Forward-Looking Volatility Estimation for Risk-Managed Investment Strategies during the COVID-19 Crisis

Abstract

Under the impact of both increasing credit pressure and low economic returns characterizing developed countries, investment levels have decreased over recent years. Moreover, the recent turbulence caused by the COVID-19 crisis has accelerated the latter process. Within this scenario, we consider the so-called Volatility Target (VolTarget) strategy. In particular, we focus our attention on estimating volatility levels of a risky asset to perform a VolTarget simulation over two different time horizons. We first consider a 20 year period, from January 2000 to January 2020, then we analyse the last 12 months to emphasize the effects related to the COVID-19 virus’s diffusion. We propose a hybrid algorithm based on the composition of a GARCH model with a Neural Network (NN) approach. Let us underline that, as an alternative to standard allocation methods based on realized and backward oriented volatilities, we exploited an innovative forward-looking estimation process exploiting a Machine Learning (ML) solution. Our solution provides a more accurate volatility estimation, allowing us to derive an effective investor risk-return profile during market crisis periods. Moreover, we show that, via a forward-looking VolTarget strategy while using an ML-based prediction as the input, the average outcome for an investment in a drawdown plan is more sustainable while representing an efficient risk-control solution for long time period investments.

1. Introduction

In order to deal with the extreme complexity of the stock market, a hybrid method based on the GARCH model combined with a Long Short-Term Memory (LSTM) Neural Network (NN) appears to be an accurate and effective tool to predict market behaviour, in particular for volatility forecasting, Kim and Won (2018). LSTM NNs are developed starting from Recurrent Neural Networks (RNNs), and they can be considered an ideal candidate to predict financial time series. Indeed, they store past information avoiding long-term dependence issues due to their unique storage unit structure, Qiu et al. (2020). Furthermore, the combination with a GARCH-type method improves the precision of the volatility estimates dealing with non-controllable data showing a clustering tendency.

Our contribution aims at investigating the effectiveness of a hybrid approach to estimate volatility exploiting a mix of the GARCH model and the LSTM-NN method. In particular, historical realized volatilities are used as input time series to implement a forward-looking simulation. Let us underline that the idea of exploiting volatility forecasts as an investment hedging strategy is a key point of several research papers; see, e.g., Chang et al. (2013); Donaldson and Kamstra (2005); Duan and Zhang (2014); McDonnel et al. (2012), and the references therein. Alternatively, we derive a volatility forecast to the hybrid economic-ML algorithm to realize a risk-controlled portfolio strategy, i.e., the VolTarget one (see, e.g., Albeverio et al. (2013); Berganza and Broto (2012)), dynamically adjusting the asset allocation between a risk-less bond and a risky asset depending on the predicted market volatility. This allows significantly reducing risky asset exposure (see Baker et al. (2020)) during periods characterized by an extraordinary increase in volatility (see, e.g., Balduzzi et al. (1998); Neely et al. (1999)), as happened during the 2008 worldwide financial crisis or the current ups and downs caused by the COVID-19 pandemic. In particular, we focus our attention on long time period investments for which a possible strategy consists of investing in equities, hence taking advantage of volatility predictions. Indeed, volatility is used as an effective tool to predict the market behaviour: higher volatility implies higher returns along with the possibility of significant drawdowns. Therefore, the total risk of the portfolio connected to equity dangerously increases.

We emphasize that the novelty of our approach concerns the opportunity to estimate realized volatility obtained from a hybrid GARCH-LSTM NN model, instead of using historical volatilities, to then directly feed a VolTarget-based portfolio. The strategy is performed by considering a single risky asset, whose volatility is computed, in first approximation, by means of the univariate GARCH model. In a future work, we shall provide a generalization of our solution to a basket of diversified risky assets, possibly depending on underlyings such as oil or gold (see, e.g., Boţoc and Anton (2020)), exploiting a multivariate GARCH model.

The paper is organized as follows. In Section 2, we develop the basics about both the GARCH process and LSTM-NN tools, also discussing the motivations inspiring our hybrid solution and providing the VolTarget strategy details, as well as the corresponding portfolio dynamics; while, in Section 3, we present the numerical evidence obtained, starting with ML-based volatility estimates to then considering a Monte Carlo simulation approach to the VolTarget, considering the S&P 500 index as the risky asset reference. Section 4 presents the discussion of the obtained results, focusing on the connection with other studies and on the novelty introduced by the research.

2. Materials and Methods

In this section, we examine the theoretical background and the methods exploited to estimate the historical realized volatility computed as the standard deviation or through the hybrid algorithm, in order to run a VolTarget strategy.

2.1. Literature Review

Various studies have been conducted in order to predict volatility based on financial time series models aiming at reducing investments’ exposure during turbulent volatility periods. Classical forecast models mainly deal with statistical inference from a regression point of view; see, e.g., Engle (1982). An example is given by considering the Generalized Auto Regressive Conditional Heteroscedasticity (GARCH) process, Bollerslev (1986), hence assuming a heteroscedastic condition of the time series. The latter implies variables’ variance not be assumed to be constant over time. Additionally, it is useful to predict the phenomenon known as volatility clustering, namely the tendency of a rather steady low, resp. high, state for volatility’s levels. It is worth mentioning that methods allowing taking the trace of the aforementioned clusterization phenomena fail to capture long-term features. That is why we combine the latter approach with a Machine Learning (ML) one. This allows us to overcome the problem, taking care of cluster phenomena, as well as long-term features at the same time, indeed providing accurate estimates also when sudden volatility changes occur.

Let us note that similar approaches have been already adopted as, e.g., in Kim and Won (2018) and Qiu et al. (2020), where the authors examined the advantages of combining an ML model with econometric ones to improve the predictions’ accuracy w.r.t. stock price volatility. Recent works such as, e.g., Murali et al. (2020), were more focused on numerical procedures, again based on hybrid models. Further, Anton (2012); Guo et al. (2014); Hajizadeh et al. (2012); Lu et al. (2016) proposed a hybrid algorithm between an artificial neural network and a GARCH model to predict the volatility of the S&P 500 index return. The main novelty we introduce in the present paper consists of exploiting such approaches, together with fine tuned ML predictions, to perform a VolTarget strategy. Let us also recall how several studies have already considered the volatility as a risk index to control the exposure of allocation strategies; see, e.g., Krein and Fernandez (2012) or Zakamulin (2013). In Albeverio et al. (2013), the authors introduced the foundations of the theoretical framework for a VolTarget investment, developed also in Albeverio et al. (2018), while Jawaid (2015) presented the results of numerical simulations for VolTarget strategies based on different financial models. In the context of the recent global financial market drawdown caused by the COVID-19 pandemic (see Baker et al. (2020)), we propose (see also Albeverio et al. (2019); Bai and Wallbaum (2020)) an innovative combined algorithm integrating the VolTarget portfolio strategy aiming at reducing the investment risk.

2.2. The GARCH(1,1) Process

One of the major challenges in the prediction of financial time series is the existence of heteroscedastic effects, denoting that the volatility of the time series is generally not constant, Williams (2011). Considering $P_t$ as the value of a stock price evaluated at time t, the log returns are defined by:

$$X_t=log{P}_{t+1}-log{P}_t.$$

(1)

The volatility $\sigma$ can be defined as the square root of the conditional variance of the log return process:

$${\sigma }_t^2=\mathit{Var}\left[X_t^2\right|F_{t-1}],$$

(2)

where $F_{t-1}$ is the $\sigma$-algebra generated by $X_0,\dots ,X_{t-1}$. Heteroscedasticity is not considered in some classical financial models, like the Black–Scholes one, which widespread for computing the price of European style options. The main limitations of this kind of models are the hypothesis of considering a stationary process and a constant realized volatility, which are unrealistic in general. In this context, ARCH models were introduced by Engle (1982) to consider a more complex setting: the conditional variance process has an autoregressive structure, and the returns are considered as white noise that multiplies the volatility:

$$\begin{array}{cc}\hfill X_t& ={ϵ}_t{\sigma }_t,\hfill \\ \hfill {\sigma }_t^2& =\omega +{\alpha }_1{X}_{t-1}^2+\dots +{\alpha }_p{X}_{t-p}^2,\hfill \end{array}$$

(3)

where ${ϵ}_t$ are independent and identically distributed (i.i.d.) random variables with expectation 0 and variance 1, independent of ${\sigma }_k$ for all $k\le t$. The lag length $p\ge 0$ is itself a parameter for the model, and the case $p=0$ represents a trivial scenario representing a white noise process.

Bollerslev (1986) improved the ARCH model allowing ${\sigma }_t^2$ to have an additional autoregressive structure within itself. The GARCH(p,q) (Generalized ARCH) model, where p is the order of the GARCH terms ${\sigma }^2$ and q is the order of the ARCH terms ${ϵ}^2$, is given by:

$$\begin{array}{cc}\hfill X_t& ={ϵ}_t{\sigma }_t,\hfill \\ \hfill {\sigma }_t^2& =\omega +{\alpha }_1{X}_{t-1}^2+...+{\alpha }_p{X}_{t-p}^2+{\beta }_1{\sigma }_{t-1}^2+\dots +{\beta }_q{\sigma }_{t-q}^2.\hfill \end{array}$$

(4)

For our purposes, we chose a GARCH(1,1) model to predict the volatility of the period 2000–2020 for the S&P 500 index given its relatively simple implementation. The solution is given in terms of a system of stochastic difference equations in discrete time, and the likelihood function is easier to handle than continuous-time models. The GARCH(1,1) used for this computation can be expressed by:

$${\sigma }_t^2={\alpha }_1{\sigma }_{t-1}^2+\beta {ϵ}_{t-1}^2+{\alpha }_0.$$

Starting from the historical data, a weighted sum of the observed volatility is computed. The prediction by the constant mean-GARCH Model, shown in Figure 1, helps in the recognition of the well-known phenomenon called volatility clustering. The main limitation is clearly the lack of forecasting accuracy.

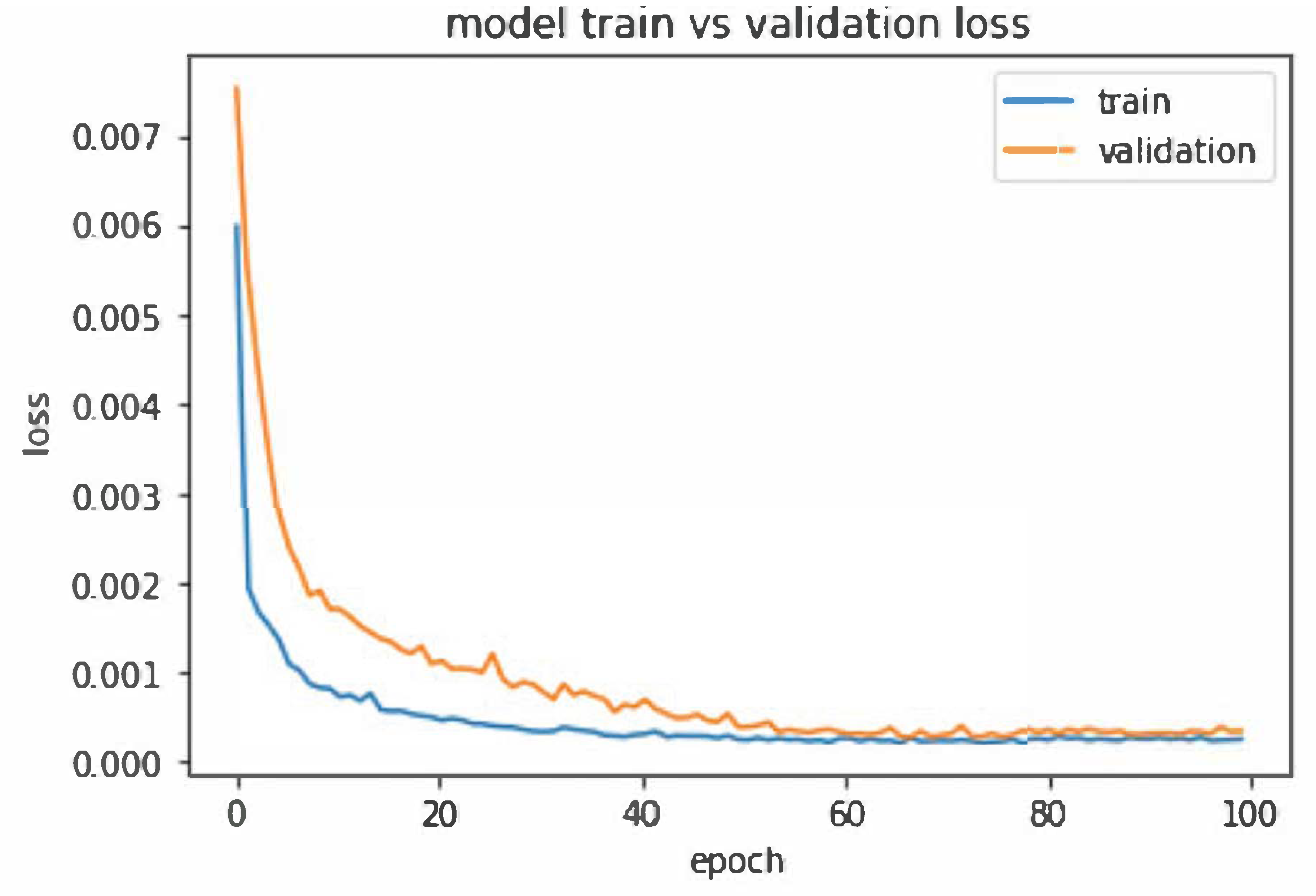
2.3. Long Short-Term Memory Neural Network

A Recurrent Neural Network (RNN) is an NN algorithm that learns sequential patterns through internal loops by receiving input sequences. A back propagation algorithm is used to reduce the error of the value calculated by the forward propagation in order to optimize the objective function. As the values are propagated into the value function, the gradient descent algorithm could encounter the issue of a vanishing (or exploding) gradient, since it can become very small (or extremely large). To avoid this kind of problem, LSTM models were developed by Hochreiter and Schmidhuber (1997) using memory cells (a unit of computation that replaces traditional artificial neurons) and gates to store information for long periods of time and to forget unessential information.

As developed in Qiu et al. (2020), each memory cell has three sigmoid layers and one $tanh$ layer, as shown in Figure 2. The cell includes a forget gate that determines which cell state information is discarded from the model.

The memory cell accepts the state $C_{t-1}$ of the previous cell and the corresponding output $h_{t-1}$. The external information $x_t$ of the current moment is also considered as the input and combined in a long vector $[h_{t-1},x_t]$ through a transformation $\sigma$:

$$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f),$$

(5)

where $W_f$ and $b_f$ are, respectively, the weight matrix and bias of the forget gate and $\sigma$ is the sigmoid function. The forget gate controls how much of the cell state $C_{t-1}$ of the previous time should be forgotten for the cell state cell $C_t$ of the current time. The gate will output a value between 0 and 1 (1 indicates complete reservation, while 0 indicates complete discardment). The input gate determines how much of the current time network update $x_t$ is added to the state cell $C_t$:

$$i_t=\sigma (W_t·[h_{t-1},x_t]+b_t).$$

(6)

The cell state ${\widehat{C}}_t$ is updated through the tanh layer to control how much new information is added:

$${\widehat{C}}_t=tanh(W_c·[h_{t-1},x_t]+b_c).$$

(7)

The output gate controls how much of the modified cell state should leave the cell and become the next hidden state. Equation (8) is used to update the cell state of the memory cell using both saved past information at time $t-1$ and present information of time t:

$${\widehat{C}}_t=f_t·C_{t-1}+i_t·{\widehat{C}}_t.$$

(8)

The output information is first determined by a sigmoid layer, and the cell state is processed by tanh and multiplied by the output of the sigmoid layer to obtain the final output, defined as:

$$h_t=\sigma (W_{\sigma }·[h_{t-1},x_t]+b_{\sigma })·tanh\left(C_t\right).$$

(9)

Because of this special characterization in terms of selectivity, LSTM NNs are suitable for random non-stationary sequences such as stock-price time series. Another fundamental feature about LSTM NNs regards the property of avoiding long-term dependences, making them suitable candidates to predict financial time series.

2.4. Estimation of the Historical Realized Volatility

Starting from the time series of the S&P500 for the period 2000–2020 with daily data points, the realized historical volatility of the S&P500 returns were determined on a monthly basis. Historical volatility was computed as the standard deviation of the difference of the logarithmic returns considering a temporal window of 21 business days, according to Equation (2). It is expressed in annualized terms (multiplied by the square root of 252), which allows for comparisons between daily, weekly, and monthly volatility calculations. Nevertheless, we often observe that daily volatilities are greater than weekly volatilities, and weekly volatilities are greater than monthly volatilities. We chose to consider monthly stock volatility in order to reduce the effect of day-by-day price fluctuations.

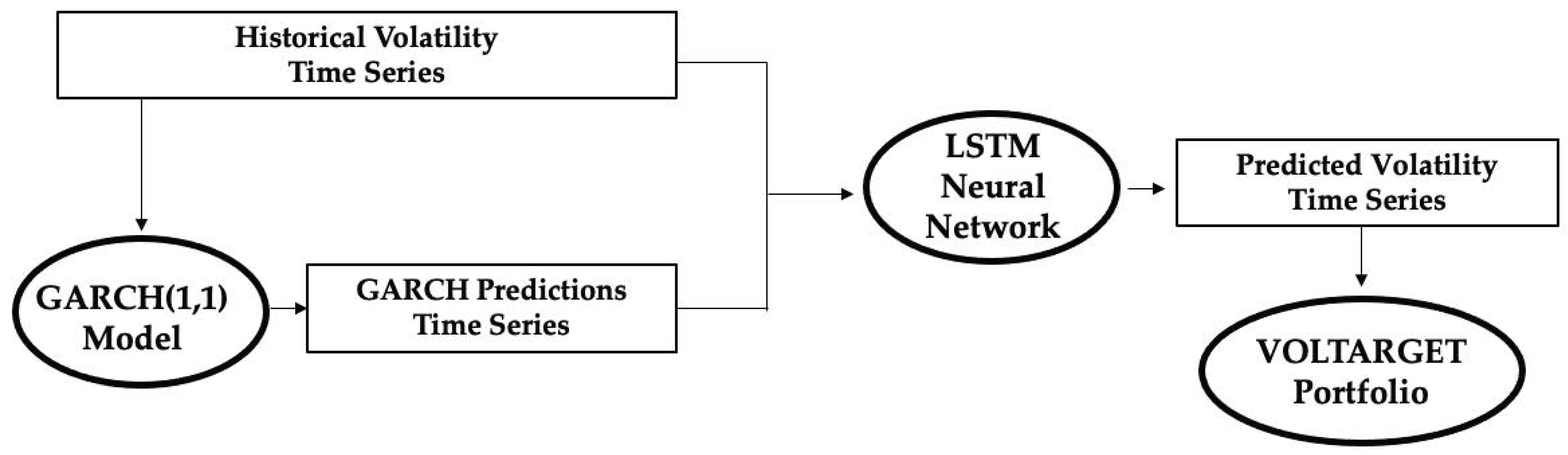
2.5. Proposed Hybrid Algorithm: LSTM Model Combined with the GARCH-Method

An integration of the LSTM model with the output coming from the GARCH helps to improve the LSTM learning procedure and its volatility predictions. In particular, as mentioned in Section 2.2, the LSTM network is suitable for capturing short-term changes and for storing past information, while the GARCH model captures volatility clustering and leptokurtosis information.

The output of the GARCH process is paired with the historical volatility data forming the input of the LSTM NN, as illustrated in Figure 3. The training set for the LSTM model is constructed in a specific way. More precisely and different from other NN applications, the construction of the training dataset for time series forecast requires the choice of a lag parameter, which directly affects the predictive performance. The key idea is to overlap rolling windows with a fixed length (the so-called lag parameter) that in our simulation we set equal to 100 days. Each of these input sequential data produces a volatility forecast for the next day, as shown in Figure 4.

The values of volatility from day $(d-100)$ to day d are used as the input to predict volatility for day $d+1$. Numerical results of this method are presented in Section 3.1.

2.6. VolTarget Strategy

The VolTarget strategy deals with dynamically adjusting the portfolio positions, based on a trend following and controlled-risk approach, according to the estimate of market volatility. The key idea is that investors should reduce the equity position during high volatility periods and, symmetrically, increase the equity position when volatility is low. More precisely, the dynamic asset allocation aims to reach a stable level of volatility in all market environments by taking advantage of the negative relationship between volatility and returns, since a higher volatility implies a greater variation of the expected returns. Additionally, we want to exploit the presence of a majority of time periods with small loss and take into account a minority of periods when there is the possibility of big gains or, on the other hand, big losses. The VolTarget mechanism is used to create and re-balance a VolTarget investment portfolio, consisting of a risk-less asset (e.g., zero-coupon bond) and a risky asset (e.g., an equity index such as the S&P 500 index, which we consider here). For the sake of simplicity, we consider just 2 assets, but the strategy remains valid if one considers more than 1 risky assets. According to Albeverio et al. (2013) and Di Persio et al. (2019), the portfolio can be modelled as a stochastic process $P\left(t\right)$ driven by the following equation:

$$P\left(t\right)={\alpha }_0\left(t\right)S_0\left(t\right)+{\alpha }_1\left(t\right)S\left(t\right)$$

(10)

where ${\alpha }_0$ and ${\alpha }_1$ define a predictable stochastic process for $t\in [0,T]$ representing, respectively, the amount invested in the risk-less $S_0\left(t\right)$ and in the risky asset $S\left(t\right)$.

The dynamics of the portfolio $P\left(t\right)$ is described by the following equation:

$$dP\left(t\right)={\alpha }_0\left(t\right)r{S}_0\left(t\right)+{\alpha }_1\left(t\right)\left(\mu S\left(t\right)dt+\sigma dW\left(t\right)\right)$$

(11)

In a VolTarget portfolio, the trading strategy is chosen in a specific way. Consider a partition of rebalancing times $0=t_0<t_1<\dots <t_n=T$ over the interval $[0,T]$. Assume that it is possible to estimate the volatility $\sigma \left(t_i\right)$ for $i\in \{1,\dots ,N\}$ and denote the estimated volatility by $\widehat{\sigma }\left(t_i\right)$. A VolTarget portfolio is a process of the form of Equation (10) where the weights ${\alpha }_0$ and ${\alpha }_1$ are defined by:

$${\alpha }_1=min\left\{\frac{VT}{\widehat{\sigma }\left(t_i\right)},LF\right\}if{t}_i\le t\le t_{i+1}forsomei\in \{0,\dots N-1\}$$

(12)

$${\alpha }_0=1-{\alpha }_1\left(t\right)$$

(13)

where $\mathit{LF}\in [0,2]$ represents the leverage factor (which in the literature can be assumed to be constant; see, e.g., Jawaid (2015)), while the parameter $\mathit{VT}$ is assumed to be positive and corresponds to the volatility target. A strategy of this kind allows having a risky asset exposure of more than $100\%$ and leveraging the investment when market volatilities are relatively low. On the other hand, the VolTarget mechanisms can be used as capital protection against turbulences in the market, which can be pivotal, especially in the years during a financial crisis.

3. Results

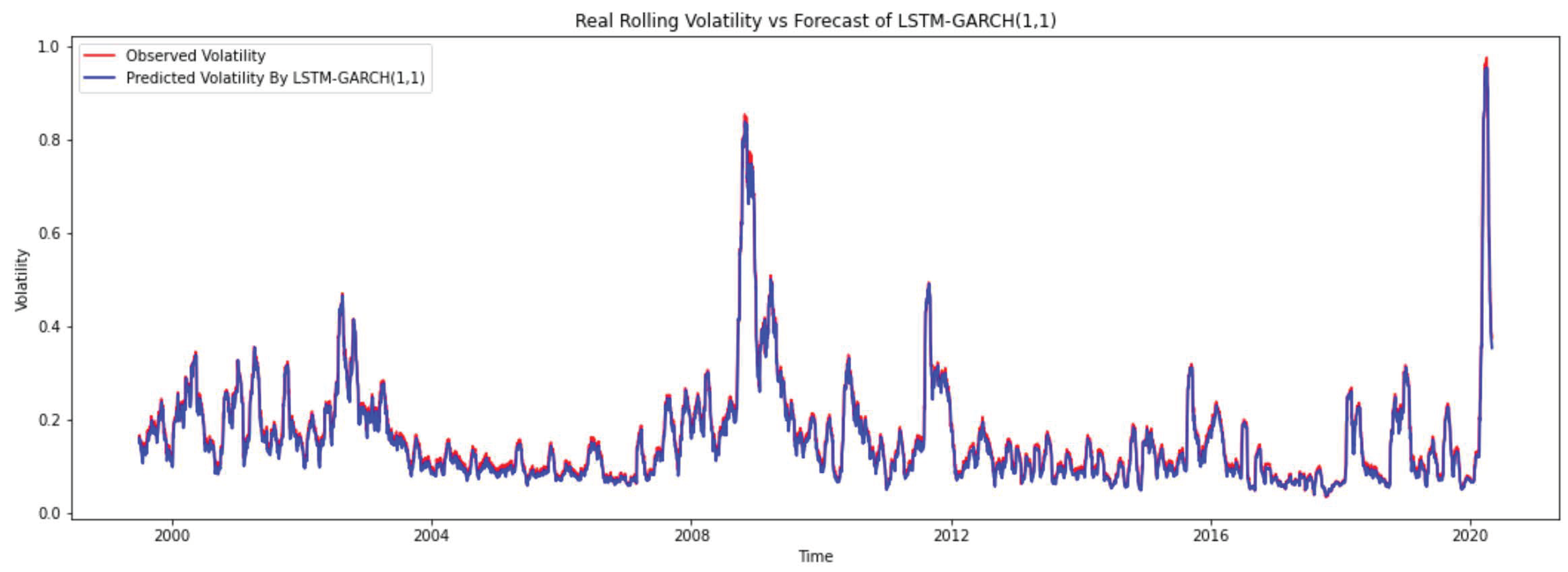
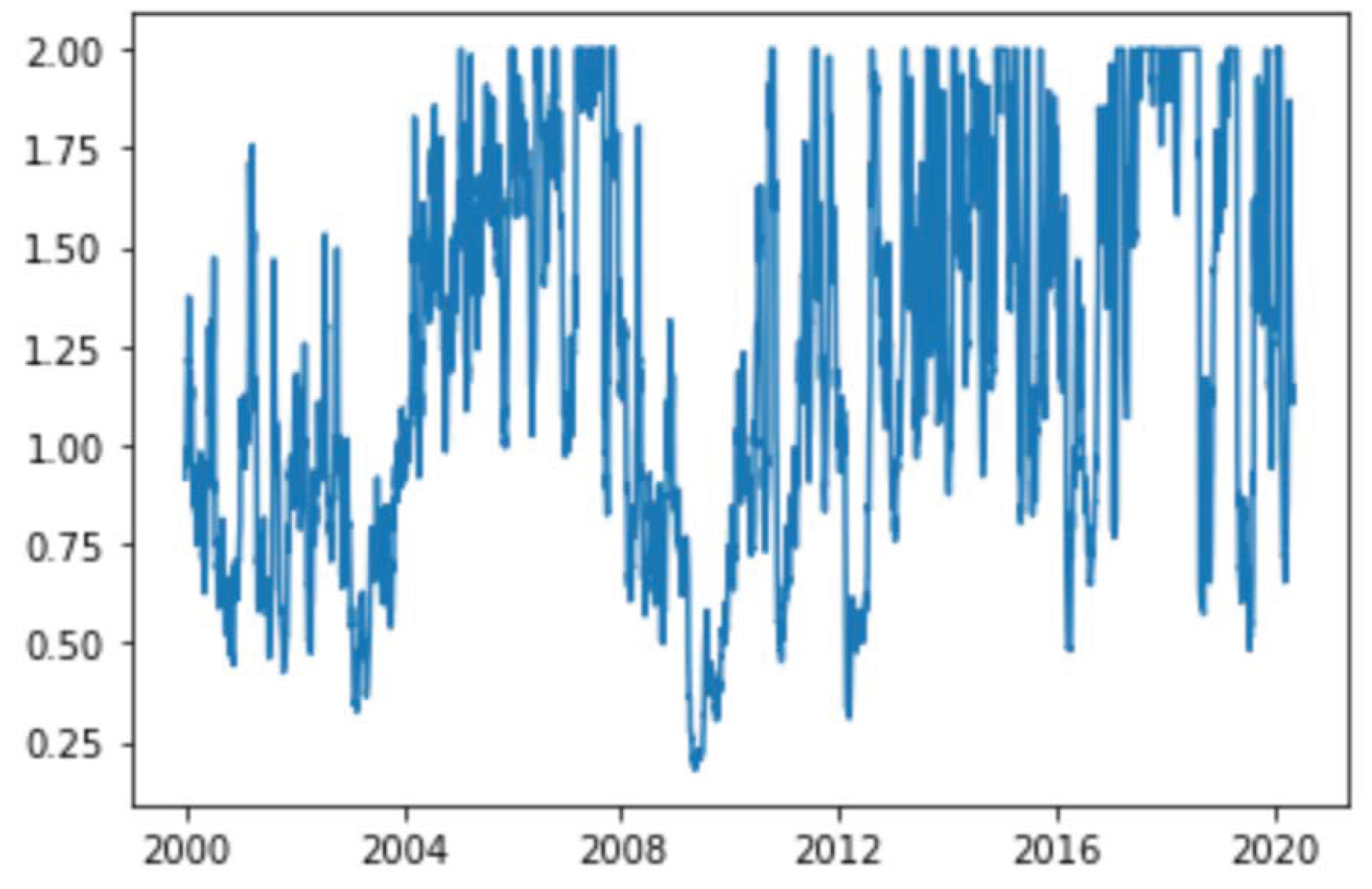
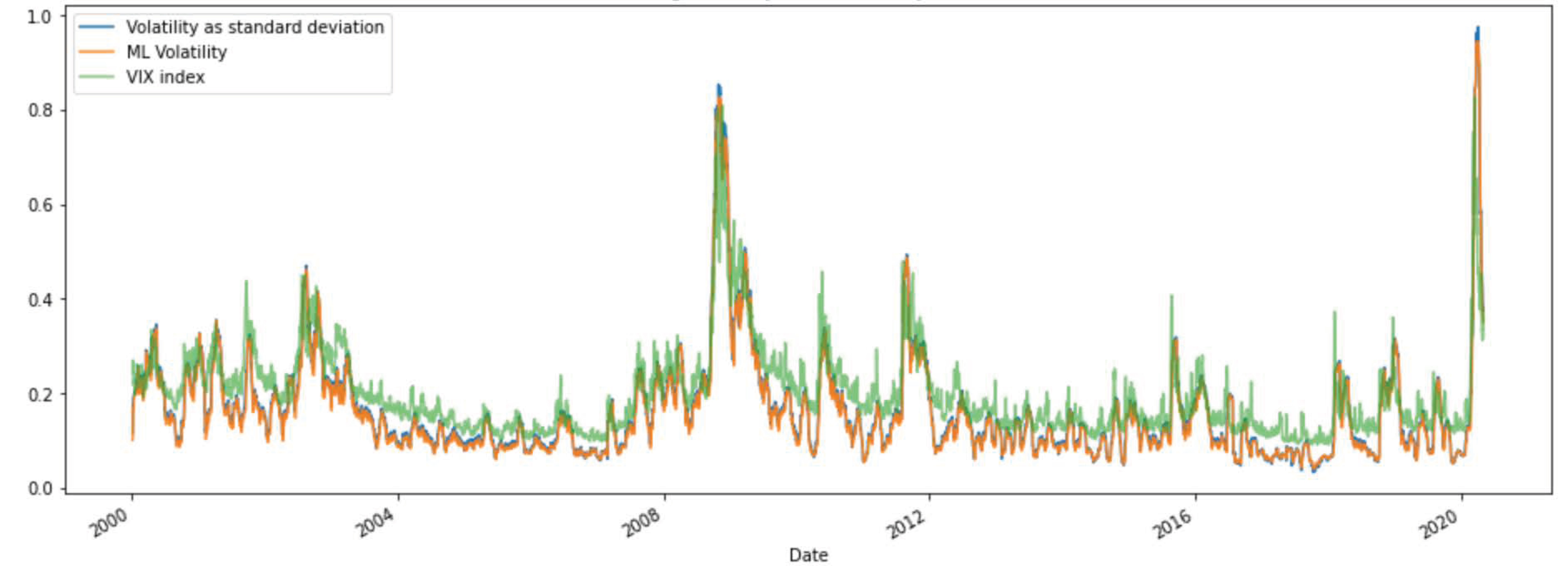
3.1. Volatility Forecasting

In this section, we present the forecasting results for the volatility of the S&P 500 index through the proposed hybrid model. In the LSTM framework, we set the lag parameter equal to 100 days, and we calibrate optimal parameters for the model, e.g., the number of layers, the number of hidden units, and the number of epochs for the training phase. We use a LSTM network formed by 2 hidden layers with respectively 32 and 16 neurons, which correspond to 7633 trainable parameters, giving the predictions for an interval of 5348 days. We show the forecast results in Figure 5, comparing them to the historical ones.

We compare the predicted ${\widehat{\nu }}_t$ and the actual volatility $R{V}_t$, which corresponds to the target value of the learning process. We present training and validation errors in Figure 6, in terms of MSE, i.e., Mean Squared Error, obtaining an error of $0.000265$ after 100 epochs.

To evaluate the effectiveness of the forecast, we consider also different loss functions, such as the MAE (Mean Absolute Error) corresponding to 0.0328 and the MAPE (Mean Absolute Percentage Error) corresponding to $0.0013$.

Finally, we consider the period from January 2020 to October 2020 as the test set in order to provide an unbiased evaluation of the trained model: this dataset has never been used in training, and it is used to verify the precision achieved. We show the results in Figure 7.

The estimated volatility is used as the input for the historical performance of the VolTarget approach. The coefficients ${\alpha }_0$ and ${\alpha }_1$ for a riskless and a risky asset are computed with regard to Equation (10), and a Monte Carlo simulation is performed, considering two different time horizons:

• January 2000–June 2020 comparing the performances of portfolios with the historical volatility and the predicted one;
• January 2020–October 2020 comparing the performance of portfolios with the historical volatility and the predicted one, which corresponds to the diffusion of COVID-19.

The choice of selecting different periods and adopting a historical perspective to perform the simulations is motivated by the fact that we want to highlight the consequences and the impact of a market crash, since the second time span corresponds to the COVID-19 pandemic.

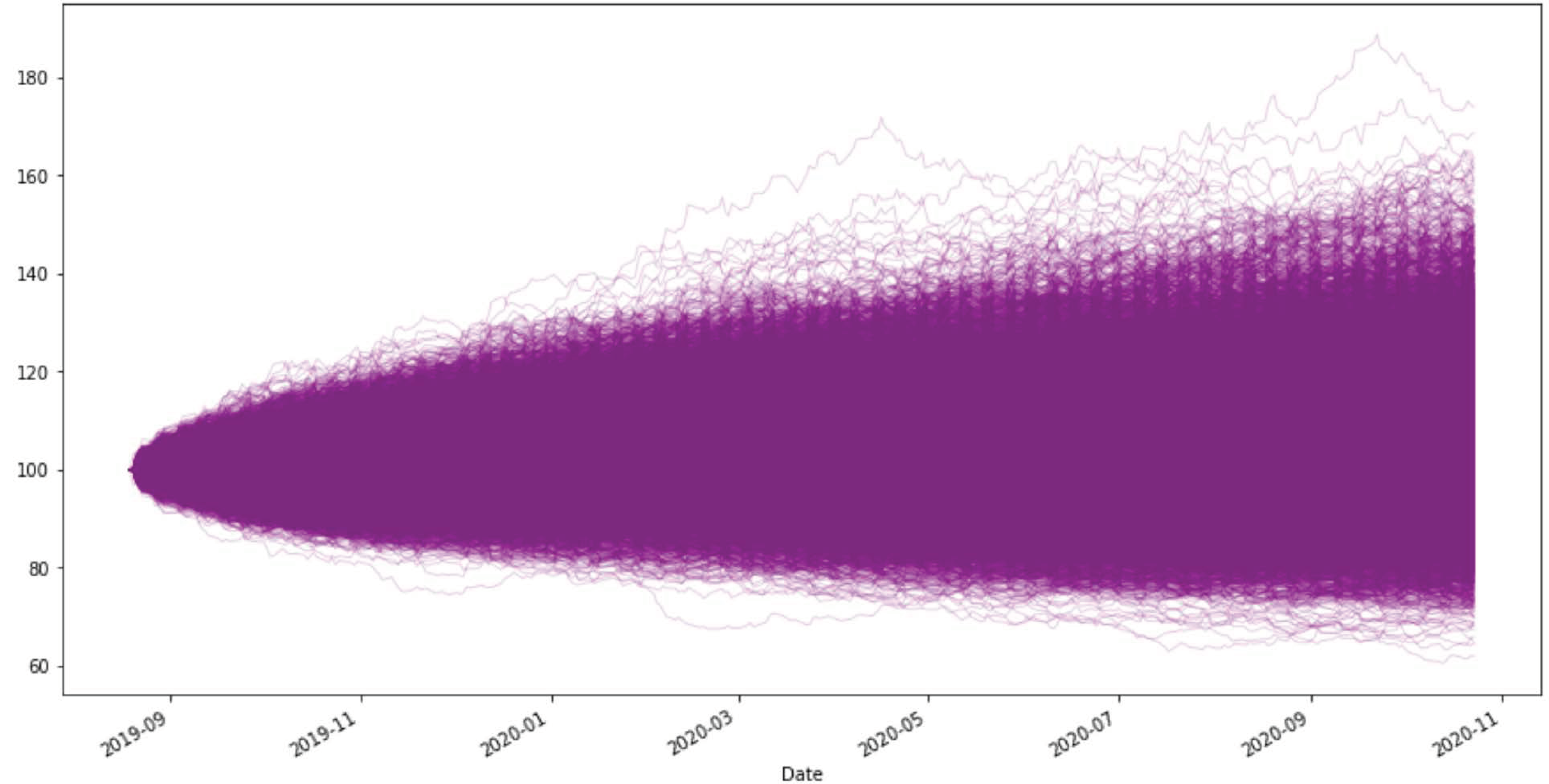
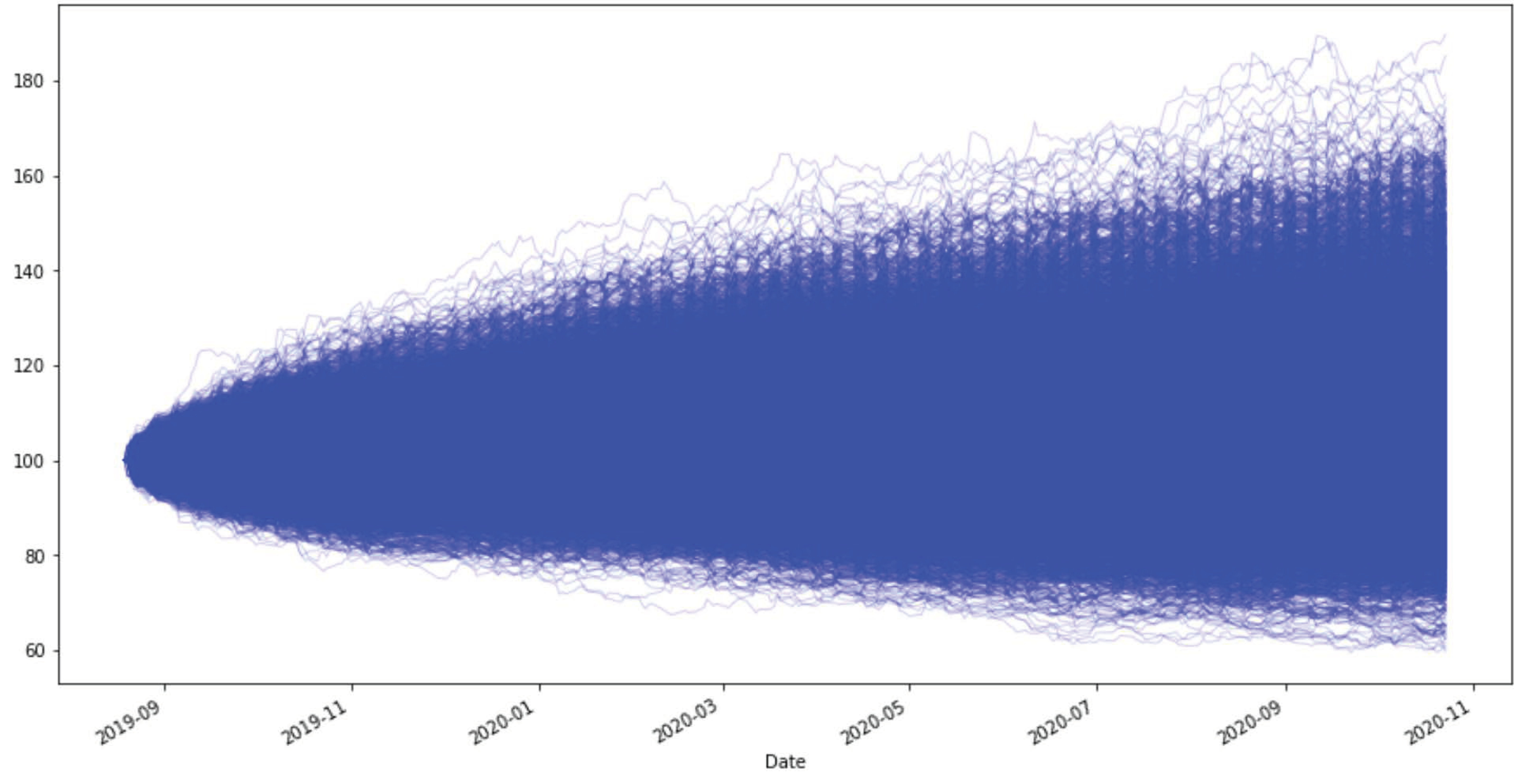
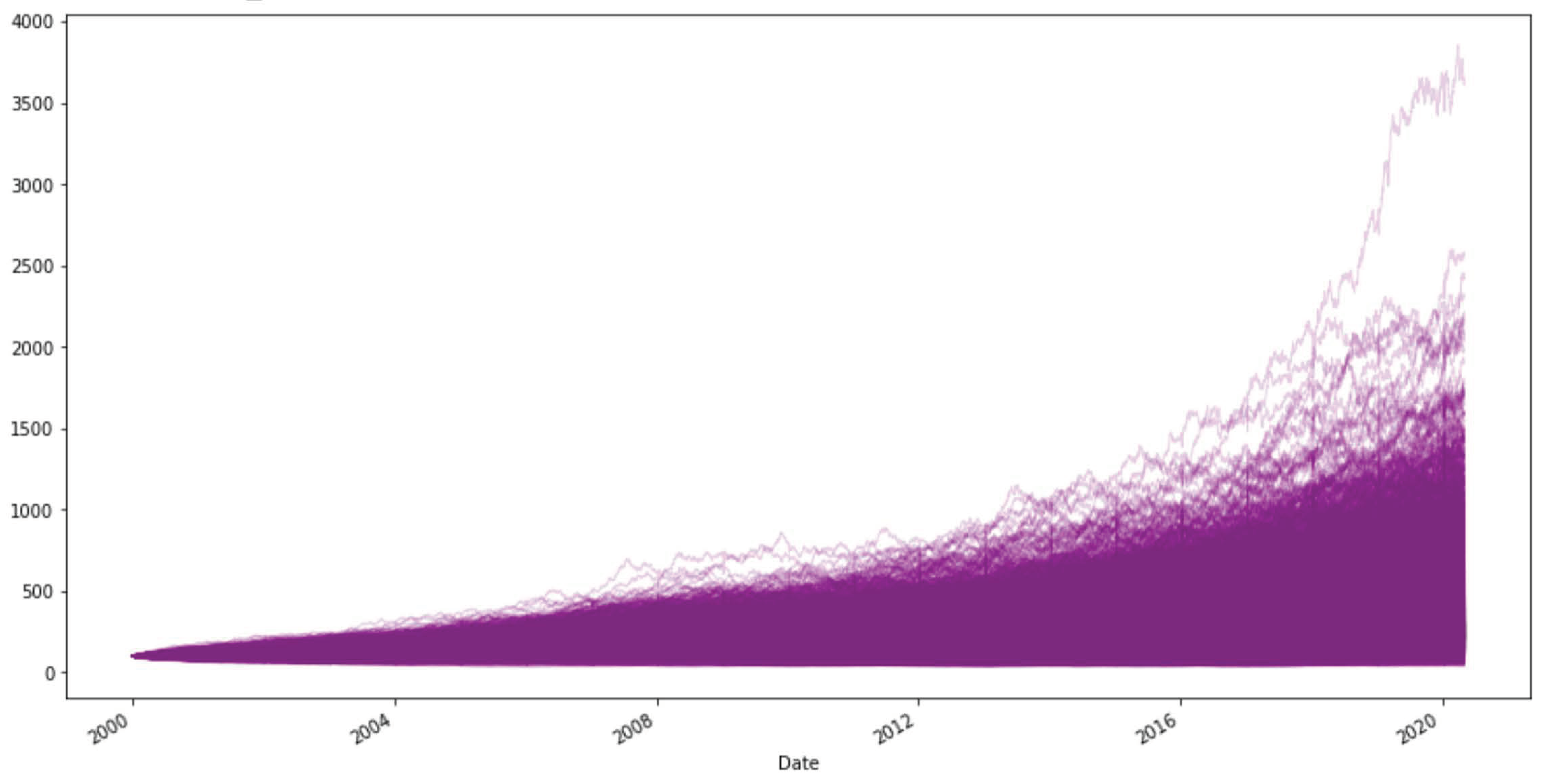
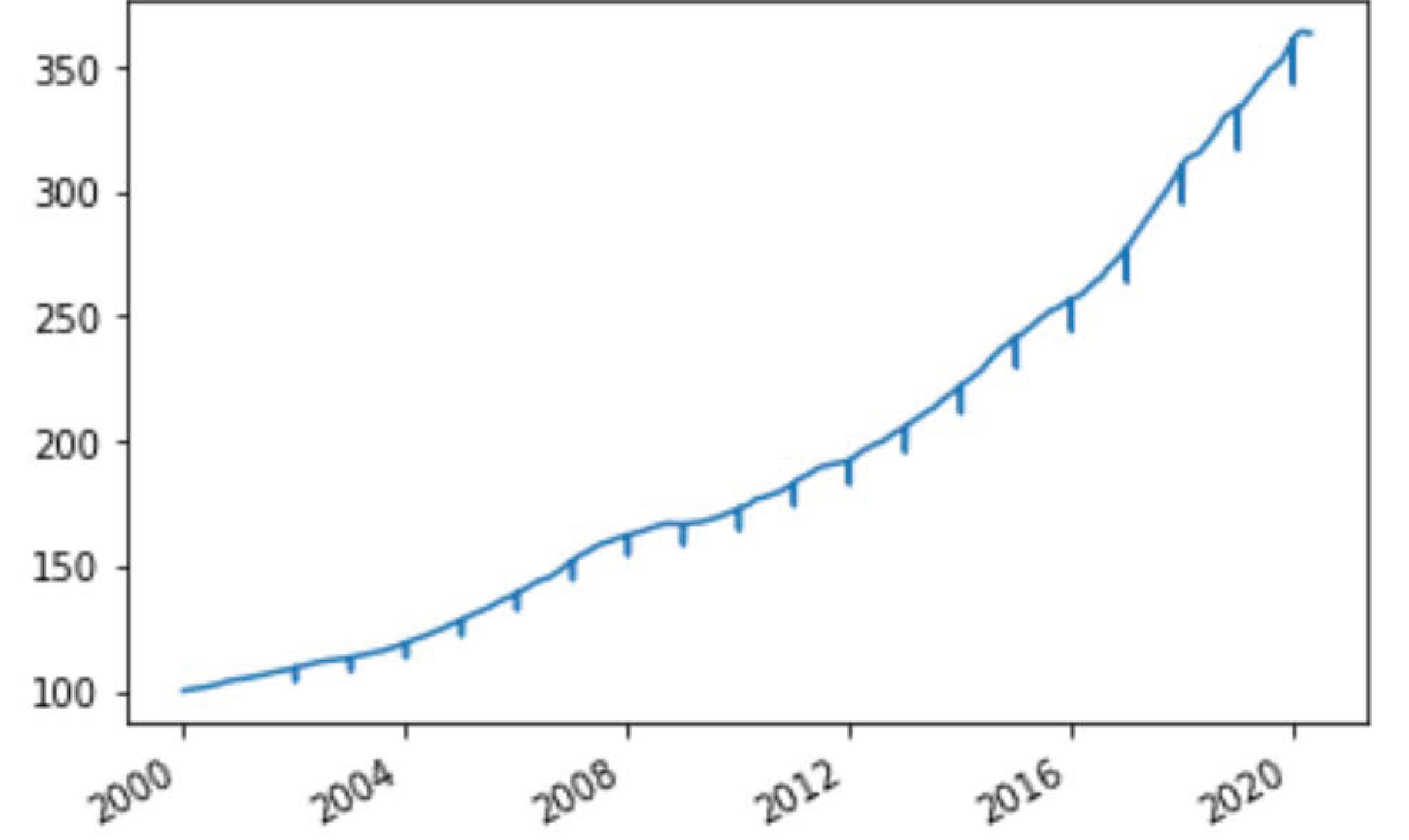
3.2. Monte Carlo Simulations

Risk measures are widely used to quantify the risk connected to the exposure of a financial portfolio. This kind of analysis is the core of many daily operations of financial institutions. It can be implemented by Monte Carlo simulations, which represent a flexible approach to deal with portfolios containing multiple investments, highly susceptible to randomness. We develop different Monte Carlo simulations in order to compare two configurations of investments that readjust their composition with daily operations:

• the classic VolTarget with historical realized volatility computed as the standard deviation w.r.t. 21 days;
• the new approach, i.e., the ML VolTarget, computed by the combined GARCH-NN method.

We consider simulations that model a portfolio following a Black–Scholes equation such as Equation (11), which describes a geometric Brownian motion. We compute the average return (considering a drawdown plan of $5\%$ for each year) and develop 10,000 different scenarios for each configuration, using a Jupyter Notebook for the numerical simulation.

To study the problem in a more realistic way, we insert some considerations about transaction costs that are heavily dependent on market volatility. We introduce these simple assumptions into the model:

• if equity markets have a volatility below $10\%$, then the transaction costs are pretty low, e.g., 10 basis points (bps);
• if equity markets have an average volatility between $10\%$ and $30\%$, the transaction costs get higher, for example 20 bps;
• if markets are getting turbulent with more than $30\%$ volatility, then transaction costs of 50 bps might be realistic.

Another crucial aspect that we want to consider is avoiding daily rebalancing: in such a way, transaction costs are minimized, and the simulation is closer to the real situation. To reduce the amount of rebalancing, one can introduce a trading filter that works as follows: as long as the (new) target allocation is not more than $3\%$ away from the current allocation, no allocation change will be done.

3.2.1. Simulation of the Portfolio Dynamics over the Period of January 2020 to October 2020

We present the results for different configurations studied in the framework of a Monte Carlo simulation with 10,000 scenarios, and then, we show the results in terms of the average return over nearly the last year (from January to October 2020), the period that was characterized by the diffusion of Covid-19 and the subsequent market crash.

Fixing volatility, the weights ${\alpha }_0$ and ${\alpha }_1$ are easily computed. These values are considered the fixed parameters for the historical simulation to study the evolution of the VolTarget portfolio.

In particular, we develop two different simulations with the volatility target set at $13\%$: in Figure 8 we report the portfolio that employs historical volatility computed as the standard deviation over 21 days, and in Figure 9, we show the portfolio with the ML predicted volatility computed by the hybrid approach. This general approach, of simulating a random process many times in order to understand its characteristics, is the particular perspective of the Monte Carlo method.

By repeating the simulation many times and taking the average, we can compute the average value of the return, which we take as the fair return, illustrated in Figure 10.

By comparing the averaged results, we deduce that the pattern obtained by studying the performance of an active volatility-targeting solution has a better trend, especially during a financial crisis.

3.2.2. Simulation of the Portfolio Dynamics over the Period of January 2000 to May 2020

After computing the estimates for the time series volatility, the weights are adapted at each step according to the value of the volatility.

We directly compute the weights ${\alpha }_0$ for the risk-free asset and ${\alpha }_1$ for the risky asset by Equations (12) and (13), and we present their evolution in Figure 11 and Figure 12.

We fix also the volatility target, which in the following example we set to $13\%$, and we set the leverage factor to two. The choice of the leverage factor is crucial to determine a well-balanced risk return profile for the portfolio. In Figure 13 and Figure 14, we present the Monte Carlo simulations for the portfolio using the historical volatility as the input for the VolTarget strategy.

In Figure 15 and Figure 16, we present the Monte Carlo simulation for the portfolio using the ML volatility as the input for the VolTarget strategy.

Figure 17 reports a modified version of Figure 5, showing volatility inputs for the three VolTarget strategies. We also added the VIXindex CBOE (2019), tge real-time market index representing the market’s expectations for volatility of the S&P500 index over the coming 30 days Cao et al. (2020), as a reference for comparison purposes. The VIX index is clearly higher since it is calculated as the 30 day expectation of volatility. We recall that realized volatility is, instead, computed as the standard deviation over 21 days.

In Figure 18, we report the evolution for the averaged return of the corresponding VolTarget portfolios starting January 2000 and with the same initial investment, i.e., 100 euros.

4. Discussion

The present paper is characterized by two main contributions. In particular, we show that hybrid GARCH-LSTM-based models provide accurate volatility forecasts for the S&P index log-return series. It is worth mentioning that the combination of ML and standard economic-based models to predict financial time series has been already investigated (see, e.g., Baffour et al. (2019); Berganza and Broto (2012); Carvalhal and Ribeiro (2007); Elsworth and Güttel (2020); Hajizadeh et al. (2012); Kim and Won (2018), and the references therein), but applying forecasting to the VolTarget-based portfolio for historical evaluations is still missing. Moreover (see Figure 10 and Figure 18), we compared averaged results, following a historical perspective: since we considered only fixed variables, other than the volatility, and we can deduce how the ML VolTarget portfolio outperforms the one constructed with historical volatility, computed as the standard deviation.

Moreover, let us underline that our ongoing research on connecting volatility estimates with portfolio dynamic simulations aims at improving the already obtained results; see, e.g., Hossain et al. (2009); Kristjanpoller and Minutolo (2016); Lahmiri (2017); Pathberiya et al. (2018); Wu et al. (2014); Yao et al. (2017). Different from these previous research works, we consider an accurate economic model in view of the VolTarget portfolio simulation.

5. Conclusions

In this research, we develop an innovative model combining the effectiveness of a classic econometric model, namely GARCH(1,1), and a ML method, i.e., a LSTM NN, to forecast volatility-based economic quantities. Let us recall that many volatility features can be captured by the GARCH model, as in the case of long-range dependency, volatility shocks’ magnitude, volatility tendency, impact, the persistence of volatility clusters, etc. Extending the GARCH tool via LSTM allows us to obtain a higher level of prediction accuracy, as witnessed by our results. Moreover, the clustering of volatility and the negative correlation between realized volatility and returns are two well-known features of equity markets, the knowledge of which motivates the use of a hybrid model that can efficiently learn more complicated and precise patterns compared to a simple NN-based method, particularly when dealing with a VolTarget portfolio. Let us underline that the VolTarget strategy constitutes an effective reaction to financially perturbed periods when investors look for a simple allocation mechanism to boost portfolio returns, aiming to both mitigate tail risks and protect investments from significant losses due to market crashes. We also tested the impact of re-balancing frequencies on the target volatility portfolios: the best performance of a VolTarget portfolio can be achieved by avoiding daily rebalancing to minimize transaction costs.

Regarding the financial framework, it is interesting to study the VolTarget problem from the sequencing risk perspective. Indeed, we can consider the occurrence of high losses at the beginning of a de-cumulation phase (see, e.g., Bai and Wallbaum (2020)) to measure risk changes according to investment periods and retirement issues. In a future work, we will extend our approach to consider structured portfolios, hence considering a combination of an LSTM-architecture with a multivariate GARCH model, possibly taking care of risky assets related to basic underlyings such as, e.g., gold or oil.