Abstract
Specially in the case of scenarios under uncertainty, the efficient management of risk when matching assets and liabilities is a relevant issue for most insurance companies. This paper considers such a scenario, where different assets can be aggregated to better match a liability (or the other way around), and the goal is to find the asset-liability assignments that maximises the overall benefit over a time horizon. To solve this stochastic optimisation problem, a simulation-optimisation methodology is proposed. We use integer programming to generate efficient asset-to-liability assignments, and Monte-Carlo simulation is employed to estimate the risk of failing to pay due liabilities. The simulation results allow us to set a safety margin parameter for the integer program, which encourage the generation of solutions satisfying a minimum reliability threshold. A series of computational experiments contribute to illustrate the proposed methodology and its utility in practical risk management.
1. Introduction
Within the enormous variety of insurance types that we can find, long-term life insurance stands out for its complexity in terms of financial management. The cash flows generated by these insurances extend over several decades and play an important role in the social sphere since they have a close relationship with pensions and retirements and, therefore, with people’s vital planning. For this reason, legislation and administrative authorities play a special role in ensuring that insurers faithfully comply with their commitments. The fact that they are extended in the long term, or in the very long term, generates a series of difficulties for their management because the insurer must plan the necessary income with enormous precision to cover its future commitments. Therefore, it is a requirement that the insurer has a range of techniques that allow for matching its assets, as long-term income generators, with its liabilities. Conventionally, we refer to this set of techniques as asset and liability management (ALM) (Ziemba et al. 1998), and it has raised the interest of numerous researchers over the last few years, with a wide variety of approaches being proposed. One of most popular solutions to this asset management problem is cash-flow matching (Iyengar and Ma 2009), whose main objective is to ensure the timely payment of the liabilities. This approach minimises the number of contractual breaches. Due to the volatility of the financial markets, we always have uncertainty regarding income, and this will be linked to the quality of financial assets. Moreover, the credit quality of assets plays a fundamental role, in particular when we deal with bonds, which are widely used in the insurance industry (Gründl et al. 2016). When the default event occurs, the price of the bond is immediately decreased, in such a way that we have lower income. Since Merton (1974), a lot of models have been developed to forecast the price under a default event.
Likewise, the obligations cannot be considered as exact or totally predictable. Those liabilities or obligations are the customer’s premium that the insurance company receives. In practice, we consider average values for obligations and we can establish certain ranges of dispersion that can be estimated based on the insurer’s own experience. Once the premium has been paid, the company invests it in the long term, so that the financial benefit envisaged in the insurance policy is secured. Finally, in the event of the customer’s retirement or death, the insurance company needs to have sufficient funds to meet its liability to the customer. Consequently, we are facing a highly complex asset allocation problem, since the amount of assets that an insurer can have is large, and the distribution of liabilities over time does not usually follow any regular pattern, both being stochastic in nature.
Heuristic and metaheuristic algorithms have become a new standard when dealing with complex and large-scale portfolio optimisation and risk management problems Doering et al. (2019); Soler-Dominguez et al. (2017). In this paper we explore an asset allocation method by means of heuristic techniques, taking into account the random nature of both assets and liabilities. The goal is to find the most efficient (minimum cost) combination of assets that meets certain requirements: they must generate sufficient income to cover the obligations of the insurer with a high probability. In a recent work, Bayliss et al. (2020) considered a simplified ALM problem, based on the net present value (NPV) concept, in which only one-to-one asset-liability assignment were allowed. Notice that, since we are comparing monetary values of assets that belong to different time periods, it makes sense to consider the NPV associated with each asset in order to make a fairer comparison of assets. Our work goes a step further and allows many-to-many, one-to-many, and many-to-one asset-liability assignments as well. Such an approach increases the efficiency with which liabilities can be covered. This also allows us to address ALM problems regardless of the number of assets and liabilities, as well as their sizes. For addressing large scale instances which could not be solved using exact integer programming techniques, previous approaches were based on the use of greedy heuristics that prioritised larger liabilities over smaller ones. This work, however, proposes an improved approach based on sorting liabilities in ascending due date order, since liabilities with earlier due dates have fewer assets combinations that can be assigned to them. Additionally, assets with earlier maturity dates have higher NPVs, which is what is to be minimised. The main methodological contribution of our approach lies in the introduction of a matheuristic algorithm, which integrates integer programming and Monte-Carlo simulation. In particular, an integer program is solved recursively to generate feasible and efficient asset-liability assignments for a deterministic scenario (where we assume average values for each random variable in the model). After each iteration, the resulting asset-liability assignment mapping (solution) is assessed under a stochastic scenario by using Monte-Carlo simulation, which also provides estimates of the mapping reliability. The simulation outcomes are also employed to update a safety margin parameter of the integer program that controls the minimum ratio between the values of the assets and the liabilities of the generated asset-liability assignments. The proposed approach is then tested in a wide variety of problem instances. The combination of simulation and optimisation methods in NPV-related financial problems under uncertainty has been also explored in Panadero et al. (2020).
The rest of the paper is structured as follows: Section 2 provides a brief literature review on ALM. Section 3 introduces a more detailed description of the specific ALM problem considered in this paper. Section 4 proposes a matheuristic algorithm for solving the aforementioned problem. A series of computational experiments are carried out in Section 5, while Section 6 provides an analysis of the obtained results. Finally, Section 7 highlights the most relevant findings of our work and points out future research lines.
2. Literature Review on ALM
One of the first relevant works on ALM theory in due to Macaulay (1938). This author formulates the theory of duration considering: a fixed liability cash flow, a fixed income as assets, and a constant interest rate. Later, Hicks (1975) introduce the term “corrected duration”, to justify variances in the present value when the interest rate changes. These authors measure duration as a percentage, while the previous one measured duration in terms of time. Fisher and Weil (1971) present the first formalised work about immunisation, defining the condition under which the value of an investment is protected against the variations of the interest rate. A fixed income portfolio, with duration equal to a given investment horizon, is studied in Fong and Vasicek (1984). Bierwag et al. (1993) contribute to the ALM topic with an analysis of the properties of cash flow dispersion in duration hedged portfolios. Zenios (1995) use a real-world scenario to highlight the mismatch between assets and liabilities in the financial industry, showcasing a case of portfolios containing mortgage-backed securities. Mulvey et al. (1997) discuss an ALM with stochastic and risk factors, where different scenarios are expressed as a tree. This strategy, known as multistage stochastic programming, is also reviewed in more recent publications. Hence, Kouwenberg and Zenios (2008) do not only study the how-to structure of assets along time, but they also consider the associated stochastic nature. Boender et al. (2008) study the role of scenarios in ALM, as a lattice of possibilities for each element in the model, each one with an associated probability.
More realistic approaches also exist. For instance, Kusy and Ziemba (1986) study a model with legal, financial, and bank-related policy considerations applied to a Canadian bank. Oguzsoy and Gu (1997) present a multi-period stochastic linear model for ALM in banking. Mulvey et al. (2000) show how Towers Perring applies ALM planning to pension management, modelling stochasticity with scenarios. Nielsen and Zenios (1996) study how to apply a multi-period stochastic program using government bonds, mortgage-backed securities, and derivative products. Consigli and Dempster (1998) develop a pension fund problem with uncertainty. Carino et al. (1998), Carino and Ziemba (1998), and Carino et al. (1998) are a series of publications that describe an ALM model adapted to the complexities of the Japanese regulations, such as legal or taxes limitations. In the Iranian regulation framework, Abdollahi (2020) studies a multi-objective ALM programming problem where the constraints are realistic legal conditions of the banking industry. Within a dynamic stochastic control approach, Sun et al. (2020) studies a mean-variance ALM problem where assets and liabilities are both stochastic, and where liabilities transfer part of their risk by means of a reinsurance.
Kouwenberg (2001) develops a scenario-generation for the ALM to minimise the expected contribution rates, taking risk into account. Gondzio and Kouwenberg (2001) focus on the computation complexity of the ALM problem, and solve a stochastic model with near 5 million scenarios, more than 12 million constraints, and 25 million variables to study a pension fund. Fleten et al. (2002) compares a fixed mix model with a multistage stochastic program. Dash and Kajiji (2005) implement a nonlinear model for the optimisation of property-liability insurers. A Monte-Carlo simulation approach to the analysis of an ALM problem can be found in Dempster et al. (2003). These authors use a model involving global assets and contribution pension plans. Hibiki (2006) compares the results of two different approaches modelling the evolution of assets. This authors check the performance of scenarios trees and hybrid trees with simulation paths. Zhang and Zhang (2009) improve the previous model by introducing new metrics and using a genetic algorithm to solve it. Consiglio et al. (2006) and Consiglio et al. (2008) study the optimisation problem derived from a liability with complex conditions, leading to a non-linear problem. For a model with just two assets, Papi and Sbaraglia (2006) solve the ALM problem with a recourse algorithm and a method that guarantees convergence. A complete handbook that describes the ALM and the multistage ALM for particular markets can be found in Zenios and Ziemba (2007). Also, Kouwenberg and Zenios (2008) review different stochastic programming models for ALM, analysing the performance of these models when they are applied to pension funds. Escudero et al. (2009) introduces a mixed integer-linear model by adding discrete variables into the model to limit the number of transactions and assets in each stage. Ferstl and Weissensteiner (2011) consider a multi-stage ALM under time-varying investment opportunities, using stochastic linear programming. Several other approaches to the ALM problem have been studied recently. Thus, Zhang and Chen (2016) focus on the mean-variance ALM with constant elasticity of variance. Wei and Wang (2017) focus on random coefficients, while Li et al. (2018) study models with stochastic volatility. Fernández et al. (2018) introduce a stochastic ALM model for a life insurance company using GPUs to run Monte-Carlo simulations. Dutta et al. (2019) uses big data analytics and stochastic linear programming under stochastic scenarios. Li et al. (2019) use a multi-period mean-variance model to analyse the ALM problem with probability constraints. Orlova (2019) develops an algorithm to solve a discrete dynamic process for cash distribution, in which the goal is to minimise the payment of fines for non-timely financing of expenses. This approach solves the problem of financial resources distribution under uncertainty over time. Kopa and Rusý (2020) formulates a complete stochastic program for ALM credit institutions that grant loans to general customers. In this paper, stochastic multi-stage scenarios are considered and the behaviour of the consumer are modelled. This behaviour impacts on the decisions the credit institution has to take and how it has to allocate its assets.
3. Problem Description and Formulation
When the conditions set out in a contract are met, insurers pay the insured. If they do not have sufficient available funds, they are subject to monetary fines issued by monetary authorities and, most likely, to lost customers. In order to ensure the insurers can meet their liabilities, they perform a process of matching assets to liabilities. Assigning assets to liabilities in an efficient manner is critical to the success of an insurance firm, since assigned (or frozen) assets cannot be used for any other purpose. Assets can only be assigned to liabilities if their maturity date precedes the due date of the liability. The value of the assets assigned to liabilities must equal or exceed the liability values. At the same time, asset maturity values and liability payment values are uncertain, thereby introducing a risk that liabilities cannot be met, even when the expected values imply that they could be met on the average.
An asset-liability assignment is the terminology used in this work to refer to a group of assets used to cover a group of liabilities. A feasible solution to the net present value asset-liability management (NPV-ALM) problem consists of a set of asset-liability assignments such that: (i) all liabilities are covered; and (ii) no individual assets or liabilities are part of more than one asset-liability assignment. Furthermore, a solution is also required to be robust under uncertain asset and liability values. Specifically, a solution must meet a minimum reliability level, where reliability is defined as the probability that all liabilities can be paid successfully using their assigned assets. Figure 1 illustrates a single asset-liability assignment consisting of three assets and two liabilities. Notice that, under the expected values for assets and liabilities (dashed lines), the liabilities can be met. However, due to uncertain asset maturity values and liability payment values, there is a risk that the assets fail to cover the liabilities in the assets-liability assignments. If is the probability that asset-liability assignment i fails to cover its liabilities, then the reliability of a set of asset-liability assignment (I) covering all of our liabilities is computed as . Following Faulin et al. (2008), we employ Monte-Carlo simulation to estimate failure probabilities associated with candidate asset-liability assignments.
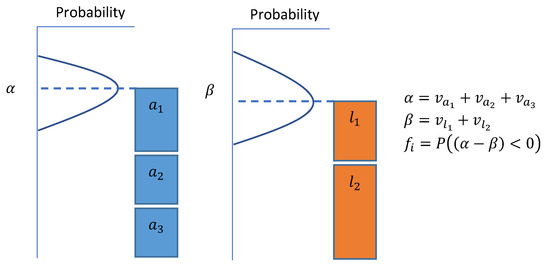
Figure 1.
An asset-liability assignment with a failure probability.
In this work, we propose a matheuristic algorithm for solving the NPV-ALM problem. A matheuristic integrates mathematical programming techniques with heuristics in order to develop an algorithm that benefits from exact optimisation as well as from fast and efficient heuristic techniques. For the case of the NPV-ALM problem, an integer program (Section 3.2) is used to calculate a set of feasible asset-liability assignment decisions that cover the liabilities. The solution is tested in a simulation to measure its reliability, and the result is employed to tune a safety margin parameter of the integer program. The safety margin parameter controls the minimum ratio between the asset values and the liability values of a generated asset-liability assignment. The process continues until a specified number of iterations have been completed. Section 3.1 formulates the NPV-ALM problem.
3.1. A Model for the Net Present Value Asset and Liability Management Problem
The objective (1) is to minimise the NPV of the assets committed to covering liabilities. In this context, is a binary decision variable indicating whether asset a is an element of asset-liability assignment g. Similarly, is a binary decision variable indicating whether liability l is an element of asset-liability assignment g. Each asset can only be part of at most one asset-liability assignment, as specified by Constraint (2). Each liability can only be part of one selected asset-liability assignment, as specified by Constraint (3). As a result of Constraints (2) and (3), the maximum number of asset-liability assignments is . A feasible asset-liability assignment requires that each of the selected assets matures before all of the selected liabilities in the asset-liability assignment. Constraint (4) introduces a continuous variable representing the latest maturity date of an asset in asset-liability assignment g. Constraint (5) introduces a continuous variable representing the earliest due date of a liability in asset-liability assignment g. Here, H is a large number which ensures the feasibility of Constraint (5) in asset-liability assignments that the liability l is not part of. Then, Constraint (6) enforces the time constraints for each asset-liability assignment. Constraint (7) requires that the sum of the asset values exceeds the value of the covered liabilities by a factor S in each asset-liability assignment g, thus ensuring that our liabilities are covered. Also, S is a multiplicative safety margin parameter for ensuring that the asset values are able to cover the liabilities under uncertain asset returns and liability values. Constraints (8) and (9) define the binary decision variables.
3.2. An Integer Programming Model for Generating Feasible Asset-Liability Assignments
Since solution time and memory requirements become an issue when solving the mixed integer program specified in Section 3.1 for realistic sized problem instances, our heuristic solution approach is based upon solving an integer program repeatedly to generate a sequence of efficient asset-liability assignments that cover all of the liabilities. This iterative approach is an alternative to generating all of the required asset-liabilities assignments in one go. This approach also vastly reduces the size and complexity of the mathematical programs that need to be solved. This integer program is denoted as . Here, U is the set of remaining uncovered liabilities, and V is the set of available assets currently unassigned to any liabilities. Initially, and . Every time a new asset-liability assignment is generated using the integer program, the selected assets are removed from V and the selected liabilities are removed from U. The integer program is solved repeatedly until the set U is empty. The input k is a randomly selected uncovered liability that must be covered by the next asset-liability assignment generated. This provides a mechanism for randomising the sets of asset-liability assignments generated. The asset-liability assignment generated is denoted as . It contains the set of selected assets and liabilities. The efficiency of an asset-liability assignment is measured by the value of the liabilities covered minus the value of the assets used, which encourages asset-liability assignments to cover as many liabilities as possible with the fewest assets possible. The net present value of the assigned assets is then subtracted, which captures our overall objective. Higher values of this efficiency measure correspond to more efficient asset-liability assignments. This efficiency objective function is expressed by Objective (10). In this expression, is a binary variable indicating which liabilities, , are part of the generated asset-liability assignment, and is a binary variable indicating which assets, , are part of the generated asset-liability assignment.
A feasible asset-liability assignment requires that each of the selected assets matures before the selected liabilities. Constraint (11) expresses this, where is the asset maturity date or liability due date of an asset or liability . Also, H is a large number which is used to ensure that Constraint (11) remains feasible in cases where liabilities are not selected. Optionally, Constraint (11) can be replaced by a constraint using the same form used in Constraints (4)–(6).
Constraint (12) requires that the sum of the asset values exceeds the value of the covered liabilities by a factor S, where S is a multiplicative safety margin parameter for ensuring that the asset values are able to cover the liabilities under uncertain asset returns and liability values.
Constraint (13) states that the randomly selected uncovered liability, k, must be included in the next asset-liability assignment generated.
4. Our Matheuristic Approach
This section describes our matheuristic algorithm, which combines integer programming and Monte-Carlo simulation for solving the NPV-ALM problem. This solving approach consists of two main phases: (i) generation of ‘promising’ solutions; and (ii) simulation and parameter tuning of the aforementioned solutions. The solution generation phase uses integer programming (specified in Section 3.2) to generate a set of asset-liability assignments that cover the liabilities. This process is iterative, i.e., each iteration generates one new asset-liability assignment from the remaining unused assets and uncovered liabilities. In order to increase the diversity of these solutions, a random factor is introduced: we randomly select one of the remaining liabilities and add a constraint which forces this liability to be part of the next asset-liability assignment. The simulation phase is used to measure the reliability of the generated solution. Monte-Carlo simulation is used estimate the failure probability associated with each asset-liability assignment. This is the probability that the sum of the maturity values of the assets, in an asset-liability assignment, is less than the corresponding sum of the liabilities. If the solution is sufficiently reliable, a best solution check is performed to see if the solution has the lowest associated NPV of any reliable solution found. The reliability result is also used to update the safety margin parameter of the integer program. The procedure followed is given in Algorithm 1.
| Algorithm 1: |
 |
5. Computational Experiments
The proposed heuristic has been implemented as a Python application running on a CPU with GHz and 16 GB of RAM. Instances from Bayliss et al. (2020) have been used to test the new approach, plus two new instances that could not be solved with the methodology presented in the former paper. Table 1 provides the details on the number of assets and liabilities for each instance, discount rate, and value modifier (if any was employed). Assets and liabilities have been distributed over time using a random uniform probability distribution from 0 to 100 and from 50 to 150, respectively. Similarly, values for assets and liabilities have been randomly generated using a uniform probability distribution from 0 to 1 and from 0 to , respectively. Asset values from instances 4 and 5 have been modified to simulate scenarios where its value varies over time, i.e.: given an asset with a value at time , a new value is computed , with and f the asset value modifier function. Likewise, instances 6 and 7 consider scenarios with liability values varying over time: given a liability with a value at time , a new value is computed , with and g the liability value modifier function. Instance 10 simulates a scenario with small assets and large liabilities, which encourages the use of multiple assets to cover a liability, while instance 11 considers a scenario with a few large assets and several small liabilities, to force the use of a single asset to cover multiple liabilities.

Table 1.
Characteristics of the set of instances.
Some initial experiments have been performed using instance 1 to set the parameter associated with the geometric probability distribution that drives the liability selection and the relative mixed integer programming optimality gap, , which is used to terminate the integer programming algorithm. Experiments to determine have been carried out in a deterministic scenario, while experiments to determine have been performed with stochastic variables. In this case, a better performance is attained with and . Figure 2 and Figure 3 present the results of the numerical tests.
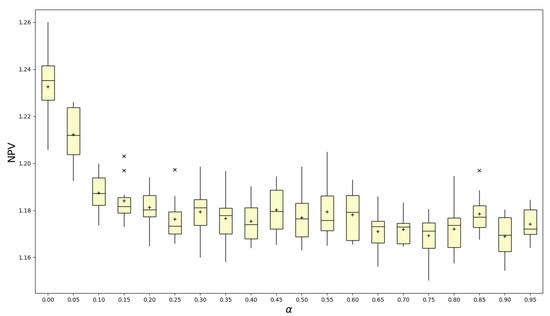
Figure 2.
Boxplot comparison of instance 1 results with different values.
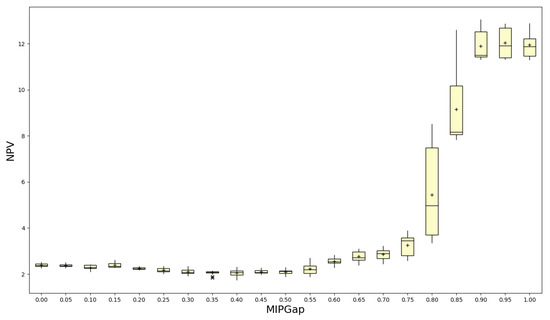
Figure 3.
Boxplot comparison of instance 1 results with different values.
Each instance in Table 1 has been solved using the integer programming algorithm presented in Algorithm 1, with a limit of 100 iterations. A time-limit of 300 seconds has also been imposed to terminate the algorithm after a solution has been generated if the aforementioned time-limit has been reached. The minimum reliability to consider a solution as feasible in the stochastic scenario is . The values of the parameters to increase and decrease the safety margin parameter S used are and . In the stochastic scenario, both asset and liability values have been considered uncertain, with a standard deviation of 5% of its expected maturity value. 500 iterations are executed for each asset-liability assignment generated in the Monte-Carlo simulation.
Table 2 provides the experimental results, compared with the results obtained in Bayliss et al. (2020). The first column contains the instance number (same as in Table 1). The second column (Cplex) contains the optimal value for each instance in a one-to-one asset-to-liability mapping. The third column (BR) contains the results of a previous biased-randomised algorithm, with its associated reliability values in the next column. Then, column 5 contains the best values obtained in the deterministic scenario with our matheuristic algorithm. Similarly, the best solutions obtained with a reliability higher than and its reliability are presented in the next two columns. Finally, some gaps between pairs of columns are also provided.

Table 2.
Results obtained for each instance.
6. Analysis of Results
As it can be seen in Table 2, the stand-alone matheuristic is providing reasonably good solutions when compared with the optimal ones given by Cplex for the deterministic scenario. Actually, Cplex is not able to solve all instances since it gets an “out of memory” (OoM) error for instance 3 (which justifies the need of using matheuristics even for the deterministic case). Also, notice that the cost of the assets-to-liabilities mapping is quite different in the deterministic scenario (Det.) and in the stochastic one (Stoch.). In other words, the deterministic scenario represents an ‘ideal’ (but not realistic) situation that provides a lower-bound to the real NPV cost under uncertainty conditions. Probably, the most interesting comparison in this table is between columns BR and Stoch. As one can see, the proposed matheuristic-simulation algorithm is usually able to outperform the previous simulation-optimisation approach proposed in Bayliss et al. (2020). This is mainly due to the fact that the methodology proposed in this paper does not require to assume a one-to-one mapping between assets and liabilities, thus allowing for an increasing number of mapping combinations. The main benefit of using the matheuristic-simulation algorithm is that it treats reliability as a hard constraint, an issue which is very important in the context of meeting liabilities. However, since the matheuristic is a more complex algorithm than BR, the 300 second time limit meant that there was not enough time for it to find solutions that met the 95% reliability constraint exactly, allowing it to achieve a low NPV. Notice that the gap between the NPVs of BR and the matheuristic are largest when the matheuristic return very reliable solution, while BR returns solution with low reliability. Figure 4 highlights the large average reliability gain attained from using the matheuristic, at the expense of a slightly higher NPV on average.
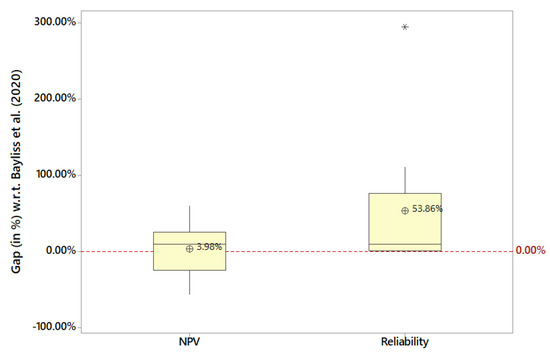
Figure 4.
Boxplot comparison of NPV and reliability results w.r.t. a previous work.
7. Conclusions
This paper proposes a hybrid matheurisctic-simulation approach to solve the stochastic version of the asset and liability management problem, where the goal is to minimise the net present value of the assets that are employed to cover the liabilities, while satisfying a reliability constraint. First, a matheuristic is designed by combining integer programming with a heuristic. The heuristic prioritises the selection of liabilities with an earlier maturity date, and it also makes use of a random procedure to increase the diversity of solutions generated. Then, the most promising solutions generated in the previous stage are simulated in a stochastic scenario. For this, a Monte-Carlo simulation is run multiple times in order to obtain estimates of the NPV-cost and the associated reliability of each solution. One of the main novelties of this paper is that approach integrates Monte-Carlo simulation with a matheuristic to provide and algorithm which can guarantee reliable solutions for the asset and liability management problem. It also considers the possibility of aggregating different assets, or different liabilities, before completing the assignment mapping, i.e.: several assets can be aggregated to cover each liability, and multiple liabilities can be covered by a single asset. To the best of our knowledge, it is the first time that this many-to-many assignment procedure is considered in the literature on asset and liability management.
The results show that the best deterministic mapping of assets to liabilities is far from being an optimal solution when uncertainty is present. Hence, simulation-optimisation methods become necessary to generate high-quality solutions whenever some components of the asset and liability management problem need to be modelled as random variables instead of deterministic values. In addition, the numerical experiments show how, by allowing many-to-many assignments between assets and liabilities, our combined matheuristic-simulation algorithm is able to outperform other simulation-optimisation approaches. As future work, we plan to: (i) include additional characteristics in the model so it fully represents the real-life problem that insurance companies and other financial institutions have to face; and (ii) introduce and test the algorithm in real-life benchmark instances.
Author Contributions
Conceptualization, C.B. and A.N.; methodology, C.B.; software, C.B. and M.S.; validation, A.A.J. and A.N.; writing–original draft preparation, C.B. and A.N.; writing–review and editing, C.B. and A.A.J.; supervision, C.B. and A.A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work has been partially supported by the cooperation agreement between Divina Pastora Seguros and the Universitat Oberta de Catalunya.
Conflicts of Interest
The authors declare no conflict of interest.
Summary of the Notation
| Sets | |
| A | Set of all assets |
| L | Set of all liabilities |
| Stochastic variables | |
| The uncertain value of asset a at maturity | |
| The uncertain value of liability l on its due date | |
| Decision variables | |
| Binary variable indicating whether asset a is selected as part of asset-liability assignment g | |
| Binary variable indicating whether liability l is selected as part of asset-liability assignment g | |
| Binary variable indicating whether asset a is selected as part of a generated asset-liability assignment | |
| Binary variable indicating whether liability l is selected as part of a generated asset-liability assignment | |
| Input parameters | |
| The expected maturity value of asset a | |
| The expected value of liability l on its due date | |
| The maturity maturity date of asset a | |
| The due date of liability l | |
| d | Discount factor used to calculate the net present value of an asset |
| Minimum reliability level | |
| m | Safety parameter decrease factor |
| h | Safety parameter increase factor |
| Other parameters | |
| Failure probability of asset-liability assignment g | |
| Asset-liability assignment g | |
| Net present value associated with Asset-liability assignment g | |
References
- Abdollahi, Hooman. 2020. Multi-objective programming for asset-liability management: The case of iranian banking industry. International Journal of Industrial Engineering & Production Research 31: 75–85. [Google Scholar]
- Bayliss, Christopher, Marti Serra, Mariem Gandouz, Angel A. Juan, and Armando Nieto. 2020. A simheuristic algorithm for reliable asset and liability management under uncertainty scenarios. Paper presented at the 2020 Winter Simulation Conference, Orlando, FL, USA, December 14–18; Piscataway: IEEE Press, pp. 1–11. [Google Scholar]
- Bierwag, Gerald O., Iraj Fooladi, and Gordon S. Roberts. 1993. Designing an immunized portfolio: Is m-squared the key? Journal of Banking & Finance 17: 1147–70. [Google Scholar]
- Boender, Guus, Cees Dert, Fred Heemskerk, and Henk Hoek. 2008. A scenario approach of ALM. In Handbook of Asset and Liability Management. Amsterdarm: Elsevier, vol. 2, pp. 829–60. [Google Scholar]
- Carino, David R., and William T. Ziemba. 1998. Formulation of the russell-yasuda kasai financial planning model. Operations Research 46: 433–49. [Google Scholar] [CrossRef]
- Carino, David R., David H. Myers, and William T. Ziemba. 1998. Concepts, technical issues, and uses of the russell-yasuda kasai financial planning model. Operations Research 46: 450–62. [Google Scholar] [CrossRef]
- Consigli, Giorgio, and Michael A. H. Dempster. 1998. Dynamic stochastic programmingfor asset-liability management. Annals of Operations Research 81: 131–62. [Google Scholar] [CrossRef]
- Consiglio, Andrea, David Saunders, and Stavros A. Zenios. 2006. Asset and liability management for insurance products with minimum guarantees: The UK case. Journal of Banking & Finance 30: 645–67. [Google Scholar]
- Consiglio, Andrea, Flavio Cocco, and Stavros A. Zenios. 2008. Asset and liability modelling for participating policies with guarantees. European Journal of Operational Research 186: 380–404. [Google Scholar] [CrossRef]
- Dash, Gordon, and Nina Kajiji. 2005. A nonlinear goal programming model for efficient asset-liability management of property-liability insurers. INFOR: Information Systems and Operational Research 43: 135–56. [Google Scholar] [CrossRef]
- Dempster, Michael A. H., Medova Germano, Elena A. Medova, and Michael Villaverde. 2003. Global asset liability management. British Actuarial Journal 9: 137–216. [Google Scholar] [CrossRef]
- Doering, Jana, Renatas Kizys, Angel A. Juan, Angels Fito, and Onur Polat. 2019. Metaheuristics for rich portfolio optimisation and risk management: Current state and future trends. Operations Research Perspectives 6: 100121. [Google Scholar] [CrossRef]
- Dutta, Goutam, Harish V. Rao, Sankarshan Basu, and Manoj Kr Tiwari. 2019. Asset liability management model with decision support system for life insurance companies: Computational results. Computers & Industrial Engineering 128: 985–98. [Google Scholar]
- Escudero, Laureano F., Araceli Garín, María Merino, and Gloria Pérez. 2009. On multistage stochastic integer programming for incorporating logical constraints in asset and liability management under uncertainty. Computational Management Science 6: 307–27. [Google Scholar] [CrossRef]
- Faulin, Javier, Angel A. Juan, Carles Serrat, and Vicente Bargueno. 2008. Predicting availability functions in time-dependent complex systems with SAEDES simulation algorithms. Reliability Engineering & System Safety 93: 1761–71. [Google Scholar]
- Fernández, José L., Ana M. Ferreiro-Ferreiro, José A. García-Rodríguez, and Carlos Vázquez. 2018. GPU parallel implementation for asset-liability management in insurance companies. Journal of Computational Science 24: 232–54. [Google Scholar] [CrossRef]
- Ferstl, Robert, and Alex Weissensteiner. 2011. Asset-liability management under time-varying investment opportunities. Journal of Banking & Finance 35: 182–92. [Google Scholar]
- Fisher, Lawrence, and Roman L. Weil. 1971. Coping with the risk of interest-rate fluctuations: Returns to bondholders from naive and optimal strategies. Journal of Business 44: 408–31. [Google Scholar] [CrossRef]
- Fleten, Stein-Erik, Kjetil Høyland, and Stein W. Wallace. 2002. The performance of stochastic dynamic and fixed mix portfolio models. European Journal of Operational Research 140: 37–49. [Google Scholar] [CrossRef]
- Fong, H. Gifford, and Oldrich A. Vasicek. 1984. A risk minimizing strategy for portfolio immunization. The Journal of Finance 39: 1541–46. [Google Scholar] [CrossRef]
- Gondzio, Jacek, and Roy Kouwenberg. 2001. High-performance computing for asset-liability management. Operations Research 49: 879–91. [Google Scholar] [CrossRef]
- Gründl, Helmut, Ming (Ivy) Dong, and Jens Gal. 2016. The evolution of insurer portfolio investment strategies for long-term investing. OECD Journal: Financial Market Trends 2016: 1–55. [Google Scholar] [CrossRef]
- Hibiki, Norio. 2006. Multi-period stochastic optimization models for dynamic asset allocation. Journal of Banking & Finance 30: 365–90. [Google Scholar]
- Hicks, John Richard. 1975. Value and Capital: An Inquiry into some Fundamental Principles of Economic Theory. Oxford: Oxford University Press. [Google Scholar]
- Iyengar, Garud, and Alfred Ka Chun Ma. 2009. Cash flow matching: A risk management approach. North American Actuarial Journal 13: 370–78. [Google Scholar] [CrossRef]
- Kopa, Milos, and Tomáš Rusý. 2020. A decision-dependent randomness stochastic program for asset–liability management model with a pricing decision. Annals of Operations Research. [Google Scholar] [CrossRef]
- Kouwenberg, Roy, and Stavros A. Zenios. 2008. Stochastic programming models for asset liability management. In Handbook of Asset and Liability Management. Amsterdam: Elsevier, pp. 253–303. [Google Scholar]
- Kouwenberg, Roy. 2001. Scenario generation and stochastic programming models for asset liability management. European Journal of Operational Research 134: 279–92. [Google Scholar] [CrossRef]
- Kusy, Martin I., and William T. Ziemba. 1986. A bank asset and liability management model. Operations Research 34: 356–76. [Google Scholar] [CrossRef]
- Li, Danping, Yang Shen, and Yan Zeng. 2018. Dynamic derivative-based investment strategy for mean-variance asset-liability management with stochastic volatility. Insurance: Mathematics and Economics 78: 72–86. [Google Scholar] [CrossRef]
- Li, Xun, Xianping Wu, and Haixiang Yao. 2019. Multi-period asset-liability management with cash flows and probability constraints: A mean-field formulation approach. Journal of the Operational Research Society 71: 1563–80. [Google Scholar] [CrossRef]
- Macaulay, Frederick R. 1938. Some Theoretical Problems Suggested by the Movements of Interest Rates, Bond Yeilds and Stock Prices in the United States Since 1856. New York: National Bureau of Economic Research. [Google Scholar]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Mulvey, John M., Daniel P. Rosenbaum, and Bala Shetty. 1997. Strategic financial risk management and operations research. European Journal of Operational Research 97: 1–16. [Google Scholar] [CrossRef]
- Mulvey, John M., Gordon Gould, and Clive Morgan. 2000. An asset and liability management system for Towers Perrin-Tillinghast. Interfaces 30: 96–114. [Google Scholar] [CrossRef][Green Version]
- Nielsen, Soren S., and Stavros A. Zenios. 1996. A stochastic programming model for funding single premium deferred annuities. Mathematical Programming 75: 177. [Google Scholar] [CrossRef]
- Oguzsoy, Cemal Berk, and Sibel Gu. 1997. Bank asset and liability management under uncertainty. European Journal of Operational Research 102: 575–600. [Google Scholar] [CrossRef]
- Orlova, E. V. 2019. Model for operational optimal control of financial recourses distribution in a company. Computer Research and Modeling 11: 343–58. [Google Scholar] [CrossRef]
- Panadero, Javier, Jana Doering, Renatas Kizys, Angel A. Juan, and Angels Fito. 2020. A variable neighborhood search simheuristic for project portfolio selection under uncertainty. Journal of Heuristics 26: 353–75. [Google Scholar] [CrossRef]
- Papi, Marco, and Simone Sbaraglia. 2006. Optimal asset–liability management with constraints: A dynamic programming approach. Applied Mathematics and Computation 173: 306–49. [Google Scholar] [CrossRef]
- Soler-Dominguez, Amparo, Angel A. Juan, and Renatas Kizys. 2017. A survey on financial applications of metaheuristics. ACM Computing Surveys 50: 1–23. [Google Scholar] [CrossRef]
- Sun, Zhongyang, Xin Zhang, and Kam Yuen. 2020. Mean-variance asset-liability management with affine diffusion factor process and a reinsurance option. Scandinavian Actuarial Journal 2020: 218–44. [Google Scholar] [CrossRef]
- Wei, Jiaqin, and Tianxiao Wang. 2017. Time-consistent mean-variance asset-liability management with random coefficients. Insurance: Mathematics and Economics 77: 84–96. [Google Scholar] [CrossRef]
- Zenios, Stavros A., and William T. Ziemba. 2007. Handbook of Asset and Liability Management: Applications and Case Studies. Amsterdam: Elsevier, vol. 2. [Google Scholar]
- Zenios, Stavros A. 1995. Asset/liability management under uncertainty for fixed-income securities. Annals of Operations Research 59: 77–97. [Google Scholar] [CrossRef]
- Zhang, Miao, and Ping Chen. 2016. Mean-variance asset-liability management under constant elasticity of variance process. Insurance: Mathematics and Economics 70: 11–18. [Google Scholar] [CrossRef]
- Zhang, Xin-Li, and Ke-Cun Zhang. 2009. Using genetic algorithm to solve a new multi-period stochastic optimization model. Journal of Computational and Applied Mathematics 231: 114–23. [Google Scholar] [CrossRef][Green Version]
- Ziemba, William T., John M. Mulvey, and H. K. Moffatt. 1998. Worldwide Asset and Liability Modeling. Cambridge: Cambridge University Press, vol. 10. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).