An Optimal Model of Financial Distress Prediction: A Comparative Study between Neural Networks and Logistic Regression
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Data Collection
3.2. Data Balancing
3.3. Training-Test Set Split
3.4. Variable Analysis
3.5. Stepwise and Lasso Selection Techniques
3.5.1. Stepwise Logistic Regression Selection
- Akaike Information Criterion (AIC):
- Bayesian Information Criterion (BIC):
- L is the likelihood of the logit model;
- K is the number of variables in the model;
- n is the number of observations.
3.5.2. Lasso Logistic Regression Selection
3.6. Prediction Models
3.6.1. Logistic Regression Model
- (resp. ) is the a priori probability that (resp. ). For simplicity, this is hereafter denoted as (resp. ).
- (resp. ) is the conditional distribution of X knowing the value taken by Y. The a posteriori probability of obtaining the modality 1 of Y (resp. 0) knowing the value taken by X is noted (resp. ).
3.6.2. Neural Networks Model: Multi-Layer Perceptron
3.7. Metrics
4. Results
4.1. Feature Selection Results
4.2. Descriptive Statistics
4.3. Estimation Results of the Stepwise and Lasso Logistic Regression Models
4.4. Performance of Logit Models
4.5. Performance of Neural Networks Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Descriptive Statistics Tables
| Variables | R5 | R7 | R14 | R15 | R21 |
|---|---|---|---|---|---|
| Entire data | |||||
| Mean | 25.730 | 0.67051 | 0.011008 | 0.025758 | 175.19 |
| Std | 101.3963 | 4.933185 | 0.02312998 | 0.08351403 | 195.8285 |
| Lilliefors (Kolmogorov–Smirnov) normality test | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 |
| Shapiro–Wilk normality test (p-value) | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | 4.554 × 10 | 4.554 × 10 |
| Distressed SMEs | |||||
| Mean | −1.037 | 1.0756 | 0.02248 | −0.0132 | 258.20 |
| Std | 12.82926 | 5.87987 | 0.03644343 | 0.08829215 | 276.327 |
| Non-distressed SMEs | |||||
| Mean | 38.135 | 0.4828 | 0.005691 | 0.04381 | 136.72 |
| Std | 120.496 | 4.441264 | 0.009236137 | 0.07494895 | 128.4722 |
| Correlation matrix | |||||
| R5 | 1.00 | ||||
| R7 | 0.04 | 1.00 | |||
| R14 | 0.08 | 0.38 | 1.00 | ||
| R15 | 0.29 | −0.12 | −0.38 | 1.00 | |
| R21 | −0.09 | −0.05 | 0.15 | −0.11 | 1.00 |
| Multicollinearity test | |||||
| VIF | 1.0485 | 1.0567 | 1.1314 | 1.1050 | 1.0602 |
| TOL | 0.9538 | 0.9463 | 0.8839 | 0.9049 | 0.9432 |
| Variables | R2 | R5 | R14 | R15 | R17 | R21 | R22 |
|---|---|---|---|---|---|---|---|
| Entire data | |||||||
| Mean | 1.1926 | 25.730 | 0.011008 | 0.025758 | 0.04643 | 175.19 | 126.67 |
| Std | 1.408321 | 101.3963 | 0.02312998 | 0.08351403 | 0.2095069 | 195.8285 | 179.956 |
| Lilliefors (Kolmogorov–Smirnov) normality test | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 |
| Shapiro–Wilk normality test (p-value) | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | 6.591 × 10 | 4.554 × 10 | <2.2 × 10 |
| Distressed SMEs | |||||||
| Mean | 1.5586 | −1.037 | 0.02248 | −0.0132 | −0.01017 | 258.20 | 183.65 |
| Std | 1.874535 | 12.82926 | 0.03644343 | 0.08829215 | 0.2715556 | 276.327 | 276.2145 |
| Non-distressed SMEs | |||||||
| Mean | 1.0230 | 38.135 | 0.005691 | 0.04381 | 0.07267 | 136.72 | 100.27 |
| Std | 1.097959 | 120.496 | 0.009236137 | 0.07494895 | 0.168407 | 128.4722 | 101.3615 |
| Correlation matrix | |||||||
| R2 | 1.00 | ||||||
| R5 | 0.03 | 1.00 | |||||
| R14 | ** | 0.08 | 1.00 | ||||
| R15 | 0.10 | *** | *** | 1.00 | |||
| R17 | 0.11 | * | −0.07 | 0.17 | 1.00 | ||
| R21 | ** | −0.09 | −0.11 | 0.09 | 1.00 | ||
| R22 | −0.08 | −0.04 | 0.23 | −0.19 | −0.02 | *** | 1.00 |
| Multicollinearity test | |||||||
| VIF | 1.1413 | 1.0507 | 1.1751 | 1.0927 | 1.0497 | 1.1929 | 1.1988 |
| TOL | 0.8762 | 0.9517 | 0.8510 | 0.9152 | 0.9527 | 0.8383 | 0.8342 |
| Variables | R5 | R8 | R14 | R15 | R17 | R21 |
|---|---|---|---|---|---|---|
| Entire data | ||||||
| Mean | 41.53 | 4.777 | 0.0121523 | 0.008771 | 0.04539 | 230.05 |
| Std | 237.3972 | 21.65186 | 0.02328563 | 0.2144745 | 0.2189421 | 394.0288 |
| Lilliefors (Kolmogorov–Smirnov) normality test | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 |
| Shapiro–Wilk normality test (p-value) | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | 4.545 × 10 | <2.2 × 10 |
| Distressed SMEs | ||||||
| Mean | 24.512 | 10.9267 | 0.025189 | −0.073553 | −0.02475 | 424.8 |
| Std | 318.6796 | 36.54885 | 0.03459138 | 0.3559114 | 0.290211 | 639.2844 |
| Non-distressed SMEs | ||||||
| Mean | 49.4224 | 1.92646 | 0.0061111 | 0.04692 | 0.07789 | 139.78 |
| Std | 189.4045 | 6.986372 | 0.0114067 | 0.06864435 | 0.1682521 | 119.4231 |
| Correlation matrix | ||||||
| R5 | 1.00 | |||||
| R8 | * | 1.00 | ||||
| R14 | −0.05 | *** | 1.00 | |||
| R15 | *** | 0.00 | *** | 1.00 | ||
| R17 | 0.04 | −0.08 | −0.12 | 0.22 | 1.00 | |
| R21 | −0.08 | 0.05 | 0.08 | −0.11 | ** | 1.00 |
| Multicollinearity test | ||||||
| VIF | 1.0132 | 1.0137 | 1.1583 | 1.0973 | 1.0052 | 1.0538 |
| TOL | 0.9869 | 0.9865 | 0.8633 | 0.9114 | 0.9949 | 0.9489 |
| Variables | R4 | R6 | R8 | R14 | R15 | R16 | R17 | R20 | R21 |
|---|---|---|---|---|---|---|---|---|---|
| Entire data | |||||||||
| Mean | 0.65687 | 0.09421 | 4.777 | 0.0121523 | 0.008771 | 1.15436 | 0.04539 | 0.4837 | 230.05 |
| Std | 1.601535 | 0.2050961 | 21.65186 | 0.02328563 | 0.2144745 | 1.20965 | 0.2189421 | 0.8906335 | 394.0288 |
| Lilliefors (Kolmogorov–Smirnov) normality test | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | 2.2 × 10 |
| Shapiro–Wilk normality test (p-value) | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | <2.2 × 10 | 4.554 × 10 | <2.2 × 10 | <2.2 × 10 |
| Distressed SMEs | |||||||||
| Mean | 1.1036 | 0.07853 | 10.9267 | 0.025189 | −0.073553 | 0.70415 | −0.02475 | 0.59976 | 424.8 |
| Std | 2.492708 | 0.1227013 | 36.54885 | 0.03459138 | 0.3559114 | 0.4777546 | 0.290211 | 1.222349 | 639.2844 |
| Non-distressed SMEs | |||||||||
| Mean | 0.449827 | 0.10148 | 1.92646 | 0.0061111 | 0.04692 | 1.3630 | 0.07789 | 0.42988 | 139.78 |
| Std | 0.8801461 | 0.2337489 | 6.986372 | 0.0114067 | 0.06864435 | 1.379693 | 0.1682521 | 0.6846804 | 119.4231 |
| Correlation matrix | |||||||||
| R4 | 1.00 | ||||||||
| R6 | *** | 1.00 | |||||||
| R8 | *** | ** | 1.00 | ||||||
| R14 | *** | *** | *** | 1.00 | |||||
| R15 | *** | ** | 0.00 | *** | 1.00 | ||||
| R16 | 0.05 | -0.04 | 0.05 | ** | *** | 1.00 | |||
| R17 | −0.09 | −0.04 | −0.08 | −0.12 | ** | 0.05 | 1.00 | ||
| R20 | 0.03 | * | *** | *** | 0.04 | 1.00 | |||
| R21 | 0.00 | 0.00 | 0.05 | 0.08 | −0.11 | *** | 0.06 | 0.05 | 1.00 |
| Multicollinearity test | |||||||||
| VIF | 1.2843 | 1.0750 | 1.2243 | 1.2359 | 1.1130 | 1.2904 | 1.0395 | 1.1583 | 1.1467 |
| TOL | 0.7786 | 0.9303 | 0.8168 | 0.8091 | 0.8985 | 0.7749 | 0.9620 | 0.8633 | 0.8721 |
Appendix B. Architectures of Neural Networks Models

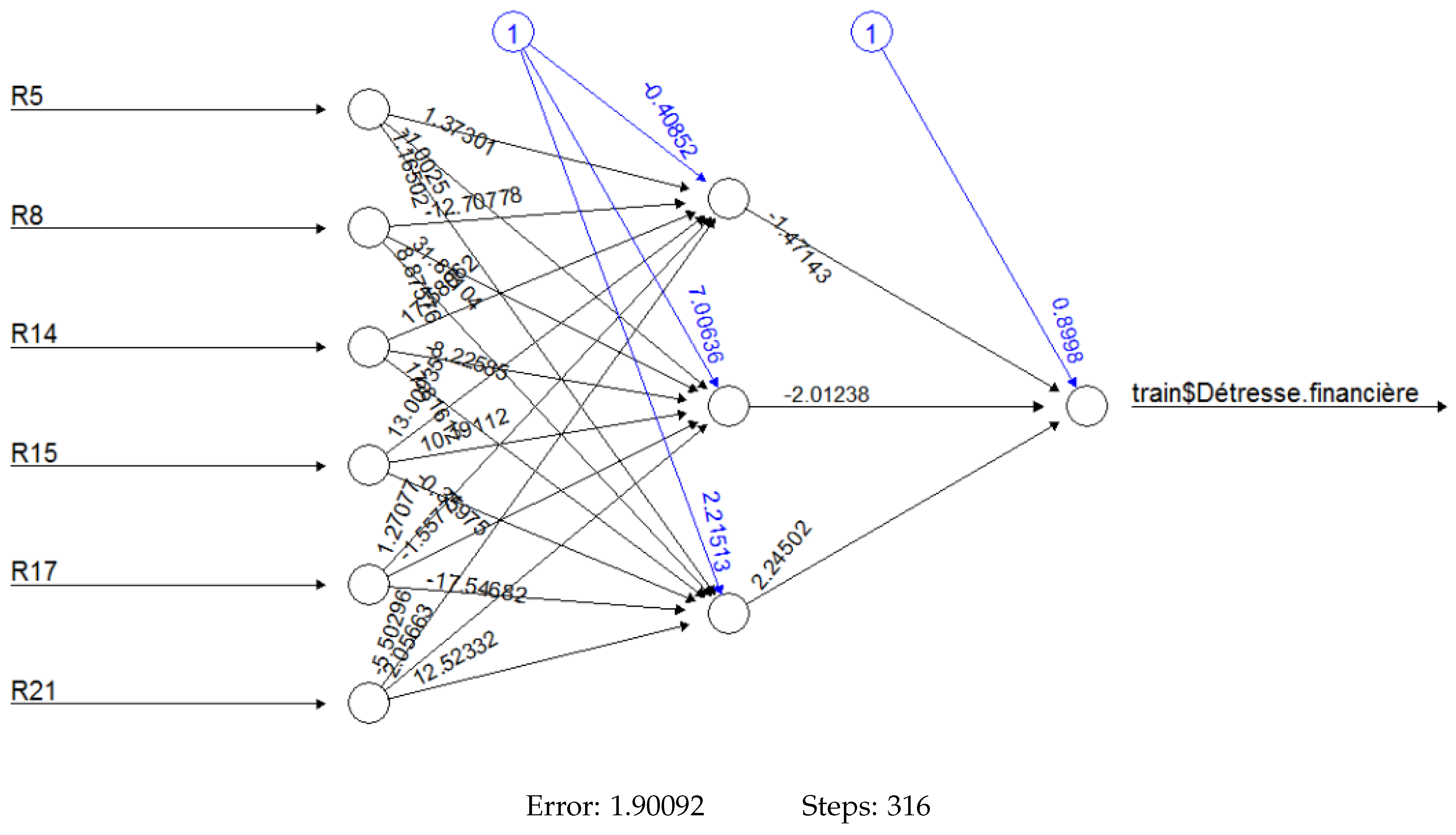
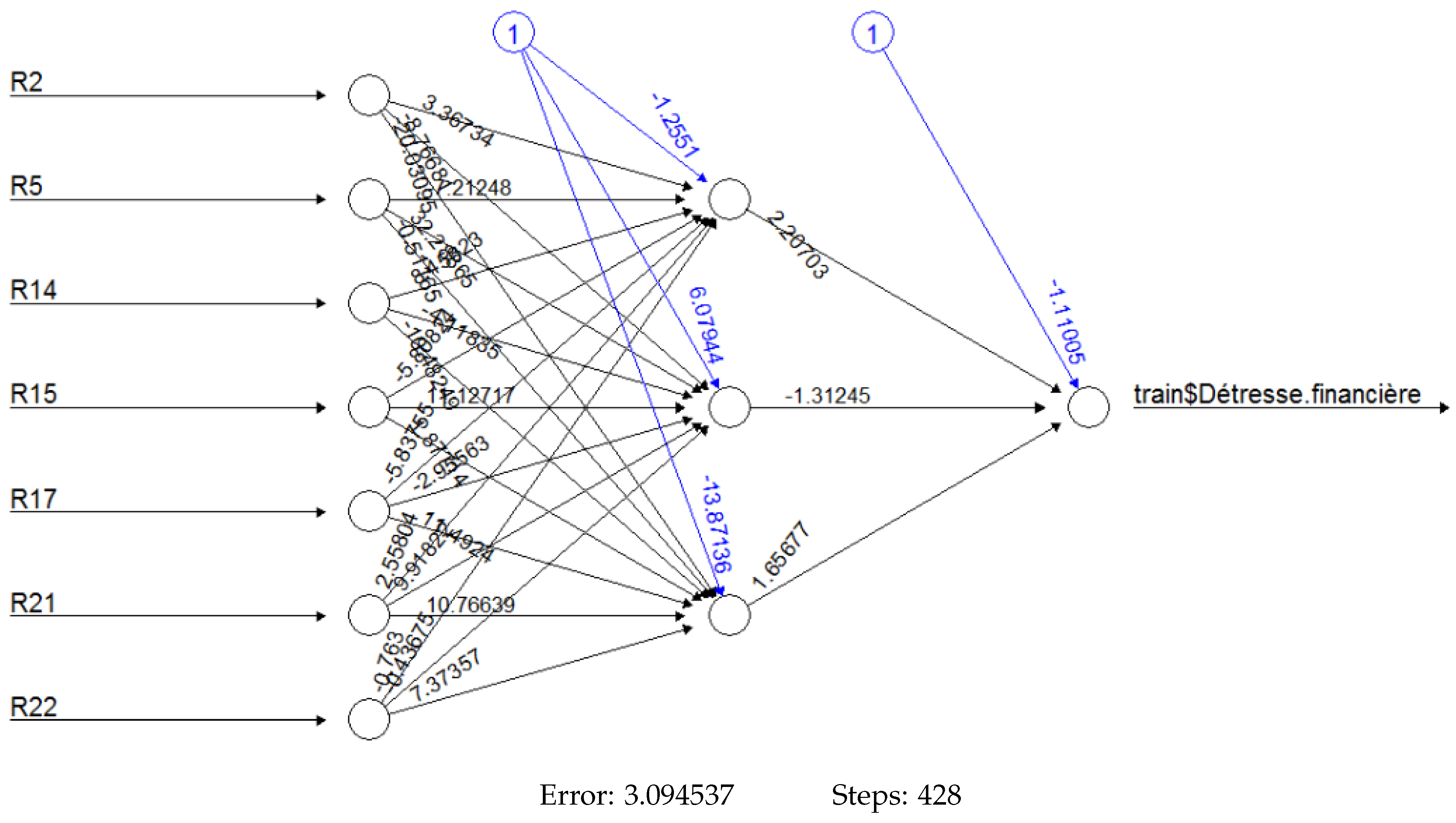
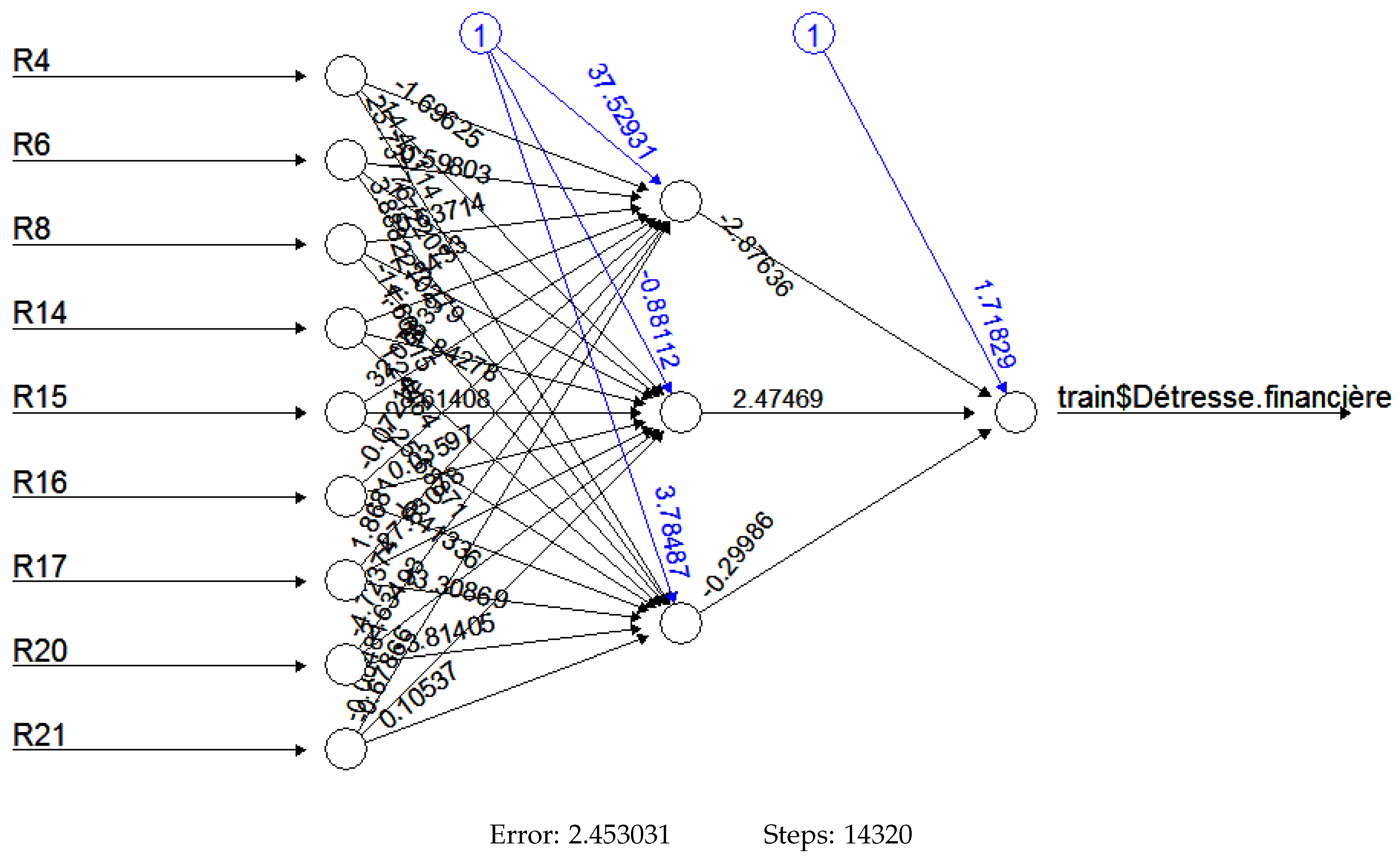
Appendix C. Machine Learning Libraries
| 1 | According to Maroc PME, SMEs are companies with a turnover of less than or equal to 200 million dirhams. |
| 2 | A graph that relates true positive rates and false positive rates. By varying the threshold S (threshold used for the assignment rule) over the interval [0, 1], the ROC curve is constructed and the true positive and false positive rates are calculated. |
References
- Affes, Zeineb, and Rania Hentati-Kaffel. 2019. Predicting US banks bankruptcy: Logit versus Canonical Discriminant analysis. Computational Economics 54: 199–244. [Google Scholar] [CrossRef]
- Altman, Edward I. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Altman, Edward I., Małgorzata Iwanicz-Drozdowska, Erkki K. Laitinen, and Arto Suvas. 2017. Financial distress prediction in an international context: A review and empirical analysis of Altman’s Z score model. Journal of International Financial Management & Accounting 28: 131–71. [Google Scholar]
- Altman, Edward I., Małgorzata Iwanicz-Drozdowska, Erkki K. Laitinen, and Arto Suvas. 2020. A race for long horizon bankruptcy prediction. Applied Economics 52: 4092–111. [Google Scholar] [CrossRef]
- Amor, S. Ben, Nabil Khoury, and Marko Savor. 2009. Modèle prévisionnel de la défaillance financière des PME québécoises emprunteuses. Journal of Small Business and Entrepreneurship 22: 517–34. [Google Scholar] [CrossRef]
- Azayite, Fatima Zahra, and Said Achchab. 2017. The impact of payment delays on bankruptcy prediction: A comparative analysis of variables selection models and neural networks. Paper presented at 2017 3rd International Conference of Cloud Computing Technologies and Applications (CloudTech), Rabat, Morocco, October 24–26; pp. 1–7. [Google Scholar]
- Back, Barbro, Teija Laitinen, Kaisa Sere, and Michiel van Wezel. 1996. Choosing Bankruptcy Predictors Using Discriminant Analysis, Logit Analysis, And Genetic Algorithms. Turku Centre for Computer Science Technical Report 40: 1–18. [Google Scholar]
- Balcaen, Sofie, and Hubert Ooghe. 2006. 35 years of studies on business failure: An overview of the classic statistical methodologies and their related problems. The British Accounting Review 38: 63–93. [Google Scholar] [CrossRef]
- Bank Al-Maghrib. 2002. Circulaire du Gouverneur de Bank Al-Maghrib n°19/G/2002 du 23 décembre 2002 (18 chaoual 1423) Relative à la Classification des Créances et à leur Couverture par les Provisions. Rabat: Bank Al-Maghrib. [Google Scholar]
- Bateni, Leila, and Farshid Asghari. 2020. Bankruptcy Prediction Using Logit and Genetic Algorithm Models: A Comparative Analysis. Computational Economics 55: 335–48. [Google Scholar] [CrossRef]
- Beaver, William H. 1966. Financial ratios as predictors of failure. Journal of Accounting Research 4: 71–111. [Google Scholar] [CrossRef]
- Bellanca, Sabrina, Loredana Cultrera, and Guillaume Vermeylen. 2015. «La faillite des PME belges». La Libre Belgique, March 28. [Google Scholar]
- Bellovary, Jodi L., Don E. Giacomino, and Michael D. Akers. 2007. A review of bankruptcy prediction studies: 1930 to present. Journal of Financial Education 1: 1–42. [Google Scholar]
- Bunn, Philip, and Victoria Redwood. 2003. Company Accounts-Based Modelling of Business Failures and the Implications for Financial Stability. Bank of England Working Paper No. 210. London: Bank of England. [Google Scholar]
- Charalambakis, Evangelos C., and Ian Garrett. 2019. On corporate financial distress prediction: What can we learn from private firms in a developing economy? Evidence from Greece. Review of Quantitative Finance and Accounting 52: 467–91. [Google Scholar] [CrossRef]
- Chawla, Nitesh V., Kevin W. Bowyer, Lawrence O. Hall, and W. Philip Kegelmeyer. 2002. SMOTE: Synthetic Minority Over-sampling Technique. Journal of Artificial Intelligence Research 16: 321–57. [Google Scholar] [CrossRef]
- Chen, Wei-Sen, and Yin-Kuan Du. 2009. Using neural networks and data mining techniques for the financial distress prediction model. Expert Systems with Applications 36: 4075–86. [Google Scholar] [CrossRef]
- Cohen, Sandra, Antonella Costanzo, and Francesca Manes-Rossi. 2017. Auditors and early signals of financial distress in local governments. Managerial Auditing Journal 32: 234–50. [Google Scholar] [CrossRef]
- Crutzen, Nathalie, and Didier Van Caillie. 2007. The Business Failure Process: Towards an Integrative Model of the Literature. Paper presented at International Workshop on Default Risk and Financial Distress, Rennes, France, September 13–14. [Google Scholar]
- Deakin, Edward B. 1972. A discriminant analysis of predictors of business failure. Journal of Accounting Research 10: 167–79. [Google Scholar] [CrossRef]
- Du Jardin, Philippe. 2015. Bankruptcy prediction using terminal failure processes. European Journal of Operational Research 242: 286–303. [Google Scholar] [CrossRef]
- Du Jardin, Philippe, and Éric Séverin. 2012. Forecasting financial failure using a Kohonen map: A comparative study to improve model stability over time. European Journal of Operational Research 221: 378–96. [Google Scholar] [CrossRef]
- Durica, Marek, L. Svabova, and Jaroslav Frnda. 2021. Financial distress prediction in Slovakia: An application of the cart algorithm. Journal of International Studies 14: 201–15. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2017. The Elements of Statistical Learning. New York: Springer Series in Statistics, vol. 1. [Google Scholar]
- Gebhardt, G. 1980. Insolvency prediction based on annual financial statements according to the company law. An assessment of the reform of annual statements by the law of 1965 from the view of external addresses. Bochumer Beitrage zur Untennehmungs und Unternehmens-Forschung 22. [Google Scholar]
- Geng, Ruibin, Indranil Bose, and Xi Chen. 2014. Prediction of financial distress: An empirical study of listed chinese companies using data mining. European Journal of Operational Research 241: 236–47. [Google Scholar] [CrossRef]
- Gregova, Elena, Katarina Valaskova, Peter Adamko, Milos Tumpach, and Jaroslav Jaros. 2020. Predicting financial distress of slovak enterprises: Comparison of selected traditional and learning algorithms methods. Sustainability 12: 3954. [Google Scholar] [CrossRef]
- Guan, Rong, Huiwen Wang, and Haitao Zheng. 2020. Improving accuracy of financial distress prediction by considering volatility: An interval-data-based discriminant model. Computational Statistics 35: 491–514. [Google Scholar] [CrossRef]
- Hafiz, Alaka, Oyedele Lukumon, Bilal Muhammad, Akinade Olugbenga, Owolabi Hakeem, and Ajayi Saheed. 2015. Bankruptcy prediction of construction businesses: Towards a big data analytics approach. Paper presented at 2015 IEEE First International Conference on Big Data Computing Service and Applications, Redwood City, CA, USA, March 30–April 2; pp. 347–52. [Google Scholar]
- Haut-Commissariat au Plan. 2018. Note D’information Relative aux Comptes Régionaux de L’année 2018. Casablanca: Haut-Commissariat au Plan. [Google Scholar]
- Haut-Commissariat au Plan. 2019. Enquête Nationale Auprès des Entreprises, Premiers Résultats 2019. Casablanca: Haut-Commissariat au Plan. [Google Scholar]
- Idrissi, Khadir, and Aziz Moutahaddib. 2020. Prédiction de la défaillance financière des PME marocaine: Une étude comparative. Revue Africaine de Management 5: 18–36. [Google Scholar]
- Inforisk. 2020. Étude Inforisk, Défaillances Maroc 2019. Casablanca: Inforisk. [Google Scholar]
- Islek, Irem, Idris Murat Atakli, and Sule Gunduz Oguducu. 2017. A Framework for Business Failure Prediction. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 10246 LNAI. Zakopane: Springer, pp. 74–83. [Google Scholar] [CrossRef]
- Iturriaga, Félix J. López, and Iván Pastor Sanz. 2015. Bankruptcy visualization and prediction using neural networks: A study of US commercial banks. Expert Systems with Applications 42: 2857–69. [Google Scholar] [CrossRef]
- Jabeur, Sami Ben. 2017. Bankruptcy prediction using Partial Least Squares Logistic Regression. Journal of Retailing and Consumer Services 36: 197–202. [Google Scholar] [CrossRef]
- Jeong, Chulwoo, Jae H. Min, and Myung Suk Kim. 2012. A tuning method for the architecture of neural network models incorporating GAM and GA as applied to bankruptcy prediction. Expert Systems with Applications 39: 3650–58. [Google Scholar] [CrossRef]
- Jones, Stewart, David Johnstone, and Roy Wilson. 2017. Predicting corporate bankruptcy: An evaluation of alternative statistical frameworks. Journal of Business Finance & Accounting 44: 3–34. [Google Scholar]
- Kamaluddin, Amrizah, Norhafizah Ishak, and Nor Farizal Mohammed. 2019. Financial distress prediction through cash flow ratios analysis. International Journal of Financial Research 10: 63–76. [Google Scholar] [CrossRef]
- Kherrazi, Soufiane, and Khalifa Ahsina. 2016. Défaillance et politique d’entreprises: Modélisation financière déployée sous un modèle logistique appliqué aux PME marocaines. La Revue Gestion et Organisation 8: 53–64. [Google Scholar] [CrossRef][Green Version]
- Khlifa, Selma Haj. 2017. Predicting default risk of SMEs in developing economies: Evidence from Morocco. Journal of WEI Business and Economics 6: 3. [Google Scholar]
- Kim, Kyoung-jae, Kichun Lee, and Hyunchul Ahn. 2018. Predicting corporate financial sustainability using Novel Business Analytics. Sustainability 11: 64. [Google Scholar] [CrossRef]
- Kisman, Zainul, and Dian Krisand. 2019. How to Predict Financial Distress in the Wholesale Sector: Lesson from Indonesian Stock Exchange. Journal of Economics and Business 2: 569–85. [Google Scholar] [CrossRef]
- Kliestik, Tomas, Katarina Valaskova, George Lazaroiu, Maria Kovacova, and Jaromir Vrbka. 2020. Remaining financially healthy and competitive: The role of financial predictors. Journal of Competitiveness 12: 74–92. [Google Scholar] [CrossRef]
- Kovacova, Maria, Tomas Kliestik, Katarina Valaskova, Pavol Durana, and Zuzana Juhaszova. 2019. Systematic review of variables applied in bankruptcy prediction models of Visegrad group countries. Oeconomia Copernicana 10: 743–72. [Google Scholar] [CrossRef]
- Long, J. Scott, and Jeremy Freese. 2006. Regression Models for Categorical Dependent Variables Using Stata. College Station: Stata Press. [Google Scholar]
- Lukason, Oliver, and Art Andresson. 2019. Tax arrears versus financial ratios in bankruptcy prediction. Journal of Risk and Financial Management 12: 187. [Google Scholar] [CrossRef]
- Lukason, Oliver, and Erkki K. Laitinen. 2019. Firm failure processes and components of failure risk: An analysis of European bankrupt firms. Journal of Business Research 98: 380–90. [Google Scholar] [CrossRef]
- Malakauskas, Aidas, and Aušrinė Lakštutienė. 2021. Financial distress prediction for small and medium enterprises using machine learning techniques. Engineering Economics 32: 4–14. [Google Scholar] [CrossRef]
- Malécot, Jean-François. 1981. Les défaillances: Un essai d’explication. [Google Scholar]
- Mselmi, Nada, Amine Lahiani, and Taher Hamza. 2017. Financial distress prediction: The case of French small and medium-sized firms. International Review of Financial Analysis 50: 67–80. [Google Scholar] [CrossRef]
- Odom, Marcus D., and Ramesh Sharda. 1990. A neural network model for bankruptcy prediction. Paper presented at 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, June 17–21; pp. 163–68. [Google Scholar]
- Ogachi, Daniel, Richard Ndege, Peter Gaturu, and Zeman Zoltan. 2020. Corporate Bankruptcy Prediction Model, a Special Focus on Listed Companies in Kenya. Journal of Risk and Financial Management 13: 47. [Google Scholar] [CrossRef]
- Ohlson, James A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef]
- Papana, Angeliki, and Anastasia Spyridou. 2020. Bankruptcy Prediction: The Case of the Greek Market. Forecasting 2: 505–25. [Google Scholar] [CrossRef]
- Park, Sunghwa, Hyunsok Kim, Janghan Kwon, and Taeil Kim. 2021. Empirics of Korean Shipping Companies’ Default Predictions. Risks 9: 159. [Google Scholar] [CrossRef]
- Paule-Vianez, Jessica, Milagros Gutiérrez-Fernández, and José Luis Coca-Pérez. 2020. Prediction of financial distress in the Spanish banking system: An application using artificial neural networks. Applied Economic Analysis 28: 69–87. [Google Scholar] [CrossRef]
- Psillaki, Maria. 1995. Rationnement du crédit et PME: Une tentative de mise en relation. Revue Internationale PME économie et Gestion de La Petite et Moyenne Entreprise 8: 67–90. [Google Scholar] [CrossRef][Green Version]
- Rahman, Mahfuzur, Cheong Li Sa, and Md KaiumMasud. 2021. Predicting Firms’ Financial Distress: An Empirical Analysis Using the F-Score Model. Journal of Risk and Financial Management 14: 199. [Google Scholar] [CrossRef]
- Refait-Alexandre, Catherine. 2004. La prévision de la faillite fondée sur l’analyse financière de l’entreprise: Un état des lieux. Economie Prevision 1: 129–47. [Google Scholar] [CrossRef]
- Sharifabadi, M. Ramezani, M. Mirhaj, and Naser Izadinia. 2017. The impact of financial ratios on the prediction of bankruptcy of small and medium companies. QUID: Investigación, Ciencia y Tecnología 1: 164–73. [Google Scholar]
- Shi, Yin, and Xiaoni Li. 2019. An overview of bankruptcy prediction models for corporate firms: A systematic literature review. Intangible Capital 15: 114–27. [Google Scholar] [CrossRef]
- Shrivastav, Santosh Kumar, and P. Janaki Ramudu. 2020. Bankruptcy prediction and stress quantification using support vector machine: Evidence from Indian banks. Risks 8: 52. [Google Scholar] [CrossRef]
- Shrivastava, Arvind, Kuldeep Kumar, and Nitin Kumar. 2018. Business distress prediction using bayesian logistic model for Indian firms. Risks 6: 113. [Google Scholar] [CrossRef]
- Sun, Jie, Hui Li, Qing-Hua Huang, and Kai-Yu He. 2014. Predicting financial distress and corporate failure: A review from the state-of-the-art definitions, modeling, sampling, and featuring approaches. Knowledge-Based Systems 57: 41–56. [Google Scholar] [CrossRef]
- Svabova, Lucia, Lucia Michalkova, Marek Durica, and Elvira Nica. 2020. Business failure prediction for Slovak small and medium-sized companies. Sustainability 12: 4572. [Google Scholar] [CrossRef]
- Tong, Yehui, and Zélia Serrasqueiro. 2021. Predictions of failure and financial distress: A study on portuguese high and medium-high technology small and midsized enterprises. Journal of International Studies 14: 9–25. [Google Scholar] [CrossRef] [PubMed]
- Valaskova, Katarina, Tomas Kliestik, Lucia Svabova, and Peter Adamko. 2018. Financial risk measurement and prediction modelling for sustainable development of business entities using regression analysis. Sustainability 10: 2144. [Google Scholar] [CrossRef]
- Van Caillie, Didier. 1993. Apports de l’analyse factorielle des correspondances multiples à l’étude de la détection des signaux annonciateurs de faillite parmi les PME. Cahier de Recherche Du Service d’Informatique de Gestion (Reprint: Cahier de Recherche Du CEPE). Ph.D. thesis, Université de Liège, Liège, Belgiquepp; pp. 1–36. [Google Scholar]
- Vu, Loan Thi, Nga Thu Nguyen, Lien Thi Vu, Phuong Thi Thuy Do, and Dong Phuong Dao. 2019. Feature selection methods and sampling techniques to financial distress prediction for Vietnamese listed companies. Investment Management and Financial Innovations 16: 276–90. [Google Scholar] [CrossRef]
- Zhang, Guoqiang, Michael Y. Hu, B. Eddy Patuwo, and Daniel C. Indro. 1999. Artificial neural networks in bankruptcy prediction: General framework and cross-validation analysis. European Journal of Operational Research 116: 16–32. [Google Scholar] [CrossRef]
- Zhang, Ling, Edward I. Altman, and Jerome Yen. 2010. Corporate financial distress diagnosis model and application in credit rating for listing firms in China. Frontiers of Computer Science in China 4: 220–36. [Google Scholar] [CrossRef]
- Zizi, Youssef, Mohamed Oudgou, and Abdeslam El Moudden. 2020. Determinants and predictors of smes’ financial failure: A logistic regression approach. Risks 8: 107. [Google Scholar] [CrossRef]
| Before Resampling | After Resampling | ||
|---|---|---|---|
| 0 | 1 | 0 | 1 |
| 0.6833 | 0.3166 | 0.5 | 0.5 |
| Liquidity | ||
| R1 | Current Ratio | |
| R2 | Quick Ratio | |
| R3 | Working Capital to Total Assets | |
| Solvency and Capital Structure | ||
| R4 | Debt to Equity Ratio | |
| R5 | Interest Coverage | |
| R6 | Cost of Debt | |
| R7 | Autonomy Ratio | |
| R8 | Repayment Capacity | |
| R9 | Bank Loans | |
| R10 | Financial Equilibrium | |
| R11 | Trade Payables to Total Liabilities | |
| Profitability | ||
| R12 | Operating Income to Sales | |
| R13 | Value added to Sales | |
| R14 | Interest to Sales | |
| R15 | Return On Assets | |
| R16 | Asset Turnover | |
| R17 | Retained Earnings to Total Assets | |
| R18 | Return On Equity | |
| R19 | Profit Margin | |
| Management | ||
| R20 | Inventory to Sales | |
| R21 | Days in Accounts Receivable | |
| R22 | Duration of Trade Payables | |
| R23 | Working Capital Requirement Management | |
| Stepwise Logistic Technique | Lasso Logistic Technique | ||||
|---|---|---|---|---|---|
| Year | 2017 | 2018 | 2017 | 2018 | |
| Selected variables | R5 | R5 | R2 | R4 | |
| R7 | R8 | R5 | R6 | ||
| R14 | R14 | R14 | R8 | ||
| R15 | R15 | R15 | R14 | ||
| R21 | R17 | R17 | R15 | ||
| R21 | R21 | R16 | |||
| R22 | R17 | ||||
| R20 | |||||
| R21 | |||||
| BIC | 132.1 | 123.67 | penalty coefficient | 0.05867105 | 0.0311904 |
| 2017 Two Years Prior to Financial Distress | ||||
|---|---|---|---|---|
| Estimate | Std.Error | Z Value Pr() | ||
| (Intercept) | −2.158 | 4.451 × 10 | −4.847 | 1.25 × 10 *** |
| R5 | 1.752 × 10 | 6.205 × 10 | 2.823 | 0.004754 ** |
| R7 | 1.015 | 3.083 × 10 | 3.291 | 0.000998 *** |
| R14 | 7.959 × 10 | 2.155 × 10 | 3.693 | 0.000221 *** |
| R15 | −2.774 × 10 | 6.603 | −4.202 | −2.65 × 10 *** |
| R21 | 4.957 × 10 | 1.305 × 10 | 3.798 | 0.000146 *** |
| 2018 One Year Prior to Financial Distress | ||||
|---|---|---|---|---|
| Estimate | Std.Error | Z Value Pr() | ||
| (Intercept) | −2.393 | 5.218 × 10 | −4.587 | 4.50 × 10 *** |
| R5 | 1.907 × 10 | 6.895 × 10 | 2.766 | 0.00568 ** |
| R8 | 3.291 × 10 | 1.783 × 10 | 1.846 | 0.06491 |
| R14 | 6.691 × 10 | 2.114 × 10 | 3.165 | 0.00155 ** |
| R15 | −3.578 × 10 | 8.646 | −4.138 | −3.50 × 10 *** |
| R17 | −3.296 × 10 | 1.281 | −2.572 | 0.01010 * |
| R21 | 7.490 × 10 | 1.792 × 10 | 4.179 | 2.92 × 10 *** |
| 2017 Two Years Prior to Financial Distress | 2018 One Year Prior to Financial Distress | ||
|---|---|---|---|
| Ratios | Coefficients | Ratios | Coefficients |
| R2 | 0.0574 | R4 | 0.0937 |
| R5 | −0.0010 | R6 | −0.9277 |
| R14 | 10.0928 | R8 | 0.0029 |
| R15 | −7.9388 | R14 | 34.9176 |
| R17 | -0.4502 | R15 | −6.5013 |
| R21 | 0.0010 | R16 | −0.0700 |
| R22 | 0.0003 | R17 | −1.2586 |
| R20 | −0.1070 | ||
| R21 | 0.0016 | ||
| Stepwise Logistic Regression | Lasso Logistic Regression | ||||
|---|---|---|---|---|---|
| 2017 two years prior to financial distress | |||||
| 0 | 1 | 0 | 1 | ||
| 0 | 28 (93.33%) a | 2 (6.67%) b | 0 | 23 (76.67%) | 7 (23.33%) |
| 1 | 2 (6.67%) c | 28(93.33%) d | 1 | 5 (16.67%) | 25 (83.33%) |
| Overall accuracy | 93.33% | Overall accuracy | 80.00% | ||
| 2018 one year prior to financial distress | |||||
| 0 | 1 | 0 | 1 | ||
| 0 | 28 (93.33%) | 2 (6.67%) | 0 | 26 (86.67%) | 4 (13.33%) |
| 1 | 1 (3.33%) | 29 (96.67%) | 1 | 4 (13.33%) | 26 (86.67%) |
| Overall accuracy | 95.00% | Overall accuracy | 86.67% | ||
| Stepwise Logistic Regression | Lasso Logistic Regression | ||||
|---|---|---|---|---|---|
| 2017 two years prior to financial distress | |||||
| 0 | 1 | 0 | 1 | ||
| 0 | 23 (76.67%) a | 7 (23.33%) b | 0 | 22 (73.33%) | 8 (26.67%) |
| 1 | 4 (13.33%) c | 26 (86.67%) d | 1 | 2 (6.67%) | 28 (93.33%) |
| Overall accuracy | 81.67% | Overall accuracy | 83.33% | ||
| 2018 one year prior to financial distress | |||||
| 0 | 1 | 0 | 1 | ||
| 0 | 26 (86.67%) | 4 (13.33%) | 0 | 26 (86.67%) | 4 (13.33%) |
| 1 | 3 (10.00%) | 27 (90.00%) | 1 | 4 (13.33%) | 26 (86.67%) |
| Overall accuracy | 88.33% | Overall accuracy | 86.67% | ||
| Stepwise Selection | ||||
|---|---|---|---|---|
| LRSt 2017 | LRSt 2018 | NNSt 2017 | NNSt 2018 | |
| Accuracy | 93.33% | 95.00% | 81.67% | 88.33% |
| Sensitivity | 93.33% | 96.67% | 86.67% | 90.00% |
| Specificity | 93.33% | 93.33% | 76.67% | 86.67% |
| Precision | 93.33% | 93.50% | 78.80% | 87.10% |
| F1-score | 93.33% | 95.10% | 82.50% | 88.50% |
| Type I error | 6.67% | 3.33% | 13.33% | 10.00% |
| Type II error | 6.67% | 6.67% | 23.33% | 13.33% |
| AUC | 0.936 | 0.959 | 0.833 | 0.880 |
| Lasso Selection | ||||
|---|---|---|---|---|
| LRL 2017 | LRL 2018 | NNL 2017 | NNL 2018 | |
| Accuracy | 80.00% | 86.67% | 83.33% | 86.67% |
| Sensitivity | 83.33% | 86.67% | 93.33% | 86.67% |
| Specificity | 76.67% | 86.67% | 73.33% | 86.67% |
| Precision | 78.10% | 86.67% | 77.80% | 86.67% |
| F1-score | 80.60% | 86.67% | 84.80% | 86.67% |
| Type I error | 16.67% | 13.33% | 6.67% | 13.33% |
| Type II error | 23.33% | 13.33% | 26.67% | 13.33% |
| AUC | 0.848 | 0.849 | 0.944 | 0.833 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zizi, Y.; Jamali-Alaoui, A.; El Goumi, B.; Oudgou, M.; El Moudden, A. An Optimal Model of Financial Distress Prediction: A Comparative Study between Neural Networks and Logistic Regression. Risks 2021, 9, 200. https://doi.org/10.3390/risks9110200
Zizi Y, Jamali-Alaoui A, El Goumi B, Oudgou M, El Moudden A. An Optimal Model of Financial Distress Prediction: A Comparative Study between Neural Networks and Logistic Regression. Risks. 2021; 9(11):200. https://doi.org/10.3390/risks9110200
Chicago/Turabian StyleZizi, Youssef, Amine Jamali-Alaoui, Badreddine El Goumi, Mohamed Oudgou, and Abdeslam El Moudden. 2021. "An Optimal Model of Financial Distress Prediction: A Comparative Study between Neural Networks and Logistic Regression" Risks 9, no. 11: 200. https://doi.org/10.3390/risks9110200
APA StyleZizi, Y., Jamali-Alaoui, A., El Goumi, B., Oudgou, M., & El Moudden, A. (2021). An Optimal Model of Financial Distress Prediction: A Comparative Study between Neural Networks and Logistic Regression. Risks, 9(11), 200. https://doi.org/10.3390/risks9110200







