In this section, we present papers that are based on the assumption of a parametric evolution of the claims data across development years:
Three articles marked with ▸ are mainly based on the use of state space models and the Kalman filter learning theory, and thus are presented in detail, while the models of the other two articles marked with ⊳ are treated in a more brief form, as state space models are not the focus of their methodologies.
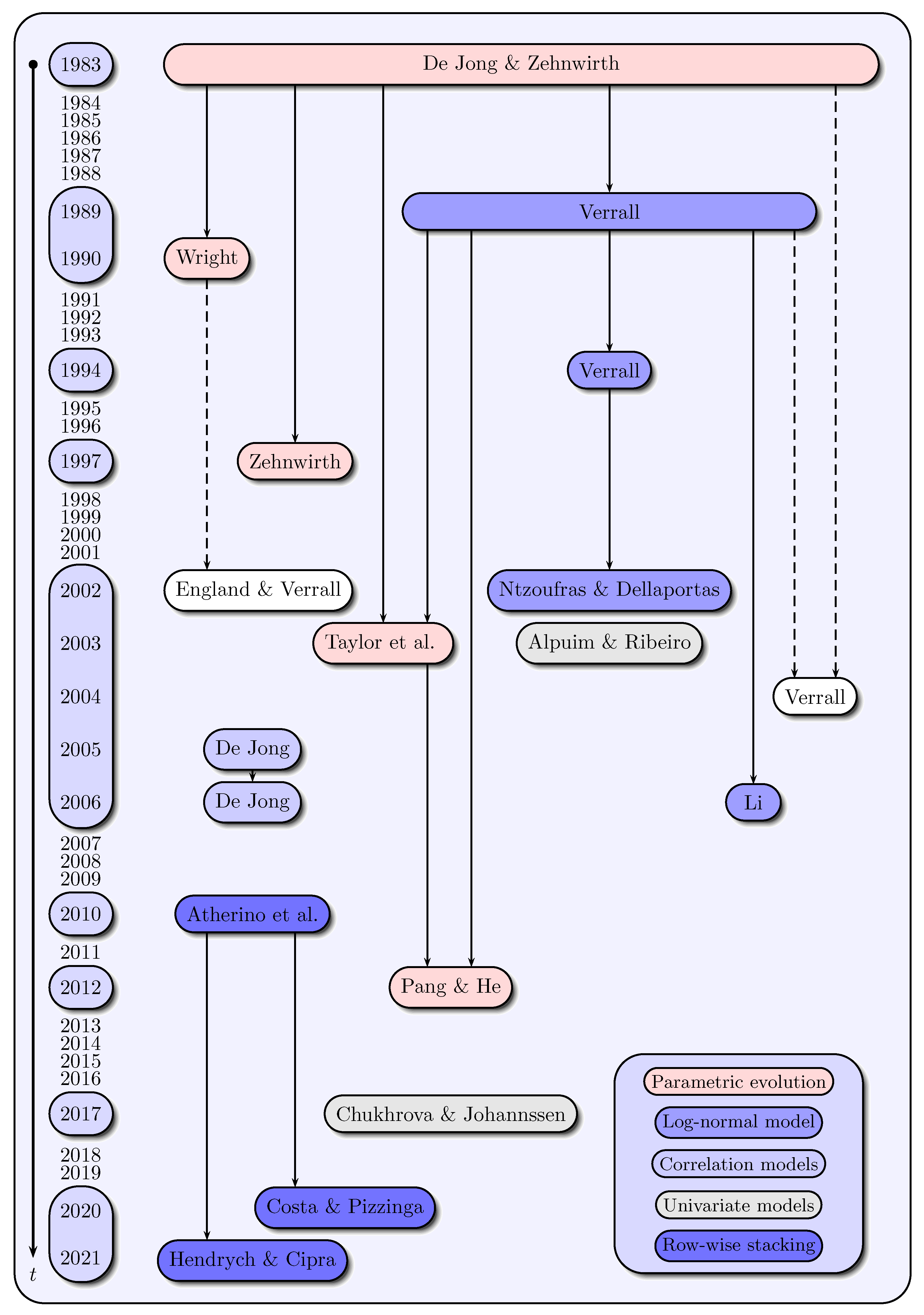
2.1. Claims Reserving, State Space Models and the Kalman Filter
De Jong and Zehnwirth (
1983) laid the foundation for the use of state space models and the Kalman filter in stochastic claims reserving with their article
“Claims Reserving, State-Space Models and the Kalman Filter”. The proposed state space model is constructed for the payment stream of the incremental payments and presumes known, time-varying system matrices.
Modeling the payment stream of incremental payments
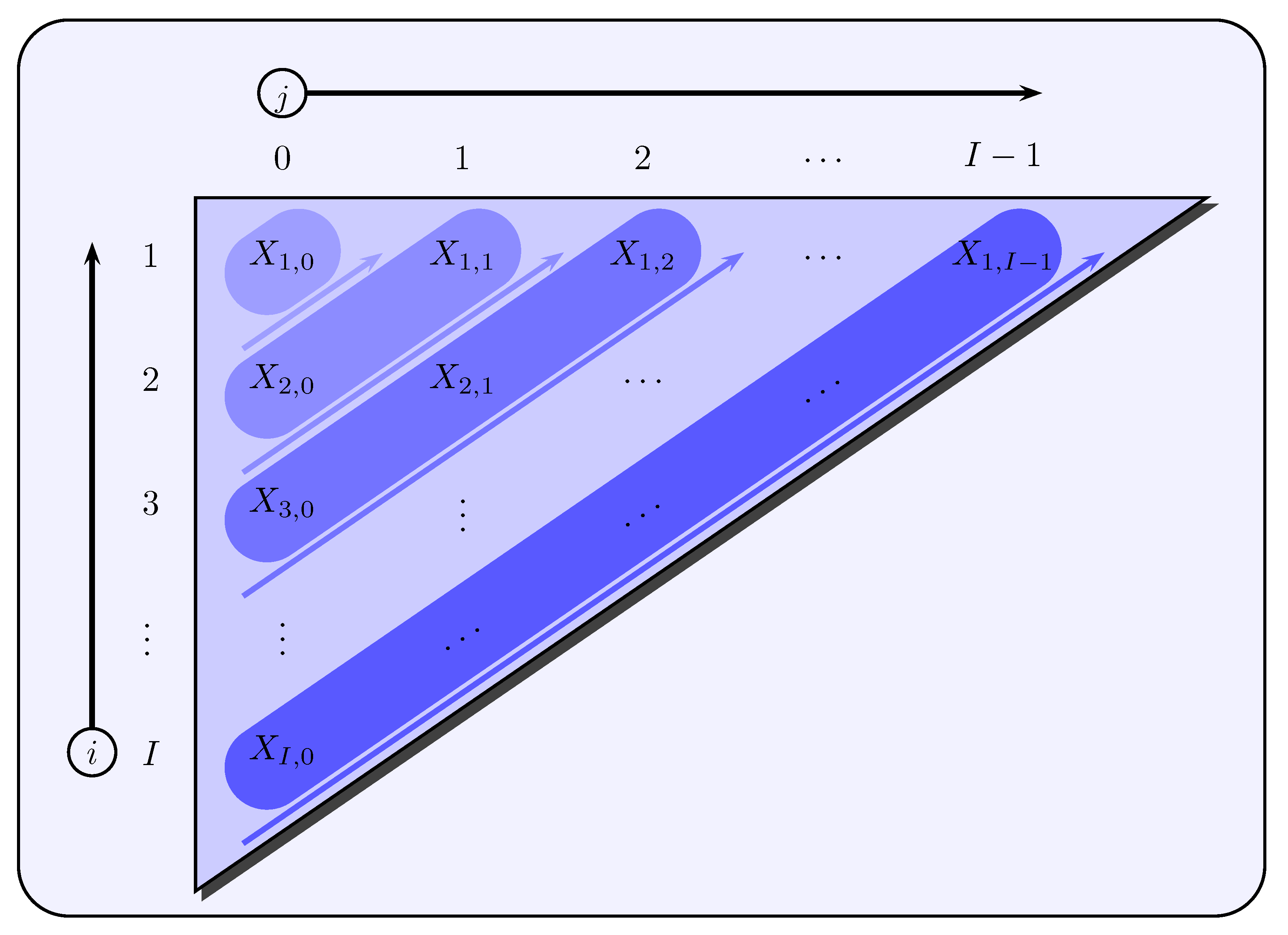
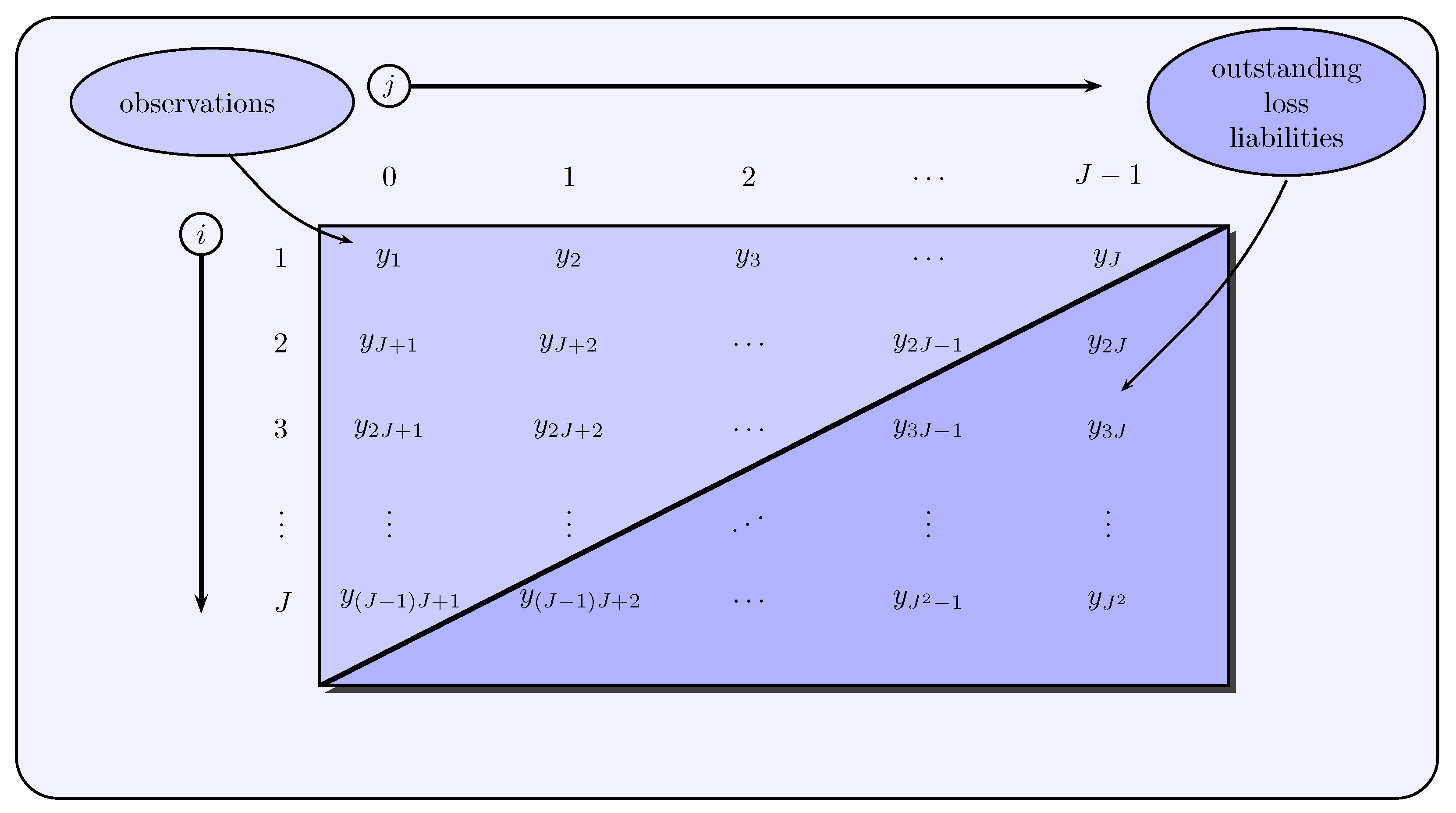
The modeling is based on claims development triangles in which incremental payments
are given for accident years
and development years
. The payment stream of incremental payments is modeled with increasing development year
and decreasing accident year
for a fixed calendar year
via
see also
Figure 2. Here, the quantity
is generally the expected claim payment to be made in accident year
i and development year
j of the
t-th calendar year, and
is a noise term with
.
De Jong and Zehnwirth (
1983) propose an optional modification of (
1) by including additional information such as the volume of business transacted in each accident year and the inflation factor for each calendar year. To this end, let
denote an appropriate index for the volume of business transacted in accident year
i and
denote an appropriate price index for payments in the
t-th calendar year. Using both these quantities, (
1) can be extended to
where
is the expected value of the inflation-adjusted and volume-weighted incremental payments in accident year
i and development year
j of calendar year
t.
Development of an appropriate state space representation
The modeling of the payment stream via (
1) and (
2) is promising with respect to the construction of an appropriate observation and state equation of a state space model, respectively. The following discussion in this regard is based on (
1), but can be applied to (
2) with minor modifications. In the first step of modeling the observation equation, (
1) is transferred into a vector representation in such a way that
represents the vector of observations
of the
t-th calendar year,
forms the vector of expected claims payments
, and
is the vector of noise terms
with
. Thus, the incremental payments made in calendar year
t can be specified via
or briefly as
. In the second step, the vector
is to be modeled in such a way that it is obtained by the product of a system matrix
and a state vector
. For this purpose,
De Jong and Zehnwirth (
1983) take
for a given accident year
i as a function depending on the development year
j and thus construct for each accident year a
distributed lag model of the form
where
are known functions in
j and
are unknown parameters depending on the respective accident year
i.
De Jong and Zehnwirth (
1983) justified the approach (
4) by an overall smooth evolution of
characterized by a firstly increasing and then decreasing behavior in
j for a given accident year
i. A variation of (
4) for
is the so-called
Hoerl curve
which
De Jong and Zehnwirth (
1983) use in their empirical application example. In addition, (
4) can be easily transferred into vector notation by using
as follows:
Substituting (
7) into (
3) then gives
or in a more compact form
with
and
for all
. Thus, given
,
, the system matrix
is a known time-varying diagonal matrix, and the state vector
contains unknown parameter vectors
for
. Assuming a Hoerl curve according to (
5), the observation Equation (
9) of the
t-th calendar year results in (due to
):
Subsequently,
De Jong and Zehnwirth (
1983) specify an appropriate state equation, in which they establish a connection between the state vector
of the
t-th calendar year and the state vector
of the
-th calendar year. The basic idea is again to model a smooth evolution, but in a slightly different form than in (
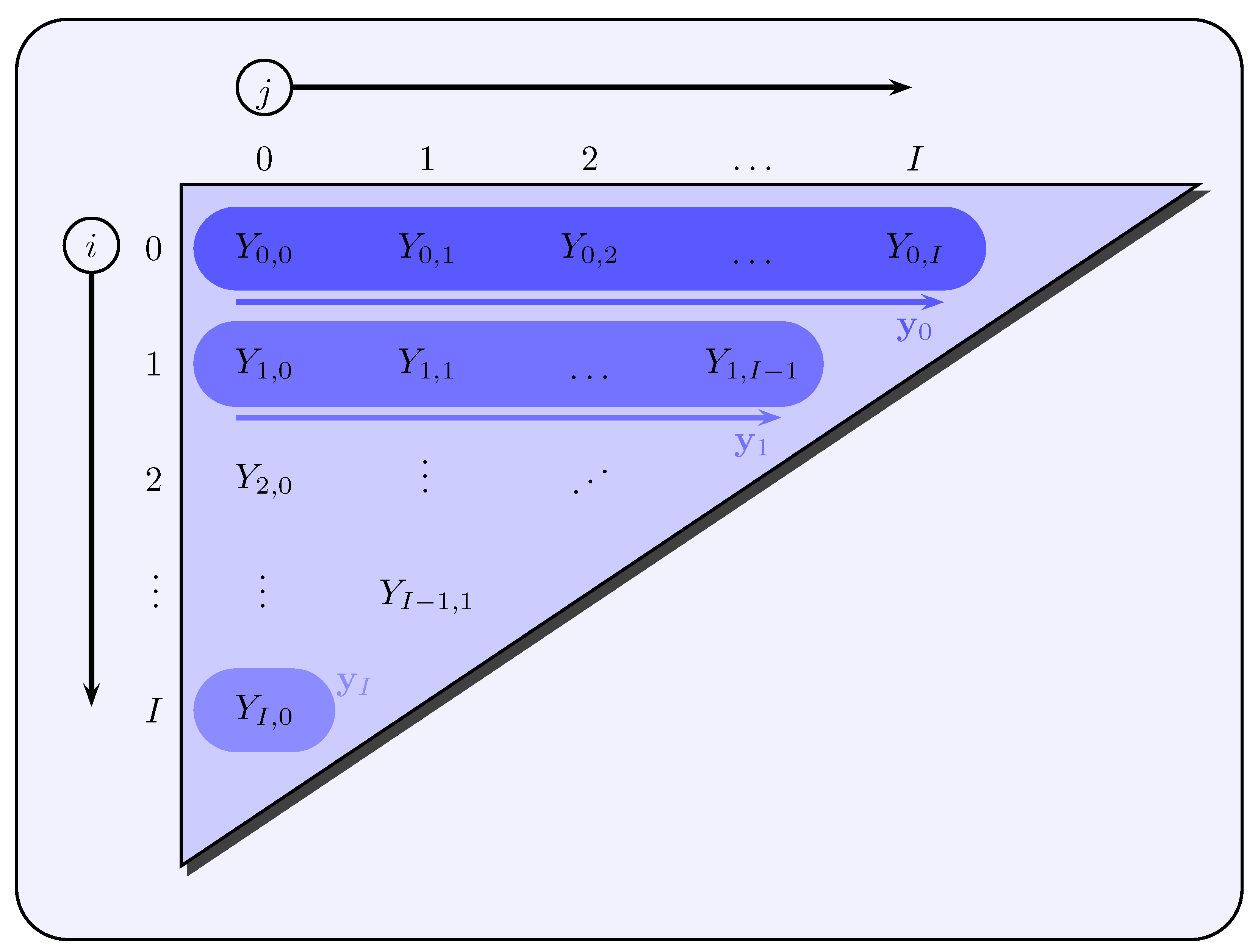
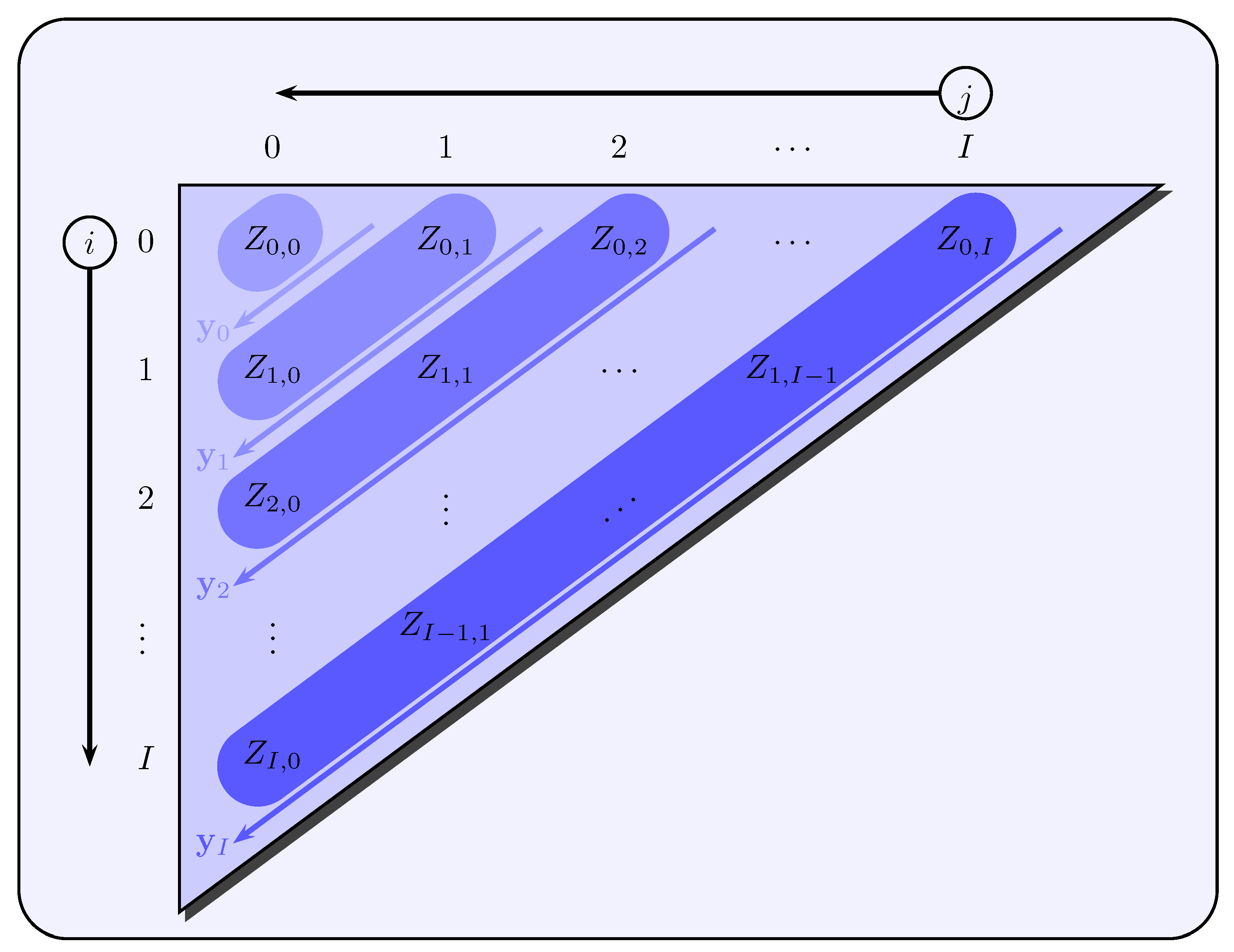
4). The starting point is the sequence
, but with the difference that for a fixed development year
j the accident years
i are varied, whereas before for a fixed calendar year
t the development years
j varied (see
Figure 3).
For a given development year
j,
De Jong and Zehnwirth (
1983) propose modeling
via
with
, where
is a noise term with
. Thus, in contrast to (
4),
is not modeled in a deterministic way but as a random variable. Further, they assume that the conditional expected value on the right-hand side of (
10) is a polynomial in
i of degree
that passes through
. This leads to
with known
for
. Substituting (
7) on both sides into (
11) for
yields
where the (
)-dimensional matrix
and the
p-dimensional vector
are given by
respectively. If both sides of Equation (
12) are multiplied from the left by the inverse
of the matrix
(the existence of the inverse is ensured, see
De Jong and Zehnwirth 1983), one obtains
Transferring (
13) into matrix notation, we obtain
or in a more compact fom
with
and
as well as
for all
. The identity matrices
, zero matrices
and scalar matrices
with
in (
14) are each of dimension
. Note also that the system matrices
and
are known in the state Equation (
15).
A variation of the state Equation (
15) is given for
(i.e., assuming a Hoerl curve as in (
5)) and the parameters
of different accident years
are connected by a random walk
that is,
,
,
. Since we have
, the relation
holds. For this reason,
De Jong and Zehnwirth (
1983) aim to obtain
and thus a state equation in the form of the random walk (
16), i.e., they choose without loss of generality the fixed development year
.
With respect to (
10) and (
13), the use of (
16) implies
for all
. Accordingly, it follows for the system matrix
that it has the value one at positions
and zeros otherwise, while
corresponds to a
t-dimensional unit vector with the value one at position
. The state Equation (
15) thus simplifies to:
If one intends to model the observation and state equations by using (
2) instead of (
1), there are only changes in the observation Equation (
9), while the state Equation (
15) remains unchanged: each row
of the system matrix
has to be multiplied by a weighting factor consisting of volume and inflation indices, i.e., by
.
Forecasting the outstanding loss liabilities
As the system matrices
are assumed to be known for all
, the outstanding loss liabilities for individual and aggregated accident years can be predicted by using
and
in a straightforward way. To this end, all future incremental payments are collected in the vector
All these future observations belong to one of the accident years
, and therefore, they are based on the corresponding state
. Accordingly, the state vector
corresponds to the vector
of the current calendar year
I, which is why the state Equation (
15) is given by
(i.e.,
,
). The system matrix
of the observation equation is obtained on the basis of (
1) similar to that in (
8), i.e., it consists mostly of zero vectors, and the entries
with
are ordered such that they are multiplied by the states
from
of the corresponding accident year
of
from
. Thus, the future observations can be predicted via
(given by (
9)) and
respectively. The variance–covariance matrix of the prediction error
is given by:
Since
,
,
are known at time
, a prediction of the outstanding loss liabilities for individual and aggregated accident years is straightforward. With respect to the aggregated accident years, all components from
are to be added to the total loss reserve, while for individual accident years only those components from
related to the respective accident year
are to be added. An extraction of these components can be carried out via a diagonal matrix
, which has a value of one at the respective positions and otherwise zeros. The variance–covariance matrix belonging to
is thus
However, if the modified payment stream according to (
2) is used, additional uncertainty is induced via the inflation index
of future calendar years
, which is unknown at time
. This is due to the unknown entries
for
instead of the known entries
in the system matrix
.
2.2. A Stochastic Method for Claims Reserving in General Insurance
Wright (
1990) primarily establishes a model for incremental payments that includes a state space approach, where the variation of the parameters is modeled over different accident years. Thus, although the model of
Wright (
1990) is not mainly based on state space models and the Kalman filter theory, it embeds them in a model framework as one component. In the following, therefore, the model for incremental payments and the state space model are presented (for further details, see
Wright 1990).
Construction of the model for claims payments
The modeling is built on development triangles that include incremental payments
in accident years
and development years
. The proposed model is based on the assumption that incremental payments
are composed of the sum of
independent and identically distributed (i.i.d.) payments
(which are stochastically independent of
), that is,
. Thus,
Wright (
1990) uses the
collective risk model and
has a mixture distribution (see, e.g.,
Kaas et al. 2009). The lags
j of individual incremental payments
between the accident year of the claim and the actual payment are modeled as i.i.d. random variables, which is why
with
is defined as the probability of payments regarding claims of accident year
i in a given development year
j. Let the number
of payments for claims of accident year
i in development year
j be Poisson-distributed with parameter
, i.e.,
; then, the incremental payments
follow a mixture Poisson distribution. Following the convolution property of the Poisson distribution, the total number of claims payments
of an accident year
i also follows a Poisson distribution with parameter
where the
for different
j are assumed to be stochastically independent random variables and the parameter
serves as a measure for the
exposure of accident year
i. As for modeling of the probability
,
Wright (
1990) gives two alternatives, the stochastic CL and the Hoerl curve model. While in the first alternative it is assumed that the probabilities
are identical over all accident years
i, the second alternative (preferred by
Wright 1990) provides a modeling via a Hoerl curve of the form
with constants
,
and
to be estimated and
and
as functions depending on
j. Using (
17), the expected value and variance of
are as follows:
In addition to the number
of payments,
Wright (
1990) also models the amount of individual payments
for claims of an accident year
i in the
j-th development year, which, like the
, are also assumed to be stochastically independent for various
j. The first two moments of
are modeled distribution-free with help of
with proper (unknown) constants
,
,
and inflation parameter
. While such a modeling of the expected value with different
and
K provides a variety of possibilities, the modeling of the variance results from the assumption that the coefficient of variation
is time-invariant and corresponds to
. The optional term
in (
19) with
and
as the average annual inflation rate between calendar years
and
k, on the other hand, are used to account for inflation; i.e.,
reflects the inflation factor from the first calendar year to calendar year
. However,
Wright (
1990) proposes using
and therefore assumes a constant inflation rate
.
Considering (
18)–(
20), and using the moments of the mixture Poisson distribution, the expected value and variance of the incremental payments
in
are obtained via
and
where
are stochastically independent for different
j due to the assumptions regarding
and
. Moreover,
Wright (
1990) normalizes the incremental payments
with the help of
with exposure defined by
By using (
17), (
21), (
23), (
24), the expected value
of the normalized incremental payments
can be stated as follows:
with
Considering (
22), (
23), (
25), the variance of
is
with
Assuming that
and
are known, one obtains a
generalized linear model of the form
with the exponential response function
, linear predictor
consisting of
and noise term
with
where the parameter estimators
and variance–covariance matrices
can be determined for all
i using the Fisher scoring algorithm such that
is approximately satisfied. However, since
and
are usually unknown,
Wright (
1990) proposes an iterative approach using parameter initializations to determine initial values for
and
. Considering this approach, all accident years are run sequentially and the results of all accident years are subsequently used to obtain new estimates of the parameters for the next run.
Modeling the parameter variation via a state space model
To increase the reliability of the estimators
,
Wright (
1990) models the variation in the parameters
for different accident years
i via
with
By defining
with the help of
and by using (
26), (
27) can be written as
with
where
and
hold for all
. Thus, Equation (
28) forms the state equation of a state space model. Considering the estimators
as observations
, the associated observation equation can be obtained via
with
and
,
and
for all
. Accordingly, a complete state space model with
and
is specified via Equations (
28) and (
29).
2.4. Loss Reserving: Past, Present and Future
Taylor et al. (
2003) give a classification scheme for claims reserving methods whose higher-level criteria make a division between static and dynamic methods. In the framework of this taxonomic classification and especially with respect to the dynamic methods, they discuss a generalized Kalman filter, which allows for non-linearities in the observation equation and noise terms following a distribution of the Exponential Dispersion Family (EDF). They present two modeling approaches based on different types of claims data and state space representations constructed specifically for these data.
Accident year-based state space modeling
In the first modeling approach, an accident year-based state space representation is constructed, which is based on Payments Per Claim Incurred (PPCI) of a workers’ compensation insurance policy as claims data. The PPCI of an accident year in the development year are denoted by and belong to the ()-th calendar year with .
The state space model considered by
Taylor et al. (
2003) is based on a linear state equation of the form
with five-dimensional random vectors
, transition matrix
,
and
for
, while the observation equation
with (
)-dimensional random vectors
, system matrix
,
and
is based on a generalized linear model with link function
h (i.e., response function
) and linear predictor
for all
. Moreover,
holds for all
, the initial state
is uncorrelated with
and
for all
and
is assumed to be EDF-distributed for all
. Thus, any strictly monotonic and differentiable link function
h (such as a logarithm function) can be used to link the EDF-distributed observations
and the systematic component
. The resulting recursive equations
Taylor et al. (
2003) refer to as the EDF filter, which include the Kalman filter as a special case, namely for the identity function as link function and normally distributed noise terms
. The observation vector
in (
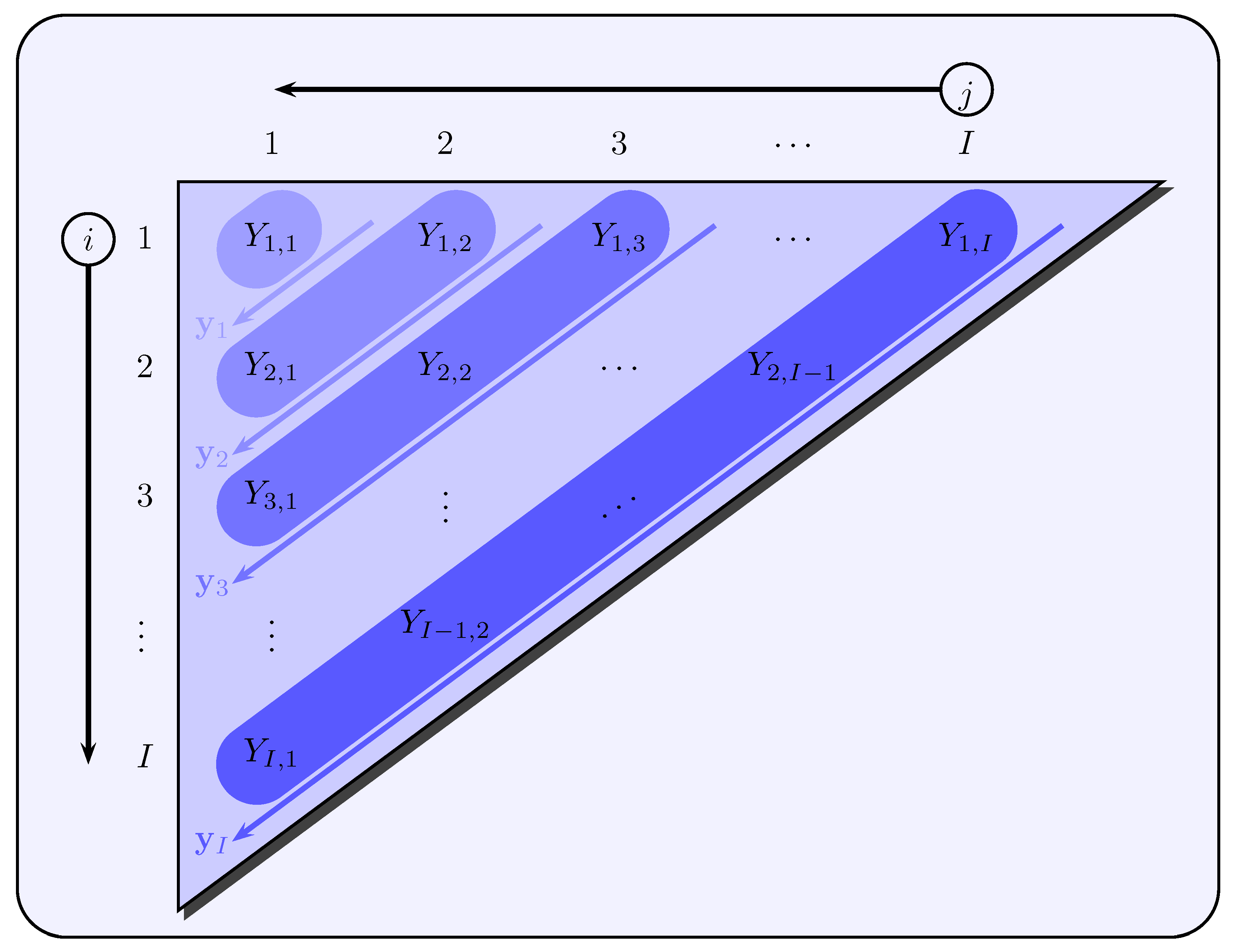
32) includes all PPCIs of an accident year
of the upper claims development triangle (see
Figure 4).
Taylor et al. (
2003) propose a logarithm function as a link function, the noise terms
are assumed to be gamma-distributed and the
-th row of the linear predictor
for an accident year
is given by
with respect to the development year
. Here,
denotes the
Kronecker delta,
which can be used to model the peak in development year
. Thus, the observation Equation (
32) of accident year
can be stated as follows:
On the other hand,
Taylor et al. (
2003) do not provide any information on the concrete form of the state Equation (
31).
Taylor et al. (
2003) model the evolution of the PPCI over the development years according to (
33) in a similar way to
De Jong and Zehnwirth (
1983),
Wright (
1990) and
Zehnwirth (
1997), who specify the evolution of incremental payments over the development years with the help of a Hoerl curve.
Taylor et al. (
2003) apply this approach to the PPCI, as their evolution over the development years is similar to that of incremental payments: They reach their peak in development year
and then drop relatively quickly to zero. This evolution of the PPCI is also the justification of
Taylor et al. (
2003) for the choice of the logarithm function as a link function and the assumption of a gamma distribution for the measurement noise.
Calendar year-based state space modeling
For the second modeling approach,
Taylor et al. (
2003) use a data set from
Taylor (
2000) that consists of motor vehicle bodily injury claim closure rates. Here, rather than collecting the observations from each accident year, they stack the observations from each calendar year into observation vectors. This is due to the fact that claim closure rates are relatively flat across development years, but are subject to calendar year effects.
The state space model proposed by
Taylor et al. (
2003) provides a linear state equation and an observation equation in the form of a generalized linear model, but differs from the first approach by the time index (calendar years
t instead of accident years
i) and by the matrix dimensions. They consider the following state space model consisting of the state equation
with (
)-dimensional random vectors
,
, a (
)-dimensional random vector
and transition matrix
for
, and the observation equation of the
t-th calendar year
with (
)-dimensional random vectors
,
, and
-dimensional system matrix
for
, where the assumptions concerning the noise terms correspond to those of the first approach (transferred to calendar years).
Taylor et al. (
2003) choose the identity function as a link function and the measurement noise is assumed to be normally distributed, which is why one obtains an ordinary linear observation equation and the usual linear Kalman filter can be used. This choice is motivated by the sufficiently high number of claims closures in the underlying claims data, and the assumption of an approximate normal distribution is justified by the central limit theorem, although the assumption of a discrete probability distribution such as the binomial distribution would be more appropriate. As for the development of the expected claim closure rate
with respect to the claims of an accident year
over the development years
,
Taylor et al. (
2003) assume
with
as effect of the
t-th calendar year and Kronecker Delta
. The observation vector
of the
t-th calendar year with
contains all
claim closure rates
of the respective calendar year
(see
Figure 5), which is why the
-dimensional state vector can be stated as
with
for
.
While the state vector
in the first modeling approach only contains the parameters of the
i-th accident year, the state vector
contains all parameters up to the
t-th accident year plus the corresponding calendar year effect. This is due to the fact that the observations of the
t-th calendar year pass through all accident years
. The observation Equation (
35) is thus given by
with
according to (
37) and
according to (
38) for all
as well as three-dimensional zero vectors
. The state Equation (
34) is then
where
and
in
are identity and zero matrices of dimensions
, respectively,
in
are three-dimensional zero vectors and
,
are given as follows:
Thus, the state equation involves a dynamic estimation of the parameters
and
via
for
. Finally,
Table 2 gives an overview of the dimensions of vectors and matrices in the state space models of
Taylor et al. (
2003).
2.5. The Application of State Space Model in Outstanding Claims Reserve
Pang and He (
2012) largely adopt the second modeling approach from
Taylor et al. (
2003), but without integrating calendar year effects. They extend the state equation by including a further lag of the state vector. Accordingly, the state space model they consider is given by
with
,
,
for all
.
Table 3 gives an overview of the dimensions of vectors and matrices in the state space model of
Pang and He (
2012).
The observation vector
contains all observations
of the
t-th calendar year, i.e., all
with
. However, the nature of the claims data is not obvious and the authors refer to it only as “times of compensation”. Therefore, in view of the magnitude of the observations and their modeling, claims data are assumed to be incremental payments. The expected incremental payments of an accident year
are assumed to have a parametric evolution over the development years
similar to (
33) via
with Kronecker Delta
. Thus, the observation Equation (
39) of the
t-th calendar year (
) results in a similar form as achieved within the second modeling approach of
Taylor et al. (
2003),
with
for all
.
Pang and He (
2012) do not give the general representation of the state equation according to (
40), but the reduced form
which solely contains the last four rows of (
40) that are of interest. For the remaining
-dimensional parameter matrices, they assume scalar matrices
and
for all
, which is why the state Equation (
42) is given by:
If, on the other hand, one intends to express the state equation in the form (
40), the upper
-dimensional part of
corresponds to an identity matrix, while the last four rows in the last four columns of
form the scalar matrix
and otherwise contain zeros. The parameter matrix
has only zeros in the
-dimensional upper part and also in the last four rows except for the last four columns, which correspond to the
-dimensional scalar matrix
. The noise vector
is equal to a zero vector in the first
rows and to the vector
in the remaining rows.