An Expectation-Maximization Algorithm for the Exponential-Generalized Inverse Gaussian Regression Model with Varying Dispersion and Shape for Modelling the Aggregate Claim Amount
Abstract
1. Introduction
2. The Exponential–Generalized Inverse Gaussian Regression Model with Varying Dispersion and Shape
3. The EM Algorithm
- E-Step: Given the current estimates taken from the rth iteration, calculate for all the pseudo-valuesandwhere , and .In this study, Equations (18)–(20) are evaluated based on the function Egig1 within the R package ghyp, which was recently created by Breymann et al. (2020).
- M-Step: Using the pseudo-values , and from the E-Step and the Newton–Raphson algorithm three times find the maximum global point of the function; i.e., obtain the updated estimates , and .Firstly, differentiate the function with respect to :andfor and .Then, the iterative procedure for the Newton–Raphson algorithm for is as follows:Secondly, differentiate the function with respect to :for and Then, the Newton–Raphson iterative algorithm for is as follows:for andFinally, differentiate the function with respect to :andfor and .Then, the iterative procedure for the Newton–Raphson algorithm for is as follows:Note that the expressions for and , and , and and which are involved in the M-step of the algorithm are given in Appendix A.
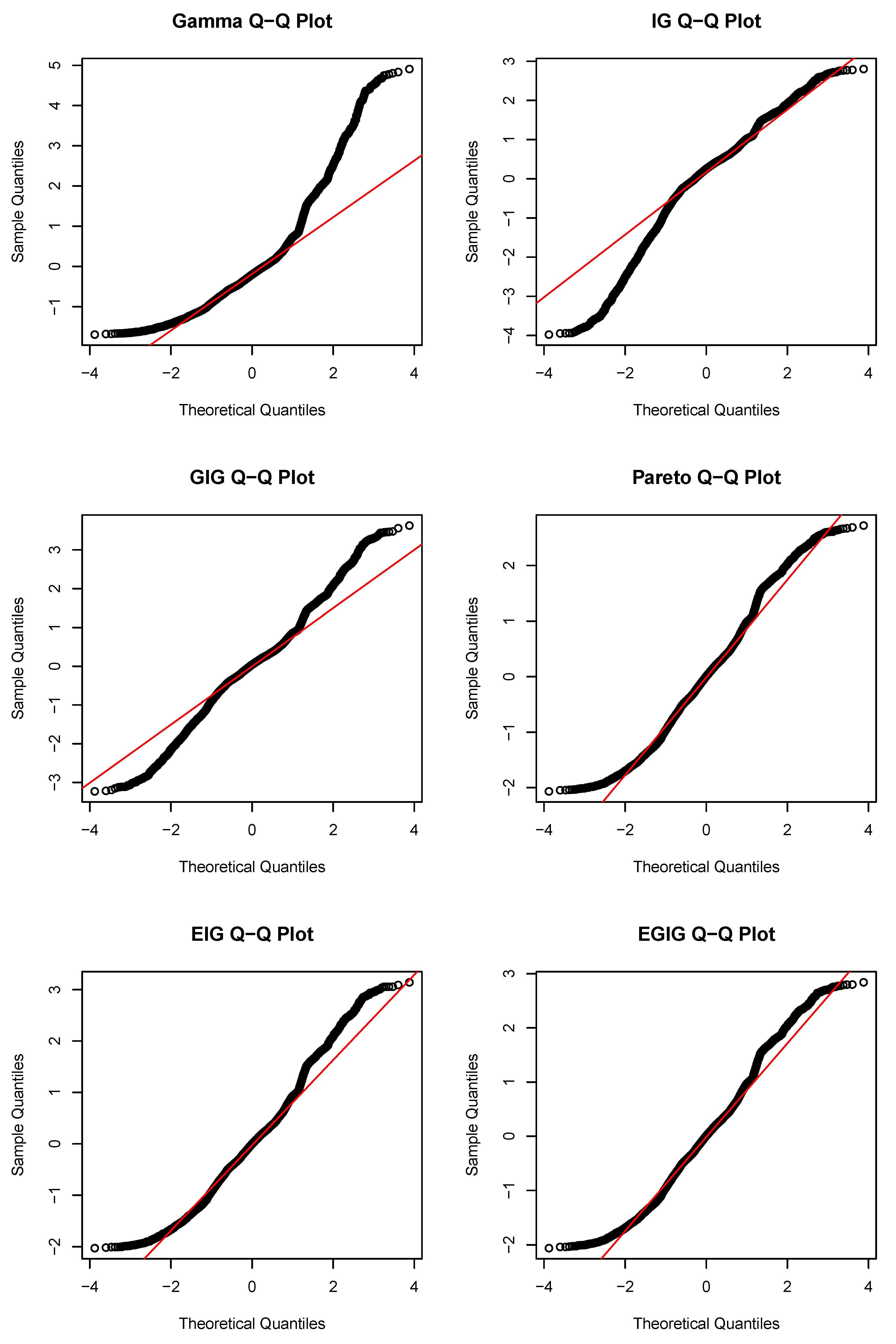
4. Empirical Analysis
- The variable YC consisted of three categories of policyholders: those who had been with the company for “less than 4 years” (C1), “between 4 to 8 years” (C2) and “more than 8 years” (C3).
- The variable AC consisted of three categories of cars: those with an age “between 0 to 7 years” (C1), “between 7 to 14 years” (C2) and “greater than 14 years” (C3).
- The variable HP consisted of three categories of cars: those with a HP of “0-1400 cc” (C1), “1400–1800 cc” (C2) and “greater than 1800 cc” (C3).
- Gamma (GA):where and .
- Inverse Gaussian (IG):where and .
- Pareto:where , and exists only if .
- Exponential–Inverse Gaussian (EIG):where and .
- GIG:where , and .
- EGIG: Defined by Equation (4).
5. Computational Aspects
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EM | Expectation-Maximization |
| EGIG | Exponential–Generalized Inverse Gaussian |
| GIG | Generalized Inverse Gaussian |
| GB2 | Generalized Beta second kind |
| GG | Generalized Gamma |
| DPLN | Double-Pareto-Lognormal |
| ELN | Exponential-Lognormal |
| EIG | Exponential-Inverse Gaussian |
| GLMGA | Generalized Log-Moyal Gamma distribution |
| MTPL | Motor third party liability |
Appendix A
References
- Abramowitz, Milton, and Irene A. Stegun. 1965. Handbook of mathematical functions with formulas, graphs, and mathematical table. In US Department of Commerce; National Bureau of Standards Applied Mathematics Series 55; Washington: U. S. Government Printing Office. [Google Scholar]
- Ahn, Soohan, Joseph H. T. Kim, and Vaidyanathan Ramaswami. 2012. A new class of models for heavy tailed distributions in finance and insurance risk. Insurance: Mathematics and Economics 51: 43–52. [Google Scholar] [CrossRef]
- Beirlant, Jan, V. Derveaux, Anna Maria De Meyer, M. J. Goovaerts, E. Labie, and B. Maenhoudt. 1992. Statistical risk evaluation applied to (belgian) car insurance. Insurance: Mathematics and Economics 10: 289–302. [Google Scholar] [CrossRef]
- Bhati, Deepesh, and Sreenivasan Ravi. 2018. On generalized log-moyal distribution: A new heavy tailed size distribution. Insurance: Mathematics and Economics 79: 247–59. [Google Scholar] [CrossRef]
- Bladt, Mogens, and Leonardo Rojas-Nandayapa. 2018. Fitting phase–type scale mixtures to heavy–tailed data and distributions. Extremes 21: 285–313. [Google Scholar] [CrossRef]
- Breymann, Wolfgang, David Luthi, and Marc Weibel. 2020. ghyp: A Package on Generalized Hyperbolic Distributions. Manual for R Package ghyp. Available online: http://ftp.uni-bayreuth.de/math/statlib/R/CRAN/doc/vignettes/ghyp/Generalized_Hyperbolic_Distribution.pdf (accessed on 8 January 2021).
- Burnham, Kenneth P., and David R. Anderson. 2002. Model Selection and Multimodel Inference. Berlin: Springer. [Google Scholar]
- Calderín-Ojeda, Enrique, Kevin Fergusson, and Xueyuan Wu. 2017. An EM algorithm for double-pareto-lognormal generalized linear model applied to heavy-tailed insurance claims. Risks 5: 60. [Google Scholar] [CrossRef]
- Dempster, Arthur P., Nan M. Laird, and Donald B. Rubin. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 39: 1–22. [Google Scholar]
- Dunn, Peter K., and Gordon K. Smyth. 1996. Randomized quantile residuals. Journal of Computational and Graphical Statistics 5: 236–44. [Google Scholar]
- Frangos, Nikolaos, and Dimitris Karlis. 2004. Modelling losses using an exponential-inverse gaussian distribution. Insurance: Mathematics and Economics 35: 53–67. [Google Scholar] [CrossRef]
- Frees, Edward W., Richard A. Derrig, and Glenn Meyers. 2014. Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press, vol. 1. [Google Scholar]
- Frees, Edward W., Gee Lee, and Lu Yang. 2016. Multivariate frequency-severity regression models in insurance. Risks 1: 4. [Google Scholar] [CrossRef]
- Frees, Edward W., and Emiliano A. Valdez. 2008. Hierarchical insurance claims modeling. Journal of the American Statistical Association 103: 1457–69. [Google Scholar] [CrossRef]
- Gallardo, Diego I., Emilio Gómez-Déniz, Jeremias Leão, and Héctor W. Gómez. 2020. Estimation and diagnostic tools in reparameterized slashed rayleigh regression model. an application to chemical data. Chemometrics and Intelligent Laboratory Systems 207: 104189. [Google Scholar] [CrossRef]
- Gilbert, P., and R. Varadhan. 2016. Numderiv: Accurate Numerical Derivatives [Software]. Available online: https://cran.r-project.org/web/packages/numDeriv/index.html (accessed on 8 January 2021).
- Gómez, Yolanda M., Diego I. Gallardo, and Mário de Castro. 2019. A regression Model for Positive Data Based on the Slashed Half-Normal Distribution. REVSTAT. Available online: https://www.ine.pt/revstat/pdf/Aregressionmodelforpositivedata.pdf (accessed on 8 January 2021).
- Gómez, Yolanda M., Diego I. Gallardo, Jeremias Leão, and Héctor W. Gómez. 2020. Extended exponential regression model: Diagnostics and application to mineral data. Symmetry 12: 2042. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, Enrique Calderín-Ojeda, and José María Sarabia. 2013. Gamma-generalized inverse gaussian class of distributions with applications. Communications in Statistics-Theory and Methods 42: 919–33. [Google Scholar] [CrossRef]
- Hassan Zadeh, Amin, and David A. Stanford. 2016. Bayesian and bühlmann credibility for phase-type distributions with a univariate risk parameter. Scandinavian Actuarial Journal 2016: 338–55. [Google Scholar] [CrossRef]
- Hürlimann, Werner. 2014. Pareto type distributions and excess-of-loss reinsurance. International Journal of Research and Reviews in Applied Sciences 18: 1. [Google Scholar]
- Jeong, Himchan. 2020. Testing for random effects in compound risk models via Bregman divergence. ASTIN Bulletin: The Journal of the IAA 50: 777–98. [Google Scholar] [CrossRef]
- Jeong, Himchan, and Emiliano A. Valdez. 2020. Predictive compound risk models with dependence. Insurance: Mathematics and Economics 94: 182–95. [Google Scholar]
- Johnson, Norman L., Samuel Kotz, and Narayanaswamy Balakrishnan. 1994. Continuous Univariate Distributions. Hoboken: John Wiley & Sons, Ltd. [Google Scholar]
- Jorgensen, Bent. 1982. Statistical Properties of the Generalized Inverse Gaussian Distribution. Berlin and Heidelberg: Springer Science & Business Media, vol. 9. [Google Scholar]
- Kleiber, Christian, and Samuel Kotz. 2003. Statistical Size Distributions in Economics and Actuarial Sciences. Hoboken: John Wiley & Sons. [Google Scholar]
- Laudagé, Christian, Sascha Desmettre, and Jörg Wenzel. 2019. Severity modeling of extreme insurance claims for tariffication. Insurance: Mathematics and Economics 88: 77–92. [Google Scholar] [CrossRef]
- Li, Zhengxiao, Jan Beirlant, and Shengwang Meng. 2020. Generalizing the Log-Moyal Distribution and Regression Models for Heavy-Tailed Loss Data. ASTIN Bulletin, 1–43. Available online: https://www.cambridge.org/core/journals/astin-bulletin-journal-of-the-iaa/article/abs/generalizing-the-logmoyal-distribution-and-regression-models-for-heavytailed-loss-data/404C21655A7BDBC001CE9C683F8CA555 (accessed on 8 January 2021). [CrossRef]
- Louis, Thomas A. 1982. Finding the observed information matrix when using the em algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 44: 226–33. [Google Scholar]
- McLachlan, Geoffrey J., and Thriyambakam Krishnan. 2007. The EM Algorithm and Extensions. Hoboken: John Wiley & Sons, vol. 382. [Google Scholar]
- Raftery, Adrian E. 1995. Bayesian model selection in social research. Sociological Methodology 25: 111–63. [Google Scholar] [CrossRef]
- Ramirez-Cobo, Pepa, Rosa E. Lillo, Simon Wilson, and Michael P. Wiper. 2010. Bayesian inference for double pareto lognormal queues. The Annals of Applied Statistics 4: 1533–57. [Google Scholar] [CrossRef]
- Rigby, Robert A., Dimitrios M. Stasinopoulos, and Calliope Akantziliotou. 2008. A framework for modelling overdispersed count data, including the poisson-shifted generalized inverse gaussian distribution. Computational Statistics & Data Analysis 53: 381–93. [Google Scholar]
- Rosenberg, Marjorie A., Edward W. Frees, Jiafeng Sun, Paul H. Johnson, Jr., and Jim Robinson. 2007. Predictive modeling with longitudinal data: A case study of wisconsin nursing homes. North American Actuarial Journal 11: 54–69. [Google Scholar] [CrossRef]
- Santos-Neto, Manoel, Francisco José A. Cysneiros, Víctor Leiva, and Michelli Barros. 2016. Reparameterized birnbaum-saunders regression models with varying precision. Electronic Journal of Statistics 10: 2825–55. [Google Scholar] [CrossRef]
- Shi, Peng, Xiaoping Feng, and Anastasia Ivantsova. 2015. Dependent frequency–severity modeling of insurance claims. Insurance: Mathematics and Economics 64: 417–28. [Google Scholar] [CrossRef]
- Stasinopoulos, Mikis, Bob Rigby, and Calliope Akantziliotou. 2008. Instructions on How to Use the Gamlss Package in R Second Edition. Available online: https://www.gamlss.com/wp-content/uploads/2013/01/gamlss-manual.pdf (accessed on 8 January 2021).
- Tzougas, George. 2020. EM estimation for the poisson-inverse gamma regression model with varying dispersion: An application to insurance ratemaking. Risks 8: 97. [Google Scholar] [CrossRef]
- Tzougas, George, and Dimitris Karlis. 2020. An EM algorithm for fitting a new class of mixed exponential regression models with varying dispersion. ASTIN Bulletin: The Journal of the IAA 50: 555–83. [Google Scholar] [CrossRef]
- Tzougas, George, Woo Hee Yik, and Muhammad Waqar Mustaqeem. 2020. Insurance ratemaking using the exponential-lognormal regression model. Annals of Actuarial Science 14: 42–71. [Google Scholar] [CrossRef]
- Wang, Yinzhi, Ingrid Hobæk Haff, and Arne Huseby. 2020. Modelling extreme claims via composite models and threshold selection methods. Insurance: Mathematics and Economics 91: 257–68. [Google Scholar] [CrossRef]
- Yang, Xipei, Edward W. Frees, and Zhengjun Zhang. 2011. A generalized beta copula with applications in modeling multivariate long-tailed data. Insurance: Mathematics and Economics 49: 265–84. [Google Scholar] [CrossRef]
| 1 | Note that the Egig function works well in practice as it can also provide an accurate numerical approximation of the first derivative of the modified Bessel function with respect to its order which, in the case of the EGIG model, is involved in the second term of Equation (20) by using the function grade from the R package numDeriv which was contributed by Gilbert and Varadhan (2016). For this reason, the Egig function was recently used by Tzougas (2020) to compute the posterior expectations at the E-Step of the EM algorithm, which was developed to estimate the parameters of the Poisson–Inverse Gamma regression model with varying dispersion. |
| Statistic | Claim Severities | Years with the Company (YC) | Age of the Car (AC) | Horsepower of the Car (HP) | |||
|---|---|---|---|---|---|---|---|
| Minimum | 75 | C1: | 2381 | C1: | 2737 | C1: | 3510 |
| Median | 3211 | C2: | 2432 | C2: | 1242 | C2: | 4064 |
| Mean | 8638 | C3: | 4712 | C3: | 5546 | C3: | 1951 |
| Maximum | − | − | − | ||||
| GA | IG | Pareto | EIG | GIG | EGIG | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 9.124 | 0.2796 | 9.123 | −3.573 | 9.3372 | 0.3649 | 9.1016 | −0.2908 | 9.1295 | 0.8555 | −0.0889 | 9.1357 | 1.1978 | −1.2825 |
| (0.0367) | (0.0137) | (0.0732) | (0.0163) | (0.1057) | (0.0585) | (0.0531) | (0.0484) | (0.047) | (0.0221) | (0.0265) | (0.062) | (0.1059) | (0.1266) | |
| YCC2 | −0.0047 | −0.0009 | 0.0284 | 0.0204 | 0.0083 | 0.0262 | ||||||||
| (0.0396) | (0.0783) | (0.0457) | (0.0461) | (0.0416) | (0.0409) | |||||||||
| YCC3 | −0.0018 | 0.0003 | 0.0098 | 0.0068 | −0.0146 | 0.0085 | ||||||||
| (0.0327) | (0.0645) | (0.0379) | (0.0382) | (0.0344) | (0.036) | |||||||||
| ACC2 | −0.0304 | −0.0249 | −0.0307 | −0.0574 | −0.1395 | 0.1115 | −0.0475 | 0.0942 | −0.032 | −0.0604 | −0.0461 | −0.2767 | ||
| (0.0441) | (0.0204) | (0.0861) | (0.0243) | (0.1183) | (0.083) | (0.0662) | (0.0712) | (0.0594) | (0.0321) | (0.0813) | (0.322) | |||
| ACC3 | −0.0625 | −0.0149 | −0.0626 | −0.0057 | −0.1316 | 0.0673 | −0.0736 | 0.061 | −0.0624 | −0.0289 | −0.0621 | −0.1342 | ||
| (0.0305) | (0.0139) | (0.061) | (0.0165) | (0.0957) | (0.0596) | (0.0468) | (0.0488) | (0.0415) | (0.0221) | (0.0673) | (0.289) | |||
| HPC2 | −0.0253 | −0.0241 | −0.0264 | −0.0207 | −0.0891 | 0.0918 | −0.0251 | 0.081 | −0.0272 | −0.0316 | 0.0697 | −0.0317 | −0.1126 | −0.1434 |
| (0.0302) | (0.0137) | (0.06) | (0.0163) | (0.0848) | (0.0566) | (0.0454) | (0.048) | (0.0407) | (0.0218) | (0.0368) | (0.0573) | (0.3683) | (0.1807) | |
| HPC3 | −0.0359 | −0.011 | −0.0374 | −0.019 | −0.0835 | 0.0409 | −0.04 | 0.024 | −0.0436 | −0.0298 | −0.0202 | −0.0456 | −0.1193 | 0.0167 |
| (0.0393) | (0.0168) | (0.0776) | (0.02) | (0.1103) | (0.0693) | (0.0585) | (0.0585) | (0.0528) | (0.0272) | (0.0454) | (0.0738) | (0.4718) | (0.2644) | |
| Deviance | 189,663 | 188,082 | 187,316 | 187,375 | 187,345 | 187,300 | ||||||||
| AIC | 189,687 | 188,106 | 187,340 | 187,399 | 187,375 | 187,330 | ||||||||
| BIC | 189,773 | 188,192 | 187,426 | 187,485 | 187,483 | 187,438 | ||||||||
| GA | IG | Pareto | EIG | GIG | EGIG | ||
|---|---|---|---|---|---|---|---|
| Min. | 8275.03 | 8283.31 | 9032.57 | 8006.52 | 8175.75 | 8333.18 | |
| 1st Quartile | 8387.38 | 8385.47 | 9194.33 | 8182.25 | 8364.69 | 8521.95 | |
| Premium | Median | 8602.25 | 8609.89 | 9953.20 | 8389.93 | 8566.93 | 8721.97 |
| Mean | 8638.44 | 8638.59 | 9918.75 | 8458.18 | 8637.75 | 8796.48 | |
| 3rd Quartile | 8882.80 | 8886.44 | 10,487.38 | 8748.00 | 8845.74 | 8991.19 | |
| Max. | 9173.15 | 9166.15 | 11,679.61 | 9154.69 | 9299.66 | 9527.14 | |
| Min. | 10,638.09 | 20,568.32 | NA | 15,619.10 | 10,786.21 | 20,367.60 | |
| 1st Quartile | 10,669.09 | 20,954.85 | NA | 15,940.62 | 10,990.80 | 21,494.80 | |
| Standard | Median | 11,209.61 | 22,214.70 | NA | 17,011.01 | 11,481.16 | 22,747.08 |
| Deviation | Mean | 11,153.58 | 22,033.36 | NA | 16,963.28 | 11,450.85 | 23,202.42 |
| 3rd Quartile | 11,522.13 | 22,841.89 | NA | 17,709.45 | 11,772.04 | 24,269.96 | |
| Max. | 12,132.53 | 24,635.57 | NA | 19,587.28 | 12,641.57 | 27,655.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzougas, G.; Jeong, H. An Expectation-Maximization Algorithm for the Exponential-Generalized Inverse Gaussian Regression Model with Varying Dispersion and Shape for Modelling the Aggregate Claim Amount. Risks 2021, 9, 19. https://doi.org/10.3390/risks9010019
Tzougas G, Jeong H. An Expectation-Maximization Algorithm for the Exponential-Generalized Inverse Gaussian Regression Model with Varying Dispersion and Shape for Modelling the Aggregate Claim Amount. Risks. 2021; 9(1):19. https://doi.org/10.3390/risks9010019
Chicago/Turabian StyleTzougas, George, and Himchan Jeong. 2021. "An Expectation-Maximization Algorithm for the Exponential-Generalized Inverse Gaussian Regression Model with Varying Dispersion and Shape for Modelling the Aggregate Claim Amount" Risks 9, no. 1: 19. https://doi.org/10.3390/risks9010019
APA StyleTzougas, G., & Jeong, H. (2021). An Expectation-Maximization Algorithm for the Exponential-Generalized Inverse Gaussian Regression Model with Varying Dispersion and Shape for Modelling the Aggregate Claim Amount. Risks, 9(1), 19. https://doi.org/10.3390/risks9010019






