On the Market-Consistent Valuation of Participating Life Insurance Heterogeneous Contracts under Longevity Risk

Abstract

The purpose of this paper is to conduct a market-consistent valuation of life insurance participating liabilities sold to a population of partially heterogeneous customers under the joint impact of biometric and financial risk. In particular, the heterogeneity between groups of policyholders stems from their offered minimum interest rate guarantees and contract maturities. We analyse the effects of these features on the company’s insolvency while embracing the insurer’s goal to achieve the same expected return for different cohorts of policyholders. Within our extensive numerical analyses, we determine the fair participation rates and other key figures, and discuss the implications for the stakeholders, taking account of various degrees of conservativeness of the insurer when pricing the contracts.

1. Introduction

This paper focuses on the market-consistent valuation of life insurance liabilities, a topic which has recently again attracted much attention both from academics and practitioners, see, for example, Sheldon and Smith (2004), Bauer et al. (2010), Broeders et al. (2013), Gambaro et al. (2019), Dorobantu et al. (2020) and Ghalehjooghi and Pelsser (2020). This growing interest mostly stems from the long-sought adoption of fair value based accounting standards in many countries, culminating with the full implementation of Solvency II in the European Union in 2016, see European Parliament and Council of the European Union (2009). According to these principles, assets and liabilities should be evaluated at the price, actual or hypothetical, they could be exchanged for in a liquid market. As in the last few decades financial markets have experienced a high volatility and permanently low (or even negative) interest rates, coupled with a steady increase in life expectancy, the introduction of these accounting standards has forced life insurers to deal with risks more carefully in valuation.

We propose a contingent claim model, along the lines of Briys and de Varenne (1994, 1997), for the valuation of the equity and the liabilities of a participating life insurance company. The pioneering model by Briys and de Varenne (1994, 1997) has been extended in several directions, e.g., by Grosen and Jørgensen (2002), Bernard et al. (2005), Chen and Suchanecki (2007), Cheng and Li (2018), Bacinello et al. (2018), Hieber et al. (2019) or Orozco-Garcia and Schmeiser (2019), just to quote a few. In most of these papers, fair valuation is carried out for individual life insurance contracts with the exception of Hieber et al. (2019), Orozco-Garcia and Schmeiser (2019) and Bacinello et al. (2018). Hieber et al. (2019) show that individual insurance contracts with an annual guaranteed return can be incorporated into an existing portfolio, resulting in no wealth transfer between two groups. Orozco-Garcia and Schmeiser (2019) examine whether contracts can be priced such that all the generations pay fair premiums and face the same level of default risk. Our paper extends Bacinello et al. (2018) who introduce biometric risk for a population of completely homogeneous policyholders, and analyze how this risk can be split into two components, namely diversifiable and systematic parts. We consider the valuation of life insurance participating contracts sold to a population of partially heterogeneous customers under the joint impact of biometric and financial risk. Here, the heterogeneity between groups of policyholders stems from their offered minimum interest rate guarantees and contract maturities. In this respect, this paper is related to Hansen and Miltersen (2002) and Burkhart (2018). Hansen and Miltersen (2002) deal with the case of participating life insurance contracts sold to heterogeneous customers, but do not take into account biometric and default risk.1 Burkhart (2018) particularly addresses surrender risk in the assessment of a heterogeneous insurance portfolio under Solvency II, and considers the interaction between minimum interest rate guarantee, surplus participation and reserving requirement.

Analyzing customers with different minimum interest rate guarantees has some interesting practical implications. As a reaction to new market conditions, in particular low interest rates, one measure insurance companies have taken was to reduce the level of the minimum interest rate guarantee drastically. For example, the German Federal Ministry of Finance has gradually decreased the maximum technical interest rate for life insurance products over the past 26 years from 4% to 2.25%, then to 1.75% and currently to 0.9%, see Eling and Holder (2013). However, these adjustments are applied exclusively to new contracts, while older customers keep enjoying higher minimum interest rate guarantees. A natural question that arises is whether new customers will then be penalized and what measures could be taken to protect the policyholders. This problem has been widely discussed in public, see, for instance, Seibel (2016).

Despite its stylized nature, this paper provides some useful insights into such and similar topics by developing a rather comprehensive contingent claim model that explicitly considers financial, default and longevity risk. We incorporate the heterogeneity of customers by dividing them into two groups. We model the liabilities for these two groups by addressing the insurer’s goal to protect both old and new customers, usually endowed with different minimum interest rate guarantees, and provide them with the same expected return. Alternatively, when the two groups have different contract maturities, the payoff of the group with the earlier maturity is structured in such a way that the other group is also adequately protected. We evaluate the outstanding liabilities in a market-consistent way and conduct an analysis of fair contracts for both specifications of the heterogeneous groups. The subject of actuarial fairness has been examined by several authors, see, for example, Meyers and Hoyweghen (2017) for a very general discussion or Knispel et al. (2011). Based on the fair combinations of parameters, we compute then the certainty equivalent returns, under the physical probability measure, for the heterogeneous policyholders. This helps answering two questions: what are the factors determining the relative magnitudes of the fair participation rates? How will the benefits of the two groups, as measured by their certainty equivalent returns, be impacted by considering both groups as a whole?

The main findings of the paper resulting from our numerical analysis can be summarized as follows: (i) The levels of the risk premium (or the degrees of prudence) arising from various longevity pricing assumptions play a substantial role in the magnitudes of the fair participation rates and of the certainty equivalent returns. (ii) Maintaining participation rates in the range 80–100% (often prescribed by law and used in practice) can severely affect the insurer’s balance sheet as some portfolio and parameter combinations actually require smaller participation rates to ensure the fairness of the contracts. Remarks (i) and (ii) are consistent with the findings in Bacinello et al. (2018). (iii) When the two groups differ in their minimum interest rate guarantees, the group with the lower rate receives a higher fair participation rate. This compensation is bound to rise if the insurance company does not explicitly aim at providing similar returns to all policyholders, as we propose to do instead by modifying the payoff structure of the group with the lower minimum interest rate guarantee. Consequently, the difference between the certainty equivalent returns would increase as well. Further, when there are few policyholders holding a lower individual guarantee, their participation in the surplus sharing must be very high to ensure fair contracts. (iv) If the two groups differ exclusively in the contract maturity, the fair participation rate for the group with the longer contract duration is much lower. As a consequence, the certainty equivalent return behaves similarly, although to a lesser extent. Further, the group with the longer contract duration receives a remarkably low fair participation rate if its size is much lower than the other group.

The remainder of this paper is structured as follows: Section 2 sets up the contract structure and describes the payoffs to the different customer groups and the modelling of the insurance and the financial risk. Section 3 focuses on the market valuation of the outstanding liabilities and explains how a fair contract analysis can be conducted in our framework. Section 4 is devoted to the numerical analysis and addresses the issue of fair pricing. Further, we find out which group benefits from specific portfolio compositions by comparing the certainty equivalent returns. Section 5 provides some concluding remarks and a short outlook on possible extensions.

2. Model Setup

We consider a life insurance company which consists of equity holders and two heterogeneous groups of policyholders. All policyholders take out their contracts at time 0. The policyholders’ heterogeneity stems from either the offered minimum interest rate guarantees or the contract maturities. In group i, $i=1,2$, there are $N_i\left(0\right)$ homogeneous policyholders, meaning that they have the same age, make the same initial contribution $l\left(0\right)$ and the contracts they hold are identical. At time 0, the insurer’s stylized balance sheet is:

Assets	Liabilities
$W\left(0\right)$	$E\left(0\right)=(1-{\alpha }_1-{\alpha }_2)W\left(0\right)$
	$L_1\left(0\right)={\alpha }_{1}W\left(0\right)$
	$L_2\left(0\right)={\alpha }_{2}W\left(0\right)$
$W\left(0\right)$	$W\left(0\right)$

The initial assets of the insurance company can be split up into three components: $W\left(0\right)=E\left(0\right)+L_1\left(0\right)+L_2\left(0\right)$, where the premiums $L_1\left(0\right)=l\left(0\right)N_1\left(0\right)$ and $L_2\left(0\right)=l\left(0\right)N_2\left(0\right)$ are contributed by the first and the second group of policyholders, respectively, and the remainder $E\left(0\right)$ by the equity holders. We denote the fraction of initial assets contributed by group i, $i=1,2$, by ${\alpha }_i=N_i\left(0\right)l\left(0\right)/W\left(0\right)=L_i\left(0\right)/W\left(0\right)\in (0,1)$, and the share of initial assets contributed by the equity holders by $e\left(0\right):=1-{\alpha }_1-{\alpha }_2\in (0,1)$.2 Note that, as we focus on the impact of different minimum interest rate guarantees and contract maturities, the individual contribution $l\left(0\right)$ is assumed to be the same for all policyholders. The benefits for each group will be determined according to the initial contribution and contract provisions.

2.1. Contract Structure

We assume that every policyholder buys from the life insurer a participating pure endowment contract whose payoff is contingent on the event that the policyholder survives the contract maturity. We discuss two different ways the heterogeneity of groups 1 and 2 could be specified. The two groups differ exclusively by

Case 1:

the minimum interest rate $g_i\ge 0$, $i=1,2$, promised by the insurer;

Case 2:

the contract maturity date $T_i$, $i=1,2$.

In both cases, the insurer provides the policyholders with some guaranteed payoff. The aggregated guaranteed payment to group i becomes due at the contract maturity $T_i$ and is defined by

$$G_i\left(T_i\right):=N_i\left(T_i\right)l\left(0\right)e^{g_i{T}_i},i=1,2,$$

(1)

where $N_i\left(t\right)$ is the (random) number of surviving policyholders at time $t\ge 0$ in group i.

In the subsequent paragraphs, we specify the outstanding liabilities $L_i\left(T_j\right)$, $i=1,2$, $j=1,2$, for Cases 1 and 2. We note that, if there are no surviving policyholders in a group, then the insurer is free from any duty of payments with respect to that group. Therefore, we will set in Case 1, involving a common maturity $T:=T_1=T_2$ for the two groups,

$$L_i\left(T\right)=\left\{\begin{array}{cc}{\Psi }_i\hfill & \mathrm{if}{N}_i\left(T\right)>0\hfill \\ 0\hfill & \mathrm{if}{N}_i\left(T\right)=0\hfill \end{array}\right.={\Psi }_i{\mathbf{𝟙}}_{\left\{N_i\left(T\right)>0\right\}},i=1,2,$$

(2)

where ${\mathbf{𝟙}}_{\{·\}}$ is the indicator function. Here, ${\Psi }_i$ represents the global payment made at maturity to surviving policyholders in group i, $i=1,2$. Case 2 involves two contract maturities and will be treated separately. The amounts ${\Psi }_i$, $i=1,2$, depend on the guaranteed payments $G_i\left(T_i\right)$, the value of the assets of the life insurance company, which is denoted by $W\left(t\right)$ at time $t\ge 0$, and on the participation rates ${\delta }_i\in [0,1]$, according to which a share of the assets exceeding the guaranteed payoff is paid to surviving policyholders as a bonus.3

Case 1. We assess the impact of different minimum interest rate guarantees. To set up this case recall that $T_1=T_2=T$ and, without loss of generality, assume that $g_1>g_2$. As a result, the payoff promised to the policyholders of group i, $i=1,2$, at maturity T is $G_i\left(T\right)=N_i\left(T\right)l\left(0\right)e^{g_{i}T}$. Such instance is common to many life insurers since older products still in force often have significantly higher guaranteed rates than those sold more recently which were penalized by the ongoing low interest environment. Although in this stylized model all contracts are issued at the same date, our findings provide some guidance on establishing some contractual parameters, in particular the participation coefficients for which there is usually some discretion on the insurer’s side.

Since several large insurance companies issuing participating contracts aim to provide the same (expected) rate of return to customers endowed with different minimum interest rate guarantees, we adjust the definition of the outstanding liabilities in order to achieve this desirable goal. Inspired by the model in Briys and de Varenne (1994, 1997), the global payment ${\Psi }_1$ in (2), relative to policyholders of the group with the higher guarantee rate $g_1$, is defined by

$${\Psi }_1=\left\{\begin{array}{cc}\frac{G_1\left(T\right)}{G\left(T\right)}W\left(T\right)\hfill & \mathrm{if}W\left(T\right)<G\left(T\right)\hfill \\ G_1\left(T\right)\hfill & \mathrm{if}G\left(T\right)\le W\left(T\right)\le \frac{G\left(T\right)}{{\alpha }_1+{\alpha }_2}\hfill \\ {\zeta }_1\hfill & \mathrm{if}\frac{G\left(T\right)}{{\alpha }_1+{\alpha }_2}<W\left(T\right)\hfill \end{array}\right.,$$

(3)

where $G\left(T\right)=G_1\left(T\right)+G_2\left(T\right)$ is the total guaranteed payment. The rationale behind (3) is as follows: if the insurance company becomes insolvent, i.e., the value of the assets at maturity $W\left(T\right)$ is insufficient to cover the total guaranteed payoff $G\left(T\right)$, the available assets are shared among the surviving policyholders according to a proportional splitting rule.4 This implies that the company has limited liability towards its customers and, in case of insolvency, nothing is left to the equity holders. If the assets perform moderately, i.e., $G\left(T\right)\le W\left(T\right)\le G\left(T\right)/\left({\alpha }_1+{\alpha }_2\right)$, the surviving policyholders of group 1 receive their guaranteed payoff $G_1\left(T\right)$, but no bonus. If the assets perform well, i.e., $G\left(T\right)/\left({\alpha }_1+{\alpha }_2\right)<W\left(T\right)$, then policyholders of group 1 are entitled to a share of the assets $W\left(T\right)$ on top of their guaranteed payments. The corresponding payoff ${\zeta }_1$ is specified further below.

The global payment ${\Psi }_2$ in (2) made to surviving policyholders of the group with the lower guarantee rate $g_2$ is defined by

$${\Psi }_2=\left\{\begin{array}{cc}\frac{G_2\left(T\right)}{G\left(T\right)}W\left(T\right)\hfill & \mathrm{if}W\left(T\right)<G\left(T\right)\hfill \\ G_2\left(T\right)e^{min\left\{(g_1-g_2)T,ln\left(\frac{W\left(T\right)-G_1\left(T\right)}{G_2\left(T\right)}\right)\right\}}\hfill & \mathrm{if}G\left(T\right)\le W\left(T\right)\le \frac{G\left(T\right)}{{\alpha }_1+{\alpha }_2}\hfill \\ {\zeta }_2\hfill & \mathrm{if}\frac{G\left(T\right)}{{\alpha }_1+{\alpha }_2}<W\left(T\right)\hfill \end{array}\right..$$

(4)

The rationale behind the expression in the middle row in (4) is as follows: after serving the minimum interest rate of the first group, the insurance company aims at endowing the second group with an identical minimum interest rate $g_1$ provided there is enough capital left for this. When this is not the case, the second group obtains the remainder $W\left(T\right)-G_1\left(T\right)(\ge G_2\left(T\right))$. On the other hand, as long as the company’s assets are sufficient to distribute some bonus (third row), group 2 will likely be compensated for its lower guaranteed payoff by receiving a higher participation coefficient.5

In order to specify the payoffs ${\zeta }_i$, $i=1,2$, we first define the quantity

$$D\left(T\right):=W\left(T\right)-\sum _{i=1}^2{\zeta }_i^{+},$$

(5)

where

$${\zeta }_i^{+}=G_i\left(T\right)+{\delta }_{i}max\left\{{\alpha }_{i}W\left(T\right)-G_i\left(T\right),0\right\}$$

(6)

is the guaranteed payment plus the regular bonus the insurance company aims at delivering to the group of policyholders i. The amount $D\left(T\right)$ represents then the excess (deficit) of the assets above (below) the target payments to both groups. If $W\left(T\right)\ge max\left\{G_1\left(T\right)/{\alpha }_1,G_2\left(T\right)/{\alpha }_2\right\}$, then $D\left(T\right)\ge 0$. If $min\left\{G_1\left(T\right)/{\alpha }_1,G_2\left(T\right)/{\alpha }_2\right\}<W\left(T\right)<max\left\{G_1\left(T\right)/{\alpha }_1,G_2\left(T\right)/{\alpha }_2\right\}$, the sign of $D\left(T\right)$ is indeterminate. Moreover, we define

$${\zeta }_i^{-}:=\left\{\begin{array}{cc}{G}_i\left(T\right)\hfill & \mathrm{if}\frac{G_i\left(T\right)}{{\alpha }_i}=max\left\{\frac{G_1\left(T\right)}{{\alpha }_1},\frac{G_2\left(T\right)}{{\alpha }_2}\right\}\hfill \\ W\left(T\right)-G_j\left(T\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right.,i=1,2,j\in \left\{1,2\right\}-\left\{i\right\},$$

(7)

and let

$${\zeta }_i={\zeta }_i^{+}{\mathbf{𝟙}}_{\left\{D\left(T\right)\ge 0\right\}}+{\zeta }_i^{-}{\mathbf{𝟙}}_{\left\{D\left(T\right)<0\right\}}.$$

(8)

As long as $D\left(T\right)\ge 0$, the firm can serve both groups with their regular bonuses. If, however, $D\left(T\right)<0$, the assets of the insurer are insufficient to generate such payments. We assume then that the group with the higher value of $G_i\left(T\right)/{\alpha }_i$ obtains only the guaranteed payment, while the other group seizes the remaining assets’ value which is larger than the guaranteed payment, but smaller than the payoff including the regular bonus.6

Case 2. We assume that the policies from the first and second group expire at time $T_1$, respectively time $T_2$, and, without loss of generality, let $T_2>T_1$. The minimum guaranteed rates are set to be equal, i.e., $g_1=g_2=:g$. The guaranteed payoffs are now $G_i\left(T_i\right)=N_i\left(T_i\right)l\left(0\right)e^{g{T}_i}$, $i=1,2$.

In order to define the outstanding liabilities $L_i\left(T_j\right)$, $i=1,2$, $j=1,2$, we need the market value $V_2\left(T_1\right)$ at the earliest maturity $T_1$ of the guaranteed payoff paid at $T_2$ to the second group. The exact specification of $V_2\left(T_1\right)$ will be given in Section 4. Define then $V\left(T_1\right):=G_1\left(T_1\right)+V_2\left(T_1\right)$ the market value at $T_1$ of the insurer’s liabilities, including the immediate guaranteed payment to the first group and the market value of future liabilities for the second group. A premature default event may occur at time $T_1$ when $W\left(T_1\right)<V\left(T_1\right)$ and $N_1\left(T_1\right)>0$. In this case, we assume that group 1 will accept less than $G_1\left(T_1\right)$ as insurance benefit, so that an equal treatment of both groups can be achieved. In other words, the two groups of policyholders have the same claiming priority in the case of bankruptcy. More specifically, the global payment made to surviving policyholders of the first group at $T_1$ is defined by

$${\Psi }_1=\left\{\begin{array}{cc}\frac{G_1\left(T_1\right)}{V\left(T_1\right)}W\left(T_1\right)\hfill & \mathrm{if}W\left(T_1\right)<V\left(T_1\right)\hfill \\ G_1\left(T_1\right)\hfill & \mathrm{if}V\left(T_1\right)\le W\left(T_1\right)\le \frac{V\left(T_1\right)}{{\alpha }_1+{\alpha }_2}\hfill \\ min\left\{{\zeta }_1^{+},W\left(T_1\right)-V_2\left(T_1\right)\right\}\hfill & \mathrm{if}\frac{V\left(T_1\right)}{{\alpha }_1+{\alpha }_2}<W\left(T_1\right)\hfill \end{array}\right..$$

(9)

Here, the target regular payment to the first group ${\zeta }_1^{+}$, defined as in (6) with T replaced by $T_1$, may be so high that the second group could not be served with the notional guaranteed amount $V_2\left(T_1\right)$. In this case, only the amount $W\left(T_1\right)-V_2\left(T_1\right)(>G_1\left(T_1\right))$ is available to the policyholders in group 1, so that the remaining assets match the market value of the guaranteed payoff to the second group.

To define the outstanding liability for group 2, we need to distinguish whether there is default at time $T_1$ or not. If default occurs, the second group obtains a rebate payment at $T_1$ amounting to

$$L_2\left(T_1\right)=\frac{V_2\left(T_1\right)}{V\left(T_1\right)}W\left(T_1\right){\mathbf{𝟙}}_{\left\{N_1\left(T_1\right)>0,N_2\left(T_1\right)>0\right\}}{\mathbf{𝟙}}_{\left\{W\left(T_1\right)<V\left(T_1\right)\right\}}.$$

(10)

If there is no default at $T_1$, i.e., when $W\left(T_1\right)\ge V\left(T_1\right)$ or when $N_1\left(T_1\right)=0$, the contract payoff for the second group becomes due at time $T_2$ and is given by

$$L_2\left(T_2\right)={\Psi }_2{\mathbf{𝟙}}_{\left\{N_2\left(T_2\right)>0\right\}}{\mathbf{𝟙}}_{\left\{N_1\left(T_1\right)=0\right\}\cup \left\{W\left(T_1\right)\ge V\left(T_1\right)\right\}},$$

(11)

with

$${\Psi }_2=\left\{\begin{array}{cc}{W}^{\prime }\left(T_2\right)\hfill & \mathrm{if}{W}^{\prime }\left(T_2\right)<G_2\left(T_2\right)\hfill \\ G_2\left(T_2\right)\hfill & \mathrm{if}{G}_2\left(T_2\right)\le W^{\prime }\left(T_2\right)\le \frac{G_2\left(T_2\right)}{{\alpha }_2^{\prime }}\hfill \\ G_2\left(T_2\right)+{\delta }_2\left({\alpha }_2^{\prime }{W}^{\prime }\left(T_2\right)-G_2\left(T_2\right)\right)\hfill & \mathrm{if}\frac{G_2\left(T_2\right)}{{\alpha }_2^{\prime }}<W^{\prime }\left(T_2\right)\hfill \end{array}\right.,$$

(12)

where ${\alpha }_2^{\prime }={\alpha }_2/\left(1-{\alpha }_1\right)$ and $W^{\prime }\left(T_2\right)$ is the assets’ value at $T_2$ taking into account the previous outflows to the policyholders of the first group. The exact specification of $W^{\prime }\left(T_2\right)$ will be given in Section 4. Note also that the events in the indicators in (10) and (11) are disjoint, so only one benefit will be paid to the second group either at $T_1$ or $T_2$.

2.2. Modelling Insurance and Financial Risk

In this section, we follow and adapt Bacinello et al. (2018) to our situation.

The insurance risk is made up of the hedgeable (also called diversifiable or unsystematic) part, which is likely to tail off once the portfolio of all policyholders of the heterogeneous groups is sufficiently large, and the systematic (or unhedgeable) part. The latter, called longevity risk, cannot be diversified away through pooling and affects all contracts equally by entailing the misestimation of the decline in mortality rates. An introduction to longevity risk is given in e.g., Barrieu et al. (2012); Biffis (2005) and Biffis et al. (2010) cover the stochastic modelling of longevity risk.

We select a risk neutral probability measure Q for pricing purposes.7 Furthermore, we let ${\tau }_i^j$ be the residual lifetime of the j-th policyholder, $j=1,\dots ,N_i\left(0\right)$, of group i, $i=1,2$. The following assumptions will remain valid throughout the paper.

Assumption 1.

There exists a positive random variable Δ, measurable with respect to the σ-algebra containing the information available to market participants at time T in Case 1, and $T_1$ in Case 2, such that

$$\begin{array}{cc}\hfill Q\left({\tau }_1^1>t_1^1,\dots ,{\tau }_1^{N_1\left(0\right)}>t_1^{N_1\left(0\right)},{\tau }_2^1>t_2^1,\dots ,{\tau }_2^{N_2\left(0\right)}>t_2^{N_2\left(0\right)}|\Delta \right)& =\prod _{i=1}^2\prod _{j=1}^{N_i\left(0\right)}Q\left({\tau }_i^j>t_i^j|\Delta \right)\hfill \\ \hfill & =\prod _{i=1}^2\prod _{j=1}^{N_i\left(0\right)}{e}^{-\Delta {\int }_0^{t_i^j}{m}_i\left(v\right)dv},\hfill \end{array}$$

(13)

for any $t_i^j\ge 0$, $i=1,2$, $j=1,\dots ,N_i\left(0\right)$, where $m_i$ is a deterministic force of mortality depending on the initial age $x_i$ of group i, non-negative, continuous, and satisfying ${\int }_0^{+\infty }{m}_i\left(v\right)dv=+\infty$.

Then, conditionally on $\Delta$, the residual lifetimes ${\tau }_i^j$, $i=1,2$, $j=1,\dots ,N_i\left(0\right)$, are independent. The random variable $\Delta$ can be thought of as a systematic risk factor whose effect is to rescale the deterministic forces of mortality $m_i$, $i=1,2$, by a random percentage. It is assumed to be the same for both groups of policyholders, so that all biometric differences between them stem from the deterministic forces of mortality, that are already equipped with safety margins, as will be specified in Section 4. Moreover, the fact that $\Delta$ is assumed to be part of the information available at the earliest maturity date means that its true value is unveiled within the (first) contract maturity, whereas today the market participants can merely anticipate the impact of the systematic risk since the rescaling amount is unknown at the valuation date 0. This greatly simplified circumstance is in some way acceptable by the fact that the insurer collects a vast quantity of demographic information from the examined and similar portfolios over the years, whose analysis can reveal the actual character of $\Delta$. As we see in Section 4, we actually exploit this property only in Case 2.

The t-years survival probability for an individual belonging to group i, $i=1,2$, can be derived from Assumption 1 through

$${}_t{p}_{x_i}:=Q\left({\tau }_i^j>t\right)=E^Q\left[e^{-\Delta {\int }_0^t{m}_i\left(v\right)dv}\right],$$

(14)

for $t\ge 0$ and $j=1,\dots ,N_i\left(0\right)$. In the following, we also set

$${}_u{p}_{y_i}^{*}:=e^{-{\int }_{y_i-x_i}^{u+y_i-x_i}{m}_i\left(v\right)dv},$$

(15)

for $y_i\ge x_i$, $i=1,2$, and $u\ge 0$, so that in particular, for $0\le t\le s$, we obtain a `deterministic’ survival probability ${}_{s-t}{p}_{x_i+t}^{*}=e^{-{\int }_t^s{m}_i\left(v\right)dv}$. Further, conditional on $\Delta$, we have $N_i\left(t\right)\sim Binomial\left(N_i\left(0\right),{\left({}_t{p}_{x_i}^{*}\right)}^{\Delta }\right)$ for $i=1,2$ and $t\ge 0$.

Concerning the modelling of the financial risk, we presume that it is entirely driven by the randomness of the assets which is captured by the next important assumption.

Assumption 2.

At time $t\ge 0$, the assets’ value $W\left(t\right)$ is defined by $W\left(t\right)=W\left(0\right)e^{R(0,t)}$, where $R(0,t)$ is the random assets’ log-return over $[0,t]$. This return is independent of Δ and the residual lifetimes ${\tau }_i^j$, $i=1,2$, $j=1,\dots ,N_i\left(0\right)$.

The possibility of having an interest risk component, that can be implemented by introducing stochastic interest rates, is ignored in this paper whereby the market short rate, denoted by r, is supposed to be constant.

3. Valuation

We denote by $V_i$ the initial market value of the outstanding liabilities for group i, $i=1,2$. The contracts issued by the insurer are fair if the following conditions hold:

$$V_1=L_1\left(0\right),V_2=L_2\left(0\right).$$

(16)

In other words, the initial market value of the claim of group i, $i=1,2$, coincides with its initial investment $L_i\left(0\right)={\alpha }_{i}W\left(0\right)$. Note that, if the Equations in (16) hold, then fairness is guaranteed for equity holders as well. Economically, we can interpret these conditions as constraints on the participation coefficients ${\delta }_i$, $i=1,2$. Nevertheless, it may happen that (16) implies participation coefficients that exceed 100% because there is a chance that the benefits of the customers are excessively low. Moreover, negative coefficients are also possible to compensate for too high benefits. We only consider fair contracts for which ${\delta }_i\in \left[0,1\right]$, $i=1,2$.

Armed with the pricing measure Q, we can calculate $V_i$, $i=1,2$. For Case 1, entailing T as the maturity date, these quantities are specified by

$$V_i=E^Q\left[e^{-rT}{L}_i\left(T\right)\right],i=1,2.$$

(17)

For Case 2 we have, for one thing,

$$V_1=E^Q\left[e^{-r{T}_1}{L}_1\left(T_1\right)\right].$$

(18)

Due to the possible premature deficit of the insurer at the earlier maturity $T_1$, the outstanding payoff to group 2 is paid out either at $T_1$ or at the regular maturity $T_2$. Then

$$V_2=E^Q\left[e^{-r{T}_1}{L}_2\left(T_1\right)+e^{-r{T}_2}{L}_2\left(T_2\right)\right].$$

(19)

4. Numerical Analysis

We conduct some numerical analyses to understand the relative size of participation rates for the heterogeneous customers and which group of policyholders is better or worse off when pooling them together. To serve this purpose, we compute for Cases 1 and 2

• firstly, the fair participation rates ${\delta }_i^{*}$, $i=1,2$, under the pricing measure Q;
• secondly, the annual certainty equivalent log-returns of the life insurance contracts under the real world measure P, henceforth just certainty equivalent returns, denoted by $C_i$, $i=1,2$, based on the fair participation rates ${\delta }_i^{*}$.8

In Case 1, the certainty equivalent returns for group i, $i=1,2,$ are given by

$$E^P\left[\frac{L_i\left(T\right)}{L_i\left(0\right)}\right]=e^{C_{i}T}\iff C_i=\frac{1}{T}ln\left(E^P\left[\frac{L_i\left(T\right)}{L_i\left(0\right)}\right]\right).$$

(20)

Depending on different pooling schemes, we can figure out, based on $C_i$, $i=1,2$, how attractive our life insurance policies are against alternative investments. Through comparing $C_1$ and $C_2$, we can also identify which group benefits more from a certain pooling scheme.

Concerning the modelling of the insurance risk under the pricing measure Q, we assume Gompertz’s law, i.e., $m_i\left(t\right)={\lambda }_i{c}_i^{x_i+t}$ for $i=1,2$ and $t\ge 0$, yielding ${}_{s-t}{p}_{x_i+t}^{*}=$$e^{-{\lambda }_i{c}_i^{x_i}\left(c_i^s-c_i^t\right)/ln\left(c_i\right)}$ for $0\le t\le s$. Furthermore, we suppose that $\Delta$ follows a Gamma distribution $\Gamma (\beta ,\theta )$ with $Va{r}_Q\left(\Delta \right)=0.1$ and $E^Q\left[\Delta \right]\in \left\{0.4,0.8,1\right\}$. The latter stipulation provides the possibility to integrate various degrees of the insurer’s conservativeness into the pricing of the contracts. Specifically, lower values of $E^Q\left[\Delta \right]$ are associated with higher risk premiums or, put it another way, with increasing conservativeness of the company concerning longevity risk.

The financial risk merely depends on the stochastic log-return of the assets $R(0,t)$, that is assumed to be normally distributed under Q with mean $(r-{\sigma }^2/2)t$ and standard deviation $\sigma \sqrt{t}$, where $\sigma$ is the assets’ volatility.

Assumption 1 shall hold under P as well, with the same rescaling random variable $\Delta$ and with deterministic forces of mortality ${\tilde{m}}_i$, $i=1,2$. However, as the considered contracts are pure endowments, we have, for all $t\ge 0$,

$${}_t{p}_{x_i}=E^Q\left[e^{-\Delta {\int }_0^t{m}_i\left(v\right)dv}\right]>E^P\left[e^{-\Delta {\int }_0^t{\tilde{m}}_i\left(v\right)dv}\right]=:{}_t{\tilde{p}}_{x_i},i=1,2.$$

(21)

In other words, the risk neutral survival probability contains a safety loading. To achieve (21), we set ${\tilde{m}}_i=m_i/\gamma$, $i=1,2$, where $\gamma <1$, and assume that the distribution of $\Delta$ under P is Gamma with the same variance as under Q, i.e., $Va{r}_P\left(\Delta \right)=Va{r}_Q\left(\Delta \right)=0.1$, but with expectation $E^P\left[\Delta \right]=1$. Under P, the distribution of the number of surviving policyholders at time $t\ge 0$ is $N_i\left(t\right)|\Delta \sim Binomial\left(N_i\left(0\right),{\left({}_t{\tilde{p}}_{x_i}^{*}\right)}^{\Delta }\right)$ with ${}_u{\tilde{p}}_{y_i}^{*}=e^{-{\int }_{y_i-x_i}^{u+y_i-x_i}{\tilde{m}}_i\left(v\right)dv}$ for $y_i\ge x_i$, $i=1,2$, and $u\ge 0$, and that of the assets’ log-return is $R(0,t)\sim \mathcal{N}\left(\left(\mu -{\sigma }^2/2\right)t,{\sigma }^{2}t\right)$, where $\mu$ is the expected instantaneous rate of return of the assets. Then, Assumption 2 shall hold under P as well.

Subsequently,

Table 1. Non case-specific parameters for numerical analyses.

Symbol	Description	Value
$l\left(0\right)$	Initial contribution of a single policyholder	35
$e\left(0\right)$	Equity holders’ share of initial assets	0.3
$x_1\left(=x_2\right)$	Initial age of policyholders	40
${\lambda }_1\left(={\lambda }_2\right)$	Age independent Gompertz parameter	$2.6743·{10}^{-5}$
$c_1\left(=c_2\right)$	Age dependent Gompertz parameter	1.098
$\beta$	Shape parameter of $\Delta$ under Q	$\left\{1.6,6.4,10\right\}$
$\theta$	Scale parameter of $\Delta$ under Q	$\left\{0.25,0.125,0.1\right\}$
r	Risk free short rate	3%
$\sigma$	Assets’ volatility	15%
$\mu$	Assets’ expected instantaneous rate of return	5%
$\gamma$	Adjustment factor to force of mortality	0.9

summarizes the assumed values for the parameters that are not case-specific and valid in all of the following numerical analyses.

The two values for the Gompertz parameters given in Table 1 were obtained by fitting the survival probabilities ${}_t{p}_{40}^{*}$ to the corresponding probabilities implied by the projected life table IPS55 in use in the Italian annuity market, see Bacinello et al. (2018). Further, combining pairwise the parameters of the Gamma distribution given in Table 1 will result in the values of $E^Q\left[\Delta \right]$ and $Va{r}_Q\left(\Delta \right)$ considered.9

Results for Case 1. We set $T\in \left\{12,25\right\}$ and consider reasonable choices for the minimum interest rate guarantees, $g_1=1.75\%$ and $g_2=1.25\%$. As previously outlined, a potentially desirable goal of an insurer is to provide all policyholders with the same (expected) rate of return regardless of the individual minimum interest rate guarantee. Hence, comparing the certainty equivalent returns $C_1$ and $C_2$ for the two groups in the present case seems particularly interesting.

Table 2. Fair participation rates and certainty equivalent returns for Case 1 with $T=12$, different portfolio sizes with $N_1\left(0\right)=N_2\left(0\right)$ and different values of $E^Q\left[\Delta \right]$. All results are in percentage.

$\mathit{T}=12$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.4$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.8$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=1$
$N_1\left(0\right)$	$N_2\left(0\right)$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$
		$C_1$	$C_2$	$C_1$	$C_2$	$C_1$	$C_2$
1	1	72.42	78.01	76.38	81.60	78.37	83.41
		4.22	4.32	4.35	4.44	4.42	4.51
10	10	70.03	75.65	71.32	76.66	71.94	77.14
		4.30	4.41	4.35	4.44	4.37	4.46
100	100	70.05	75.68	71.34	76.69	71.96	77.17
		4.30	4.41	4.35	4.44	4.37	4.46
1000	1000	70.06	75.68	71.35	76.70	71.97	77.19
		4.30	4.41	4.35	4.45	4.37	4.46
100,000	100,000	70.06	75.68	71.35	76.70	71.97	77.18
		4.30	4.41	4.35	4.45	4.37	4.46

,

Table 3. Fair participation rates and certainty equivalent returns for Case 1 with $T=12$, different portfolio sizes with $N_1\left(0\right)\ne N_2\left(0\right)$ and different values of $E^Q\left[\Delta \right]$. All results are in percentage.

$\mathit{T}=12$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.4$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.8$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=1$
$N_1\left(0\right)$	$N_2\left(0\right)$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$
		$C_1$	$C_2$	$C_1$	$C_2$	$C_1$	$C_2$
10	1000	68.51	74.59	69.80	75.66	70.44	76.18
		4.26	4.38	4.31	4.42	4.33	4.44
100	100,000	68.55	74.57	69.91	75.64	70.56	76.15
		4.26	4.37	4.31	4.41	4.33	4.43
1000	100	71.34	76.75	72.57	77.71	73.16	78.18
		4.33	4.44	4.38	4.47	4.40	4.49
100,000	10	71.63	77.01	72.84	77.96	73.43	78.43
		4.34	4.44	4.38	4.48	4.40	4.50

and

Table 4. Fair participation rates and certainty equivalent returns for Case 1 with $T=25$, different portfolio sizes with $N_1\left(0\right)\ne N_2\left(0\right)$ and different values of $E^Q\left[\Delta \right]$. All results are in percentage.

$\mathit{T}=25$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.4$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.8$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=1$
$N_1\left(0\right)$	$N_2\left(0\right)$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$
		$C_1$	$C_2$	$C_1$	$C_2$	$C_1$	$C_2$
10	1000	82.45	88.11	84.59	89.59	85.56	90.24
		4.61	4.72	4.67	4.77	4.69	4.79
100	100,000	82.56	88.09	84.80	89.57	85.81	90.22
		4.61	4.72	4.67	4.77	4.70	4.79
1000	100	85.80	90.45	87.58	91.58	88.39	92.09
		4.69	4.78	4.74	4.82	4.76	4.83
100,000	10	86.13	90.73	87.87	91.84	88.66	92.33
		4.69	4.79	4.74	4.82	4.76	4.84

contain our findings for the fair participation rates and the annual certainty equivalent returns.

From Table 2, we observe the following:

(2.1)

Group 2, endowed with a lower interest rate guarantee, is naturally provided with a higher fair participation rate ${\delta }_2^{*}$ and a perceptibly larger implied certainty equivalent return $C_2$. In order to examine the goodness of the contract design in (4), middle row, to achieve similar rates of return for different groups of customers, we further carry out the analysis under the assumption that the same payout structure of group 1 is applied to group 2 (but still with different guarantees $g_1>g_2$) and find that ${\delta }_2^{*}$ and $C_2$ are even higher. Therefore, if the insurance company aimed at treating both groups fairly when the payoff structures are identical, it should assign a much larger fair participation rate to the second group than to the first one, resulting in a greater difference between $C_1$ and $C_2$. That is why our attempt at designing contracts that potentially provide the same rate of return to customers endowed with different minimum interest rate guarantees leads to more desirable results.

(2.2)

For any portfolio size, an increase in the longevity risk premium, i.e., lower values for $E^Q[\Delta ]$, leads to smaller fair participation rates. This is because longevity improvements anticipated by the insurer increase the expected number of survivors, and consequently the value of the outstanding liabilities. To offset this effect and simultaneously ensure fairness, lower participation rates are offered. The same observation holds true for the certainty equivalent returns of the policyholders under the physical measure P. The reason for this is due to the smaller participation rates ${\delta }_i^{*}$, $i=1,2$, since a greater degree of conservativeness harms the customers’ benefits.

(2.3)

For the exceptional case where $N_1\left(0\right)=N_2\left(0\right)=1$, the fair participation rates are considerably higher than those obtained with larger portfolio sizes due to the sizeable extinction probability of the groups and the fact that the equity holders seize all the assets pertaining to the extinct group(s). As a compensation, the policyholders need to be served with substantially larger participation rates.

(2.4)

It seems that, with a very small portfolio size, e.g., $N_i\left(0\right)=10$, $i=1,2$, the portfolio is already well-diversified, i.e., the expected impact of the systematic part of the biometric risk is the only component still playing a role, since similar results are achieved as, e.g., when $N_i\left(0\right)=$ 100,000.

(2.5)

It is notable that all certainty equivalent returns lie between the risk free rate of return and the expected rate of return of the assets under P, i.e., $C_i\in (r,\mu )=(0.03,0.05)$, $i=1,2$. It is true that our life insurance policies cannot beat the pure investment into the assets due to the guaranteed interest rate, although the values obtained are much closer to $\mu$ than to r. Nevertheless, the included guarantees of the insurance products make them much less risky and are crucial for many potential customers when comparing different investment opportunities.

Table 3 displays the effect of assuming different group sizes. Our findings are listed below:

(3.1)

We observe that policyholders in the larger group obtain relatively higher fair participation rates ${\delta }_i^{*}$, $i=1,2$, and consequently mostly also relatively higher certainty equivalent returns $C_i$ on their investments when comparing them with the corresponding numbers from Table 2.

(3.2)

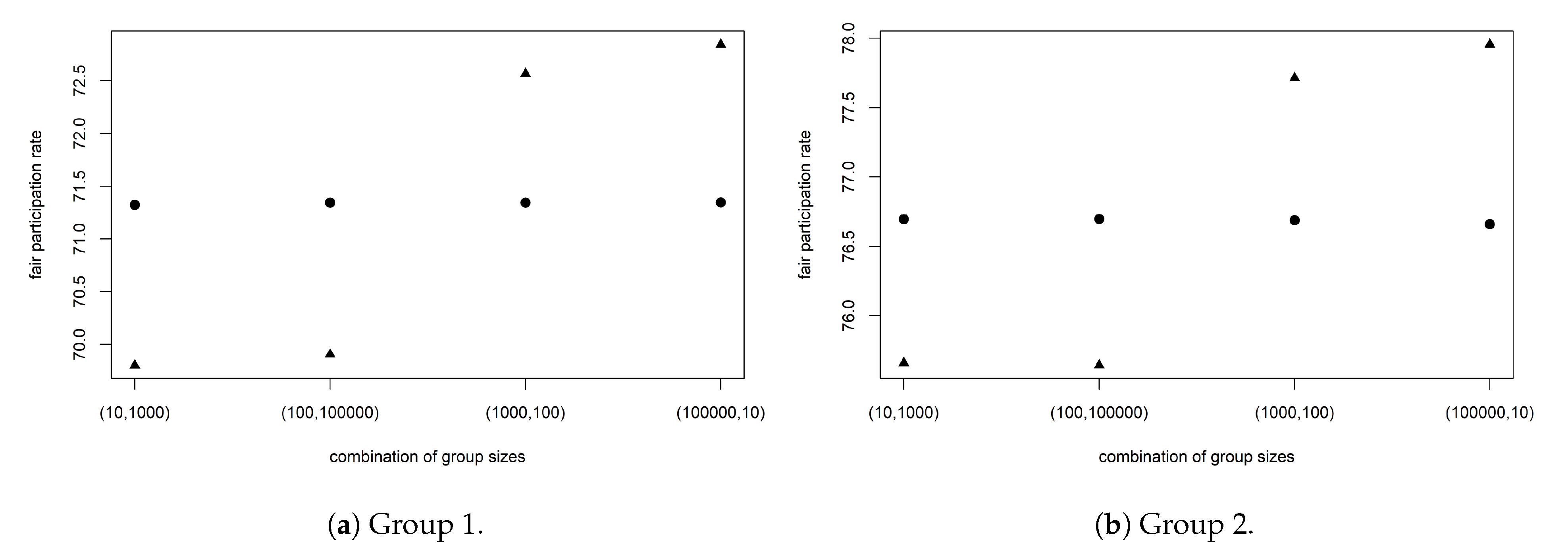
For the first group, an increase in $N_1\left(0\right)$ leads to an increase in ${\delta }_1^{*}$ and $C_1$ in general, independently of the size of the other group, while, for the second group, the opposite relations apply. We can conclude that, if there are only a few policyholders holding a lower individual guarantee than the rest, their participation in the surplus distribution must be very high to ensure fair contracts, especially if they represent a clear minority. Another related interesting fact is that a sudden spread within the values for ${\delta }_i^{*}$ and $C_i$, $i=1,2$, occurs as soon as the size ratio between the two groups shifts.

Figure 1 clearly illustrates the fact described in Remark (3.2) using the example where $E^Q\left[\Delta \right]=0.8$. In the two plots, we can further detect that the corresponding numbers from Table 2 lie in-between the ones from Table 3.

Table 4 completes Case 1 by addressing the influence of the maturity date. We observe that a longer contract duration increases both the fair participation rates ${\delta }_i^{*}$, $i=1,2$, and the certainty equivalent returns $C_i$ compared to Table 3. Moving T from 12 to 25 years implies that less policyholders are expected to survive the maturity date, consequently a lower aggregated guaranteed payment needs to be provided by the insurer. Due to the fair contract principles, the insurer is then able to provide larger participation rates for a longer contract maturity. Again, a high participation in the surplus results in a high certainty equivalent return.

Results for Case 2. In this case, the maturity dates of the groups’ policies differ. The quantity $V_2\left(T_1\right)$ in the definitions of the payoff functions (see Equations (9)–(12)) is given by

$$V_2\left(T_1\right)=E_{T_1}^Q\left[G_2\left(T_2\right)e^{-r(T_2-T_1)}\right],$$

(22)

where $E_{T_1}^Q\left[·\right]$ denotes the expectation under Q conditional on information available at time $T_1$. Since $G_2\left(T_2\right)=N_2\left(T_2\right)l\left(0\right)e^{g{T}_2}$ is proportional to $N_2\left(T_2\right)$, and by exploiting Assumptions 1 and 2 of Section 2.2, we can write (22) as

$$V_2\left(T_1\right)=e^{-r(T_2-T_1)}l\left(0\right)e^{g{T}_2}{N}_2\left(T_1\right){\left({}_{T_2-T_1}{p}_{x_2+T_1}^{*}\right)}^{\Delta }.$$

(23)

Furthermore, the remaining assets’ value $W^{\prime }\left(T_2\right)$ is defined as

$$W^{\prime }\left(T_2\right)=\left(W\left(T_1\right)-L_1\left(T_1\right)\right)e^{R\left(T_1,T_2\right)},$$

(24)

where $R\left(T_1,T_2\right)$ is the assets’ log-return for the period from $T_1$ to $T_2$, which is normally distributed with mean $\left(r-{\sigma }^2/2\right)(T_2-T_1)$ and variance ${\sigma }^2(T_2-T_1)$ under Q.10

As the first group is entirely dealt with at the earlier maturity $T_1$, its certainty equivalent return is defined as in (20). On the contrary, the second group receives a payout either at the regular maturity $T_2$, or at $T_1$ if the insurance company is then insolvent. To be able to incorporate this contingency into the computation of $C_2$, we assume that the possible payment $L_2\left(T_1\right)$ is invested into the riskless asset from $T_1$ to $T_2$ yielding an annual log-return of r, so that

$$C_2=\frac{1}{T_2}ln\left(E^P\left[\frac{L_2\left(T_1\right)e^{r(T_2-T_1)}+L_2\left(T_2\right)}{L_2\left(0\right)}\right]\right).$$

(25)

The number of surviving policyholders of the second group is now needed at both times $T_1$ and $T_2$. Consequently, under Q and conditional on $\Delta$ and $N_2\left(T_1\right)$, we obtain $N_2\left(T_2\right)\sim Binomial\left(N_2\left(T_1\right),{\left({}_{T_2-T_1}{p}_{x_2+T_1}^{*}\right)}^{\Delta }\right)$.11

Concerning the case-specific parameters, we stipulate that $\left(T_1,T_2\right)\in \left\{(10,12),(12,25)\right\}$ and $g=1.25\%$.

Table 5. Fair participation rates and certainty equivalent returns for Case 2 with $\left(T_1,T_2\right)=(10,12)$, different portfolio sizes with $N_1\left(0\right)=N_2\left(0\right)$ and different values of $E^Q\left[\Delta \right]$. All results are in percentage.

$\left({\mathit{T}}_1,{\mathit{T}}_2\right)=(10,12)$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.4$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.8$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=1$
$N_1\left(0\right)$	$N_2\left(0\right)$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$
		$C_1$	$C_2$	$C_1$	$C_2$	$C_1$	$C_2$
1	1	75.52	49.27	78.36	52.07	79.90	53.47
		4.26	4.04	4.36	4.16	4.42	4.22
10	10	73.62	47.73	74.51	48.80	74.92	49.32
		4.34	4.13	4.37	4.18	4.39	4.20
100	100	73.63	47.74	74.53	48.82	74.95	49.34
		4.34	4.13	4.37	4.18	4.39	4.20
1000	1000	73.64	47.74	74.53	48.82	74.96	49.34
		4.34	4.13	4.37	4.18	4.39	4.20
100,000	100,000	73.63	47.74	74.53	48.82	74.96	49.35
		4.34	4.13	4.37	4.18	4.39	4.20

,

Table 6. Fair participation rates and certainty equivalent returns for Case 2 with $\left(T_1,T_2\right)=(10,12)$, different portfolio sizes with $N_1\left(0\right)\ne N_2\left(0\right)$ and different values of $E^Q\left[\Delta \right]$. All results are in percentage.

$\left({\mathit{T}}_1,{\mathit{T}}_2\right)=(10,12)$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.4$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.8$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=1$
$N_1\left(0\right)$	$N_2\left(0\right)$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$
		$C_1$	$C_2$	$C_1$	$C_2$	$C_1$	$C_2$
10	1000	72.82	53.45	73.65	54.45	74.04	54.94
		4.32	4.11	4.35	4.16	4.37	4.19
100	100,000	72.84	53.52	73.71	54.53	74.14	55.02
		4.32	4.11	4.35	4.16	4.37	4.19
1000	100	74.30	38.77	75.21	39.88	75.65	40.43
		4.36	4.15	4.39	4.20	4.41	4.22
100,000	10	74.45	35.60	75.36	36.68	75.80	37.21
		4.36	4.16	4.40	4.20	4.41	4.23

and

Table 7. Fair participation rates and certainty equivalent returns for Case 2 with $\left(T_1,T_2\right)=(12,25)$, different portfolio sizes with $N_1\left(0\right)\ne N_2\left(0\right)$ and different values of $E^Q\left[\Delta \right]$. All results are in percentage.

$\left({\mathit{T}}_1,{\mathit{T}}_2\right)=(12,25)$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.4$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=0.8$		${\mathit{E}}^{\mathit{Q}}\left[\mathbf{\Delta }\right]=1$
$N_1\left(0\right)$	$N_2\left(0\right)$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$	${\delta }_1^{*}$	${\delta }_2^{*}$
		$C_1$	$C_2$	$C_1$	$C_2$	$C_1$	$C_2$
10	1000	70.61	51.90	71.29	53.75	71.66	54.62
		4.25	4.39	4.27	4.48	4.29	4.52
100	100,000	70.62	51.99	71.35	53.83	71.75	54.71
		4.25	4.39	4.28	4.48	4.29	4.52
1000	100	77.35	39.07	78.24	41.06	78.67	42.01
		4.44	4.33	4.47	4.43	4.48	4.48
100,000	10	78.19	36.59	79.13	38.59	79.58	39.52
		4.46	4.33	4.49	4.43	4.51	4.47

show our values for ${\delta }_i^{*}$ and $C_i$, $i=1,2$, for this second case.

Table 5 delivers the fair participation rates and certainty equivalent returns for the two heterogeneous and equal-sized groups of policyholders with $T_1=10$ and $T_2=12$. We can establish the following:

(5.1)

One of the main questions is: why are fair participation coefficients for the second group so much smaller compared to group 1, even though in Case 1 it was seen that a longer duration leads to higher fair participation rates? A possible explanation is the fact that only a portion of the assets ${\alpha }_{1}W\left(T_1\right)$, pertaining to the first group at $T_1$, is paid out to its policyholders if the insurer is able to achieve a surplus. As a consequence, group 2 profits from the residual amount staying in the company which boosts the probability of gaining relatively high assets’ values in the future. To maintain fairness, a lower ${\delta }_2^{*}$ is required.

(5.2)

The spread between $C_1$ and $C_2$ is always significantly positive, although it decreases as $E^Q[\Delta ]$ increases. Clearly, the substantially higher fair participation rates for group 1 play a major role here. Nevertheless, these differences are much less relevant than those between ${\delta }_1^{*}$ and ${\delta }_2^{*}$.

Figure 2 illustrates the situation described in (5.1) and shows that obtaining fairness is associated with providing the second group with a much smaller participation coefficient.

As before, the case when $N_1\left(0\right)\ne N_2\left(0\right)$ holds is evaluated for Case 2 and the corresponding results are presented in Table 6 and Table 7. As far as Table 6 is concerned, two striking features are:

(6.1)

The fair participation rates ${\delta }_i^{*}$, $i=1,2$, grow with $N_i\left(0\right)$. Therefore, it is surprising that, unlike the certainty equivalent return $C_1$ of the first group, $C_2$ declines as the second group size $N_2\left(0\right)$ increases (as in Table 3 where this also holds for ${\delta }_2^{*}$). Yet, this finding reinforces the fact that low values of ${\delta }_2^{*}$, when $N_2\left(0\right)$ is small, are necessary.

(6.2)

The most remarkable feature is given by the variation in the values of ${\delta }_2^{*}$ for a given mortality pricing assumption when changing the composition of the portfolio (in particular, when comparing cases with $N_1\left(0\right)<N_2\left(0\right)$ to cases with $N_1\left(0\right)>N_2\left(0\right)$).

To get a better understanding of Remark (6.2), a key example is shown in Figure 3 where, on the left-hand side, ${\delta }_2^{*}$ is plotted against numbers of policyholders in group 1. An increase in $N_1\left(0\right)$ results in a remarkable decrease of the participation coefficient ${\delta }_2^{*}$. The adjoining graph in Figure 3 displays, inter alia, the development of the assets’ value $W^{\prime }\left(T_2\right)$ at time $T_2$, which is relevant for the contract payoff of the second group if the insurer is solvent at $T_1$. The rise of $W^{\prime }\left(T_2\right)$ stems from the fact that the two quantities $W\left(T_1\right)$ and $L_1\left(T_1\right)$ occurring in (24) evolve differently, i.e., $W\left(T_1\right)$ grows faster than $L_1\left(T_1\right)$. Thus, the second group would benefit from a bigger size of group 1 and consequently ${\delta }_2^{*}$ needs to be lowered.

As far as Table 7 is concerned, we further observe the following:

(7.1)

Compared to Remark (6.2), the fair participation rate of the second group seems to smooth out over time within one longevity pricing assumption since the fluctuations between the varying pooling schemes subside. Specifically, ${\delta }_2^{*}$ goes down if $N_2\left(0\right)/N_1\left(0\right)$ is large (unlike Table 4 when compared to Table 3) and it goes up if $N_2\left(0\right)/N_1\left(0\right)$ is small (as in Table 4 when compared to Table 3). Looking at the values of ${\delta }_1^{*}$, the same pattern is observed, i.e., a high $N_2\left(0\right)/N_1\left(0\right)$ results in lower fair participation coefficients and a low $N_2\left(0\right)/N_1\left(0\right)$ leads to (much) higher ones.

(7.2)

Concerning the certainty equivalent returns, those of group 1 behave quite as expected, i.e., for the first two pooling schemes (low ${\delta }_1^{*}$), smaller figures of $C_1$ are obtained and for the last two combinations (high ${\delta }_1^{*}$), larger values occur, compared to Table 6. By contrast, the relevant values of $C_2$ are always significantly higher than their counterparts in the previous table. A possible reason for that is our assumption made in the specific definition of this quantity given in (25), namely that the premature payoff to the second group conditioned by a default event at time $T_1$ is invested into the riskless asset until $T_2$.

5. Concluding Remarks

Participating life insurance products with minimum guarantees still represent a large portion of the contract portfolios of many life insurers. Due to the challenges these products have had to face in the recent past, such as the ongoing low interest rate environment, it is of special importance to adequately assess the financial standing of the firms. For this purpose, we seek to establish a model which strives to include several possible influencing factors. In addition to the introduction of a financial risk component, i.e., the uncertainty about future developments of the assets, and of the default risk, i.e., the chance of a distress of the company, we also integrate the longevity risk that is specifically crucial for life insurers. Especially in the light of the fact that people steadily get older on average and because of our focus on products cashing out only the claims of surviving policyholders, like pure endowments, it is reasonable to enhance our exploration by taking this risk into account. In this way, we can also study the effects of different longevity pricing assumptions made by the insurance company that reflect its degree of conservativeness. Furthermore, we aim to incorporate an often unconsidered circumstance, namely that customers and their contracts are (partially) heterogeneous. Therefore, we simplistically divide them into two homogeneous groups. As a consequence, crucial issues, such as the impact of the usually high guarantees of old policyholders on the payout structures of new customers who are endowed with much lower guaranteed interest rates, can be surveyed.

After modelling the liabilities, we value them on a market-consistent basis leading to the feasibility of a fair contract analysis. With the aid of such an analysis, it is possible to determine appropriate policy parameters and in particular the participation rates. Building on the outcomes, we are also able to compute other interesting key figures, like the physical returns for the diverse insured persons. Eventually, we detect the effects of the different elements included in the model on the life insurer’s and the policyholders’ positions. Our main findings are listed in the following overview:

• If the insurer decides to heavily load risk premiums for the systematic part of the insurance risk, lower fair participation rates result. This in turn also hits the customers’ returns, particularly if the presumptions on the longevity risk are very prudent.
• Maintaining usual practised participation rates of $\sim 80–100\%$ (often prescribed by law) can give rise to severe financial problems for the insurer, as certain portfolio and parameter combinations actually imply smaller participation coefficients ensuring the fairness of the contracts.
• If the two groups differ exclusively in the promised minimum interest rate guarantee provided by the insurer (Case 1), the group endowed with the lower minimum interest rate guarantee receives a larger fair participation rate. This increase is intensified if the insurance company does not explicitly aim to provide similar returns to all policyholders. Consequently, the difference between the actual returns widens as well. Thus, the proposed definition of the payoff structure for this case turns out to be an option the insurer can exploit in order to protect the customers and advance the desirable goal of achieving similar returns for everyone.
• In Case 1, another observation leads to the insight that, if there are only a few policyholders holding a lower individual guarantee than the rest, their participation in the surplus sharing must be really high to ensure fair contracts, especially if they represent a clear minority.
• If the two groups differ exclusively in the contract maturity date (Case 2), the fair participation rate for the group with the longer contract duration is much lower, and so is the resulting actual return, although on a considerably smaller scale.
• In Case 2, the group with the longer contract duration receives a remarkably low fair participation rate if it outnumbers the members of the other group.

While the paper at hand is not able to capture every facet, in the given context, of a modern insurance company acting in an open market economy, we think that our setup, paired with the wide numerical analyses and related findings, helps to get a better understanding of the interaction between the several influencing variables and to assess more thoroughly possibly occurring situations with their inherent chances.

Potential aspects of future research can include, for instance, the study of alternative splitting rules in the event of bankruptcy, the allowance for a stochastic short rate model, the combination of different elements of heterogeneity, or the adoption of more sophisticated assumptions concerning the systematic biometric risk.