Abstract
In insurance mathematics, optimal control problems over an infinite time horizon arise when computing risk measures. An example of such a risk measure is the expected discounted future dividend payments. In models which take multiple economic factors into account, this problem is high-dimensional. The solutions to such control problems correspond to solutions of deterministic semilinear (degenerate) elliptic partial differential equations. In the present paper we propose a novel deep neural network algorithm for solving such partial differential equations in high dimensions in order to be able to compute the proposed risk measure in a complex high-dimensional economic environment. The method is based on the correspondence of elliptic partial differential equations to backward stochastic differential equations with unbounded random terminal time. In particular, backward stochastic differential equations—which can be identified with solutions of elliptic partial differential equations—are approximated by means of deep neural networks.
Keywords:
backward stochastic differential equations; semilinear elliptic partial differential equations; stochastic optimal control; unbounded random terminal time; machine learning; deep neural networks MSC:
60H35; 65N75; 68T07
1. Introduction
Classical optimal control problems in insurance mathematics include finding risk measures like the probability of ruin or the expected discounted future dividend payments. Mathematically, these are problems over a potentially infinite time horizon, ending at an unbounded random terminal time—the time of ruin of the insurance company. In recent models which take multiple economic factors into account, the problems are high dimensional. For computing these risk measures, optimal control problems need to be solved numerically. A standard method for solving control problems is to derive the associated Hamilton–Jacobi–Bellman (HJB) equation—a semilinear (sometimes integro) partial differential equation (PDE)—and show that its (numerical) solution also solves the original control problem. In the case of infinite time horizon problems, these HJB equations are (degenerate) elliptic. In this paper we propose a novel deep neural network algorithm for semilinear (degenerate) elliptic PDEs associated to infinite time horizon control problems in high dimensions.
We apply this method to solve the dividend maximization problem in insurance mathematics. This problem originates in the seminal work by De Finetti (1957), who introduced expected discounted future dividend payments as a valuation principle for a homogeneous insurance portfolio. This constitutes an alternative risk measure to the (even more) classical probability of ruin. Classical results on the dividend maximization problem are Asmussen and Taksar (1997); Jeanblanc-Picqué and Shiryaev (1995); Radner and Shepp (1996); Shreve et al. (1984). Overviews can be found in Albrecher and Thonhauser (2009); Avanzi (2009); for an introduction to optimization problems in insurance we refer to Azcue and Muler (2014); Schmidli (2008). Recent models for the surplus of an insurance company allow for changes in the underlying economy. Such models have been studied, e.g., in Jiang and Pistorius (2012); Leobacher et al. (2014); Sotomayor and Cadenillas (2011); Zhu and Chen (2013); Szölgyenyi (2013, 2016); Reppen et al. (2020). In Leobacher et al. (2014); Szölgyenyi (2013, 2016) hidden Markov models for the underlying economic environment were proposed that allow for taking (multiple) exogenous, even not directly observable, economic factors into account. While these authors study the dividend maximization problem from a theoretical perspective, we are interested in computing the risk measure. However, classical numerical methods fail when the problem becomes high-dimensional, that is for example when exogenous economic factors are taken into account. In this paper we propose a novel deep neural network algorithm to solve high-dimensional problems. As an application we use it to solve the dividend maximization problem in the model from Szölgyenyi (2016) in high dimensions numerically.
Classical algorithms for solving semilinear (degenerate) elliptic PDEs like finite difference or finite element methods suffer from the so-called curse of dimensionality—the computational complexity for solving the discretized equation grows exponentially in the dimension. In high-dimensions (say ) one has to resort to costly quadrature methods such as multilevel-Monte Carlo or the quasi-Monte Carlo-based method presented in Kritzer et al. (2019). In recent years, deep neural network (DNN) algorithms for high-dimensional PDEs have been studied extensively. Prominent examples are Han et al. (2017, 2018), where semilinear parabolic PDEs are associated with backward stochastic differential equations (BSDEs) through the (nonlinear) Feynman-Kac formula and a DNN algorithm is proposed that solves these PDEs by solving the associated BSDEs. In the literature there exists a variety of DNN approaches for solving PDEs, in particular (degenerate) parabolic ones. Great literature overviews are given, e.g., in Beck et al. (2020); Grohs et al. (2019a), out of which we list some contributions here: (Beck et al. 2018, 2019b, 2019c; Becker et al. 2019a, 2019b; Berg and Nyström 2018; Chan-Wai-Nam et al. 2019; Chen and Wan 2020; Dockhorn 2019; E and Yu 2018; Farahmand et al. 2017; Fujii et al. 2019; Goudenѐge et al. 2019; Han and Long 2020; Han et al. 2020; Henry-Labordѐre 2017; Huré et al. 2019; Jacquier and Oumgari 2019; Long et al. 2018; Lu et al. 2019; Lye et al. 2020; Magill et al. 2018; Pham et al. 2019; Raissi 2018; Sirignano and Spiliopoulos 2018).
While mathematical finance control problems (e.g., investment problems) are studied over relatively short time horizons, leading to (degenerate) parabolic PDEs, in insurance mathematics they are often considered over the whole lifetime of the insurance company, leading to (degenerate) elliptic PDEs. For elliptic PDEs, a multilevel Picard iteration algorithm is studied in Beck et al. (2020), a derivative-free method using Brownian walkers without explicit calculation of the derivatives of the neural network is studied in Han et al. (2020), and a walk-on-the-sphere algorithm is introduced in Grohs and Herrmann (2020) for the Poisson equation, where the existence of DNNs that are able to approximate the solution to certain elliptic PDEs is shown.
In the present article we propose a novel DNN algorithm for a large class of semilinear (degenerate) elliptic PDEs. For this, we adopt the approach from Han et al. (2018) for (degenerate) parabolic PDEs. The difference here is that we use the correspondence between the PDEs we seek to solve and BSDEs with random terminal time. This correspondence was first presented in Pardoux (1998), and elaborated afterwards, e.g., in Briand and Hu (1998); Briand and Confortola (2008); Darling and Pardoux (1997); Pardoux (1999); Royer (2004).
As these results are not as standard as the BSDE correspondence to parabolic PDEs, we summarize the theory in Section 2 for the convenience of the reader. In Section 3 we present the DNN algorithm, and test it in Section 4.1 and Section 4.2. In Section 4.3 we present the model from Szölgyenyi (2016) in which we seek to solve the dividend maximization problem and hence to compute the risk measure. That this method works also in high dimensions is demonstrated at the end of Section 4.3, where numerical results are presented.
The method presented here can be applied to many other high-dimensional semilinear (degenerate) elliptic PDE problems in insurance mathematics, such as the calculation of ruin probabilities, but we emphasize that its application possibilities are not limited to insurance problems.
2. BSDEs Associated with Elliptic PDEs
This section contains a short survey on scalar backward stochastic differential equations with random terminal times and on how they are related to a certain type of semilinear elliptic partial differential equations.
2.1. BSDEs with Random Terminal Times
Let be a filtered probability space satisfying the usual conditions and let be a d-dimensional standard Brownian motion on it. We assume that is equal to the augmented natural filtration generated by W. For all real valued row or column vectors x, let denote their Euclidean norm. We need the following notations and definitions for BSDEs.
Definition 1.
A BSDE with random terminal time is a triple f), where
- the terminal time is an -stopping time,
- the generator f: is a process which satisfies that for all , the process is progressively measurable,
- the terminal condition is an -measurable random variable with on .
Definition 2.
A solution to the BSDE f) is a pair of progressively measurable processes with values in , where
- Y is continuous -a.s. and for all , the trajectories belong to , and is in ,
- for all and all it holds a.s. that
- and on .
Results on existence of solutions of BSDEs with random terminal time can be found in Pardoux’ seminal article Pardoux (1998) (see (Pardoux 1998, Theorem 3.2)), in Briand and Confortola (2008) for generators with quadratic growth (see (Briand and Confortola 2008, Theorem 3.3)), and, e.g., in Briand and Hu (1998); Briand et al. (2003); Darling and Pardoux (1997); Pardoux (1999); Royer (2004); many of them cover multidimensional state spaces for the Y-process.
Optimal control problems which can be treated using a BSDE setting have for example been studied in (Briand and Confortola 2008, Section 6). For this they consider generators of the forward-backward form
where X is a forward diffusion (see also the notation in the following subsection), is a Banach space, r is a Hilbert space-valued function (in their setting z takes values in the according dual space) with linear growth, g a real valued function with quadratic growth in u, and . In the sequel we focus on generators of forward-backward form.
2.2. Semilinear Elliptic PDEs and BSDEs with Random Terminal Time
In this subsection we recall the connection between semilinear elliptic PDEs and BSDEs with random (and possibly infinite) terminal time. The relationship between the theories is based on a nonlinear extension of the Feynman-Kac formula, see (Pardoux 1998, Section 4).
We define the forward process X as the stochastic process satisfying a.s.,
where and and are globally Lipschitz functions.
In this paper we consider the following class of PDEs.
Definition 3.
- A semilinear (degenerate) elliptic PDE on the whole is of the formwhere the differential operator acting on is given byand is such that the process is a generator of a BSDE in the sense of Definition 1.
- We say that a function u satisfies Equation (4) with Dirichlet boundary conditions on the open, bounded domain , ifwhere is a bounded, continuous function.
Definition 4.
- 1.
- 2.
In order to keep the notation simple, we do not highlight the dependence of on x.
For later use we also introduce the following notion of solutions of PDEs, which we will use later.
Definition 5.
- A function is called viscosity subsolution of (4), if for all and all points where has a local maximum,
- A function is called viscosity supersolution of (4), if for all and all points where has a local minimum,
- A function is called viscosity solution of (4), if it is a viscosity sub- and supersolution.
A similar definition of viscosity solutions can be given for the case of Dirichlet boundary conditions (6), see Pardoux (1998).
For later use, note that (8) can be rewritten in forward form as
Theorem 1
((Pardoux 1998, Theorem 4.1)). Let meet the assumptions of (Pardoux 1998, Theorem 3.2) and let satisfy
with λ as in (Pardoux 1998, Theorem 3.2). If u is a classical solution of the PDE (4), then
solve the BSDE (7). An equivalent statement can be established for the system with boundary conditions (6) and Equation (8), see Pardoux (1998).
Note that for all , Y and Z are stochastic processes adapted to . Therefore, , are -measurable and hence a.s. deterministic. For us, the connection between PDEs and BSDEs is of relevance because of the converse result, where delivers a solution to the respective PDE.
Theorem 2
((Pardoux 1998, Theorem 4.3)). Assume that for some , the function F satisfies for all
- (i)
- ,
- (ii)
- ,
- (iii)
- .
The case of the Dirichlet problem requires additional assumptions on the domain G and the exit time from (8). We refer to (Pardoux 1998, Theorem 4.3). A corresponding result for BSDEs with quadratic generator is (Briand and Confortola 2008, Theorem 5.2).
To conclude, the correspondence between PDE (6) and BSDE (8) is given by , , . For tackling elliptic PDEs which are degenerate (as it is the case for our insurance mathematics example) we need to take the relationship a little further in order to escape the not so convenient structure of the Z-process. We factor for cases where this equation is solvable for ( needs not necessarily be invertible) and define 1, giving the correspondence , , . This relationship motivates us to solve semilinear degenerate elliptic PDEs by solving the corresponding BSDEs forward in time (cf. (9))
for by approximating the paths of by a DNN, see Section 3. Doing so, we obtain an estimate of a solution value for a given .
3. Algorithm
The idea of the proposed algorithm is inspired by Han et al. (2018), where the authors use the correspondence between BSDEs and semilinear parabolic PDEs to construct a DNN algorithm for solving the latter. In the same spirit, we construct a DNN algorithm based on the correspondence to BSDEs with random terminal time for solving semilinear elliptic PDEs.
The details of the algorithm are described in three steps of increasing specificity. First we explain the DNN algorithm mathematically. This is done below. Second, Algorithm 1 at the end of this section provides a pseudocode. Third, our program code is provided on Github2 under a creative commons license. The algorithm is implemented in a generic manner so that it can be reused for other elliptic PDE problems.
The goal of the algorithm is to calculate solution values of the semilinear (degenerate) elliptic PDE of interest. For the construction of the algorithm we use the correspondence to a BSDE with random terminal time. Recall from Section 2 that such a BSDE is given by a triplet that can be determined from the given PDE and by
and
Furthermore, recall that we have identified , where u is the solution of the PDE we are interested in.
The first step for calculating u is to approximate (10) up to the stopping time . To make this computationally feasible, we choose T large and stop at , hence at T at the latest. Now let , . We simulate M paths of the Brownian motion W. With this we approximate the forward process using the Euler–Maruyama scheme, that is and
In the next step we compute . For all , are approximated by DNNs, each mapping G to . As noted above, the implementation of this (and all other steps) is provided.
Now, we initialize and use the above approximations to compute the solution to the BSDE forward in time by approximating (11):
Note that due to this construction, indirectly is also approximated by a DNN as a combination of DNNs.
For the training of the involved DNNs, we compare with the terminal value . This defines the loss function for the training:
After a certain number of training epochs the loss function is minimized and we obtain an approximate solution value of the PDE.
Remark 1.
Several approximation errors arise in the proposed algorithm:
- 1.
- the approximation error of the Euler–Maruyama method, which is used for sampling the forward equation,
- 2.
- the error of approximating the expected loss,
- 3.
- the error of cutting off the potentially unbounded random terminal time at time T,
- 4.
- the approximation error of the deep neural network model for approximating for each .
It is well known that for any continuous function we can find DNNs that approximate the function arbitrarily well, see Hornik (1991); Hornik et al. (1989). This is, however, not sufficient to make any statement about the approximation quality. Results on convergence rates are required. Though this question is already studied in the literature (see, e.g., Beck et al. 2019a, 2020; Berner et al. 2020; Elbrächter et al. 2018; Gonon et al. 2019; Grohs et al. 2018, 2019a, 2019b; Hutzenthaler et al. 2018, 2020a, 2020b; Jentzen et al. 2018; Kutyniok et al. 2019; Reisinger and Zhang 2019), results on convergence rates for given constructions are yet scarce and hence many questions remain open while the number of proposed DNN algorithms grows.
We close this section with some comments on the implementation.
Remark 2.
- All DNNs are initialized with random numbers.
- For each value of x we average over 5 independent runs. The estimator for is calculated as the mean value of in the last 3 network training epochs of each run, sampled according to the validation size (see below).
- We choose a nonequidistant time grid in order to get a higher resolution for earlier (and hence probably closer to the stopping time) time points.
- We use tanh as activation function.
- We compute simultaneously for 8 values of x by using parallel computing.
| Algorithm 1 Elliptic PDE Solver for a BSDE with stopping time |
| Require: number of training epochs E, maximal time T, step-size , number of timesteps N, number of sample paths M, number of hidden layer neurons dim, initial (random) starting values 1: function TrainableVariables() ▹ see Pytorch or Tensorflow return a trainable variable with dimension initialized by . 2: end function 3: function Subnetwork(x) ▹ allowing x to be a tensor containing M rows (samples) return a trainable DNN, evaluated at x. 4: end function 5: for do 6: ▹ Initialize nonequidistant timesteps 7: end for 8: for do 9: Sample Brownian motion trajectory 10: Sample path from forward process 11: calculate stopping time 12: calculate terminal value 13: set for all 14: end for 15: = TrainableVariables) ▹ Initialize u 16: TrainableVariables) ▹ Initialize 17: for do 18: 19: 20: end for 21: for do 22: for do 23: for do 24: 25: if then break 26: end if 27: end for 28: = Subnetwork 29: end for 30: update all trainable variables and the subnetwork’s weights according to the loss function 31: end for return |
4. Examples
In this section we apply the proposed algorithm to three examples. The first one serves as a validity check, the second one as an academic example with a nonlinearity. Finally, we apply the algorithm to solve the dividend maximization problem under incomplete information.
4.1. The Poisson Equation
The first example we study is the Poisson equation—a linear PDE.
Let , , , , and
Solving (14) is equivalent to solving the BSDE with
up to the stopping time .
To obtain a reference solution for this linear BSDE we use an analytic formula for the expectation of , see (Øksendal 2003, Example 7.4.2, p. 121). This yields
Numerical Results
We compute on the and the for 15 different values of x. Figure 1 shows the approximate solution of u obtained by the DNN algorithm on the diagonal points (in blue) and the analytical reference solution (in green). Table 1 contains the parameters we use.
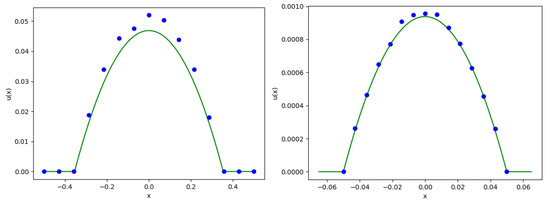
Figure 1.
Approximate solution (blue) and reference solution (green) for the Poisson equation on the (left) and on the (right).

Table 1.
Parameters for the Poisson equation.
Note that as the expected value of decreases linearly in d, we adapt the cut off time T for accordingly.
4.2. Quadratic Gradient
The second example is a semilinear PDE with a quadratic gradient term.
Let , , and . We consider the PDE
corresponding to the BSDE
In addition, for this example we have an analytic reference solution given by
Numerical Results
As in the previous example we compute for 15 different values of x on the and the . Figure 2 shows the approximate solution of u obtained by the DNN algorithm on the diagonal points (in blue) and the analytical reference solution (in green). Table 2 contains the parameters we use.
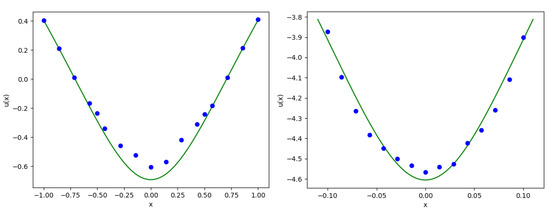
Figure 2.
Approximate solution (blue) and reference solution (green) for the equation with quadratic gradient on the (left) and on the (right).

Table 2.
Parameters for the equation with quadratic gradient.
While classical numerical methods for PDEs would be a much better choice in the case , their application would not be feasible in the case .
4.3. Dividend Maximization
The goal of this paper is to show how to use the proposed DNN algorithm to solve high-dimensional control problems that arise in insurance mathematics. We finally arrived at the point where we are ready to do so.
Our example comes from Szölgyenyi (2016), where the author studies De Finetti’s dividend maximization problem in a setup with incomplete information about the current state of the market. The hidden market-state process determines the trend of the surplus process of the insurance company and is modeled as a d-state Markov chain. Using stochastic filtering, in Szölgyenyi (2016) they achieve to transform the one-dimensional problem under incomplete information to a d-dimensional problem under complete information. The cost is additional dimensions in the state space. We state the problem under complete information using different notation than in Szölgyenyi (2016) in order to avoid ambiguities.
The probability that the Markov chain modeling the market-state is in state is given by
where
, B is a one-dimensional Brownian motion, are the values of the surplus trend in the respective market-states of the hidden Markov chain, and denotes the intensity matrix of the chain.
Let be the dividend rate process. The surplus of the insurance company is given by
where . For later use we define also the dividend free surplus
The processes (18) and (20) form the d-dimensional state process underlying the optimal control problem we aim to solve.
The goal of the insurance company is to determine its value by maximizing the discounted dividends payments until the time of ruin , that is it seeks to find
where is a discount rate, A is the set of admissible controls, and denotes the expectation under the initial conditions for and . Admissible controls are -progressively measurable, -valued for and fulfill for , cf. Szölgyenyi (2016).
In order to tackle the problem, we solve the corresponding Hamilton–Jacobi–Bellmann (HJB) equation4 from Szölgyenyi (2016),
where is the second order degenerate elliptic operator
The supremum in (23) is attained at
The boundary conditions in direction are given by
No boundary conditions are required for the other variables, cf. Szölgyenyi (2016).
In (Szölgyenyi 2016, Corollary 3.6) it is proven that the unique viscosity solution to (24) solves the optimal control problem (22). Hence, we can indeed solve the control problem by solving the HJB equation.
For the numerical approximation we cut off at . Hence, and .
For the convenience of the reader we derive the BSDE corresponding to (24). The forward equation is given by
that is
where , , and
We claim that the BSDE associated to (24) is given in forward form by
Applying Itô’s formula to yields
Canceling terms verifies (in a heuristic manner) (24).
Hence, the corresponding BSDE has the parameters
and
if .
Numerical Results
As for this example we have no analytic reference solution at hand, we use the solution from Szölgyenyi (2016) for the case , which was obtained by a finite difference method and policy iteration. Then we show that the DNN algorithm also provides an approximation in high dimensions in reasonable computation time.
As in the previous examples we compute on the and on the for 15 different values of x. Figure 3 shows the approximate solution of the HJB equation and hence the value of the insurance company obtained by the DNN algorithm (in blue) and the reference solution from Szölgyenyi (2016) (in green) for the case . For we have no reference solution at hand. Figure 4 shows the loss for a fixed value of x in the case . Table 3 and Table 4 contain the parameters we use.
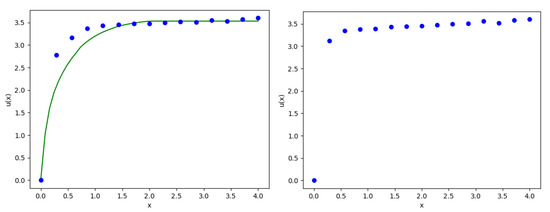
Figure 3.
Approximate solution (blue) and reference solution (green) for the dividend problem on the for fixed (left) and on the for fixed (right, without reference solution).
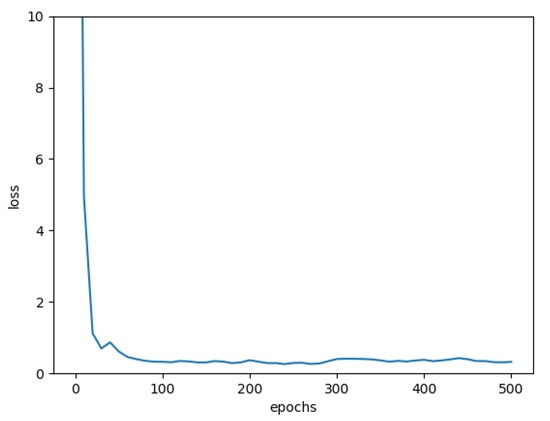
Figure 4.
Interpolated loss for the case .

Table 3.
Parameters for the dividend problem.

Table 4.
Intensity matrix values for the dividend problem.
5. Conclusions
The goal of this paper was to compute the risk measure given by the expected discounted future dividend payments in a complex high-dimensional economic environment. This demonstrates the effectiveness of using DNN algorithms for solving some high-dimensional PDE problems in insurance mathematics that cannot be solved by classical methods. In the literature the focus so far was on parabolic PDE problems; however, in insurance mathematics we often face problems up to an unbounded random terminal time, e.g., the time of ruin of the insurance company, leading to (degenerate) elliptic problems.
Hence, we have proposed a novel deep neural network algorithm for a large class of semilinear (degenerate) elliptic PDEs associated to infinite time horizon control problems in high dimensions. The method extends the DNN algorithm proposed by Han, Jetzen, and E Han et al. (2018), which was developed for parabolic PDEs, to the case of (degenerate) elliptic semilinear PDEs. We have attacked the problem inspired by a series of results by Pardoux Pardoux (1998).
Of course, in low dimensions one would not use the proposed DNN algorithm—classical methods are more efficient. However, recent models are frequently high dimensional, in which case classical methods fail due to the curse of dimensionality. Then the DNN algorithm presented here can be applied to compute the desired quantity.
We emphasize that the method presented here can also be applied to many other high-dimensional semilinear (degenerate) elliptic PDE problems in insurance mathematics and beyond.
An implementation of the algorithm is provided on Github5 under a creative commons license.
Author Contributions
Writing–original draft, S.K., A.S. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
Stefan Kremsner was supported by the Austrian Science Fund (FWF): Project F5508-N26, which is part of the Special Research Program “Quasi-Monte Carlo Methods: Theory and Applications”.
Acknowledgments
The authors thank Gunther Leobacher for discussions and suggestions that improved the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Albrecher, Hansjörg, and Stefan Thonhauser. 2009. Optimality results for dividend problems in insurance. RACSAM Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas 103: 295–320. [Google Scholar] [CrossRef]
- Asmussen, Søren, and Michael Taksar. 1997. Controlled diffusion models for optimal dividend pay-out. Insurance: Mathematics and Economics 20: 1–15. [Google Scholar] [CrossRef]
- Avanzi, Benjamin. 2009. Strategies for dividend distribution: A review. North American Actuarial Journal 13: 217–51. [Google Scholar] [CrossRef]
- Azcue, Pablo, and Nora Muler. 2014. Stochastic Optimization in Insurance—A Dynamic Programming Approach. Springer Briefs in Quantitative Finance. New York, Heidelberg, Dordrecht and London: Springer. [Google Scholar]
- Beck, Christian, Sebastian Becker, Philipp Grohs, Nor Jaafari, and Arnulf Jentzen. 2018. Solving stochastic differential equations and Kolmogorov equations by means of deep learning. arXiv arXiv:1806.00421. [Google Scholar]
- Beck, Christian, Fabian Hornung, Martin Hutzenthaler, Arnulf Jentzen, and Thomas Kruse. 2019a. Overcoming the curse of dimensionality in the numerical approximation of Allen-Cahn partial differential equations via truncated full-history recursive multilevel Picard approximations. arXiv arXiv:1907.06729. [Google Scholar]
- Beck, Christian, Sebastian Becker, Patrick Cheridito, Arnulf Jentzen, and Ariel Neufeld. 2019b. Deep splitting method for parabolic PDEs. arXiv arXiv:1907.03452. [Google Scholar]
- Beck, Christian, Weinan E, and Arnulf Jentzen. 2019c. Machine learning approximation algorithms for high-dimensional fully nonlinear partial differential equations and second-order backward stochastic differential equations. Journal of Nonlinear Science 29: 1563–619. [Google Scholar] [CrossRef]
- Beck, Christian, Lukas Gonon, and Arnulf Jentzen. 2020. Overcoming the curse of dimensionality in the numerical approximation of high-dimensional semilinear elliptic partial differential equations. arXiv arXiv:2003.00596. [Google Scholar]
- Becker, Sebastian, Patrick Cheridito, and Arnulf Jentzen. 2019a. Deep optimal stopping. Journal of Machine Learning Research 20: 74. [Google Scholar]
- Becker, Sebastian, Patrick Cheridito, Arnulf Jentzen, and Timo Welti. 2019b. Solving high-dimensional optimal stopping problems using deep learning. arXiv arXiv:1908.01602. [Google Scholar]
- Berg, Jens, and Kaj Nyström. 2018. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 317: 28–41. [Google Scholar] [CrossRef]
- Berner, Julius, Philipp Grohs, and Arnulf Jentzen. 2020. Analysis of the generalization error: Empirical risk minimization over deep artificial neural networks overcomes the curse of dimensionality in the numerical approximation of Black–Scholes partial differential equations. SIAM Journal on Mathematics of Data Science 3: 631–57. [Google Scholar] [CrossRef]
- Briand, Philippe, and Ying Hu. 1998. Stability of BSDEs with random terminal time and homogenization of semi-linear elliptic PDEs. Journal of Functional Analysis 155: 455–94. [Google Scholar] [CrossRef]
- Briand, Philippe, Bernard Delyon, Ying Hu, Étienne Pardoux, and Lucretiu Stoica. 2003. Lp solutions of backward stochastic differential equations. Stochastic Processes and their Applications 108: 109–29. [Google Scholar] [CrossRef]
- Briand, Philippe, and Fulvia Confortola. 2008. Quadratic BSDEs with random terminal time and elliptic PDEs in infinite dimension. Electronic Journal of Probability 13: 1529–61. [Google Scholar]
- Chan-Wai-Nam, Quentin, Joseph Mikael, and Xavier Warin. 2019. Machine learning for semi linear PDEs. Journal of Scientific Computing 79: 1667–712. [Google Scholar] [CrossRef]
- Chen, Yangang, and Justin W. L. Wan. 2020. Deep neural network framework based on backward stochastic differential equations for pricing and hedging american options in high dimensions. Quantitative Finance, 1–23. [Google Scholar] [CrossRef]
- Darling, Richard W. R., and Étienne Pardoux. 1997. Backwards SDE with random terminal time and applications to semilinear elliptic PDE. The Annals of Probability 25: 1135–59. [Google Scholar] [CrossRef]
- De Finetti, Bruno. 1957. Su un’impostazione alternativa della teoria collettiva del rischio. Transactions of the XVth International Congress of Actuaries 2: 433–43. [Google Scholar]
- Dockhorn, Tim. 2019. A discussion on solving partial differential equations using neural networks. arXiv arXiv:1904.07200. [Google Scholar]
- E, Weinan, and Bing Yu. 2018. The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems. Communications in Mathematics and Statistics 6: 1–12. [Google Scholar] [CrossRef]
- Elbrächter, Dennis, Philipp Grohs, Arnulf Jentzen, and Christoph Schwab. 2018. DNN expression rate analysis of high-dimensional PDEs: Application to option pricing. arXiv arXiv:1809.07669. [Google Scholar]
- Farahmand, Amir-Massoud, Saleh Nabi, and Daniel Nikovski. 2017. Deep reinforcement learning for partial differential equation control. Paper presented at 2017 American Control Conference (ACC), Seattle, WA, USA, May 24–26; pp. 3120–27. [Google Scholar]
- Fujii, Masaaki, Akihiko Takahashi, and Masayuki Takahashi. 2019. Asymptotic expansion as prior knowledge in deep learning method for high dimensional BSDEs. Asia-Pacific Financial Markets 26: 391–408. [Google Scholar] [CrossRef]
- Gonon, Lukas, Philipp Grohs, Arnulf Jentzen, David Kofler, and David Šiška. 2019. Uniform error estimates for artificial neural network approximations. arXiv arXiv:1911.09647. [Google Scholar]
- Goudenège, Ludovic, Andrea Molent, and Antonino Zanette. 2019. Machine learning for pricing American options in high dimension. arXiv arXiv:1903.11275. [Google Scholar]
- Grohs, Philipp, Fabian Hornung, Arnulf Jentzen, and Philippe Von Wurstemberger. 2018. A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black-Scholes partial differential equations. arXiv arXiv:1809.02362. [Google Scholar]
- Grohs, Philipp, Arnulf Jentzen, and Diyora Salimova. 2019a. Deep neural network approximations for Monte Carlo algorithms. arXiv arXiv:1908.10828. [Google Scholar]
- Grohs, Philipp, Fabian Hornung, Arnulf Jentzen, and Philipp Zimmermann. 2019b. Space-time error estimates for deep neural network approximations for differential equations. arXiv arXiv:1908.03833. [Google Scholar]
- Grohs, Philipp, and Lukas Herrmann. 2020. Deep neural network approximation for high-dimensional elliptic PDEs with boundary conditions. arXiv arXiv:2007.05384. [Google Scholar]
- Han, Jiequn, Arnulf Jentzen, and Weinan E. 2017. Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations. Communications in Mathematics and Statistics 5: 349–80. [Google Scholar]
- Han, Jiequn, Arnulf Jentzen, and Weinan E. 2018. Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences 115: 8505–10. [Google Scholar] [CrossRef]
- Han, Jiequn, and Jihao Long. 2020. Convergence of the deep BSDE method for coupled FBSDEs. Probability, Uncertainty and Quantitative Risk 5: 1–33. [Google Scholar] [CrossRef]
- Han, Jihun, Mihai Nica, and Adam Stinchcombe. 2020. A derivative-free method for solving elliptic partial differential equations with deep neural networks. Journal of Computational Physics 419: 109672. [Google Scholar] [CrossRef]
- Henry-Labordère, Pierre. 2017. Deep primal-dual algorithm for BSDEs: Applications of machine learning to CVA and IM. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Hornik, Kurt. 1991. Approximation capabilities of multilayer feedforward networks. Neural Networks 4: 251–57. [Google Scholar] [CrossRef]
- Hornik, Kurt, Maxwell Stinchcombe, and Halbert White. 1989. Multilayer feedforward networks are universal approximators. Neural Networks 2: 359–66. [Google Scholar] [CrossRef]
- Huré, Côme, Huyên Pham, and Xavier Warin. 2019. Some machine learning schemes for high-dimensional nonlinear PDEs. arXiv arXiv:1902.01599. [Google Scholar]
- Hutzenthaler, Martin, Arnulf Jentzen, Thomas Kruse, Tuan Anh Nguyen, and Philippe von Wurstemberger. 2018. Overcoming the curse of dimensionality in the numerical approximation of semilinear parabolic partial differential equations. arXiv arXiv:1807.01212. [Google Scholar]
- Hutzenthaler, Martin, Arnulf Jentzen, and Philippe von Wurstemberger. 2020a. Overcoming the curse of dimensionality in the approximative pricing of financial derivatives with default risks. Electronic Journal of Probability 25: 73. [Google Scholar] [CrossRef]
- Hutzenthaler, Martin, Arnulf Jentzen, Thomas Kruse, and Tuan Anh Nguyen. 2020b. A proof that rectified deep neural networks overcome the curse of dimensionality in the numerical approximation of semilinear heat equations. SN Partial Differential Equations and Applications 1: 1–34. [Google Scholar] [CrossRef]
- Jacquier, Antoine Jack, and Mugad Oumgari. 2019. Deep PPDEs for rough local stochastic volatility. arXiv arXiv:1906.02551. [Google Scholar] [CrossRef]
- Jeanblanc-Picqué, Monique, and Albert Nikolaevich Shiryaev. 1995. Optimization of the flow of dividends. Russian Mathematical Surveys 50: 257–77. [Google Scholar] [CrossRef]
- Jentzen, Arnulf, Diyora Salimova, and Timo Welti. 2018. A proof that deep artificial neural networks overcome the curse of dimensionality in the numerical approximation of Kolmogorov partial differential equations with constant diffusion and nonlinear drift coefficients. arXiv arXiv:1809.07321. [Google Scholar]
- Jiang, Zhengjun, and Martijn Pistorius. 2012. Optimal dividend distribution under markov regime switching. Finance and Stochastics 16: 449–76. [Google Scholar] [CrossRef]
- Kritzer, Peter, Gunther Leobacher, Michaela Szölgyenyi, and Stefan Thonhauser. 2019. Approximation methods for piecewise deterministic markov processes and their costs. Scandinavian Actuarial Journal 2019: 308–35. [Google Scholar] [CrossRef] [PubMed]
- Kutyniok, Gitta, Philipp Petersen, Mones Raslan, and Reinhold Schneider. 2019. A theoretical analysis of deep neural networks and parametric PDEs. arXiv arXiv:1904.00377. [Google Scholar]
- Leobacher, Gunther, Michaela Szölgyenyi, and Stefan Thonhauser. 2014. Bayesian dividend optimization and finite time ruin probabilities. Stochastic Models 30: 216–49. [Google Scholar] [CrossRef][Green Version]
- Long, Zichao, Yiping Lu, Xianzhong Ma, and Bin Dong. 2018. PDE-Net: Learning PDEs from Data. Paper presented at 35th International Conference on Machine Learning, Stockholm, Sweden, July 10–15; pp. 3208–16. [Google Scholar]
- Lu, Lu, Xuhui Meng, Zhiping Mao, and George Karniadakis. 2019. DeepXDE: A deep learning library for solving differential equations. arXiv arXiv:1907.04502. [Google Scholar]
- Lye, Kjetil O, Siddhartha Mishra, and Deep Ray. 2020. Deep learning observables in computational fluid dynamics. Journal of Computational Physics 410: 109339. [Google Scholar] [CrossRef]
- Magill, Martin, Faisal Qureshi, and Hendrick de Haan. 2018. Neural networks trained to solve differential equations learn general representations. Advances in Neural Information Processing Systems 31: 4071–81. [Google Scholar]
- Øksendal, Bernt. 2003. Stochastic Differential Equations. Berlin: Springer. [Google Scholar]
- Pardoux, Étienne. 1998. Backward stochastic differential equations and viscosity solutions of systems of semilinear parabolic and elliptic PDEs of second order. In Stochastic Analysis and Related Topics VI. Berlin: Springer, pp. 79–127. [Google Scholar]
- Pardoux, Étienne. 1999. BSDEs, weak convergence and homogenization of semilinear PDEs. In Nonlinear Analysis, Differential Equations and Control. Berlin: Springer, pp. 503–49. [Google Scholar]
- Pham, Huyen, Xavier Warin, and Maximilien Germain. 2019. Neural networks-based backward scheme for fully nonlinear PDEs. arXiv arXiv:1908.00412. [Google Scholar]
- Radner, Roy, and Larry Shepp. 1996. Risk vs. profit potential: A model for corporate strategy. Journal of Economic Dynamics and Control 20: 1373–93. [Google Scholar] [CrossRef]
- Raissi, Maziar. 2018. Deep hidden physics models: Deep learning of nonlinear partial differential equations. The Journal of Machine Learning Research 19: 932–55. [Google Scholar]
- Reisinger, Christoph, and Yufei Zhang. 2019. Rectified deep neural networks overcome the curse of dimensionality for nonsmooth value functions in zero-sum games of nonlinear stiff systems. arXiv arXiv:1903.06652. [Google Scholar]
- Reppen, A Max, Jean-Charles Rochet, and H. Mete Soner. 2020. Optimal dividend policies with random profitability. Mathematical Finance 30: 228–59. [Google Scholar] [CrossRef]
- Royer, Manuela. 2004. BSDEs with a random terminal time driven by a monotone generator and their links with PDEs. Stochastics and Stochastic Reports 76: 281–307. [Google Scholar] [CrossRef]
- Schmidli, Hanspeter. 2008. Stochastic Control in Insurance. Probability and its Applications. London: Springer. [Google Scholar]
- Shreve, Steven E., John P. Lehoczky, and Donald P. Gaver. 1984. Optimal consumption for general diffusions with absorbing and reflecting barriers. SIAM Journal on Control and Optimization 22: 55–75. [Google Scholar] [CrossRef]
- Sirignano, Justin, and Konstantinos Spiliopoulos. 2018. DGM: A deep learning algorithm for solving partial differential equations. Journal of Computational Physics 375: 1339–64. [Google Scholar] [CrossRef]
- Sotomayor, Luz R., and Abel Cadenillas. 2011. Classical and singular stochastic control for the optimal dividend policy when there is regime switching. Insurance: Mathematics and Economics 48: 344–54. [Google Scholar] [CrossRef]
- Szölgyenyi, Michaela. 2013. Bayesian dividend maximization: A jump diffusion model. In Handelingen Contactforum Actuarial and Financial Mathematics Conference, Interplay between Finance and Insurance, February 7–8. Brussel: Koninklijke Vlaamse Academie van België voor Wetenschappen en Kunsten, pp. 77–82. [Google Scholar]
- Szölgyenyi, Michaela. 2016. Dividend maximization in a hidden Markov switching model. Statistics & Risk Modeling 32: 143–58. [Google Scholar]
- Zhu, Jinxia, and Feng Chen. 2013. Dividend optimization for regime-switching general diffusions. Insurance: Mathematics and Economics 53: 439–56. [Google Scholar] [CrossRef]
| 1 | Since is solvable for , f is well-defined. |
| 2 | |
| 3 | The numerical examples were run on a Lenovo Thinkpad notebook with an Intel Core i7 processor (2.6 GHz) and 16 GB memory, without CUDA. |
| 4 | For abbreviation we use for etc. |
| 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).