Abstract
Risk taking is an inherent element of the banking business. Banks make conscious decisions regarding risk taking as they expect to make more return if they take more risk. The primary objective of this study is to empirically investigate the efficiency of Indian banks in generating return relative to the risk they take. If the efficiency measurement is not adjusted for different risk preferences, then a bank earning lower return at lower risk may be misclassified as less efficient compared to peers earning the same level of return, but operating at a higher level of risk. This paper uses measures of liquidity risk, credit risk, market risk, and insolvency risk to develop a risk-return stochastic frontier in order to examine the risk efficiency of banks, a novel attempt in the Indian context. The paper further analyzes the efficiency of banks with respect to bank specific characteristics and risk management regimes. The models are estimated using data from a sample of 47 major banks for the period 2009–2018. The study reveals that Indian banks, on average, exhibited lower efficiency in trading risk against return during the sample period.
JEL Classification:
G21; G28; G32
1. Introduction
Modern banking theory emphasizes that risk taking is an inherent element of the banking business. Banks make conscious decisions regarding risk taking as they expect to make a higher return if they take more risk. However, taking excessive risk increases the possibility of banks losing heavily. Thus, the objective of risk management for banks has two key goals: first, to ensure that the risk being taken matches the bank’s capacity to absorb losses in case of unexpected, extreme adverse events; second, to ensure that the bank generates adequate profits relative to that risk. In order to ensure financial stability in the banking sector, banking regulators demand banks to hold sufficient capital to support unexpected losses, and the Basel Capital Accords provide a common regulatory framework for capital allocation. While capital requirements and adequacy have been well researched, banks’ efficiency to make profits relative to the risks they take has been less explored in the literature.
As the risk level of the operating plan is an important factor affecting the profitability of banks, when a bank takes lending or investment decisions, the bank not only considers risks but also evaluates its return relative to that risk (Marrison 2002). If the efficiency measurement is not adjusted for different risk preferences, then a bank earning lower return at lower risk may be misclassified as less efficient compared to peers earning the same level of return, but operating at a higher risk. Koetter (2008) has pointed out that the traditional efficiency measures that focus on cost minimization and profit maximization seem not to account well for the risk associated with the banks’ chosen operating plans. However, with the adoption of Basel standards for risk measurement, a new strand of literature has emerged that models efficiency according to risk preference. To the best of our knowledge, no such study has been carried out to measure the efficiency of Indian banks in trading risk against return.
Against this backdrop, this paper aims to measure the risk efficiency of Indian banks in generating return relative to the risk they take. Efficiency is analyzed by developing a multi-parameter risk efficiency model using the Stochastic Frontier approach. Risk-return frontiers are developed by considering the risk level of banks with respect to the major risks faced by them, such as credit, market, liquidity and insolvency risks, as inputs and operating profit over total assets as output. We use data from a sample of Indian banks for the period 2009–2018 to estimate the models. Our sample period covers two regulatory regimes, Basel II from March 2009 to March 2013 and Basel III from April 2013 onwards. The Basel III regulatory reform required banks to maintain higher capital quality and higher capital ratios as one of the key prudential tools to reduce insolvency risk (BIS 2017). Further, Basel III focused on enhancing the robustness and risk sensitivity of risk measurement methods. In addition, in India during Basel III, many banks have progressed to advanced measurement methods from standardized approaches to risk measurement, and hence better risk recognition is expected. This paper, therefore, specifically compares the risk efficiency of banks between the two regulatory regimes. As the literature on cost and profit efficiency of Indian banks (e.g., Kumbhakar and Sarkar 2003; Das and Kumbhakar 2010) has well established the existence of ownership and size effects in the Indian banking system, we further examine whether risk efficiency also varies between public sector banks (PSBs) and private sector banks (PVBs) as well as between small and large banks.
The paper is divided into six sections. In Section 2, we have reviewed the literature, followed by a discussion on methodology in Section 3. In Section 4, we discuss the variables used in our analysis and the econometric models. Section 5 presents the results of the analysis and discusses the findings. The final section summarizes the findings of the study with suggestions.
2. Review of the Literature
The literature on the analysis of bank efficiency is comprehensive. There are two broad approaches followed to explain bank efficiency; non-structural and structural (Hughes and Mester 2008). The non-structural approach compares performance among banks using a variety of financial ratios that capture various aspects of performance and study the relationship of the ratio with bank specific and environment specific factors, such as investment strategy, ownerships, size, etc. On the other hand, the structural approach relies on a theoretical model of the banking firm and the concept of optimization. The older literature followed the structural approach and applied the traditional microeconomic theory of production to banking firms. This assumes that banks choose a production plan that either minimizes costs, given its output mix and input prices, or maximizes profits, given the prices of its inputs and outputs (see Berger and Mester 2001; Kumbhakar and Sarkar 2003; Nurboja and Kosak 2017; Lee and Huang 2017). However, these approaches neglect the risk taking behavior of banks and consider only inputs, outputs, and their respective prices for modeling efficiency. While some studies have attempted to account for the risk associated with the chosen operating plans, they treat various risks as exogenous variables and model them as constraints under the traditional cost-minimizing or profit-maximizing framework. Thus, such measures may fail to fully capture the risk associated with the banks’ objectives and chosen operating plans (Koetter 2008). This is because risk preferences and profit expectations are potentially heterogeneous across banks, possibly due to the different objectives they follow. This has led to a new stream of literature modeling bank performance within a utility maximizing framework (see Hughes and Moon 1995; Hughes et al. 2001; Hughes and Mester 2013). The utility maximizing approach assumes that banks select the optimum production plan according to the utility they get from it (Hughes and Moon 1995). For example, banks may choose riskier plans with the objective of getting a higher rate of return. Accordingly, the bank performance is modeled in the risk-return space that incorporates the trade-off between return and risk.
Studies that employ the utility maximization approach are relatively fewer. Hughes and Mester (2008) estimated how the scale depends on a banks’ capital structure and examined the risk-taking of US banks using the value-maximizing approach, rather than cost-minimizing. They find that better diversification is associated with larger-scale economies, while increased and inefficient risk taking is associated with smaller-scale economies. Koetter (2008) analyzed the risk efficiency of banks in Germany by using a risk-return stochastic frontier model with expected return on equity as the output and the standard deviation of the return as risk input. He reported that the mean risk-return efficiency was higher than cost and profit efficiency. Ozyildirim and Ozdincer (2008) analyzed the risk efficiency of Turkish banks by taking operational income over total assets as output and three inputs as risk specifications, viz. capital adequacy ratio for insolvency risk, the ratio of non-performing loans over total loans (NPL) for credit risk, and the deposits to third party fund ratio for liquidity risk.
In the Indian context, studies have investigated the efficiency and productivity of the Indian banking system. Das and Kumbhakar (2010), Kumar et al. (2016), Kaur and Gupta (2015) and Bhatia and Mahendru (2015) focused on the technical efficiency of Indian banks. Kumbhakar and Sarkar (2003), Ray and Das (2010) and Smitha et al. (2018) focused on their cost and profit efficiency. In general, these studies have reported an improvement in the efficiency of Indian banks over the years. They have observed that public sector banks (PSBs) are more profit efficient and less cost efficient relative to private sector banks (PVBs), and the banks which are bigger in size in terms of assets are more efficient compared to smaller banks. Few of these studies analyzed the impact of risk on cost or profit efficiency, by including NPL and capital ratio as exogenous variables. In this study, we have attempted to analyze the risk efficiency of Indian banks in the risk-return framework.
As the objective of this study is to analyze the efficiency of banks in managing risk-return trade-off, we have adopted the utility maximization approach, using the stochastic frontier analysis, similar to Koetter (2008) and Ozyildirim and Ozdincer (2008); however, this differs from the previous risk efficiency studies. First, this study includes several forward-looking risk measures, detailed in Section 4, adapted from the Basel methodology to represent various risks, instead of using ex-post realizations of risks, such as the NPL, used in previous studies. Second, the study analyses the effect of bank specific factors, such as ownership, size, and risk management regime (Basel II/III) on banks’ efficiency to manage risk-return trade-off. Moreover, to the best of our knowledge, this is the first study attempting to assess the risk efficiency of Indian banks using stochastic frontier analysis with a risk-return frontier.
3. Methodology
The standard framework for efficiency estimation consists of developing a production frontier or a boundary, consisting of the best performing decision making units (DMU) that produce optimum possible outputs for a given set of inputs. Then, the production frontier is used as a benchmark to measure the relative performance of other DMUs in the sample. Broadly, two different approaches are followed in the literature for estimating the efficiency of DMUs, viz. parametric approach and non-parametric approach. Data Envelopment Analysis (DEA), popularly known as the non-parametric approach, uses the linear programming technique to identify efficient DMUs. The parametric approach utilizes econometric estimation to define the best performing DMUs (Mastromarco 2008). The parametric or statistical approach requires a production function, a specification about the functional form of the relationship between the output and input variables, to be defined. In addition, the inefficiency deviation from the production frontier, is modeled as an additional stochastic term.
The stochastic frontier model is written in general form as suggested by Greene (2002), as follows:
where the function ‘f’ defines the production function (a cost or profit or utility function) containing regressors as input quantities. β is a vector of parameters of . The term () in the model represents the deviations of the DMUs from the frontier, where ‘S’ denotes sign of , which takes a positive/negative sign when the production function is for output maximization/minimization. The economic logic behind this specification is that the production process is subject to two economically distinguishable random disturbances: statistical noise represented by , and technical inefficiency represented by .
The error term, , is assumed to follow iid , which captures the measurement errors and other noises that are neglected by non-parametric models. The inefficiency terms, are assumed to be independent of , and to satisfy ≥ 0. The composed error term, () is an asymmetric variable, with negative skewness for profit or utility functions (output maximization) and positive skewness for cost functions (output minimization).
Since the error and inefficiency terms are independent, their variance is . The proportion of to the total variance, defined as is an important parameter that measures the deviation from the efficiency frontier, due to inefficiency. If is zero, this implies that the error term dominates and that there is no inefficiency, and all deviations from the frontier representing best performance units result from the error term. If is close to 1, then the inefficiency term dominates, and most of the deviations from the frontier result from inefficiency.
The is generally modelled as exponential, half-normal, truncated normal, or gamma distribution. Given the specification for the random variables and , the maximum likelihood (ML) technique is used to estimate the parameters of the stochastic frontier model (Mastromarco 2008). To test the hypothesis , the Wald statistic (W) or Likelihood ratio (LR) test statistic is used. The likelihood ratio test statistic is given by , where and are the values of the log-likelihood function under the null () and alternative () hypotheses. Since the alternative hypothesis is 0 < γ < = 1, the one-sided test is performed. When the null hypothesis is true, the test statistic (W) is asymptotically distributed as a standard normal random variable. Coelli (1995) reported that under the null hypothesis H0, the LR statistic is asymptotically distributed as a mixture of chi-square distributions, with degrees of freedom (DF) equal to the number of restrictions. The critical values of the statistic LR were given by Kodde and Palm (1986). The technical efficiencies of ith DMU is computed from the estimated stochastic frontier as:
The literature shows a large variance of efficiency models depending on assumptions about the distribution of , and how DMU specific factors such as size of the firm, operating environments, etc., that represent observable heterogeneity unrelated to the production structure, are modelled. If DMU specific factors are assumed to influence the structure of the technology, using which conventional inputs are converted into outputs but not efficiency, then they are included in the production function “f” (Kumbhakar and Sarkar 2003). If DMU specific factors are considered the source of inefficiency, then they are used for modelling the parameters of the distribution of uit. Among the various stochastic frontier specifications used in the literature, the models used by Battese and Coelli (1992) and Battese and Coelli (1995) are widely used in the literature. In this paper, we follow their 1992 specification for estimating time behavior of risk efficiencies, and their 1995 model to estimate the effects of bank size, bank ownership and risk management regimes on banks’ efficiency to trade risk against return. Since in the utility maximization framework the functional form of the production process is unknown, we have employed a linear model in this study.
4. Variables and Econometric Models
Following the literature, we use the operating profit over total assets (OPOA) as the output variable to represent return and several forward looking risk measures as inputs representing liquidity risk, credit risk, market risk and insolvency risk. Though many studies on cost and profit efficiency have used return on asset (ROA) as the output variable, we preferred OPOA because the ROA is highly influenced by the provision taken for non-performing loans that cease to generate returns. Hence, ROA is not appropriate to gauge banks’ ability to price their product against likely risks. Moreover, studies that use ROA consider NPL as one of the inputs of the production process along with other non-risk variables such as deposits, labor, etc., but in the risk return framework, only risk variables that affect future returns are considered. However, for the sake of ensuring the robustness of the efficiency estimates, we also evaluate the model with ROA as the input.
The leverage ratio (LVR), the ratio for Tier1-1 capital to the total exposure, proposed in the Basel III framework is used as a measure of insolvency risk instead of of Capital to Risk Weighted Asset Ratio (CRAR) used in earlier studies. This is because CRAR encapsulates other risks that are captured separately in our analysis. Highly capitalized banks are likely to have lower bankruptcy costs, which in turn reduces their funding costs, thus generating higher profits (Berger 1995). Moreover, highly capitalized banks engage more in prudent lending and borrow less, which in turn reduces their costs and increases their profitability (Tan 2016). We, therefore, expect banks with higher LVR to generate a higher return.
The risk density of credit exposure (RDCE), defined as the ratio of risk weighted credit exposure to total credit exposure, and the ratio of restructured loans to total loans (RSL), are used as measures of credit risk. As risk weighted assets are calculated by the banks based on the risk assessment of creditworthiness of the borrower, the RDCE, based on Basel guidelines, can be considered a measure of the ex-ante credit risk assumed by banks when they assign loans. The RSL is used as a measure of ex-post realizations of credit risks instead of the NPL, as NPL ceases to generate returns, whereas the restructured loans continue to do so. Banks with a higher risk density are expected to earn higher returns to be risk efficient. Similarly, as a higher proportion of restructured loans in the portfolio indicates higher credit risk, a risk efficient bank with higher RSL is expected to earn a higher return.
The risk density of market risk exposure (RDME), defined as the ratio of risk weighted market risk exposure to the total market exposure, and the asset liability gap (GAP) in the portfolio, are included as measures of market risk. RDME captures market risk associated with investments in all types of instruments, such as interest rate related products, shares, foreign exchange, and other derivative products such as options, forward rate agreements, other forward contracts, bond futures, interest rates and cross-currency swaps, forward foreign exchange positions, etc. However, as interest rate risk is a major market risk in banks’ investment portfolios (Gonzalez-Hermosillo 1999), we also use the ratio of difference between risk sensitive assets and risk sensitive liabilities maturing in one year to total assets (GAP), as a traditional measure to capture interest rate risk. As the GAP ratio decreases (negative), the value of long term assets financed with short term liabilities increases and the portfolio becomes more exposed to interest rate risk. Hence, a higher return is expected when the ratio falls.
The ratio of current assets over total assets (CATA) is used as a measure of liquidity risk. Though measures such as ratio of liquid assets to short-term liabilities, customer deposits to total (non-interbank) loans, government securities/total assets, etc., are also used in the literature as measures of liquidity risk, we use CATA mainly because it allows us to directly relate return and liquidity risk. As liquid assets prevent banks from losses due to rapid price deterioration, and due to the maturity mismatch, as short term assets normally earn lower returns compared to long terms assets, banks with higher liquidity risks (lower CATA) are expected to earn higher returns.
We have not included some risks faced by banks such as sovereign risk, concentration risk, operational risks, etc., in this study because banks’ expectations of returns are either not directly influenced by such risks, or measuring such risks is difficult. Moreover, as the credit and market risks account for a major portion of the risk faced by Indian banks (in terms of the Risk Weighted Assets), we do not expect any major variation in estimated risk efficiency due to the exclusion of such risks.
Accordingly, the following stochastic frontier model is postulated for analysis:
where are random variables assumed to be iid , and independent of the .
We assume two different specifications for . Following Battese and Coelli (1992), the first specification of is as follows:
where are non-negative random variables which are assumed to account for technical inefficiency and are assumed to be iid , bounded below by the truncation point zero, η is a parameter to be estimated, and T is the last period. If η < 0, then increases as t increases, implying an increasing inefficiency. If η > 0, then decreases, which leads to a decrease in inefficiency as t increases. For η = 0 and μ > 0, then follow a truncated normal distribution and we obtain a time invariant model. When η = 0 and μ = 0, follow a half normal distribution.
Following Battese and Coelli (1995), the second specification of is as follows:
where
Furthermore, are assumed to be distributed as truncated , bounded below by the variable truncation point and follow iid .
Where the control variable REGIME represents the Basel II/III regimes, it takes the value 0 for the Basel II regime and 1 for the Basel III regime. As the Basel III regulation was implemented in India in April 2013, the period from 2014–2019 is considered as Basel III regime, and the earlier period as Basel II regime. The variable OWNERSHIP represents ownership of the bank and takes the value 0 for public sector banks and 1 for private sector banks. The variable SIZE represents the size of the bank measured as the log value of total assets.
The bank level data of 47 major banks from 2009 to 2018, collected from their respective websites as well as from the website of Reserve Bank of India (RBI), has been used for this study. It constitutes a panel data of 461 bank years, with 23 PVBs and 24 PSBs. As of March 2018, the banks included in our sample accounted for 95.9% of the total assets of all scheduled commercial banks operating in India. The models are estimated using FRONTIER application software.
5. Results and Discussion
We start our analysis with the visualization of input and output variables used in the risk efficiency models. Figure 1 presents the average return (OPOA) (on the right-hand scale) of banks included in our study plotted against various risk variables. The mean of the variables measured across bank groups, regulatory regimes and bank size is given in Table 1. It can be seen from the last panel of Figure 1 that, on average, profitability of banks declined sharply over the sample period. At the same time, the value of most risk variables exhibited an increasing trend, particularly during the Basel III regime (2014–2018), indicating a decline in risk efficiency post implementation of Basel III guidelines. The operating profit, on average, declined to 1.94% of the total assets during the Basel III regime as against 2.14% during the Basel II regime (Table 1). However, barring the insolvency risk, the level of all other risks remained higher during the Basel III regime.
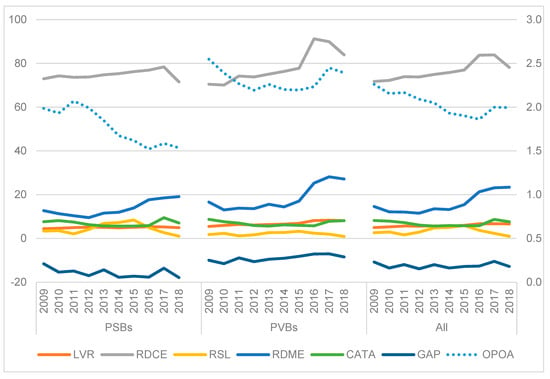
Figure 1.
Return and Risks: Bank Groups. Source: Author’s calculation.

Table 1.
Mean of the Variables.
A comparison of the data of PSBs and PVBs shown in the first and second panel of Figure 1 reveals that PVBs, on average, were more profitable as compared to PSBs. Though PVBs and PSBs had comparable risk levels during the Basel II regime, the risk level of PVBs, particularly the forward looking measures of credit risk (RDCE) and market risk (RDME), increased at a higher pace during the Basel III regime. However, unlike PSBs, the PVBs could improve their profitability during the Basel III regime despite slow credit off take. It appears that PVBs were more risk efficient than PSBs. However, the comparison of data of small and big size1 banks, does not provide any conclusive view on the difference in risk-efficiency between them (Table 1).
Though Figure 1 and Table 1 provide an overall view of the relative position of the risk and return of public and private sector banks, of Basel II and III regimes, and of small and large banks, it is somewhat difficult to make conclusions about efficiency using aggregate values of these indicators reported in Table 1. Although the risk variables are strictly not comparable, an analysis of the composition of risk-weighted assets of the banks included in our sample indicates that RWA for credit exposure accounts for a major portion of the total RWA of Indian banks, followed by market risk and operational risk. Hence, the variables RDCE and RSL assume more importance in the efficiency analysis. A comparison of OPOA vs. RDCE and RSL across bank groups indicates that PVBs earn higher returns compared to those of PSBs for the given level of credit risk. The significant value of t-statistic for the mean difference of the variables across bank ownership, size and regulatory regimes justifies the use of these control variables in the efficiency analysis. Further, it also indicates a structural break and role reversal between public and private sector banks during the Basel III regime. Whether such differences are due to change in the general economic condition or due to the results of just a few banks in a particular year needs to be studied in a statistical framework. This necessitates the need for the estimation of stochastic frontier models that measure returns relative to risk frontier level and explain efficiency in terms of exogenous variables, such as time, ownership, and size.
Table 2 presents the results of the maximum likelihood estimation of the two stochastic frontier models that we considered for our analysis. In model 1, the risk return frontier is modeled as Equation (3) with the inefficiency function given in Equation (4), whereas in model 2, Equation (3) is used with the specification of inefficiency function given in Equation (5). Model 1, wherein the inefficiency is assumed to be time variant, is estimated for the whole sample as well as separately for PSBs and PVBs to understand how efficiency of these banks behaved over time. Model 2, wherein the inefficiency is modeled as a function of risk management regimes, bank size, and ownership, is estimated primarily to validate the results of model 1. The coefficients of models 1 and 2 show that all input risk variables, except CATA in model 1 and CATA and RSL in model 2 are significant and have the same sign in both models. However, coefficients of model 1 estimated separately for PSBs and PVBs indicate that both managed risk-return trade-off differently.

Table 2.
Results of the Estimated Models.
As our primary objective is to estimate risk efficiency of individual banks in comparison to the best performing banks in the whole sample, we first check whether the coefficients of models 1 and 2 are theoretically consistent. The positive and significant coefficient of LVR suggests that banks with low insolvency risks (well capitalized) generate higher returns. The result is consistent with the findings of earlier studies that leverage ratio and profitability are positively associated (Ghosh and Chatterjee 2015). The results further confirm theories on the optimum capital decision of banks, particularly the trade-off theory used in corporate finance, which suggests that the decision-maker, typically a manager, balances the various costs and benefits of the leverage (Frank and Goyal 2007). The negative coefficients of RDCE and RSL, the variables representing the credit risk, in models 1 and 2 indicate banks’ inefficiency in pricing advances and loans according to the perceived risk. As advances and loans form a major portion of the banks’ portfolios, this is a matter of great concern. Regarding market risk, both RDME and GAP have a positive and significant impact on operating profit, confirming the banks’ efficiency in managing risks in their investment portfolios. This could also be attributed to the low risk in their investment portfolio because it consists of a higher proportion of long-term government securities that attract low capital charges under the standard duration approach used for RDME calculation. The negative coefficient of CATA indicates that profitability increases with a decrease in CATA (increase in liquidity risk). As interest earned on current assets, which are of short-term maturity, are lower compared to those on assets with long-term maturity, banks having lower proportions of such current assets (higher liquidity risk) make higher profits. Therefore, in general, it can be noted that estimated coefficients of risk return frontiers are theoretically consistent.
Turning to the parameters of the inefficiency function, the relatively high and significant value of in model 1 suggests that about 70 per cent of the variation in return from the frontier is due to inefficiency. The LR statistic, which is greater than the critical value (5.528) of the mixed chi-square statistic with three degrees of freedom at 1% significant level, further confirms the overall fitness of the model and the presence of bank-specific inefficiency (Kodde and Palm 1986).
The negative and significant value of η indicates that, on average, efficiency has declined over the sample period. A comparison of η between PSBs and PVBs shows that the efficiency of PSBs, on average, declined at a higher rate than that of PVBs. An analysis of estimated efficiency of individual banks from model 1, using Equation (2), further reveals that PSBs, on average, were less efficient than PVBs in trading risk against return and the efficiency of public sector banks declined at a higher pace as seen in the value of η (Figure 2). To check the robustness of the model, we also estimated model 1 with ROA as the output variable. However, the estimated and η are found to be similar to those produced by model 1 with OPOA as output.
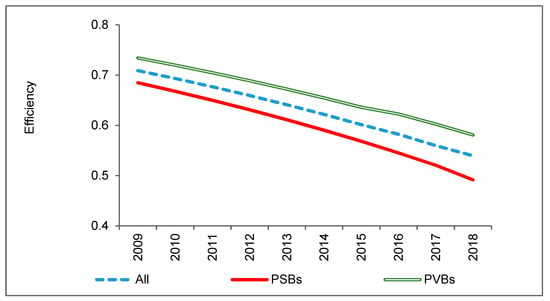
Figure 2.
Bank group–mean efficiency. Source: Author’s calculation.
In model 2, the value of declined substantially and is not found to be statistically significant indicating that the control variables included in the model explain the bank specific inefficiency to a large extent. As in the case of model 1, the LR statistic of model 2 is also significant confirming the appropriateness of modeling the risk inefficiency of banks in the stochastic frontier framework.
Moving on to the behavior of inefficiency with respect to the specific control variables, the positive and significant coefficient of REGIME indicates that the mean risk inefficiency of the banks was higher during the Basel III regime as compared to the Basel II regime which is again in sync with the efficiency estimates of model 1. There are multiple reasons for this. First, the profitability of banks declined substantially during the Basel III regime, particularly that of PSBs. This is because the PSBs followed an aggressive lending strategy during the Basel II regime. A significant portion of those assets later became NPA and had to be restructured or written off during the Basel III period. This has led to the depletion of their capital. At the same time, Basel III norms required the banks to increase their capital ratio progressively from 9% in 2013 to 11.5% by 2019, to augment additional capital as counter cyclical buffer. Therefore, banks, in particular, PSBs, had to resort to cutting back their lending activities to maintain the desired level of capital ratio. Reduction in credit growth together with a higher level of restructured loans contributed to a reduction in profitability. Second, rising interest rates and steep increase in loans during 2012–2015, can be attributed to the buildup of risk, particularly credit risk, during the Basel III period. Third, increased risk recognition through the adoption of advanced risk measurement methods, particularly by PVBs, could have also attributed to the increase in reported risk. Therefore a decline in profitability together with an increase in risk, particularly credit and market risk, can be attributed to the decline in efficiency during the Basel III regime.
The negative and significant coefficient of OWNERSHIP in model 2 reveals that PVBs, on average, were more risk efficient than PSBs during the entire sample period, which is again in line with the results of model 1. The coefficients of the interaction terms REGIME × OWNERSHIP in model 2 is not statistically significant. However, the behaviour of banks in managing risk-return trade-off significantly varied between PSBs and PVBs. While both return and risks of PVBs increased during the Basel III regime, a declining trend is seen for PSBs (Figure 1). The counter-cyclical lending strategy followed by PVBs helped them to maintain asset growth and profitability during the entire sample period. However, their risk level, particularly ex-ante credit and market risks, RDCE and RDME, were higher than that of PSBs despite lower NPAs. This was because PSBs could clean up a higher proportion of advances through write-offs of the NPAs that attract higher risk weight in RDCE calculation than that of PVBs. Moreover, PVBs’ portfolios consisted of a higher proportion of off-balance sheet items that are exposed to both market and credit risks. However, the asset liability GAP was higher for PSBs. Therefore, our study establishes that PVBs are not only profit and cost efficient as reported in the previous studies, but they are also more risk efficient when compared to PSBs. The negative and significant value of the estimated coefficient of the control variable SIZE indicates that bigger banks were more efficient in managing risks. Mean efficiency of small and large banks obtained from model 1 also confirms this (Figure 3). In fact, the efficiency of small banks, on average declined at a higher rate compared to large banks. This result is in alignment with previous studies on profit and cost efficiencies of Indian Banks (Kumbhakar and Sarkar 2003), and it reconfirms theories on the scale of the economy, which facilitates banks in putting in place more sophisticated risk measurement processes and gives them more pricing power.
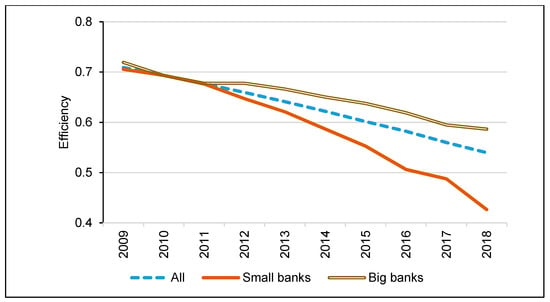
Figure 3.
Bank size–mean efficiency. Source: Author’s calculation.
6. Conclusions
This paper has analyzed the efficiency of Indian banks in managing risk-return trade-off by adopting the utility maximization approach and using the stochastic frontier models. The study has used two models proposed by Battese and Coelli (1992, 1995), wherein technical inefficiency is modeled as a truncated normal distribution, with a time varying parameter in the first model and as a function of bank specific factors in the second model. The risk-return frontier was estimated using several forward-looking risk measures, adapted from the Basel methodology, covering major risks faced by banks such as credit risk, market risk, liquidity risk and insolvency risk as inputs. The results indicate that Indian banks, on average, exhibited inefficiency in managing risk-return tradeoff. The inefficiency, on average, increased over time during the sample period and was higher during the Basel III regime. A dip in profitability due to factors such as low credit growth, increased NPA and restructured loans, coupled with regulatory changes that warranted higher capital ratio and increased risk recognition, contributed to the deterioration of risk efficiency during Basel III. The results show that PVBs are not only profit and cost efficient as seen in other studies, but also more risk efficient. The counter-cyclical lending strategy followed by PVBs together with the adoption of sound risk management practices could have facilitated PVBs to earn higher returns than PSBs for the given level of risk. Though the efficiency of both PSBs and PVBs declined over the period, the efficiency of public sector banks declined at a higher pace. The results also revealed that bigger banks were more efficient in managing risk-return trade-off due to economies of scale.
Thus, to summarize, banks in India need to improve their efficiency in generating returns on the risk they take. The ownership effect points out that, for the banks to become more risk efficient, they need to have independent, professional and risk conscious management. Banks also need to adopt measures to enhance risk recognition and implement risk based pricing, using measures such as risk adjusted return on capital (RAROC). The size effect of the risk efficiency points towards a need for greater bank consolidation so that economies of scale will help them to manage risk-return trade-off more efficiently.
Author Contributions
Conceptualization, Methodology, J.N., P.D., D.L.; Analysis and Writing—Original Draft Preparation, J.N.; Writing—Review & Editing, P.D., D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Disclaimer
The opinions expressed in this paper are those of authors and not of the institutions they are affiliated.
References
- Battese, George, and Timothy James Coelli. 1992. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. Journal of Productivity Analysis 1: 153–69. [Google Scholar] [CrossRef]
- Battese, George, and Timothy James Coelli. 1995. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empirical Economics 20: 325–32. [Google Scholar] [CrossRef]
- Berger, Allen N. 1995. The Profit-Structure Relationship in Banking—Tests of Market-Power and Efficient-Structure Hypotheses. Journal of Money Credit and Banking 27: 404–31. [Google Scholar] [CrossRef]
- Berger, Allen N., and Mester Loretta J. 2001. Explaining the Dramatic Changes in Performance of US Banks: Technological Change, Deregulation, and Dynamic Changes in Competition. Working Paper. Pennsylvania: University of Pennsylvania. Available online: https://pdfs.semanticscholar.org/21e8/7e6d74195eaf8359d542a32657e4d3738b3f.pdf (accessed on 1 January 2018).
- Bhatia, Aparna, and Mahendru Megha. 2015. Assessment of technical efficiency of public sector banks in India using data envelopment analysis. Eurasian Journal of Business and Economics 8: 115–40. [Google Scholar] [CrossRef]
- Bank for International Settlement (BIS). 2017. Basel III: Finalising post-crisis reforms. Available online: https://www.bis.org/bcbs/publ/d424.htm (accessed on 1 January 2018).
- Coelli, Tim. 1995. Estimators and hypothesis tests for a stochastic frontier function: A monte carlo analysis. Journal of Productivity Analysis 6: 247–268. [Google Scholar] [CrossRef]
- Das, Abhiman, and Subal C. Kumbhakar. 2010. Productivity and efficiency dynamics in Indian banking: An input distance function approach incorporating quality of inputs and outputs. Journal of Applied Econometrics 27: 205–34. [Google Scholar] [CrossRef]
- Frank, Murray Z., and Vidhan K. Goyal. 2007. Trade-Off and Pecking Order Theories of Debt. Handbook of Corporate Finance: Empirical Corporate Finance. Handbooks in Finance Series; North-Holland: Elsevier. Available online: https://pdfs.semanticscholar.org/e05f/12544c3ca1aa47cf2c61ac4c56e4abeb7b03.pdf (accessed on 31 March 2018).
- Ghosh, Saibal, and Goutam Chatterjee. 2015. Capital Structure, Ownership and Crisis: How Different Are Banks. RBI working paper series (DEPR) 06; Mumbai: Reserve Bank of India. [Google Scholar]
- Gonzalez-Hermosillo, Brenda. 1999. Determinants of Ex-Ante Banking System Distress: A Macro-Micro Empirical Exploration of Some Recent Episodes. IMF Working Paper 99/33. Washington: International Monetary Fund. [Google Scholar]
- Greene, W. 2002. Fixed and Random Effects in Stochastic Frontier Models. Working Paper no. 02-16. New York: New York University, Stern School of Business. [Google Scholar]
- Hughes, Joseph P., and Loretta J. Mester. 2013. Who said large banks don’t experience scale economies? Evidence from a risk-return-driven cost function. Journal of Financial Intermediation 22: 559–85. [Google Scholar] [CrossRef]
- Hughes, Joseph P., and Choon-Goel Moon. 1995. Measuring Bank Efficiency When Managers Trade Return for Reduced Risk. Working Paper, Department of Economics. Available online: https://ideas.repec.org/p/rut/rutres/199520.html (accessed on 1 January 2018).
- Hughes, Joseph P., Loretta J. Mester, and Choon-Geol Moon. 2001. Are scale economies in banking elusive or illusive? Evidence obtained by incorporating capital structure and risk-taking into models of bank production. Journal of Banking and Finance 25: 2169–208. [Google Scholar] [CrossRef]
- Hughes, Joseph P., and Loretta J. Mester. 2008. Efficiency in Banking: Theory, Practice, and Evidence. In The Oxford Handbook of Banking. Edited by N. Allen and P. Berger. Available online: https://www.econstor.eu/obitstream/10419/31302/1/568268954.pdf (accessed on 1 January 2018).
- Kaur, Sandeepa, and P. K. Gupta. 2015. Productive efficiency mapping of the Indian banking system using data envelopment analysis. Procedia Economics and Finance 25: 227–38. [Google Scholar] [CrossRef]
- Kodde, David A., and Franz C. Palm. 1986. Wald criteria for jointly testing equality and inequality restrictions. Econometrica 54: 1243–48. [Google Scholar] [CrossRef]
- Michael, Koetter. 2008. The stability of efficiency rankings when risk-preferences and objectives are different. The European Journal of Finance 14: 115–35. [Google Scholar]
- Kumar, Mukesh, Vincent Charles, and Chandra Sekhar Mishra. 2016. Evaluating the performance of Indian Banking sector using DEA during post-reform and global financial crisis. Journal of Business Economics and Management 17: 156–72. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., and Subrata Sarkar. 2003. Deregulation, ownership, and productivity growth: Evidence from Indian banks. Journal of Money, Credit, and Banking 35: 403–24. [Google Scholar] [CrossRef]
- Lee, Chi-chuan, and Tai-Hsin Huang. 2017. Cost efficiency and technological gap in Western European Banks: A stochastic meta-frontier analysis. International Review of Economics and Finance 48: 161–78. [Google Scholar] [CrossRef]
- Marrison, Christoppher. 2002. Fundamentals of Risk Measurement, 1st ed. New York: McGraw-Hill Education. [Google Scholar]
- Marrison, Christoppher. 2008. Stochastic Frontier Models. Statistics CIdE 2008—University of Salento Department of Economics and Mathematics—September, 2008. Available online: http://www.camillamastromarco.it/CIDE/STFR.pdf (accessed on 30 March 2018).
- Nurboja, Bashkim, and Marko Kosak. 2017. Banking efficiency in South East Europe: Evidence for financial crises and the gap between new EU members and candidate countries. Economic Systems 41: 122–38. [Google Scholar] [CrossRef]
- Ozyildirim, Cenktan, and Begumhan Ozdincer. 2008. Risk specifications in risk efficiency analysis. International Journal of Mathematics and Computers in Simulation 2: 36–41. [Google Scholar]
- Ray, Subhash C., and Abhiman Das. 2010. Distribution of cost and profit efficiency: Evidence from Indian Banking. European Journal of Operational Research 201: 297–307. [Google Scholar] [CrossRef]
- Nair, Smitha, V. Gopikumar, and V. Asha. 2018. An empirical analysis of banking Sector efficiency in emerging economies. International Journal of Pure and Applied Mathematics 118: 467–83. [Google Scholar]
- Tan, Yong. 2016. The impact of risk and competition on bank profitability in China. International Financial Markets, Institutions and Money 40: 85–110. [Google Scholar] [CrossRef]
| 1 | Classified based on median asset size. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).