EM Estimation for the Poisson-Inverse Gamma Regression Model with Varying Dispersion: An Application to Insurance Ratemaking
Abstract
1. Introduction
2. The Poisson-Inverse Gamma Regression Model with Varying Dispersion
3. The EM Algorithm
- E-step: Given the estimates obtained from the rth iteration, compute for all , the pseudo-valuesandThe Equations (13)–(15) involved in the E-step of the algorithm have closed form expressions. However, unlike the case with Equations (13) and (14), which can be easily evaluated, as is well known, see, for instance, Mencía and Sentana (2012), it is not always possible to obtain numerically reliable direct derivatives of the Bessel function with respect to its order, which is involved in the second term of Equation (15). In this study, in order to compute Equations (13)–(15) we rely on the function Egig within the R package ghyp, which was contributed by Weibel et al. (2020). Note that, in the case of Equation (15), Egig can provide an accurate numerical approximation of the first derivative of the modified Bessel function with respect to its order by using the function grad from the R package numDeriv, see Gilbert and Varadhan (2019).
- M-step: Using , and from the E-step and the Newton-Raphson algorithm twice, find the maximum global point of the function, i.e., obtain the updated estimates and .
- -
- Firstly, taking the derivatives of the function with respect to we obtain the following results:andfor and and whereSubsequently, the iterative procedure for the Newton–Raphson algorithm for goes, as follows:
- -
- Secondly, differentiating the function with respect to givesfor and , where and are the digamma and trigamma functions, and where.Then, the Newton-Raphson iterative algorithm for is as follows:for and .
- Finally, it should be noted that when the regression structures for the mean and dispersion parameters of the model are limited to the constants and this EM type algorithm can be employed for the ML estimation of the ‘univariate’, without regression components, model.
4. Numerical Illustration
- The variable AD consists of two categories of policyholders, those of age: C1 = “between 18 and 25 years” and C2 = “greater than 25 years”.
- The variable HP consists of two categories of vehicles, those with a HP: C1 = “0–5000 cc” and C2 = “greater than 5000 cc”.
- The variable AC consists of two categories of vehicles, those of age: C1 = “between 0 and 5 years” and C2 = “greater than 5 years”.
- The NBI and PIG claim frequency models can be constructed as follows. Consider a policyholder i, , whose number of claims, denoted as , with , are independent and suppose that given a continuous random variable , with pdf defined on and where , follows a Poisson distribution with pmf given by Equation (1). Additionally, we assume that that as this ensures that the model is identifiable. The following results are very well known, see, for example, Dionne and Vanasse (1989, 1992) and Boucher et al. (2007, 2008).
- -
- Let follow a Gamma distribution with pdf given byParameterization (22) ensures thatSubsequently, the unconditional distribution of becomes a NBI distribution, with pmf given byThe mean and the variance of the NBI distribution are given byand
- -
- Let follow a Inverse Gaussian distribution with pdf given byParameterization (26) also ensures that . Then, the unconditional distribution of becomes a PIG distribution, with pmf given bywhere is the modified Bessel function of the third kind of order with argument with integral representation given by Equation (4).The mean and the variance of the PIG distribution are given byand
- -
- We consider that the mean and dispersion parameters of the NBI and PIG distributions are modelled as functions of explanatory variableswhere and are covariate vectors with dimensions and , respectively, with and the corresponding parameter vectors and where it is assumed that the matrices and with rows given by and , respectively, are of full rank.
- -
- Finally, it should be noted that when the regression components in each of the NBI and PIG models are limited to the constants and , we obtain the univariate, without regression components, models.
4.1. Modelling Results
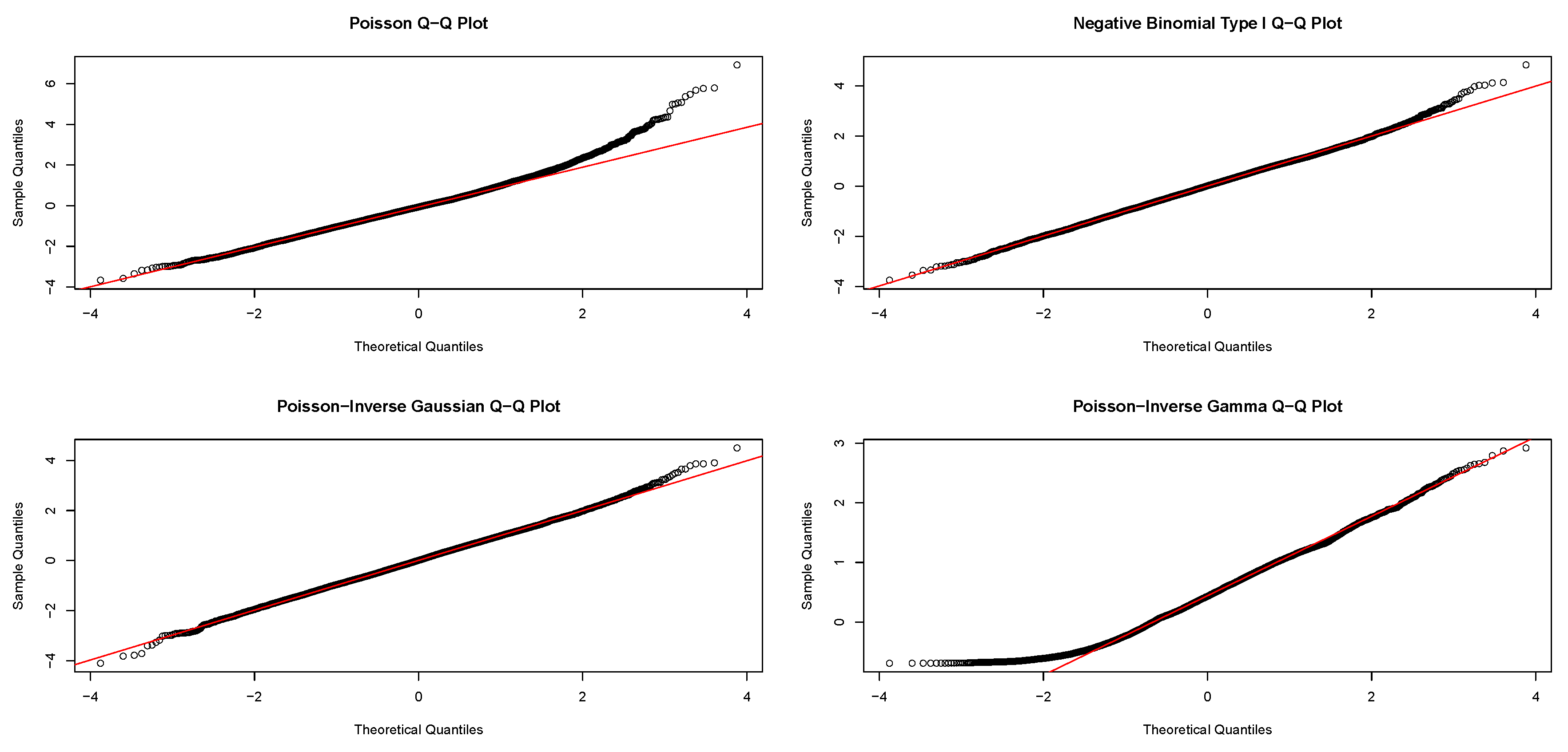
4.2. Models Comparison
4.3. Application to Ratemaking
5. Computational Aspects
6. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Abramowitz, Milton, and Irene A. Stegun. 1965. Handbook of Mathematical Functions. New York: Dover Publications, pp. 241–47. [Google Scholar]
- Altun, Emrah. 2019. A new model for over-dispersed count data: Poisson quasi-Lindley regression model. Mathematical Sciences 13: 241–47. [Google Scholar] [CrossRef]
- Barreto-Souza, Wagner, and Alexandre B. Simas. 2016. General mixed Poisson regression models with varying dispersion. Statistics and Computing 26: 1263–80. [Google Scholar] [CrossRef]
- Böhning, Dankmar. 1999. Computer Assisted Analysis of Mixtures and Applications in Meta-Analysis, Disease Mapping and Others. Boca Raton: CRC Press. [Google Scholar]
- Boucher, Jean-Philippe, Michel Denuit, and Montserrat Guillén. 2007. Risk classification for claim counts: A comparative analysis of various zero-inflated mixed Poisson and hurdle models. North American Actuarial Journal 11: 110–31. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Michel Denuit, and Montserrat Guillén. 2008. Models of Insurance Claim Counts with Time Dependence Based on Generalisation of Poisson and Negative Binomial Distributions. Variance 2: 135–62. [Google Scholar]
- Brouhns, Natacha, Montserrat Guillén, Michel Denuit, and Jean Pinquet. 2003. Bonus-Malus Scales in Segmented Tariffs With Stochastic Migration Between Segments. Journal of Risk and Insurance 70: 577–99. [Google Scholar] [CrossRef]
- Burnham, Kenneth P., and David R. Anderson. 2002. A Practical Information-Theoretic Approach. Model Selection and Multimodel Inference, 2nd ed. New York: Springer. [Google Scholar]
- Cameron, A. Colin, and Pravin K. Trivedi. 1998. Regression Analysis of Count Data. Cambridge: Cambridge University Press, vol. 53. [Google Scholar]
- Cohen, A. Clifford, Jr. 1966. A note on certain discrete mixed distributions. Biometrics 22: 566–72. [Google Scholar] [CrossRef]
- Cole, Timothy J., and Pamela J. Green. 1992. Smoothing reference centile curves: The LMS method and penalized likelihood. Statistics in Medicine 11: 1305–19. [Google Scholar] [CrossRef]
- De Jong, Piet, and Gillian Z. Heller. 2008. Generalized Linear Models for Insurance Data. Cambridge: Cambridge University Press, vol. 10. [Google Scholar]
- Dean, Charmaine, J. F. Lawless, and G. E. Willmot. 1989. A mixed poisson–inverse-gaussian regression model. Canadian Journal of Statistics 17: 171–81. [Google Scholar] [CrossRef]
- Dempster, Arthur P., Nan M. Laird, and Donald B. Rubin. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 39: 1–22. [Google Scholar]
- Denuit, Michel, and Stefan Lang. 2004. Non-life rate-making with Bayesian GAMs. Insurance: Mathematics and Economics 35: 627–47. [Google Scholar] [CrossRef]
- Denuit, Michel, Xavier Maréchal, Sandra Pitrebois, and Jean-François Walhin. 2007. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. Hoboken: John Wiley & Sons. [Google Scholar]
- Dionne, Georges, and Charles Vanasse. 1989. A generalization of actuarial automobile insurance rating models: The negative binomial distribution with a regression component. ASTIN Bulletin 19: 199–212. [Google Scholar] [CrossRef]
- Dionne, Georges, and Charles Vanasse. 1992. Automobile insurance ratemaking in the presence of asymmetrical information. Journal of Applied Econometrics 7: 149–65. [Google Scholar] [CrossRef]
- Dunn, Peter K., and Gordon K. Smyth. 1996. Randomized quantile residuals. Computational and Graphical Statistics 5: 236–45. [Google Scholar]
- Frangos, Nicholas E., and Spyridon D. Vrontos. 2001. Design of optimal bonus-malus systems with a frequency and a severity component on an individual basis in automobile insurance. ASTIN Bulletin 31: 1–22. [Google Scholar] [CrossRef]
- Frees, Edward W. 2010. Regression Modeling with Actuarial and Financial Applications. Cambridge: Cambridge University Press. [Google Scholar]
- Gilbert, Paul, and Ravi Varadhan. 2019. Accurate Numerical Derivatives R Package Manual. Version 2016.8-1.1. Available online: https://cran.r-project.org/web/packages/numDeriv/numDeriv.pdf (accessed on 6 June 2019).
- Giuricich, Mario Nicoló, and Krzysztof Burnecki. 2019. Modelling of left-truncated heavy-tailed data with application to catastrophe bond pricing. Physica A: Statistical Mechanics and Its Applications 525: 498–13. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, and Enrique Calderín-Ojeda. 2016. The Mixture Poisson Exponential-Inverse Gaussian Regression Model: An application in Health Services. Metodoloski Zvezki 13: 71. [Google Scholar]
- Gómez-Déniz, Emilio, and Enrique Calderín-Ojeda. 2018a. Properties and applications of the Poisson-reciprocal inverse gaussian distribution. Journal of Statistical Computation and Simulation 88: 269–89. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, and Enrique Calderín-Ojeda. 2018b. Multivariate Credibility in Bonus-Malus Systems Distinguishing between Different Types of Claims. Risks 6: 34. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, and F. J. Vázquez-Polo. 2003. Robustness in Bayesian model for Bonus-Malus systems. In Intelligent And Other Computational Techniques In Insurance: Theory and Applications. Toh Tuck: World Scientific Publishing, pp. 435–63. [Google Scholar]
- Gómez-Déniz, Emilio, Agustín Hernández-Bastida, and M. Pilar Fernández-Sánchez. 2014. Computing credibility bonus-malus premiums using the aggregate claims distribution. Hacettepe Journal of Mathematics and Statistics 43: 1047–61. [Google Scholar]
- Gómez-Déniz, Emilio, José María Sarabia, and Enrique Calderín-Ojeda. 2008. Univariate and multivariate versions of the negative binomial-inverse Gaussian distributions with applications. Insurance: Mathematics and Economics 42: 39–49. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, M.E. Ghitany, and Ramesh C. Gupta. 2016. Poisson-mixed inverse gaussian regression model and its application. Communications in Statistics - Simulation and Computation 45: 2767–81. [Google Scholar] [CrossRef]
- Haberman, Steven, and Arthur E. Renshaw. 1996. Generalized linear models and actuarial science. Journal of the Royal Statistical Society: Series D (The Statistician) 45: 407–36. [Google Scholar] [CrossRef]
- Hilbe, Joseph M. 2008. Negative Binomial Regression. Cambridge: Cambridge University Press. [Google Scholar]
- Insurance Europe. European Motor Insurance Markets 2019. Available online: https://www.insuranceeurope.eu/european-motor-insurance-markets-2019 (accessed on 8 February 2019).
- Johnson, Norman L., Samuel Kotz, and Narayanaswamy Balakrishnan. 1994. Continuous Univariate Distributions. Hoboken: John Wiley & Sons, vol. 1. [Google Scholar]
- Jørgensen, Bent. 2012. Statistical Properties of the Generalized Inverse Gaussian Distribution. Cham: Springer Science & Business Media, vol. 9. [Google Scholar]
- Kaas, Rob, Marc Goovaerts, Jan Dhaene, and Michel Denuit. 2008. Modern Actuarial Risk Theory: Using R. Cham: Springer Science & Business Media, vol. 128. [Google Scholar]
- Karlis, Dimitris, George Tzougas, and Nicholas Frangos. 2018. Confidence intervals of the premiums of optimal bonus malus systems. Scandinavian Actuarial Journal 2: 129–44. [Google Scholar] [CrossRef]
- Karlis, Dimitris. 2001. A general EM approach for maximum likelihood estimation in mixed Poisson regression models. Statistical Modelling 1: 305–18. [Google Scholar] [CrossRef]
- Karlis, Dimitris. 2005. EM algorithm for mixed Poisson and other discrete distributions. ASTIN Bulletin 35: 3–24. [Google Scholar] [CrossRef][Green Version]
- Khazraee, S. Hadi, Valen Johnson, and Dominique Lord. 2018. Bayesian Poisson hierarchical models for crash data analysis: Investigating the impact of model choice on site-specific predictions. Accident Analysis & Prevention 117: 181–95. [Google Scholar]
- Klein, Nadja, Michel Denuit, Stefan Lang, and Thomas Kneib. 2014. Nonlife ratemaking and risk management with Bayesian generalized additive models for location, scale, and shape. Insurance: Mathematics and Economics 5: 225–49. [Google Scholar] [CrossRef]
- Lambert, Diane. 1992. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics 34: 1–14. [Google Scholar] [CrossRef]
- Lawless, Jerald F. 1987. Negative binomial and mixed Poisson regression. The Canadian Journal of Statistics 15: 209–25. [Google Scholar] [CrossRef]
- Lemaire, Jean, Sojung Carol Park, and Kili C. Wang. 2015. The Impact of Covariates on a Bonus-Malus System: An Application of Taylor’s Model. European Actuarial Journal 5: 1–10. [Google Scholar] [CrossRef]
- Lemaire, Jean, Sojung Carol Park, and Kili C. Wang. 2016. The Use of Annual Mileage as a Rating Variable. ASTIN Bulletin 46: 39–69. [Google Scholar] [CrossRef]
- Lemaire, Jean. 1995. Bonus-Malus Systems in Automobile Insurance. New York: Kluwer Academic Publishers. [Google Scholar]
- Louis, Thomas A. 1982. Finding the observed information matrix when using the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 44: 226–33. [Google Scholar]
- Mahmoudvand, Rahim, and Hossein Hassani. 2009. Generalized bonus-malus systems with a frequency and a severity component on an individual basis in automobile insurance. ASTIN Bulletin 39: 307–15. [Google Scholar] [CrossRef]
- Majeske, Karl D. 2007. A non-homogeneous Poisson process predictive model for automobile warranty claims. Reliability Engineering & System Safety 92: 243–51. [Google Scholar]
- McLachlan, Geoffrey J., and Thriyambakam Krishnan. 2007. The EM Algorithm and Extensions. Hoboken: John Wiley & Sons, vol. 38. [Google Scholar]
- Mencía, Javier, and Enrique Sentana. 2005. Estimation and Testing of Dynamic Models with Generalized Hyperbolic Innovations. CEPR Discussion Papers, No. 5177. London: Centre for Economic Policy Research (CEPR). [Google Scholar]
- Mert, Mehmet, and Yasemin Saykan. 2005. On a bonus-malus system where the claim frequency distribution is geometric and the claim severity distribution is Pareto. Hacettepe Journal of Mathematics and Statistics 34: 75–81. [Google Scholar]
- Ni, Weihong, Bo Li, Corina Constantinescu, and Athanasios A. Pantelous. 2014. Bonus-Malus Systems with Hybrid Claim Severity Distributions. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management. Liverpool: American Society of Civil Engineers, pp. 1234–44. [Google Scholar]
- Ni, Weihong, Corina Constantinescu, and Athanasios A. Pantelous. 2014. Bonus-Malus systems with Weibull distributed claim severities. Annals of Actuarial Science 8: 217–233. [Google Scholar] [CrossRef]
- Ord, J. Keith, and G. Alex Whitmore. 1986. The Poisson-inverse gaussian distribution as a model for species abundance. Communications in Statistics-theory and Methods 15: 853–71. [Google Scholar] [CrossRef]
- Perline, Richard. 1998. Mixed Poisson Distributions Tail Equivalent to their Mixing Distributions. Statistics and Probability Letters 38: 229–33. [Google Scholar] [CrossRef]
- Picech, Liviana. 1994. The Merit-Rating Factor in a Multiplicating Rate-Making model. In ASTIN Colloquium, Cannes. Cannes: Cambridge University Press. [Google Scholar]
- Pinquet, Jean. 1997. Allowance for cost of claims in bonus-malus systems. ASTIN Bulletin 27: 33–57. [Google Scholar] [CrossRef]
- Pinquet, Jean. 1998. Designing Optimal Bonus-Malus Systems From Different Types of Claims. ASTIN Bulletin 28: 205–20. [Google Scholar] [CrossRef]
- Raftery, Adrian E. 1995. Bayesian model selection in social research. Sociological Methodology 25: 111–63. [Google Scholar] [CrossRef]
- Rigby, Robert A., and D. M. Stasinopoulos. 1996. A semi-parametric additive model for variance heterogeneity. Statistics and Computing 6: 57–65. [Google Scholar] [CrossRef]
- Rigby, Robert A., and Dimitrios M. Stasinopoulos. 1996. Mean and dispersion additive models. In Statistical Theory and Computational Aspects of Smoothing. Edited by Wolfgang Härdle and Michael Schimek. Heidelberg: Physica, pp. 215–30. [Google Scholar]
- Rigby, Robert A., and Dimitrios M. Stasinopoulos. 2005. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society: Series C (Applied Statistics) 54: 507–54. [Google Scholar] [CrossRef]
- Rigby, Robert A., Dimitrios M. Stasinopoulos, and Calliope Akantziliotou. 2008a. A framework for modelling overdispersed count data, including the Poisson-shifted generalized inverse Gaussian distribution. Computational Statistics & Data Analysis 53: 381–93. [Google Scholar]
- Rigby, Robert A., Dimitrios M. Stasinopoulos, and Calliope Akantziliotou. 2008b. Instructions on How to Use the Gamlss Package in R, 2nd Edition. Available online: http://www.gamlss.org (accessed on 11 January 2008).
- Romaniuk, Maciej. 2020. Imprecise Approaches to Analysis of Insurance Portfolio with Catastrophe Bond. Paper presented at International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Lisbon, Portugal, 15–19 June 2020; Cham: Springer. [Google Scholar]
- Schiegl, Magda. 2010. About the Justification of Experience Rating: Bonus Malus System and a new Poisson Mixture Model. arXiv arXiv:1009.4142. [Google Scholar]
- Shared, Moshe. 1980. On mixtures from exponential families. Journal of the Royal Statistical Society: Series B (Methodological) 42: 192–98. [Google Scholar] [CrossRef]
- Trembley, Luc. 1992. Using the Poisson inverse Gaussian in bonus-malus systems. ASTIN Bulletin 22: 97–106. [Google Scholar] [CrossRef]
- Tzougas, George, and Dimitris Karlis. 2020. An EM algorithm for fitting a new class of mixed exponential regression models with varying dispersion. Astin Bulletin 50: 555–83. [Google Scholar] [CrossRef]
- Tzougas, George, Spyridon Vrontos, and Nicholas Frangos. 2014. Optimal Bonus-Malus Systems Using Finite Mixture Models. ASTIN Bulletin 44: 417–44. [Google Scholar] [CrossRef]
- Tzougas, George, Spyridon Vrontos, and Nicholas Frangos. 2015. Risk Classification for Claim Counts and Losses Using Regression Models for Location, Scale and Shape. Variance 9: 140–57. [Google Scholar]
- Tzougas, George, Spyridon Vrontos, and Nicholas Frangos. 2018. Bonus-Malus Systems with Two-Component Mixture Models Arising from Different Parametric Families. North American Actuarial Journal 22: 55–91. [Google Scholar] [CrossRef]
- Tzougas, George, Wei Li Hoon, and Jun Ming Lim. 2019. The negative binomial-inverse Gaussian regression model with an application to insurance ratemaking. European Actuarial Journal 9: 323–44. [Google Scholar] [CrossRef]
- Weibel, Mark, David Lóthi, and Wolfgang Breymann. 2020. ghyp: Generalized Hyperbolic Distribution and Its Special Cases. Available online: https://cran.r-project.org/web/packages/ghyp/ghyp.pdf (accessed on 27 April 2020).
- Willmot, Gordon E. 1987. The Poisson-inverse Gaussian distribution as an alternative to the negative binomial. Scandinavian Actuarial Journal 3–4: 113–27. [Google Scholar] [CrossRef]
- Willmot, Gordon E. 1990. Asymptotic tail behaviour of Poisson mixtures with applications. Advances in Applied Probability 22: 147–59. [Google Scholar] [CrossRef]
- Willmot, Gordon E. 1993. On recursive evaluation of mixed Poisson probabilities and related quantities. Scandinavian Actuarial Journal 2: 114–33. [Google Scholar]
- Yip, Karen C. H., and Kelvin K. W. Yau. 2005. On modeling claim frequency data in general insurance with extra zeros. Insurance: Mathematics and Economics 36: 153–63. [Google Scholar] [CrossRef]
| 1 | Note that Schiegl (2010) used a different parameterization of the PIGA distribution to derive a Bonus-Malus system for the case without covariates, i.e., based only on the a posteriori criteria. Note also that, the Bonus-Malus premium functions determined by the classic NBI and PIG models were not included for the sake of brevity. Those functions can be found, for instance, in Dionne and Vanasse (1989, 1992), Frangos and Vrontos (2001), Mahmoudvand and Hassani (2009) and Tzougas et al. (2014, 2018) respectively. Note also that, the Bounus-Malus premium rates for the case when only on the a posteriori criteria are used can be obtained if the regression components of the NBI, PIG, and PIGA models are limited to constants. |
| Statistic | Value | Age of the Driver (AD) | Horsepower of the Car (HP) | Age of the Car (AC) | |||
|---|---|---|---|---|---|---|---|
| # Observations | 14,143 | C1: | 3238 | C1: | 5042 | C1: | 4318 |
| Minimum | 0 | C2: | 10,905 | C2: | 9101 | C2: | 9825 |
| Median | 0 | - | - | - | |||
| Mean | 0.4827 | - | - | - | |||
| Variance | 0.6988 | - | - | - | |||
| Maximum | 12 | - | - | - | |||
| NBI | PIG | PIGA |
|---|---|---|
| NBI | PIG | PIGA | |||
|---|---|---|---|---|---|
| Coeff. | Coeff. | Coeff. | |||
| Intercept | Intercept | Intercept | |||
| AD | CS | CS | |||
| C2 | C2 | C2 | |||
| HP | AC | AC | |||
| C2 | C2 | C2 | |||
| AC | HP | HP | |||
| C2 | C2 | C2 | |||
| Coeff. | Coeff. | Coeff. | |||
| Intercept | Intercept | Intercept | |||
| AD | CS | CS | |||
| C2 | C2 | C2 | |||
| Panel A: Distributions | Panel B: Regression Models with Varying Dispersion | |||||
|---|---|---|---|---|---|---|
| Model | AIC | SBC | Model | DEV | AIC | SBC |
| NBI | 17,829.1 | 17,843.5 | NBI | 15,885.1 | 15,897.1 | 15,940.1 |
| PIG | 17,799.2 | 17,813.5 | PIG | 15,867.3 | 15,879.4 | 15,922.3 |
| PIGA | 17,780.4 | 17,794.8 | PIGA | 15,848.6 | 15,860.6 | 15,903.6 |
| Risk | Explanatory Variables | A Priori Premiums | ||||
|---|---|---|---|---|---|---|
| Class | AD | HP | AC | NBI | PIG | PIGA |
| 1 | C1 | C1 | C1 | |||
| 2 | C1 | C1 | C2 | |||
| 3 | C1 | C2 | C1 | |||
| 4 | C1 | C2 | C2 | |||
| 5 | C2 | C1 | C1 | |||
| 6 | C2 | C1 | C2 | |||
| 7 | C2 | C2 | C1 | |||
| 8 | C2 | C2 | C2 | |||
| NBI | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIG | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIGA | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| NBI | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIG | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIGA | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| NBI | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIG | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIGA | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| NBI | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIG | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIGA | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| NBI | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIG | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| PIGA | |||||
| Year | Number of Claims | ||||
| t | 0 | 1 | 2 | 3 | 4 |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzougas, G. EM Estimation for the Poisson-Inverse Gamma Regression Model with Varying Dispersion: An Application to Insurance Ratemaking. Risks 2020, 8, 97. https://doi.org/10.3390/risks8030097
Tzougas G. EM Estimation for the Poisson-Inverse Gamma Regression Model with Varying Dispersion: An Application to Insurance Ratemaking. Risks. 2020; 8(3):97. https://doi.org/10.3390/risks8030097
Chicago/Turabian StyleTzougas, George. 2020. "EM Estimation for the Poisson-Inverse Gamma Regression Model with Varying Dispersion: An Application to Insurance Ratemaking" Risks 8, no. 3: 97. https://doi.org/10.3390/risks8030097
APA StyleTzougas, G. (2020). EM Estimation for the Poisson-Inverse Gamma Regression Model with Varying Dispersion: An Application to Insurance Ratemaking. Risks, 8(3), 97. https://doi.org/10.3390/risks8030097





