Numerical Algorithms for Reflected Anticipated Backward Stochastic Differential Equations with Two Obstacles and Default Risk
Abstract
1. Introduction
1.1. Basics of the Defaultable Model
1.2. Basic Notions
- is a -measurable random variable and ;
- is -progressively measurable and ;
- is -progressively measurable rcll process and ;
- is -progressively measurable and satisfies ;
- is a -adapted rcll increasing process and , ;
1.3. Reflected Anticipated BSDEs with Two Obstacles and Default Risk
- (a)
- ;
- (b)
- Lipschitz condition: for any , , y, , z, , u, , , , there exists a constant such that
- (c)
- for any , , y, , z, , u, , , , the following holds:where , is the i-th element of u.
- (a)
- for any , , L and V are separated, i.e., , ;
- (b)
- L and V are rcll and their jumping times are totally inaccessible and satisfy
- (c)
- there exists a process of the following form:where , , , and are -adapted increasing processes, , such that
2. Discrete Time Framework
2.1. Random Walk Approximation of the Brownian Motion
2.2. Approximation of the Defaultable Model
2.3. Computing the Conditional Expectations
2.4. Approximations of the Anticipated Processes and the Generator
- (a)
- there exists a constant , such that for all ,
- (b)
- for any , y, , z, , u, , , , there exists a constant , such thatwhere , .
2.5. Approximation of the Obstacles
3. Discrete Penalization Scheme
3.1. Implicit Discrete Penalization Scheme
3.2. Explicit Discrete Penalization Scheme
- If , we can get ;
- If , we can get , . From (12), we know that p should be much larger than n to keep above the lower obstacle ;
- If , we can get , . From (12), we know that p should be much larger than n to keep under the upper obstacle .
4. Discrete Reflected Scheme
4.1. Implicit Discrete Reflected Scheme
4.2. Explicit Discrete Reflected Scheme
5. Convergence Results
5.1. Convergence of the Penalized ABSDE to RABSDE (2)
5.2. Convergence of the Implicit Discrete Penalization Scheme
5.3. Convergence of the Explicit Discrete Penalization Scheme
5.4. Convergence of the Implicit Discrete Reflected Scheme
5.5. Convergence of the Explicit Discrete Reflected Scheme
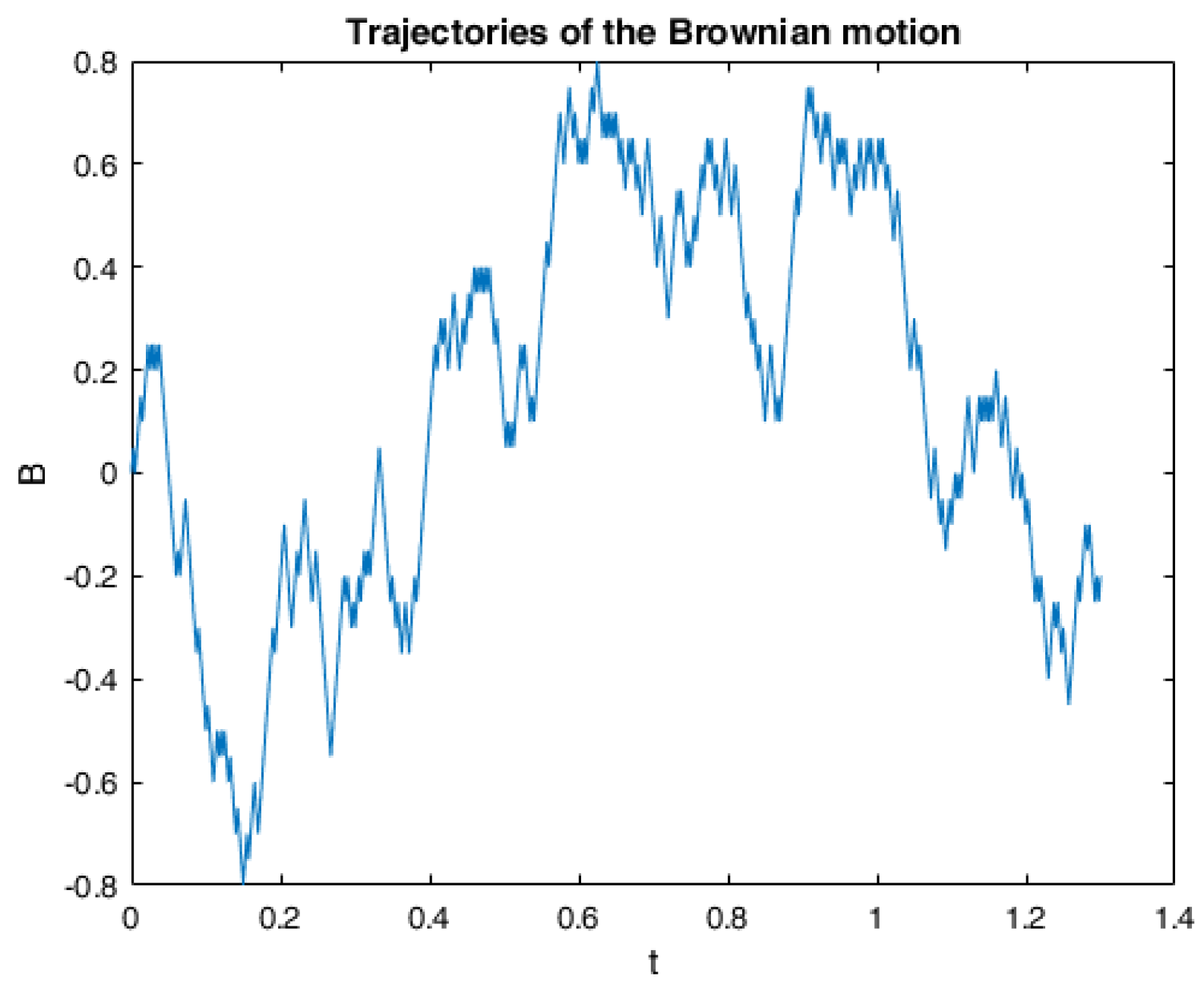
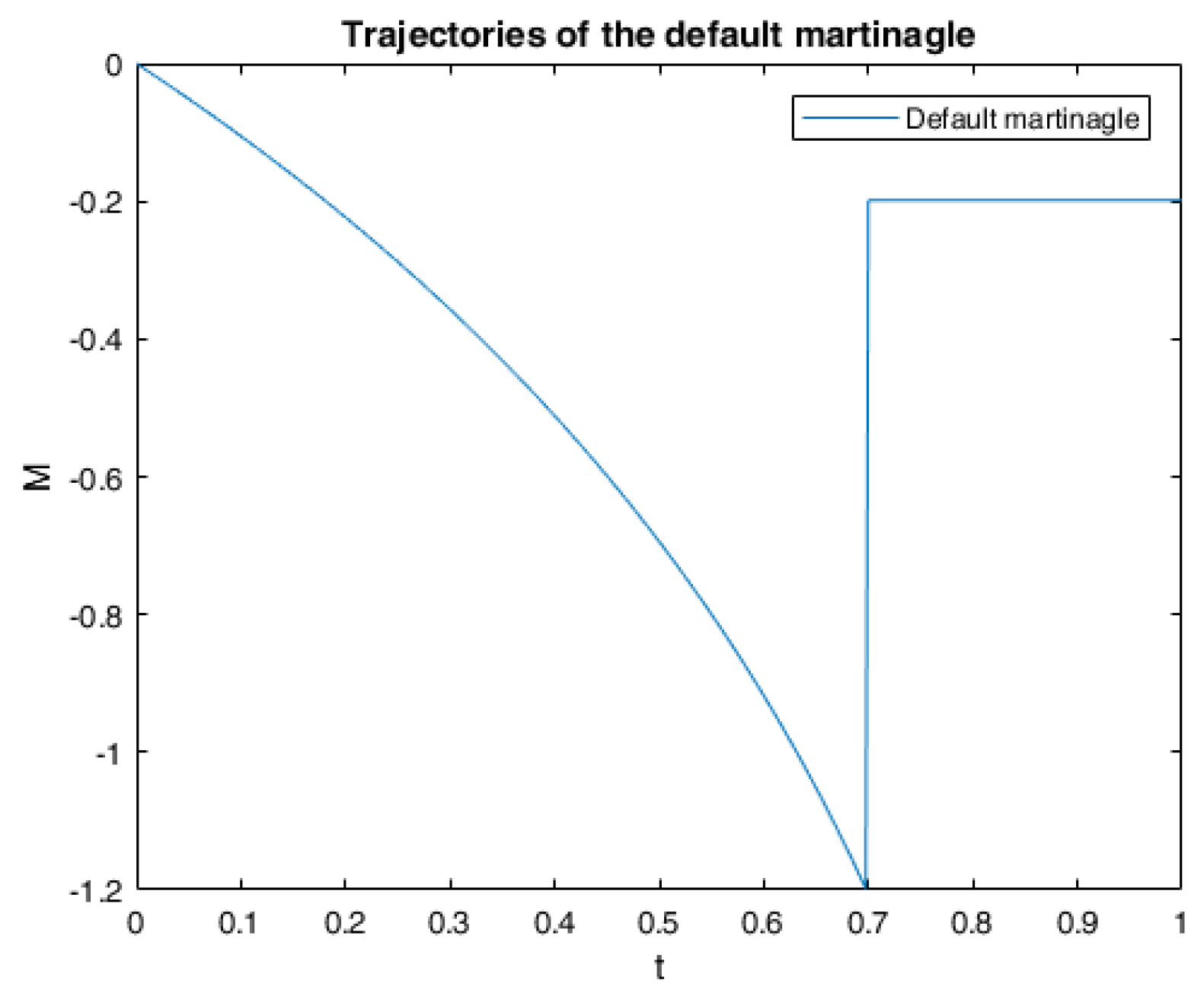
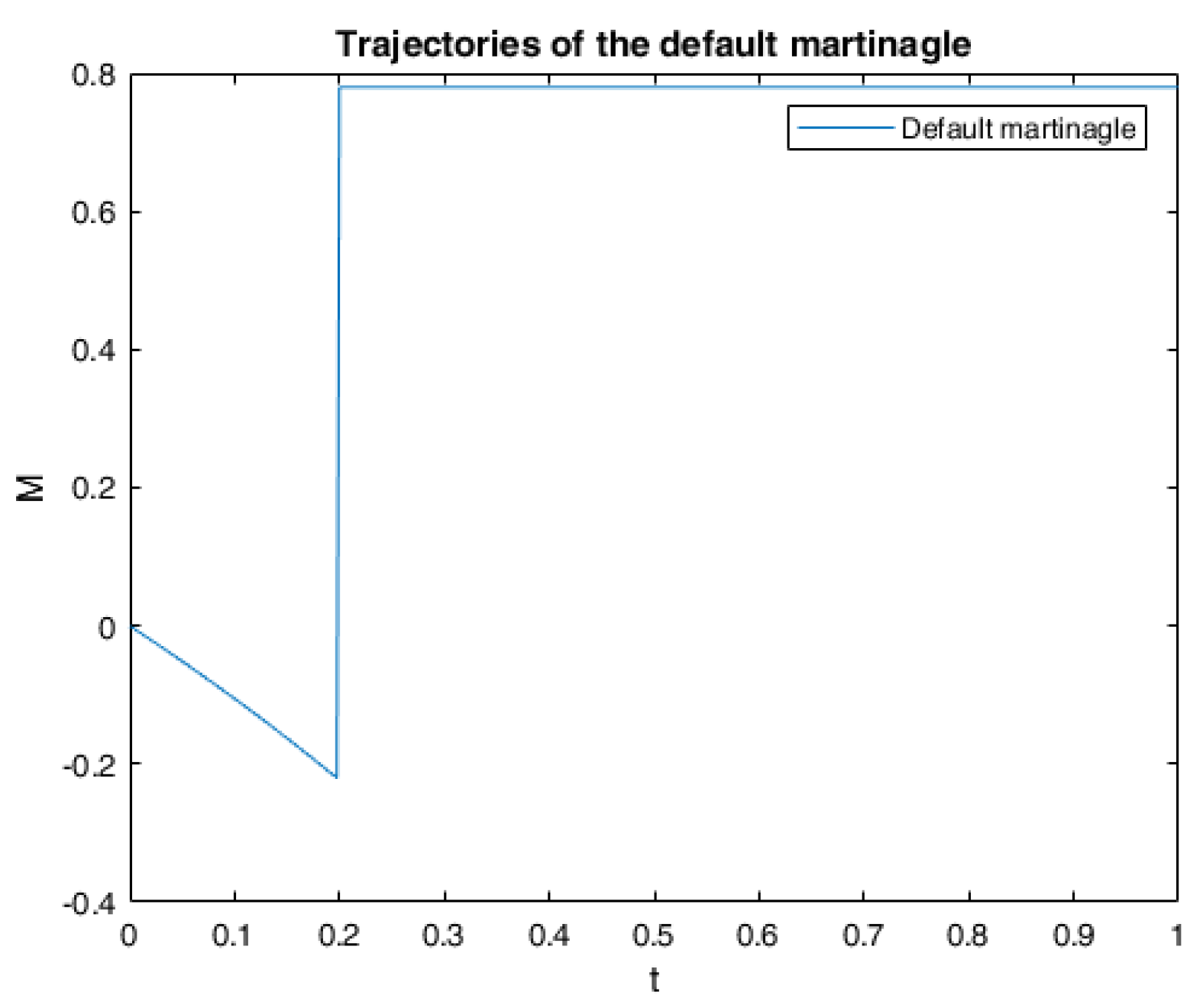
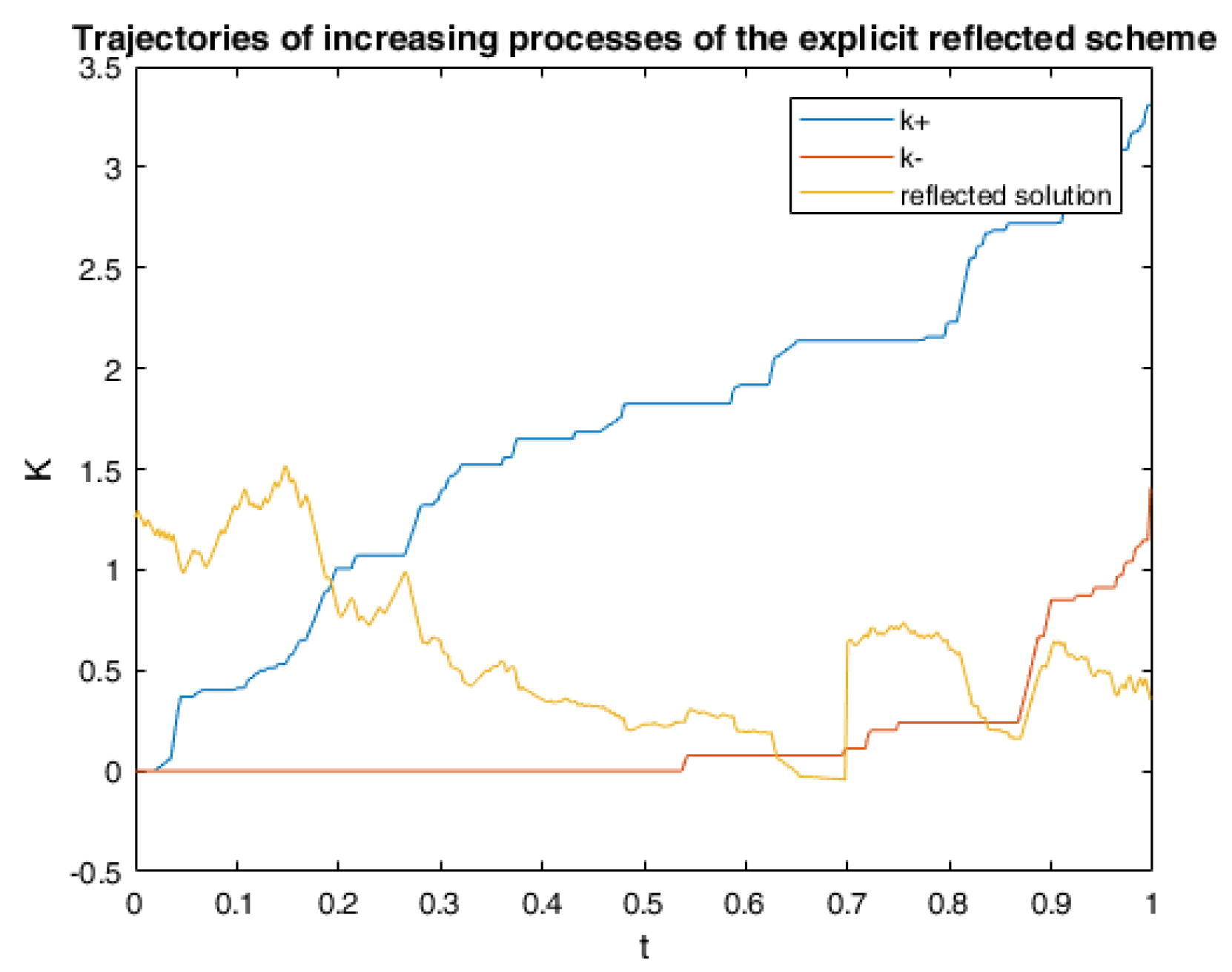
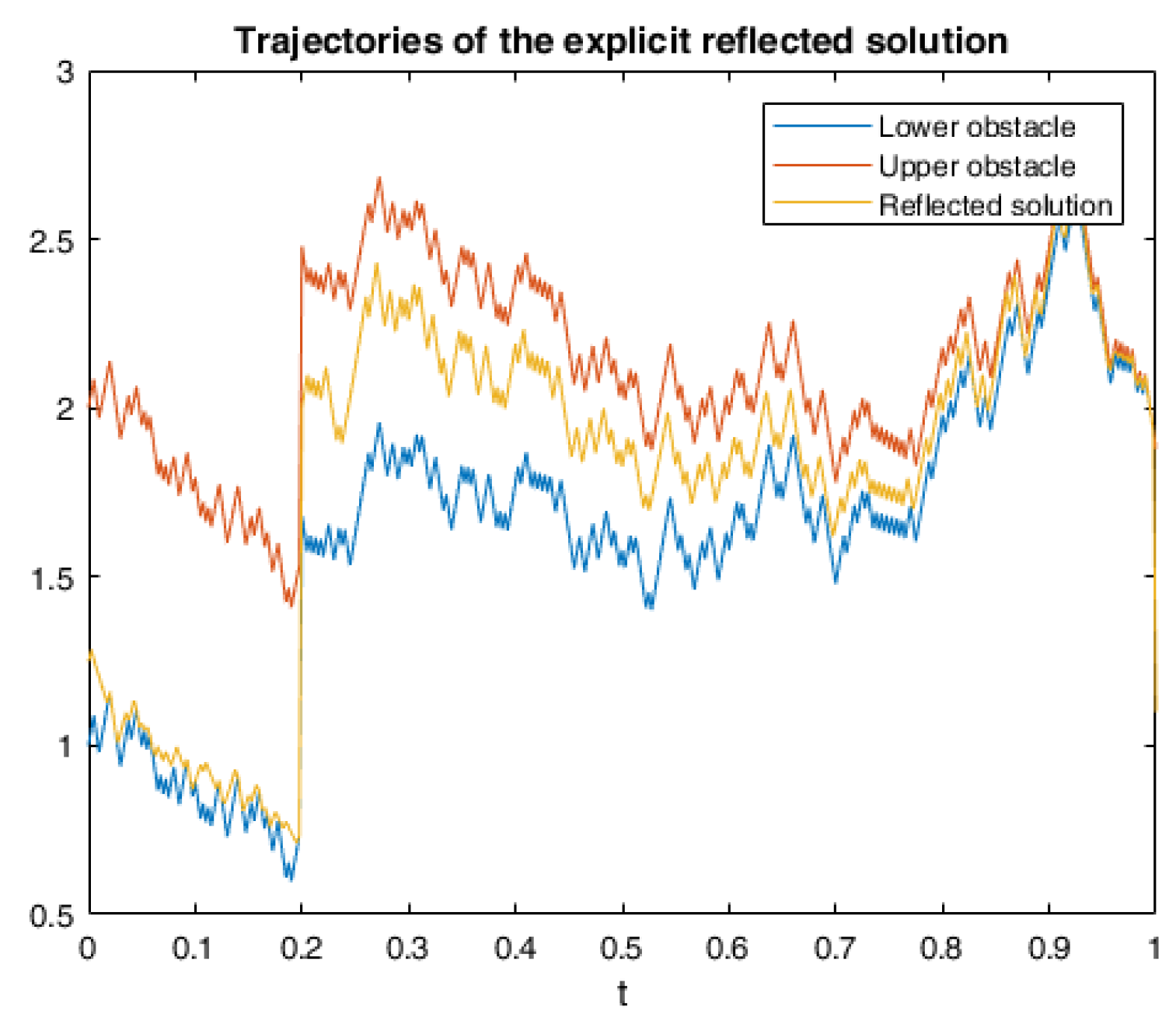
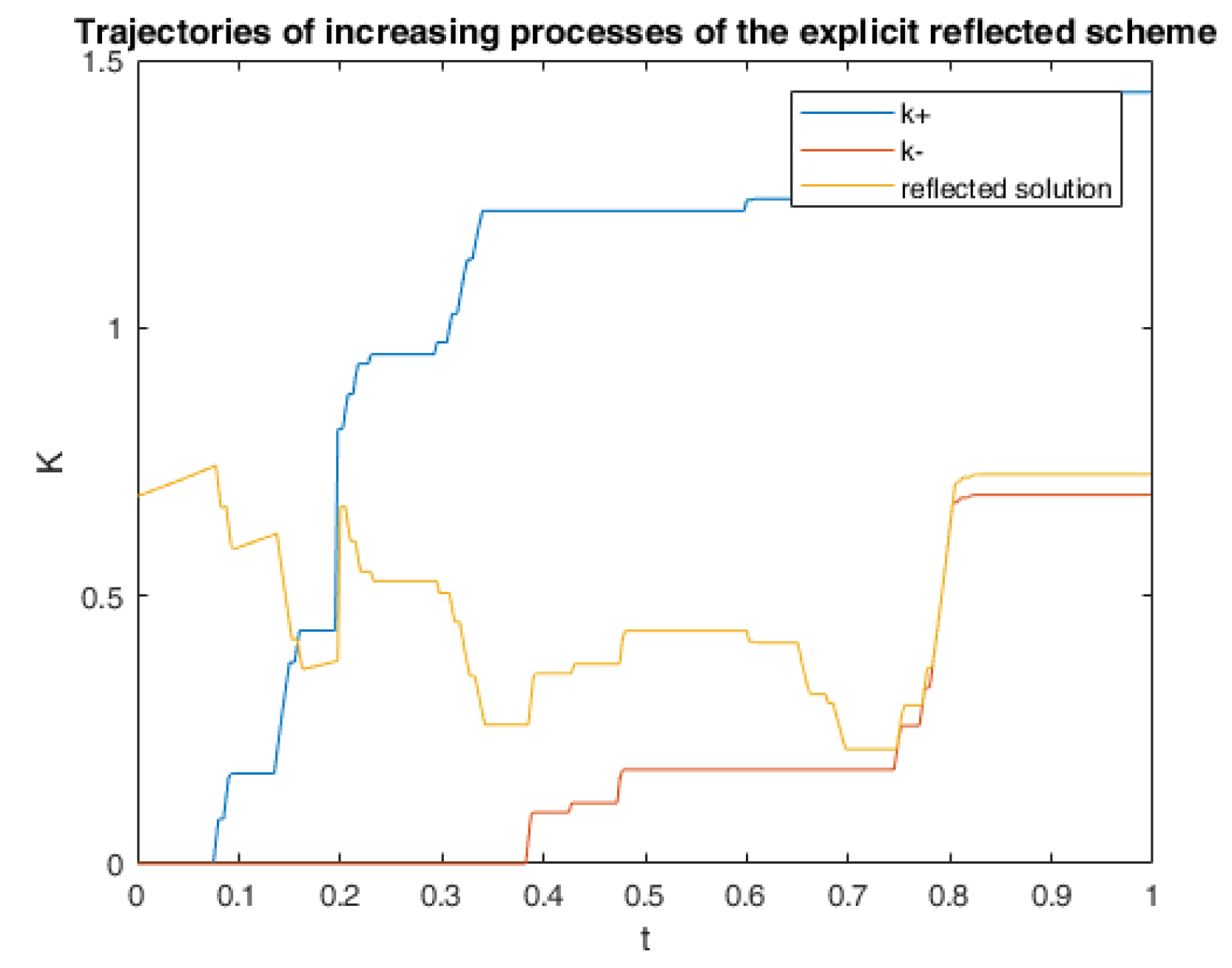
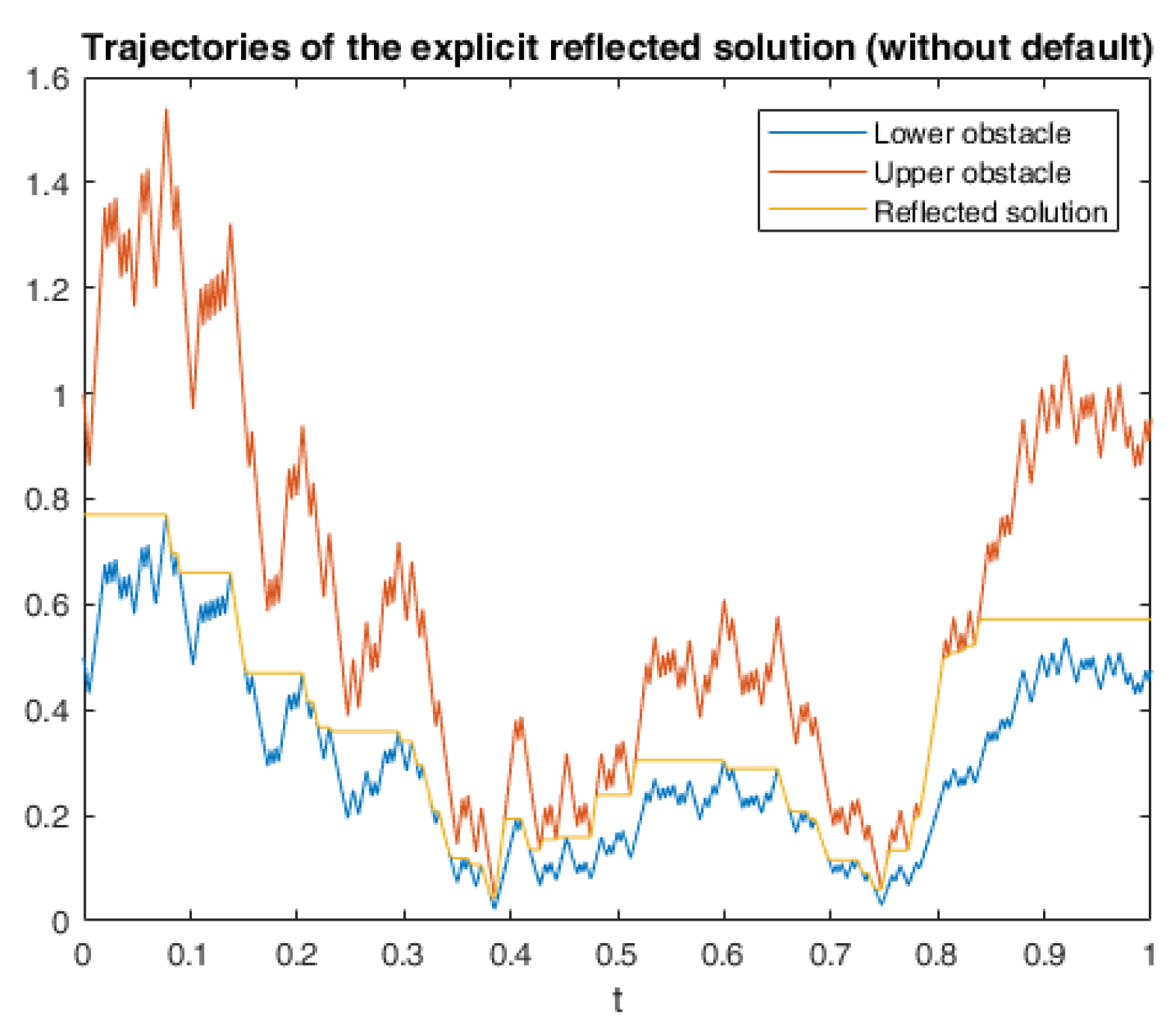
6. Numerical Calculations and Simulations
6.1. One Example of RABSDE with Two Obstacles and Default Risk
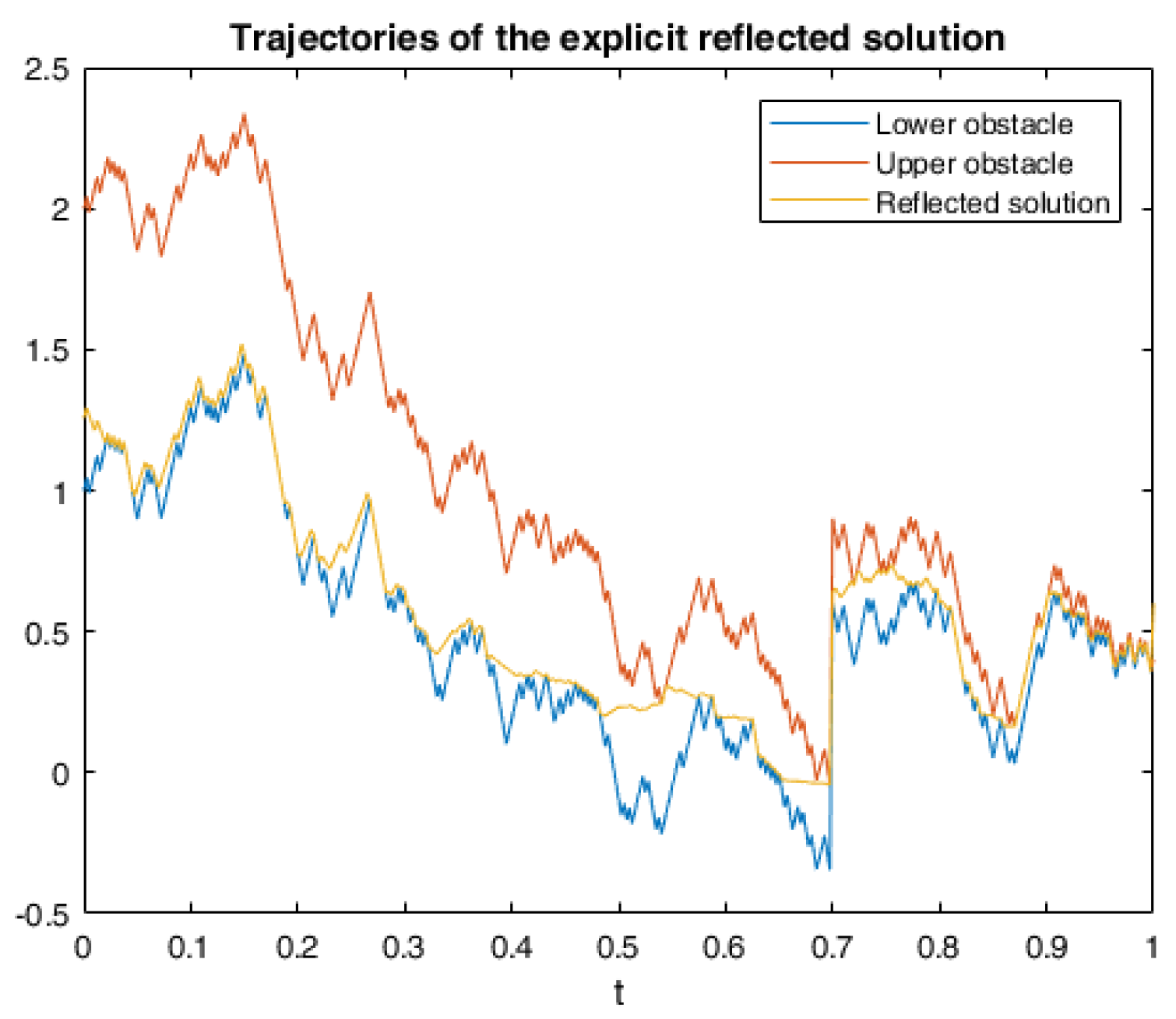
6.2. Application in American Game Options in a Defaultable Setting
6.2.1. Model Description
- The broker has the right to cancel the contract at any time before the maturity T, while the trader has the right to early exercise the option;
- the trader pays an initial amount (the price of this option) which ensures an income from the broker , where is an -stopping time;
- the broker has the right to cancel the contract before T and needs to pay to . Here, the payment amount of the broker should be greater than his payment to the trader (if trader decides for early exercise), i.e., , is the premium that the broker pays for his decision of early cancellation. is an -stopping time;
- if and both decide to stop the contract at the same time , then the trader gets an income equal to .
6.2.2. The Hedge for the Broker
6.2.3. Numerical Simulation
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Barles, Guy, Rainer Buckdahn, and Étienne Pardoux. 1997. Backward stochastic differential equations and integral-partial differential equations. Stochastics: An International Journal of Probability and Stochastic Processes 60: 57–83. [Google Scholar] [CrossRef]
- Bielecki, Tomasz, Monique Jeanblanc, and Marek Rutkowski. 2007. Introduction to Mathematics of Credit Risk Modeling. Stochastic Models in Mathematical Finance. Marrakech: CIMPA–UNESCO–MOROCCO School, pp. 1–78. [Google Scholar]
- Bismut, Jean Michel. 1973. Conjugate convex functions in optimal stochastic control. Journal of Mathematical Analysis and Applications 44: 384–404. [Google Scholar] [CrossRef]
- Briand, Philippe, Bernard Delyon, and Jean Mémin. 2002. On the robustness of backward stochastic differential equations. Stochastic Processes and their Applications 97: 229–53. [Google Scholar] [CrossRef]
- Cordoni, Francesco, and Luca Di Persio. 2014. Backward stochastic differential equations approach to hedging, option pricing, and insurance problems. International Journal of Stochastic Analysis 2014: 152389. [Google Scholar] [CrossRef]
- Cordoni, Francesco, and Luca Di Persio. 2016. A bsde with delayed generator approach to pricing under counterparty risk and collateralization. International Journal of Stochastic Analysis 2016: 1059303. [Google Scholar] [CrossRef]
- Cvitanic, Jaksa, and Ioannis Karatzas. 1996. Backward stochastic differential equations with reflection and dynkin games. Annals of Probability 24: 2024–56. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Larry Epstein. 1992. Stochastic differential utility. Econometrica: Journal of the Econometric Dociety 60: 353–94. [Google Scholar] [CrossRef]
- Dumitrescu, Roxana, and Céline Labart. 2016. Numerical approximation of doubly reflected bsdes with jumps and rcll obstacles. Journal of Mathematical Analysis and Applications 442: 206–43. [Google Scholar] [CrossRef]
- El Karoui, Nicole, Christophe Kapoudjian, Étienne Pardoux, Shige Peng, and Marie Claire Quenez. 1997a. Reflected solutions of backward sdes and related obstacle problems for pdes. Annals of Probability 25: 702–37. [Google Scholar] [CrossRef]
- El Karoui, Nicole, Étienne Pardoux, and Marie Claire Quenez. 1997b. Reflected backward sdes and american options. Numerical Methods in Finance 13: 215–31. [Google Scholar]
- Hamadène, Said. 2006. Mixed zero-sum stochastic differential game and american game options. SIAM Journal on Control and Optimization 45: 496–518. [Google Scholar]
- Hamadène, Said, Jean Pierre Lepeltier, and Anis Matoussi. 1997. Double barrier backward sdes with continuous coefficient. Pitman Research Notes in Mathematics Series 41: 161–76. [Google Scholar]
- Hamadène, Said, and Jean Pierre Lepeltier. 2000. Reflected bsdes and mixed game problem. Stochastic Processes and Their Applications 85: 177–88. [Google Scholar] [CrossRef]
- Jeanblanc, Monique, Thomas Lim, and Nacira Agram. 2017. Some existence results for advanced backward stochastic differential equations with a jump time. ESAIM: Proceedings and Surveys 56: 88–110. [Google Scholar] [CrossRef]
- Jiao, Ying, Idris Kharroubi, and Huyen Pham. 2013. Optimal investment under multiple defaults risk: A bsde-decomposition approach. The Annals of Applied Probability 23: 455–91. [Google Scholar] [CrossRef]
- Jiao, Ying, and Huyên Pham. 2011. Optimal investment with counterparty risk: A default-density model approach. Finance and Stochastics 15: 725–53. [Google Scholar] [CrossRef]
- Karatzas, Ioannis, and Steven Shreve. 1998. Methods of Mathematical Finance. New York: Springer, vol. 39. [Google Scholar]
- Kusuoka, Shigeo. 1999. A remark on default risk models. Advances in Mathematical Economics 1: 69–82. [Google Scholar]
- Lejay, Antoine, Ernesto Mordecki, and Soledad Torres. 2014. Numerical approximation of backward stochastic differential equations with jumps. Research report. inria-00357992v3. Available online: https://hal.inria.fr/inria-00357992v3/document (accessed on 30 June 2020).
- Lepeltier, Jean Pierre, and Jaime San Martín. 2004. Backward sdes with two barriers and continuous coefficient: An existence result. Journal of Applied Probability 41: 162–75. [Google Scholar] [CrossRef]
- Lepeltier, Jean Pierre, and Mingyu Xu. 2007. Reflected backward stochastic differential equations with two rcll barriers. ESAIM: Probability and Statistics 11: 3–22. [Google Scholar] [CrossRef]
- Lin, Yin, and Hailiang Yang. 2014. Discrete-time bsdes with random terminal horizon. Stochastic Analysis and Applications 32: 110–27. [Google Scholar] [CrossRef][Green Version]
- Mémin, Jean, Shige Peng, and Mingyu Xu. 2008. Convergence of solutions of discrete reflected backward sdes and simulations. Acta Mathematicae Applicatae Sinica, English Series 24: 1–18. [Google Scholar] [CrossRef]
- Øksendal, Bernt, Agnes Sulem, and Tusheng Zhang. 2011. Optimal control of stochastic delay equations and time-advanced backward stochastic differential equations. Advances in Applied Probability 43: 572–96. [Google Scholar] [CrossRef]
- Pardoux, Étienne, and Shige Peng. 1990. Adapted solution of a backward stochastic differential equation. Systems and Control Letters 14: 55–61. [Google Scholar] [CrossRef]
- Peng, Shige, and Mingyu Xu. 2011. Numerical algorithms for backward stochastic differential equations with 1-d brownian motion: Convergence and simulations. ESAIM: Mathematical Modelling and Numerical Analysis 45: 335–60. [Google Scholar] [CrossRef][Green Version]
- Peng, Shige, and Xiaoming Xu. 2009. Bsdes with random default time and their applications to default risk. arXiv arXiv:0910.2091. [Google Scholar]
- Peng, Shige, and Zhe Yang. 2009. Anticipated backward stochastic differential equations. Annals of Probability 37: 877–902. [Google Scholar] [CrossRef]
- Potter, Philip. 2005. Stochastic Integration and Differential Equations. Berlin/Heidelberg: Springer. [Google Scholar]
- Tang, Shanjian, and Xunjing Li. 1994. Necessary conditions for optimal control of stochastic systems with random jumps. SIAM: Journal on Control and Optimization 32: 1447–75. [Google Scholar] [CrossRef]
- Wang, Jingnan. 2020. Reflected anticipated backward stochastic differential equations with default risk, numerical algorithms and applications. Doctoral dissertation, University of Kaiserslautern, Kaiserslautern, Germany. [Google Scholar]
- Xu, Mingyu. 2011. Numerical algorithms and simulations for reflected backward stochastic differential equations with two continuous barriers. Journal of Computational and Applied Mathematics 236: 1137–54. [Google Scholar] [CrossRef][Green Version]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Korn, R. Numerical Algorithms for Reflected Anticipated Backward Stochastic Differential Equations with Two Obstacles and Default Risk. Risks 2020, 8, 72. https://doi.org/10.3390/risks8030072
Wang J, Korn R. Numerical Algorithms for Reflected Anticipated Backward Stochastic Differential Equations with Two Obstacles and Default Risk. Risks. 2020; 8(3):72. https://doi.org/10.3390/risks8030072
Chicago/Turabian StyleWang, Jingnan, and Ralf Korn. 2020. "Numerical Algorithms for Reflected Anticipated Backward Stochastic Differential Equations with Two Obstacles and Default Risk" Risks 8, no. 3: 72. https://doi.org/10.3390/risks8030072
APA StyleWang, J., & Korn, R. (2020). Numerical Algorithms for Reflected Anticipated Backward Stochastic Differential Equations with Two Obstacles and Default Risk. Risks, 8(3), 72. https://doi.org/10.3390/risks8030072





