1. Introduction
It is widely recognized that the volatility of stocks evolves in a stochastic fashion rather than being constant or deterministic over time. Many empirical studies on stock options reveal that the implied volatility in option price data exhibit the so-called volatility smile/skew, which cannot be explained by the constant-volatility stock price models, say, the geometric Brownian motion model adopted in the
Black and Scholes (
1973) formula. Tremendous effort has been made to articulate this issue, and various stochastic volatility models have been developed to capture the volatility smile/skew as observed in the market. See, for example,
French et al. (
1987),
Hull and White (
1987),
Wiggins (
1987),
Stein and Stein (
1991), and
Heston (
1993). Among these stochastic volatility models, the most commonly used is certainly Heston’s model (
Heston 1993). Indeed, the variance process described by Heston’s model follows a single-factor square-root process with mean-reversion, i.e., a Cox-Ingersoll-Ross (CIR) process, which is mathematically tractable even when the instantaneous volatility/variance is assumed to be correlated with the stock price.
The early research of Heston’s model focuses on option pricing under this model. Recently, there has been emerging interest in portfolio selection problems under Heston’s model as well as other stochastic volatility models. One direction of research is on maximizing the expected utility from investment and consumption.
Kraft (
2005) investigates a utility maximization problem and provides an explicit solution of the problem under specific conditions on model parameters. With the help of a martingale criterion,
Kallsen and Muhle-Karbe (
2010) derive explicit solutions for a power utility maximization problem in a number of affine-form stochastic volatility models.
Zeng and Taksar (
2013) study an optimal portfolio selection problem under a general stochastic volatility model and obtain closed-form solutions for Heston’s model under more relaxed assumptions. Other relevant works along this direction include, for example,
Zariphopoulou (
2001),
Fleming and Hernández-Hernández (
2003),
Liu et al. (
2003), and
Chacko and Viceira (
2005). Another direction of research explores the mean-variance hedging, that is, the problem of approximating a given final payoff by a self-financing trading strategy so as to minimize the mean-squared error. Preceding works include
Laurent and Pham (
1999),
Biagini et al. (
2000),
Hobson (
2004),
Černý and Kallsen (
2008), to name but only a few.
Although portfolio selection problems under Heston’s model have been extensively studied, most existing works concentrate on portfolio selection under the utility-maximization or the mean-variance hedging criteria and few attention has been paid to that under
Markowitz (
1952)’s mean-variance paradigm. In fact,
Markowitz (
1952)’s mean-variance criterion and
Merton (
1969,
1971)’s utility-maximization criterion are both considered precursors of modern portfolio optimization theory, and, to some degree, they are of equal importance in the field. On the other hand, the history of the mean-variance portfolio selection is much longer than that of the mean-variance hedging. In
Markowitz (
1952), the mean-variance portfolio selection problem is proposed in a single-period discrete-time setting. Using some delicate embedding techniques,
Zhou and Li (
2000) apply the linear-quadratic (LQ) control theory to solve a continuous-time mean-variance portfolio selection problem analytically. Subsequently,
Lim and Zhou (
2002),
Lim (
2004) and
Lim (
2005) study mean-variance portfolio selection problems with random parameters by using the LQ control and backward stochastic differential equations (BSDEs). At first glance, one may consider nesting the mean-variance portfolio selection problem under Heston’s model in Lim and Zhou’s framework. However, this is impossible since the variance process in Heston’s model is unbounded, which violates the boundedness assumption of model parameters in Lim and Zhou’s framework. In fact, a class of nonlinear BSDEs is used to solve mean-variance problems, and this class is termed backward stochastic differential Riccati equations (BSREs). Because there are no general results for BSREs with unbounded coefficients, it is challenging to use BSREs to solve mean-variance problems under Heston’s model. This attracts recent attention to studying mean-variance portfolio selection problems with unbounded random coefficients. See
Chiu and Wong (
2011,
2014),
Shen et al. (
2014),
Shen and Zeng (
2015),
Shen (
2015),
Li et al. (
2018), etc.
The focus of the the current paper is on demonstrating that volatility derivatives (e.g., variance swap) is effective tool to manage volatility risk when the stock price dynamics is only partially correlated with the stochastic volatility dynamics. Particularly, the advantage of using variance swap contracts is that there is no cost of entering into these contracts since swaps are worth zero at issuance. Compared with other volatility derivatives, e.g., variance and volatility options, variance swaps provide non-directional exposure to volatility risk, which then reduces the need for delta-hedging residual volatility risk.
To investigate the effect of variance swaps in hedging volatility risk, in this paper we consider two dynamic mean-variance portfolio selection problems under Heston’s stochastic volatility model in a complete market and an incomplete market, respectively. More specifically, we assume that a bank account, a stock and a variance swap are traded in the complete market and that only the bank account and the stock are traded in the incomplete market. The variance process of the stock is described by Heston’s model and is correlated with the stock price process. Throughout this paper, we make a standing assumption that the variance process/the market price of risk process is exponentially integrable. We employ a combined LQ control and BSDE approach to solve the two problems. To address the issue in the solvability of BSREs with unbounded coefficients, we use measure change techniques and study several transformed BSDEs under equivalent probability measures first. Based on the exponential-integrability assumption, Girsanov’s theorem, Hölder’s inequality and the one-to-one correspondence relationships between the solutions to the original BSREs and the transformed BSDEs, the uniqueness and existence of solutions to the original BSREs are proved under the real-world probability measure. Due to the Markovian structure, the unique solutions to these BSREs can be represented by the solutions to some Riccati-type ordinary differential equations (ODEs). With the unique solutions to related BSREs, a straightforward application of the LQ control theory leads to the explicit expressions of the efficient portfolio strategies and the efficient frontiers immediately. To examine the differences of the two problems and the effect of adding the variance swap in the portfolio, we provide numerical examples of the efficient frontiers with different parameter values in the complete and the incomplete markets. It is shown that the variance swap can reduce the overall risk of the terminal wealth through hedging against the volatility risk. In addition, we verify that if the stock price and variance processes are perfectly correlated, the complete market and the incomplete one are indistinguishable. Therefore, the variance swap is an effective tool to hedge idiosyncratic volatility risk.
On technical side, this paper somehow extends
Shen (
2015) and
Shen and Zeng (
2015) to cater for the current setting.
Shen et al. (
2014)) consider a mean-variance problem under a constant elasticity of variance (CEV) model. The efficient strategy found in
Shen et al. (
2014) indeed is in a space smaller than the square-integrable space since the BSDE therein is proved to admit a unique solution in a space accommodating stochastic Lipschitz coefficients, which is smaller than the usually used square-integrable solution space for BSDEs.
Shen and Zeng (
2015) study an optimal investment-reinsurance problem for insurers under the mean-variance optimization criterion. They impose an exponential integrability condition of order 2 and solve the problem for a modified admissible control set. A similarly modified definition of the admissible set is adopted by
Li et al. (
2018) to investigate a mean-variance asset-liability management under with stochastic volatility. Though
Shen and Zeng (
2015) have considered Heston’s model in their framework, they only find the almost surely square-integrable efficient strategy. We should note that in most preceding works as well as the current one, admissible strategies are required to be square-integrable (in an expected sense). By extending some techniques in
Shen (
2015) developed exclusively for a complete market environment and increasing the order of exponential integrability of the market price of risk, in this paper we manage to find square-integrable efficient portfolio strategies under Heston’s model, where the market may be incomplete.
The rest of this paper is structured as follows.
Section 2 introduces the basic notation, model dynamics and standing assumption. In
Section 3, we formulate two mean-variance portfolio selection problems, one in the complete market with the variance swap and the other in the incomplete market without the variance swap. Using the combined LQ control and BSDE approach, we derive the explicit expressions of the efficient portfolio strategies and the efficient frontiers of the two problems in
Section 4 and
Section 5, respectively.
Section 6 provides numerical examples to illustrate the differences of the two problems and the effectiveness of the variance swap in hedging volatility risk. Finally,
Section 7 concludes the paper. The Appendix contains proofs that can be adapted from the literature.
2. Model Dynamics
This section introduces the complete market and the incomplete market, and sets up the model dynamics of primitive assets, including a bank account, a stock and a variance swap. To begin with, we fix a complete probability space , carrying two one-dimensional, independent standard Brownian motions and . We further equip with a right-continuous, -complete filtration generated by and . Here is a real-world probability measure. We denote by the expectation taken under , the conditional expectation under given , the Euclidean norm of , and the transpose of any vector or matrix A. Let be a finite horizon, where .
For later use, we introduce several spaces of random variables and stochastic processes on . For any , we define
: the space of -valued, -measurable random variables such that ;
: the space of -valued, -adapted processes such that ;
: the space of -valued, -adapted, càdlàg processes such that ;
: the space of -valued, -adapted, essentially bounded, càdlàg processes over under ;
: the space of -valued, -adapted, càdlàg processes such that the random variable has exponential moments of all orders.
Replacing the expectation by , where is the expectation under some probability measure equivalent to , we can define similar spaces of random variables and stochastic processes on , i.e., , , , and . Furthermore, we define the following two spaces of deterministic functions:
: the space of continuous functions ;
: the space of continuous, uniformly bounded functions .
Throughout this paper, we will take to be either or in different circumstances.
We let
be the risk-neutral probability measure, which will be specified after we introduce our standing assumption. Suppose that the market prices of risks of
and
are given by two
-adapted processes
and
. We denote by
the vector process of the market prices of risks, where
. We will specify the structure of the market prices of risks later. Indeed,
is a probability measure equivalent to
and the processes
and
defined by
and
are two one-dimensional,
-standard Brownian motions. We denote by
the expectation taken under
, and
the conditional expectation under
given
.
The price process of the bank account
is given by
where
represents the risk-free, instantaneous interest rate. In what follows, we introduce the dynamics of the stock and variance processes under the risk-neutral measure
and the real-world measure
sequentially. Under
, the stock price process
is governed by
where
is the instantaneous volatility of the stock at time
t; the variance process
evolves according to Heston’s model
Here
and
are the speed of mean-reversion and the long-run average of
under
;
is the volatility of volatility; the correlation coefficient satisfies
. We require that the Feller condition is satisfied, i.e.,
, so that
is positive,
-a.s. (refer to Chapter 9 in
Elliott and Kopp 2005). Though the Feller condition may not be satisfied in practice, market volatility seldom becomes zero. Hence, having the Feller condition in place is meaningful in our model, which guarantees a strictly positive volatility.
As in other literature on Heston’s model (see, for example,
Zeng and Taksar 2013), we assume that the market prices of risks at time
t are given by
and
The above specification of the market prices of risks ensures that the evolution of the variance process under the real-world probability measure
has a similar structure of affine drift and square-root volatility of volatility as that under the risk-neutral probability measure
(see Equation (
5)). Indeed, this specification is closely related to the completely affine and the essentially affine specifications proposed by
Duffee (
2002). Furthermore, we require
, which rules out the case that the real-world probability measure
coincides with the risk-neutral probability measure
. Otherwise, the portfolio selection problems do not have non-trivial solutions.
Under
, the stock price process
follows
Here
can be considered as the appreciation rate of the stock at time
t. The variance process
under
satisfies
where
Even when
, we still have
in view of the convention
. Then Equation (
5) is well-defined even if
. Hence, we do not require that
in this paper. The equivalence between
and
implies that
is also positive,
-a.s.. In fact, this is guaranteed by the Feller condition under
, i.e.,
. In Heston’s model (
5),
can be considered as the common shock of the stock price and the variance, while
as the idiosyncratic shock of the variance. Therefore,
and
represent the market price of the common risk of the stock and the variance and that of the idiosyncratic risk of the variance, respectively.
We now introduce our assumption:
Standing Assumption. For any
,
where
The Standing Assumption states that the variance process/the market price of risk is exponentially integrable of all orders under
. This assumption allows us to define a family of probability measures equivalent to
through a family of Radon-Nikodým derivatives. Indeed, under the Standing Assumption, it holds that
The above equation will be used frequently throughout this paper. Particularly, if we take
in (
6) or
in the Standing Assumption, then we can specify the risk-neutral probability measure
as follows
Moreover, it will turn out that the Standing Assumption ensures that a set of BSDEs admits unique solutions in proper spaces and mean-variance portfolio selection problems have optimal solutions.
We now introduce the dynamics of a variance swap under Heston’s model. The research on pricing variance swaps can be dated back to the early works of
Neuberger (
1990,
1994) and
Dupire (
1992,
1993). Simply speaking, a variance swap contract is a financial contract with two legs on the future realized variance of the price changes of the underlying asset. One leg of the variance swap is floating and pays a variable amount based upon the annualized realized variance over a specified period, while the other leg is fixed and pays a fixed amount. This fixed amount is called the strike, which is usually chosen such that there is no cost of entering the contract at the issue time. The terminal payoff of the variance swap is equal to the realized variance minus the strike multiplying a notational amount. Under the continuous sampling scheme, we consider a variance swap written on the realized variance of the stock
S over
with a one-unit notational amount. Mathematically, the time-
t value of this variance swap is given by
where the strike
is
Substituting (
9) into (
8) gives
Here the first equality is obtained via canceling out the first two deterministic terms on the right hand side of (
9) and noting that the third term on the right hand side of (
9) is a
-martingale and hence has a zero expectation under
; the second equality comes from interchanging the order of integration; the third equality is due to the martingale property of the Itô integral inside the conditional expectation
.
Therefore, differentiating both sides of (
10) with respect to
t, we obtain the dynamics of the variance swap
where
3. Problem Formulation
In this section, we formulate two mean-variance portfolio selection problems for an economic agent. In the first problem, the agent can invest in the bank account, the stock and the variance swap; in the second problem, the agent can only invest in the bank account and the stock. Since the variance process is driven by the common shock and the idiosyncratic shock , the market in the first problem is complete, while that in the second problem is incomplete in general. Note when or , the idiosyncratic shock disappears in the dynamics of the variance process and the variance swap. The randomness of the financial market is entirely driven by the common shock . In this case, the variance swap becomes a redundant asset, and the market in the second problem becomes complete. The special case of or will be discussed in detail in the rest of the paper.
In what follows, we introduce the mean-variance portfolio selection problem in the complete market. In this circumstance, the agent can allocate his wealth to the bank account, the stock and the variance swap over the finite-horizon
. Here we assume that the investment horizon is not longer than the term of the variance swap, i.e.,
. Let
denote the amount of the agent’s wealth invested in the stock at time
t, and
the notational amount invested in the variance swap at time
t. We call
a portfolio strategy of the agent. Let
be the total wealth of the agent at time
t when the portfolio strategy
is adopted. Suppose that the market is frictionless, short-selling is allowed and the portfolio strategy is self-financing. Then the amount of the agent’s wealth invested in the bank account at time
t is equal to
. Thus, the agent’s wealth process
satisfies the following stochastic differential equation (SDE):
where
and
represent the risk premium vector and the volatility matrix of the risky assets (i.e., the stock and the variance swap), respectively. Denote by
the variance-covariance matrix of the risky assets. If
, the market price of risk (vector) and its squared-norm satisfy
and
However, if
or
, the volatility matrix and the variance-covariance matrix are singular. To integrate this singular case into a unified framework, we define an auxiliary market price of risk (vector) and its squared-norm as
and
It should be noted that the following equality holds
for any
.
Definition 1. In the complete market, a portfolio strategy is said to be admissible if (1) is -adapted; (2) and . The set of admissible portfolio strategies is denoted by .
From the standard theory of SDEs (refer to Chapter 1 in
Yong and Zhou 1999), we know that for any
, the SDE (
12) has a unique strong solution
such that
, for any
. The agent’s objective is to find a portfolio
, such that the expected terminal wealth satisfies
for a given
, while the variance of the terminal wealth
is minimized. We specify the mean-variance problem in the complete market as follows:
Definition 2. In the complete market, the mean-variance portfolio selection is the following stochastic control problem with a terminal state constraint, parameterized by : Here denotes an optimal portfolio strategy of the above problem, and denotes the wealth process associated with . The optimal portfolio strategy is called an efficient portfolio strategy, the pair is called an efficient point, and the set of all efficient points is called an efficient frontier.
The Lagrangian duality theorem (refer to
Luenberger 1968) is a useful tool to deal with the state constraint
. We consider the following min-max stochastic control problem:
By the end of this section, we will show that the mean-variance portfolio selection problem (
18) is feasible under a mild condition. Then solving the mean-variance problem (
18) is equivalent to finding an optimal control
over
in the inner minimization problem first and then finding an optimal value
over
in the outer maximization problem in the min-max problem (
19). Note that
Denote by
. Therefore, the solution of the inner minimization problem is the same as that of the following problem
This problem is called a quadratic-loss minimization problem.
Next we formulate the mean-variance portfolio selection problem in the incomplete market. Note that the agent can only invest in the bank account and the stock in the incomplete market. Now the portfolio strategy is
and the associated wealth process is denoted by
, which evolves as follows
Definition 3. In the incomplete market, a portfolio strategy is said to be admissible if (1) is -adapted; (2) and . The set of admissible portfolio strategies is denoted by .
Again, by the standard theory of SDEs, for any
, the SDE (
21) has a unique strong solution
such that
, for any
. The mean-variance portfolio selection problem in the incomplete market is specified as follows:
Definition 4. In the incomplete market, the mean-variance portfolio selection is the following stochastic control problem with a terminal state constraint, parameterized by : Here denotes an optimal portfolio strategy of the above problem, and denotes the wealth process associated with . The optimal portfolio strategy is called an efficient portfolio strategy, the pair is called an efficient point, and the set of all efficient points is called an efficient frontier.
Similarly, the related min-max problem and quadratic-loss minimization problem are defined, respectively, as follows
and
where
.
The mean-variance problem (
18) is said to be feasible for every
if there always exists a portfolio
such that
. The feasibility of the mean-variance problem (
22) can be defined similarly. It can be shown as in previous works (see, for example,
Lim (
2004)) that the two mean-variance problems (
18) and (
22) are feasible if and only if
and
respectively. In the rest of the paper, we assume that
, which ensures that both problems are feasible.
Moreover, we restrict
and
in Problems (
18) and (
22), respectively, in the remainder of the paper. This is reasonable and in line with the existing literature. Otherwise, if
and
, Problems (
18) and (
22) have trivial solutions: the agent can achieve not only the terminal state constraint but also a zero variance by investing only part of his wealth, i.e.,
, in the risk-free bank account during the entire investment horizon.
Remark 1. Whether the variance swap is traded in the market makes the two problems fundamentally different. Although the more complicated derivative, i.e., the variance swap, is introduced in the first problem, its market is complete and hence the problem is easier. On the contrary, the second problem with less and simpler assets is more complicated due to market incompleteness.
4. Solutions to the Complete Market Case
In this section, we derive the explicit expressions of the efficient portfolio strategy and the efficient frontier of the mean-variance problem (
18). Our derivation relies on the LQ control and BSDE approach.
First of all, we consider a pair of processes
and
satisfying the following backward stochastic differential Riccati equation (BSRE):
Lim (
2004) discussed the solvability of a class of BSREs with bounded coefficients. However, the method in
Lim (
2004) cannot be applied to study the solvability of (
27), since its coefficients are random and unbounded. We instead use a transformation method to prove the existence and uniqueness of a solution to (
27).
Under the Standing Assumption, the following Novikov condition holds:
Thus, we can define a new probability measure
equivalent to
as follows
Hence by Girsanov’s theorem, the process
defined by
is a two-dimensional,
-standard Brownian motion. We denote by
the expectation taken under
, and
the conditional expectation under
given
.
Lemma 1. Suppose that the Standing Assumption holds. The BSRE (27) admits a unique solution , where the first component of the solution satisfies Proof. Let us consider a pair of processes
and
, which is governed by the following linear BSDE under
:
Evidently, the driver of (
29) is Lipschitz continuous. In addition, by Hölder’s inequality and the Standing Assumption, we can show
That is,
, for any
. Thus, Equation (
29) is a BSDE with
p-standard data (see Theorem 5.1 in
El Karoui et al. (
1997)), which admits a unique solution
, for any
. Furthermore, using Proposition 2.2 in
El Karoui et al. (
1997), we obtain
Since , we must have , a.e. , -a.s..
Consider a pair of transformed processes
and
defined by
and
An application of Itô’s differentiation rule to
gives
which is exactly the BSRE (
27). Observing (
31) and (
32), we can see that
has a one-to-one correspondence relationship with
. Therefore,
is the unique solution to the BSRE (
27).
Combining (
30)–(
32) gives
a.e.
,
-a.s.. Since
and
are equivalent, we have that
and the above inequalities also hold
-a.s.. Furthermore, using Hölder’s inequality, the Standing Assumption and Equation (
6) and taking
in the above
p-standard data, we obtain
where
C is a positive constant. Therefore,
. □
Remark 2. The basic idea in the above proof is to relate the BSRE (27) to a linear BSDE (29) that satisfies the Lipschitz continuity condition. By doing this, we can use the -solution theory of BSDEs and the transformation method to prove the uniqueness and existence of the original BSRE in appropriate spaces. Furthermore, from the linear BSDE and the reciprocal transformation, we can represent the first component in terms of an expectation, which will be used to derive explicit expressions of the solution to the BSRE (27). Remark 3. The derivations of (34) is based on the following reasoning: under the Standing Assumption, an adapted stochastic process, which is dominated by another adapted, -integrable process under an equivalent probability measure, is -integrable under the original probability measure. Similar derivations can be also conducted for processes in . We will refer to (34) and this remark whenever similar derivations are needed in the sequel. Since the (auxiliary) market prices of risk vector
are deterministic functions of the variance
, it is Markovian with respect to
. Therefore, we can derive the explicit expressions of the unique solution to (
27) via partial differential equations (PDEs).
Lemma 2. Suppose that the Standing Assumption holds. The unique solution pair of the BSRE (27) is given byand Here and are the solutions of the following Riccati and linear ODEs:and Remark 4. In Lemma 2, deriving the solution to the BSRE (27) is reduced to calculating an expectation. Due to the Markovian and square-root structure of Heston’s model, we use the Feynman-Kac formula and obtain the exponential affine-form expression for the first component of the solution. Indeed, the Feynman-Kac formula relates the solutions of Markovian BSDEs to those of PDEs. Similar calculations are frequently conducted in zero-coupon bond pricing under affine-form term-structure models. Lemma 3. The explicit solutions to (38) and (39) are given byandwhere , and . Define a stochastic exponential
by
Before we derive the efficient strategy and the efficient frontier, we study the integrability of . This integrability result will be used in the proof of Theorem 1.
Lemma 4. Under the Standing Assumption, the stochastic exponential belongs to , for any .
Proof. It can be easily verified that for any given
, the following equation
has two positive roots
with the first root satisfying
. From the Standing Assumption, we know
This completes the proof. □
Theorem 1. Suppose that the Standing Assumption holds. The efficient portfolio strategy of the mean-variance portfolio selection problem (18) is given byorwhereand the efficient frontier is given bywhich can be also written as Proof. Denote by
which solves the same SDE as
in Equation (
12) but has a different initial value
. Hence for any
, we know
, for
. By Itô’s differentiation rule, we have
We employ a localization technique and define a sequence of stopping times as follows
Here we adopt the convention
. Since
and
, for any
, and
, the sequence of the stopping times
is increasing and converges to
,
-a.s., when
n approaches
. Moreover, we note
where the right hand side is a
-integrable random variable.
Integrating from 0 to
and taking expectations on both sides of (
49) yield
Sending
in the above equation and using the dominated convergence theorem and the monotone convergence theorem, we obtain
Depending on the value of correlation coefficient, the optimal strategy of the quadratic-loss minimization problem (
20) is given by the following two cases
or
The optimal cost functional is given by
From the Lagrangian duality theorem, solving the original problem (
18) is reduced to maximizing the following cost functional
over
. From Lemma 1, we know
Using the first-order condition to (
55) with respect to
, we obtain the following optimal value of
:
Substituting
into (
52) or (
53) and (
54) leads to the efficient portfolio strategy (
43) or (
44) and the efficient frontier (
46) and (
47).
Next we claim that the efficient portfolio strategy (
43) or (
44) is admissible. Evidently,
is
-adapted, i.e., Condition (1) in Definition 1 is satisfied. For both (
43) and (
44), we can see
Then substituting
into (
12) gives
where
and
By Itô’s differentiation rule, we can verify
where
is the unique solution of the BSRE (
29) and
is defined by
Using Lemmas 1 and 4, we deduce that
Furthermore, we derive that
Hence, . In the same vein, we can show . This implies that Condition (2) in Definition 1 is satisfied. Therefore, we can conclude . This completes the proof. □
Remark 5. Although the efficient strategy has the same parametric form as that in the market with bounded coefficients, the admissibility of the efficient strategy needs to be carefully discussed. Simply speaking, this is because the product of two square-integrable variables is not necessarily square-integrable unless additional conditions (refer to Remark 3), i.e., Standing Assumption, are imposed.
Remark 6. From Lemmas 2 and 3, we can see that is independent of the term of the variance swap, i.e., . Therefore, the efficient frontier (45) or (46) in the complete market does not depend on . This is interesting since investing in the variance swaps with different maturities does not make any difference to the efficient frontier. Remark 7. Depending on the correlation coefficient, the efficient portfolio strategies have different representations. Particularly, if or 1, the optimal (notational) amounts allocated to the stock and the variance swap cannot be disentangled, since the volatility matrix now is singular and hence not invertible. Indeed, when or 1, the stock and the variance swap play essentially the same role in the market and the existence of any one of them makes the market complete and the other a redundant asset.
5. Solution to the Incomplete Market Case
In this section, we consider the mean-variance portfolio selection problem (
22), where the variance swap is absent. Although the market with only the bank account and the stock in this section seems simpler than the market in the previous section, the derivations of the efficient portfolio strategy and the efficient frontier are more complicated due to market incompleteness. The derivations in this section also rely on the LQ control and BSDE approach.
Consider a pair of processes
and
satisfying the following BSDE
As in the previous section, Equation (
58) is a BSRE with random and unbounded coefficients, thereby the existing theory of BSREs cannot be used directly. Similarly, we apply a transformation method to prove the existence and uniqueness of a solution to BSRE (
58). Indeed, in
Section 4 we use a reciprocal transformation to relate the BSRE (
27) to the linear BSDE (
29). Since the market is incomplete in this section, the structure of BSRE (
58) is different from that of (
27). We cannot use the same reciprocal transformation in this section. Instead, we use a logarithmic transformation to relate BSRE (
58) to a quadratic BSDE. In that sense, this section is not a trivial repetition of the previous section.
Under the Standing Assumption, we can define a new probability measure
equivalent to
as follows
By Girsanov’s theorem, the process
defined by
and
is a two-dimensional,
-standard Brownian motion. We denote by
the expectation taken under
, and
the conditional expectation under
given
.
Lemma 5. Suppose that the Standing Assumption holds. The BSRE (58) admits at least one solution . Proof. We consider a pair of processes
and
following a quadratic BSDE under
:
From the Standing Assumption, we can see that the BSDE (
59) belongs to a class of quadratic BSDEs satisfying the exponential integrability condition, as considered by
Briand and Hu (
2008). Therefore, under the Standing Assumption, there exists at least one solution
, for any
(see Corollary 4 in
Briand and Hu 2008).
We consider a pair of transformed processes
and
defined by
and
Applying Itô’s differentiation rule to
gives
which is exactly the BSRE (
58). Therefore, by relationships (
60) and (
61), there also exists at least one solution
to the BSRE (
58). By
, where
, Hölder’s inequality and the Standing Assumption (see also Remark 3), we derive
and
Therefore, . □
Remark 8. As is not uniformly bounded in t, the classical theory of quadratic BSDEs established by Kobylanski (2000) is not working for (59). Furthermore, since the driver of (59) is neither convex nor concave in the second (control) component of the solution, the uniqueness result for quadratic BSDEs in Briand and Hu (2008) cannot be applied. Therefore, the BSDE (59) does not necessarily have a unique solution, and neither does the BSRE (58). Fortunately, we can find an explicit solution to the BRSE (58), thanks to its Markovian structure, and verify that this solution is exactly the unique solution. Lemma 6. Suppose that the Standing Assumption holds. A solution pair to the BSRE (58) is given byand Here and are the solutions of the following Riccati and linear ODEs:and Remark 9. Unlike the proof of Lemma 2, the solution of the BSRE (58) is found by trial and error in Lemma 6. This is because we cannot find a linear BSDE related to BSRE (58). In fact, it seems very difficult, if not impossible, to represent the solution in terms of an expectation expression. The difficulty is caused by market incompleteness. Lemma 7. The first component of the solution to the BSRE (58), i.e., given by (62), is in . More specifically, , a.e. , -a.s.. Proof. From the second line of Equation (
A11), we see
Since
is bounded, a.e.
,
-a.s. and
, we have that the process
is a square-integrable
-martingale. Then taking expectations gives
a.e.
,
-a.s.. Furthermore, since
,
,
-a.s., and
is not the solution of (
65), the upper bound is strict, for any
. □
Remark 10. Although we have already obtained the solution space of in Lemma 5, that space is not delicate enough to be used in our following applications. Lemma 7 gives a more accurate estimate for the first component of the solution . The upper bound of guarantees that the first-order condition is satisfied in Theorem 2 for the outer maximization problem.
As in the previous section, we provide the explicit representations of the solutions to (
65) and (
66).
Lemma 8. The explicit solutions to (65) and (66) are given byand - (i)
- (ii)
if and , then - (iii)
if and , then
where , and .
Proof. The proof is similar to that of Lemma 3. We omit it here. □
Lemma 9. Suppose that the Standing Assumption holds. The solution given by (67) is non-negative and non-explosive over . Proof. Consider the following Riccati equation for
:
Obviously,
is the solution to (
71). Observe
and
Thus, using the comparison theorem for Riccati equations (see Theorem 2.1 in
Freiling et al. 1996) gives
Since
is Markovian with respect to
, we can derive as in Lemma 2 that there exists
and
such that
The dynamics of
under
is given by
As in Lemmas 2 and 6, we have
and
Observe that
and
Again, using the comparison theorem for Riccati equations gives
It follows from Jensen’s inequality, the tower property, Hölder’s inequality and the Standing Assumption that
Therefore,
does not explode over
, i.e., the investment horizon
T is shorter than the first explosion time of
, and
This completes the proof. □
The next lemma states that
given in Lemma 6 is, in fact, the unique solution to the BSRE (
58).
Lemma 10. Suppose that the Standing Assumption holds. The BSRE (58) admits a unique solution , which is given by (62)–(64). Proof. From relationships (
60) and (
61), we have
and
is a solution pair of the quadratic BSDE (
59). Suppose that
, where
, is another solution pair to the BSDE (
59), i.e.,
By the Standing Assumption and Lemma 9, the following Novikov condition holds:
Thus, we can define a new probability measure
equivalent to
as follows
By Girsanov’s theorem, the process
defined by
and
is a two-dimensional,
-standard Brownian motion. Under
,
and
satisfy the following two equations
and
Denote by
. Then subtracting (
76) by (
77) gives
Indeed, Equation (
78) is a BSDE with quadratic growth and bounded terminal value considered by
Kobylanski (
2000), hence admits a unique solution. Clearly,
and
form the unique solution pair to (
78). Therefore,
is the unique solution to the quadratic BSDE (
59). By definition,
is the unique solution to the BSRE (
58). Furthermore, by Lemmas 5 and 7, we conclude that
. □
Next we derive the closed-form expressions of the efficient portfolio strategy and the efficient frontier of the mean-variance portfolio selection problem (
22).
Theorem 2. The efficient portfolio strategy of the mean-variance portfolio selection problem (22) is given bywhereand the efficient frontier is given bywhich can be also written as Proof. As in
Section 4, a two-step procedure is employed to derive the efficient portfolio strategy and the efficient frontier. Since the derivations are similar to those of Theorem 1, we only present key steps here.
We first consider the quadratic-loss minimization problem (
24). Applying Itô’s differentiation rule to
, where
, using the technique of localization, and taking integrations and expectations, we obtain
Therefore, the optimal control and the associated cost functional of the quadratic-loss minimization problem (
24) are given by
and
Then we consider the following cost functional
Since
, using the Lagrangian method, we can achieve the desired results (
79)–(
82). The admissibility of the efficient portfolio strategy (
79) can be verified as in the proof of Theorem 1, and is omitted here. □
Remark 11. From Theorems 1 and 2, the efficient portfolio strategies in the complete and the incomplete markets can be, respectively, decomposed into two components:and The first terms capture the market prices of risks of the stock and the variance swap, while the second terms quantify the dollar amounts that should be reserved to hedge the volatility risk arising in Heston’s model.
Remark 12. From the explicit solution of , the efficient frontier is independent of , i.e., the market price of the idiosyncratic risk, in the incomplete market. As seen in the above remark, although the agent allocates part of his wealth to hedge against the volatility risk, only the common risk can be hedged in the incomplete market. The idiosyncratic risk is still unhedgable unless volatility derivatives (e.g., variance swaps) can be traded as in the complete market case. From this observation, we conjecture that the residual risk on the efficient frontier of the complete market should be smaller than that of the incomplete market unless these two markets are indistinguishable, i.e., when or 1.
6. Numerical Examples
In this section, we provide numerical examples to illustrate the differences between the complete and the incomplete market scenarios discussed in
Section 4 and
Section 5, respectively. We are particularly interested in when the two markets are indistinguishable and whether the variance swap is an effective tool to reduce the volatility risk in the portfolio.
Intuitively speaking, the variance swap can hedge against the volatility risk and hence adding the variance swap into the portfolio should reduce the overall risk, as measured by the variance of the terminal wealth. Indeed, in the complete market, the agent would walk away from the variance swap, invest only in the bank account and the stock, and achieve at least the same level of the variance as in the incomplete market if there were any possibility that the variance swap would increase the overall risk of the agent’s terminal wealth. When
, we have
Then using the comparison theorem for Riccati equations (see Theorem 2.1 in
Freiling et al. 1996), we know that
, for all
. By Lemmas 1, 6 and 7, we further have
and hence
, for all
. Therefore, given that
and with all other parameters being identical in the two markets, we can confirm
analytically. However, when
, the comparison theorem cannot be applied and this case needs to be analyzed numerically.
Before proceeding to numerical results, we briefly explain our principle of selecting parameter values. Clearly, it is financially reasonable that v, , and take positive values. In addition to that, we require that the Feller condition holds, i.e., . The values of , and should be discussed carefully.
From the empirical evidence, the correlation coefficient should take negative values due to the leverage effect, i.e., the instantaneous volatility decreases as the stock price increases. Typically, the appreciation rate is greater than the risk-free interest rate. So it is not unreasonable to assume that
and
. Therefore, the situation with
is extremely important and practically meaningful. In what follows, we will verify the impact of the variance swap on the overall risk in the case of
and investigate that in the case of
.
Table 1 presents a set of parameter values adopted as our benchmark. We will vary the value of one parameter each time when others are fixed, and provide sensitivity analysis of the efficient frontier with respect to model parameters
,
and
. These parameters determine the differences between the complete and the incomplete market examples. Recall the restrictions
and
in the complete and the incomplete markets, respectively. The benchmark values of model parameters allow us to consider the efficient frontiers for
in both markets.
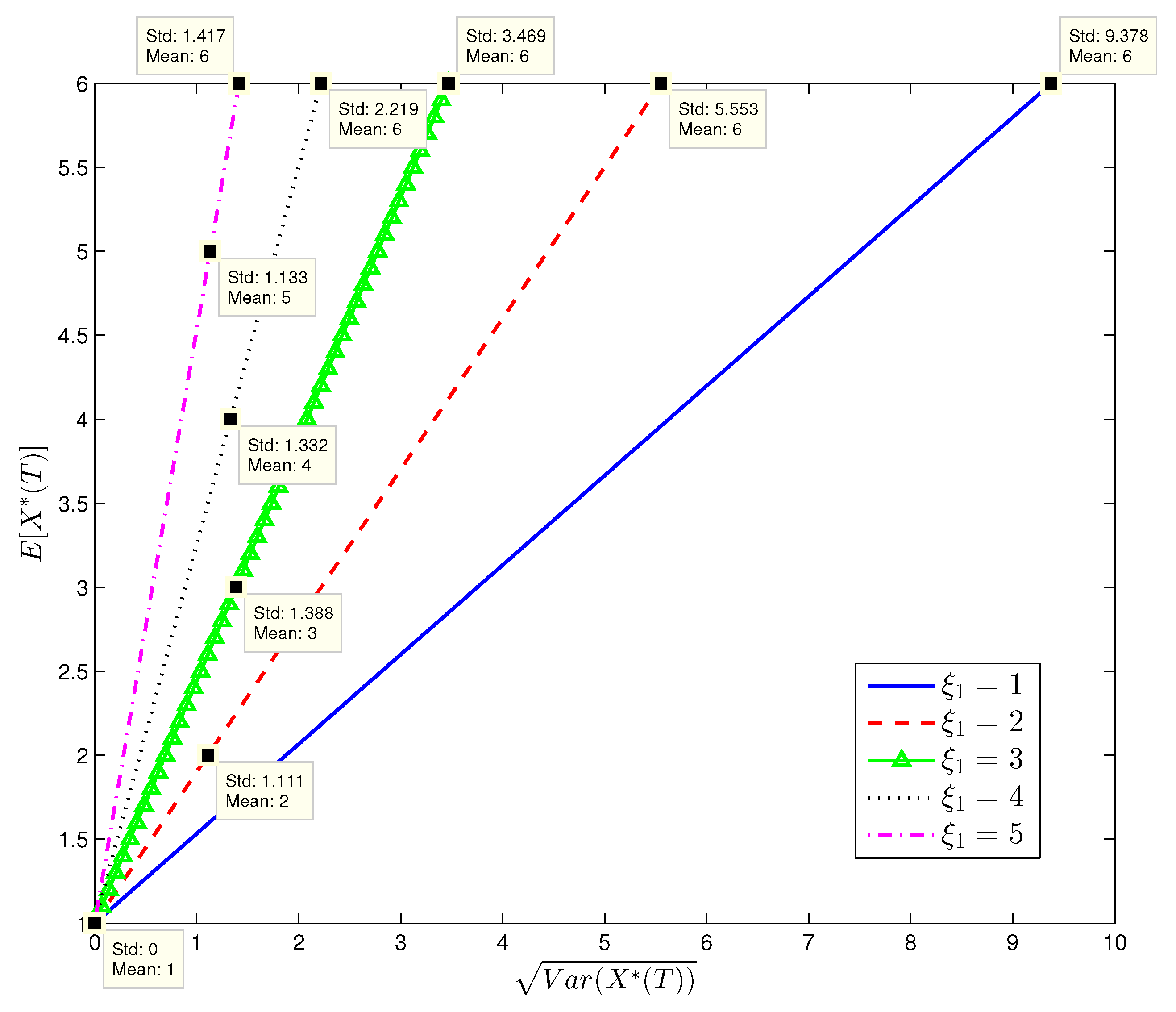
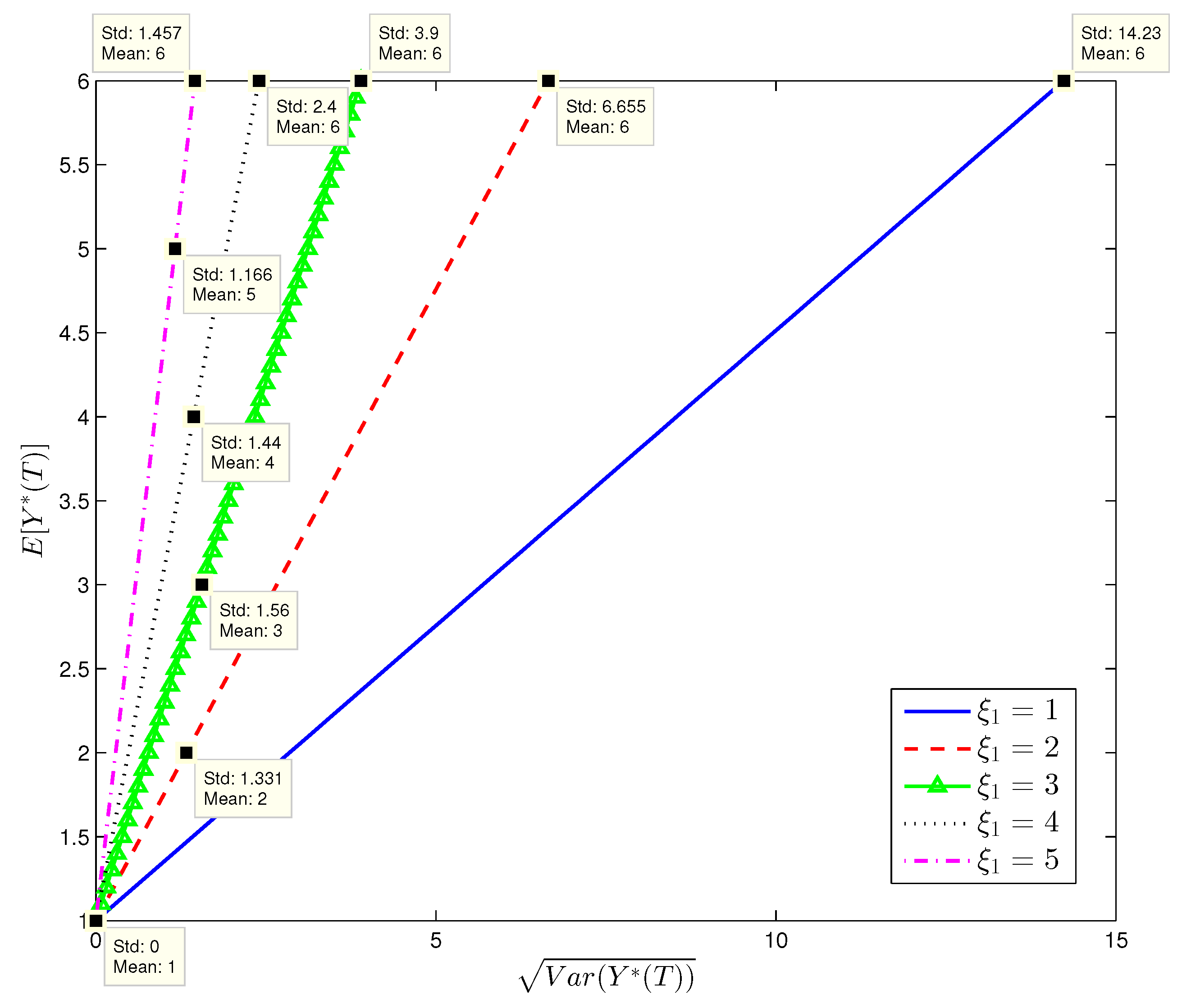
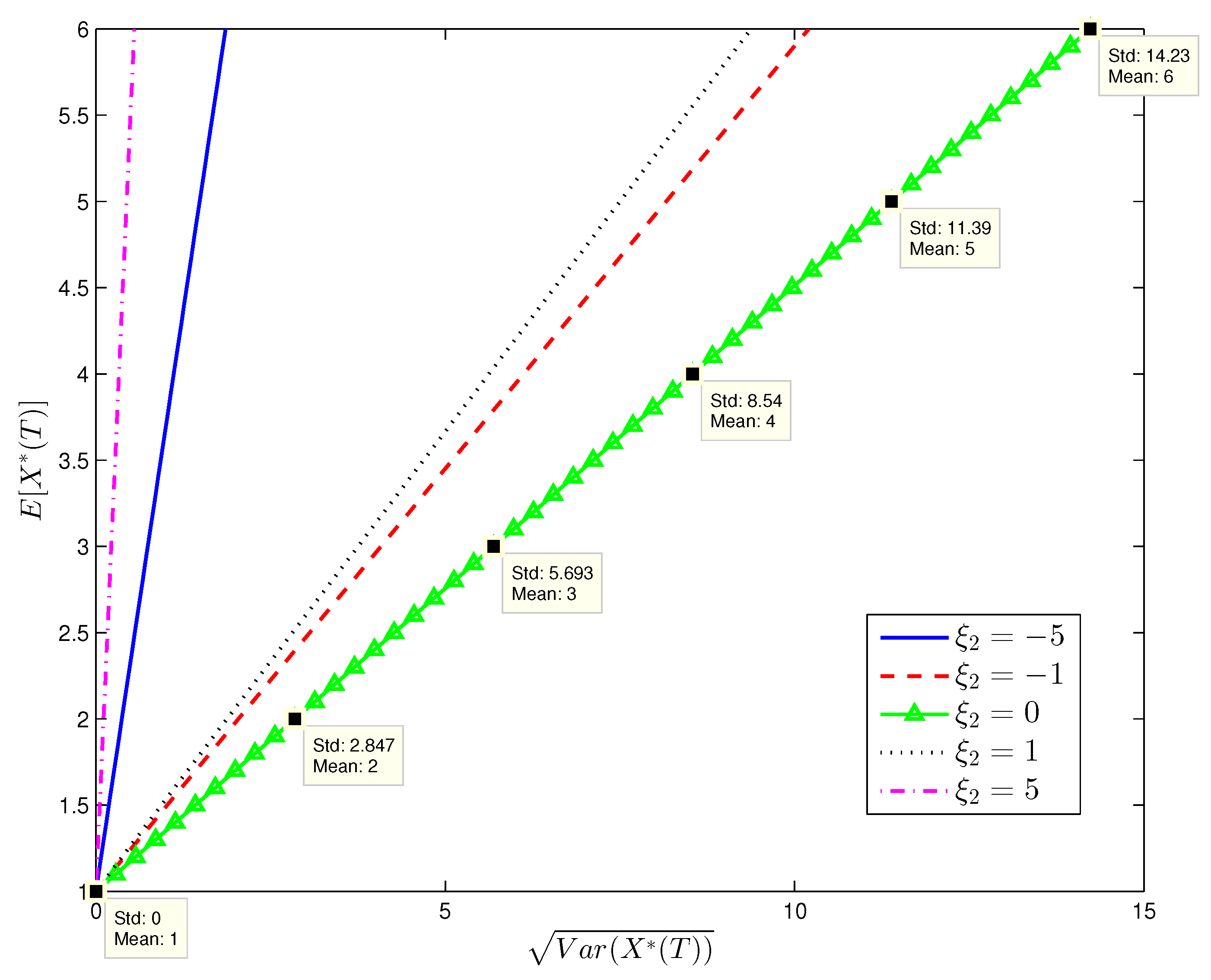
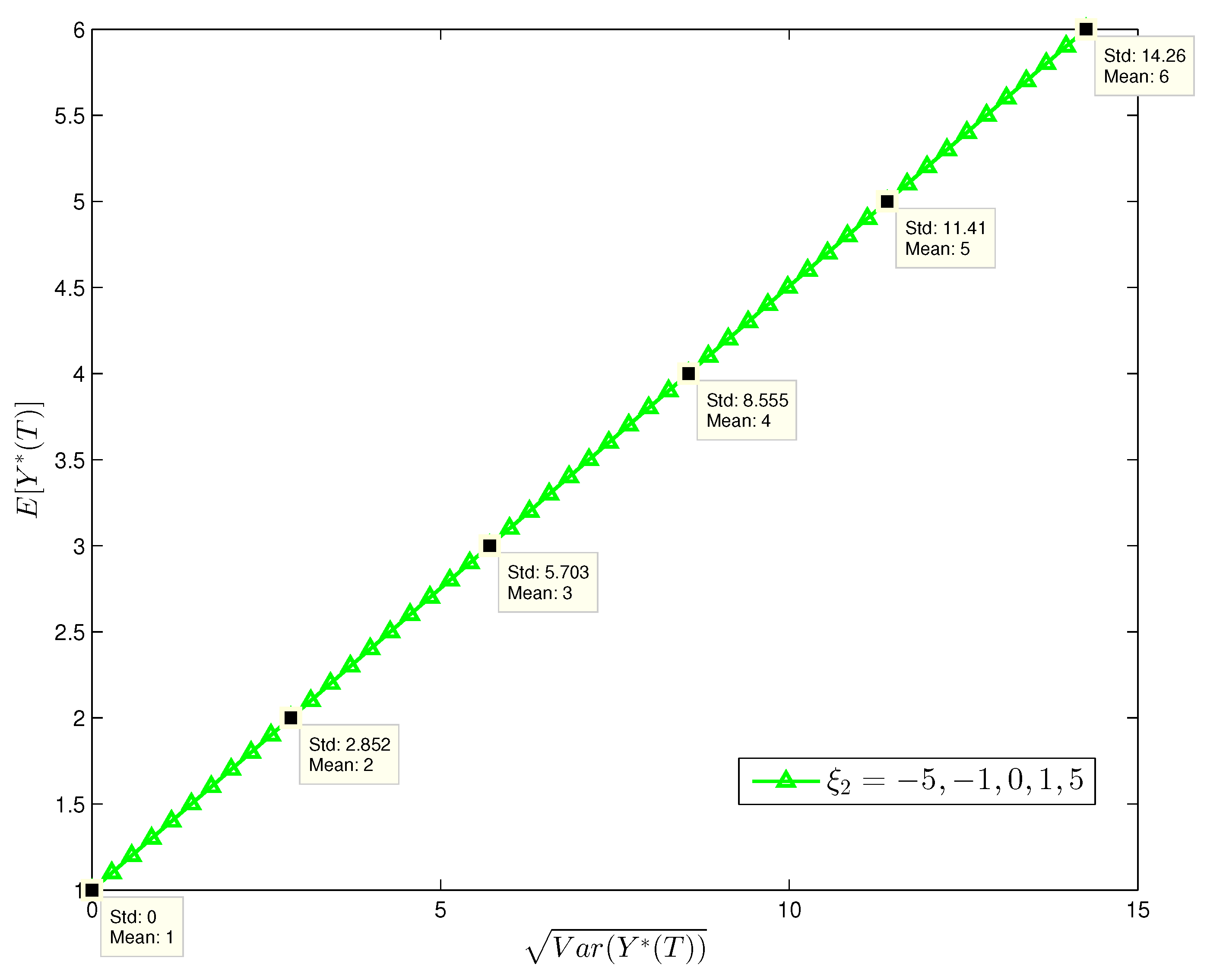
Figure 1,
Figure 2,
Figure 3 and
Figure 4 show the efficient frontiers (standard deviation v.s. mean) with different values of
and
. From
Figure 1,
Figure 2,
Figure 3 and
Figure 4, the efficient frontiers in the complete market is always on the left hand side of those in the incomplete market when all parameter values are identical. Note that the efficient frontier on the left hand side has a greater slope and a greater slope indicates a lower overall portfolio risk. This shows that introducing the variance swap to the financial market is an effective way to hedge the volatility risk, thereby reducing the overall risk of the agent’s terminal wealth. From
Figure 1 and
Figure 2, we can see that the overall risk of the agent’s terminal wealth decreases with
. On the one hand, observing two matrices in Equation (
83) and using the comparison theorem for Riccati equations, we know that both
and
are increasing functions of
when the values of other model parameters are specified in
Table 1. In addition, the greater is
or
, the greater is the slope in (
47) or (
82). Thus, the efficient frontiers with greater
are on the left hand side of those with smaller
. If the market price of the common risk
is higher, the excessive returns on both the stock and the variance are greater. Therefore, the agent can achieve a same level of expected terminal wealth by holding less risky assets and hence bearing less risk.
In
Figure 4, it is shown that
has no impact on the efficient frontiers in the incomplete market. In the incomplete market, the agent cannot invest in the variance swap and does not bear the idiosyncratic risk of the variance process in his wealth. So the efficient frontiers in the incomplete market are independent of
. On the other hand,
Figure 3 shows that the efficient frontiers in the complete market with the variance swap do vary with
. Regardless of whether
is negative or positive, the variance of the terminal wealth in the complete market is smaller than that in the incomplete market for any given level of expected terminal wealth. Moreover, the higher is the absolute value of
, the smaller variance of the terminal wealth can be achieved in the complete market. Note that
is proportional to the market price of the idiosyncratic risk of the variance process. This implies that the higher is the market price of the idiosyncratic risk, the more volatility risk can be hedged by the variance swap. We note that even if
is zero, the variance is also slightly smaller in
Figure 3 than in
Figure 4 (refer to the green lines in both figures). This implies that even when the idiosyncratic risk is not priced, the volatility risk still amplifies the variance of the terminal wealth and the variance swap can be still used to hedge the volatility risk in the complete market.
Table 2 and
Table 31 report the efficient frontiers with different
in the complete and the incomplete markets, respectively. Though
is a condition to incorporate the leverage effect in our modeling framework, we also show the efficient frontiers with
, as this case corresponds to a degenerate incomplete market, which is in fact complete as discussed throughout this paper. We observe that as the correlation increases from
to 0, the variance of the terminal wealth is decreasing in both markets. This is because that the increase of
reduces the leverage effect, which makes the stock price risk and volatility risk less interactive. Thus, the diminished interaction decreases the overall risk of the terminal wealth.
It is particularly interesting, as shown in the first and the last rows of
Table 2 and
Table 3, that the efficient frontiers are exactly the same in the complete and the incomplete markets when
. This verifies our conjecture, that is,
is a condition that the complete and the incomplete markets are indistinguishable. The equivalence of two markets can be also confirmed by the comparison theorem of Riccati equations. More precisely, the following equality holds
if and only if
. Once Equation (
84) is satisfied, the slopes in (
47) and (
82) are identical and so are the efficient frontiers. If the variance process and the stock price process are perfectly positive/negative-correlated (i.e.,
), the variance swap becomes a redundant asset. Note that even if the idiosyncratic risk is not priced, i.e.,
, the two matrices in (
84) may be still different due to their last entries (see
Figure 3 and
Figure 4). This reflects that the differences of the complete market and the incomplete market are primarily determined by
rather than
.