Longevity Risk Measurement of Life Annuity Products
Abstract
1. Introduction
2. The Model’s Features
2.1. Mortality Model
2.2. Insurer’s Liability
3. Solvency Capital Valuation
3.1. Deferred Period
- -
- be the fund value at the end of the contract, where the available asset at time t is defined as
- -
- be the value at time n of the liability of the insurer;
- -
- is then the final surplus of the contract.
- -
- is the real number of survivors at time t;
- -
- is the survival index of an annuitant initially aged 65, alive at age and living at least up to age . This term guarantees that a policyholder in the cohort must be alive at the end of the deferred period;
- -
- guarantees that benefits are paid if the annuitant is alive at each payment time on the payment period.
3.2. Payment Period
4. Numerical Results
4.1. Simulation Framework
4.2. Results and Comparative Remarks
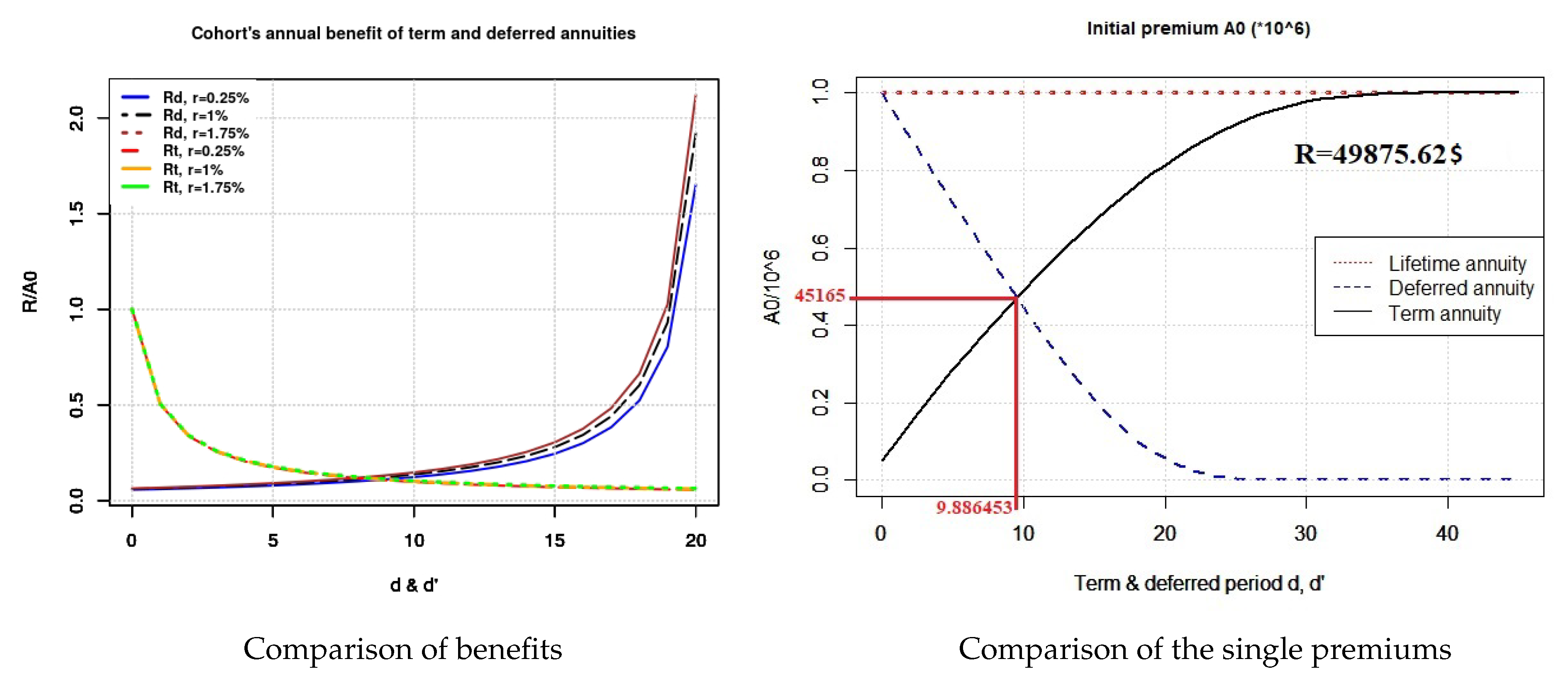
- : This comes from the fact that , where is shared for the benefits for the lifetime annuity, whereas is shared for the benefits for term annuity. This can be explained by the fact that the survival probabilities are high for the first years following the retirement.
- : Similarly, the unique premium is distributed into benefits for a lifetime annuity, whereas it is distributed into benefits for the deferred annuity.
- •
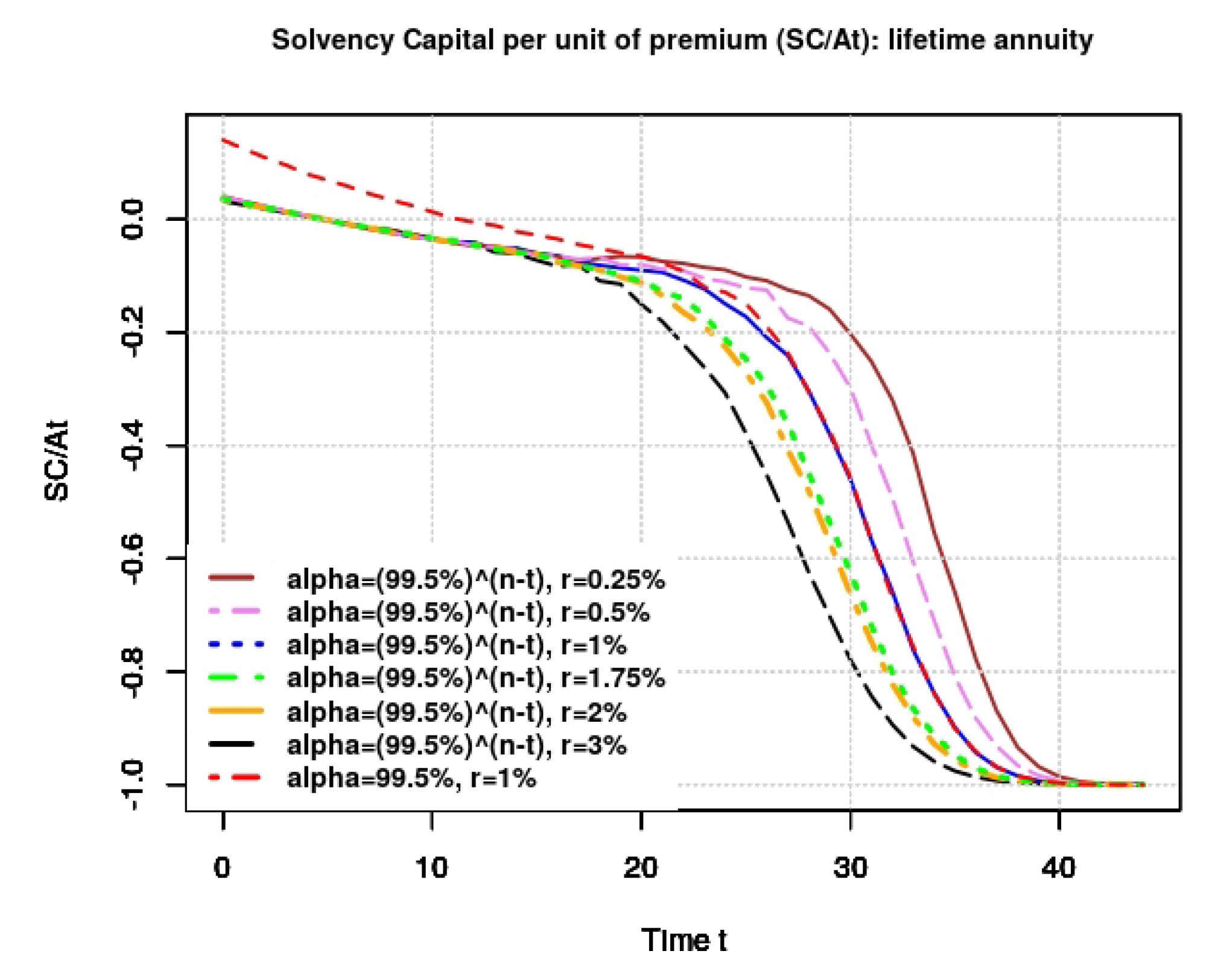
- Lifetime annuity:Figure 2 shows how the SC changes with respect to the computational time for different values of the confidence level and the short rate. We observe that the SC decreases when the short rate increases. We can also see that the SC decreases as t increases. Moreover the values of SC obtained with a variable confidence level are smaller than those obtained with a constant confidence level.Note that a negative value of SC means no additional capital is required from the insurer; that is, . In other words, means that the insurer is solvent with a confidence level without any additional capital.
- •
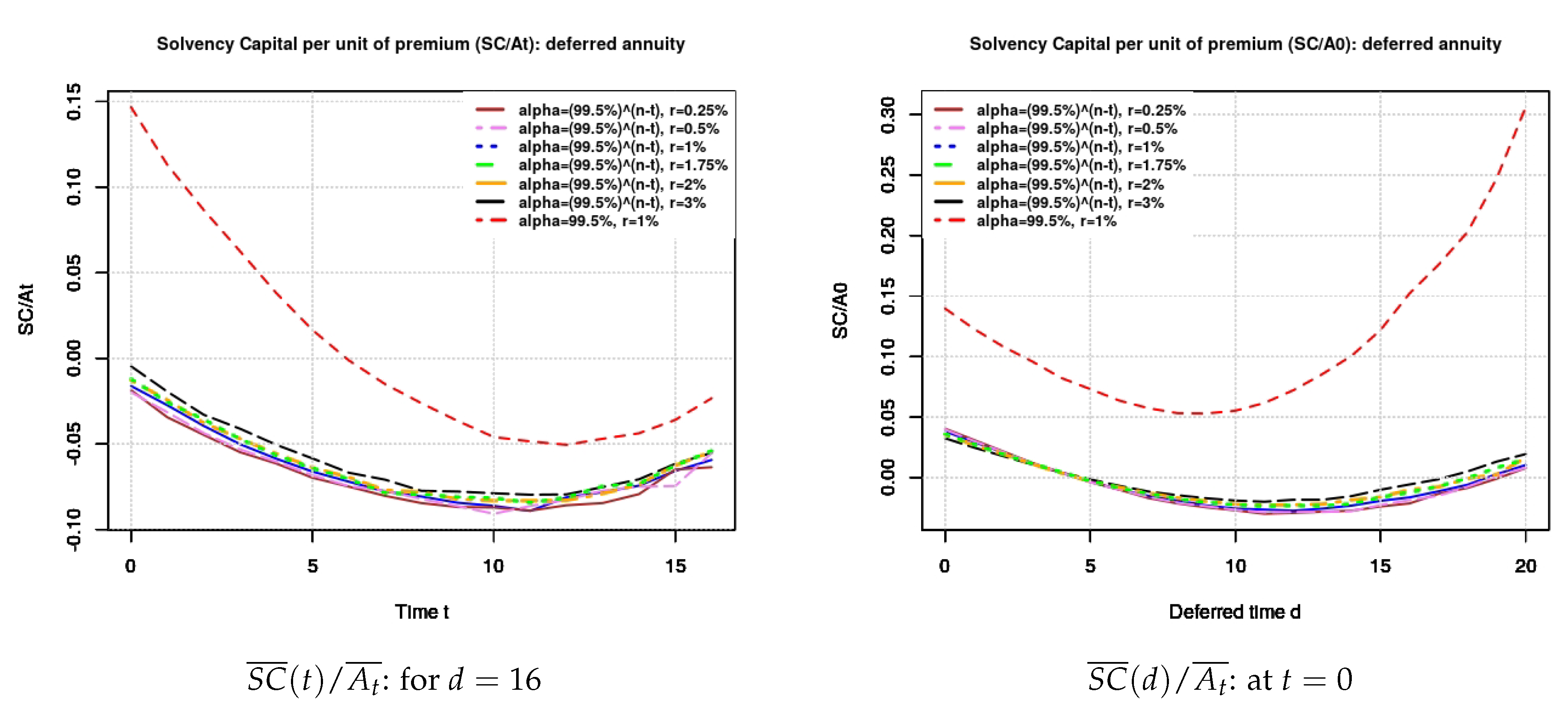
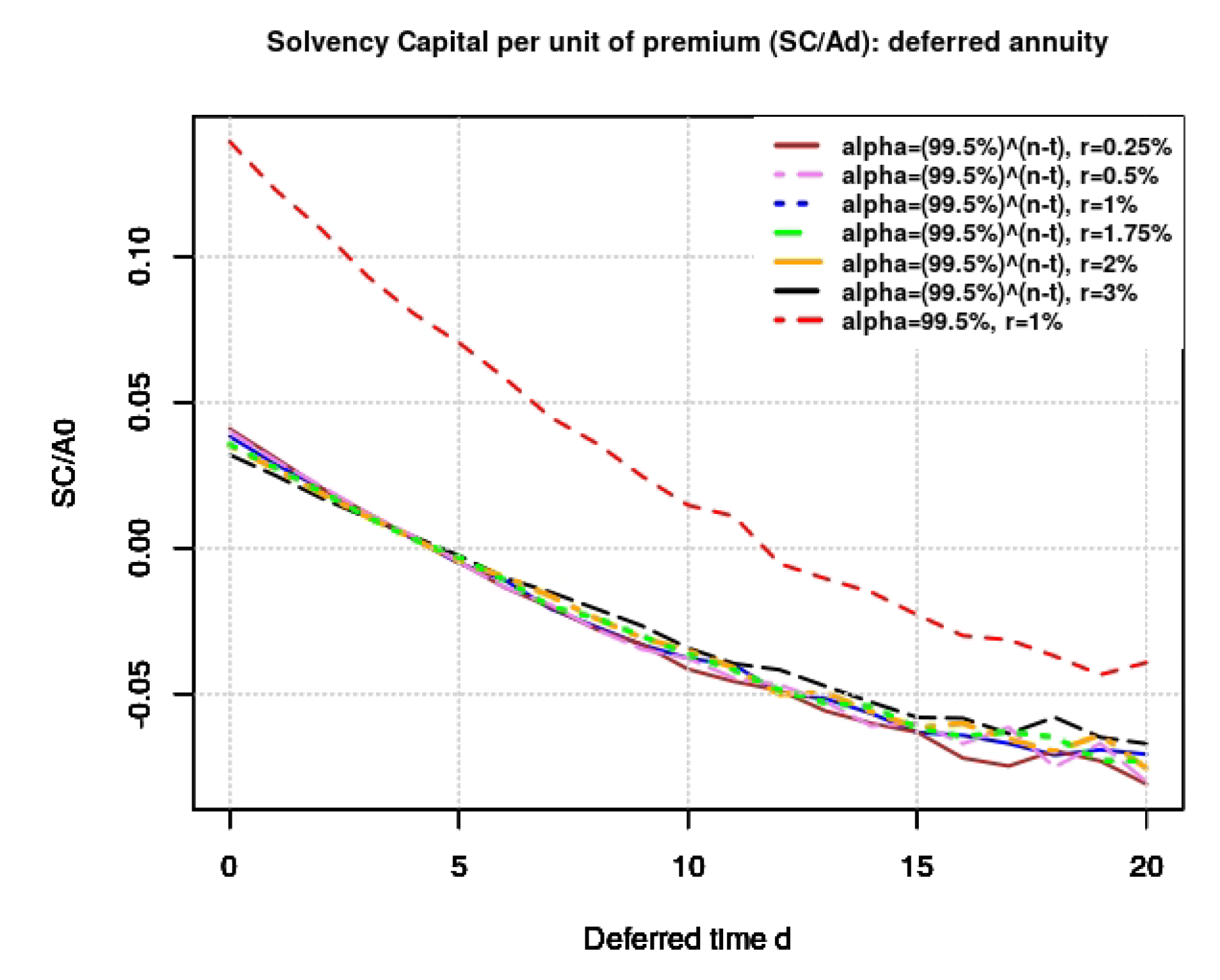
- Deferred annuity: Below are presented the graphs of the SC with respect to t; to d on the deferred period in Figure 3, and with respect to d on the payment period in Figure 4 respectively.From Figure 3 it comes out that the SC decreases for both values of and slightly decreases with respect to r. Furthermore, for a constant confidence level we obtain a higher value of SC; it decreases for small values of d and increases for larger values of t. Moreover, the SC have a convex form with respect to d and with respect to t. This implies that there exist optimal values of d and t that minimize the SC of the insurer.Regarding Figure 4, it can be seen how the SC decreases with d in the payment period. Moreover, we find that the SC is strictly negative with respect to and for any value of r and .
- •
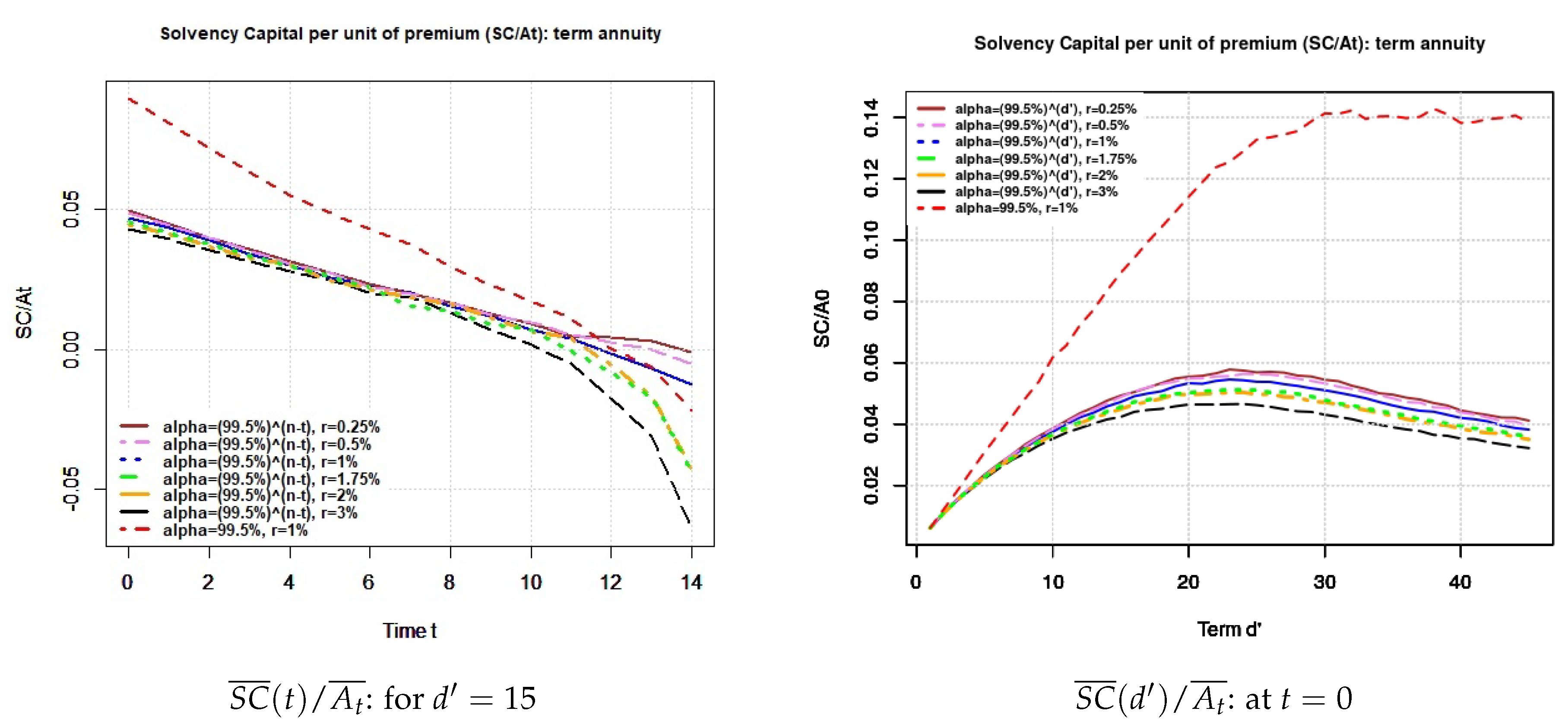
- Term annuity:Figure 5 below shows the SC with respect to t and to both .It comes out that the SC decreases with and r. Moreover, the SC is strictly positive and increases with for constant and takes a concave form when increases for variable values of .
- (i)
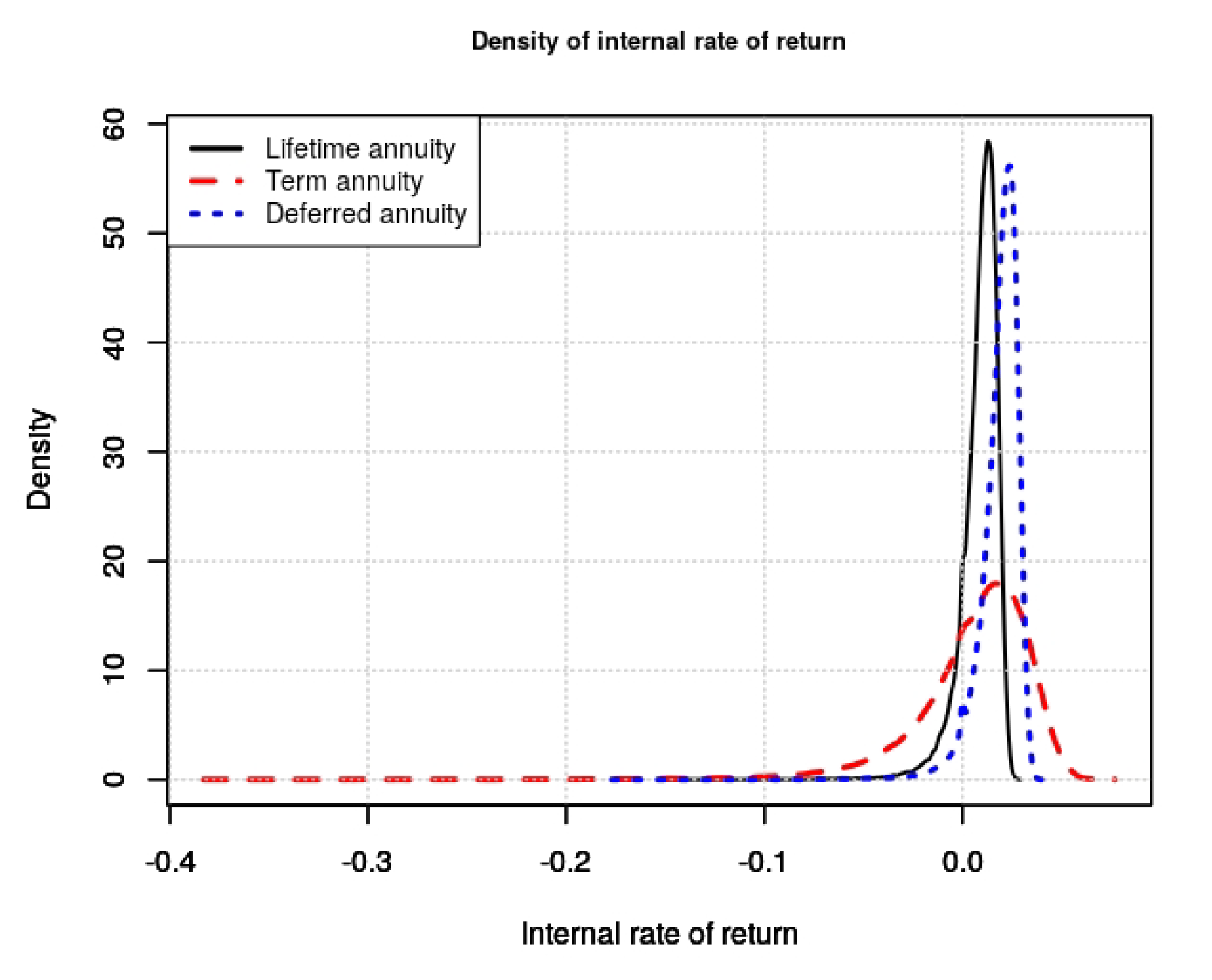
- On the policyholder side, buying a term annuity will provide the annuitant with a good level of annual benefits but he will not be fully hedged against the longevity risk, whereas buying a deferred annuity will give a better level of annual benefits until death. In these cases, the longevity risk will partly be borne by the policyholders. The lifetime annuity gives the smallest level of annual benefits and fully hedges the annuitants against the longevity risk. Furthermore, for a fixed unique premium (respectively annual benefit), we can always find a pair of deferred time and term time such that the deferred and the term annuities provide the same annual benefits (respectively, the same unique premium). Note that combining successive term annuities could be a way to fully protect the annuitant against longevity risk, but in this case, the policyholder will face a pricing risk. The latter refers to the risk of rising annuity prices as a consequence of a high survival probability.
- (ii)
- On the insurer side, we can see that a positive SC is not always bad for an insurer, since it could yield a return even greater than a simple risk-free investment. Thus, the choice of the product to invest in depends on the risk aversion of the shareholders. Furthermore, identifying the product with the higher SC is subject to the computational time.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Term Annuity | Deferred Annuity | |||
|---|---|---|---|---|
| Values of and | Constant | Variable | Constant | Variable |
| 1 | 0.006156096 | 0.006153251 | 0.12403064 | 0.028944735 |
| 2 | 0.012352836 | 0.011125707 | 0.10912764 | 0.020232837 |
| 3 | 0.018453675 | 0.015353574 | 0.09544175 | 0.011929853 |
| 4 | 0.024303704 | 0.019543642 | 0.08413130 | 0.003968597 |
| 5 | 0.030369315 | 0.023229284 | 0.07259427 | −0.002910031 |
| 6 | 0.036514168 | 0.026574362 | 0.06354518 | −0.009368481 |
| 7 | 0.042701852 | 0.029546813 | 0.05693445 | −0.015076207 |
| 8 | 0.049113252 | 0.032413929 | 0.05428510 | −0.019060104 |
| 9 | 0.054907241 | 0.035345726 | 0.05368941 | −0.022470205 |
| 10 | 0.061024635 | 0.037834998 | 0.05721433 | −0.024729544 |
| 11 | 0.066085821 | 0.040194102 | 0.06270525 | −0.027540167 |
| 12 | 0.071862367 | 0.042155518 | 0.07390130 | −0.026949580 |
| 13 | 0.078535718 | 0.044084758 | 0.08444255 | −0.025193941 |
| 14 | 0.081923754 | 0.045936822 | 0.10052367 | −0.022804985 |
| 15 | 0.088126534 | 0.047274945 | 0.12330174 | −0.020479482 |
| 16 | 0.094834232 | 0.048906110 | 0.14671319 | −0.017047308 |
| 17 | 0.099364414 | 0.049970686 | 0.17094055 | −0.008042942 |
| 18 | 0.104767967 | 0.051177807 | 0.20153683 | −0.005249659 |
| 19 | 0.108327306 | 0.052016609 | 0.24425237 | 0.003488531 |
| 20 | 0.114894825 | 0.052853503 | 0.28521635 | 0.008879507 |
| 21 | 0.117501784 | 0.053364122 | 0.32288946 | 0.022371629 |
| 22 | 0.124528607 | 0.053879230 | 0.38329314 | 0.030489628 |
| 23 | 0.125890879 | 0.054244362 | 0.46111143 | 0.043680410 |
| 24 | 0.129962889 | 0.053597210 | 0.56054421 | 0.059427455 |
| 25 | 0.132918217 | 0.054048539 | 0.63835185 | 0.074547151 |
| 26 | 0.135450581 | 0.053696949 | 0.77494507 | 0.089206222 |
| 27 | 0.134558526 | 0.053324689 | 0.89920010 | 0.106217807 |
| 28 | 0.138901767 | 0.052551723 | 1.04882551 | 0.122351220 |
| 29 | 0.137323859 | 0.051922851 | 1.18591028 | 0.145081812 |
| 30 | 0.139340024 | 0.050700867 | 1.59980240 | 0.153899525 |
| 31 | 0.138424839 | 0.050212237 | 1.56913581 | 0.178013360 |
| 32 | 0.140725493 | 0.049092220 | 1.87843064 | 0.192808945 |
| 33 | 0.140501927 | 0.048290239 | 2.22641035 | 0.220370419 |
| 34 | 0.139830293 | 0.047356370 | 2.51850546 | 0.250856412 |
| 35 | 0.140390117 | 0.046204732 | 2.93846784 | 0.244808218 |
| 36 | 0.139532337 | 0.045694537 | 3.52777988 | 0.248769619 |
| 37 | 0.142093689 | 0.044263673 | 4.06141286 | 0.267697773 |
| 38 | 0.140524473 | 0.043942408 | 4.23378876 | 0.281096107 |
| 39 | 0.141067107 | 0.043023385 | 5.32838507 | 0.283869613 |
| 40 | 0.139819819 | 0.041877271 | 5.84001265 | 0.293670850 |
References
- Antolin, Pablo. 2007. Longevity Risk and Private Pensions. Available online: http://www.oecd.org/daf/fin/private-pensions/37977228.pdf (accessed on 25 May 2019).
- Antonio, Katrien, Lize Devolder, and Sander Devriendt. 2015. The IA| BE 2015 Mortality Projection for the Belgian Population. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2576167 (accessed on 15 March 2020).
- Barrieu, Pauline, Harry Bensusan, Nicole El Karoui, Caroline Hillairet, Stéphane Loisel, Claudia Ravanelli, and Yahia Salhi. 2012. Understanding, modelling and managing longevity risk: Key issues and main challenges. Scandinavian Actuarial Journal 3: 203–31. [Google Scholar] [CrossRef]
- Bauer, Daniel, Andreas Reuss, and Daniela Singer. 2012. On the calculation of the solvency capital requirement based on nested simulations. ASTIN Bulletin: The Journal of the IAA 42: 453–99. [Google Scholar]
- Bauer, Daniel, Daniela Bergmann, and Andreas Reuss. 2010. Solvency II and nested simulations: A least-squares Monte Carlo approach. Paper presented at 2010 ICA Congress, Sydney, Australia, 23–27 August 2010. [Google Scholar]
- Blake, David, and William Burrows. 2001. Survivor bonds: Helping to hedge mortality risk. Journal of Risk and Insurance 68: 339–48. [Google Scholar] [CrossRef]
- Brown, Jeffrey R., Olivia S. Mitchell, and James M. Poterba. 2000. National Bureau of Economic Research, Working Paper. Available online: https://www.nber.org/papers/w7812.pdf (accessed on 10 April 2019).
- Christiansen, Marcus C., and Andreas Niemeyer. 2014. Fundamental definition of the solvency capital requirement in solvency II. ASTIN Bulletin: The Journal of the IAA 44: 501–33. [Google Scholar] [CrossRef]
- Devineau, Laurent, and Stéphane Loisel. 2009. Risk aggregation in Solvency II: How to converge the approaches of the internal models and those of the standard formula? Bulletin Français d’Actuariat 9: 107–45. [Google Scholar]
- Devolder, Pierre, and Adrien Lebègue. 2017. Iterated VaR or CTE measures: A false good idea? Scandinavian Actuarial Journal 4: 287–318. [Google Scholar] [CrossRef]
- European Insurance and Occupational Pensions Authority. 2014a. Technical Specification for the Preparatory Phase (Part I). Available online: https://eiopa.europa.eu/Publications/ (accessed on 20 January 2018).
- European Insurance and Occupational Pensions Authority. 2014b. The Underlying Assumptions in the Standard Formula for the Solvency Capital Requirement Calculation. Available online: https://eiopa.europa.eu/Publications/ (accessed on 20 January 2018).
- Fung, Simon Man Chung, Katja Ignatieva, and Michael Sherris. 2019. Managing Systematic Mortality Risk in Life Annuities: An Application of Longevity Derivatives. Risks 7: 2. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2013. Monte Carlo Method in Financial Engineering. New York: Springer Science and Business Media, vol. 53, p. 7. [Google Scholar]
- Gompertz, Benjamin. 1825. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical transactions of the Royal Society of London 115: 513–83. [Google Scholar]
- Gronchi, Sandro. 1986. On investment criteria based on the internal rate of return. Oxford Economic Papers 38: 174–80. [Google Scholar] [CrossRef]
- Hainaut, Donatien, Pierre Devolder, and Antoon Pelsser. 2007. Robust evaluation of SCR for participating life insurances under Solvency II. Insurance: Mathematics and Economics 79: 107–23. [Google Scholar] [CrossRef]
- Hari, Norbert, Anja De Waegenaere, Bertrand Melenberg, and Theo E. Nijman. 2008. Longevity risk in portfolios of pension annuities. Insurance: Mathematics and Economics 42: 505–19. [Google Scholar] [CrossRef]
- Kochanski, Michael, and Bertel Karnarski. 2011. Solvency capital requirement for hybrid products. European Actuarial Journal 1: 173–98. [Google Scholar] [CrossRef]
- Lichters, Roland, Roland Stamm, and Donal Gallagher. 2015. Hull-White Model. In Modern Derivatives Pricing and Credit Exposure Analysis. New York: Springer, pp. 403–22. [Google Scholar]
- Liebwein, Peter. 2006. Risk models for capital adequacy: Applications in the context of solvency II and beyond. The Geneva Papers on Risk and Insurance-Issues and Practice 31: 528–50. [Google Scholar] [CrossRef]
- Ng, Andrew Cheuk-Yin, and Johnny Siu-Hang Li. 2011. Valuing variable annuity guarantees with the multivariate Esscher transform. Insurance: Mathematics and Economics 49: 393–400. [Google Scholar] [CrossRef]
- Ohlsson, Esbjörn, and Jan Lauzeningks. 2009. The one-year non-life insurance risk. Insurance: Mathematics and Economics 45: 203–208. [Google Scholar] [CrossRef]
- Olivieri, Annamaria, and Ermanno Pitacco. 2008. Solvency Requirements for Life Annuities: Some Comparisons. Working Paper. Available online: http://ssrn.com/abstract=1266094 (accessed on 15 June 2019).
- Pfeifer, Dietmar, and Doreen Strassburger. 2008. Solvency II: stability problems with the SCR aggregation formula. Scandinavian Actuarial Journal 2: 61–77. [Google Scholar] [CrossRef]
- Vasicek, Oldrich A., and H. Gifford Fong. 2015. Term structure modeling using exponential splines. In Finance, Economics, and Mathematics. New York: John Wiley & Sons. [Google Scholar]
- Zeddouk, Fadoua, and Pierre Devolder. 2019. Mean Reversion in Stochastic Mortality: Why and How? ISBA Discussion Paper, UClouvain. Available online: http://hdl.handle.net/2078.1/219343 (accessed on 20 January 2020).
| A | B | a | MSE | ||
|---|---|---|---|---|---|
| 0.0105677 | 0.0005749505 | 0.1304207503 | 0.0014965354 | 0.0083530153 | 0.000303644 |
| Constant | Variable | |
|---|---|---|
| Lifetime annuity | 0.1403933 | 0.03822095 |
| Term annuity | 0.08871471 | 0.04748606 |
| Deferred annuity | 0.1467654 | −0.01588651 |
| Constant | Variable | |||
|---|---|---|---|---|
| Mean | Variance | Mean | Variance | |
| Lifetime annuity | ||||
| Term annuity | ||||
| Deferred annuity | / | / | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngugnie Diffouo, P.M.; Devolder, P. Longevity Risk Measurement of Life Annuity Products. Risks 2020, 8, 31. https://doi.org/10.3390/risks8010031
Ngugnie Diffouo PM, Devolder P. Longevity Risk Measurement of Life Annuity Products. Risks. 2020; 8(1):31. https://doi.org/10.3390/risks8010031
Chicago/Turabian StyleNgugnie Diffouo, Pauline Milaure, and Pierre Devolder. 2020. "Longevity Risk Measurement of Life Annuity Products" Risks 8, no. 1: 31. https://doi.org/10.3390/risks8010031
APA StyleNgugnie Diffouo, P. M., & Devolder, P. (2020). Longevity Risk Measurement of Life Annuity Products. Risks, 8(1), 31. https://doi.org/10.3390/risks8010031






