The Determinants of Market-Implied Recovery Rates
Abstract
1. Introduction
2. Related Literature
2.1. Factors Driving Historical Recovery Rates
- Debt contract-specific variables: Coupon rate, seniority, collateral.
- Firm-specific variables: Size, asset tangibility, market-to-book ratio, liquidity ratio, interest coverage ratio, profit margin, leverage, firm age.
- Industry-specific variables: industry dummy, utilities dummy, industry sales growth, industry stock return.
- Macroeconomic variables: Bond default rate, GDP growth, S&P500 index return, S&P500 index volatility, unemployment rate, Fama-French factors, economic uncertainty.
2.2. Inferring Recovery Rates from Market Data
3. Methodology
3.1. The Recovery Model
3.2. Data and Model Calibration
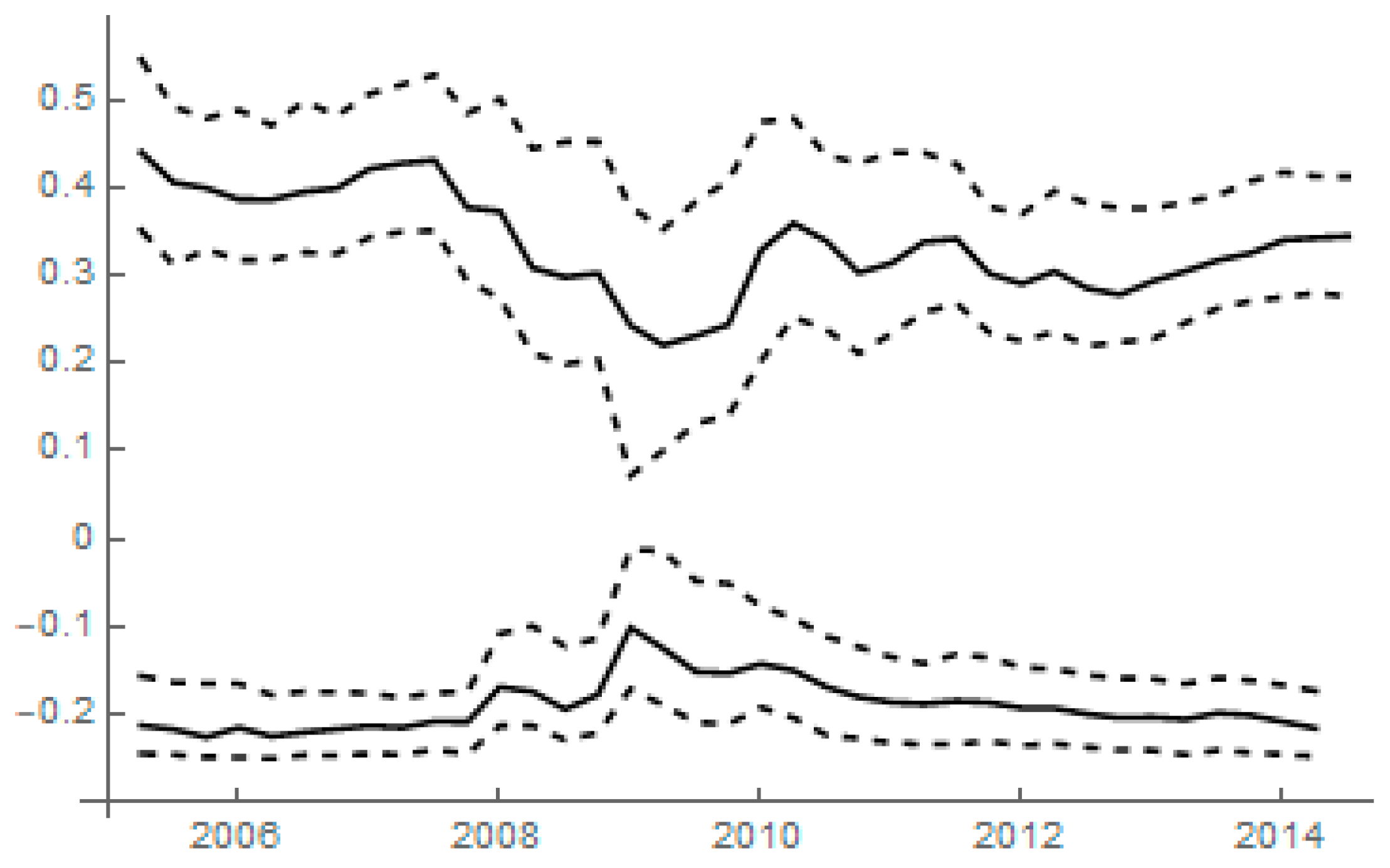
3.3. Comparison with Historical Recoveries
- The actual recovery rates from CDS auctions are slightly lower than actual recovery rates on the underlying bonds. Chernov et al. (2013) and Gupta and Sundaram (2015) find a downward bias of about 15% of the bond price (which represents a smaller fraction of par) and attribute it to a liquidity premium.
- Market-implied recovery rates from CDS might contain a premium for the CDS writer’s counterparty risk. That being said, Arora et al. (2012) find that the negative relation between CDS spreads and CDS writer credit quality is economically very small because of risk mitigation techniques, such as overcollateralization and bilateral netting.
- Historical recovery rates (as reported by Moody’s for instance) are, by definition, calculated on a sample of defaulting firms. The market-implied recoveries are extracted from a sample of firms underlying a CDS contract. The difference in the two populations of firms could generate a bias in the comparison of recoveries.6
- Most importantly, market-implied recoveries are risk-neutral expectations of random recovery rates. By contrast, historical recoveries are calculated once the default event has materialized. In some studies, the historical recovery rates are computed at the resolution of financial distress and they can be viewed as the realizations of random recovery. In other studies, the historical recovery rates are computed using 30-day post default bond prices. Such historical recovery rates are still expectations about ultimate recovery, but they are conditionally calculated on default having occurred.
4. Factor Analysis
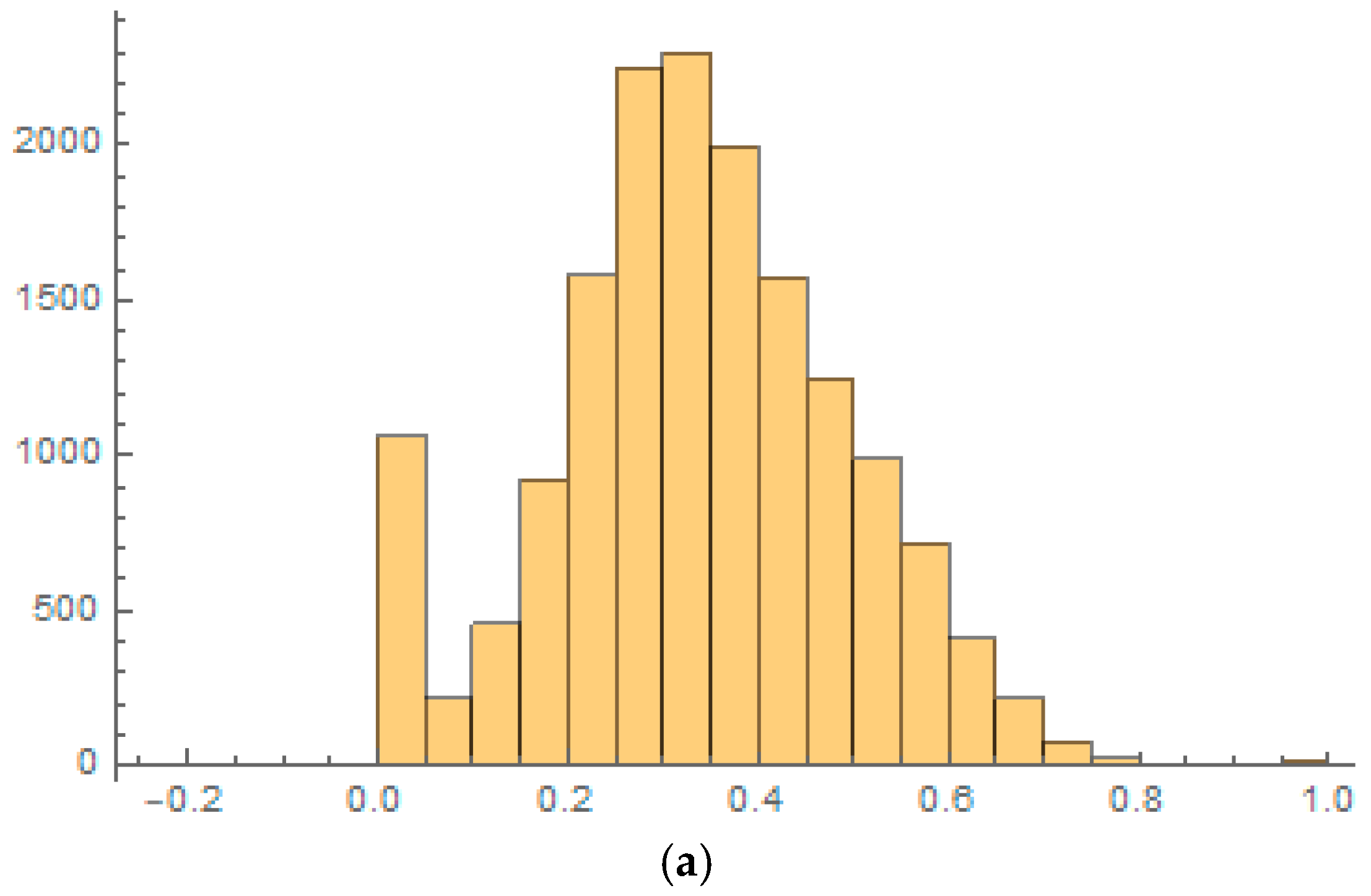
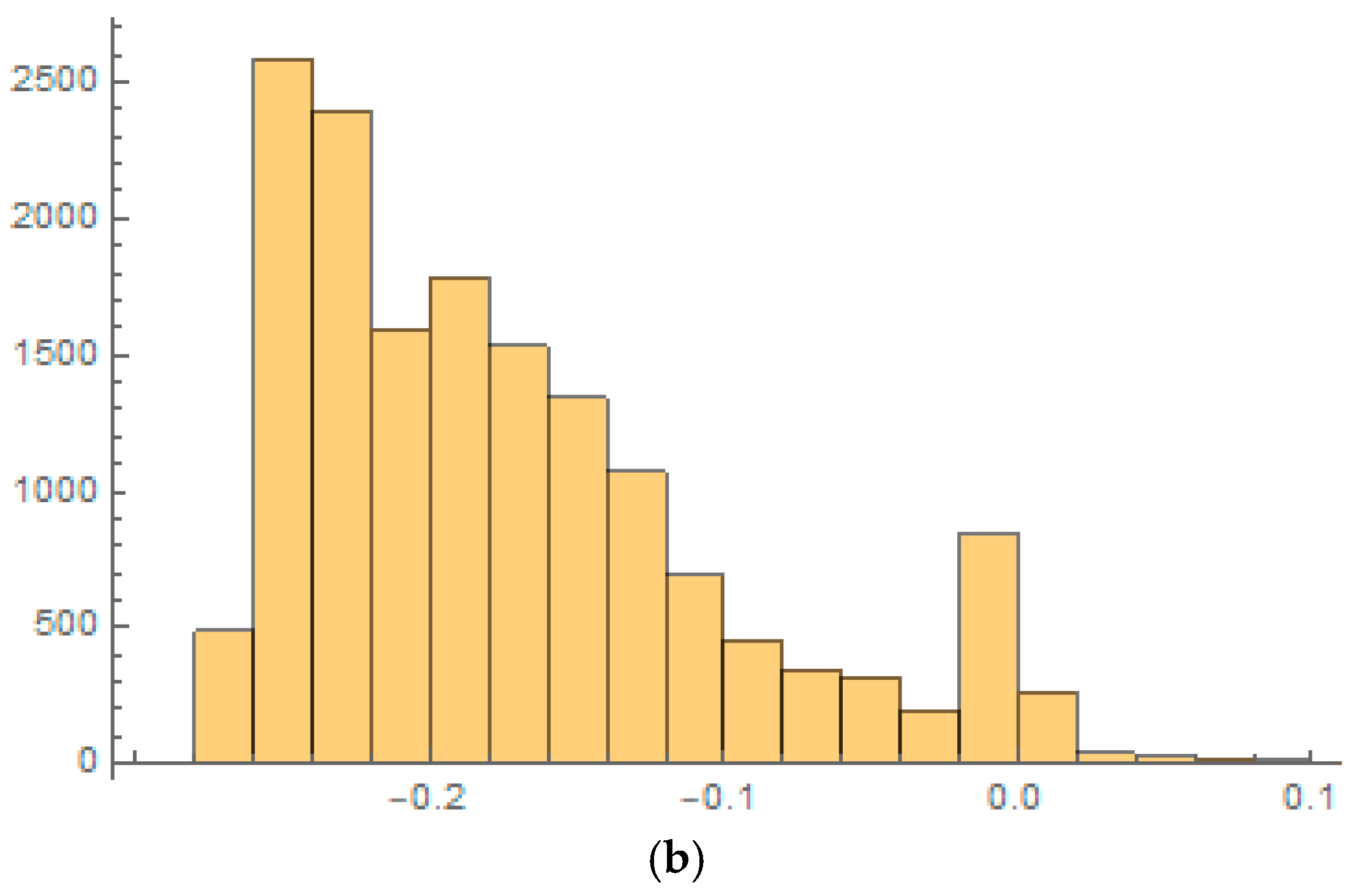
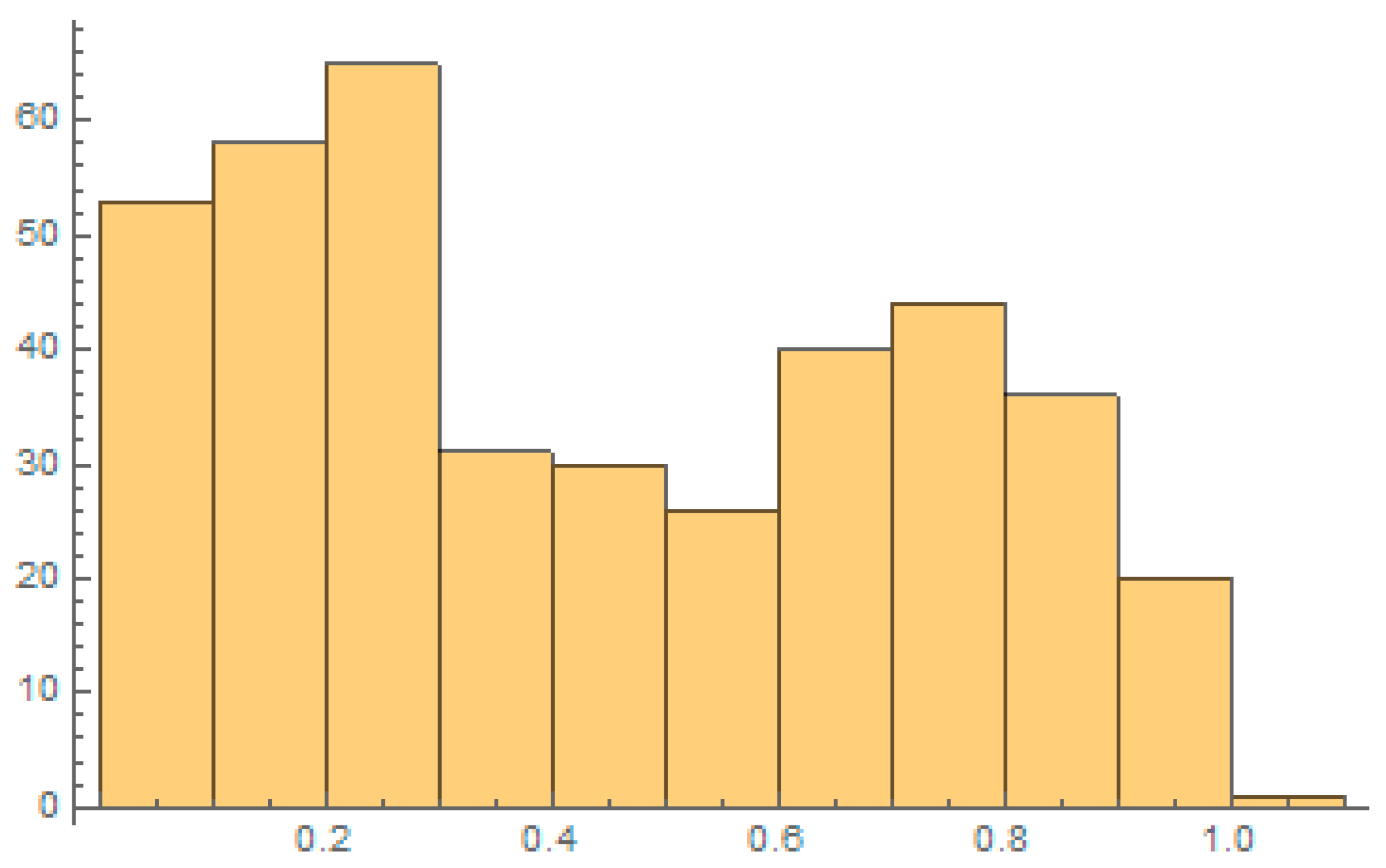
4.1. Descriptive Statistics
4.2. Linear Regression Results
4.3. Tobit Regression Results
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Acharya, Viral, Sreedhar Bharath, and Anand Srinivasan. 2007. Does industry-wide distress affect defaulted firms? Evidence from creditor recoveries. Journal of Financial Economics 85: 787–821. [Google Scholar] [CrossRef]
- Altman, Edward, and Egon Kalotay. 2014. Ultimate recovery mixtures. Journal of Banking and Finance 40: 116–29. [Google Scholar] [CrossRef]
- Altman, Edward, and Brenda Karlin. 2009. The re-emergence of distressed exchanges in corporate restructurings. Journal of Credit Risk 5: 43–55. [Google Scholar] [CrossRef]
- Altman, Edward, and Vellore Kishore. 1996. Almost everything you wanted to know about recoveries on defaulted bonds. Financial Analyst Journal 52: 57–64. [Google Scholar] [CrossRef]
- Altman, Edward, Brooks Brady, Andrea Resti, and Andrea Sironi. 2005. The link between default and recovery rates: Theory, empirical evidence, and implications. The Journal of Business 78: 2203–28. [Google Scholar] [CrossRef]
- Arora, Navneet, Priyank Gandhi, and Francis Longstaff. 2012. Counterparty credit risk and the credit default swap market. Journal of Financial Economics 103: 280–93. [Google Scholar] [CrossRef]
- Bastos, Joao. 2009. Forecasting bank loan loss-given-default. Journal of Banking and Finance 34: 2510–17. [Google Scholar] [CrossRef]
- Bris, Arturo, Iwo Welch, and Ning Zhu. 2006. The costs of bankruptcy: Chapter 7 liquidation versus Chapter 11 reorganization. Journal of Finance 61: 1253–303. [Google Scholar] [CrossRef]
- Bruche, Max, and Carlos Gonzalez-Aguado. 2010. Recovery rates, default probabilities and the credit cycle. Journal of Banking and Finance 34: 713–23. [Google Scholar] [CrossRef]
- Chava, Sudheer, Catalina Stefanescu, and Stuart Turnbull. 2011. Modeling the loss distribution. Management Science 57: 1267–87. [Google Scholar] [CrossRef]
- Chernov, Mikhail, Alexander Gorbenko, and Igor Makarov. 2013. CDS auctions. Review of Financial Studies 26: 768–805. [Google Scholar] [CrossRef]
- Cox, John, Steven Ross, and Mark Rubinstein. 1979. Option pricing: A simplified approach. Journal of Financial Economics 7: 229–63. [Google Scholar] [CrossRef]
- Das, Sanjiv, and Paul Hanouna. 2009. Implied recovery. Journal of Economic Dynamics and Control 33: 1837–57. [Google Scholar] [CrossRef]
- Denis, Diane, and Kimberly Rodgers. 2007. Chapter 11: Duration, outcome, and post-reorganization performance. Journal of Financial and Quantitative Analysis 42: 101–18. [Google Scholar] [CrossRef]
- Doshi, Hitesh, Redouane Elkamhi, and Chayawat Ornthanalai. 2018. The term structure of expected recovery rates. Journal of Financial and Quantitative Analysis 53: 2619–61. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth Singleton. 1999. Modeling term structures of defaultable bonds. Review of Financial Studies 12: 687–720. [Google Scholar] [CrossRef]
- Düllmann, Klaus, and Monika Trapp. 2004. Systematic Risk in Recovery Rates—An Empirical Analysis of U.S. Corporate Credit Exposures. Discussion Paper, Series 2: Banking and Financial Supervision, No. 2004,02; Frankfurt am Main: Deutsche Bundesbank Research Centre. [Google Scholar]
- François, Pascal, and Weiyu Jiang. 2019. Credit value adjustment with market-implied recovery. Journal of Financial Services Research. forthcoming. [Google Scholar]
- Franks, Julian, and Walter Torous. 1994. A comparison of financial recontracting in distressed exchanges and Chapter 11 reorganizations. Journal of Financial Economics 35: 349–70. [Google Scholar] [CrossRef]
- Frye, Jon. 2000. Collateral damage. RISK 13: 91–94. [Google Scholar]
- Gambetti, Paolo, Geneviève Gauthier, and Frédéric Vrins. 2019. Recovery Rates: Uncertainty Certainly Matters. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3366889 (accessed on 15 April 2019).
- Giesecke, Kay, Francis Longstaff, Stephen Schaefer, and Ilya Strebulaev. 2011. Corporate bond default risk: A 150-year perspective. Journal of Financial Economics 102: 233–55. [Google Scholar] [CrossRef]
- Gupta, Sudip, and Rangarajan Sundaram. 2015. Mispricing and arbitrage in CDS auctions. Journal of Derivatives 22: 79–91. [Google Scholar] [CrossRef]
- Jankowitsch, Rainer, Florian Nagler, and Marti Subrahmanyam. 2014. The determinants of recovery rates in the U.S. corporate bond market. Journal of Financial Economics 114: 155–77. [Google Scholar] [CrossRef]
- Jaskowski, Marcin, and Michael McAleer. 2012. Estimating Implied Recovery Rates from the Term Structure of CDS Spreads. Working paper. Amsterdam, The Netherlands: Tinbergen Institute. [Google Scholar]
- Loterman, Gert, Iain Brown, David Martens, Christophe Mues, and Bart Baesens. 2012. Benchmarking regression algorithms for loss given default modeling. International Journal of Forecasting 28: 161–70. [Google Scholar] [CrossRef]
- Merton, Robert. 1974. On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance 29: 449–70. [Google Scholar]
- Mora, Nada. 2012. What determines creditor recovery rates? Federal Reserve Bank of Kansas City Economic Review 97: 79–109. [Google Scholar]
- Nazemi, Abdolreza, and Frank Fabozzi. 2018. Macroeconomic variable selection for creditor recovery rates. Journal of Banking and Finance 89: 14–25. [Google Scholar] [CrossRef]
- Nazemi, Abdolreza, Konstantin Heidenreich, and Frank Fabozzi. 2018. Improving corporate bond recovery rate prediction using multi-factor support vector regressions. European Journal of Operational Research 271: 664–75. [Google Scholar] [CrossRef]
- Qi, Min, and Xinlei Zhao. 2011. Comparison of modeling methods for loss given default. Journal of Banking and Finance 35: 2842–55. [Google Scholar] [CrossRef]
- Shleifer, Andrei, and Robert Vishny. 1992. Liquidation values and debt capacity: A market equilibrium approach. Journal of Finance 47: 1343–66. [Google Scholar] [CrossRef]
- Siao, Jhao-Siang, Ruey-Ching Hwang, and Chih-Kang Chu. 2016. Predicting recovery rates using logistic quantile regression with bounded outcomes. Quantitative Finance 16: 777–92. [Google Scholar] [CrossRef]
- Ünal, Haluk, Madan Dilip, and Levent Güntay. 2003. Pricing the risk of recovery in default with APR violation. Journal of Banking and Finance 27: 1001–25. [Google Scholar] [CrossRef]
- Varma, Praveen, and Richard Cantor. 2005. Determinants of recovery rates on defaulted bonds and loans for North American corporate issuers: 1983–2003. Journal of Fixed Income 14: 29–44. [Google Scholar] [CrossRef]
| 1 | The aggregation is performed through a recursive algorithm. See Das and Hanouna (2009) for details. |
| 2 | The denominator is the expected present value of all the premiums to be paid. The numerator is the expected present value of the compensation for the loss given default. |
| 3 | All CDS are U.S. dollar denominated and senior unsecured single-name contracts. |
| 4 | Before September 2010, the data was provided by CMA via Datastream. After that date, the data is provided by Thomson Reuters. The data is combined from the two providers by using the function “SPLC” of Datastream. |
| 5 | For instance, empirical studies on U.S. bankruptcy filings (Bris et al. 2006; Denis and Rodgers 2007) report that firms in financial distress spend between two and three years on average under bankruptcy. |
| 6 | When regressing historical recovery rates, Jankowitsch et al. (2014) find a positive and significant coefficient for CDS availability. |
| 7 | Altman and Kalotay (2014) propose a mixture of normals to model the bimodal distribution of historical recovery rates. Siao et al. (2016) opt for a quantile-based regression. |
| 8 | Since CDS in the sample are written on the same type of bonds (senior unsecured), the factor analysis precludes those variables that are specific to the debt contract such as coupon, seniority, or collateral. |
| Determinant | Examples of Studies | Effect | Method |
|---|---|---|---|
| Panel A: Debt contract-specific variables | |||
| Coupon rate | Chava et al. (2011) | + | PR |
| Collateral | Frye (2000) | + | LR |
| Qi and Zhao (2011) | + | RT | |
| Seniority | Varma and Cantor (2005) | + | LR |
| Acharya et al. (2007) | + | LR | |
| Siao et al. (2016) | + | LQ | |
| Rating | Jankowitsch et al. (2014) | + | LR |
| Panel B: Firm-specific variables | |||
| Size | Acharya et al. (2007); Chava et al. (2011) | +/− | LR, PR |
| Market-to-book | Chava et al. (2011) | − | PR |
| Asset tangibility | Varma and Cantor (2005) | + | LR |
| Chava et al. (2011) | + | PR | |
| Liquidity | Varma and Cantor (2005) | + | LR |
| Profit margin | Acharya et al. (2007) | + | LR |
| Leverage | Varma and Cantor (2005) | − | LR |
| Default event severity | Franks and Torous (1994); Altman and Karlin (2009) | − | LR |
| Panel C: Industry-specific variables | |||
| Industry dummies | Acharya et al. (2007); Chava et al. (2011) | +/− | LR, PR |
| Industry sales growth dummy | Acharya et al. (2007) | + | PR |
| Industry stock return dummy | Acharya et al. (2007) | + | PR |
| Industry default rate | Jankowitsch et al. (2014) | − | LR |
| Panel D: Macroeconomic variables | |||
| Default rate | Frye (2000); Altman et al. (2005) | − | LR |
| GDP growth | Altman et al. (2005); Chava et al. (2011) | + | LR, PR |
| Fed fund rate | Jankowitsch et al. (2014) | + | LR |
| Stock index return | Nazemi et al. (2018) | + | SVR, RT |
| Corporate bond spread | Nazemi et al. (2018) | − | SVR, RT |
| Unemployment rate | Nazemi et al. (2018) | − | SVR, RT |
| Statistic | Initial Sample | Restricted Sample | ||
|---|---|---|---|---|
| RMSE | RRMSE | RMSE | RRMSE | |
| Mean | 23 | 10.23 | 9 | 7.19 |
| Median | 3 | 4.76 | 2 | 4.44 |
| Standard deviation | 222 | 17.12 | 17 | 7.58 |
| Maximum | 9389 | 440.08 | 93 | 39.34 |
| 95% percentile | 93 | 39.34 | 51 | 24.59 |
| Variable | Description |
|---|---|
| Size | Logarithm of total assets. |
| Asset tangibility | Property, plant and equipment/total assets. |
| Liquidity | (Cash plus short-term investments)/total assets. |
| Profit margin | EBITDA/sales. |
| Leverage | Long-term debt/total assets. |
| Rating | Dummy = 1 if issuer is investment grade. |
| Industry stress | Dummy = 1 if quarterly industry index return is below −30%. |
| GDP growth | Seasonally adjusted, quarterly growth rate of U.S. GDP. |
| Unemployment | Seasonally adjusted, quarterly U.S. unemployment rate. |
| Stock index | S&P500 index adjusted, quarterly return. |
| Default rate | Quarterly default rate reported by Moody’s and S&P. |
| NAICS | Industry | GICS Stock Index | Ticker |
|---|---|---|---|
| 11 | Agriculture, forestry and fishing | Agriculture | S5AGRI |
| 21 | Minerals and gases | Energy | SPN |
| 22 | Utilities | Utilities | S5UTIL |
| 23 | Construction | Construction and engineering | S5CSTEX |
| 31 | Food manufacturing | Food and beverage | SPSIFBUP |
| 32 | Wood and concrete manufacturing | Materials | S5MATR |
| 33 | Metal manufacturing | Metal and mining | SPSIMM |
| 42 | Wholesale trade | Retail | SPSIRE |
| 44 | Retail trade | Retail | SPSIRE |
| 45 | Sporting goods and book stores | Retail | SPSIRE |
| 48 | Transportation and warehousing | Transportation | SPSITN |
| 49 | Postal service | Transportation | SPSITN |
| 51 | Information and newspaper | Media and entertainment | S5MEDA |
| 52 | Finance and insurance | Financials | SPF |
| 53 | Real estate, rental and leasing | Real estate | S5RLST |
| 54 | Professional and technical services | Commercial and professional services | S5COMS |
| 56 | Administrative and support services | Consumer services | S5HOTR |
| 62 | Health care | Health care | S5HLTH |
| 72 | Food services | Restaurants | S5REST |
| 81 | Other non-public services | Consumer services | S5HOTR |
| Variable | Mean | Std Dev | Min | Q1 | Q2 | Q3 | Max |
|---|---|---|---|---|---|---|---|
| Size | 9.5283 | 1.3598 | 4.7791 | 8.5894 | 9.3755 | 10.2807 | 14.8302 |
| Asset tangibility | 0.3120 | 0.2461 | 0.0000 | 0.1009 | 0.2534 | 0.5050 | 0.9530 |
| Liquidity | 0.1619 | 0.2233 | 0.0000 | 0.0336 | 0.0877 | 0.1975 | 3.4089 |
| Profit margin | 0.2015 | 0.3369 | −7.7214 | 0.1043 | 0.1735 | 0.2771 | 24.1566 |
| Leverage | 0.2767 | 0.1973 | 0.0000 | 0.1445 | 0.2428 | 0.3714 | 2.3640 |
| GDP growth | 0.0177 | 0.0267 | −0.0840 | 0.0050 | 0.0225 | 0.0360 | 0.0540 |
| Unemployment | 0.0688 | 0.0187 | 0.0440 | 0.0500 | 0.0655 | 0.0880 | 0.1000 |
| Stock index | 0.0153 | 0.0688 | −0.2356 | −0.0207 | 0.0335 | 0.0605 | 0.1314 |
| Default rate | 0.0042 | 0.0039 | 0.0008 | 0.0020 | 0.0022 | 0.0047 | 0.0174 |
| Industry | Count | Industry | Count |
|---|---|---|---|
| Agriculture | 1 (0.2%) | Professional services | 149 (30.0%) |
| Minerals and gases | 80 (16.1%) | Health care | 9 (1.8%) |
| Manufacturing | 186 (37.4%) | Food services | 9 (1.8%) |
| Transportation and trade | 62 (12.5%) | Other non-public services | 1 (0.2%) |
| Variable | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Intercept | 0.5762 *** | 0.5762 *** | 0.4369 *** | 0.3977 *** | 0.3850 *** |
| (−0.0366) | (0.1025) | (0.1021) | (0.0209) | (0.0656) | |
| Size | −0.0137 *** | −0.0137 | −0.0125 | - | 0.0077 ** |
| (0.0021) | (0.0104) | (0.0104) | - | (0.0030) | |
| Asset tangibility | 0.0286 | 0.0286 | 0.0254 | 0.0324 | 0.0210 |
| (0.0589) | (0.0486) | (0.0486) | (0.0491) | (0.0174) | |
| Liquidity | 0.0214 | 0.0214 | 0.0181 | 0.0258 | 0.0201 ** |
| (0.0142) | (0.0186) | (0.0186) | (0.0189) | (0.0103) | |
| Profit margin | 0.0032 | 0.0032 | 0.0031 | 0.0035 | 0.0037 |
| (0.0070) | (0.0065) | (0.0067) | (0.0068) | (0.0034) | |
| Leverage | −0.1214 ** | −0.1214 *** | −0.1220 *** | −0.1223 *** | −0.1202 *** |
| (0.0449) | (0.0326) | (0.0326) | (0.0328) | (0.0140) | |
| Rating | 0.0091 | 0.0091 | 0.0098 | 0.0085 | 0.0220 *** |
| (0.0049) | (0.0067) | (0.0073) | (0.0074) | (0.0043) | |
| Industry stress | 0.0046 | 0.0046 | −0.0068 | −0.0043 | 0.0039 |
| (0.0058) | (0.0067) | (0.0064) | (0.0063) | (0.0062) | |
| GDP growth | 0.1339 * | 0.1339 *** | - | 0.1497 *** | 0.1362 ** |
| (0.0595) | (0.0485) | - | (0.0483) | (0.0621) | |
| Unemployment | −0.8287 | −0.8287 *** | - | - | −0.7864 *** |
| (0.6827) | (0.2794) | - | - | (0.2827) | |
| Stock index | −0.0353 | −0.0353 * | - | −0.0304 * | −0.0356 |
| (0.0208) | (0.0182) | - | (0.0184) | (0.0249) | |
| Default rate | −3.5229 *** | −3.5229 *** | - | - | −3.4103 *** |
| (0.6149) | (0.6956) | - | - | (0.6752) | |
| L_ GDP growth | - | - | 0.1401 *** | - | - |
| - | - | (0.0470) | - | - | |
| L_ Unemployment | - | - | 1.2948 *** | - | - |
| - | - | (0.2692) | - | - | |
| L_ Stock index | - | - | −0.0183 | - | - |
| - | - | (0.0161) | - | - | |
| L_ Default rate | - | - | 3.7581 *** | - | - |
| - | - | (0.4939) | - | - | |
| Industry fixed effects | Yes | No | No | No | Yes |
| Firm fixed effects | No | Yes | Yes | Yes | No |
| R2 within | 0.1182 | 0.1182 | 0.1198 | 0.1142 | - |
| R2 between | 0.0458 | 0.0458 | 0.0598 | 0.1567 | - |
| R2 overall | 0.0928 | 0.0928 | 0.1013 | 0.1447 | - |
| Variable | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Intercept | −0.1164 ** | −0.1164 ** | −0.0740 ** | −0.1980 *** | −0.1605 *** |
| (0.0435) | (0.0585) | (0.0335) | (0.0116) | (0.0340) | |
| Size | −0.0173 *** | −0.0173 *** | −0.0077 *** | −0.0077 *** | |
| (0.0044) | (0.0059) | (0.0015) | (0.0016) | ||
| Asset tangibility | 0.0721 ** | 0.0721 *** | 0.0404 *** | 0.1149 *** | 0.0392 *** |
| (0.0240) | (0.0223) | (0.0089) | (0.0260) | (0.0090) | |
| Liquidity | 0.0031 | 0.0031 | 0.0053 | 0.0140 | 0.0044 |
| (0.0114) | (0.0129) | (0.0053) | (0.0124) | (0.0052) | |
| Profit margin | −0.0111 * | −0.0111 ** | −0.0113 *** | −0.0122 ** | −0.0111 *** |
| (0.0050) | (0.0049) | (0.0017) | (0.0056) | (0.0017) | |
| Leverage | 0.0624 *** | 0.0624 *** | 0.0614 *** | 0.0972 *** | 0.0602 *** |
| (0.0146) | (0.0203) | (0.0072) | (0.0208) | (0.0072) | |
| Rating | −0.0181 *** | −0.0181 *** | −0.0198 *** | −0.0219 *** | −0.0194 *** |
| (0.0040) | (0.0042) | (0.0022) | (0.0047) | (0.0022) | |
| Industry stress | 0.0085 | 0.0085 ** | 0.0200 *** | 0.0246 *** | 0.0087 *** |
| (0.0064) | (0.0038) | (0.0030) | 0.0036) | (0.0031) | |
| GDP growth | 0.0143 | 0.0143 | - | −0.2603 *** | 0.0140 |
| (0.0287) | (0.0264) | - | (0.0301) | (0.0316) | |
| Unemployment | 1.0304 *** | 1.0304 *** | - | - | 1.0447 |
| (0.2230) | (0.1548) | - | - | (0.1438) | |
| Stock index | −0.0445 *** | −0.0445 *** | - | −0.0459 *** | −0.0444 *** |
| (0.0109) | (0.0090) | - | (0.0113) | (0.0127) | |
| Default rate | 2.0635 *** | 2.0635 *** | - | - | 2.1315 *** |
| (0.4733) | (0.3694) | - | - | (0.3434) | |
| L_ GDP growth | - | - | −0.1958 *** | - | - |
| - | - | (0.0330) | - | - | |
| L_ Unemployment | - | - | −0.4481 *** | - | - |
| - | - | (0.1436) | - | - | |
| L_ Stock index | - | - | 0.0327 *** | - | - |
| - | - | (0.0127) | - | - | |
| L_ Default rate | - | - | 0.8050 ** | - | - |
| - | - | (0.3444) | - | - | |
| Industry fixed effects | Yes | No | Yes | No | Yes |
| Firm fixed effects | No | Yes | No | Yes | No |
| R2 within | 0.2142 | 0.2142 | 0.2048 | 0.1543 | - |
| R2 between | 0.0722 | 0.0722 | 0.1274 | 0.0601 | - |
| R2 overall | 0.1377 | 0.1377 | 0.1848 | 0.0984 | - |
| Variable | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Intercept | 0.3853 *** | 0.3775 *** | 0.2449 *** | 0.4329 *** |
| (0.0710) | (0.0350) | (0.0709) | (0.0589) | |
| Size | 0.0086 *** | 0.0077 ** | 0.0091 *** | - |
| (0.0032) | (0.0032) | (0.0033) | - | |
| Asset tangibility | 0.0129 | 0.0055 | 0.0105 | 0.0089 |
| (0.0187) | (0.0166) | (0.0186) | (0.0189) | |
| Liquidity | 0.0212 ** | 0.0206 * | 0.0182 * | 0.0188 * |
| (0.0108) | (0.0109) | (0.0108) | (0.0108) | |
| Profit margin | 0.0050 | 0.0049 | 0.0049 | 0.0058 |
| (0.0036) | (0.0036) | (0.0036) | (0.0036) | |
| Leverage | −0.1348 *** | −0.1386 *** | −0.1350 *** | −0.1406 *** |
| (0.0150) | (0.0150) | (0.0150) | (0.0150) | |
| Rating | 0.0221 *** | 0.0228 *** | 0.0227 *** | 0.0241 *** |
| (0.0046) | (0.0046) | (0.0046) | (0.0045) | |
| Industry stress | 0.0047 | 0.0051 | −0.0072 | −0.0049 |
| (0.0065) | (0.0065) | (0.0061) | (0.0061) | |
| GDP growth | 0.1268 * | 0.1264 * | - | 0.1414 ** |
| (0.0656) | (0.0656) | - | (0.0656) | |
| Unemployment | −0.9115 *** | −0.9145 *** | - | - |
| (0.2998) | −0.2998 | - | - | |
| Stock index | −0.0342 | −0.0342 | - | −0.0273 |
| (0.0263) | (0.0263) | - | (0.0252) | |
| Default rate | −3.4702 *** | −3.4672 *** | - | - |
| (0.7143) | (0.7143) | - | - | |
| L_ GDP growth | - | - | 0.1497 ** | - |
| - | - | (0.0681) | - | |
| L_ Unemployment | - | - | 1.2966 *** | - |
| - | - | (0.2968) | - | |
| L_ Stock index | - | - | −0.0192 | - |
| - | - | (0.0262) | - | |
| L_ Default rate | - | - | 3.9085 *** | - |
| - | - | (0.7104) | - | |
| Industry fixed effects | Yes | No | Yes | Yes |
| Log-likelihood | 7047.49 | 7043.20 | 7058.31 | 7020.83 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
François, P. The Determinants of Market-Implied Recovery Rates. Risks 2019, 7, 57. https://doi.org/10.3390/risks7020057
François P. The Determinants of Market-Implied Recovery Rates. Risks. 2019; 7(2):57. https://doi.org/10.3390/risks7020057
Chicago/Turabian StyleFrançois, Pascal. 2019. "The Determinants of Market-Implied Recovery Rates" Risks 7, no. 2: 57. https://doi.org/10.3390/risks7020057
APA StyleFrançois, P. (2019). The Determinants of Market-Implied Recovery Rates. Risks, 7(2), 57. https://doi.org/10.3390/risks7020057




