Default Ambiguity

Abstract

This paper discusses ambiguity in the context of single-name credit risk. We focus on uncertainty in the default intensity but also discuss uncertainty in the recovery in a fractional recovery of the market value. This approach is a first step towards integrating uncertainty in credit-risky term structure models and can profit from its simplicity. We derive drift conditions in a Heath–Jarrow–Morton forward rate setting in the case of ambiguous default intensity in combination with zero recovery, and in the case of ambiguous fractional recovery of the market value.

1. Introduction

Recently, an increasing amount of literature focuses on uncertainty as it relates to financial markets. The problem is that, the probability distribution of randomness in these markets is unknown. Typically, the unknown distribution is either estimated by statistical methods or calibrated to given market data by means of a model for the financial market. For example, in credit risk, the default probability is not observed, hence, have to be estimated from observable data. These methods introduce a large model risk.

Already, Knight (1921) pointed towards a formulation of risk which is able to treat such challenges in a systematic way. He was followed by Ellsberg (1961), who called random variables with known probability distribution certain, and those where the probability distribution is not known uncertain.

In this paper, we address these problems by constructing a model such that the parameters are characterised by uncertainty. Then, a single probability measure in a classical model is replaced by a family of probability measures, that is, a full class of models.

Following the modern literature in the area, we will call the feature that the probability distribution is not entirely fixed or, cannot be modelled by a single probability measure, ambiguity. This area has recently renewed the attention of researchers in mathematical finance to fundamental subjects such as arbitrage conditions, pricing mechanisms, and super-hedging. In equity markets, volatility uncertainty plays a crucial role, and has been extensively investigated, see for example, Avellaneda et al. (1995); Denis and Martini (2006); Lyons (1995); Vorbrink (2014). A major difficulty in this setting is that volatility uncertainty is characterized (at least in continuous time) by probabilities measures being mutually singular. Thus, the classical fundamental theorem of asset pricing fails to justify the no-arbitrage conditions, and new techniques are demanded, see Bayraktar and Zhang (2013); Bouchard and Nutz (2015); Burzoni et al. (2017), and Biagini et al. (2017).

In this paper, we introduce the concept of ambiguity to defaultable term structure models. The starting point for term structure models are typically bond prices of the form

$$\begin{array}{c}\hfill P(t,T)=e^{-{\int }_t^{T}f(t,u)du},0\le t\le T,\end{array}$$

(1)

where ${\left(f(t,T)\right)}_{0\le t\le T}$ is the instantaneous forward rate and T is the maturity time. This follows the seminal approach proposed in Heath et al. (1992). The presence of credit risk1 in the model introduces an additional factor known as the default time. In this setting, bond prices are assumed to be absolutely continuous with respect to the maturity of the bond. This assumption is typically justified by the argument that, in practice, only a finite number of bonds are liquidly traded and the full term structure is obtained by interpolation, thus is smooth. There are two classical approaches to model market default risk: the structural approach Merton (1974) and the reduced-form approach (see for example, Artzner and Delbaen (1995); Duffie et al. (1996); Lando (1994) for some of the first works in this direction).

Structural models of credit risk describe the modelling of credit events specific to a particular corporate firm. Here, the underlying state is the value of a firm’s assets which is observable. Default time is define as the first time the firm’s asset value falls below a certain barrier level (for example, its liabilities). Hence, default is not a surprise. The approach links the default events to the firm’s economic fundamentals, consequently, default time is endogenously within the model. However, the assumption that the firm’s asset value is observable is often too strong in real applications, see Duffie and Lando (2001) and the survey article Frey and Schmidt (2011). Structural models in credit risk have been studied under many different viewpoints, see Black and Cox (1976); Frey and Schmidt (2009, 2012); Gehmlich and Schmidt (2018); Geske (1977); Kim et al. (1993); Leland and Toft (1996); Merton (1974).

In comparison to the structural approach, reduced form approaches take a less stringent viewpoint regarding the mechanisms leading to default and model default events via an additional random structure. This additional degree of freedom together with their high tractability led to a tremendous success of this model class in credit risk modelling. For more details on the reduced form approach, we refer to Bielecki and Rutkowski (2002), and the references therein. Structural models can be embedded into (generalized) reduced form models as pointed out in Bélanger et al. (2004) and Fontana and Schmidt (2018).

Reduced-form models typically postulate that default time is totally inaccessible and, consequently, bond prices are absolutely continuous with respect to the maturity. Under the assumption of zero recovery2, this implies that credit risky bond prices $P(t,T)$ are given by

$$\begin{array}{c}\hfill P(t,T)={𝟙}_{\{\tau >t\}}{e}^{-{\int }_t^{T}f(t,u)du}\end{array}$$

(2)

with $\tau$ denoting the random default time. Since $\tau$ is totally inaccessible, it has an intensity $\lambda$. For example, if the intensity is constant, the default time is the first jump of a Poisson process with constant arrival rate $\lambda$. More generally, ${\lambda }_t$ may be viewed as the conditional rate of occurrence of default at time t, given information up to that time. In a situation where the owner of a defaultable claim recovers part of its initial investment upon default, the associated survival process ${𝟙}_{\{\tau >t\}}$ in (2), is replaced by a semimartingale. The quantity of the investment recovered is the so-called recovery.

Under ambiguity, we suggest that there is some prior information at hand which gives a upper and lower bounds on the intensity. The implicit assumption that the probability distribution of default is known is quite restrictive. Thus, we analyse our problem in a multiple priors model which describe uncertainty about the “true probability distribution". By means of the Girsanov theorem, we construct the set of priors from the reference measure. The assumption is that all priors are equivalent.

In view of our framework, it is only important to acknowledge that a rating class provides an estimate of the one-year default probability in terms of a confidence interval. Also estimates for 3-, and 5-year default probabilities can be obtained from the rating migration matrix. Thus, leading to a certain amount of model risk.

The aim of this paper is to incorporate ambiguity into the context of single-name credit risk. We focus on ambiguity on the default intensity, and also discuss ambiguity on the recovery.

The main results are as follows: we obtain a necessary and sufficient condition for a reference probability measure to be a local martingale measure for credit risky bond markets under default ambiguity, thereby ensuring the absence of arbitrage in a sense to be precisely specified below. Furthermore, we consider the case where we have partial information on the amount that the owner of a defaulted claim receives upon default.

The next section of this paper introduces homogeneous ambiguity, and its example. Section 3 introduces the fundamental theorem of asset pricing (FTAP) under homogeneous ambiguity. In Section 4 and Section 6, we derive the no-arbitrage conditions for defaultable term structure models with zero-recovery, and fractional recovery of the market value, in our framework. We conclude in Section 7.

2. Intensity-Based Models

Intensity-based models are the most used model class for modeling credit risk (see (Bielecki and Rutkowski 2002, Chapter 8) for an overview of relevant literature). The default intensity, however, is difficult to estimate and therefore naturally carries a lot of uncertainty. This has led to the emergence of rating agencies which, since the early 20th century, estimate bond’s credit worthiness3.

Modeling of credit risk has up to now incorporated uncertainty in the default intensity in a systematic way. On the other side, a number of Bayesian approaches exist, utilizing filtering technologies (see, for example, Duffie and Lando (2001); Frey and Schmidt (2009), among many others).

Here, we introduce an alternative treatment of the lack of precise knowledge of the default intensity based on the concept of ambiguity following the seminal ideas from Frank Knight in Knight (1921).

Uncertainty in our setting will be captured through a family of probability measures $\mathcal{P}$ replacing the single probability measure $\mathbb{P}$ in classical approaches. Intuitively, each $\mathbb{P}$ represents a model and the family $\mathcal{P}$ collects models which we consider equally likely.

In this spirit, working with a single $\mathbb{P}$, or with a set $\mathcal{P}=\left\{\mathbb{P}\right\}$ which contains only one element, is in a one-to-one correspondence to assuming that the parameters of the underlying processes are exactly known. In financial markets, this is certainly not the case and ambiguity helps to incorporate this uncertainty into the used models.

We consider throughout a fixed finite time horizon $T^{*}>0$. In light of our discussion above, let $(\mathsf{\Omega },\mathcal{F})$ be a measurable space and $\mathcal{P}$ be a set of probability measures on the measurable space $(\mathsf{\Omega },\mathcal{F})$. In particular, there is no fixed and known measure $\mathbb{P}$ (except in the special case where $\mathcal{P}$ contains only one element which we treat en passant).

Intensity-based default models correspond to the case where the ambiguity is homogeneous, i.e., there is a measure ${\mathbb{P}}^{\prime }$ such that $\mathbb{P}\sim {\mathbb{P}}^{\prime }$ for all $\mathbb{P}\in \mathcal{P}$. Here, $\mathbb{P}\sim {\mathbb{P}}^{\prime }$ means that $\mathbb{P}$ and ${\mathbb{P}}^{\prime }$ are equivalent, that is, they have the same nullsets. The reference measure ${\mathbb{P}}^{\prime }$ only has the role of fixing events of measure zero for all probability measures under consideration. Intuitively, this means there is no ambiguity on these events of measure zero. In the following, $E^{\prime }$ is the expectation with respect to the reference measure ${\mathbb{P}}^{\prime }$.

Remark 1.

As a consequence of the equivalence of all probability measures in $\mathcal{P}$, all equalities and inequalities will hold almost-surely with respect to any probability measure $\mathbb{P}\in \mathcal{P}$, or, respectively, to ${\mathbb{P}}^{\prime }$.

Ambiguity in Intensity-Based Models

In this section, we introduce ambiguity in intensity-based models. Our goal is not the most general approach in this setting: we rather focus on simpler, but still practically highly relevant cases. For a more general treatment, we refer the reader to Biagini and Zhang (2017). The main mathematical tool we use here is enlargement of filtrations and we refer the reader to Aksamit and Jeanblanc (2017) for further details and a guide to the literature.

Assume that under ${\mathbb{P}}^{\prime }$ we have a d-dimensional Brownian motion W with canonical and augmented4 filtration $\mathbb{F}={\left({\mathcal{F}}_t\right)}_{0\le t\le T^{*}}$ and a standard exponential random variable $\tau$, independent of ${\mathcal{F}}_{T^{*}}$, that is, ${\mathbb{P}}^{\prime }(t<\tau |{\mathcal{F}}_t)=exp(-t)$, $0\le t\le T^{*}$. The Brownian motion W has the role of modelling market movements and general information, excluding default information. We therefore call $\mathbb{F}$ the market filtration in the following. The filtration $\mathbb{G}={\left({\mathcal{G}}_t\right)}_{0\le t\le T^{*}}$ includes default information and is obtained by a progressive enlargement of $\mathbb{F}$ with $\tau$, i.e.,

$$\begin{array}{c}\hfill {\mathcal{G}}_t=\bigcap _{ϵ>0}\sigma ({𝟙}_{\{t\ge \tau \}},W_s:0\le s\le t+ϵ),0\le t\le T^{*}.\end{array}$$

To finalize our setup, we assume that $\mathcal{F}={\mathcal{G}}_{T^{*}}$.

Note that up to now, everything has been specified under the reference measure ${\mathbb{P}}^{\prime }$ and nothing was said about the concrete models we are interested in (except about the nullsets). These models will now be introduced using the Girsanov theorem, i.e., by changing from ${\mathbb{P}}^{\prime }$ to the measures we are interested in.

Consequently, the next step is to construct measures ${\mathbb{P}}^{\lambda }$ with appropriate processes $\lambda$ – under ${\mathbb{P}}^{\lambda }$, the default time $\tau$ will have the intensity $\lambda$. More precisely, assume that $\lambda$ is some positive process which is predictable with respect to the market filtration, $\mathbb{F}$. Define the density process $Z^{\lambda }$ by

$$\begin{array}{c}\hfill Z_t^{\lambda }:=\left\{\begin{array}{cc}exp\left({\int }_0^t(1-{\lambda }_s)ds\right),\hfill & t<\tau \hfill \\ {\lambda }_{\tau }exp\left({\int }_0^{\tau }(1-{\lambda }_s)ds\right)\hfill & t\ge \tau .\hfill \end{array}\right.\end{array}$$

(3)

Note that $Z^{\lambda }$ is a $\mathbb{G}$-local martingale and corresponds to a Girsanov-type change of measure (see Theorem VI.2.2 in Brémaud (1981)). If $E^{\prime }\left[Z_{T^{*}}^{\lambda }\right]=1$ we obtain an equivalent measure ${\mathbb{P}}^{\lambda }\sim {\mathbb{P}}^{\prime }$ via

$$\begin{array}{c}\hfill {\mathbb{P}}^{\lambda }\left(A\right):=E^{\prime }\left[{𝟙}_A{Z}_{T^{*}}^{\lambda }\right]\forall A\in \mathcal{F}.\end{array}$$

(4)

Under the measure ${\mathbb{P}}^{\lambda }$, $\tau$ has intensity $\lambda$: more precisely, this means that the process

$$\begin{array}{c}\hfill M_t^{\lambda }:={𝟙}_{\{t\le \tau \}}-{\int }_0^{t\wedge \tau }{\lambda }_{s}ds,0\le t\le T^{*},\end{array}$$

(5)

is a ${\mathbb{P}}^{\lambda }$-martingale.

Now we introduce a precise definition of ambiguity on the default intensity which is very much in spirit of the G-Brownian motion in Peng (2010): we consider an interval $[\underline{\lambda },\overline{\lambda }]\subset (0,\infty )$ where $\underline{\lambda }$ and $\overline{\lambda }$ denote lower (upper) bounds in the default intensity. Intuitively, we include all possible intensities lying in these bounds in our family of models $\mathcal{P}$. More precisely, we define the set of density generators H by

$$H:=\{\lambda :\lambda \mathrm{is}\mathbb{F}-\text{predictable}\mathrm{and}{\mathbb{P}}^{\prime }(\underline{\lambda }\le {\lambda }_t\le \overline{\lambda },t\in [0,T^{*}])=1\}.$$

Ambiguity on the default intensity is now covered by considering the concrete family of probability measures

$$\begin{array}{c}\hfill \mathcal{P}:=\{{\mathbb{P}}^{\lambda }:\lambda \in H\}.\end{array}$$

(6)

In the following, we will always consider this $\mathcal{P}$. First, we observe that this set is convex.

Lemma 1.

$\mathcal{P}$ is a convex set.

Proof. 

Consider ${\mathbb{P}}^{{\lambda }^{\prime }},{\mathbb{P}}^{{\lambda }^{″}}\in \mathcal{P}$ and $\alpha \in (0,1)$. Then,

$$\begin{array}{cc}\hfill \alpha {\mathbb{P}}^{{\lambda }^{\prime }}\left(A\right)+(1-\alpha ){\mathbb{P}}^{{\lambda }^{″}}\left(A\right)& =E^{\prime }\left[{𝟙}_A(\alpha Z_{T^{*}}^{{\lambda }^{\prime }}+(1-\alpha )Z_{T^{*}}^{{\lambda }^{″}})\right].\hfill \end{array}$$

Now consider the (well-defined) intensity $\lambda$, given by

$${\int }_0^t{\lambda }_{s}ds:=t-log\left[\alpha e^{{\int }_0^t(1-{\lambda }_s^{\prime })ds}+(1-\alpha )e^{{\int }_0^t(1-{\lambda }_s^{″})ds}\right],$$

$0\le t\le T^{*}$. Then,

$$\alpha Z_{T^{*}}^{{\lambda }^{\prime }}+(1-\alpha )Z_{T^{*}}^{{\lambda }^{″}}=Z_{T^{*}}^{\lambda }$$

such that by (4), ${\mathbb{P}}^{\lambda }\sim {\mathbb{P}}^{\prime }$ refers to an equivalent change of measure. Finally, we have to check that $\lambda \in H$, which means that $\lambda \in [\underline{\lambda },\overline{\lambda }]$, $0\le t\le T^{*}$: note that

$$\begin{array}{c}{\displaystyle t-log\left[\alpha e^{{\int }_0^t(1-{\lambda }_s^{\prime })ds}+(1-\alpha )e^{{\int }_0^t(1-{\lambda }_s^{″})ds}\right]}\hfill \\ \le t-log\left[\alpha e^{{\int }_0^t(1-\overline{\lambda })ds}+(1-\alpha )e^{{\int }_0^t(1-\overline{\lambda })ds}\right]\hfill \\ \le t-t(1-\overline{\lambda })=\overline{\lambda }t,\hfill \end{array}$$

and ${\lambda }_t\le \overline{\lambda }$ follows. Similarly, $\underline{\lambda }\le {\lambda }_t$ and the claim follows since t was arbitrary. □

Remark 2.

Intuitively, the requirement $\underline{\lambda }>0$ states that there is always a positive risk of experiencing a default, which is economically reasonable. Technically it has the appealing consequence that all considered measures in $\mathcal{P}$ are equivalent.

It turns out that the set of possible densities will play an important role in connection with measure changes. In this regard, we define admissible measure changes with respect to $\mathcal{P}$ by

$$\mathcal{A}:=\{{\lambda }^{*}:{\lambda }^{*}\mathrm{is}\mathrm{positive},\mathbb{F}-\text{predictable}\mathrm{and}{E}^{\prime }\left[Z_{T^{*}}^{{\lambda }^{*}}\right]=1\}.$$

The associated Radon-Nikodym derivatives $Z_{T^{*}}^{{\lambda }^{*}}$ for ${\lambda }^{*}\in \mathcal{A}$ are the possible Radon-Nikodym derivatives for equivalent measure changes.

Remark 3.

It is of course possible to consider an ambiguity setting more general than the specific one in (6). One possibility is to consider only a subset of $\mathcal{P}$. Another possibility is to allow the bounds $\underline{\lambda }$ and $\overline{\lambda }$ to depend on time, or even on the state of the process – this latter case is important for considering affine processes under uncertainty and we refer to Fadina et al. (2019) for further details. In Section 5, we consider indeed such a more general setting.

3. Absence of Arbitrage under Ambiguity

Absence of arbitrage and the respective generalizations, no free lunch (NFL), and no free lunch with vanishing risk (NFLVR), are well established concepts when the underlying probability measure $\mathbb{P}$ is known and fixed. Here, we give a small set of sufficient conditions for absence of arbitrage extended to the setting with ambiguity. In this regard, consider, a fixed set $\mathcal{P}$ of probability measures on the measurable space $(\mathsf{\Omega },\mathcal{F})$. In addition, let $\mathbb{G}={\left({\mathcal{G}}_t\right)}_{0\le t\le T^{*}}$ be a right-continuous filtration.

Discounted price processes of the traded assets are given by a finite dimensional $\mathbb{G}$-semimartingale $X={\left(X_t\right)}_{0\le t\le T^{*}}$. The semimartingale property holds equivalently in any of the filtration ${\mathbb{G}}_{+}$ or the augmentation of ${\mathbb{G}}_{+}$, see (Neufeld and Nutz 2014, Proposition 2.2). It is well known that then X is a semimartingale for all $\mathbb{P}\in \mathcal{P}$.

A self-financing trading strategy is a predictable and X-integrable process $\mathsf{\Phi }$ and the associated discounted gains process is given by the stochastic integral of $\mathsf{\Phi }$ with respect to X,

$${(\mathsf{\Phi }·X)}_t={\int }_0^t{\mathsf{\Phi }}_{u}d{X}_u,0\le t\le T^{*}.$$

Intuitively, an arbitrage is an admissible self-financing trading strategy which starts from zero initial wealth, has non-negative pay-off under all possible future scenarios, hence for all $P\in \mathcal{P}$, there is at least one $P\in \mathcal{P}$, such that the pay-off is positive. This is formalized in the following definition, compare for example Vorbrink (2014). As usual a trading strategy is called a-admissible, if ${(\mathsf{\Phi }·X)}_t\ge -a$ for all $0\le t\le T^{*}$.

Definition 1.

A self-financing trading strategy Φ is called$\mathcal{P}$-arbitrage if it is a-admissible for some $a>0$ and

(i) 

for every $\mathbb{P}\in \mathcal{P}$ we have that ${(\mathsf{\Phi }·X)}_{T^{*}}\ge 0$, $\mathbb{P}$-almost surely, and

(ii) 

for at least one $\mathbb{P}\in \mathcal{P}$ it holds that $\mathbb{P}({(\mathsf{\Phi }·X)}_{T^{*}}>0)>0$.

Since all probability measures $\mathbb{P}\in \mathcal{P}$ are considered as possible, a $\mathcal{P}$-arbitrage is a riskless trading strategy for all possible models (i.e., for all $\mathbb{P}\in \mathcal{P}$) while it is a profitable strategy for at least one scenario (i.e., for at least one $\mathbb{P}\in \mathcal{P}$).

The main tool for classifying arbitrage free markets will be local martingale measures, even in the setting with ambiguity. In this regard, we call a probability measure $\mathbb{Q}$ a local martingale measure if X is a $\mathbb{Q}$-local martingale.

It is well-known that no arbitrage or, more precisely, no free lunch with vanishing risk (NFLVR) in a market where discounted price processes are locally bounded semimartingales is equivalent to the existence of an equivalent local martingale measure (ELMM), see Delbaen and Schachermayer (1994, 1998). The technically difficult part of this result is to show that a precise criterion of absence of arbitrage implies the existence of an ELMM. In the following, we will not aim at such a deep result under ambiguity, but utilize the easy direction, namely that existence of an ELMM implies the absence of arbitrage as formulated below.

From the classical fundamental theorem of asset pricing (FTAP), the following result follows easily.

Theorem 1.

If, for every $\mathbb{P}\in \mathcal{P}$ there exists an equivalent local martingale measure $\mathbb{Q}\left(\mathbb{P}\right)$, then there is no arbitrage in the sense of Definition 1.

Proof. 

Indeed, assume on the contrary that there is an arbitrage $\mathsf{\Phi }$ with respect to some measure $\mathbb{P}\in \mathcal{P}$ which we fix for the remainder of the proof. If there exists an ELMM $\mathbb{Q}\left(\mathbb{P}\right)$ then $\mathsf{\Phi }$ would be an arbitrage strategy together with an ELMM, a contradiction to the classical FTAP. □

This (sufficient) condition directly corresponds to the existing results in the literature (see, for example, Biagini et al. (2017)) where arbitrages of the first kind are studied under the additional assumption of continuity for the traded assets.

4. Ambiguity on the Default Intensity

Our aim is to discuss dynamic term structure models under default risk with ambiguity on the default intensity. The relevance of this issue has, for example, already been reported in Riedel (2015). Here, we take this as motivation to propose a precise framework taking ambiguity on the default intensity into account.

4.1. Dynamic Defaultable Term Structures

We specialize the considerations of absence of arbitrage in Section 3 to defaultable bond markets. Recall that we have a filtration $\mathbb{G}$ at hand and that $\tau$ is the $\mathbb{G}$-stopping time at which the company defaults. We define the default indicator process H by

$$H_t={𝟙}_{\{t\ge \tau \}},0\le t\le T^{*}.$$

The associated survival process is $1-H.$ A credit risky bond with a maturity time $T\le T^{*}$ is a contingent claim promising to pay one unit of currency at T. We denote the price of such a bond at time $t\le T$ by $P(t,T)$. If no default occurs prior to T, $P(T,T)=1$. We will first consider zero recovery, i.e., assume that the bond loses its total value at default. Then $P(t,T)=0$ on $\{t\ge \tau \}$.

Besides zero recovery, we only make the weak assumption that bond-prices prior to default are positive and absolutely continuous with respect to maturity T. This follows the well-established approach by Heath et al. (1992). More formally, we assume that

$$P(t,T)={𝟙}_{\{\tau >t\}}exp\left(-{\int }_t^{T}f(t,u)du\right)0\le t\le T.$$

(7)

The initial forward curve $T\mapsto f(0,T)$ is then assumed to be sufficiently integrable and the forward rate processes $f(·,T)$ are assumed to follow Itô processes satisfying

$$\begin{array}{c}\hfill f(t,T)=f(0,T)+{\int }_0^{t}a(s,T)ds+{\int }_0^{t}b(s,T)d{W}_s,\end{array}$$

(8)

for $0\le t\le T$. Recall that W was chosen to be a Brownian motion. We denote by $\mathcal{O}$ the optional $\sigma$-algebra and by $\mathcal{B}$ the Borel $\sigma$-algebra.

Assumption 1.

We require the following technical assumptions:

(i) 

the initial forward curve is measurable, and integrable on $[0,T^{*}]$:

$${\int }_0^{T^{*}}\left|f(0,u)\right|du<\infty ,$$

(ii) 

the drift parameter $a(\omega ,s,t)$ is $\mathbb{R}$-valued $\mathcal{O}\otimes \mathcal{B}$-measurable and integrable on $[0,T^{*}]$:

$${\int }_0^{T^{*}}{\int }_0^{T^{*}}\left|a(s,t)\right|dsdt<\infty ,$$

(iii) 

the volatility parameter $b(\omega ,s,t)$ is ${\mathbb{R}}^d$-valued, $\mathcal{O}\otimes \mathcal{B}$-measurable, and

$$\underset{s,t\le T^{*}}{sup}\parallel b(s,t)\parallel <\infty .$$

(iv) 

Let $r_t$ be the short rate process at time t, for $0\le t\le T^{*}$. With probability one, it holds that

$$0<f(t,t)-r_t,0\le t\le T^{*}.$$

Set for $0\le t\le T\le T^{*}$,

$$\begin{array}{cc}\hfill \overline{a}(t,T)& ={\int }_t^{T}a(t,u)du,\hfill \\ \hfill \overline{b}(t,T)& ={\int }_t^{T}b(t,u)du.\hfill \end{array}$$

Lemma 2.

Under Assumption 1 it holds that,

$${\int }_t^{T}f(t,u)du={\int }_0^{T}f(0,u)du+{\int }_0^t\overline{a}(·,u)du+{\int }_0^t\overline{b}(·,u)d{W}_u-{\int }_0^{t}f(u,u)du$$

for $0\le t\le T\le T^{*}$, almost surely.

This follows as in Heath et al. (1992): for the case W is a Brownian motion, this is Lemma 6.1 in Filipović (2009). This result could also be generalized where W is replaced by a semimartingale with absolutely continuous characteristics, see Proposition 5.2 in Björk et al. (1997). Note that the strong condition (iii) of uniform boundedness of b in Assumption 1 is needed for the application of the stochastic Fubini theorem.

4.2. Absence of Arbitrage without Ambiguity on the Default Intensity

The first step towards the study of term structure models with default ambiguity is the study of absence of arbitrage in (classical) intensity-based dynamic term structure models. Consider $\lambda ={\left({\lambda }_t\right)}_{0\le t\le T^{*}}\in \mathcal{A}$ and the probability measure ${\mathbb{P}}^{\lambda }$. Then, the dual predictable projection $H^p$ of H is given by $H_t^p={\int }_0^{t\wedge \tau }{\lambda }_{s}ds$ (under ${\mathbb{P}}^{\lambda })$. Moreover, the Doob-Meyer decomposition yields that

$$M^{\lambda }:=H-{\int }_0^{·\wedge \tau }{\lambda }_{s}ds$$

is ${\mathbb{P}}^{\lambda }$-martingale, compare equation (5).

For discounting, we use the bank account. Its value is given by a stochastic process starting with 1 which is then upcounted by the short rate r, i.e., the value process of the bank account is $\gamma \left(t\right)=exp\left({\int }_0^t{r}_{s}ds\right)$ with an $\mathbb{G}$-predictable process r.

In the bond market context considered here, a measure $\mathbb{Q}$ is called local martingale measure if, for any maturity $T\in (0,T^{*}]$, the discounted bond price process for the bond with maturity T is a $\mathbb{Q}$-local martingale. Then, we obtain the following result.

Proposition 1.

Assume that Assumption 1 holds. Consider a measure $\mathbb{Q}$ on $(\mathsf{\Omega },\mathcal{F})$, such that $M^{\lambda }$ is a $\mathbb{Q}$-martingale, that W is a $\mathbb{Q}$-Brownian motion and that $\mathbb{Q}\left({\int }_0^{T^{*}}\right|r_s|ds<\infty )=1$. Then $\mathbb{Q}$ is a local martingale measure if and only if

(i) 

$f(t,t)=r_t+{\lambda }_t,$

(ii) 

the drift condition

$$\begin{array}{c}\hfill \overline{a}(t,T)=\frac{1}{2}{∥\overline{b}(t,T)∥}^2,\end{array}$$

holds $dt\otimes dQ$-almost surely for $0\le t\le T\le T^{*}$ on $\{\tau >t\}$.

Proof. 

We set $E=1-H$ and $F(t,T)=exp\left(-{\int }_t^{T}f(t,u)du\right)$. Then (7) can be written as $P(t,T)=E\left(t\right)F(t,T).$ Integrating by part yields

$$dP(t,T)=F(t-,T)dE\left(t\right)+E(t-)dF(t,T)+d{[E,F(·,T)]}_t.$$

For $\{t<\tau \}$,

$$\begin{array}{cc}\hfill dP(t,T)& =P(t-,T)\left(-{\lambda }_{t}dt+\left(f(t,t)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{a}(t,T)\right)dt\right)\hfill \\ & -P(t-,T)\left(d{M}^{\lambda }+\overline{b}(t,T)d{W}_t\right).\hfill \end{array}$$

(9)

The discounted bond price process is a local martingale if and only if the predictable part in the semimartingale decomposition vanishes, i.e.,

$$f(t,t)-r_t-{\lambda }_t-\overline{a}(t,T)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2=0.$$

(10)

Letting $T=t$ we obtain (i) and (ii) and the result follows. □

4.3. Absence of Arbitrage with Ambiguity on the Default Intensity

Next, we derive the no-arbitrage conditions for the forward rate in term of the intensity and the short rate, and also the conditions for the drift and volatility parameters, under ambiguity on the default intensity. In this regard, we require a bit more structure: we assume that the setting detailed in Section 2 holds, in particular, we consider the family of probability measures $\mathcal{P}$ constructed in equation (6). Recall that for all ${\mathbb{P}}^{\lambda }\in \mathcal{P}$, W is a Brownian motion and that ${\mathbb{P}}^{\lambda }\sim {\mathbb{P}}^{\prime }$. We may, for the moment, safely assume that the market filtration $\mathbb{F}$ satisfies the usual conditions under ${\mathbb{P}}^{\prime }$.

For a generic real-valued, $\mathbb{F}$-progressive process $\theta ={\left({\theta }_t\right)}_{t\ge 0}$, let the process $z^{\theta }={\left(z_t^{\theta }\right)}_{0\le t\le T^{*}}$ be given as the unique strong solution of

$$\begin{array}{c}\hfill d{z}_t^{\theta }={\theta }_t{z}_t^{\theta }d{W}_t,z_0^{\theta }=1.\end{array}$$

(11)

Then, $z^{\theta }$ is a continuous local martingale. If $E^{\prime }\left[z_{T^{*}}^{\theta }\right]=1$, we can define a probability measure ${\tilde{\mathbb{P}}}^{\theta }$ by letting

$$\begin{array}{c}\hfill {\tilde{\mathbb{P}}}^{\theta }\left(A\right):=E^{\prime }\left[{𝟙}_A{z}_{T^{*}}^{\theta }\right],\forall A\in \mathcal{F},\end{array}$$

(12)

just as in equation (4). Under ${\tilde{\mathbb{P}}}^{\theta }$ the process $\tilde{W}=W-{\int }_0^{·}{\theta }_{s}ds$ is a Brownian motion, i.e., W itself became a Brownian motion with drift $\theta$, see Theorem 5.1 in Chapter 3 of Karatzas and Shreve (1998).

Moreover, set ${\tilde{\lambda }}_t:=(f(t,t)-r_t)·{\lambda }_t^{-1},t\in [0,T^{*}].$ Note that under Assumption 1, $\tilde{\lambda }$ is positive (which is necessary for an equivalent change of measure). The associated density is abbreviated by

$$Z_{T^{*}}^{*}=Z_{T^{*}}^{\tilde{\lambda }}.$$

Theorem 2.

Consider ${\mathbb{P}}^{\lambda }\in \mathcal{P}$. Under Assumption 1, there exists an ELMM to ${\mathbb{P}}^{\lambda }$, if there exists an $\mathbb{F}$-progressive process ${\theta }^{*}$ such that

(i) 

$E^{{\mathbb{P}}^{\lambda }}\left[Z_{T^{*}}^{*}{z}_{T^{*}}^{{\theta }^{*}}\right]=1$,

(ii) 

the drift condition

$$\overline{a}(t,T)=\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{b}(t,T){\theta }_t^{*},0\le t\le T\le T^{*}$$

holds $dt\otimes d{\mathbb{P}}^{\lambda }$-almost surely on $\{t<\tau \}$.

Intuitively, the theorem states that for the probability measure ${\mathbb{P}}^{\lambda }$, we find an ELMM if we are able to perform an equivalent change of measure (condition (i)) in such a way that under the new measure the drift condition holds for the Brownian motion with drift ${\theta }^{*}$ (condition (ii)).

Proof. 

We start from some ${\mathbb{P}}^{\lambda }\in \mathcal{P}$ and fix this measure in the following. This means that, under ${\mathbb{P}}^{\lambda }$, W is a Brownian motion and $\tau$ has intensity $\lambda$. In the search for an ELMM we are looking for an equivalent measure ${\mathbb{P}}^{*}$ which satisfies the conditions of Proposition 1.

In this regard, note the following: by its definition, (11), together with condition (i), $z^{{\theta }^{*}}$ is a density process for a change of measure via the Girsanov theorem for Itô processes, see Theorem 5.1 in Chapter 3 of Karatzas and Shreve (1998). Moreover, by (3) together with (i), $Z^{*}=Z^{\tilde{\lambda }}$ is the density for the change in intensity from $\lambda$ under ${\mathbb{P}}^{\lambda }$ to the intensity given by ${\lambda }_t^{*}:={(f(t,t)-r_t)}_{0\le t\le T^{*}}$, see (Brémaud 1981, Theorem VI.2.T2). We set

$$d{\mathbb{P}}^{*}:=Z_{T^{*}}^{*}{z}_{T^{*}}^{{\theta }^{*}}d{\mathbb{P}}^{\lambda }.$$

According to Theorem 3.40 in Chapter III of Jacod and Shiryaev (2003), this refers to a Girsanov-type (and equivalent) change of measure. Moreover, $W_t^{*}=W_t-{\int }_0^t{\theta }_s^{*}ds,$$0\le t\le T^{*},$ is a ${\mathbb{P}}^{*}$-Brownian motion and $M^{{\lambda }^{*}}$ is a ${\mathbb{P}}^{*}$-martingale.

We now show that ${\mathbb{P}}^{*}$ is also a local martingale measure. Recall from (9) that, under ${\mathbb{P}}^{\lambda }$,

$$\begin{array}{cc}\hfill \frac{dP(t,T)}{P(t-,T)}& =\left(f(t,t)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{a}(t,T)\right)dt-d{H}_t-\overline{b}(t,T)d{W}_t,\hfill \end{array}$$

for $\{t<\tau \}$; here $H_t={𝟙}_{\{t\ge \tau \}}$ is the default indicator. We introduce the martingales $W^{*}$ and $M^{{\lambda }^{*}}$ into this representation: note that

$$\begin{array}{cc}\hfill \frac{dP(t,T)}{P(t-,T)}& =\left(-{\lambda }^{*}\left(t\right)+f(t,t)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{a}(t,T)-\overline{b}(t,T){\theta }_t^{*}\right)dt\hfill \\ & -d{M}_t^{{\lambda }^{*}}-\overline{b}(t,T)d{W}_t^{*},\hfill \end{array}$$

again on $\{t<\tau \}$. Since, by assumption, $-{\lambda }_t^{*}+f(t,t)=r_t$, together with the drift condition (ii), we obtain for the discounted bond price process $\tilde{P}(t,T)=P(t,T)/{\gamma }_t$,

$$\begin{array}{cc}\hfill d\tilde{P}(t,T)& =\tilde{P}(t-,T)·\left(-d{M}_t^{{\lambda }^{*}}-\overline{b}(t,T)d{W}_t^{*}\right),\hfill \end{array}$$

which is a ${\mathbb{P}}^{*}$-local martingale and the proof is finished. □

5. Examples

The setting proposed above can, in dimension one, be directly linked to a special case of the non-linear affine processes introduced in Fadina et al. (2019). Indeed, note that for a progressive process $\lambda$, the integral

$$X_t:=x+{\int }_0^t{\lambda }_{s}ds,0\le t\le T^{*}$$

is a special semimartingale. Moreover, there are affine bounds on drift and volatility (the bound of the volatility is simply zero) since

$$\underline{\lambda }\le {\lambda }_t\le \overline{\lambda },$$

such that X is a non-linear affine process.

The major advantage of this setting is that numerical methods via non-linear PDE come into reach. More precisely, Theorem 4.1 in Fadina et al. (2019) shows that whenever $\psi$ is Lipschitz, the non-linear expectation

$$\begin{array}{c}\hfill \mathcal{E}\left[\psi \left(X_{T^{*}}\right)\right]:=\underset{\mathbb{P}\in \mathcal{P}}{sup}{E}^{\mathbb{P}}\left[\psi \left(X_{T^{*}}\right)\right]\end{array}$$

(13)

can be expressed as viscosity solution of the fully non-linear PDE

$$\left\{\begin{array}{cc}-{\partial }_{t}v(t,x)-G\left(x,{\partial }_{x}v(t,x)\right)=0\hfill & \mathrm{on}[0,T^{*})\times [\underline{\lambda },\overline{\lambda }],\hfill \\ \phantom{-{\partial }_{t}v(t,x)-G(x,}v(T,x)=\psi \left(x\right)\hfill & x\in [\underline{\lambda },\overline{\lambda }],\hfill \end{array}\right.$$

(14)

where G is defined by

$$\begin{array}{c}\hfill G(x,p):=\underset{\lambda \in [\underline{\lambda },\overline{\lambda }]}{sup}\left\{\lambda p\right\}\end{array}$$

(15)

and $v(0,x)=\mathcal{E}\left[\psi \left(X_{T^{*}}\right)\right]$ (the dependency on x arises through $X_0=x$).

Clearly, when p is either strictly positive (hence ${\partial }_{x}v(t,x)$) or negative, then the supremum in (15) is immediate and the PDE (14) can be solved using standard methods. This means that the solution to the non-linear expectation is obtained simply by the upper bound $\overline{\lambda }$ (or the lower bound $\underline{\lambda }$, respectively). Such a condition holds if $\psi$ is monotone. The more general case has to be solved using numerical methods and we provide a simple example now.

Example 1.

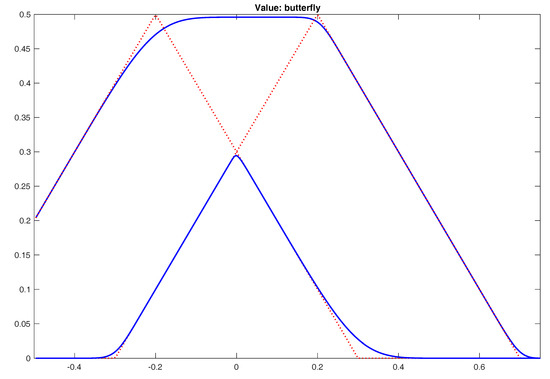
Consider a butterfly on $X_{T^{*}}$, i.e., the derivative with the payoff

$$\psi \left(x\right)={(x-K_1)}^{+}-2{(x-K_2)}^{+}+{(x-K_3)}^{+},$$

where we choose $K_1=-0.2$, $K_2=0.3$, and $K_3=0.8$. Moreover, let $\underline{\lambda }=0.1$ and $\overline{\lambda }=0.5$. Then the upper and lower price bounds for the butterfly are shown in Figure 1 (the upper prices are given by the nonlinear expectation in equation (13), while the lower prices are obtained by replacing the supremum in (13) by an infimum).

6. Ambiguity on the Recovery

A detailed study of bond markets beyond zero recovery is often neglected, the high degree of uncertainty about the recovery mechanism being a prime reason for this. This motivates us to take some time for developing a deeper understanding of a suitable recovery model under ambiguity.

We start from the observation that intensity-based models always need certain recovery assumptions, as for example, zero recovery, fractional recovery of treasury, and fractional recovery of par value, see (Bielecki and Rutkowski 2002, Chapter 8). We have so far considered the case where the credit risky bond becomes worthless at default (zero recovery). In the following, we will consider fractional recovery of market value where the credit risky bond looses a fraction of its market value upon default. Other recovery models can be treated in a similar fashion.

6.1. Fractional Recovery without Ambiguity

Fractional recovery of market value (RMV) is specified through a marked point process ${(T_n,R_n)}_{n\ge 1}$ where the stopping times $\left(T_n\right)$ denote the default times and $R_n\in (0,1]$ denotes the associated fractional recovery. Let

$$\begin{array}{c}\hfill R_t=\prod _{T_n\le t}{R}_n,0\le t\le T^{*},\end{array}$$

(16)

denote the recovery process. Then, R is non-increasing, positive with $R_0=1$. The recovery process replaces the default indicator in (7). More precisely, we assume that the family of defaultable bond prices under RMV satisfy

$$P_R(t,T)=R_{t}exp\left(-{\int }_t^{T}f(t,u)du\right),0\le t\le T\le T^{*}.$$

(17)

Remark 4.

If a default occurs at $t=T_n$, the bond looses a random fraction $q_t=1-R_{T_n}\in [0,1)$ of its pre-default value. Thus, the value $(1-q_t)P(t-,T)$ is immediately available to the bond owner at default. It is still subject to default risk because of the possible future defaults occurring at $T_{n+1},T_{n+2},\cdots$.

First, we state a generalization of Proposition 1 to this setting. To this end, we require more structure and continue in the setting of the Section 2. Assume that the marked point process ${(T_n,R_n)}_{n\ge 1}$ is independent from W and standard in the following sense: the random times $\left(T_n\right)$ are the jumping times from a Poisson process with intensity one, and the recovery values $\left(R_n\right)$ are independent from $\left(T_n\right)$ and W, and uniformly distributed in $[\underline{r},\overline{r}]\subset (0,1]$.

The filtration $\mathbb{G}={\left({\mathcal{G}}_t\right)}_{0\le t\le T^{*}}$ is obtained by a progressive enlargement of $\mathbb{F}$ with default and recovery information (given by R), i.e.,

$$\begin{array}{c}\hfill {\mathcal{G}}_t=\bigcap _{ϵ>0}\sigma (R_s,W_s:0\le s\le t+ϵ),0\le t\le T^{*}.\end{array}$$

We assume again $\mathcal{F}={\mathcal{G}}_{T^{*}}$. As next step, we introduce measure changes for the marked point process. Let

$${\mathsf{\Phi }}_t=\sum _{T_n\le t}{R}_n,0\le t\le T^{*}.$$

This implies that the defaultable bond prices under RMV, $P_R(0,t)$, at maturity time t of this bond, pays out ${\mathsf{\Phi }}_t$, the accumulated fractional default losses. Then, $\mathsf{\Phi }$ is a special semimartingale w.r.t. $\mathbb{G}$. Let

$${\mu }^{\mathsf{\Phi }}(dt,dx)=\sum _{n\ge 1}{\delta }_{(T_n,R_n)}(dt,dx)$$

denote the associated jump measure and let ${\nu }^{\mathsf{\Phi }}(dt,dx)$ denote its compensator, see Chapter II.1 in Jacod and Shiryaev (2003) or Chapter VIII.1 in Brémaud (1981). Note that ${\nu }^{\mathsf{\Phi }}(dt,dx)={𝟙}_{\{x\in [\underline{r},\overline{r}]\}}{(\overline{r}-\underline{r})}^{-1}dxdt$.

We introduce the densities

$$\begin{array}{c}\hfill L^{\mu ,h}=\left(\prod _{T_n\le T^{*}}{\mu }_{T_n}h(T_n,R_n)\right)·e^{{\int }_0^{T^{*}}{\int }_{\underline{r}}^{\overline{r}}(1-{\mu }_{t}h(t,x)){(\overline{r}-\underline{r})}^{-1}dxdt},\end{array}$$

(18)

where the predictable process $\mu$ is positive and, for any $x\in [\underline{r},\overline{r}]$, the $\mathbb{G}$-predictable process ${\left(h(t,x)\right)}_{0\le t\le T^{*}}$ is also positive. If $E\left[L_{T^{*}}\right]=1$, we can define the equivalent measure ${\mathbb{P}}^{\mu ,h}$ by

$$\begin{array}{c}\hfill d{\mathbb{P}}^{\mu ,h}=L_{T^{*}}d{\mathbb{P}}^{\prime }.\end{array}$$

(19)

By ${\mathcal{A}}^{*}$ we denote all pairs $(\mu ,h)$ which satisfy the above properties. Then, the compensator of the jump measure ${\mu }^{\mathsf{\Phi }}$ under $P^{\mu ,h}$ is

$$\begin{array}{c}\hfill {\mu }_{t}h(t,x){\nu }^{\mathsf{\Phi }}(dt,dx)={\mu }_{t}h(t,x){𝟙}_{\{x\in [\underline{r},\overline{r}]\}}{(\overline{r}-\underline{r})}^{-1}dxdt=:K_t^{\mu ,h}\left(dx\right)dt,\end{array}$$

(20)

see T10 in Section VIII.3 of Brémaud (1981). Next, we compute the compensator of R. We obtain from (16) that

$$\begin{array}{c}\hfill R_t-{\int }_0^t\int R_{s-}(x-1)K_s^{\mu ,h}\left(dx\right)ds,0\le t\le T^{*}\end{array}$$

(21)

is a ${\mathbb{P}}^{\mu ,h}$-martingale. For a $\mathbb{G}$-progressive process g, we denote

$$M^g=R+{\int }_0^{·}{R}_{s-}{g}_{s}ds.$$

Proposition 2.

Assume that Assumption 1 holds and let g be a positive and $\mathbb{G}$-predictable process. Consider a measure $\mathbb{Q}$ on $(\mathsf{\Omega },\mathcal{F})$, such that $M^g$ is a $\mathbb{Q}$-martingale, W is a $\mathbb{Q}$-Brownian motion, and $\mathbb{Q}\left({\int }_0^{T^{*}}\right|r_s|ds<\infty )=1$. Then $\mathbb{Q}$ is a local martingale measure if and only if

(i) 

$f(t,t)=r_t+g_t,$

(ii) 

the drift condition

$$\begin{array}{c}\hfill \overline{a}(t,T)=\frac{1}{2}{∥\overline{b}(t,T)∥}^2,0\le t\le T\le T^{*},\end{array}$$

holds $dt\otimes d\mathbb{Q}$-almost surely.

Proof. 

We generalize the proof of Proposition 1 to the case of RMV. To this end, let $F(t,T)=exp\left(-{\int }_t^{T}f(t,u)du\right)$. Then (17) reads $P_R(t,T)=R\left(t\right)F(t,T).$ Integrating by part yields

$$d{P}_R(t,T)=F(t-,T)dR\left(t\right)+R(t-)dF(t,T)+d{[R,F(·,T)]}_t.$$

Note that, by assumption,

$$M_t^g=R_t+{\int }_0^t{R}_{s-}{g}_{s}ds,0\le t\le T^{*},$$

is a Q-martingale and that $[R,F(.,T\left)\right]=0$ since R is of finite variation and $F(.,T)$ is continuous. Hence, by Lemma 2,

$$\begin{array}{cc}\hfill d{P}_R(t,T)& =P_R(t-,T)\left(-g_t+f(t,t)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{a}(t,T)\right)dt\hfill \\ & +P_R(t-,T)\left(r_{t}dt+d{M}^g-\overline{b}(t,T)d{W}_t\right),\hfill \end{array}$$

(22)

and we obtain the result as in the proof of Proposition 1. □

Example 2.

A classical example is when the defaults $\left(T_n\right)$ arrive at rate $\lambda >0$, and the recovery values $\left(R_n\right)$ are i.i.d. Then, $\int (x-1){\nu }^{\mathsf{\Phi }}(dt,dx)=\lambda E[R_1-1]dt$. We obtain that the instantaneous forward rate of the defaultable bond $f(t,t)$ equals $r_t+\lambda E[1-R_1]$. In the case of zero recovery, we recover $f(t,t)=r_t+\lambda$, and, in the case of full recovery (the case without default risk), $f(t,t)=r_t$.

6.2. Fractional Recovery with Ambiguity

We introduce ambiguity in this setting by changing from the standardized measure ${\mathbb{P}}^{\prime }$ to various appropriate measures via the Girsanov theorem. We also generalize the setting for ambiguity from the quite specific $\mathcal{P}$ to a general set of probability measures ${\mathcal{P}}^{*}$ here, see Remark 3. The reason for this is also economic: while bounding the intensity from above and below seems to be quite plausible, an upper/lower bound on the recovery (i.e., on $\left(R_n\right)$) sounds too strong for some applications.

Recall that ${\mathcal{A}}^{*}$ was the set of all candidates $(\mu ,h)$ which induce the measure changes via (19). Ambiguity is introduced by the set ${\mathcal{P}}^{*}$ of probability measures satisfying

$$\begin{array}{c}\hfill \varnothing \ne {\mathcal{P}}^{*}\subset \{{\mathbb{P}}^{\mu ,h}:(\mu ,h)\in {\mathcal{A}}^{*}\}.\end{array}$$

(23)

If ${\mathcal{P}}^{*}$ contains only one probability measure, we are in the classical setting, otherwise there is ambiguity in the market. Measure changes from ${\mathbb{P}}^{\mu ,h}$ to a new measure are done via the density $L^{{\mu }^{*},h^{*}}$ (see (18)) where, as above, ${\mu }^{*},h^{*}(.,x),x\in [\underline{r},\overline{r}]$ are positive and progressive. Recall the definition of the density $z^{\theta }$ in (11).

Theorem 3.

Let $g_t^{*}:=f(t,t)-r_t,$$t\in [0,T^{*}]$, and assume that Assumption 1 holds. Then there exists an ELMM for ${\mathbb{P}}^{\mu ,h}\in {\mathcal{P}}^{*}$ if

(i) 

there exists an $\mathbb{F}$-progressive ${\theta }^{*}$ such that $E^{\prime }\left[z_{T^{*}}^{{\theta }^{*}}\right]=1$,

(ii) 

there exist ${\mu }^{*}$ and $h^{*}(t,x)$, such that $E\left[L^{{\mu }^{*},h^{*}}\right]=1$ and

$$g_t^{*}=\int (x-1){\mu }_t^{*}{h}^{*}(t,x)K_t^{\mu ,h}\left(dx\right),0\le t\le T^{*},$$

$dt\otimes d{P}^{\prime }$-almost surely, and

(iii) 

the drift condition

$$\overline{a}(t,T)=\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{b}(t,T){\theta }_t^{*},0\le t\le T\le T^{*},$$

holds $dt\otimes d{P}^{\prime }$-almost surely.

Absence of arbitrage in this general ambiguity setting can now be classified, thanks to Theorem 1 as follows: if an ELMM exists for each ${\mathbb{P}}^{\mu ,h}\in {\mathcal{P}}^{*}$, then the market is free of arbitrage in the sense of Definition 1.

Proof. 

Fix ${\mathbb{P}}^{\mu ,h}\in {\mathcal{P}}^{*}$. We can define an equivalent measure ${\mathbb{P}}^{*}\sim {\mathbb{P}}^{\mu ,h}$ by

$$d{\mathbb{P}}^{*}:=L^{{\mu }^{*},h^{*}}{z}_{T^{*}}^{{\theta }^{*}}d{\mathbb{P}}^{\mu ,h},$$

with ${\mu }^{*}$ and $h^{*}$ as in (ii). According to Theorem 3.40 in Chapter III of Jacod and Shiryaev (2003), this refers to a Girsanov-type (and equivalent) change of measure. Moreover, $W^{*}=W-{\int }_0^{·}{\theta }_s^{*}ds$ is a ${\mathbb{P}}^{*}$-Brownian motion. Next, note that the compensator of the jump measure ${\mu }^{\mathsf{\Phi }}$ under ${\mathbb{P}}^{*}$ computes, according to T10 in Section VIII.3 in Brémaud (1981), to

$$\begin{array}{c}\hfill {\nu }^{*}(dt,dx):={\mu }_t^{*}{h}^{*}(t,x)K_t^{\mu ,h}\left(dx\right)dt\end{array}$$

with $K_t^{\mu ,h}$ from Equation (20). This implies that

$$\begin{array}{c}\hfill M_t^{g^{*}}=R_{s-}(x-1){\nu }^{*}(ds,dx)=R_t-{\int }_0^t{R}_{s-}{g}_s^{*}ds\end{array}$$

(24)

is a ${\mathbb{P}}^{*}$-martingale.

Now, we show that ${\mathbb{P}}^{*}$ is indeed a martingale measure: from (22) we obtain that

$$\begin{array}{cc}\hfill \frac{d{P}_R(t,T)}{P_R(t-,T)}& =\left(f(t,t)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{a}(t,T)\right)dt+d{R}_t-\overline{b}(t,T)d{W}_t.\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill \frac{d{P}_R(t,T)}{P_R(t-,T)}& =\left(f(t,t)+\frac{1}{2}{∥\overline{b}(t,T)∥}^2-\overline{a}(t,T)-\overline{b}(t,T){\theta }_t^{*}\right)dt+d{M}_t^g-\overline{b}(t,T)d{W}_t^{*}\hfill \\ & =r_{t}dt+d{M}_t^g-\overline{b}(t,T)d{W}_t^{*},\hfill \end{array}$$

by the definition of $g^{*}$ and the drift condition (iii). Hence, discounted bond prices are ${\mathbb{P}}^{*}$-local martingales and the proof is finished. □

Remark 5.

We can view zero recovery in the above setting by assuming that ${\mathbb{P}}^{\prime }(R_1=0)=1$ and letting $\tau =T_1$. Note that this case is excluded in RMV setting, since, under this assumption, at the first default all prices drop to zero and further defaults can not occur.

7. Conclusions

This paper provides a first step towards including ambiguity in intensity based models for credit risk. Many research questions are still open: first, the extension of constant boundaries $\underline{\lambda }$, $\overline{\lambda }$ to time-dependent, or, as in Fadina et al. (2019), state-dependent boundaries. Second, the extension to two or more defaultable assets, where default dependence comes into play. Third, estimation and determination of the bounds by statistical methods or calibration to market data. We hope that our paper provides the foundation for future works in these directions.