Abstract
Banks make profits from the difference between short-term and long-term loan interest rates. To issue loans, banks raise funds from capital markets. Since the long-term loan rate is relatively stable, but short-term interest is usually variable, there is an interest rate risk. Therefore, banks need information about the optimal leverage strategies based on the current economic situation. Recent studies on the economic crisis by many economists showed that the crisis was due to too much leveraging by “big banks”. This leveraging turns out to be close to Kelly’s optimal point. It is known that Kelly’s strategy does not address risk adequately. We used the return–drawdown ratio and inflection point of Kelly’s cumulative return curve in a finite investment horizon to derive more conservative leverage levels. Moreover, we carried out a sensitivity analysis to determine strategies during a period of interest rates increase, which is the most important and risky period to leverage. Thus, we brought theoretical results closer to practical applications. Furthermore, by using the sensitivity analysis method, banks can change the allocation sizes to loans with different maturities to mediate the risks corresponding to different monetary policy environments. This provides bank managers flexible tools in mitigating risk.
1. Introduction
Banks’ loan operations issue long-term loans at relatively high fixed interest rates and fund these loans with their own equity, low interest customer deposits, and short-term loans borrowed from the open market. However, since the short-term loan rate fluctuates with the health of the economy, bank loan operations always involve risk. Since the 2008 financial crisis, many researchers have pointed out that banks’ over leveraging on their loan balance sheet was one of the main triggers of the crisis. On the other hand, the interest rates difference between a long-term loan and a short-term loan normally is in the range of 2–3 percent annually. If a bank is too conservative on short-term borrowing, it will lose profit opportunities. Thus, establishing the right leverage level becomes an important issue.
Limiting the leverage will hold down credit access and disrupt economic growth since it is a built-in process of the banking business. Gornall and Strebulaev (2013) built a quantitative model of banking that explains bank capital structure and the decisions of banks and their borrowers. Their analysis gives great knowledge on fundamental questions about the behavior of nature. Harding et al. (2013) studied the effect of capital requirements, deposit insurance, and franchise value on a bank’s capital structure. They found that banks that are regulated accordingly preferred to maintain capital above the minimum required. The deep and accurate understanding of the model gives guidance to the discussion of financial regulatory reforms.
The recent financial crisis in 2008 also emphasized the importance of appropriate risk management. Banking experts and researchers have been highly engaged to find methods to manage risks effectively and efficiently in the balance sheet while maintaining profitability. Birge and Judice (2012) proposed a balance sheet management problem which contains the main risks. It is an optimization problem to determine a bank asset-liability management strategy by a simulation of bank balance sheets, using time series analysis, over time for multi-period model, and optimizing the utility function of equity for the single-period model.
Retail deposits are considered the core liabilities of the banking sector and the other components of bank funding as the non-core liabilities as in Hahm et al. (2013). The rate of credit growth relative to the trend of the risk premium is reflected by the ratio of the non-core to core liabilities. This gives an overview of the risk premiums as one of the main functions in the economy. Hahm et al. (2013) formulate a model of credit supply as the reverse of a credit risk model where a large stock of non-core liabilities serves as an indicator of the erosion of risk premiums. Therefore, they are exposed to the possibility of an economic crisis. They found supporting empirical evidence in their study of emerging and developing economies.
The model used in this research extends that of Birge and Judice (2012) by viewing the problem as a portfolio optimization problem with one risky asset. The growth optimal portfolio (GOP) theory of Kelly (1956), Thorp (1971, 2011) and MacLean et al. (2011) and its extension by Vince and Zhu (2015) has been applied to the model that is discussed in detail in the model chapter. We calibrated historical information of interest rates and defined a random variable X as the net rate difference of higher long-term loan interest and the lower short-term wholesale interest. GOP theory uses the function:
This is simply the log expected return under the log utility function, which is concave and has a unique maximum in the case of one risky investment. This maximum is often referred to as the Kelly optimal allocation size .
The results of calibrating the historical US loan interest rates shows that the leverage level of the US major banks right before the 2008 financial crisis was 20–30 times of bank equity. This level was close to what is suggested by the growth optimal portfolio theory in Latane (1959), a well-known theoretical optimal leverage. On the other hand, it is well known that the growth optimal portfolio theory does not adequately account for investment risk. Kelly’s point may be a large fraction when the wager is favorable and the risk of loss is very small. For such a large fraction, if the loss has occurred, then the amount left may be a small fraction of what one had initially; it may be even less than the initial size if the loss has occurred in more than one consecutive period. An example can be found in Ziemba and Hash (1986). MacLean et al. (2010), discussed these properties of the Kelly criterion and the idea of “fractional Kelly”. To overcome this risk, an alternative approach was recently developed by Vince and Zhu (2015), which modifies the growth optimal portfolio theory to more explicitly account for the risk. Besides the leverage level suggested by the growth optimal portfolio theory, their analysis also suggests two other reasonable risk-adjusted optimal leverage levels: The return to drawdown ratio optimal and the inflection point of marginal increase of return. Using the historical interest data in the US, the alternative two optimal points yield optimal leverage levels that are around 5–8 times that of bank equity. These leverage levels are much more conservative than the Kelly point.
The approaches suggested by Vince and Zhu essentially account for the expected drawdown risk approximated by the position size and are much easier to implement in practice than the alternatives, such as utility maximization, which needs a risk aversion coefficient which is difficult to calibrate. Drawdown is probably the most relevant risk measure in practice since while most risk measures usually focus on an outcome over a one-period horizon, such as value at risk or expected shortfall, in the case of banks it is important to account for periods of consecutive losses, as it is the case of drawdown. It is known among both theoretical researchers and practitioners that the drawdown accounts for portfolio losses better in the long run. Moreover, limiting drawdowns helps smooth the performance of investments. Finally, in real investment drawdown is where investors feel the pain investors. We refer to Chekhlov et al. (2005); Grossman and Zhou (1993) and Maier-Paape and Zhu (2018) and the references therein for additional discussion on drawdown. From the point of view of risk allocation, the inflection point is also highly relevant. It is the point at which the marginal change of return with respect to the risk turns from an increase to a decrease. Thus, it represents the risk level at which it would be more efficient to allocate capital to other projects or other corporations. The risk that is not incurred by using the inflection point can therefore be used in other projects or corporations where the marginal increase in profitability is higher per unit of risk.
Next, we turn to the more challenging issue of sensitivity analysis—how does the change in parameters impact the optimal leverage level? The focus is on the impact of change of short term interest rates on the optimal leverage level. Then analysis has been done on how to use the changes of a loan portfolio to mitigate the need to change the leverage level. Both are pertinent issues in practice. A sound quantitative analysis provides a theoretical foundation for important bank business decisions. However, these issues are mathematically challenging. The foundation for the sensitivity analysis is to calculate the derivatives of the optimal leverage levels with respect to the changes of return and loan portfolio mix. The available data is limited but can be used to estimate the general leverage level. Unfortunately, they are clearly insufficient to estimate the derivative numerically. Empirically, the PERT distribution fits the data series best by using the maximum likelihood method. This provides a handle on the problem. However, analyzing the qualitative behavior of the derivatives is still non-trivial. Formulae have been developed for the derivative of the growth optimal leverage level with respect to the expected return and show that this derivative is positive. In other words, qualitatively, if the environment becomes more profitable for loan operations, then it is reasonable to increase the leverage level. This confirmed the intuition of practitioners’ experiences. The formula for the derivative also enables us to estimate quantitatively the adjustment needed for the leverage level as the economic environment changes. However, a similar qualitative analysis for the return to drawdown ratio optimal and the inflection point turns out to be much more involved and has eluded us so far. Therefore, we approximated using the Taylor expansion and numerical analysis. This derivation guaranteed high accurate approximations that informs practitioners about the correct amount of changes of either the leverage level or the loan portfolio changes to respond to different loan profitability scenarios. Once the optimal points were in hand, the performance was tested using US historical data and comparing different strategies. Firstly, a test was developed for the three optimal leverage levels to investigate which one performs better in terms of risk adjusted return. As the theory suggested, Kelly’s point should give the highest return, which has very high risk, then the return–drawdown ratio and the inflection point respectively, which lower the risk and provide better risk-adjusted returns. Secondly, we performed a test, with the most conservative leverage level (inflection point), to compare changing the optimal leverage level with (Fed) interest rates changes vs. fixing the leverage level.
The final step provides practical strategies for a bank loan operation during different phases of the monetary policies of increasing or decreasing short-term interest rates. Possible adjustments of the loan portfolios include: (1) Adjustment of the leverage level or (2) adjustment of the allocation of 15-year and 30-year loans. This leads to the derivatives’ development of three allocation levels with respect to the return and the allocation percentages. Then we simulated the historical data to compare the above two strategies of adjusting the allocation between 15-year and 30-year loans to fixing the leverage level according to the aggregated data. This analysis provides a reasonable leverage level for banks’ mortgage operations. Moreover, adjustment strategies are suggested for the loan operation in order to deal with different monetary policy environments.
2. Model
2.1. Methodology
This chapter introduces growth portfolio theory and the related results. Growth portfolio theory starts with Kelly’s new interpretation of Shannon’s information rate Kelly (1956) in 1956 and has a long history. The maximum exponential rate of growth of an investor’s capital is related to the rate of accurate transmission of information over the noisy communication channel defined by Shannon (1948) in 1948. Latane (1959) independently discovered the GOP in 1959 and it attracted much attention. The main idea is to maximize the compounded expected growth of a portfolio, which is equivalent to maximizing log utility. Since log is concave, the maximum is unique, called Kelly’s Point. Many researchers studied and developed GOP. For example; Thorp (1971) extended Kelly’s idea and result to portfolio problems in 1972. Various properties of the GOP were discussed by Bell and Cover (1980); Barron and Cover (1988), Cover (1991); Ordentlich and Cover (1998), and MacLean et al. (2005). Thereafter Phelps (1962) developed an utility analysis of personal saving for one risky asset. Due to this risky asset, the effect of the optimal consumption policy is analyzed by dynamic programming. Hakansson (1970) developed Phelps’ theory for multiple risky assets with one riskiness asset with the consumption policy. Hakansson gave an explicit solution for the optimal investment and consumption strategy by using dynamic programming.
GOP has the obvious advantage of maximizing the growth but is also well known to practitioners as too risky. Some of the criticisms are reflected in Samuelson (1979); Markowitz (1976); Thorp (2011), and MacLean et al. (2010). Various “fractioned” Kelly points were proposed by MacLean et al. (1992); Browne (2000), and Davis and Lleo (2010). The textbook by MacLean et al. (2012) is an excellent source for Kelly’s criterion and GOP.
The method of Kelly’s criterion (growth portfolio theory) Kelly (1956) is used to approach the loan leverage problem. Recently, Vince and Zhu (2015) have developed and analyzed the optimal strategy of Kelly, adding the practical consideration that investment in practice is always over a finite time horizon, and it maximizes risk-adjusted returns. Their work of theoretical analysis and computer simulation shows that these three alternative strategies are more conservative than the Kellyt-Thorp theory suggested. The two alternatives they have analyzed are:
- Kelly’s optimal point;
- The maximum return–risk ratio;
- Inflection point.
Kelly’s formula has a unique maximum but to explicitly account for risk, a risk measure needs to be used. Out of many risk measures, "drawdown" is an appropriate risk measure in gambling (investment) problems. The maximum of the "return–drawdown" ratio and the inflection point of Kelly’s return curve will address this issue.
Vince and Zhu (2015) suggested focusing on the cumulative return curve over a finite investment horizon Q,
where s is the allocation or leverage, , and X is the random variable of aggregated return.
2.1.1. Kelly Optimal Point
Kelly’s maximum point always exists for any portfolio with a positive expected return. Solving the following equation maximizes Kelly’s cumulative return :
which is the same as solving:
2.1.2. Return–Risk Ratio
As mentioned before, Kelly’s allocation level does not account for risk adequately. Out of many risk measures, "drawdown" is considered appropriate in investment problems. When the return for each period is relatively small, it is approximately proportional to the investment size s. Thus we use:
as an approximation for the return–drawdown ratio. We follow Vince and Zhu (2015), where one can also find additional information.
2.1.3. Inflection Point
We solve the following equation to find the inflection point(s):
or equivalently:
The inflection point also depends on Q and it denotes by . This point also exists for sufficiently large Q. For details refer to Vince and Zhu (2015).
A bank benefits from issuing loans by making profits from the difference between the higher long term loan interest and the lower short term wholesale interest. Doing so involves interest rate risk because the long term mortgage rate r is fixed, yet the short term wholesale rate f can vary. Thus, the net rate difference can be viewed as a random variable and calibrated using the historical information on the rates.
For the one period model, Birge and Judice (2012) optimize an utility function for shareholders preferences. Time-series analysis is used for the multi-period model. A difficulty in applying this procedure is that the historical data is not long enough to calibrate time series with high confidence. Therefore, the model presented here focuses on the one period model, using GOP related criteria as discussed above.
2.2. Assumptions
In this study we make the following assumptions that are identified:
- The bank issues the same amount of loans every year;
- The bank does not distribute dividends to shareholders;
- The ratio of deposits to equity () is known and it is 6.6. See (A1);
- Refinancing facility is available. When the market interest rates on loans decrease, borrowers have and always take the option to reduce their interest rates by refinancing.
2.3. Problem Formulation
A bank has three types of liabilities: Equity (E), deposits (D), and non-core funding (N). Then the total liabilities L are:
The ratio of deposit to equity, , is known (A1). Then the appropriate proportion is seeked as needed by bank managers. The bank has to pay interest on the deposit in the year n and the bank receives interest , still remaining on the loan issued on year .
Bank issues loans of various lengths. First, consider a model with loans of fixed maturity of t-year, assume that the same size of the loan is issued in every year, and call it l. At any given year n, denote the percentage of t-year loan issued on year on banks account at year n. Then:
where is the t-year loan rate in year k. The total loan balance is:
L is funded by three different categories: Equity, deposits (core funding), and non-core funding which, is borrowed from capital markets. Then:
Next we discuss returns. The return from the loan issued in year is the balance of the loan issued in year, , which is , times the interest difference of . Since the refinancing facility is available, the total return rate funded by deposits in year n is:
Then the total return on the deposits is:
where or:
is the portion of l that is covered by deposits. Similarly we can calculate the return from equity assuming no dividend payments:
where or:
is the portion of l that is funded by equity. Then . Similarly, the total return from the leverage is:
where is the short term rate of borrowing money from the open market on year n. Since the total capital in hand is E, total return T can be calculated by:
where , , , and are defined as follows:
We then analyze the the expected log return. Let:
Let us view as a sample for a random variable X,
and as a sample from Y.
Both X and Y can be calibrated with historical data.
Theoretically,
Note that is a constant w.r.t s. We have:
To calculate , and , we need t-year loan data. The next chapter describes the data in detail. They are regarded as sample data and are used to calibrate the random variables X and Y respectively.
3. Estimating the Leverage Level
This chapter estimates the appropriate leverage levels for the bank loan balance-sheet according to the methods discussed in chapter 03 using, historical data from the US market. Furthermore, this section discusses the data sources and simulation results for two different maturities of loans in the US using the leverage level discussed in chapter 02. Then we compare the existing results with our calculation results. The simulation shows and points are appropriate levels to consider in practice and point is too risky. Finally, we discuss the importance of sensitivity analysis.
3.1. Description of Data
The following data was obtained from the Federal Reserve Bank of St. Louis for:
- A 5-year treasury constant maturity rate, percent, annual, not seasonally adjusted (1954–2016).
- A 30-year fixed rate mortgage average in the United States, percent, annual, not seasonally adjusted (1971–2016).
- A 15-year fixed rate mortgage average in the United States, percent, annual, not seasonally adjusted (1992–2016).
The above data have different lengths. Therefore we must fill the missing values by extrapolating the available data. The following method of calculation was used.
3.1.1. Projecting 30-Year Maturity Interest Rates from 1954 to 1970
Historically, the difference between the long-term mortgage rates and the short-term 5-year treasury rates has been relatively stable. Thus, we use the available data of 30-year maturity interest rates (Appendix C) and 5-year treasury rates(Appendix C) from 1971–2016, and fit a linear regression to predict the missing values of the 30-year mortgage rates from 1954–1970 (Figure 1).
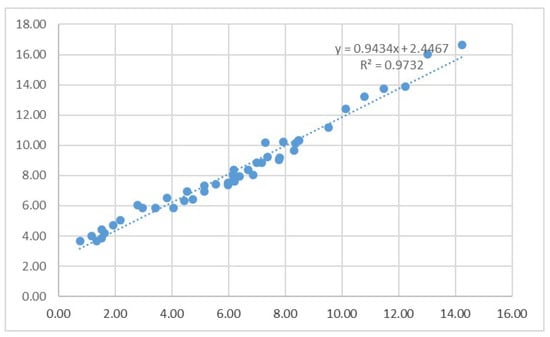
Figure 1.
The 5-year treasury constant maturity rate (X) vs. the 30-year fixed rate mortgage average (Y) in the United States.
The regression equation is:
which is used to complete the values of 30-year mortgage rates from 1954–1970, since we have 5-year treasury rates from 1954–1970. See
3.1.2. Projecting 15-Year Maturity Interest Rates from 1954 to 1991
The rate difference between the 30-year and the 15-year mortgage is more stable than the difference between the 30-year loan and the short term borrowing rate. Thus, we use the available data of the 15-year maturity interest rates and 30-year mortgage rates from 1992–2016, and fit a linear regression to predict missing values of the 15-year mortgage rates from 1954–1991 (Figure 2).
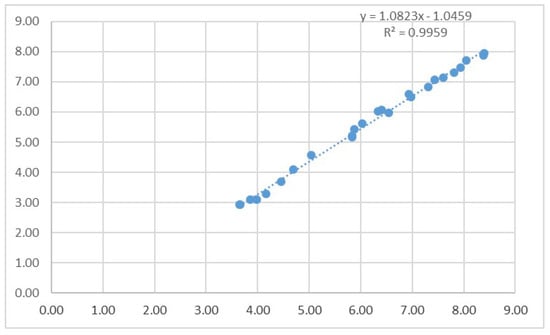
Figure 2.
The 30-year (X) vs. 15-year (Y) fixed rate mortgage average in the United States.
The regression equation is:
which is used to complete the values of the 15-year mortgage rates from 1954–1991, since we have 30-year mortgage rates from 1954–1991 from the prediction above.
3.2. Numerical Simulation
We use historical data from 1956–2016 on US yearly loan rates as discussed in the previous section. This data includes two loan rates for two maturities: 15-year and 30-years of loans. It also includes a wholesale rate, which is the rate the bank borrows in the short term to fund the loans (). In the previous chapter, we calculated formulae for , and in Equation (11) for the net rate. Using those formulae and computer programing (R), we calculate net rates X and Y. Then we find the three critical leverage levels.
Computation Results
In this section, we present our numerical results of three optimal leverage levels using the historical data described above. The calculations are based on , (A1), and the operating cost for different maturities of loans.
Table 1 and Table 2 show the optimal leverage levels for different investment horizons , and 20. The investment horizon, Q, represents how long the bank is expected to follow this strategy. The decision has to be taken by bank managers.

Table 1.
Leverage level for 30-year loans.

Table 2.
Leverage level for 15-year loans.
The relationship among those three optimal points is clear as follows:
where is the inflection point, is maximum of the return–drawdown ratio, and is Kelly’s optimal point.
Kelly’s optimal point yields a larger return, but it is too risky for investments shown by simulation in the data (Figure 3). Return–drawdown ratio maximizes your return adjusted to the investment size as a proxy for risk. If you go beyond you could gain more but the percentage of the gain will be lower. The inflection point is the lowest. Before the inflection point your rate of return is increasing (derivative is positive or convex) and afterward, it will be decreasing (derivative is negative or concave).
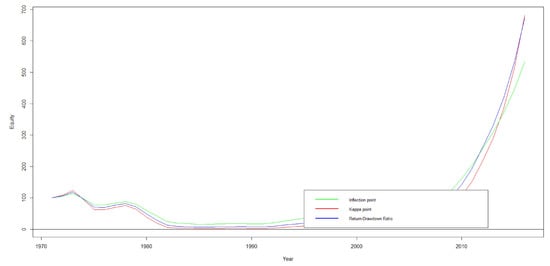
Figure 3.
Equity for -red, -blue, and -green vs. year in x-axis.
3.3. Performance Comparison
To see the effect of the three leverage levels , , and , we conduct a simulation of the following analysis for the 30-year loan for 50-years investment horizon. All three points are calculated using all historical data. Assuming E (equity) starts with 100 in 1970, then deposits are and respectively. We process this for all years from 1971 through 2016 and plot the return from each three points vs. year (in x-axis). The comparison uses two accounting methods to compare the performances assuming:
- Varying equity and;
- Fixed equity.
It turns out that the point performed better in the sense that it has a lower risk than the other two in an increasing pace of Fed interest rates in both methods.
3.3.1. Varying Equity
The varying equity method accumulates the return from the previous year. If there is a profit, then the equity increases, else it decreases. This assumes bank does not distribute profits as dividends to their shareholders or issue any new shares.
The performance test for the varying equity method shows that the bank almost reaches bankruptcy when using point, and that the inflection point performs better in the sense that it has a lower risk compared to the Kelly’s investment size and return–drawdown ratio. Therefore, point is the safest. The following graph (Figure 3) shows how equity changes and also shows that around 1981, equity reduced to almost zero when using point. Figure 4 provides a better view.
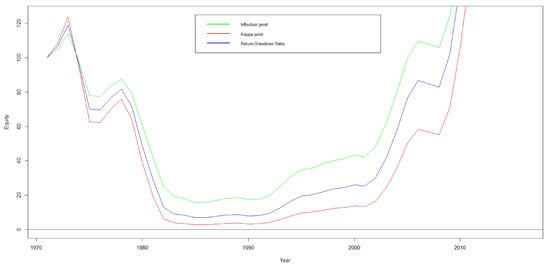
Figure 4.
Equity -red, -blue, and -green vs. year in x-axis (zoom).
3.3.2. Fixed Equity
Graph (Figure 5) shows how individual points perform (year (X) vs. return (Y)) when fixing equity. Negative returns occur in the period of interest rates increase by the Federal Reserve Bank.
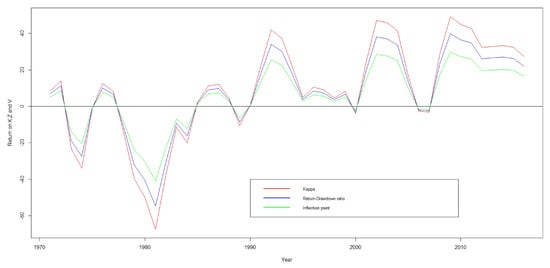
Figure 5.
Returns from -red, -blue, and -green vs. year in x-axis for fixed equity.
It shows that has the highest loss and highest profit where risk is higher and it is the maximum of Kelly’s cumulative return curve. The lowest loss is shown by the point and this confirms that the inflection point is more conservative than the other two. It performs better in the sense of generating a risk-adjusted return.
In the next chapter we discuss sensitivity analysis, how the leverage amount can be changed when the Fed interest rates change, or simply how to switch the allocation between loans of different maturities. Then we compare the performance of these two strategies at the end of the next chapter.
3.4. Comparison with Existing Results
In recent years, many other researchers have also studied the bank loan leverage levels using different approaches. Harding et al. (2013) studied the impact of capital requirements, deposit insurance, and franchise value on a bank’s capital structure assuming that the market value follows a standard geometric Brownian motion process. The maximum leverage reported is and the minimum leverage reported is . Gornall and Strebulaev (2013) used a supply chain model that links the bank with the firm to derive a unified model of the financing supply chain. This research reports a minimum leverage of and a maximum leverage of . Berg and Gider (2017) used a joint sample of banks and non-banks between 1965 and 2013 to analyze the determinants of this leverage difference according to the Basel type definitions. The reported median leverage level is .
The optimal leverage levels this research presents are within the range that are observed in existing literature. The higher values, even in the range of existing literature, almost cause bankruptcy which is shown by simulating the data in the performance test. Among the three allocation levels that we discussed in this section, is too risky.
Our model also allows us to link the level of interest rate risk on mortgages, essentially determined by mortgage maturity, with the optimal leverage level the bank should have.
4. Sensitivity Analysis
The model we presented has considered all the historical data together from 1956 to 2016. During that period there were periods of Fed interest rates increases as well as decreases. Increasing cycles are the most important periods for bankers. In these times, loans which have long maturity (30-year) will have a lower average rate (mean) than shorter maturity loans (15-year), or banks make losses from loans that have long maturity. Therefore, it encourages us to see how the loan size adjusts during the periods of Fed interest rates increases. This gives a strategy that issues more short-term loans and reduces long-term loans. However, the question is by how much? This leads to the derivatives’ analysis of those optimal points w.r.t, the distribution parameter that affects the mean return directly. This will be handled by a sensitivity analysis that discusses the behavior of the derivatives and gives more information about these strategies in this chapter.
A sensitivity analysis is needed to address the issue of: How does the change in parameters impact the optimal leverage level? This chapter focuses on the impact of the change of short-term interest rates on the optimal leverage level. A sound quantitative analysis provides a theoretical foundation for important bank business decisions. However, these issues are mathematically challenging. The available data is limited but can be used to estimate the general leverage level. Unfortunately, they are clearly insufficient to estimate the derivatives numerically.
We seek a continuous distribution that is defined on a bounded interval and negatively skewed (skewness is shown in the histograms of the returns). We use the Kolmogorov–Smirnov, Anderson Darling, and Chi-Squared tests and rank about 30 distributions. It turns out that PERT distribution is among the first five distributions. Also, the PERT distribution is one of which has the above properties and it is widely used in risk analysis. Therefore, we find that the PERT distribution is a suitable distribution for the return data series.
We will discuss the sensitivity of the three types of optimal allocation points with respect to the distribution parameters of the random variable X (aggregated return). The numerical example with the empirical distribution that we used in the previous chapter shows us the most suitable distribution is the PERT distribution. The data has a left-skewed distribution and must be in a bounded continuous interval. The PERT distribution fits the characteristics of the data. The maximum likelihood method is used to estimate parameters when needed.
The pdf of the PERT distribution is given by:
where,
The histograms in Figure 6 were created from the empirical distribution of the aggregated return X. These histograms are negatively skewed in a finite interval. This is consistent with our initial assumption that the data follows PERT distribution with mode “b” as a parameter of the distribution.
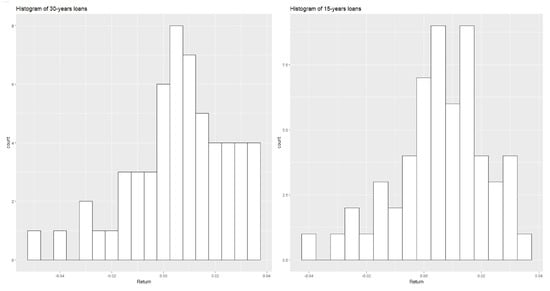
Figure 6.
Histogram of t-year of loans.
It is reasonable to fix the bounds of the interval a and c, and consider the mode b as a variable parameter to analyze the sensitivity of the three leverage levels above with respect to b. i.e., consider the derivatives of the optimal three leverage levels with respect to b. Chopra and Ziemba (1993) observed that the impact of a perturbation in mean to a Kelly type of optimal allocation is much larger than that of variance. Thus, in sensitivity analysis, we focused more on the mean which is directly related to the mode b through (23).
4.1. One Fixed Loan Maturity
We first consider the case that there is only one kind of loan with a fixed maturity.
4.1.1. Kelly’s Point
Let us assume that X has a PERT distribution on whose probability density function is given by Equation (21). Under the assumption that a and c are fixed, the distribution can be characterized by through b. Thus, substituting and in Equation (21),
It follows that,
Notice that the Kelly optimal point is determined by the equation,
4.1.2. Approximations
Exact computation for and eluded us so far. It turns out that approximating up to the second moment is adequate in this particular application. This approximation study is based on our data and the approximation fits into the situation that the data represents. It is of course not practical to model all situations in reality. The approximation is developed under certain conditions, which can be applied to the situation that the data represents and most of the real scenarios.
Let , then using second order Taylor’s expansion around , can be approximated by . Then taking the expectation of , is given by:
Kelly’s original utility function is the expectation of the log while our approximation model is a quadratic function which is concave but not strictly monotone. Fortunately, the monotonicity is only lost after the function reaches its maximum, whereas the interesting leverage levels are all reached before the maximum. This approximation works best when for all . Notice that for so that and , for all . Thus, the approximation is a suitable method for the allocation sizes and as this follows Vince and Zhu (2015) results. The accuracy of these two allocations using the approximation is high when compared with the actual numerical computation.
Figure 7 shows the comparison of the two curves. The expected log-return curve is almost symmetrically concave and closer to the approximate curve if the distribution is symmetric as in the diagram. The lower curve is the approximate curve and the upper curve is the expected log-return curve. Moreover, the skewness of the distribution makes the right side (after the maximum) of the log return curve steeper. Every time, the deviation of approximate curve happens around the maximum point, but before it, they are almost identical. This also shows us the approximations for and are accurate.
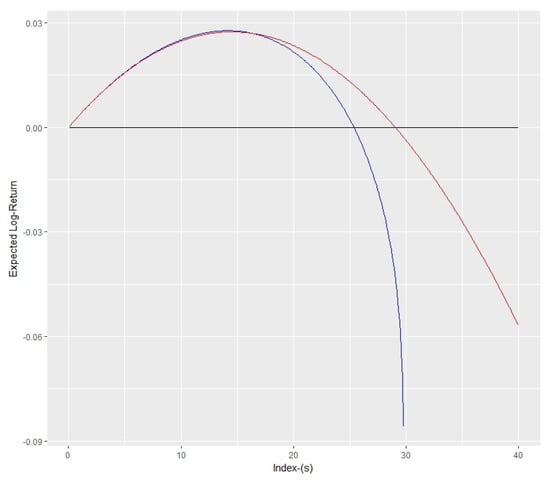
Figure 7.
Expected log return vs. approximated curve.
If the distribution is more skewed, then the two graphs in Figure 7 also significantly deviate from one another. The more skewness, the more deviation. Therefore the approximation works best when the distribution of the return is almost symmetric as in our scenario. Since our analysis is based on the PERT distribution, we will find out the conditions for b (mode) where this analysis is valid.
Table 3 presents the third moment of the random variable and the skewness of the distribution of the historical data. It shows that the third moment is very small and therefore, it is reasonable to ignore the terms beyond the third moment in the approximation.

Table 3.
Skewness of the return distribution.
The existence of satisfies the inequality:
This implies equivalently that:
The approximation is valid only under this condition.
4.1.3. Return–Drawdown Ratio
The return–drawdown ratio, , is determined by Equation (28). It also depends on Q, therefore the notation is introduced here. It follows from the definition that satisfies:
Taking derivative w.r.t in Equation (28) gives Equation (A6) and simplifies to:
as in the Appendix B.3.
4.1.4. Inflection Point
The inflection point is derived by solving Equation (4). Approximately,
Then can be given as:
Then, as noticed from the relationship in the numerical simulation, is true. Now, calculate the derivative of w.r.t :
Details can be found in the Appendix B.4.
The discussion in the above three sections has shown that all three optimal points of leveraging increase as the mode of the distribution increases. The distribution of returns may take negative values as well. Therefore, there is a probability of losing your investment. The investment size should not exceed the capital on hand, i.e., for all . This shows us we should not increase our investment size, , beyond the limits as discussed before. These limits provide guides for the investors to not lose more than what investors have on their hand as capital. To avoid this danger, there should be limits for increasing as well as the other two leverage levels.
This whole discussion is based on an approximation, so we will carry out a sensitivity analysis (by numerical simulation) in Section 4.2 to verify what we observe here by using an approximation.
4.2. Simulation Study
To show the approximation gives a reliable analysis, we created a random sample of returns from a PERT distribution and calculated these three optimal points using 100 different random samples by changing the mode b. For each b, we calculated three optimal points 100 times, creating 100 different random samples. Then we considered the means of all 100 for a particular b.
The graph in Figure 8 shows the result for three optimal points when changing b with the simulation described above.
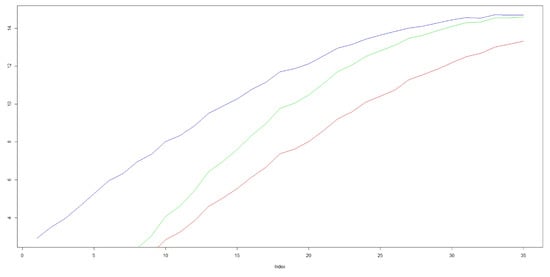
Figure 8.
Simulation of variation of .
Figure 9 shows how point and are increasing functions of b with the bounds of b described in the previous section.
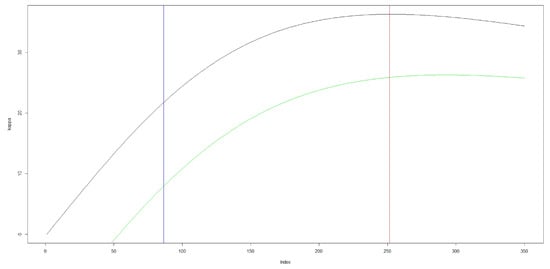
Figure 9.
Variation of .
4.3. Mixed of Loan Maturities in One Model
Next, we discuss the general situation where we consider all types of loans available together as a portfolio. Assume that the allocation proportion is for each loan with maturity i. Assume there are k different types of loans. Then define the total loan balance as follows. Denote as the duration for the loan maturity of the loan and l as the total size issued in every year, which is the same for each year. Then,
Then the total return is:
where,
Similar to as in single loan, the new random variable of return would be:
Details are in the Appendix B.5.
The effect on , and is similar when interest rates change. Therefore the effect on the denominator is approximately constant when interest rates change. The differences of and approximately cancel off the change of effects. Therefore it is reasonable to assume that is approximately linear w.r.t :
where:
Thus,
Kelly’s point gives the solution to the following equation for (approximation) s.
Taking the derivative of Equation (43) w.r.t ,
As in the above equation, Equation (44) can be used to estimate the change of w.r.t .
The optimal return–drawdown ratio is given by solving the following equation:
Taking derivative w.r.t , after cancellations and replacement with estimates,
After substituting approximations and solving for ,
The inflection point is given by solving:
Taking the derivative w.r.t , then replace with estimation,
After substituting approximate derivatives of l,
4.4. Banker’s Strategies
We applied the above analysis to the case that there are two loans of duration, 15-year and 30-year, respectively. The results on Table 1 and Table 2 show that the 15-year loan is safer than 30-year loan in the sense that it has lower risk. Therefore, when interest rates increase we can increase the allocation for the 15-year loan and transfer those amounts, decreasing the allocation of the 30-year loans. Therefore, there are two options that banks can do when interest rates rise:
- Change the leverage size by or;
- Change the allocation sizes, ’s.
To affect the change of leverage size with reallocation the total derivative has to be zero. For example, in the case of Kelly’s point, one solves the following equation:
where and to determine the changes on allocation. Since there are only two different maturities of loans the corresponding changes of and can be found easily from above equation.
Consider the 15-year and the 30-year loan maturities. Then we only have two allocation sizes, which satisfy:
It follows that:
Then we find the percentage of change in the Equation (51), which is a linear relationship between and .
The regression coefficient of average return (vs. Fed interest rates) shows that, on average, when interest rates increase by % then the average return decreases by . For example, if the allocation sizes start with 50% on each maturity, then the allocation change for a 15-year loan (if we use inflection point) for a 50-year investment horizon is (Table 4) per 0.25% increase of Fed fund rates. That means that when Fed interest rates increase by 0.25%, then the new allocation for a 15-year loan should be % and for a 30-year loan, it should be %

Table 4.
Percentage change of 15-year loan allocation when Fed fund rate increases by 0.25%.
4.5. Mixed-Model: Performance Test
Varying Equity
Figure 10 shows how equity changes when using a constant leverage level. We see that point almost causes bankruptcy during the late 1980s.
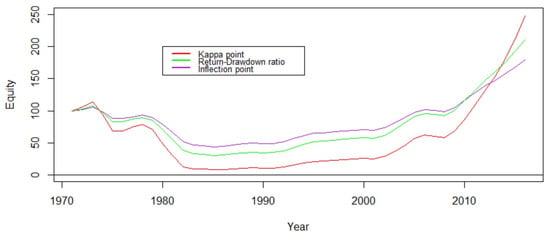
Figure 10.
Equity for -red, -blue, and -green vs. year in x-axis.
Fixing Equity
Figure 11 shows the return when changing the optimal leverage levels when Fed interest rates change. The point again causes the highest loss during the peak of Fed interest rates in the 1980s except at 1982. This is because is too sensitive to change according to interest rates change. Also, we noticed that in the peak points of return curve inflection point gives a higher return than return–drawdown ratio.
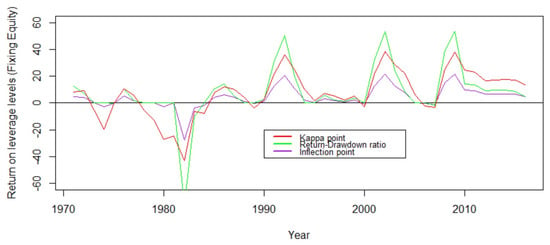
Figure 11.
Return on changing leverage levels -red, -blue, and -green vs. year in x-axis.
In the above case we have seen that inflection point performs better in terms of risk-adjusted return. Therefore, next we will compare the inflection point with different strategies.
Figure 12 shows that changing the total leverage level while fixing the allocation yields a higher return. On the other hand, fixing total leverage level and changing the allocation between loans of different maturities yields lower risk.
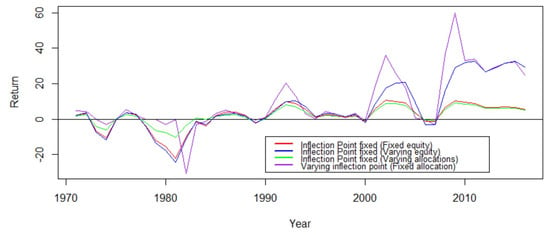
Figure 12.
Return on changing leverage levels -red, -blue, and -green vs. year in x-axis.
5. Conclusions
Testing the growth optimal leverage level (Kelly’s point) on the US mortgage market using historical data leads to almost bankruptcy during the period of 1970–1980, when the short-term interest rate was rapidly increased. The other two are more conservative compared to the Kelly point, with the inflection point as the most conservative among the three. Testing on the same historical data of the US mortgage market with 15- and 30-year fixed rate mortgages showed that both and suggest acceptable levels of leverage. Moreover, backtests on historical data also show that the 15-year loan was more favorable in producing better risk-adjusted returns when compared to the 30-year loan.
When the short-term loan interest rate was rising, the cost of financing long-term mortgages increased too, which chips away the profit margin. By sensitivity analysis we approached an important issue: The adjustment of the loan portfolio to mitigate such risks. Our sensitivity analysis qualitatively showed that the three leverage levels , , and are positively correlated to the return. Furthermore, using regression analysis on historical market data showed that the return was negatively correlated to the short-term interest rate. This means that the bank should reduce the loan portfolio leverage in an environment when the short-term interest rate was increasing and increase leverage level when the short-term interest rate was decreasing. Possible adjustments of the loan portfolios include the adjustment of the leverage level or the adjustment of the allocation into the mix of the 15-year and 30-year loan. The derivative of the point was too large to be stable in practice. On the other hand, the derivative of the point was more reasonable. Indeed, the simulation on historical data showed that adjusting either the leverage level or fixing the leverage level according to the aggregated data yielded better results compared to fixing at the level suggested by the aggregated data and adjusting the allocation between the 15-year and 30-year loan, but the later strategy lowered the risk. Based on our analysis we believe that is a reasonable leverage level for banks mortgage operations. Moreover, adjustment strategies are suggested for the loan operation to deal with different monetary policy environments.
While our analysis provided a new framework to analyze the appropriate level of loan leverages, the analysis was idealized in assuming that the empirical data rich enough to conduct estimates or calibrate the PERT distribution. The sensitivity analysis relied on an approximation using the moments up to the second order. More importantly, in practice a loan portfolio is not liquid. Changing the leverage levels or the allocation is either costly or time consuming. These are important directions for further investigation.
Author Contributions
The three authers contributed equally.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GOP | Growth Optimal Portfolio |
| Fed | Federal Reserve Bank |
Appendix A. Deposit to Equity Ratio
The total equity capital is 1.803 trillion USD according the https://fred.stlouisfed.org/series/USTEQC, and the total deposits are 12.022 trillion USD according to the https://fred.stlouisfed.org/series/DPSACBW027SBOG.
Appendix B. Calculations
Appendix B.1. Total Returns—Single Model
Appendix B.2. Derivative of κ
Taking the derivative with respect to b in Equation (25),
where is the derivative of P w.r.t b, which calculated using log differentiation:
Since:
is an increasing function of b as expected. The rate of increase can be estimated using the expression of .
Appendix B.3. Derivative of ζQ
Since:
we use as an approximation for .
Similarly, we can replace with , and respectively.
Solving for gives:
We can rewrite the denominator as follows:
Notice that the first term of the denominator of the above equation becomes zero, when the inflection point occurs (referring to Equation (4)). Before the inflection point, the expression becomes positive and after it becomes negative. point occurs after the inflection point, therefore the term is always negative at . The second term, is positive because it is before the point where the maximum of the curve occurs. Therefore the denominator is negative. Now we need that numerator to be negative.
Consider the numerator of Equation (A11). If or, equivalently, , the numerator becomes negative. According to historical data, this is not the case for this problem. For the two different loans of maturities, 15 and 30 years, respectively. Therefore we focus on :
Rearrange Equation (A11) as follows:
can be found as:
from the approximation. Then we seek the condition(s) for .
For our bank loan leverage problem, the data shows that always holds. Those values for the two different loans of maturities, 15 and 30 years, are respectively.
If ;
The numerical analysis of historical data shows that whenever the inequality of Equation (27) is satisfied. Thus under the same conditions of existence for , is also an increasing function of b (or equivalently ).
Appendix B.4. Derivative of Inflection Point
Solving the above equation for , an approximate explicit solution can be found for the inflection point (notice that this depends on Q):
The inflection point exist when:
To see how this point varies with respect to the mean (), rewrite Equation (A21) as:
Then, as noticed from the numerical simulation, is true.
Now, calculate the derivative of w.r.t :
As discussed before with the data, it shows that . Since we already know , that means . When the same condition for Equation (27) satisfied, the inflection point will also increase.
Appendix B.5. Mixed of Loan—Derivatives
Distribute of the total loan amount for each of the funding resources and calculate them as follows for equity, deposits and non-core funding respectively:
Then the total return is:
Let us define some notation below to conveniently to write the above equation:
Then,
Let,
Then,
Similarly, define and as follows:
Then the new random variable of return would be:
The effect on , and is similar when interest rates change. Therefore the effect on the denominator is approximately constant when interest rates change. The differences of and approximately cancel off the change of effects. Therefore it is reasonable to assume that is approximately linear w.r.t :
where is as defined in Equation (40). Thus,
Let , be the mean and variance of each and covariance of and respectively. Then,
Use the Taylor’s second order approximation to estimate the effect of changes w.r.t ’s,
Appendix B.5.1. Kelly’s Point (GOP)
Kelly’s point gives the solution to the following equation for s.
Taking the derivative of Equation (A46) w.r.t ,
As in the above equation, Equation (A47) it can be used to estimate the change of w.r.t .
Appendix B.5.2. Return–Drawdown Ratio
The optimal return–drawdown ratio is given by solving the following equation:
Taking derivative w.r.t ,
After cancellations and replacement with estimates,
Let us calculate important derivatives to substitute into the above Equation (A50). Then, when interest change, it estimates the effect of . Following short-hand notations defined for convenience, let be the derivative of w.r.t s at , and the partial derivative of w.r.t at .
Solving for ,
Appendix B.5.3. Inflection Point
The inflection point is given by solving:
Taking the derivative w.r.t ,
then replace with estimation,
Since the approximation is second order, , it needs few more derivatives as follows:
Appendix C. Raw Data
All data are annual averages Federal Reserve Economic Data.
- Economic Research Division, Federal Reserve Bank of St. Louis GS5: 5-year Treasury Constant Maturity Rate, Percent, Annual, Not Seasonally Adjusted.
- MORTGAGE15US: 15-year Fixed Rate Mortgage Average in the United States, Percent, Annual, Not Seasonally Adjusted.
- MORTGAGE30US: 30-year Fixed Rate Mortgage Average in the United States, Percent, Annual, Not Seasonally Adjusted.
References
- Barron, Andrew R., and Thomas M. Cover. 1988. A Bound on the Financial Value of Information. IEEE Transactions of Information Theory 34: 1097–988. [Google Scholar] [CrossRef]
- Bell, Robert M., and Thomas M. Cover. 1980. Competitive Optimality of Logarithmic Investment. Mathematics of Operations Research 5: 161–166. [Google Scholar] [CrossRef]
- Berg, Tobias, and Jasmin Gider. 2017. What Explains the Difference in Leverage between Banks and Non-Banks? Journal of Financial and Quantitative Analysis 52: 2677–702. [Google Scholar] [CrossRef]
- Birge, John R., and Pedro Júdice. 2012. Long-term Bank Balance Sheet Management: Estimation and Simulation of Risk-Factors. Journal of Banking and Finance 37: 4711–20. [Google Scholar] [CrossRef]
- Browne, Sid. 2000. Risk-Constrained Dynamic Active Portfolio Management. Management Science 46: 1188–99. [Google Scholar] [CrossRef]
- Chekhlov, Alexei, Stanislav Uryasev, and Michael Zabarankin. 1993. Drawdown Measure in Portfolio Optimization. International Journal of Theoretical and Applied Finance 8: 13–58. [Google Scholar] [CrossRef]
- Chopra, Vijaya K., and William T. Ziemba. 1993. The Effect of Errors in Mean, Variance and Covariance Estimates on Optimal Portfolio Choice. Journal of Portfolio Management 19: 6–11. [Google Scholar] [CrossRef]
- Cover, Thomas M. 1991. Universal Portfolio. Mathematical Finance 1: 1–29. [Google Scholar] [CrossRef]
- Davis, Mark, and Sébastien Lleo. 2010. Fractional Kelly Strategies for Benchmarked Asset Management. Kelly Capital Growth Investment Criterion 10: 387–409. [Google Scholar]
- Gornall, Will, and Ilya A. Strebulaev. 2013. Financing as a Supply Chain: The Capital Structure of Banks and Borrowers. The National Bureau of Economic Research 43: 127–48. [Google Scholar]
- Grossman, Sanford J., and Zhongquan Zhou. 1993. Optimal investment strategies for controlling drawdowns. Mathematical Finance 3: 241–76. [Google Scholar] [CrossRef]
- Hahm, Joon-ho, Hyun Song Shin, and Kwanho Shin. 2013. Non-Core Bank Liabilities and Financial Vulnerability. Journal of Money, Credit and Banking 45: 3–36. [Google Scholar] [CrossRef]
- Hakansson, Nils H. 1970. Optimal Investment and Consumption Strategies Under Risk for a Class of Utility Functions. Econometrica 38: 587–607. [Google Scholar] [CrossRef]
- Harding, John P., Xiaozhong Liang, and Stephen L. Ross. 2013. Bank Capital Requirements, Capital Structure and Regulation. Journal of Financial Services Research 43: 127–48. [Google Scholar] [CrossRef]
- Kelly, John. L. 1956. A New Interpretation of Information Rate. Bell System Technical Journal 35: 917–26. [Google Scholar] [CrossRef]
- Latane, Henry. A. 1959. Criteria for Choice among Risky Ventures. Journal of Political Economy 67: 144–55. [Google Scholar] [CrossRef]
- MacLean, Leonard C., William T. Ziemba, and George Blazenko. 1992. Growth versus Security in Dynamic Investment Analysis. Management Science 38: 1562–85. [Google Scholar] [CrossRef]
- MacLean, Leonard C., William. T. Ziemba, and Yuming Li. 2005. Time to Wealth Goals in Capital Accumulation. Quantitative Finance 5: 343–55. [Google Scholar] [CrossRef][Green Version]
- MacLean, Leonard C., Edward O. Thorp, and William T. Ziemba. 2010. Good and Bad Properties of Kelly Criterion. In Kelly Capital Growth Investment Criterion. Hackensack: World Scientific, pp. 32–58. [Google Scholar]
- MacLean, Leonard C., Edward. O. Thorp, and William T. Ziemba. 2011. Introduction to the Relationship of Kelly Optimization to Asset Allocation. In Kelly Capital Growth Investment Criterion. Hackensack: World Scientific, pp. 303–6. [Google Scholar]
- MacLean, Leonard C., Edward O. Thorp, and William. T. Zeimba. 2012. The Kelly Capital Growth Investment Criterion. Singapore: World Scientific, vol. 3. [Google Scholar]
- Maier-Paape, Stanislaus, and Qiji Zhu. 2018. A General Framework for Portfolio Theory—Part II: Drawdown risk measures. Risks 6: 76. [Google Scholar] [CrossRef]
- Markowitz, Harry M. 1976. Investment for the Long Run: New Evidence for an Old Rule. Journal of Finance 31: 273–86. [Google Scholar] [CrossRef]
- Ordentlich, Erik, and Thomas M. Cover. 1998. The Cost of Achieving the Best Portfolio in Hindsight. Mathematics of Operations Research 23: 960–82. [Google Scholar] [CrossRef]
- Phelps, Edmund S. 1962. The Accumulation of Risky Capital: A Sequential Utility Analysis. Econometrica 30: 729–43. [Google Scholar] [CrossRef]
- Samuelson, Paul A. 1979. Why We Should Not Make Mean Log of Wealth Big Though Years to Act are Long. Journal of Banking and Finance 3: 305–7. [Google Scholar] [CrossRef]
- Shannon, Claude E. 1948. A Mathematical Theory of Communication. Bell System Technical Journal 27: 379–423. [Google Scholar] [CrossRef]
- Thorp, Edward O. 1971. Portfolio Choice and Kelly Criterion. Proceedings of the Business and Economics Section of the American Statistical Association, Fort Collins, CO, USA, August 23–26; pp. 215–224. [Google Scholar]
- Thorp, Edward O. 2011. Understanding the Kelly Criterion. Kelly Capital Growth Investment Criterion 3: 511–25. [Google Scholar]
- Vince, Ralph, and Qiji Jim Zhu. 2015. Optimal Betting Size for the Game of Blackjack. Risk Journals: Portfolio Management 4: 53–75. [Google Scholar] [CrossRef]
- Ziemba, William T., and Donald B. Hausch. 1986. Betting at the Racetrack. San Luis Obispo: Dr. Z. Investments. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).