1. Introduction
In this paper, we analyze the optimal excess-of-loss reinsurance problem from the insurer’s point of view, under the criterion of maximizing the expected utility of the terminal wealth. It is well known that the reinsurance policies are very effective tools for risk management. In fact, by means of a risk sharing agreement, they allow the insurer to reduce unexpected losses, to stabilize operating results, to increase business capacity and so on. Among the most common arrangements, the proportional and the excess-of-loss contracts are of great interest. The former was intensively studied in
Irgens and Paulsen (
2004);
Liu and Ma (
2009);
Liang et al. (
2011);
Liang and Bayraktar (
2014);
Zhu et al. (
2015);
Brachetta and Ceci (
2019) and references therein. The latter was investigated in these articles: in
Zhang et al. (
2007) and
Meng and Zhang (
2010), the authors proved the optimality of the excess-of-loss policy under the criterion of minimizing the ruin probability, with the surplus process described by a Brownian motion with drift; in
Zhao et al. (
2013) the Cramér-Lundberg model is used for the surplus process, with the possibility of investing in a financial market represented by the Heston model; in
Sheng et al. (
2014) and
Li and Gu (
2013) the risky asset is described by a Constant Elasticity of Variance (CEV) model, while the surplus is modelled by the Cramér-Lundberg model and its diffusion approximation, respectively; finally, in
Li et al. (
2018) the authors studied a robust optimal strategy under the diffusion approximation of the surplus process.
The common ground of the cited works is the underlying risk model, which is the Cramér-Lundberg model (or its diffusion approximation)
1. In the actuarial literature it is of great importance, because it is simple enough to perform calculations. In fact, the claims arrival process is described by a Poisson process with constant intensity (or a Brownian motion, in the diffusion model). Nevertheless, as noticed by many authors (e.g.,
Grandell (
1991);
Hipp (
2004)), it needs generalization in order to take into account the so called
size fluctuations and
risk fluctuations, i.e., variations of the number of policyholders and modifications of the underlying risk, respectively.
The main goal of our work is to extend the classical risk model by modelling the claims arrival process as a marked point process with dual-predictable projection affected by an exogenous stochastic process Y. More precisely, both the intensity of the claims arrival process and the claim size distribution are influenced by Y. Thanks to this environmental factor, we achieve a reasonably realistic description of any risk movement. For example, in automobile insurance Y may describe weather conditions, road conditions, traffic volume and so on. All these factors usually influence the accident probability as well as the damage size.
Some noteworthy attempts in that direction can be found in
Liang and Bayraktar (
2014) and
Brachetta and Ceci (
2019), where the authors studied the optimal proportional reinsurance. In the former, the authors considered a Markov-modulated compound Poisson process, with the (unobservable) stochastic factor described by a finite state Markov chain. In the latter, the stochastic factor follows a general diffusion. In addition, in
Brachetta and Ceci (
2019) the insurance and the reinsurance premia are not evaluated by premium calculation principles (see
Young (
2006)), because they are stochastic processes depending on
Y. In our paper, we extend further the risk model, because the claim size distribution is influenced by the stochastic factor, which is described by a diffusion-type stochastic differential equation (SDE). In addition, we study a different reinsurance contract, which is the excess-of-loss agreement.
To the best of our knowledge stochastic risk factor models in insurance have not been considered so far. This is in contrast with financial literature where risky asset dynamics affected by exogenous stochastic factors have been largely considered, see for instance
Ceci (
2009);
Ceci and Gerardi (
2009,
2010);
Zariphopoulou (
2009) and
Ceci (
2012).
In our model the insurer is also allowed to lend or borrow money at a given interest rate
r. During recent years, negative interest rates drew the attention of many authors. For example, since June 2016 the European Central Bank (ECB) fixed a negative Deposit facility rate, which is the interest banks receive for depositing money within the ECB overnight. Presently, it is
. As a consequence, in our framework
. We point out that there is no loss of generality due to the absence of a risky asset, because as long as the insurance and the financial markets are independent (which is a standard hypothesis in non-life insurance), the optimal reinsurance strategy turns out to depend only on the risk-free asset (see
Brachetta and Ceci (
2019) and references therein). As a consequence, the optimal investment strategy can be eventually obtained using existing results in the literature.
The paper is organized as follows: in
Section 2, we formulate the model assumptions and describe the maximization problem; in
Section 3 we derive the Hamilton-Jacobi-Bellman (HJB) equation; in
Section 4, we investigate the candidate optimal strategy, which is suggested by the HJB derivation; in
Section 5, we provide the verification argument with a probabilistic representation of the value function; finally, in
Section 6 we perform some numerical simulations.
2. Model Formulation
Let be a complete probability space endowed with a filtration which satisfies the usual conditions, where is the insurer’s time horizon. We model the insurance losses through a marked point process with local characteristics influenced by an environment stochastic factor . Here, the sequence describes the claim arrival process and the corresponding claim sizes. Precisely, , , are stopping times such that a.s. and , , are -random variables such that , is -measurable.
The stochastic factor
Y is defined as the unique strong solution to the following SDE:
where
is a standard Brownian motion on
. We assume that the following conditions hold true:
We will denote by the natural filtration generated by the process Y.
The random measure corresponding to the losses process
is given by
where
denotes the Dirac measure located at point
. We assume that its
-dual predictable projection
has the form
where
is such that , is a distribution function, with ;
is a strictly positive measurable function.
In the sequel, we will assume the following integrability conditions:
and
According to the definition of dual predictable projection, for every nonnegative,
-predictable and
-indexed process
we have that
2In particular, choosing
with
any nonnegative
-predictable process
i.e., the claims arrival process
is a point process with stochastic intensity
.
Now we give the interpretation of
as conditional distribution of the claim sizes
3.
Proposition 1. and the following equality holds:where is the strict past of the σ-algebra generated by the stopping time : This means that in our model both the claim arrival intensity and the claim size distribution are affected by the stochastic factor
Y. This is a reasonable assumption; for example, in automobile insurance
Y may describe weather, road conditions, traffic volume, and so on. For a detailed discussion of this topic see also
Brachetta and Ceci (
2019).
Remark 1. Let us observe that for any -predictable and -indexed process such thatthe processturns out to be an -martingale. If in additionthen is a square integrable -martingale and Moreover, the predictable covariation process of is given bythat is is an -martingale4.
In this framework we define the cumulative claims up to time
as follows
and the insurer’s reserve process is described by
where
is the initial wealth and
is a nonnegative
-adapted process representing the gross insurance risk premium. In the sequel we assume
, for a suitable function
such that
. Let us notice that Equation (
7) implies that
Now we allow the insurer to buy an excess-of-loss reinsurance contract. By means of this agreement, the insurer chooses a retention level
and for any future claim the reinsurer is responsible for all the amount which exceeds that threshold
(e.g.,
means full reinsurance). For any dynamic reinsurance strategy
, the insurer’s surplus process is given by
where
is a nonnegative
-adapted process representing the reinsurance premium rate. In addition, we suppose that the following assumption holds true.
Assumption 1. (Excess-of-loss reinsurance premium) Let us assume that for any reinsurance strategy the corresponding reinsurance premium process admits the following representation:where is a continuous function in α, with continuous partial derivatives in , such that - 1.
for all , since the premium is increasing with respect to the protection level;
- 2.
, because the cedant is not allowed to gain a profit without risk.
In the rest of the paper, should be intended as a right derivative. Moreover, we assume that Assumption 1 formalizes the minimal requirements for a process
to be a reinsurance premium. In the next examples we briefly recall the most famous premium calculation principles, because they are widely used in optimal reinsurance problems solving. In
Appendix B the reader can find a rigorous derivation of the formulas (
10) and (
11) below.
Example 1. The most famous premium calculation principle is the expected value principle (abbr. EVP)5. The underlying conjecture is that the reinsurer evaluates her premium in order to cover the expected losses plus a load which depends on the expected losses. In our framework, under the EVP the reinsurance premium is given by the following expression:for some safety loading .
Example 2. Another important premium calculation principle is the variance premium principle (abbr. VP). In this case, the reinsurer’s loading is proportional to the variance of the losses. More formally, the reinsurance premium admits the following representation:for some safety loading .
Furthermore, the insurer can lend or borrow money at a fixed interest rate . More precisely, every time the surplus is positive, the insurer lends it and earns interest income if (or pays interest expense if ); on the contrary, when the surplus becomes negative, the insurer borrows money and pays interest expense (or gains interest income if ).
Under these assumptions, the total wealth dynamic associated with a given strategy
is described by the following SDE:
It can be verified that the solution to (
12) is given by the following expression:
Our aim is to find the optimal strategy
in order to maximize the expected exponential utility of the terminal wealth, that is
where
is the risk-aversion parameter and
is the set of all admissible strategies as defined below.
Definition 1. We denote by the set of all admissible strategies, that is the class of all nonnegative -predictable processes . With the notation we refer to the same class, restricted to the strategies starting from .
Remark 3. We need additional integrability conditions in order to ensure that under (full reinsurance) and (null reinsurance) the expected utility is finite. Precisely, under conditionwe get thatand underwith K given in (14), we have that In the next proposition we give a sufficient condition for Equation (
17).
Proposition 2. Assume that there exists an integrable function such thatwhere the constant K is given in (14). Then Equation (17) is fulfilled.
Proof. Since
is a pure-jump process, we have that
Taking the expectation, by Equation (
8) we get that
Applying Gronwall’s lemma we obtain that
□
As usual in stochastic control problems, we focus on the corresponding dynamic problem:
where
denotes the insurer’s wealth process starting from
evaluated at time
T.
3. HJB Formulation
In order to solve the optimization problem (
19), we introduce the
value function associated with it, that is
This function, if sufficiently regular, is expected to solve the Hamilton-Jacobi-Bellman (HJB) equation:
where
denotes the Markov generator of the couple
associated with a constant control
. In what follows, we denote by
the class of all bounded functions
, with
, with bounded first order derivatives
and bounded second order derivatives with respect to the spatial variables
.
Lemma 1. Let be a function in . The Markov generator of the stochastic process for all constant strategies is given by the following expression: Proof. For any
, applying Itô’s formula to the stochastic process
, we get the following expression:
where
is defined in (
22) and
In order to complete the proof, we have to show that
is an
-martingale. For the first term, we observe that
because the partial derivative is bounded and using the assumption (
2). For the second term, it is sufficient to use the boundedness of
f and the condition (
6). □
Remark 4. Since the couple is a Markov process, any Markovian control is of the form , where denotes a suitable function. The generator associated with a general Markovian strategy can be easily obtained by replacing α with in (
22).
In order to simplify our optimization problem, we present a preliminary result.
Remark 5. Let be an integrable function such that . For any , the following equation holds true:where . In fact, by integration by parts we get that Now let us consider the ansatz , which is motivated by the following proposition.
Proposition 3. Let us suppose that there exists a function solution to the following Cauchy problem:with final condition , , where Then the functionsolves the HJB problem given in (21).
Proof. From the expression (
26) we can easily verify that
By Remark 5, taking
, we can rewrite the last integral in this more convenient way:
Now we define
by means of the Equation (
25), obtaining the following equivalent expression:
Taking the infimum over
, by (
24) we find out the PDE in (
21). The terminal condition in (
21) immediately follows by definition. □
The previous result suggests to focus on the minimization of the function (
25), that is the aim of the next section.
4. Optimal Reinsurance Strategy
In this section, we study the following minimization problem:
where
is defined in (
25).
In particular, we provide a complete characterization of the optimal reinsurance strategy. In the sequel we assume .
Proposition 4. Let us suppose that is strictly convex in and let us define the set as follows: If the equationadmits at least one solution in for any , denoted by , then the minimization problem (27) admits a unique solution given by Proof. The function
is continuous in
by definition (see Assumption 1) and for any
its derivative is given by the following expression:
Since is convex in by hypothesis, if then , and , because the derivative is increasing in and there is no stationary point in . Else, if then , and coincides with the unique stationary point of , which is . Let us notice that it exists by hypothesis and it is unique because is strictly convex. □
By the previous proposition, we observe that is an important threshold for the insurer: as long as the marginal cost of the full reinsurance falls in the interval , the optimal choice is full reinsurance.
Unfortunately, it is not always easy to check whether
is strictly convex in
or not. In the next result such an hypothesis is relaxed, while the uniqueness of the solution to (
29) is required.
Proposition 5. Suppose that Equation (29) admits a unique solution for any . Moreover, let us assume that Then the minimization problem (27) admits a unique solution given by (
30).
Proof. Recalling the proof of Proposition 4, if
then
and
. For any
, by hypothesis there exists a unique stationary point
. By simple calculations, using (
32) we notice that
hence
is the unique minimizer and this completes the proof. □
The next result deals with the existence of a solution to (
29). In particular, it is sufficient to require that the claim size distribution is heavy-tailed, which is a relevant case in non-life insurance (see
Rolski et al. (
1999), chp. 2), plus a technical condition for the reinsurance premium.
Proposition 6. Let us assume that the reinsurance premium is such that6and the claim size distribution is heavy-tailed in this sense: Then, for any , the Equation (29) admits at least one solution in .
Proof. The following property of heavy-tailed distributions is a well known implication of our assumption:
Hence, by Equation (
31), for any
On the other hand, we know that
As a consequence, being continuous in , there exists such that . □
Now we turn the attention to the other crucial hypothesis of Proposition 4, which is the convexity of . The reader can easily observe that the reinsurance premium convexity plays a central role.
Proposition 7. Suppose that the reinsurance premium is convex in and for some function such that . Then the function defined in (25) is strictly convex in .
Proof. Recalling the expression (
25), it is sufficient to prove the convexity of the following term:
For this purpose, let us evaluate its second order derivative:
Now the term in brackets is
The proof is complete. □
By Proposition 1, the hypothesis on the claim sizes distribution above may be read as assuming that the claims are exponentially distributed conditionally to Y.
4.1. Expected Value Principle
Now we investigate the special case of the expected value principle introduced in Example 1.
Proposition 8. Under the EVP (see Equation (10)), the optimal reinsurance strategy is given by Proof. Using Remark 5, we can rewrite the Equation (
10) as follows:
As a consequence, we have that
For
, we have that
hence
and by Proposition 4 the minimizer belongs to
. Now we look for the stationary points, i.e., the solutions to the Equation (
29), that in this case reads as follows:
Solving this equation, we obtain the unique solution given by (
33). In order to prove that it coincides with the unique minimizer to (
27), it is sufficient to show that
For this purpose, observe that
The proof is complete. □
Remark 6. Formula (33) was found by Zhao et al. (2013) (see eq. 3.31, p. 508). We point out that it is a completely deterministic strategy. This fact is crucially related to the use of the EVP rather than the underlying model; in fact, in Zhao et al. (2013) the authors considered the Cramér-Lundberg model under the EVP7.
From the economic point of view, by Equation (
33) it is easy to show that the optimal retention level is decreasing with respect to the interest rate and the risk-aversion; on the contrary, it is increasing with respect to the reinsurer’s safety loading. In addition, the sensitivity with respect to the time-to-maturity depends on the sign of
r.
Another relevant aspect of (
33) is that it is independent of the claim size distribution. To the authors this result seems quite unrealistic. In fact, any subscriber of an excess-of-loss contract is strongly worried about possibly extreme events, hence the claims distribution is expected to play an important role.
4.2. Variance Premium Principle
This subsection is devoted to derive an optimal strategy under the variance premium principle (see Example 2).
Proposition 9. Let us suppose that is strictly convex in andfor some (eventually ).
Under the VP (see Equation (11)) the optimal reinsurance strategy is the unique solution to the following equation: Proof. The proof is based on Proposition (4). By Equation (
11) we get its derivative:
It is clear that the set
defined in (
28) is empty, because for any
Hence the minimizer should coincide with the unique stationary point of
, i.e., the solution to (
36). In order to prove it, we need to ensure the existence of a solution to (
36). For this purpose, we notice that on the one hand
On the other hand, for
, by (
35) we get
As a consequence, by the continuity of there exists a point such that . Such a solution is unique because is strictly convex by hypothesis. □
Conversely to Proposition 8, the optimal retention level given in Proposition 9 is still dependent on the stochastic factor Y. Such a dependence is spread through the claim size distribution.
Remark 7. We observe that any heavy-tailed distribution (see the proof of Proposition 6) satisfies the condition (35) with .
Now we specialize the variance premium principle to conditionally exponentially distributed claims.
Proposition 10. Under the VP, suppose that for some function such that . The optimal reinsurance strategy is given by Proof. By the proof of Proposition 9, we know that under VP
. Now, under our hypotheses, by Equation (
31) we readily get
The equation
admits a unique solution, given by Equation (
37). At this point
, the function
is strictly convex, because
It follows that
is the unique minimizer by Proposition
30. □
Contrary to Equation (
33), the explicit formula (
37) keeps the dependence on the stochastic factor
Y. In addition, the following result holds true.
Remark 8. Suppose that for some function such that . We consider two different reinsurance safety loadings , referring to the EVP and VP, respectively. Moreover, let us denote by and the optimal retention level under the EVP and VP, given in Equations (33) and (37), respectively. It is easy to show that From the practical point of view, as long as the stochastic factor fluctuations result in a rate parameter higher than the threshold , the optimal retention level evaluated through the expected value principle turns out to be larger than the variance principle.
6. Numerical Results
In this section, we show some numerical results, mostly based on Propositions 8 and 10. We assumed the following dynamic of the stochastic factor
Y for performing simulations:
The
-dual predictable projection
(see Equation (
5)) is determined by these functions:
The parameters are set according to
Table 1 below.
The SDEs are approximated through a classical Euler’s scheme with steps length , while the expectations are evaluated by means of Monte Carlo simulations with parameter M.
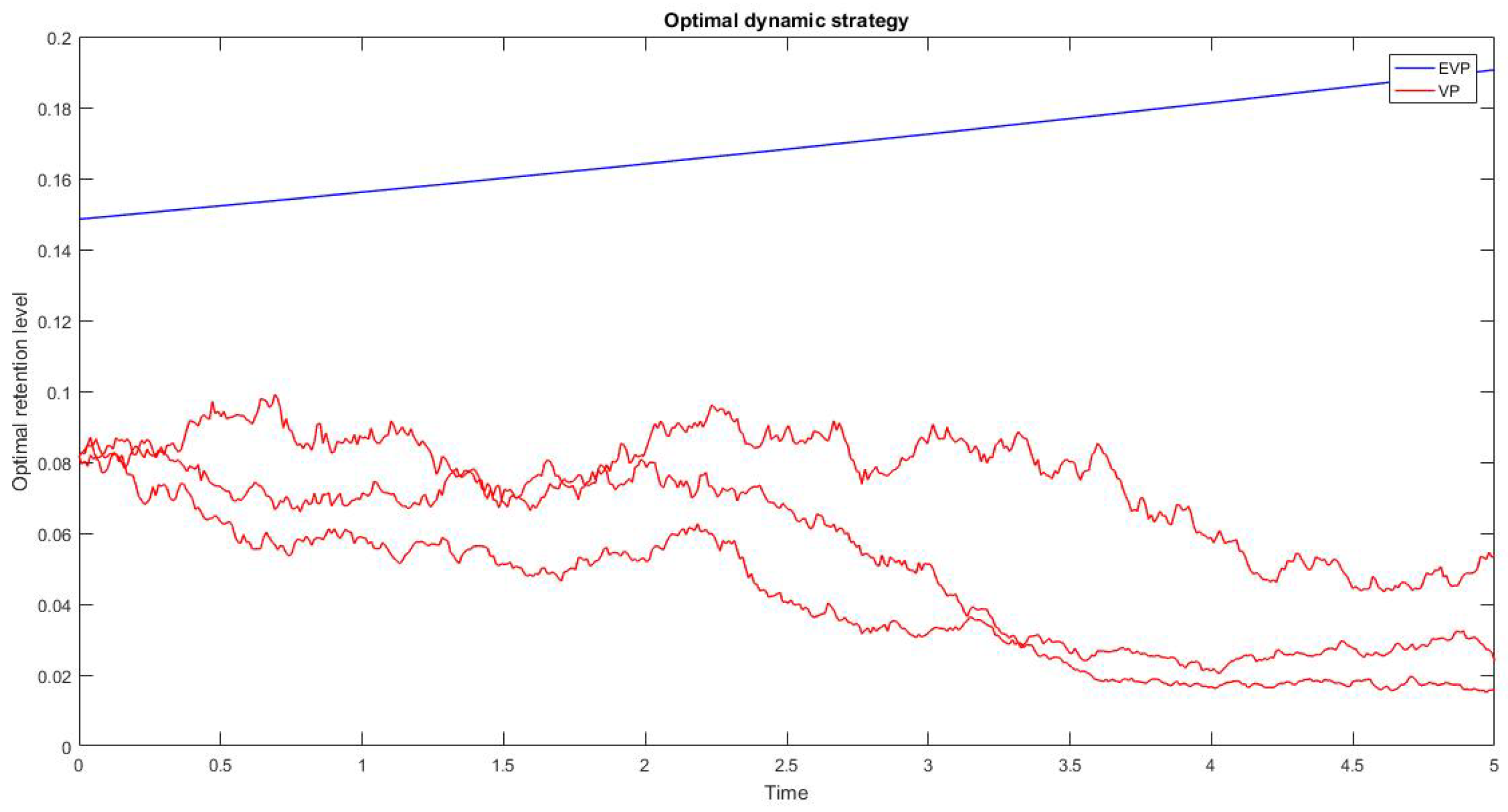
In
Figure 1 we show the dynamic strategies under EVP and VP, computed by the Equations (
33) and (
37), respectively.
In
Figure 2 we start the sensitivity analysis investigating the effect of the risk aversion parameter on the optimal strategy at time
. As expected, there is an inverse relationship. Notice that for high values of
the two strategies tend to the same level.
Figure 3 refers to the sensitivity analysis with respect to the reinsurance safety loading
. When
the strategies coincide (because the premia coincide), then they diverge for increasing values of
.
In
Figure 4 we observe that the distance between the retention levels in the two cases is larger when
and it decreases as long as
r increases. Nevertheless, even for positive values of the risk-free interest rate the distance is not negligible (see the pictures above, with
).
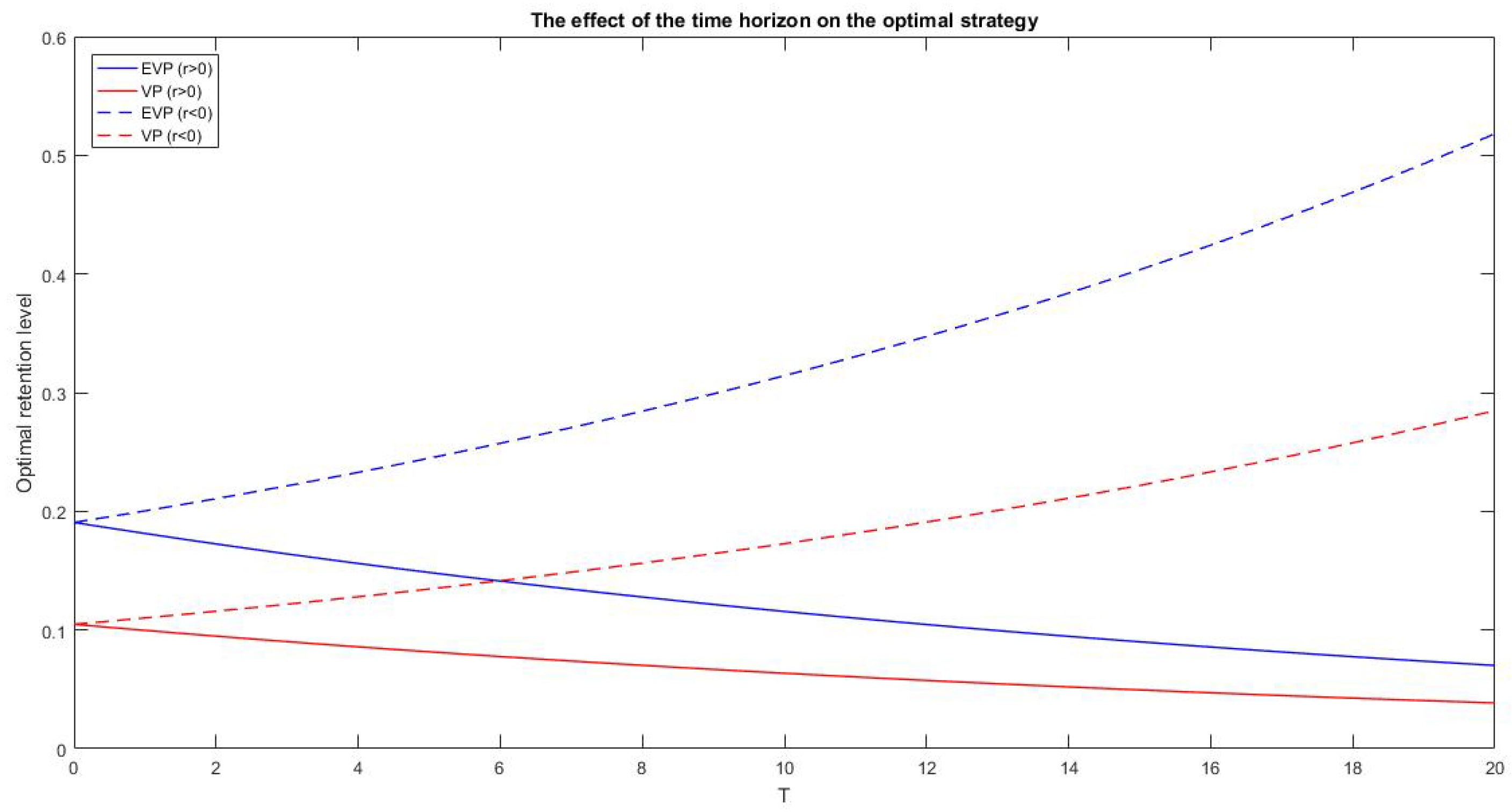
In
Figure 5 we study the response of the optimal strategy to variations of the time horizon. The two cases exhibit the same behavior, which is strongly influenced by the sign of the interest rate. In fact, if
the retention level increases with the time horizon, while if
the optimal strategy decreases with
T.
Finally, thanks to Proposition 11 we are able to numerically approximate the value function by simulating the trajectories of
Y. The graphical result (under VP) is shown in
Figure 6 below.