Imbalance Market Real Options and the Valuation of Storage in Future Energy Systems

Abstract

As decarbonisation progresses and conventional thermal generation gradually gives way to other technologies including intermittent renewables, there is an increasing requirement for system balancing from new and also fast-acting sources such as battery storage. In the deregulated context, this raises questions of market design and operational optimisation. In this paper, we assess the real option value of an arrangement under which an autonomous energy-limited storage unit sells incremental balancing reserve. The arrangement is akin to a perpetual American swing put option with random refraction times, where a single incremental balancing reserve action is sold at each exercise. The power used is bought in an energy imbalance market (EIM), whose price we take as a general regular one-dimensional diffusion. The storage operator’s strategy and its real option value are derived in this framework by solving the twin timing problems of when to buy power and when to sell reserve. Our results are illustrated with an operational and economic analysis using data from the German Amprion EIM.

1. Introduction

In today’s electric grids, power system security is managed in real time by the system operator, who coordinates electricity supply and demand in a manner that avoids fluctuations in frequency or disruption of supply (see, for example, New Zealand Electricity Authority 2016). In addition, the system operator carries out planning work to ensure that supply can meet demand, including the procurement of non-energy or ancillary services such as operating reserve, the capacity to make near real-time adjustments to supply and demand. These services are provided principally by network solutions such as the control of large-scale generation, although from a technical perspective they can also be provided by smaller, distributed resources such as demand response or energy storage (National Grid ESO 2019a; Xu et al. 2016). Such resources have strongly differing operating characteristics: when compared to thermal generation, for example, energy storage is energy limited but can respond much more quickly. Storage also has important time linkages, since each discharge necessitates a corresponding recharge at a later time.

The coming decades are expected to bring a period of “energy transition” in which markets for ancillary services will evolve, among other highly significant changes to generation, consumption and network operation. The UK government, for example, has an ambition that “new solutions such as storage or demand-side response can compete directly with more traditional network solutions” (UK Office of Gas and Electricity Markets 2017, p. 29). In harmony, the UK System Operator National Grid has recently declared its intention to “create a marketplace for balancing that encourages new and existing providers, and all new technology types” (National Grid ESO 2019b). In anticipation of changes such as these, we will examine the participation of autonomous energy storage in a future marketplace for balancing.

Operating reserve is typically procured via a two-price mechanism, with a reservation payment plus an additional utilisation payment each time the reserve is called for (Ghaffari and Venkatesh 2013; Just and Weber 2008). Since the incentivisation and efficient use of operating reserve for system balancing is of increasing importance with growing penetration of variable renewable generation (King et al. 2011), several system operators have recently introduced real-time energy imbalance markets (EIMs) in which operating reserve is pooled, including in Germany (Ocker and Ehrhart 2017) and California (Lenhart et al. 2016; Western EIM 2019). Such markets typically involve the submission of bids and offers from several providers for reserves running across multiple time periods, which are then accepted, independently in each period, in price order until the real-time balancing requirement is met. As one provider can potentially be called upon over multiple consecutive periods, this reserve procurement mechanism is not well suited to energy-limited reserves such as energy storage. However, storage-oriented solutions are being pioneered in a number of countries including a recent tender by the National Grid in the UK (National Grid ESO 2019a) and various trials by state system operators in the US (Xu et al. 2016).

This paper considers operating reserve contracts for energy limited storage devices such as batteries. In contrast to previous work on the pricing and hedging of energy options where settlement is financial (see, for example, Benth et al. (2008) and references therein), we take account of the physical settlement required in system balancing, considering also the limited energy and time linkages of storage. The potential physical feedback effects of such contracts are investigated by studying the operational policy of the storage or battery operator. To address the limited nature of storage, the considered reserve contract is for a fixed quantity of energy. In this way, each contract written can be physically covered with the appropriate amount of stored energy. We consider a simple arrangement where the system operator sets the contract parameters, namely the premia (the reservation and utilisation payments) plus an EIM price level $x^{*}$ at which the energy is delivered. That is, rather than being the outcome of a price formation process, these parameters are set administratively. Our analysis thus focuses exclusively on the timing of the battery operator’s actions. This dynamic modelling contrasts with previous economic studies of operating reserve in the literature, which have largely been static (Just and Weber 2008).

To quantify the economic opportunity for the storage operator, we use real options analysis. Real Options analysis is the application of option pricing techniques to the valuation of non-financial or ‘real’ investments with flexibility (Borison 2005; Dixit and Pindyck 1994). Here, the energy storage unit is the real asset, and is coupled with the timing flexibility of the battery operator, who observes the EIM price in real time. The arrangement may be viewed as providing the battery operator with a real perpetual American put option on the reserve contract described above. This option is either of swing type (called the lifetime problem in this paper) or of single exercise type (the single problem). The feature that sets it apart from the existing literature on swing options is the random refraction time (cf. Carmona and Touzi 2008).

A key question in Real Options analyses is the specification of the driving randomness (Borison 2005). In this paper, we model the EIM price to resemble the historical statistical dynamics of imbalance prices. In common with electricity spot prices and commodity prices more generally but unlike the prices of financial assets, imbalance prices typically exhibit significant mean reversion (Ghaffari and Venkatesh 2013; Pflug and Broussev 2009).

To avoid trivial cases, we impose the following, mild, sustainability conditions on the arrangement:

S1. 

The battery operator has a positive expected profit from the arrangement.

S2. 

The reserve contract cannot lead to a certain financial loss for the system operator.

Condition S1 is also known as the individual rationality or participation condition (Fudenberg et al. 1991). While the battery operator is assumed to be a profit maximiser, the system operator may engage in the arrangement for wider reasons than profit maximisation. To acknowledge the potential additional benefits provided by batteries, for example in providing response quickly and without direct emissions, condition S2 is less strict than individual rationality.

By considering reserve contracts for incremental capacity (defined as an increase in generation or equivalently a decrease in load), we are able to provide complete solutions whose numerical evaluation is straightforward. Contracts for a decrease in generation, or an increase in load, lead to a fundamentally different set of optimisation problems which have been partially solved by Szabó and Martyr (2017).

This study extends earlier work (Moriarty and Palczewski 2017) with two important differences. Firstly, the dynamics of the imbalance price is described there by an exponential Brownian motion. In the present paper, by employing a different methodological approach, we obtain explicit results for mean-reverting processes (and also other general diffusions) which better describe the statistical properties of imbalance prices (Ghaffari and Venkatesh 2013; Pflug and Broussev 2009). Secondly, the present paper takes into account deterioration of the store. Without this feature, it was found that the value of storage is either very small (corresponding roughly to writing a single reserve contract) or infinite.

Through a benchmark case study, we obtain the following economic recommendations. Firstly, investments in battery storage to provide reserve will be profitable on average for a wide range of the contract parameters. Secondly, the EIM price level $x^{*}$ at which energy is delivered is an important consideration. This is because, as $x^{*}$ increases, the EIM price reaches $x^{*}$ significantly less frequently and the reserve contract starts to provide cover for rare events, resulting in infrequent power delivery and low utilisation of the battery, which may make the business case unattractive. These observations suggest that the contractual arrangement studied in this paper is more suitable for the frequent balancing of less severe imbalance.

1.1. Objectives

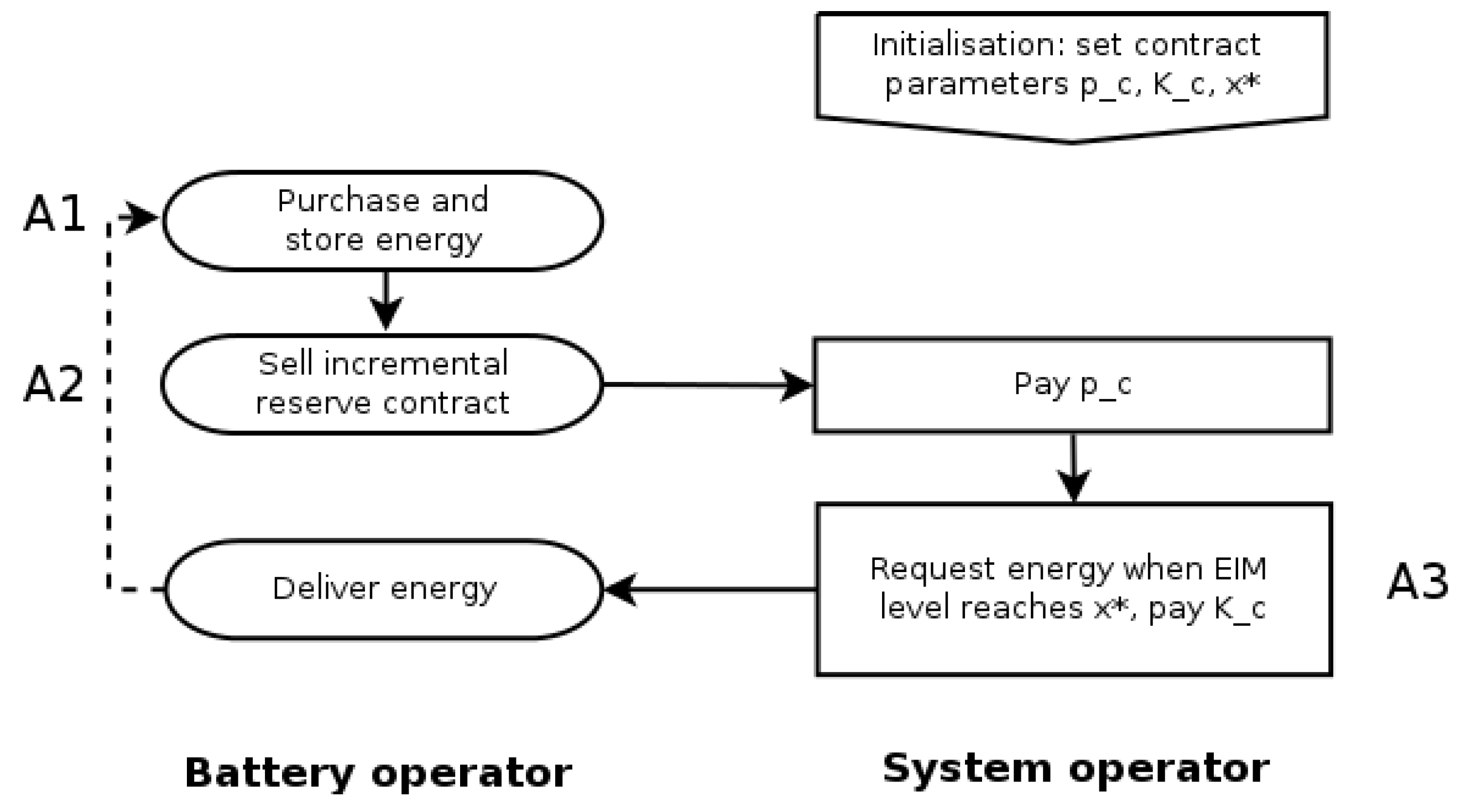
Given the model parameters $x^{*}$, $p_c\ge 0$ and $K_c\ge 0$, we wish to analyse the actions A1–A3 below (a graphical description of this sequence of actions is provided in Figure 1):

A1

The battery operator selects a time to purchase a unit of energy on the EIM and stores it.

A2

With this physical cover in place, the battery operator then chooses a later time to sell the incremental reserve contract to the system operator in exchange for the initial premium $p_c$.

A3

The system operator requests delivery of power when the EIM price X first lies above the level $x^{*}$ and immediately receives the contracted unit of energy in return for the utilisation payment $K_c$.

Thus, the system operator obtains incremental reserve from the arrangement in preference to using the EIM, when the EIM price is higher than the level $x^{*}$ specified by the system operator. When the sequence A1–A3 is carried out once, we refer to this as the single problem; when it is repeated indefinitely back-to-back, we refer to it as the lifetime problem.

In the lifetime problem, because storage is energy limited, action A3 must be completed before the sequence A1–A3 can begin again. Thus, if the arrangement is considered as a real swing put option, the time between A2 and A3 is a random refraction period during which no exercise is possible. Note that, after action A3, the battery operator will perform action A1 again when the EIM price has fallen sufficiently. Mathematically, therefore, we have the following objectives:

M1

For the single and lifetime problems, find the highest EIM price $\check{x}$ at which the battery operator may buy energy when acting optimally.

M2

For the single and lifetime problems, find the expected value of the total discounted cash flows (value function) for the battery operator corresponding to each initial EIM price $x\ge \check{x}$.

We also aim to provide a straightforward numerical procedure to explicitly calculate $\check{x}$ and the value function (for $x\ge \check{x}$) in the lifetime problem.

1.2. Approach and Related Work

We take the EIM price to be a continuous time stochastic process ${\left(X_t\right)}_{t\ge 0}$. Since markets operate in discrete time, this is an approximation, made for analytical tractability. Nevertheless, it is consistent with the physical fact that the system operator’s system balancing challenge is both real-time and continuous.

Mathematically, the problem is one of choosing two optimal stopping times corresponding to the two actions A1 and A2, based on the evolution of the stochastic process X (The reader is refered to Peskir and Shiryaev (2006, chp. 1) for a thorough presentation of optimal stopping problems). We centre our solution techniques around ideas of Beibel and Lerche (2000), who characterise optimal stopping times using the Laplace transforms of first hitting times for the process X (see, for example, Borodin and Salminen (2012, sec. 1.10)). Methods and results from the single problem are then combined with a fixed point argument for the lifetime analysis.

Our methodological results feed into a growing body of research on timing problems in trading. In a financial context, Zervos et al. (2013) optimise the performance of “buy low, sell high” strategies, using the same Laplace transforms to provide a candidate value function, which is later verified as a solution to certain quasi-variational inequalities. An analogous strategy in an electricity market using hydroelectric storage is studied in Carmona and Ludkovski (2010) where the authors use Regression Monte Carlo methods to approximately solve the dynamic programming equations for a related optimal switching problem. Our results differ from the above papers in two aspects. Our analysis is purely probabilistic, leading to arguments that do not refer to the theory of PDEs and quasi-variational inequalities. Secondly, our characterisation of the value function and the optimal policy is explicit up to a single, one-dimensional nonlinear optimisation, which, as we demonstrate in an empirical experiment, can be performed in milliseconds using standard scientific software. Related to our lifetime analysis, Carmona and Dayanik (2008) apply probabilistic techniques to study the optimal multiple-stopping problem for a general linear regular diffusion process and reward function. However, the latter work deals with a finite number of option exercises in contrast to our lifetime analysis which addresses an infinite sequence of exercises via a fixed point argument. Our work thus yields results with a significantly simpler and more convenient structure.

The contracts we consider have features in common with the reliability options used in Colombia, Ireland and the ISO New England market and currently being introduced in Italy (Mastropietro et al. 2018). Reliability options pay an initial premium to a generator, usually require physical cover, and have a reference market price and a strike price that plays a similar role to $x^{*}$. Typically, the strike price is set at the variable cost of the technology used to satisfy demand peaks, and the generator is contracted to pay back the difference between the market price and the strike price in periods when energy is delivered and the market price is higher. However, instead of being designed for system balancing, the purpose of reliability options is to ensure sufficient investment in generation capacity.

The remainder of the paper is organised as follows. The mathematical formulation and main tools are developed in Section 2. In the results of Section 3, we show that, for a range of price processes X incorporating mean reversion, solutions for all initial values x can be obtained. Furthermore, an empirical illustration using data from the German Amprion system operator is provided and qualitative implications are drawn, while Section 5 presents the conclusions. Auxiliary results are collected in the appendices.

2. Methodology

2.1. Formulation and Preliminary Results

In this section, we characterise the real option value in the single and lifetime problems using the theory of regular one-dimensional diffusions. Denoting by ${\left(W_t\right)}_{t\ge 0}$ a standard Brownian motion, let $X={\left(X_t\right)}_{t\ge 0}$ be a (weak) solution of the stochastic differential equation:

$$d{X}_t=\mu \left(X_t\right)dt+\sigma \left(X_t\right)d{W}_t,$$

(1)

with boundaries $a\in \mathbb{R}\cup \{-\infty \}$ and $b\in \mathbb{R}\cup \{\infty \}$. The solution of this equation with the initial condition $X_0=x$ defines a probability measure ${\mathbb{P}}^x$ and the related expectation operator ${\mathbb{E}}^x$. We assume that the boundaries are natural or entrance-not-exit, i.e., the process cannot reach them in finite time, and that X is a regular diffusion process, meaning that the state space $I:=(a,b)$ cannot be decomposed into smaller sets from which X cannot exit. The existence and uniqueness of such an X is guaranteed if the functions $\mu$ and $\sigma$ are Borel measurable in I with ${\sigma }^2>0$, and

$$\forall y\in I,\exists \epsilon >0\mathrm{such}\mathrm{that}{\int }_{y-\epsilon }^{y+\epsilon }\frac{1+\left|\mu \right(\xi \left)\right|}{{\sigma }^2\left(\xi \right)}d\xi <+\infty$$

(2)

(see Karatzas and Shreve (1991, Theorem 5.5.15); condition (2) holds if, for example, $\mu$ is locally bounded and $\sigma$ is locally bounded away from zero). Necessary and sufficient conditions for the boundaries a and b to be non-exit points, i.e., natural or entrance-not-exit, are formulated in Karatzas and Shreve (1991, Theorem 5.5.29). In particular, it is sufficient that the scale function

$$p\left(x\right):={\int }_c^{x}exp\left(-2{\int }_c^z\frac{\mu \left(u\right)}{{\sigma }^2\left(u\right)}du\right)dz,x\in I$$

(3)

converges to $-\infty$ when x approaches a and to $+\infty$ when x approaches b. (Here, $c\in I$ is arbitrary and the condition stated above does not depend on its choice.) These conditions are mild, in the sense that they are satisfied by all common diffusion models for commodity prices, including those in Section 3.

Denote by ${\tau }_x$ the first time that the process X reaches $x\in I$:

$${\tau }_x=inf\{t\ge 0:X_t=x\}.$$

(4)

For $r>0$, define

$${\psi }_r\left(x\right)=\left\{\begin{array}{cc}{\mathbb{E}}^x\left\{e^{-r{\tau }_c}\right\},\hfill & x\le c,\hfill \\ 1/{\mathbb{E}}^c\left\{e^{-r{\tau }_x}\right\},\hfill & x>c,\hfill \end{array}\right.{\varphi }_r\left(x\right)=\left\{\begin{array}{cc}1/{\mathbb{E}}^c\left\{e^{-r{\tau }_x}\right\},\hfill & x\le c,\hfill \\ {\mathbb{E}}^x\left\{e^{-r{\tau }_c}\right\},\hfill & x>c,\hfill \end{array}\right.$$

(5)

for any fixed $c\in I$ (different choices of c merely result in a scaling of the above functions). It can be verified directly that function ${\varphi }_r\left(x\right)$ is strictly decreasing in x while ${\psi }_r\left(x\right)$ is strictly increasing, and, for $x,y\in I$, we have

$${\mathbb{E}}^x\left\{e^{-r{\tau }_y}\right\}=\left\{\begin{array}{cc}{\psi }_r\left(x\right)/{\psi }_r\left(y\right),\hfill & x<y,\hfill \\ {\varphi }_r\left(x\right)/{\varphi }_r\left(y\right),\hfill & x\ge y.\hfill \end{array}\right.$$

(6)

Since the boundaries $a,b$ are natural or entrance-not-exit, we have ${\psi }_r(a+)\ge 0$, ${\varphi }_r(b-)\ge 0$ and ${\psi }_r(b-)={\varphi }_r(a+)=\infty$ (Borodin and Salminen 2012, Sec. II.1).

2.1.1. Optimal Stopping Problems and Solution Technique

The class of optimal stopping problems which we use in this paper is

$$v\left(x\right)=\underset{\tau }{sup}{\mathbb{E}}^x\left\{e^{-r\tau }\vartheta \left(X_{\tau }\right){\mathbf{1}}_{\tau <\infty }\right\},$$

(7)

where the supremum is taken over the set of all (possibly infinite) stopping times. Here, $\vartheta$ is the payoff function and v is the value function. If a stopping time ${\tau }^{*}$ exists which attains the supremum in (7), we call this an optimal stopping time. In addition, if v and $\vartheta$ are continuous, then the set

$$\mathsf{\Gamma }:=\{x\in I:v(x)=\vartheta (x\left)\right\}$$

(8)

is a closed subset of I. Under general conditions (Peskir and Shiryaev 2006, chp. 1), which are satisfied by all stopping problems studied in this paper, ${\tau }^{*}=inf\{t\ge 0:X_t\in \mathsf{\Gamma }\}$ is the smallest optimal stopping time and the set $\mathsf{\Gamma }$ is then called the stopping set.

Appendix A contains three lemmas providing a classification of solutions to the stopping problem (7) which will be used below.

2.1.2. Single Problem

Let ${\left(X_t\right)}_{t\ge 0}$ denote the EIM price. We will develop a mathematical representation of actions A1–A3 (see Section 1.1) when only one reserve contract is traded. Considering A3, the time of power delivery is the first time that the EIM price exceeds a predetermined level $x^{*}$:

$${\widehat{\tau }}_e=inf\{t\ge 0:X_t\ge x^{*}\}.$$

Given the present level x of the EIM price, the expected net present value of the utilisation payment exchanged at time ${\widehat{\tau }}_e$ can be expressed as follows thanks to (6):

$$h_c\left(x\right)=E^x\{e^{-r{\widehat{\tau }}_e}{K}_c\}=\left\{\begin{array}{cc}{K}_c,\hfill & x\ge x^{*},\hfill \\ K_c\frac{\psi \left(x\right)}{\psi \left(x^{*}\right)},\hfill & x<x^{*}.\hfill \end{array}\right.$$

(9)

Therefore, the optimal timing of action A2 corresponds to solving the following optimal stopping problem:

$$\underset{\tau }{sup}{\mathbb{E}}^x\left\{e^{-r\tau }\left(p_c+h_c\left(X_{\tau }\right)\right){\mathbf{1}}_{\tau <\infty }\right\}.$$

Since the utilisation payment $K_c$ obtained when the EIM price exceeds $x^{*}$ is positive and constant, as is the initial premium $p_c$, it is best to obtain these cashflows as soon as possible. The solution of the above stopping problem is therefore trivial: the contract should be sold immediately after completing action A1, i.e., immediately after providing physical cover for the reserve contract. Optimally timing the simultaneous actions A1 and A2, the purchase of energy and sale of the incremental reserve contract, is therefore the core optimisation task. It corresponds to solving the following optimal stopping problem:

$$V_c\left(x\right)=\underset{\tau }{sup}{E}^x\left\{e^{-r\tau }\left(-X_{\tau }+p_c+h_c\left(X_{\tau }\right)\right){\mathbf{1}}_{\tau <\infty }\right\}=\underset{\tau }{sup}{E}^x\left\{e^{-r\tau }h\left(X_{\tau }\right){\mathbf{1}}_{\tau <\infty }\right\},$$

(10)

where the payoff

$$h\left(x\right)=-x+p_c+h_c\left(x\right)$$

(11)

is non-smooth since $h_c$ is non-smooth. The function $V_c\left(x\right)$ is the real option value in the single problem.

2.1.3. Lifetime Problem Formulation and Notation

In addition, to having a design life of multiple decades, thermal power stations have the primary purpose of generating energy rather than providing ancillary services. In contrast, electricity storage technologies such as batteries have a design life of years and may be dedicated to providing ancillary services. In this paper, we take into account the potentially limited lifespan of electricity storage by modelling a multiplicative degradation of their storage capacity: each charge–discharge cycle reduces the capacity by a factor $A\in (0,1)$.

We now turn to the lifetime problem. To this end, suppose that a nonnegative continuation value $\zeta (x,\alpha )$ is also received at the same time as action A3. It is a function of the capacity of the store $\alpha \in (0,1)$ and the EIM price x, and represents the future proceeds from the arrangement.

The expected net present value of action A3 is now

$$h^{\zeta }(x,\alpha ):=E^x\{e^{-r{\widehat{\tau }}_e}\left(\alpha K_c+\zeta (X_{{\widehat{\tau }}_e},A\alpha )\right)\}=\left\{\begin{array}{cc}\left(\alpha K_c+\zeta (x^{*},A\alpha )\right)\frac{\psi \left(x\right)}{\psi \left(x^{*}\right)},\hfill & x<x^{*},\hfill \\ \alpha K_c+\zeta (x,A\alpha ),\hfill & x\ge x^{*},\hfill \end{array}\right.$$

(12)

where $A\in (0,1)$ is the multiplicative decrease of storage capacity per cycle. Here, the optimal timing of action A2 may be non trivial due to the continuation value $\zeta (x,\alpha )$. We will show, however, that, for the functions $\zeta$ of interest in this paper, it is optimal to sell the reserve contract immediately after action A1, identically as in the single problem. The timing of action A1 requires the solution of the optimal stopping problem

$$\mathcal{T}\zeta (x,\alpha ):=\underset{\tau }{sup}{E}^x\left\{e^{-r\tau }\left(-\alpha X_{\tau }+\alpha p_c+h^{\zeta }(X_{\tau },\alpha )\right){\mathbf{1}}_{\tau <\infty }\right\}.$$

(13)

The optimal stopping operator $\mathcal{T}$ makes the dependence on $\zeta$ explicit: it maps $\zeta$ onto the real option value of a selling a single reserve contract followed by continuation according to $\zeta$. We define the lifetime value function $\widehat{V}$ as the limit

$$\widehat{V}\left(x\right)=\underset{n\to \infty }{lim}\left({\mathcal{T}}^n\mathbf{0}\right)(x,1)$$

(14)

(if the limit exists), where ${\mathcal{T}}^n$ denotes the n-fold iteration of the operator $\mathcal{T}$ and $\mathbf{0}$ is the function identically equal to 0. Thus, ${\mathcal{T}}^n\mathbf{0}$ is the real option value of selling at most n reserve contracts under the arrangement. (Note that a priori it may not be optimal to sell all n contracts in this case, since it is possible to offer fewer contracts and refrain from trading afterwards by choosing $\tau =\infty$.)

Calculation of the lifetime value function requires the analysis of a two-argument function. We will show now that this computation may be reduced to a function of the single argument x. Define ${\zeta }_0(x,\alpha )=0$ and ${\zeta }_{n+1}(x,\alpha )=\mathcal{T}{\zeta }_n(x,\alpha )$. We interpret ${\zeta }_n(x,\alpha )$ as the maximum expected wealth accumulated over at most n cycles of the actions A1–A3 when the initial capacity of the store is $\alpha$.

Lemma 1.

We have ${\zeta }_n(x,\alpha )=\alpha {\widehat{\zeta }}_n\left(x\right)$, where ${\widehat{\zeta }}_n\left(x\right)={\zeta }_n(x,1)$. Moreover, ${\widehat{\zeta }}_n\left(x\right)={\widehat{\mathcal{T}}}^n\mathbf{0}\left(x\right)$, where

$$\widehat{\mathcal{T}}\widehat{\zeta }\left(x\right)=\underset{\tau }{sup}{\mathbb{E}}^x\{e^{-r\tau }(-X_{\tau }+p_c+{\widehat{h}}^{\widehat{\zeta }}\left(X_{\tau }\right)){\mathbf{1}}_{\tau <\infty }\},$$

(15)

and

$${\widehat{h}}^{\widehat{\zeta }}\left(x\right)=\left\{\begin{array}{cc}(K_c+A\widehat{\zeta }\left(x^{*}\right))\frac{\psi \left(x\right)}{\psi \left(x^{*}\right)},\hfill & x<x^{*},\hfill \\ K_c+A\widehat{\zeta }\left(x\right),\hfill & x\ge x^{*}.\hfill \end{array}\right.$$

(16)

Proof. 

The proof is by induction. Clearly, the statement is true for $n=0$. Assume it is true for $n\ge 0$. Then,

$${\zeta }_{n+1}(x,\alpha )=\mathcal{T}{\zeta }_n(x,\alpha )=\alpha \underset{\tau }{sup}{\mathbb{E}}^x\{e^{-r\tau }(-X_{\tau }+p_c+\frac{1}{\alpha }{h}^{{\zeta }_n}(X_{\tau },\alpha )){\mathbf{1}}_{\tau <\infty }\},$$

and

$$\frac{1}{\alpha }{h}^{{\zeta }_n}(x,\alpha )=E^x\{e^{-r{\widehat{\tau }}_e}(K_c+\frac{1}{\alpha }{\zeta }_n(X_{{\widehat{\tau }}_e},A\alpha ))\}=E^x\{e^{-r{\widehat{\tau }}_e}(K_c+A{\widehat{\zeta }}_n\left(X_{{\widehat{\tau }}_e}\right))\}.$$

Hence, ${\zeta }_{n+1}(x,\alpha )=\alpha \widehat{\mathcal{T}}{\widehat{\zeta }}_n\left(x\right)=\alpha {\zeta }_{n+1}(x,1)$. Consequently, ${\widehat{\zeta }}_n={\widehat{\mathcal{T}}}^n\mathbf{0}$. ☐

Assume that ${\zeta }_n(x,\alpha )$ converges to $\zeta (x,\alpha )$ as $n\to \infty$. Then, clearly, ${\widehat{\zeta }}_n$ converges to $\widehat{\zeta }\left(x\right)=\zeta (x,1)$. It is also clear that $\zeta$ is a fixed point of $\mathcal{T}$ if and only if $\widehat{\zeta }$ is a fixed point of $\widehat{\mathcal{T}}$. Therefore, we have simplified the problem to that of finding a limit of ${\widehat{\mathcal{T}}}^n\mathbf{0}\left(x\right)$. The stopping problem $\widehat{\mathcal{T}}\widehat{\zeta }$ will be called the normalised stopping problem and its payoff denoted by

$$\widehat{h}(x,\widehat{\zeta })=\left\{\begin{array}{cc}-x+p_c+\frac{{\psi }_r\left(x\right)}{{\psi }_r\left(x^{*}\right)}\left(K_c+A\widehat{\zeta }\left(x^{*}\right)\right),\hfill & x<x^{*},\hfill \\ -x+p_c+K_c+A\widehat{\zeta }\left(x\right),\hfill & x\ge x^{*}.\hfill \end{array}\right.$$

(17)

In particular, $\widehat{\mathcal{T}}\mathbf{0}$ coincides with the single problem’s value function $V_c$.

Notation. In the remainder of this paper, a caret (hat) will be used over symbols relating to the normalised lifetime problem:

$$\widehat{V}\left(x\right)=\underset{n\to \infty }{lim}{\widehat{\mathcal{T}}}^n\mathbf{0}\left(x\right).$$

2.1.4. Sustainability Conditions Revisited

The sustainability conditions S1 and S2 introduced in Section 1 are our standing economic assumptions. The next lemma, proved in the appendices, expresses them quantitatively. This makes way for their use in the mathematical considerations below.

Lemma 2.

When taken together, the sustainability conditionsS1andS2are equivalent to the following quantitative conditions:

S1*:

${sup}_{x\in (a,b)}h\left(x\right)>0$, and

S2*:

$p_c+K_c<x^{*}$.

Notice that S1* is always satisfied when $a\le 0$.

2.2. Three Exhaustive Regimes in the Single Problem

In this section, we consider the single problem. Recall that the sustainability assumptions, or equivalently assumptions S1* and S2*, are in force. For completeness, the notation and general optimal stopping theory used below is presented in Appendix A.

Since the boundary a is not-exit, we have ${\varphi }_r(a+)=\infty$. When h is given by (11), the limit L of (A3) is then

$$L_c:=\underset{x\to a}{lim\; sup}\frac{-x}{{\varphi }_r\left(x\right)}.$$

(18)

It can also be verified that the analogous constant R defined in (A4) in the appendices satisfies $R<\infty$ since, by S2*, h is negative on $[x^{*},\infty )$. The following theorem completes our aim M2.

Theorem 1.

(Single problem) Assume that conditionsS1*andS2*hold. With the definition (18), there are three exclusive cases:

(A) 

$L_c\le \frac{h\left(x\right)}{{\varphi }_r\left(x\right)}$ for some x$⟹$there is $\widehat{x}<x^{*}$ that maximises $\frac{h\left(x\right)}{{\varphi }_r\left(x\right)}$, and then, for $x\ge \widehat{x}$, ${\tau }_{\widehat{x}}$ is optimal, and

$$V_c\left(x\right)={\varphi }_r\left(x\right)\frac{h\left(\widehat{x}\right)}{{\varphi }_r\left(\widehat{x}\right)},x\ge \widehat{x}.$$

(19)

(B) 

$\infty >L_c>\frac{h\left(x\right)}{{\varphi }_r\left(x\right)}$ for all x $⟹V_c\left(x\right)=L_c{\varphi }_r\left(x\right)$ and there is no optimal stopping time.

(C) 

$L_c=\infty ⟹V_c\left(x\right)=\infty$ and there is no optimal stopping time.

Moreover, in cases A and B, the value function $V_c$ is continuous.

Proof. 

By condition S1*, $h\left(y\right)$ is positive for some $y\in I$ and the value function $V_c\left(x\right)>0$. For case A, note first that the function h is negative on $[x^{*},b)$ by S2*, see (9) and (11). Therefore, the supremum of $\frac{h}{{\varphi }_r}$ is positive and must be attained at some (not necessarily unique) $\widehat{x}\in (a,x^{*})$. The optimality of ${\tau }_{\widehat{x}}$ for $x\ge \widehat{x}$ then follows from Lemma A1. Case B follows from Lemma A2 and the fact that $L_c>0$. Lemma A2 proves case C. The continuity of $V_c$ follows from Lemma A3. ☐

The optimal strategy in case A is of a threshold type. When an arbitrary threshold strategy ${\tau }_{\tilde{x}}$ is used, the resulting expected value for $x\ge \tilde{x}$ is given by ${\varphi }_r\left(x\right)h\left(\tilde{x}\right)/{\varphi }_r\left(\tilde{x}\right)$. Figure 2 (whose problem data fall into case A) shows the potentially high sensitivity of the expected value of discounted cash flows for the single problem with respect to the level of the threshold $\tilde{x}$. It is therefore important in general to identify the optimal threshold accurately.

We now show that, for commonly used diffusion price models, it is case A in the above theorem which is of principal interest. This is due to the mild sufficient conditions established in the following lemma which are satisfied, for example, by the examples in Section 3. Although condition 2(b) in Lemma 3 is rather implicit, it may be interpreted as requiring that the process X does not ‘escape relatively quickly to $-\infty$’ (see Appendix D for a further discussion and examples) and it is satisfied, for example, by the Ornstein-Uhlenbeck process.

Lemma 3.

If conditionS1${}^{*}$holds, then:

1.

The equality $L_c=0$ implies case A of Theorem 1.

2.

Any of the following conditions is sufficient for $L_c=0$:

(a) 

$a>-\infty$,

(b) 

$a=-\infty$ and ${lim}_{x\to -\infty }\frac{x}{{\varphi }_r\left(x\right)}=0$.

Proof. 

Condition S1${}^{*}$ ensures that h takes positive values. Hence, the ratio $\frac{h\left(x\right)}{{\varphi }_r\left(x\right)}>0=L_c$ for some x. For assertion 2(a), recall from Section 2 that ${\varphi }_r(a+)=\infty$ since the boundary a is not-exit. Then, we have $L_c={lim\; sup}_{x\to a}(-x)/{\varphi }_r\left(x\right)=0$ as $a>-\infty$. In 2(b), the equality $L_c=0$ is immediate from the definition of $L_c$. ☐

Turning now to aim M1, we have

Corollary 1.

In the setting of Theorem 1 for the single problem, either

(a) 

the quantity

$$\check{x}:=max\left\{x\in I:\frac{h\left(x\right)}{{\varphi }_r\left(x\right)}=\underset{y\in I}{sup}\frac{h\left(y\right)}{{\varphi }_r\left(y\right)}\right\}$$

(20)

is well-defined, i.e., the set is non-empty. Then, $\check{x}$ is the highest price at which the battery operator may buy energy when acting optimally, and we have $\check{x}<x^{*}$ (this is case A); or

(b) 

there is no price at which it is optimal for the battery operator to purchase energy. In this case, the single problem’s value function may either be infinite (case C) or finite (case B).

Proof. 

(a) Since the maximiser $\widehat{x}$ in case A of Theorem 1 is not necessarily unique, the set in (20) may contain more than one point. Since h and ${\varphi }_r$ are continuous and all maximisers lie to the left of $x^{*}$, this set is closed and bounded from above, so $\check{x}$ is well-defined and a maximiser in case A. For any stopping time $\tau$ with ${\mathbb{P}}^x\{X_{\tau }>\check{x}\}>0$, it is immediate from assertion 3 of Lemma A1 that $\tau$ is not optimal for the problem $V_c\left(x\right)$, $x\ge \check{x}$. Part (b) follows directly from cases B and C of Theorem 1. ☐

Corollary 1 confirms that it is optimal for the battery operator to buy energy only when the EIM price is strictly lower than the price $x^{*}$ which would trigger immediate power delivery to the system operator. Thus, the battery operator (when acting optimally) does not directly conflict with the system operator’s balancing actions.

2.3. Two Exhaustive Regimes in the Lifetime Problem

Turning to the lifetime problem, we begin by letting $\widehat{\zeta }\left(x\right)$ in definition (16) be a general nonnegative continuation value depending only on the EIM price x, and studying the normalised stopping problem (15) in this case (the payoff $\widehat{h}$ is therefore defined as in (17)).

We now wish to study the value of n cycles A1–A3, and hence the lifetime value, by iterating the operator $\widehat{\mathcal{T}}$. To justify this approach, it is necessary to check the timing of action A2 in the lifetime problem. With the actions A1–A3 defined as in Section 1.1, recall that the timing of action A2 is trivial in the single problem: after A1 it is optimal to perform A2 immediately. Lemma A5, which may be found in Appendix B, confirms that the same property holds in the lifetime problem.

We may now provide the following answer to objective M1 for the lifetime problem.

Corollary 2.

Assume that conditionsS1*andS2*hold. In the lifetime problem with $\widehat{\zeta }=\widehat{V}$, either:

(a) 

the quantity

$$\check{x}:=max\left\{x\in I:\frac{\widehat{h}(x,\widehat{\zeta })}{{\varphi }_r\left(x\right)}=\underset{y\in I}{sup}\frac{\widehat{h}(y,\widehat{\zeta })}{{\varphi }_r\left(y\right)}\right\}$$

(21)

is well-defined, i.e., the set is non-empty. Then, $\check{x}$ is the highest price at which the battery operator can buy energy when acting optimally in the lifetime problem, and we have $\check{x}<x^{*}$ (cases 1 and 2a in Lemma A4 in Appendix B); or

(b) 

there is no price at which it is optimal for the battery operator to purchase energy. In this case, the lifetime value function may either be infinite (case 3) or finite (case 2b in Lemma A4 in Appendix B).

Proof. 

The proof proceeds exactly as that of Corollary 1 with the exception of showing that $\check{x}<x^{*}$ (this is because Lemma A4 in the appendices, which characterises the possible solution types in the lifetime problem, does not guarantee the strict inequality $\check{x}<x^{*}$). Assume then $\check{x}=x^{*}$. At the EIM price $X_t=\check{x}=x^{*}$, the power delivery to the system operator is immediately followed by the purchase of energy by the battery operator and this cycle can be repeated instantaneously, arbitrarily many times. However, since each such cycle is loss making for the battery operator by condition S2${}^{*}$, this strategy would lead to unbounded losses almost surely in the lifetime problem started at EIM price $x^{*}$ leading to $\widehat{V}\left(x^{*}\right)=-\infty$. This would contradict the fact that $\widehat{V}>0$, so we conclude that $\check{x}<x^{*}$. ☐

Pursuing aim M2, we will show now that there are two regimes in the lifetime problem: either the lifetime value function is strictly greater than the single problem’s value function (and the cycle A1–A3 is repeated infinitely many times), or the lifetime value equals the single problem’s value. Although the latter case appears counterintuitive, it is explained by the fact that the lifetime problem’s value is then attained only in the limit when the purchase of energy (action A1) is made at a decreasing sequence of prices converging to a, the left boundary of the process $\left(X_t\right)$. In this limit, the benefit of future payoffs becomes negligible, equating the lifetime value to the single problem’s value.1

Theorem 2.

There are two exclusive regimes:

($\alpha$)

$\widehat{V}\left(x\right)>V_c\left(x\right)$ for all $x\ge x^{*}$,

($\beta$)

$\widehat{V}\left(x\right)=V_c\left(x\right)$ for all $x\ge x^{*}$ (or both are infinite for all x).

Moreover, in regime (α), an optimal stopping time exists when the continuation value is $\widehat{\zeta }={\widehat{\zeta }}_n={\widehat{\mathcal{T}}}^n\mathbf{0}$ for $n>0$ (that is, for a finite number of reserve contracts), and when $\widehat{\zeta }=\widehat{V}$ (for the lifetime value function).

Proof. 

We take the continuation value $\widehat{\zeta }=V_c$ in Lemma A4 from Appendix B and consider separately its cases 1, 2a, 2b and 3. Firstly, in case 3, we have $V_c=\infty$, implying that also $\widehat{V}=\infty$ and we have regime $\left(\beta \right)$.

Case 2 of Lemma A4 corresponds to case B of Theorem 1, when there is no optimal stopping time in the single problem and $V_c\left(x\right)=L_c{\varphi }_r\left(x\right)$ for all $x\in I$. Considering first case 2b and defining ${\widehat{\zeta }}_n$ as in Lemma A6 in Appendix B, it follows that ${\widehat{\zeta }}_2\left(x\right)=L_c{\varphi }_r\left(x\right)=V_c\left(x\right)$ for $x\in I$ and consequently $\widehat{V}=V_c$, which again corresponds to regime ($\beta$).

In case 2a of Lemma A4, suppose first that the maximiser $\widehat{x}\le x^{*}$ is such that $\frac{\widehat{h}(\widehat{x},{\widehat{\zeta }}_1)}{{\varphi }_r\left(\widehat{x}\right)}=L_c$. Then, for $x\ge x^{*}\ge \widehat{x}$, we have ${\widehat{\zeta }}_2\left(x\right)={\varphi }_r\left(x\right)\frac{\widehat{h}(\widehat{x},{\widehat{\zeta }}_1)}{{\varphi }_r\left(\widehat{x}\right)}=L_c{\varphi }_r\left(x\right)$, which also yields regime ($\beta$). On the other hand, when $\frac{\widehat{h}(\widehat{x},{\widehat{\zeta }}_1)}{{\varphi }_r\left(\widehat{x}\right)}>L_c$, we have for $x\ge x^{*}\ge \widehat{x}$ that ${\widehat{\zeta }}_2\left(x\right)={\varphi }_r\left(x\right)\frac{\widehat{h}(\widehat{x},{\widehat{\zeta }}_1)}{{\varphi }_r\left(\widehat{x}\right)}>L_c{\varphi }_r\left(x\right)={\widehat{\zeta }}_1\left(x\right)$, and so regime ($\alpha$) applies by the monotonicity of the operator $\widehat{\mathcal{T}}$. From the definition of $\widehat{h}$ in (17), and holding the point $\widehat{x}\le x^{*}$ constant, this monotonicity implies that $\frac{\widehat{h}(\widehat{x},{\widehat{\zeta }}_n)}{{\varphi }_r\left(\widehat{x}\right)}>L_c$ for all $n>1$ and that $\frac{\widehat{h}(\widehat{x},\widehat{V})}{{\varphi }_r\left(\widehat{x}\right)}>L_c$. We conclude that case 2a of Lemma A4 applies (rather than case 2b) for a finite number of reserve contracts and also in the lifetime problem.

Considering now the maximiser $\widehat{x}$ defined in case 1 of Lemma A4, we have for $x\ge x^{*}\ge \widehat{x}$ that

$${\widehat{\zeta }}_2\left(x\right)={\varphi }_r\left(x\right)\frac{\widehat{h}(\widehat{x},{\widehat{\zeta }}_1)}{{\varphi }_r\left(\widehat{x}\right)}\ge \frac{\widehat{h}({\widehat{x}}_0,{\widehat{\zeta }}_1)}{{\varphi }_r\left({\widehat{x}}_0\right)}>\frac{\widehat{h}({\widehat{x}}_0,\mathbf{0})}{{\varphi }_r\left({\widehat{x}}_0\right)}={\widehat{\zeta }}_1\left(x\right)=V_c\left(x\right),$$

and regime $\left(\alpha \right)$ again follows by monotonicity. In addition, trivially, case 1 of Lemma A4 applies for $\widehat{\zeta }={\widehat{\zeta }}_n$ and $\widehat{\zeta }=\widehat{V}$. ☐

The following corollary follows immediately from the preceding proof.

Corollary 3.

Regime (β) holds if and only if ${\widehat{\mathcal{T}}}^2\mathbf{0}\left(x\right)=\widehat{\mathcal{T}}\mathbf{0}\left(x\right)$ for all $x\ge x^{*}$.

To address the implicit nature of our answers to M1 and M2 for the lifetime problem, in the next section, we provide results for the construction and verification of the lifetime value function and corresponding stopping time. For this purpose, we close this section by summarising results obtained above (making use of additional results from Appendix C).

Theorem 3.

In the setting of Theorem 2, assume that regime (α) holds. Then, the lifetime value function $\widehat{V}$ is continuous, is a fixed point of the operator $\widehat{\mathcal{T}}$ and ${\widehat{\mathcal{T}}}^n\mathbf{0}$ converges to $\widehat{V}$ exponentially fast in the supremum norm. Moreover, there is $\check{x}<x^{*}$ such that ${\tau }_{\check{x}}$ is an optimal stopping time for $\widehat{\mathcal{T}}\widehat{V}\left(x\right)$ when $x\ge \check{x}$ and, furthermore, $\check{x}$ is the highest price at which the battery operator can buy energy when acting optimally.

2.4. Construction of the Lifetime Value Function

In this section, we discuss a numerical procedure for solution of the lifetime problem. It is based on the problem’s structure as summarised in Theorem 3. Lemma 4 provides a means of constructing the lifetime value function, together with the value $\check{x}$ of Theorem 3, using a one-dimensional search. We assume that regime ($\alpha$) of Theorem 2 holds.

In the circumstance when the above procedure is not followed, complementary findings in Appendix E enable one to verify if a candidate buy price $\widehat{x}$ is optimal for the lifetime problem.

Lemma 4.

The lifetime value function evaluated at $x^{*}$ satisfies

$$\widehat{V}\left(x^{*}\right)=\underset{z\in (a,x^{*})}{max}y\left(z\right),$$

(22)

where

$$y\left(z\right):=\frac{-z+p_c+\frac{{\psi }_r\left(z\right)}{{\psi }_r\left(x^{*}\right)}{K}_c}{\frac{{\varphi }_r\left(z\right)}{{\varphi }_r\left(x^{*}\right)}-\frac{{\psi }_r\left(z\right)}{{\psi }_r\left(x^{*}\right)}A}.$$

(23)

Proof. 

Fix $z\in (a,x^{*})$. In the normalised lifetime problem of Section 2.1.3, suppose that the strategy ${\tau }_z$ is used for each energy purchase. Writing y for the total value of this strategy under ${\mathbb{P}}^{x^{*}}$, by construction we have the recursion

$$y=\frac{{\varphi }_r\left(x^{*}\right)}{{\varphi }_r\left(z\right)}\left(-z+p_c+\frac{{\psi }_r\left(z\right)}{{\psi }_r\left(x^{*}\right)}\left(K_c+Ay\right)\right).$$

Rearranging, we obtain (23). By Theorem 3, there exists an optimal strategy ${\tau }_{\check{x}}$ of the above form under ${\mathbb{P}}^{x^{*}}$ and (22) follows. ☐

Hence, under ${\mathbb{P}}^{x^{*}},$ an optimal stopping level $\widehat{x}$ can be found by maximising $y\left(z\right)$ over $z\in (a,x^{*})$. The value $\check{x}$ of Theorem 3 is given by $\check{x}=max\{x:y\left(x\right)={max}_{z\in (a,x^{*})}y\left(z\right)\}$.

3. Results

The general theory presented above provides optimal stopping times for initial EIM prices $x\ge \check{x}$, where $\check{x}$ is the highest price at which the battery operator can buy energy optimally. In this section, for specific models of the EIM price, we derive optimal stopping times for all possible initial EIM prices $x\in I$ when the sustainability conditions S1* and S2* hold. In the examples of this section, the stopping sets $\mathsf{\Gamma }$ for the single and lifetime problems take the form $(a,\check{x}]$ although, in general, stopping sets may have much more complex structure. Interestingly, the stopping sets for the single and lifetime problem are either both half-lines or both compact intervals.

Note that condition S2* is ensured by the explicit choice of parameters. Verification of condition S1${}^{*}$ is straightforward by checking, for example, if the left boundary a of the interval I satisfies $a<p_c+{lim}_{x\to a}\frac{{\psi }_r\left(x\right)}{{\psi }_r\left(x^{*}\right)}{K}_c$, i.e., that ${lim\; sup}_{x\to a}h\left(x\right)>0$. In particular, S1${}^{*}$ always holds if $a=-\infty$.

Our approach is to combine the above general results with the geometric method drawn from Section 5 of Dayanik and Karatzas (2003). Although Proposition 5.12 of the latter paper gives results for natural boundaries, we note that the same arguments apply to entrance-not-exit boundaries. In particular, we construct the least concave majorant W of the obstacle $H:[0,\infty )\to \mathbb{R}$, where

$$H\left(y\right):=\left\{\begin{array}{cc}\frac{\widehat{h}(F^{-1}\left(y\right),\widehat{\zeta })}{{\varphi }_r\left(F^{-1}\left(y\right)\right)},\hfill & y>0,\hfill \\ \underset{x\to a}{lim\; sup}\frac{\widehat{h}(x,\widehat{\zeta })}{{\varphi }_r\left(x\right)}=L_c,\hfill & y=0\hfill \end{array}\right.$$

(24)

(the latter equality was given in (A5) in the appendices). Here, the function $F\left(x\right)={\psi }_r\left(x\right)/{\varphi }_r\left(x\right)$ is strictly increasing with $F(a+)=0$. Writing $\widehat{\mathsf{\Gamma }}$ for the set on which W and H coincide, under appropriate conditions, the smallest optimal stopping time is given by the first hitting time of the set $\mathsf{\Gamma }:=F^{-1}(\widehat{\mathsf{\Gamma }})$ (Dayanik and Karatzas 2003, Propositions 5.13 and 5.14).

The Ornstein-Uhlenbeck (OU) process is a continuous-time stochastic process with dynamics

$$d{X}_t=\theta (\mu -X_t)dt+\sigma d{W}_t,$$

(25)

where $\theta ,\sigma >0$ and $\mu \in \mathbb{R}$. It has two natural boundaries, $a=-\infty$ and $b=\infty$. This process extends the scaled Brownian motion model by introducing a mean reverting drift term $\theta (\mu -X_t)dt$. The mean reversion is commonly observed in commodity price time series and may have several causes (Lutz 2009). In the present context, the mean reversion can also be interpreted as the impact on prices of the system operator’s corrective balancing actions. Appendix F collects some useful facts about the Ornstein-Uhlenbeck process. In particular, when constructing W, it is convenient to note that $H^{″}\circ F$ has the same sign as $(\mathcal{L}-r)h$, where $\mathcal{L}$ is the infinitesimal generator of X defined as in Appendix F.

3.1. OU Price Process

Assume now that the EIM price follows the OU process (25) so that $L_c=0$ (see Equation (A19) in Appendix F) and, by Lemma 3, case A of Theorem 1 applies. We are able to deal with the single and lifetime problems simultaneously by setting $\widehat{\zeta }$ equal to 0 for the single problem and equal to (the positive function) $\widehat{V}$ in the lifetime problem. The results of Section 2.2 and Section 2.3 yield that, in both problems, the right endpoint of the set $\widehat{\mathsf{\Gamma }}$ equals $F\left(\check{x}\right)$ for some $\infty <\check{x}<x^{*}$. Furthermore, since ${\psi }_r$ is a solution to $(\mathcal{L}-r)v=0$ and since $\check{x}<x^{*}$, for $x\le x^{*}$, we have

$$\begin{array}{ccc}\hfill (\mathcal{L}-r)\widehat{h}(x,\widehat{\zeta })& =& (\mathcal{L}-r)\left(-x+p_c+\frac{{\psi }_r\left(x\right)}{{\psi }_r\left(x^{*}\right)}\left(K_c+A\widehat{\zeta }\left(x^{*}\right)\right)\right)\hfill \end{array}$$

(26)

$$\begin{array}{cc}=& (\mathcal{L}-r)(-x+p_c)\hfill \end{array}$$

(27)

$$\begin{array}{cc}=& (r+\theta )x-r{p}_c-\theta \mu .\hfill \end{array}$$

(28)

Therefore, the function $(\mathcal{L}-r)\widehat{h}(·,\widehat{\zeta })$ is negative on $(-\infty ,B_0)$ and positive on $(B_0,\infty )$, where $B_0=\frac{r{p}_c+\theta \mu }{r+\theta }$. This implies that H is strictly concave on $(0,F\left(B_0\right))$ and strictly convex on $(F\left(B_0\right),\infty )$. Since the concave majorant W of H cannot coincide with H in any point of convexity, so necessarily $\check{x}<B_0$ and H is concave on $(0,F\left(\check{x}\right))$. Hence, we conclude that W is equal to H on the latter interval and so $\mathsf{\Gamma }=(-\infty ,\check{x}]$.

3.2. General Mean-Reverting Processes

The above reasoning can be extended to mean-reverting processes with general volatility

$$d{X}_t=\theta (\mu -X_t)dt+\sigma \left(X_t\right)d{W}_t$$

for a measurable function $\sigma$ such that the above equation admits a unique solution, cf. Section 2, and $L_c=0$ (cf. (24)). Recall that we assume that $\left(X_t\right)$ has two non-exit boundaries $a,b$ (natural or entrance-not-exit boundaries) satisfying $a<x^{*}<b$. Since $\mathcal{L}=\theta (\mu -x)\frac{d}{dx}+\frac{1}{2}{\sigma }^2\left(x\right)\frac{d^2}{d{x}^2}$, Equations (26)–(28) still apply. In particular, we see that the diffusion coefficient $\sigma (·)$ does not affect the sign of (28) and thus does not influence the concavity properties of H on $(0,F\left(x^{*}\right))$. Proceeding as above, we argue that case A of Theorem 1 applies and the single and lifetime problems can be solved simultaneously. Particularly, the largest buy price is given by $a<\check{x}<x^{*}$ (different for the single and lifetime problems). Note that the form of the stopping set is purely determined by $\mu ,\theta$, the left boundary a and the initial premium $p_c$. Obviously, the mean price level $\mu$ satisfies $\mu >a$ because a is an unreachable boundary.

Lemma 5.

If $p_c>a$, then the stopping sets for the single and lifetime problems are of the form $\mathsf{\Gamma }=(a,\check{x}]$.

Proof. 

The same arguments as in the OU case are directly applicable to the present setting and, under the assumptions of the lemma, we have $B_0=\frac{r{p}_c+\theta \mu }{r+\theta }>a$. Hence, for each problem, the stopping set has the form $\mathsf{\Gamma }=(a,\check{x}]$ for some $\check{x}<B_0$. ☐

In the particular case of the CIR model (Cox et al. 1985)

$$d{X}_t=\theta (\mu -X_t)dt+\sigma \sqrt{X_t}d{W}_t,$$

(29)

we have $a=0$, $b=\infty$. Then:

Corollary 4.

If X is the CIR process (29) with $2\theta \mu \ge {\sigma }^2$ and $\mu >0$, then the boundary $a=0$ is entrance-not-exit. Furthermore, if $p_c>0$, then the stopping sets for the single and lifetime problems are of the form $\mathsf{\Gamma }=(0,\check{x}]$.

Proof. 

It follows from (Cox et al. 1985, p. 391) that the condition $2\theta \mu \ge {\sigma }^2$ is necessary and sufficient for the boundary 0 to be entrance-not-exit. By Lemma 3, we have $L_c=0$. An application of Lemma 5 concludes. ☐

Remark 1.

More generally, suppose that the imbalance price process follows

$$d{X}_t=\theta (\mu -X_t)dt+\sigma X_t^{\gamma }d{W}_t$$

for some $\gamma >0.5$. Then, the left boundary $a=0$ is entrance-not-exit for any choice of parameters $\theta ,\mu ,\sigma >0$ since the scale function p given in (3) converges to negative infinity at 0. Therefore, the arguments in the above corollary apply and the stopping sets for the single and lifetime problems are also of the form $\mathsf{\Gamma }=(0,\check{x}]$.

3.3. Shifted Exponential Price Processes

In order to first recover and then generalise previously obtained results (Moriarty and Palczewski 2017), take the following shifted exponential model for the price process:

$$\begin{array}{ccc}\hfill f\left(z\right)& :=& D+d{e}^{bz},\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill X_t& =& f\left(Z_t\right),\hfill \end{array}$$

(31)

where Z is a regular one-dimensional diffusion with non-exit (natural or entrance-not-exit) boundaries $a^Z$ and $b^Z$ (we will use the superscripts X and Z where necessary to emphasise the dependence on the stochastic process). The idea is that Z models the physical system imbalance process while f represents a price stack of bids and offers which is used to form the EIM price. In this case, the left boundary for X is $a=f\left(a^Z\right)\ge D$ and, by Lemma 3, $L_c=0$ and case A of Theorem 1 applies. Rather than working with the implicitly defined process X, however, we may work directly with the process Z by setting:

$$\begin{array}{ccc}\hfill z^{*}& :=& f^{-1}\left(x^{*}\right),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill h_f\left(z\right)& :=& -f\left(z\right)+p_c+\left\{\begin{array}{cc}\frac{{\psi }_r^Z\left(z\right)}{{\psi }_r^Z\left(z^{*}\right)}{K}_c,\hfill & z<z^{*},\hfill \\ K_c,\hfill & z\ge z^{*},\hfill \end{array}\right.\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\widehat{h}}_f(z,\widehat{\zeta })& :=& \left\{\begin{array}{cc}-f\left(z\right)+p_c+\frac{{\psi }_r^Z\left(z\right)}{{\psi }_r^Z\left(z^{*}\right)}\left(K_c+A\widehat{\zeta }\left(z^{*}\right)\right),\hfill & z<z^{*},\hfill \\ -f\left(z\right)+p_c+K_c+A\widehat{\zeta }\left(z\right),\hfill & z\ge z^{*},\hfill \end{array}\right.\hfill \end{array}$$

(34)

and modifying the definitions for $\mathcal{T},\widehat{\mathcal{T}},V_c$ and $\widehat{V}$ accordingly. We then have

Theorem 4.

Taking definitions (30) and (32)–(34), assume that conditions S1* and S2* hold. Then,

$$L_c:=\underset{z\to a^Z}{lim\; sup}\frac{-f\left(z\right)}{{\varphi }_r^Z\left(z\right)}=0.$$

In addition:

(i) 

(Single problem) There exists $\widehat{z}<z^{*}$ that maximises $\frac{h_f\left(z\right)}{{\varphi }_r^Z\left(z\right)}$, the stopping time ${\tau }_{\widehat{z}}$ is optimal for $z\ge \widehat{z}$, and

$$V_c\left(z\right)={\varphi }_r^Z\left(z\right)\frac{h_f\left(\widehat{z}\right)}{{\varphi }_r^Z\left(\widehat{z}\right)},z\ge \widehat{z}.$$

(ii) 

(Lifetime problem) The lifetime value function $\widehat{V}$ is continuous and a fixed point of $\widehat{\mathcal{T}}$. There exists $\tilde{z}\in (\widehat{z},z^{*})$ which maximises $\frac{\widehat{h}(z,\widehat{V})}{{\varphi }_r^Z\left(z\right)}$ and ${\tau }_{\tilde{z}}$ is an optimal stopping time for $z\ge \tilde{z}$ with

$$\widehat{V}\left(z\right)=\widehat{\mathcal{T}}\widehat{V}\left(z\right)={\varphi }_r^Z\left(z\right)\frac{\widehat{h}(\tilde{z},\widehat{V})}{{\varphi }_r^Z\left(\tilde{z}\right)},z\ge \tilde{z}.$$

Proof. 

The proof follows from the one-to-one correspondence between the process X and the process Z, and direct transfer from Theorems 1 and 3. ☐

In some cases, explicit necessary and/or sufficient conditions for S1${}^{*}$ may be given in terms of the problem parameters. Assume that $a^Z=-\infty$ as in the examples studied below. If $p_c>D$ and $K_c\ge 0$, this is sufficient for the condition S1${}^{*}$ to be satisfied as then $h_f\left(z\right)\ge -f\left(z\right)+p_c>0$ for sufficiently small z. When $p_c=D$ and $K_c>0$, it is sufficient to verify that $e^{bz}=o\left({\psi }_r^Z\left(z\right)\right)$ as $z\to -\infty$ since then $h_f\left(z\right)=-d{e}^{bz}+{\psi }_r^Z\left(z\right)K_c/{\psi }_r^Z\left(z^{*}\right)$ for $z<z^{*}$. On the other hand, our assumption that S1${}^{*}$ holds necessarily excludes parameter combinations with $p_c-D=K_c=0$, since the reserve contract writer then cannot make any profit because $h_f\left(z\right)\le 0$ for all z.

In Section 3.3.1, we take Z to be the standard Brownian motion and recover results from the single problem of Moriarty and Palczewski (2017) (the lifetime problem is formulated differently in the latter reference, where degradation of the store is not modelled). In Section 3.3.2, we generalise to the case when Z is an OU process.

3.3.1. Brownian Motion Imbalance Process

When the imbalance process $Z=W$, the Brownian motion, we have

$$(\mathcal{L}-r){\widehat{h}}_f(z,\widehat{\zeta })=(\mathcal{L}-r)(-f\left(z\right)+p_c)=d{e}^{bz}\left\{r-\frac{1}{2}{b}^2\right\}+r(D-p_c).$$

We have several cases depending on the sign of $(D-p_c)$ and $(r-\frac{1}{2}{b}^2)$.

• Assume first that $r>\frac{1}{2}{b}^2$:

  (i)

  We may exclude the subcase $p_c\le D$, since then $H\left(y\right)=\frac{\widehat{h}(z,\widehat{\zeta })}{{\varphi }_r^Z\left(z\right)}{|}_{z={\left(F^Z\right)}^{-1}\left(y\right)}$ is strictly convex on $(0,F^Z\left(z^{*}\right))$ for any $\widehat{\zeta }$ and $\mathsf{\Gamma }$ cannot intersect this interval, contradicting Theorem 4 and, consequently, violating S1${}^{*}$ or S2${}^{*}$.

  (ii)

  If $p_c>D$, H is concave on $(0,F^Z\left(B\right))$ and convex on $(F^Z\left(B\right),\infty )$, where

  $$B=\frac{1}{b}log\left(\frac{r(p_c-D)}{d(r-\frac{1}{2}{b}^2)}\right).$$

  By Theorem 4 and the positivity of H on $(0,F^Z\left(\widehat{z}\right)),$ we have $\mathsf{\Gamma }=(-\infty ,\widehat{z}]$ and $\mathsf{\Gamma }=(-\infty ,\tilde{z}]$ for the single and lifetime problems, respectively, with $\tilde{z}<\widehat{z}<B$.

• Suppose that $r<\frac{1}{2}{b}^2$.

  (i)

  When $p_c\ge D$, the function H is concave on $(0,\infty )$. Hence, the stopping sets $\mathsf{\Gamma }$ for single and lifetime problems have the same form as in case 1(ii) above.

  (ii)

  If $p_c<D$, the function H is convex on $(0,F^Z\left(B\right))$ and concave on $(F^Z\left(B\right),\infty )$. The set $\mathsf{\Gamma }$ must then be an interval, respectively $[{\widehat{z}}_0,\widehat{z}]$ and $[{\tilde{z}}_0,\tilde{z}]$. For explicit expressions for the left and right endpoints for the single problem, as well as sufficient conditions for S1${}^{*}$, the reader is refered to Moriarty and Palczewski (2017).

• In the boundary case $r=\frac{1}{2}{b}^2$, the convexity of H is determined by the sign of the difference $D-p_c$. As above, the possibility $D>p_c$ is excluded since then H is strictly convex. Otherwise, H is concave and the stopping sets $\mathsf{\Gamma }$ have the same form as in case 1(ii) above.

3.3.2. OU Imbalance Process

When Z is the Ornstein-Uhlenbeck process, by adjusting d and b in the price stack function f (see (30)), we can restrict our analysis to the OU process with zero mean and unit volatility, that is:

$$d{Z}_t=-\theta Z_{t}dt+d{W}_t.$$

Then, for $z<z^{*},$

$$\begin{array}{ccc}\hfill (\mathcal{L}-r){\widehat{h}}_f(z,\widehat{\zeta })& =& (\mathcal{L}-r)(-f\left(z\right)+p_c)\hfill \end{array}$$

(35)

$$\begin{array}{cc}=& d{e}^{bz}\left\{b\left(\theta z-\frac{1}{2}b\right)+r\right\}+r(D-p_c)=:\eta \left(z\right).\hfill \end{array}$$

(36)

Differentiating $\eta$, we obtain

$${\eta }^{\prime }\left(z\right)=db\theta e^{bz}\left(bz+1+\frac{r-\frac{1}{2}{b}^2}{\theta }\right),$$

which has a unique root at $z^{\diamond }=\frac{1}{b}\left(\frac{\frac{1}{2}{b}^2-r}{\theta }-1\right)$. The function $\eta$ decreases from $r(D-p_c)$ at $-\infty$ until $\eta \left(z^{\diamond }\right)=-d{e}^{b{z}^{\diamond }}\theta +r(D-p_c)$ at $z^{\diamond }$ and then increases to positive infinity.

• If $p_c\ge D$, then the function $\eta$ is negative on $(-\infty ,u)$, where u is the unique root of $\eta$. Hence, H is concave on $(0,F^Z\left(u\right))$ and convex on $(F^Z\left(u\right),\infty )$. The stopping sets $\mathsf{\Gamma }$ for the single and lifetime problems must then be of the form $(-\infty ,\widehat{z}]$ and $(-\infty ,\tilde{z}]$, respectively, cf. case 1(ii) in Section 3.3.1.
• The case $p_c<D$ is more complex:

  (i)

  Let $z^{\diamond }\ge z^{*}$. We exclude the possibility $\eta \left(z^{*}\right)\ge 0$, since then the function H is convex on $(0,F^Z\left(z^{*}\right))$ and the set $\mathsf{\Gamma }$ has empty intersection with this interval, contradicting Theorem 4 and, consequently, violating S1${}^{*}$ or S2${}^{*}$. When $\eta \left(z^{*}\right)<0$, H is convex on $(0,F^Z\left(u\right))$ and concave on $(F^Z\left(u\right),F^Z\left(z^{*}\right))$, where u is the unique root of $\eta$ on $(0,z^{*})$. Therefore, the stopping sets $\mathsf{\Gamma }$ for the single and lifetime problems are of the form $[{\widehat{z}}_0,\widehat{z}]$ and $[{\tilde{z}}_0,\tilde{z}]$, respectively, with $min({\widehat{z}}_0,{\tilde{z}}_0)>u$, cf. case 2(ii) in Section 3.3.1.

  (ii)

  Consider now $z^{\diamond }<z^{*}$. As above, we exclude the case $\eta \left(z^{\diamond }\right)\ge 0$, since then H is convex on $(0,F^Z\left(z^{*}\right))$. The remaining case $\eta \left(z^{\diamond }\right)<0$ implies that the stopping sets $\mathsf{\Gamma }$ have the same form as in case 2(i) above, as H is convex and then concave if $\eta \left(z^{*}\right)\le 0$, and convex–concave–convex if $\eta \left(z^{*}\right)>0$.

4. Benchmark Case Study and Economic Implications

In this section, we use a case study to draw qualitative implications from the above results. An OU model is assumed, which captures both the mean reversion and random variability present in EIM prices, and is fitted to relevant data. The interest rate is taken to be $3\%$ per annum, and the degradation factor for the store to be $A=0.9999$.

Our data is the ‘balancing group price’ from the German Amprion system operator, which is available for every 15 min period (AMPRION 2016). Summary statistics for the period from 1 June 2012 to 31 May 2016 are presented in

Table 1. Summary statistics for the 15 min balancing group price per MWh in the German Amprion area, 1 June 2012 to 31 May 2016.

Min.	1st Qu.	Median	Mean	3rd Qu.	Max.
−6002.00	0.27	33.05	31.14	66.97	6344.00

. To address the issue of its extreme range, which impacts the fitting of both volatility and mean reversion in the OU model, the data was truncated at the values −150 and 150. The parameters obtained by maximum likelihood fitting were then $\theta =68.69$ (the rate of mean reversion), $\sigma =483.33$ (the volatility), $\mu =30.99$ (the mean-reversion level). The effect of the truncation step was to approximately halve the fitted volatility.

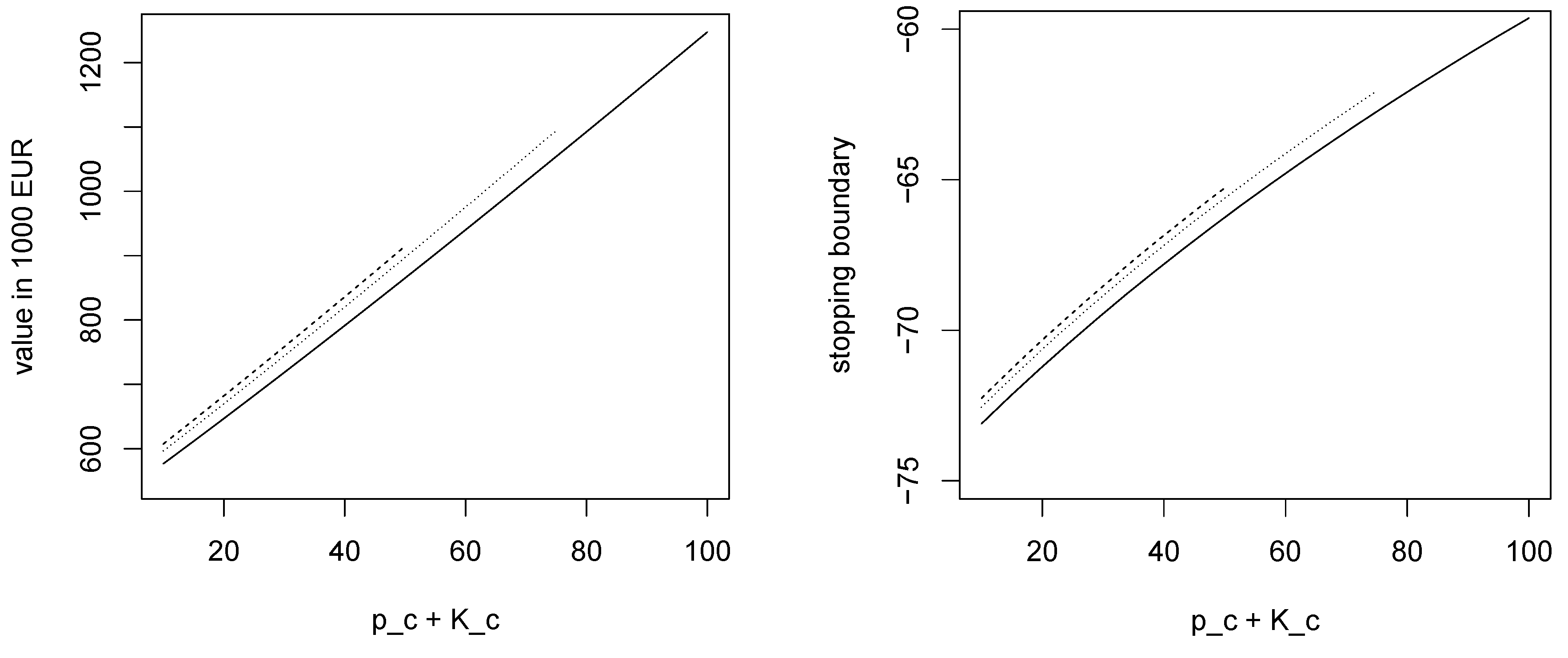
The left panel of Figure 3 and Figure 4 show the lifetime value $\widehat{V}\left(x^{*}\right)$, while the right panel of Figure 3 plots the stopping boundary $\check{x}$, which is the maximum price at which the battery operator can buy energy optimally. These values of $\check{x}$ are significantly below the long-term mean price D, indeed the former value is negative while the latter is positive. Thus, in this example, the battery operator purchases energy when it is in excess supply, further contributing to balancing. To place the negative values on the stopping boundary in Figure 3 in the statistical context, recall from Table 1 that the first quartile of the price distribution is approximately zero. Indeed, negative energy prices usually occur several times per day in the German EIM. In the present dataset of 1461 days, there are only 11 days without negative prices and the longest observed time between negative prices is $41.5$ h.

We make the following empirical observations. Firstly, defining the total premium as the sum $p_c+K_c$, altering its distribution between the initial premium $p_c$ (which is received at $x=\check{x}$) and the utilisation payment $K_c$ (which is received at $x=x^{*}$) results in insignificant changes to the graphs, with relative differences on the vertical axes of the order ${10}^{-3}$ (data not shown). It is for this reason that the figures are indexed by the total premium $p_c+K_c$ rather than by individual premia. Secondly, it is seen from the right-hand panel of Figure 3 that the (negative valued) stopping boundary increases with the total premium, making exercise more frequent. Thus, as the total premium increases, both the frequency and size of the cashflows increase, yielding a superlinear relationship in the left-hand panel of Figure 3. This superlinearity is not very pronounced since the stopping boundary is relatively insensitive to the total premium in the range presented in the graphs (see the right hand panel), so that the lifetime value is driven principally by the size of the cashflows. Thirdly, the grey horizontal line of Figure 4 is placed at a level indicative of recent costs for lithium-ion batteries per MWh (megawatt hour). Thus, the investment case for battery storage providing reserve is significantly positive for a wide range of the contract parameters. Finally, the contours in Figure 4 have an S-shape, the marginal influence of $x^{*}$ being smaller in the range $x^{*}<110$ and larger for greater values of $x^{*}$ (with the marginal influence eventually decreasing again in the limit of large $x^{*}$).

These phenomena are explained by the presence of mean reversion in the OU price model. The timings of the cashflows to the battery operator are entirely determined by the successive passage times of the price process between the levels $x^{*}$ and $\check{x}$. These passage times are relatively short on average for the fitted OU model. This means that the premia are received at almost the same time under each reserve contract, and it is the total premium which drives the real option value. Furthermore, the passage times between $x^{*}$ and $\check{x}$ may be decomposed into passage times between $x^{*}$ and D, and between D and $\check{x}$. Since the OU process is statistically symmetric about D, let us compare the distances $|\check{x}-D|$ and $|x^{*}-D|$. From Figure 3, we have $\check{x}\approx -70$ so that $|\check{x}-D|\approx 100$. Therefore, for $x^{*}<110$, we have $|x^{*}-D|\ll |\check{x}-D|$ and the passage time between D and $\check{x}$, which varies little, dominates that between $x^{*}$ and D. Correspondingly, we observe in Figure 4 that the value function changes relatively little as $x^{*}$ varies below 110. Conversely, as $x^{*}$ increases beyond 110, it is the distance between $x^{*}$ and D which dominates, and the value function begins to decrease relatively rapidly.

These results provide insights into the suitability of the considered arrangement for correcting differing levels of imbalance. As the distance between $x^{*}$ and the mean level D grows, the energy price reaches $x^{*}$ significantly less frequently and the reserve contract starts to provide insurance against rare events, resulting in infrequent power delivery and low utilisation of the battery. These observations suggest that the contractual arrangement studied in this paper is more suitable for the frequent balancing of less severe imbalance. In contrast, the more rapid reduction in the lifetime value for large values of $x^{*}$ suggests that such arrangements based on real-time markets are not suitable for balancing relatively rare events such as large system disturbances due to unplanned outages of large generators. The system operator may prefer to use alternative arrangements, based, for example, on fixed availability payments, to provide security against such events.

5. Conclusions

In this paper, we investigate the procurement of operating reserve from energy-limited storage using a sequence of physically covered incremental reserve contracts. This leads to the pricing of a real perpetual American swing put option with a random refraction time. We model the underlying energy imbalance market price as a general linear regular diffusion, which, in particular, is capable of modelling the mean reversion present in imbalance prices. Both the optimal operational policy and the real option value of the store are characterised explicitly. Although the solutions are generally not available in an analytical form, we have provided a straightforward procedure for their numerical evaluation together with empirical examples from the German energy imbalance market.

The results of the lifetime analysis in particular have both managerial implications for the battery operator and policy implications for the system operator. From the operational viewpoint, under the setup described in Section 1.1, we have established that the battery operator should purchase energy as soon as the EIM price falls to the level $\check{x}$, which may be calculated as described in Section 2.4. Furthermore, the battery operator should then sell the reserve contract immediately. Our real options valuation may be taken into account when deciding whether to invest in an energy store, and whether to sell such reserve contracts in preference to trading in other markets (for example, performing price arbitrage in the spot energy market).

Turning to the perspective of the system operator, we have demonstrated that the proposed arrangement can be mutually beneficial to the system operator and battery operator. More precisely, the system operator can be protected against guaranteed financial losses from the incremental capacity contract purchase while the battery operator has a quantifiable profit. The analysis also provides information on feedback due to battery charging by determining the highest price $\check{x}$ at which the battery operator buys energy, hence identifying conditions under which the battery operator’s operational strategy is aligned with system stability.

We address incremental reserve contracts, which are particularly valuable to the system operator when the margin of electricity generation capacity over peak demand is low. Decremental reserve may also be studied in the above framework, although the second stopping time (action A2) is non-trivial, which leads to a nested stopping problem beyond the scope of the present paper. Furthermore, we assume that the energy storage unit is dedicated to providing incremental reserve contracts, so that the opportunity costs of not operating in other markets or providing other services are not modelled. The extension to a finite expiry time, the lifetime analysis with decremental reserve contracts, and also the opportunity cost of not operating in other markets would be interesting areas for further work.

The methodological advances of this paper reach beyond energy markets. In particular, they are relevant to real options’ analyses of storable commodities where the timing problem over the lifetime of the store is of primary interest. The lifetime analysis via optimal stopping techniques, developed in Section 2.3, provides an example of how timing problems can be addressed for rather general dynamics of the underlying stochastic process. In this context, we provide an alternative method to quasi-variational inequalities, which are often dynamics-specific and technically more involved.