Model-Free Stochastic Collocation for an Arbitrage-Free Implied Volatility, Part II

Abstract

This paper explores the stochastic collocation technique, applied on a monotonic spline, as an arbitrage-free and model-free interpolation of implied volatilities. We explore various spline formulations, including B-spline representations. We explain how to calibrate the different representations against market option prices, detail how to smooth out the market quotes, and choose a proper initial guess. The technique is then applied to concrete market options and the stability of the different approaches is analyzed. Finally, we consider a challenging example where convex spline interpolations lead to oscillations in the implied volatility and compare the spline collocation results with those obtained through arbitrage-free interpolation technique of Andreasen and Huge.

1. Introduction

Financial markets provide option prices for a discrete set of strike prices and maturity dates. In order to price over-the-counter vanilla options with different strikes, or to hedge complex derivatives with vanilla options, it is useful to have a continuous arbitrage-free representation of the option prices, or equivalently of their implied volatilities. For example, the variance swap replication of Carr and Madan consists in integrating a specific function over a continuum of vanilla put and call option prices (Carr and Madan 2001; Carr and Lee 2009). More generally, Breeden and Litzenberger (1978) have shown that any path-independent claim can be valued by integrating over the probability density implied by market option prices. An arbitrage-free representation is also particularly important for the Dupire local volatility model (Dupire 1994), where arbitrage will translate to a negative local variance. In this paper, we describe a new technique to interpolate the market option prices in an arbitrage-free manner.

A rudimentary, but popular, representation is to interpolate market implied volatilities with a cubic spline across option strikes. Unfortunately, this may not be arbitrage-free as it does not preserve the convexity of option prices in general. A typical convex interpolation of the call option prices by quadratic splines or rational splines is also not satisfactory in general since it may generate unrealistic oscillations in the corresponding implied volatilities, as evidenced in (Jäckel 2014). Kahalé (2004) designs an arbitrage-free interpolation of the call prices, which however requires convex input quotes, employs two embedded non-linear minimizations, and it is not proven that the algorithm for the interpolation function of class $C^2$ converges. In reality, it is often not desirable to strictly interpolate option prices as those fluctuate within a bid-ask spread. Interpolation will lead to a noisy estimate of the probability density (which corresponds to the second derivative of the undiscounted call option price).

More recently, Andreasen and Huge (2011) have proposed to calibrate the discrete piecewise constant local volatility corresponding to a single-step finite difference discretization of the forward Dupire equation. In their representation of the local volatility, the authors use as many constants as the number of market option strikes for an optimal fit. It is thus sometimes considered to be “non-parametric”. Their technique works well but often yields a noisy probability density estimate, as the prices are typically over-fitted. Furthermore the output of their technique is a discrete set of option prices, which, while relatively dense, must still be interpolated carefully to obtain the price of options whose strike falls in between nodes.

This paper considers another approach, based on the stochastic collocation technique of Grzelak and Oosterlee (2017). Instead of collocating on a polynomial as in Le Floc’h and Oosterlee (2019), we explore various ways to use a monotonic spline, including B-spline parametrizations. This allows for a richer representation, with as many parameters as there are market option strikes. A direct consequence is the ability to capture more complex implied probability distributions, such as multi-modal distributions. We pay attention to avoid over-fitting by adding some appropriate regularization. This is reminiscent of the penalized B-spline technique for volatility modelling of Corlay (2016), where a B-spline parameterization of the Radon–Nikodym derivative of the underlying’s risk-neutral probability density with respect to a roughly calibrated base model is used. Concretely, Corlay’s method translates to an explicit probability density representation where the probability density is a spline multiplied by a base probability density function, such as the lognormal or normal probability density function. Corlay’s technique however limits the implied volatility shapes allowed, and often requires the use of a more elaborate base probability density function, such as the one stemming from the SVI1 parameterization of Gatheral (2004), to properly fit the market in practice. We will see that the stochastic collocation on a spline is more flexible and can fit the market very well when collocating to a simple Gaussian variable.

The outline of the paper is as follows. Section 2 presents how to apply the stochastic collocation on a monotonic cubic spline, while still preserving the first moment exactly. The collocation on an exponential spline is explored in Section 3, which results in analytical formulas not only for the price of vanilla options but also for the price of variance swaps. Section 4 considers B-spline representations which take into account the monotonicity and the martingale constraints explicitly. Section 5 details the calibration towards market option prices of each kind of representation. Section 6 explains how to filter the market quotes so that the spline collocation technique can be applied directly. The filtering may be used independently of the B-spline collocation. Finally, Section 7 explores the stability of the calibration on concrete market data, for the different parametrizations considered. We compare the quality of fit and the implied probability density with the Andreasen–Huge technique, regularized. In Section 8, we look at a challenging example of Jäckel (2014), where interpolation splines applied to call prices lead to oscillations in the interpolation.

2. Spline Collocation

Collocation methods are commonly used to solve ordinary or partial differential equations (LeVeque 2007). The underlying principle is to solve the equations in a specific finite dimensional space of solutions, such as polynomials up to a certain degree. In contrast, the stochastic collocation method (Mathelin and Hussaini 2003) consists in mapping a physical random variable Y to a point X in an artificial stochastic space. Collocation points $x_i$ are used to approximate the function mapping X to Y, $F_X^{-1}⚬F_Y$, typically by a polynomial, where $F_X,F_Y$ are respectively the cumulative distribution functions (CDF) of X and Y. Thus, only a small number of inversions of Y (and evaluations of $F_Y$) are used. This allows the problem to be solved in the “cheaper” artificial space.

In the context of option price interpolation, the stochastic collocation allows us to interpolate the market CDF in a better set of coordinates. In particular, we follow Grzelak and Oosterlee (2017) and use a Gaussian distribution for X.

In (Grzelak and Oosterlee 2017), the stochastic collocation is applied to the survival distribution function $G_Y$, where $G_Y\left(y\right)=1-F_Y\left(y\right)$ with $F_Y$ being the cumulative density function of the asset price process. When the survival density function is known for a range of strikes, their method can be summarized by the following steps:

• Given a set of collocation strikes $y_i$, $i=0,\dots ,N$, compute the survival density $p_i$ at those points: $p_i=G_Y\left(y_i\right)$.
• Project on the Gaussian distribution by transforming the $p_i$ using the inverse cumulative normal distribution ${\mathsf{\Phi }}^{-1}$ resulting in $x_i={\mathsf{\Phi }}^{-1}(1-p_i)$.
• Interpolate $(x_i,y_i)$ with a monotonic and derivable function g on $\mathbb{R}$. Grzelak and Oosterlee (2017) use a Lagrange polynomial for g but the technique can be applied to any derivable and monotonic function. Further on, we will consider a monotonic spline.
• Price by integrating the density with the integration variable $x={\mathsf{\Phi }}^{-1}(1-G_Y\left(y\right))$, using the approximation g to map the coordinates x to the strikes y.

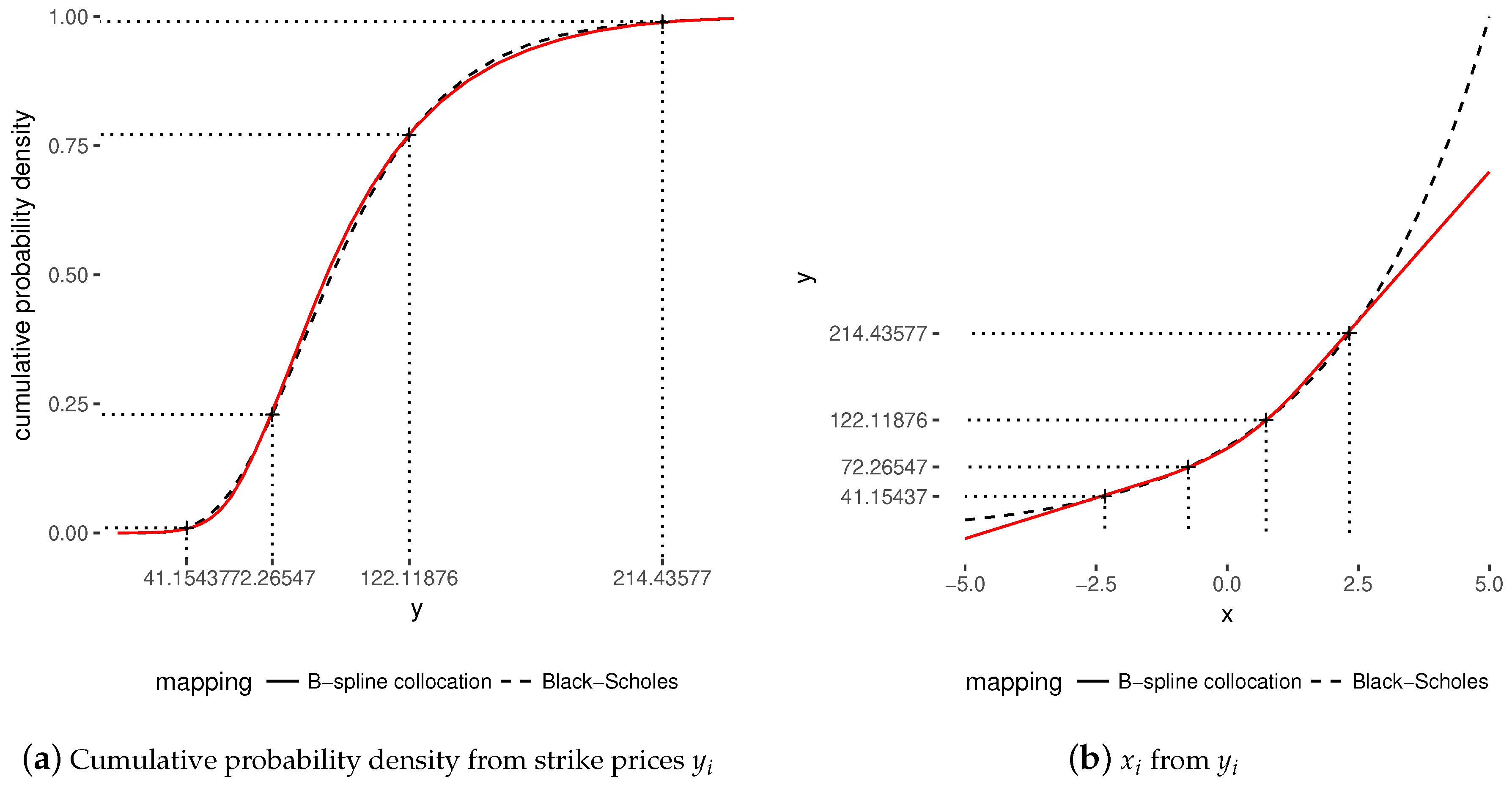
In order to illustrate the mapping involved in the stochastic collocation technique, we consider four options with strikes $y_0=40$, $y_1=70$, $y_2=120$, $y_3=215$ and maturity time $T=2$ in the Black–Scholes model with constant volatility $\sigma =20\%$ and forward price to maturity $F=100$. Figure 1a details the mapping from the four market strikes $y_i$ to the cumulative probability density $p_i$ (step 1) and Figure 1b shows the mapping from the coordinate $x_i$ to $y_i$ (step 2). The initial goal of step 3 is to find a smooth function that approximates the theoretical mapping in the coordinates from x to y well. The mapping function only needs to be monotonic, and to conserve the first moment, in order for the collocation method to be arbitrage-free. The figures show the mapping with the Black–Scholes model, which constitutes the reference, and with the B-spline collocation presented in this paper, based on the four options. The cumulative density for the B-spline collocation is obtained after computing the optimal collocation B-spline in the $x,y$ coordinates, based on the four points ${(x_i,y_i)}_{i=0,\dots ,3}$.

In reality, we are really interested in minimizing the error in terms of option prices (or equivalently implied volatilities). The discrete set of reference option prices either come directly from the financial markets, or from a prior model. This is where step 4 also becomes critical.

Let us now detail step 4. The undiscounted price of an option with strike price K is obtained by integrating over the probability density Breeden and Litzenberger (1978):

$$\begin{array}{cc}\hfill C\left(K\right)& ={\int }_0^{+\infty }max\left(y-K,0\right)f\left(y\right)dy,\hfill \end{array}$$

where f is the probability density implied by the options prices. We then perform the change of variable $x={\mathsf{\Phi }}^{-1}(1-G_Y\left(y\right))$ to obtain

$$\begin{array}{cc}\hfill C\left(K\right)& ={\int }_{{\mathsf{\Phi }}^{-1}\left(0\right)}^{{\mathsf{\Phi }}^{-1}\left(1\right)}max\left(G_Y^{-1}(1-\mathsf{\Phi }\left(x\right))-K,0\right)\varphi \left(x\right)dx.\hfill \end{array}$$

As $g\left(x\right)\approx G_Y^{-1}(1-\mathsf{\Phi }\left(x\right))$, we have

$$\begin{array}{cc}\hfill C\left(K\right)& \approx {\int }_{-\infty }^{\infty }max\left(g\left(x\right)-K,0\right)\varphi \left(x\right)dx\hfill \\ & ={\int }_{x_K}^{\infty }\left(g\left(x\right)-K\right)\varphi \left(x\right)dx,\hfill \end{array}$$

(1)

where $\varphi \left(x\right)$ is the Gaussian density function and

$$x_K=g^{-1}\left(K\right).$$

(2)

The change of variables is valid when the survival density is continuous and its derivative is integrable. In particular, it is not necessary for the derivative to be continuous.

When g is a piecewise cubic polynomial defined on the knots ${(x_i,y_i)}_{i=0,\dots ,N}$, the call option price can be obtained analytically. Let $g\left(x\right)=g_i\left(x\right)=a_i+b_i(x-x_i)+c_i{(x-x_i)}^2+d_i{(x-x_i)}^3$ for $x\in [x_i,x_{i+1}]$, and k the index such that $y_k\le K<y_{k+1}$, assuming that $0\le i<N$ exists, Equation (1) becomes

$$\begin{array}{cc}\hfill C\left(K\right)& =I({\tilde{x}}_{-1},x_0)+I({\tilde{x}}_N,\infty )-K\mathsf{\Phi }(-{\tilde{x}}_k)\hfill \\ & +\sum _{i=k}^{N-1}\left[a_i-(b_i+d_i({\tilde{x}}_i^2+3))x_i+c_i(x_i^2+1)\right]\left(\mathsf{\Phi }(-{\tilde{x}}_i)-\mathsf{\Phi }(-{\tilde{x}}_{i+1})\right)\hfill \\ & +\sum _{i=k}^{N-1}\left[b_i+c_i({\tilde{x}}_i-2x_i)+d_i(3x_i^2-3{\tilde{x}}_i{x}_i+{\tilde{x}}_i^2+2)\right]\varphi \left({\tilde{x}}_i\right)\hfill \\ & -\sum _{i=k}^{N-1}\left[b_i+c_i({\tilde{x}}_{i+1}-2x_i)+d_i(3x_i^2-3x_i{\tilde{x}}_{i+1}+{\tilde{x}}_{i+1}^2+2)\right]\varphi \left({\tilde{x}}_{i+1}\right),\hfill \end{array}$$

(3)

with ${\tilde{x}}_k=g^{-1}\left(K\right)$, ${\tilde{x}}_{-1}=x_0$ and ${\tilde{x}}_i=x_i$ for $i>k$. The integral I corresponding to the left and right extrapolations is defined by

$$I(a,b)={\int }_a^{b}g\left(x\right)\varphi \left(x\right)dx.$$

In the case of a linear extrapolation with slope s and starting at the point $(x,y)$, we have

$$\begin{array}{cc}\hfill I_L(a,b)& =(y-sx)\left(\mathsf{\Phi }\right(b)-\mathsf{\Phi }(a\left)\right)-s\left(\varphi \right(b)-\varphi (a\left)\right).\hfill \end{array}$$

with the abuse of notation $\mathsf{\Phi }(\infty )=1,\mathsf{\Phi }(-\infty )=0$ and $\varphi (\infty )=\varphi (-\infty )=0$. We use $s=s_L$, and $x=x_0,y=y_0$ for the left wing extrapolation, and $s=s_R$, and $x=x_N,y=y_N$ for the right wing extrapolatioin.

When $K<y_0$ and in the case of a linear extrapolation, Equation (3) is still valid, but with ${\tilde{x}}_{-1}=\frac{K-y_0}{s_L}+x_0$. When $K>y_N$, $C_K=I_R({\tilde{x}}_N,\infty )$ with ${\tilde{x}}_N=\frac{K-y_N}{s_R}+x_N$.

The cut-off point ${\tilde{x}}_k=g_k^{-1}\left(K\right)$ can be found analytically through Cardano’s formula (Nonweiler 1968).

The first moment is given by

$$\begin{array}{cc}\hfill M_1\left(g\right)& =I(-\infty ,x_0)+I(x_N,\infty )\hfill \\ & +\sum _{i=0}^{N-1}\left[a_i-(b_i+d_i(x_i^2+3))x_i+c_i(x_i^2+1)\right]\left(\mathsf{\Phi }\left(x_{i+1}\right)-\mathsf{\Phi }\left(x_i\right)\right)\hfill \\ & +\sum _{i=0}^{N-1}\left[b_i-c_i{x}_i+d_i(x_i^2+2)\right]\varphi \left(x_i\right)\hfill \\ & -\sum _{i=0}^{N-1}\left[b_i+c_i(x_{i+1}-2x_i)+d_i(3x_i^2-3x_i{x}_{i+1}+x_{i+1}^2+2)\right]\varphi \left(x_{i+1}\right).\hfill \end{array}$$

(4)

In practice, the preservation of the martingale property (and the put-call parity relation) imposes $M_1=F$ where F is the market forward price to maturity T.

The put option price is calculated through the put-call parity relation, namely

$$C\left(K\right)-P\left(K\right)=F-K,$$

(5)

where $P\left(K\right)$ is the undiscounted price today of a put option of maturity T, and F is the forward price to maturity.

When put option prices are very small, and assuming that the first moment equals exactly the forward price, it is preferable to use a more direct approach. Equation (5) does not allow to compute prices below machine epsilon. Using the same change of variables as for the call option (Equation (1)), we have for a put option with strike K:

$$\begin{array}{cc}\hfill P\left(K\right)& ={\int }_0^{+\infty }max\left(K-y,0\right)f\left(y\right)dy\hfill \\ & ={\int }_{-\infty }^{x_K}(g\left(x\right)-K)\varphi \left(x\right)dx.\hfill \end{array}$$

This leads to

$$\begin{array}{cc}\hfill P\left(K\right)& =K\mathsf{\Phi }\left({\tilde{x}}_k\right)-I(-\infty ,{\tilde{x}}_{-1})-I({\tilde{x}}_N,x_N)\hfill \\ & +\sum _{i=0}^{k-1}\left[a_i-(b_i+d_i(x_i^2+3))x_i+c_i(x_i^2+1)\right]\left(\mathsf{\Phi }\left({\tilde{x}}_{i+1}\right)-\mathsf{\Phi }\left({\tilde{x}}_i\right)\right)\hfill \\ & +\sum _{i=0}^{k-1}\left[b_i+c_i({\tilde{x}}_i-2x_i)+d_i(3x_i^2-3x_i{\tilde{x}}_i+{\tilde{x}}_i^2+2)\right]\varphi \left({\tilde{x}}_i\right)\hfill \\ & -\sum _{i=0}^{k-1}\left[b_i+c_i({\tilde{x}}_{i+1}-2x_i)+d_i(3x_i^2-3x_i{\tilde{x}}_{i+1}+{\tilde{x}}_{i+1}^2+2)\right]\varphi \left({\tilde{x}}_{i+1}\right),\hfill \end{array}$$

(6)

with ${\tilde{x}}_k=g^{-1}\left(K\right)$, ${\tilde{x}}_{-1}=x_0$ and ${\tilde{x}}_i=x_i$ for $0\le i<k$.

3. Exponential Spline Collocation

3.1. Vanilla Options

Instead of interpolating on the strikes (the points ${(x_i,y_i)}_{i=0,\dots ,N}$), we will interpolate the log strikes (the points ${(x_i,ln{y}_i)}_{i=0,\dots ,N}$) with a piecewise polynomial. This presupposes that the strikes are strictly positive and that the probability of the asset being negative equals zero. The undiscounted call price of an option with strike K is then

$$C\left(K\right)={\int }_{-\infty }^{\infty }max(e^{g\left(x\right)}-K,0)\varphi \left(x\right)dx,$$

(7)

where g is a monotonic piecewise polynomial function interpolating ${(x_i,ln{y}_i)}_{i=0,\dots ,N}$. We cannot obtain a closed-form formula for a general g function, if we assume that g is a quadratic spline. Let ${\left({\overline{x}}_j\right)}_{j=0,\dots ,M}$ be the spline knots, and $g\left(x\right)=a_j+b_j(x-{\overline{x}}_j)+c_j{(x-{\overline{x}}_j)}^2$ on $[{\overline{x}}_j,{\overline{x}}_{j+1}]$, with k the index such that ${\overline{y}}_k\le K<{\overline{y}}_{k+1}$, we have then

$$\begin{array}{cc}\hfill C\left(K\right)& =I({\tilde{x}}_{-1},{\overline{x}}_0)+I({\tilde{x}}_M,\infty )+K\mathsf{\Phi }(-{\tilde{x}}_k)\hfill \\ & +\sum _{j=k}^{M-1}{e}^{a_j-b_j{\overline{x}}_j+c_j{\overline{x}}_j^2+\frac{1}{2}{m}_j^2}\frac{\mathsf{\Phi }\left({\overline{x}}_{j+1}\sqrt{1-2c_j}-m_j\right)-\mathsf{\Phi }\left({\tilde{x}}_j\sqrt{1-2c_j}-m_j\right)}{\sqrt{1-2c_j}},\hfill \end{array}$$

with $m_j=\frac{b_j-2c_j{\overline{x}}_j}{\sqrt{1-2c_j}}$ and defining ${\tilde{x}}_k=g^{-1}(lnK)$, ${\tilde{x}}_i={\overline{x}}_i$ for $i>k$. When $1-2c_j<0$, we can use the imaginary error function erfi as we have for $a,b\in \mathbb{R}$,

$$-\mathrm{i}\frac{\mathsf{\Phi }\left(\mathrm{i}b\sqrt{2c_j-1}\right)-\mathsf{\Phi }\left(\mathrm{i}a\sqrt{2c_j-1}\right)}{\sqrt{2c_j-1}}=\frac{\mathrm{erfi}\left(b\sqrt{\frac{2c_j-1}{2}}\right)-\mathrm{erfi}\left(a\sqrt{\frac{2c_j-1}{2}}\right)}{2\sqrt{2c_j-1}}.$$

For a linear extrapolation with slope s and passing by the point $(x,y)$, corresponding to $g\left(u\right)=s(u-x)+y$, we find

$$\begin{array}{cc}\hfill I(a,b)& ={\int }_a^b{e}^{s(u-x)+y}\varphi \left(u\right)du\hfill \\ & =e^{y-sx+\frac{1}{2}{s}^2}\left(\mathsf{\Phi }(b-s)-\mathsf{\Phi }(a-s)\right),\hfill \end{array}$$

(8)

with some abuse of notation $\mathsf{\Phi }(-\infty )=0$, $\mathsf{\Phi }(\infty )=1$. The left wing extrapolation corresponds to $x={\overline{x}}_0$ and $y={\overline{y}}_0$, with $s=s_L$ a free parameter and the right wing extrapolation corresponds to $x={\overline{x}}_M,y={\overline{y}}_M$ with $s=s_R$. In order to keep the continuity of the derivative at the boundaries, we choose $s_R=g^{\prime }\left(x_N\right)$ and $s_L=g^{\prime }\left(x_0\right)$.

The first moment is given by

$$\begin{array}{cc}\hfill M_1& ={\int }_{-\infty }^{\infty }{e}^{g\left(x\right)}\varphi \left(x\right)dx\hfill \\ & =I(-\infty ,{\overline{x}}_0)+I({\overline{x}}_M,\infty )\hfill \\ & +\sum _{j=0}^{M-1}{e}^{a_j-b_j{\overline{x}}_j+c_j{\overline{x}}_j^2+\frac{1}{2}{m}_j^2}\frac{\mathsf{\Phi }\left({\overline{x}}_{j+1}\sqrt{1-2c_j}-m_j\right)-\mathsf{\Phi }\left({\overline{x}}_j\sqrt{1-2c_j}-m_j\right)}{\sqrt{1-2c_j}}\hfill \\ & =I(-\infty ,{\overline{x}}_0)+I({\overline{x}}_M,\infty )\hfill \\ & +\sum _{j=0}^{M-1}{e}^{a_j+\frac{b_j^2-2b_j{\overline{x}}_j+2c_j{\overline{x}}_j^2}{2(1-2c_j)}}\frac{\mathsf{\Phi }\left({\overline{x}}_{j+1}\sqrt{1-2c_j}-m_j\right)-\mathsf{\Phi }\left({\overline{x}}_j\sqrt{1-2c_j}-m_j\right)}{\sqrt{1-2c_j}}.\hfill \end{array}$$

(9)

3.2. Variance Swap

Variance swaps contracts allow a buyer to receive the future realized variance of the price changes until a specific maturity date against a fixed strike price, paid at maturity. Conventionally, these price changes are daily log returns of a specific stock, equity index, or exchange rate based upon the most commonly used closing price (or exchange rate reset price). Variance swaps became particularly popular after Demeterfi et al. showed that a single contract could be statically replicated by a portfolio of vanilla options (Demeterfi et al. 1999). In the absence of jumps2 and assuming the observations to be continuous, the problem of pricing a variance swap can be reduced to the pricing of a log-contract. The price V of a variance swap, by continuous replication, has a particularly simple closed-form expression with the exponential spline parametrization. For a newly issued variance swap with zero strike, and a transition probability density f from $t=0$ to $t=T$, following Carr and Lee (2009), we have

$$\begin{array}{cc}\hfill V(0,T)& =-\frac{2}{T}{\int }_0^{\infty }ln\left[\frac{y}{F(0,T)}\right]f\left(y\right)dy\hfill \\ & =-\frac{2}{T}{\int }_{-\infty }^{\infty }\left(g\left(x\right)-lnF(0,T)\right)\varphi \left(x\right)dx.\hfill \end{array}$$

(10)

In Equation (10), $\tilde{g}=g-F(0,T)$ is a piecewise quadratic spline. The value of the integral corresponds to the first moment of the collocation variable with the spline $\tilde{g}$, which is given explicitly by Equation (4). The standard replication formula from Carr and Madan (2001) implies to choose an integration cut-off and to use of a numerical quadrature, typically an adaptive Gauss–Lobatto quadrature. This is not necessary with the exponential spline collocation approach. The price of the variance swap can be adjusted by changing the slope of the linear extrapolation. This allows for a fast joint calibration of the collocating B-spline to market option prices and variance swaps. The market variance swap prices give some additional information on the tail of the distribution, not covered by vanilla options.

4. B-Spline Collocation

We recall that the goal of the stochastic collocation is to find a smooth monotonic function to represent the function g mapping the abscissas ${\left(x_i\right)}_{i=0,\dots ,N}$ to the ordinates (the strikes) ${\left(y_i\right)}_{i=0,\dots ,N}$ (see Figure 1b), by minimizing the error in option prices in a least-squares sense. From the previous sections, we now know how to price vanilla options by collocating on a spline, which passes through the specific points ${(x_i,y_i)}_{i=0,\dots N}$. We can then choose to optimize either the abscissas or the ordinates of those points in order to minimize the least squares error in option prices, on the condition that we use a monotonicity preserving spline and make sure to conserve the first moment in the optimization.

Instead of using an exact interpolation function on a set of points, and optimizing this interpolation through the choice of points, we can rely on a B-spline representation and optimize directly the B-spline coefficients. The method will work both on the direct strikes, or on the log strikes. We consider a quadratic B-spline representation, that is, B-splines of order $k=3$. The B-spline representation of g on $N+1+k$ knots reads (De Boor 1978)

$$g\left(x\right)=\sum _{i=0}^N{\alpha }_i{B}_{i,3}\left(x\right).$$

(11)

We choose the nearly optimal knots $t_{i+3}=\frac{x_{i+1}+x_{i+2}}{2}$ for $i=0,\dots ,N-3$ according to (De Boor 1978, p. 193) with the boundary knots $t_0=t_1=t_2=x_0$ and $t_{N+1}=t_{N+2}=t_{N+3}=x_N$. This choice of knots ensures that g is $C^1$ on $[x_0,x_N]$.

Because the derivative of the equivalent piecewise polynomial representation is linear between two distinct knots, g will be monotonically increasing on an interval $[t_{i-1},t_i]$ if and only if the derivative at the endpoints is positive. Thus, g will be monotonically increasing on the interval $[x_0,x_N]$ if and only if ${\alpha }_i-{\alpha }_{i-1}>0$ for $i=1,\dots ,N$ in Equation (11).

It is then particularly simple to impose the monotonicity constraints when we optimize the coefficients ${\alpha }_i$ during the calibration to market quotes. Furthermore, a least-squares fit of g directly to some input ${(x_i,y_i)}_{i=0,\dots ,N}$ reduces to a simple quadratic programming problem:

$$\tilde{\alpha }=\underset{\alpha \in {\mathbb{R}}^{N+1}}{arg\; min}\frac{1}{2}{\alpha }^{T}Q\alpha +q^T\alpha$$

(12)

subject to ${\alpha }_i-{\alpha }_{i-1}>0$ for $i=1,\dots ,N$, with $Q=P^{T}P$, $q=-P^{T}y$ and P the matrix defined by $P_{i,j}=B_{i,3}\left(y_j\right)$. In particular, P is a banded matrix (De Boor 1978).

The quadratic programming problem is fast to solve using a standard optimization library such as CVXOPT (Andersen et al. 2013), OSQP (Stellato et al. 2017), or quadprog (Turlach and Weingessel 2007), when compared to the total time taken to calibrate the spline. This will allow starting the optimization from a reasonable initial guess.

In order to price an option or to evaluate the first moment, we simply transform the B-spline representation to a piecewise quadratic polynomial (De Boor 1978, p. 117–19) and rely on Section 2 and Section 3 in this paper, for respectively a direct B-spline collocation, and an exponential B-spline collocation.

In the case of the direct B-spline collocation, the first moment is a linear combination of the B-spline coefficients. Indeed, the first moment is a linear combination of the piecewise polynomial coefficients in Equation (4) and the piecewise polynomial coefficients themselves are a linear combination of the B-spline coefficients:

$$\begin{array}{cc}\hfill a_j& =\frac{t_{j+2}-t_{j+1}}{t_{j+3}-t_{j+1}}\left({\alpha }_{j+1}-{\alpha }_j\right)+{\alpha }_j,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill b_j& =2\frac{{\alpha }_{j+1}-{\alpha }_j}{t_{j+3}-t_{j+1}},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill c_j& =\frac{1}{t_{j+3}-t_{j+2}}\left(\frac{{\alpha }_{j+2}-{\alpha }_{j+1}}{t_{j+4}-t_{j+2}}+\frac{{\alpha }_j-{\alpha }_{j+1}}{t_{j+3}-t_{j+1}}\right).\hfill \end{array}$$

(15)

We can thus add the martingale constraint directly to the quadratic programming problem as an additional equality constraint.

5. Calibration of the Spline Collocation to Market Quotes

We wish to minimize the weighted ${\ell }_2$ error norm between the volatilities implied from the prices obtained by spline collocation and the market implied volatilities. For this, we can optimize the location of either the spline knots abscissas $x_i$ or the spline knots ordinates $y_i$, or in the case of the B-spline representation, the coefficients ${\alpha }_i$.

5.1. Coordinate Transformation

In order to preserve the order of the knots, we rely on the following mapping:

$$\left\{\begin{array}{c}{z}_i=x_i-x_{i-1},\mathrm{for}i>0,\hfill \\ z_0=x_0,\hfill \end{array}\right.$$

and enforce $z_i\ge 0$ as box constraints in the least-squares minimization. Box constraints can be added in a relatively straightforward manner to any Levenberg-Marquardt algorithm, such as the one of Klare and Miller (2013), through the projection technique described in (Kanzow et al. 2004).

We use the same mapping if the ordinates or the B-spline coefficients are optimized, using $y_i$, respectively ${\alpha }_i$, instead of $x_i$ in the above equations.

5.2. Moment Conservation

We also wish to preserve the first moment exactly in order for the spline representation to be fully arbitrage-free. Let $M_1\left(g\right)$ be the first moment computed by Equation (4) and F be the market forward price to the option maturity time T. In order to make $M_1$ match F, we shift the coefficient $a_i$ of each piecewise polynomial ${\left(g_i\right)}_{i=0,\dots ,N-1}$ and use

$${\widehat{a}}_i=a_i+F-M_1,\mathrm{for}0\le i\le N.$$

(16)

For the exponential spline representation on $M+1$ unique knots, the adjustment is almost the same, but based on the log values we use

$${\widehat{a}}_i=a_i+lnF-ln{M}_1,\mathrm{for}0\le i\le M.$$

(17)

The new spline $\widehat{g}$ with updated coefficients ${\widehat{a}}_i$ will satisfy exactly $M_1=F$.

With this adjustment, there is a fundamental difference between the optimization of the abscissas $x_i$ and the ordinates $y_i$: when the abscissas are optimized, the adjustment will also implicitly adjust the $y_i$ as we have $y_i={\widehat{a}}_i$. Furthermore, when optimizing the ordinates $y_i$ or the B-spline coefficients ${\alpha }_i$, the first coordinate $y_0$ (respectively ${\alpha }_0$) can be directly deduced from the martingale adjustment. Indeed, the adjustment only impacts the value of $z_0$ and has no effect on $z_i=u^{-1}(y_i-y_{i-1})$ for $i>0$. This allows to reduce the number of dimensions of the optimization problem by one.

5.3. Choice of Coordinates

In our experiments, the optimization of the abscissas ${\left(x_i\right)}_{i=0,\dots ,N}$ appeared to be the least stable. In particular, the outcome was highly dependent on the initial guess. Only with a proper regularization and a good smooth initial guess (for example, the constant Bachelier guess) was the outcome satisfactory.

In comparison, the optimization of the ordinates ${\left(y_i\right)}_{i=0,\dots ,N}$ was found to be more stable, and the optimization of the B-spline coefficients was the most stable of all choices. One reason for this stability, is the initial guess for the B-spline coefficients respects the martingale constraint. Another is that the B-spline formulation is simply more stable than the piecewise-polynomial version (De Boor 1978). Values from the B-spline representation are obtained from a linear combination of the coefficients, while values obtained from the monotonic cubic spline representation are neither a linear combination of the abscissas nor of the ordinates, because of the monotonicity constraint.

The flexibility of choosing a different variety of monotonic splines such as the cubic spline of Hyman (1983) or Huynh (1993) when optimizing the knots abscissas or ordinates does not translate to a better fit of the reference option prices. In some specific cases, such as the one we explore in Section 8, the optimization the abscissas led to a better fit, but this consists in fitting towards the prices of a pre-existing model at hypothetical strikes, and not directly towards the market prices.

From now on, for clarity, we will thus focus only on the B-spline or exponential B-spline collocations where the B-spline coefficients are optimized.

5.4. Regularization

We will see through real examples that it can be useful to add regularization to the minimization as well, in order to avoid an implied probability density with many spikes. An interesting candidate for the regularization is to minimize the strain energy of the beam that is forced to pass through the given data points (Glass 1966):

$$E=\sum _{i=0}^m{\mu }_i^2{\left(\sigma (\xi ,K_i)-{\sigma }_i\right)}^2+{\lambda }^2\sum _{i=0}^{m-1}\frac{{\mu }_i^2{g}^{″}{\left(x_i\right)}^2}{{\left[1+g^{\prime }{\left(x_i\right)}^2\right]}^{\frac{5}{2}}}(x_{i+1}-x_i),$$

(18)

where $\sigma (\xi ,K)$ is the implied volatility corresponding to the option prices obtained with the spline collocation and ${\sigma }_i$ is the market implied volatility at strike $K_i$. For the maturity T considered, $m+1$ is the number of market strikes. We allow the number of strikes to be greater than or equal to the number of spline interpolation nodes $N+1$. The parameter $\xi$ represents a specific spline configuration on $N+1$ nodes. For a B-spline, we have $\xi ={\left({\alpha }_j\right)}_{j=0,\dots ,N}$, where ${\left({\alpha }_j\right)}_{j=0,\dots ,N}$ are the coefficients of the B-spline representation.

The first term of the objective E corresponds to the square of the root mean square error (RMSE), while the second term is the regularization. The regularization parameter $\lambda$ controls the smoothness of the spline interpolation.

In the case of the B-spline representation, Eilers and Marx (1996) propose a simpler regularization. Their penalized spline (P-spline) minimizes the total variation of the second derivative. This regularization, expressed in terms of the B-spline coefficients, reads

$$E=\sum _{i=0}^m{\mu }_i^2{\left(\sigma (\xi ,K_i)-{\sigma }_i\right)}^2+{\lambda }^2\sum _{j=1}^{N-1}\frac{4{\mu }_i^2}{{(t_{j+2}-t_{j+1})}^2}{\left(\frac{{\alpha }_{j+1}-{\alpha }_j}{t_{j+3}-t_{j+1}}+\frac{{\alpha }_{j-1}-{\alpha }_j}{t_{j+2}-t_j}\right)}^2,$$

(19)

where ${\left(t_j\right)}_{j=0,\dots ,N+3}$ are the spline knots. In particular, the latter regularization is linear in the coefficients ${\left({\alpha }_j\right)}_{j=0,\dots ,N}$ and can thus be directly included in the quadratic programming problem described in Section 4.

6. Making Market Call Prices Arbitrage-Free

For each strike and maturity, at a given time, the market quotes two prices for an option contract: the bid price and the ask price. In order to calibrate directly the collocation spline to the market quotes, we need a single estimate of the implied cumulative probability density. It is common practice to use the average of the bid and ask prices, the mid price for this purpose. Alternatively, we could also build two distinct representations: one for the bid prices and one or the ask prices.

When considered separately, the bid, ask, or mid prices are not guaranteed to be arbitrage-free in theory: there can be theoretical arbitrages within the bid-ask spread that cannot be taken advantage of in practice. Like most financial models, the collocation method is really only well defined in the absence of arbitrage: the implied cumulative probability density needs to be monotonic. We will explore in this section different ways to smooth the quotes and make them arbitrage-free. The goal is to obtain a good initial guess of the implied cumulative probability density in order to calibrate the spline nodes to the market prices afterwards.

6.1. No-Arbitrage Properties

Let ${\left(y_i\right)}_{i=0,\dots ,m}$ be the market strikes and ${\left(c_i\right)}_{i=0,\dots ,m}$ the undiscounted market call option prices corresponding to each strike, with $y_0<y_1<\dots <y_n$. Lemma 1 of Kahalé (2004) states that there is no arbitrage in those prices if and only if

$$-1<\frac{c_i-c_{i-1}}{y_i-y_{i-1}}<\frac{c_{i+1}-c_i}{y_{i+1}-y_i}<0,\mathrm{for}i=1,\dots ,m-1.$$

(20)

To be more precise, we should also have $max(F-y_i,0)<c_i<F$, where F is the underlying forward price to the option maturity.

6.2. A Quadratic Programming Problem

When the undiscounted call option prices $c_i$ contain some arbitrage, we need to solve the following quadratic programming problem:

$$\tilde{c}=\underset{z\in {\mathbb{R}}^{n+1}}{arg\; min}{∥W·(z-c)∥}_2^2$$

(21)

subject to

$$-1<\frac{z_i-z_{i-1}}{y_i-y_{i-1}}<\frac{z_{i+1}-z_i}{y_{i+1}-y_i}<0,\mathrm{for}i=1,\dots ,m-1,$$

(22)

where W is a diagonal matrix of weights. For equal weights W is the identity matrix $I_{n+1}$. We can include information on the bid-ask spread, for example by taking $w_i$ to be the inverse of the bid-ask spread at strike $y_i$.

We have

$$\begin{array}{cc}\hfill {∥W·(z-c)∥}_2^2& =z^T{W}^{T}Wz-2{\left(W^{T}Wc\right)}^{T}z+{\left(Wc\right)}^{T}Wc.\hfill \end{array}$$

The minimization problem can thus be formulated as a quadratic programming problem:

$$\tilde{c}=\underset{z\in {\mathbb{R}}^{n+1},Gz\le h}{arg\; min}\frac{1}{2}{z}^{T}Qz+q^{T}z$$

(23)

with

$$\begin{array}{cc}\hfill Q& =W^{T}W,\hfill \\ \hfill q& =-W^{T}Wc,\hfill \end{array}$$

and the elements $G_{i,j}$ of the matrix G, that specifies the linear constraints in (23), are

$$G_{i,i-1}=-\frac{1}{y_i-y_{i-1}},G_{i,i}=\frac{1}{y_i-y_{i-1}}+\frac{1}{y_{i+1}-y_i},G_{i,i+1}=-\frac{1}{y_{i+1}-y_i},$$

for $i=1,\dots ,n-1$, and

$$\begin{array}{cc}\hfill G_{0,0}=\frac{1}{y_1-y_0},& G_{0,1}=-\frac{1}{y_1-y_0},\hfill \\ \hfill G_{n,n}=\frac{1}{y_n-y_{n-1}},& G_{n,n-1}=-\frac{1}{y_n-y_{n-1}}.\hfill \end{array}$$

and the vector h by $h_0=1.0-ϵ$, $h_i=-ϵ$ for $i>0$. The constant $ϵ$ defines a maximum acceptable slope and ensures that the call prices are strictly convex.

In order to tune the smoothing of option prices, we could add a Tikhonov regularization, using the matrix of second order differences as Tikhonov matrix. This is, however, not necessary for the B-spline collocation, as we already add a regularization when computing the B-spline representation based on the initial guess.

Once the quadratic programming problem has been solved3, we can estimate the call price slope $c_i^{\prime }$ at each strike $y_i$ using the parabola that passes through the three points $c_{i-1},c_i,c_{i+1}$ (see Le Floc’h and Oosterlee (2019)):

$$c_i^{\prime }\approx \frac{l_i(y_{i+1}-y_i)+l_{i+1}(y_i-y_{i-1})}{y_{i+1}-y_{i-1}}\mathrm{where}{l}_i=\frac{c_i-c_{i-1}}{y_i-y_{i-1}}$$

(24)

for $i=1,\dots ,m-1$, and with $c_0^{\prime }=l_1$, $c_m^{\prime }=l_m$. It will lead to $-1<c_i^{\prime }<0$ and increasing $c_i^{\prime }$ assuming that the call prices $c_i$ obeys the conditions of lemma 1 of Kahalé (2004). This gives a direct estimate of the survival density $p_i=-c_i^{\prime }$ and thus of the abscissa $x_i$.

Another approach to find an initial guess is to rely on a very rough estimate, which may be a good starting point for the optimization. A straightforward initial guess for the implied cumulative probability density is to consider the density implied by a flat Bachelier volatility. The at-the-money market implied volatility is a natural choice. For a given option price, the Bachelier implied volatility ${\sigma }_N$ can be found in closed form using the rational expansions of Le Floc’h (2016). The collocation points can then be obtained directly:

$$x_i=-\frac{F-y_i}{\sigma \sqrt{T}}.$$

(25)

With a constant Bachelier volatility, x is an affine function of y and vice-versa.

7. Example of Calibration on TSLA Options

We consider options on the stock with ticker TSLA expiring on 17 January 2020 as of 15 June 2018. We first imply the forward price from the put-call parity relation at-the-money and then imply the Black–Scholes volatility from the mid price for each option strike (

Table A1. Implied volatilities against strikes K for TSLA options expiring on 17 January 2020 as of 15 June 2018. This corresponds to a maturity $T=1.59178$ and the forward is $f=356.73$.

Strike	Implied Volatility	Strike	Implied Volatility
20	1.217 45	330	0.507 12
25	1.152 97	335	0.504 29
50	1.001 35	340	0.501 40
55	1.008 70	350	0.496 19
75	0.905 59	360	0.491 45
100	0.819 65	370	0.485 71
120	0.779 70	380	0.482 10
125	0.753 93	390	0.477 66
140	0.725 53	400	0.468 23
150	0.703 70	410	0.469 13
160	0.687 09	420	0.465 20
175	0.663 15	430	0.462 10
180	0.654 28	440	0.459 70
195	0.631 00	450	0.456 14
200	0.623 20	460	0.454 18
210	0.615 45	470	0.451 55
230	0.586 62	480	0.445 42
240	0.578 38	490	0.445 28
250	0.562 50	500	0.443 04
255	0.562 55	510	0.439 39
260	0.557 23	520	0.441 32
270	0.548 52	550	0.433 63
275	0.545 61	580	0.429 71
280	0.540 06	590	0.428 44
285	0.538 48	600	0.424 11
290	0.532 53	650	0.422 27
300	0.522 24	670	0.420 34
310	0.520 24	680	0.419 34
315	0.516 84	690	0.419 35
320	0.512 74	700	0.417 59
325	0.510 04

). In this example, the options mid prices are not arbitrage free.

We will measure the RMSE between the volatilities implied by the calibrated stochastic collocation and the market implied volatilities, with and without regularization. We use equal weights in this example. Although it is not particularly realistic, it has the advantage of making the plots of the implied volatility more explicit.

The calibration consists firstly in computing an arbitrage-free (convex) set of call option prices from the market mid quotes according to Section 6.2, secondly in computing the B-spline initial guess following Section 4, and thirdly in minimizing the error measure represented by Equation (18) with a Levenberg–Marquardt minimizer.

7.1. B-Spline

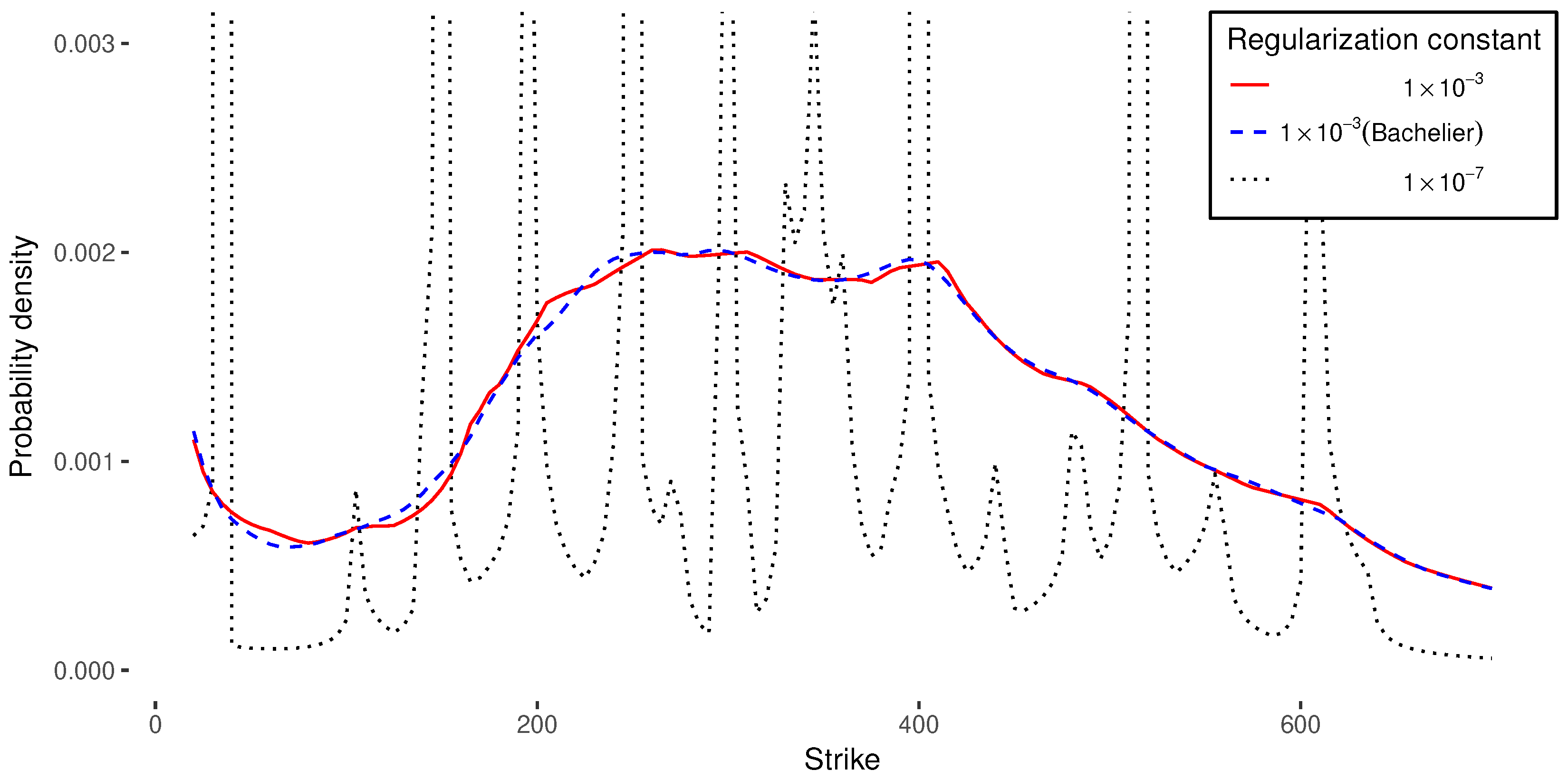
With a small (or zero) regularization parameter $\lambda$, the resulting implied probability density possesses many spurious spikes (Figure 2a). The use of a larger regularization parameter $\lambda$, during the non-linear minimization of the objective E described in Equation (18), helps smoothing the spikes, but it increases the RMSE slightly (see

Table 1. Root mean square error (RMSE) of the collocation method implied volatilities against the market implied volatilities of the TSLA 1 m options as of 18 June 2018.

Method	Regularization	RMSE	Time (ms)
Exponential B-spline collocation	$\lambda =1\times {10}^{-3}$	0.00437	43
B-spline collocation	$\lambda =6\times {10}^{-6}$	0.00397	71
Andreasen–Huge	none	0.00356	890
Exponential B-spline collocation	$\lambda =1\times {10}^{-7}$	0.00345	150
B-spline collocation	$\lambda =1\times {10}^{-10}$	0.00326	37
Schumarker quadratic spline	none	0.00313	0.5

).

In Table 1, we also compute the RMSE with a simple convexity preserving quadratic spline (Schumaker 1983) on the filtered market option prices (Equation (23)). This interpolation leads to a positive and piecewise-constant probability density. On convex prices, the interpolation is exact. The RMSE is thus purely due to the filtering of the market quotes by quadratic programming.

Andreasen and Huge (2011) propose a different non-parametric arbitrage-free volatility interpolation, where a discrete local volatility is calibrated to market option prices in a one-step finite-difference discretization of the forward Dupire partial differential equation. The number of free parameters corresponds effectively to the number of quotes, as in the spline collocation, and their technique will also tend to overfit. It is known to lead to a nearly exact interpolation on arbitrage-free option prices. It does however not lead to a more accurate representation of the market implied volatilities than the B-spline collocation with a small regularization constant. The corresponding implied probability density also possesses spikes.

The B-spline collocation is not only at least as accurate as the technique of Andreasen and Huge (2011) on this example, it is also significantly faster. In the latter, the involved finite difference grid must be relatively large (we used 800 points) and the corresponding tridiagonal system must be solved for each set of piecewise constant volatilities considered by the minimizer. Furthermore, the B-spline collocation offers a continuous interpolation of the option prices. In the technique of Andreasen and Huge (2011), options prices are given only at the finite difference grid points. Another careful4 arbitrage-free interpolation must be used to compute the price in between grid points. Finally, the B-spline collocation offers the ability to tune the probability density smoothness against the RMSE.

The optimal regularization parameter can be found using the L-curve method (Hansen 1992). On Figure 3b we plot the L-curve for the calibrated B-spline collocation, that is the regularization norm against residual norm, in logarithmic scale, or equivalently, the second sum against the first sum of Equation (19), varying the regularization parameter $\lambda$. For most regularization techniques, such a curve is L-shaped, because, on linear problems, the regularization norm is a strictly decreasing function of the regularization parameter $\lambda$, and the residual norm is a strictly increasing function of $\lambda$. A good regularization parameter will achieve a good compromise between the two errors, and will correspond to a regularized solution near the “corner” of the L-curve. On non-linear least-squares problems in general, the regularization and residual norms will not be strictly monotonic, they will however be nearly monotonic and the L-curve method may still be applied (Aster et al. 2018, p. 241).

Our choice $\lambda =6\times {10}^{-6}$ is the point located in the corner of the L-curve (see Figure 3b). Performing multiple calibrations to find the optimal regularization parameter, following one of the algorithms of Hansen and O’Leary (1993), may be time-consuming. An alternative is to apply the L-curve method to the B-spline initial guess based on the convex option prices5 (Figure 3a).

7.2. Exponential B-Spline

The exponential B-spline initial guess does not preserve the first moment. As a consequence, its calibration tends to be less stable than the calibration of the regular B-spline. The choice of initial guess plays then an important role, and the inclusion of the regularization in the calculation of the exponential B-spline initial guess is particularly important. The RMSE in the implied volatilities is comparable to the one obtained by the Andreasen and Huge technique, and is larger than the RMSE of the regular B-spline collocation (Table 1). In spite of the larger error, the implied probability density is not as smooth as the one implied from the regular B-spline collocation (Figure 4). A smoother initial guess, such as the constant Bachelier volatility, is then preferable.

7.3. Starting from Arbitrage-Free Prices

It is also interesting to take the filtered convex option prices (from Equation (23)) as a basis to compare the different techniques. We expect the RMSE to be lower, eventually zero, if the interpolation is exact at the market strikes. For example, the convexity-preserving Schumaker quadratic spline results in an RMSE of exactly zero (but the associated implied probability density is a staircase). The B-spline collocation results in an RMSE of around 0.0005 without regularization constant. This is lower than the RMSE produced by the Andreasen–Huge technique. In theory, their technique should be able to attain a lower RMSE, but the number of strikes, and thus the number of constants to optimize is relatively large on our problem and this creates difficulties for the numerical optimization. The collocation on an exponential B-spline leads to an RMSE similar to the one obtained with the Andreasen–Huge technique (

Table 2. Root mean square error (RMSE) of the collocation method implied volatilities against the implied volatilities of the TSLA 1 m options as of 18 June 2018, based on convexity adjusted prices.

Method	Regularization	RMSE	Time (ms)
Exponential B-spline collocation	$\lambda ={10}^{-3}$	0.00287	35
B-spline collocation	$\lambda =6\times {10}^{-6}$	0.00239	39
Exponential B-spline collocation	$\lambda ={10}^{-7}$	0.00118	160
Andreasen–Huge	none	0.00112	890
B-spline collocation	$\lambda ={10}^{-10}$	0.00042	78
Schumaker quadratic spline	none	0	0.02

). Of course, with a small regularization constant, the corresponding probability density possesses many spikes and is not very practical.

On other market data, for example, options on NFLX from July 2018, the same conclusions can be drawn.

8. A More Extreme Example—Wiggles in the Implied Volatility

Jäckel (2014) shows that undesired oscillations can appear in the graph of the implied volatility against the option strikes when the option prices are interpolated by a monotonic and convex spline.

Table A2. Implied volatilities against moneyness $\frac{K}{F}$ for an option of maturity $T=5.0722$, corresponding to the example 1 of Jäckel (2014).

Moneyness	Implied volatility
0.035 12	0.642 41
0.049 10	0.621 68
0.068 62	0.590 58
0.095 92	0.553 14
0.134 08	0.511 40
0.187 41	0.466 70
0.261 96	0.420 23
0.366 17	0.373 30
0.511 82	0.327 56
0.715 42	0.285 11
1	0.249 33
1.397 78	0.228 97
1.953 80	0.220 86
2.730 99	0.218 76
3.817 33	0.218 74
5.335 80	0.218 43
7.458 29	0.217 20
10.425 07	0.215 74
14.572 00	0.214 62
20.368 49	0.214 11
28.470 74	0.214 58

in Appendix A presents a concrete example6. Here, the option quotes are not direct market quotes, but the solution of a sparse finite difference discretization of a local stochastic volatility model: the market never quotes so far out-of-the-money option prices. His data has a few interesting properties:

• some of the option prices are extremely small: the interpolation must be very accurate numerically.
• the option prices are free of arbitrage. In theory, an arbitrage-free interpolation can be exact.
• a cubic spline interpolation on the volatilities or the variances, often used by practitioners, is not arbitrage-free.
• a convexity preserving $C^1$-quadratic, or $C^2$-rational spline results in strong oscillations in the implied volatility.

The interpolation proposed in (Jäckel 2014) possesses unnatural spikes at the points of clamping, in particular, the implied density is not continuous.

For this example, the B-spline collocation leads to a relatively large RMSE when compared to Andreasen–Huge method. As a consequence, we can see an oscillation of small amplitude in the corresponding implied volatility for large strikes (Figure 5b). This is very mild compared to the spline interpolations presented in (Jäckel 2014). The higher error is mostly located in the left wing. The exponential B-spline collocation results in a much lower RMSE, albeit still larger than the Andreasen and Huge technique (

Table 3. Root mean square error (RMSE) of the collocation method implied volatilities against the implied volatilities of Table A2 in Appendix A.

Method	Regularization	RMSE	Time (ms)
Septic polynomial	none	$1\times {10}^{-2}$	230
B-spline	$\lambda ={10}^{-12}$	$2\times {10}^{-4}$	10
Exponential B-spline	$\lambda ={10}^{-7}$	$6\times {10}^{-5}$	10
Andreasen–Huge (800 nodes)	none	$1\times {10}^{-6}$	25
Andreasen–Huge (3200 nodes)	none	$9\times {10}^{-8}$	67
Schumaker convex spline	none	0	0.02

). The volatility implied by the exponential B-spline collocation does not oscillate.

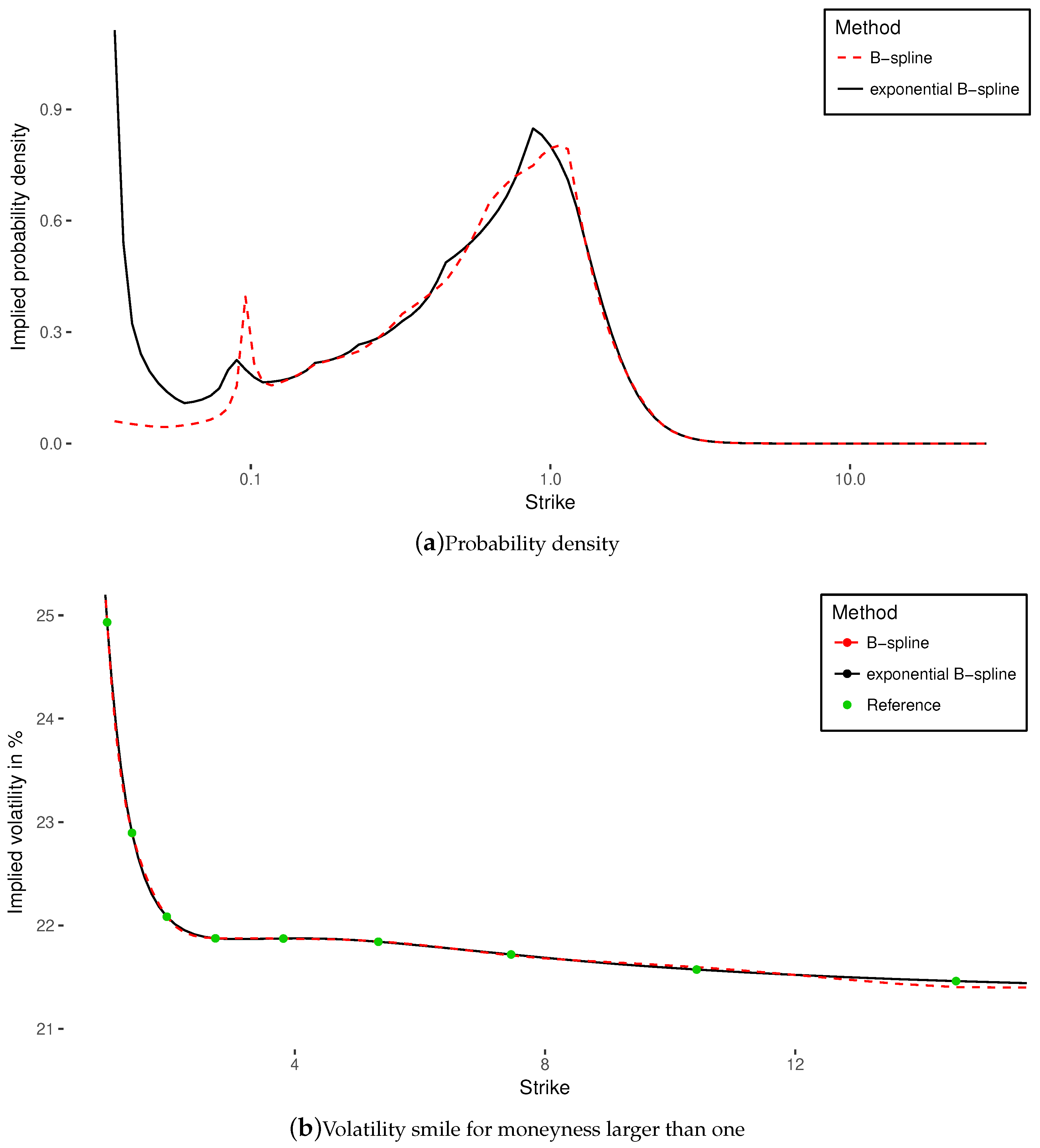
The optimal implied probability density is relatively smooth, but possesses a few visible modes (Figure 5a). This makes the monotonic polynomial collocation of Le Floc’h and Oosterlee (2019) ineffective, even when using a high degree polynomial. Polynomials of degree seven and higher lead to a RMSE larger than one vol point.

It is possible to obtain a better fit with the B-spline collocation with a better choice of knots, for example, if we compute the knots implied by the calibrated B-spline collocation, and calibrate one more time. In

Table 4. Root mean square error (RMSE) of the collocation method implied volatilities starting the calibration with the Bachelier, the convex, or the “best” initial guess, and using a small regularization constant.

Market Data	Collocation Method	Bachelier	Convex	Best
Peter Jäckel	B-spline	0.00063	0.00025	0.00001
	Exponential B-spline	0.00016	0.00006	0.00003
TSLA raw	B-spline	0.00330	0.00326	0.00322
	Exponential B-spline	0.00343	0.00345	0.00343
TSLA convex	B-spline	0.00054	0.00042	0.00034
	Exponential B-spline	0.00108	0.00118	0.00108

, we denote this technique as “Best”. It improves significantly the accuracy on the example of Peter Jäckel, but not on the filtered and non filtered TSLA market option quotes, where the different choices for the initial knots lead to a very similar RMSE.

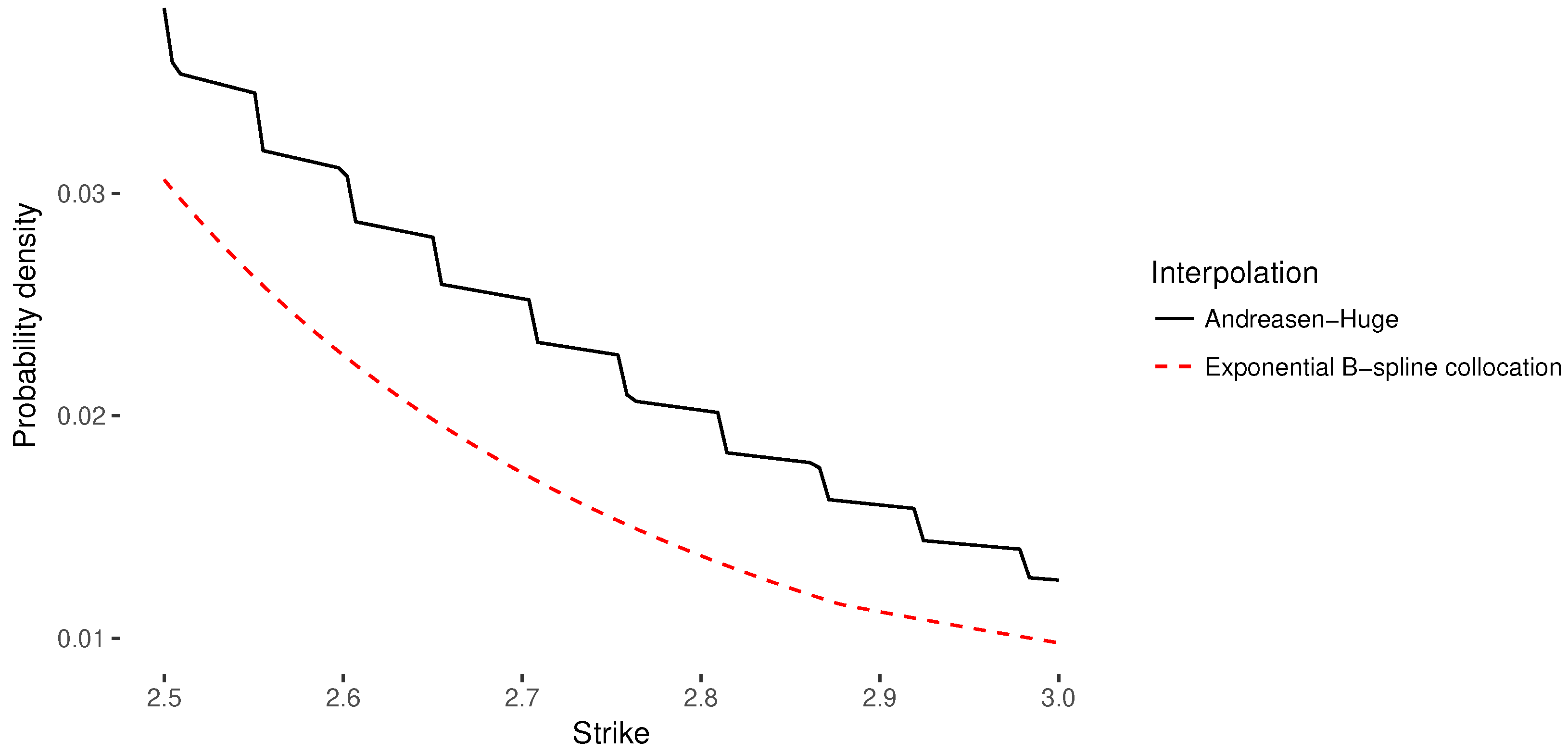
On Peter Jäckel’s example, the optimal implied probability density is relatively smooth everywhere, and especially for strike moneyness larger than one. Figure 6 shows however that the probability density implied by technique of Andreasen and Huge (2011) exhibits a staircase shape when zoomed-in. This is due to the interpolation in between the finite difference grid nodes. In contrast, the probability density implied by the (exponential) B-spline collocation stays very smooth, and is continuous by construction.

9. Conclusions

The monotonic B-spline and exponential B-spline collocations allow a more flexible arbitrage-free representation as compared to the monotonic polynomial collocation. They can capture multi-modal distributions well. In practice, when the goal is to fit market option prices, we have shown that is important to add a regularization during the optimization in order to stabilize the calibration and produce a smooth implied probability density, and we have described which regularization is appropriate.

We have also presented a simple non-parametric technique to de-arbitrage a set of option prices, which may be used independently of the B-spline collocation method.

In some specific cases, such as the example from Jäckel (2014), the outcome of the B-spline calibration may be dependent on the choice of the initial fixed knots. In the latter example, the exponential B-spline collocation behaved better, however.

On actual market options quotes, corresponding to various equity or equity indices, we did not observe this strong dependence on the choice of initial knots. We observed a quality of fit in terms of implied volatilities similar to or better than the best non-parametric arbitrage-free methods, such as the technique of Andreasen and Huge (2011). Compared to the latter, the spline collocation has the advantage of providing a natural continuous interpolation and extrapolation. The technique from Andreasen and Huge is based on a fine discretization of the problem, and requires an additional careful arbitrage-free interpolation scheme to compute the prices for option strikes not placed on the discretization grid. The B-spline collocation is also less computationally intensive, as the Andreasen and Huge technique mainly works well on a dense grid, typically composed of thousand points or more.

An additional interesting property of the exponential B-spline representation is the simple analytical expression we obtain for the price of a variance swap. The latter is a linear combination of the B-spline parameters. This allows including the market prices of variance swaps very easily into the calibration and thus obtaining a better representation of the wings of the implied volatility.

Finally, the B-spline and exponential B-spline collocations can be used directly to price exotic derivatives within the collocated local volatility model of Grzelak (2016).

We leave for further research the definition of an algorithm for an automatic selection of the best B-spline knots, as well as an extension to B-splines of order four.