Mortality Forecasting: How Far Back Should We Look in Time?
Abstract
:1. Introduction
2. Models for Comparison
2.1. Notation
- as the observed number of deaths in calender year t aged x.
- as the exposure data that measure the average population in calendar year t aged x.
- as the central mortality rate, which reflects the death probability at age x in the middle of the year. It is calculated by:
- as the initial mortality rate, which is the one-year death probability for a person who is aged exactly x at time t.
2.2. CBD Model and a Local Linear Approach
- and , where denotes age groups.
- where and are smooth functions of t.
2.3. 2D LOP Model and 2D KS Model
2.4. A Discussion on the Two Groups of Mortality Models
3. Case Study: GB Male Mortality Data from 1950–2016, Ages 50–89
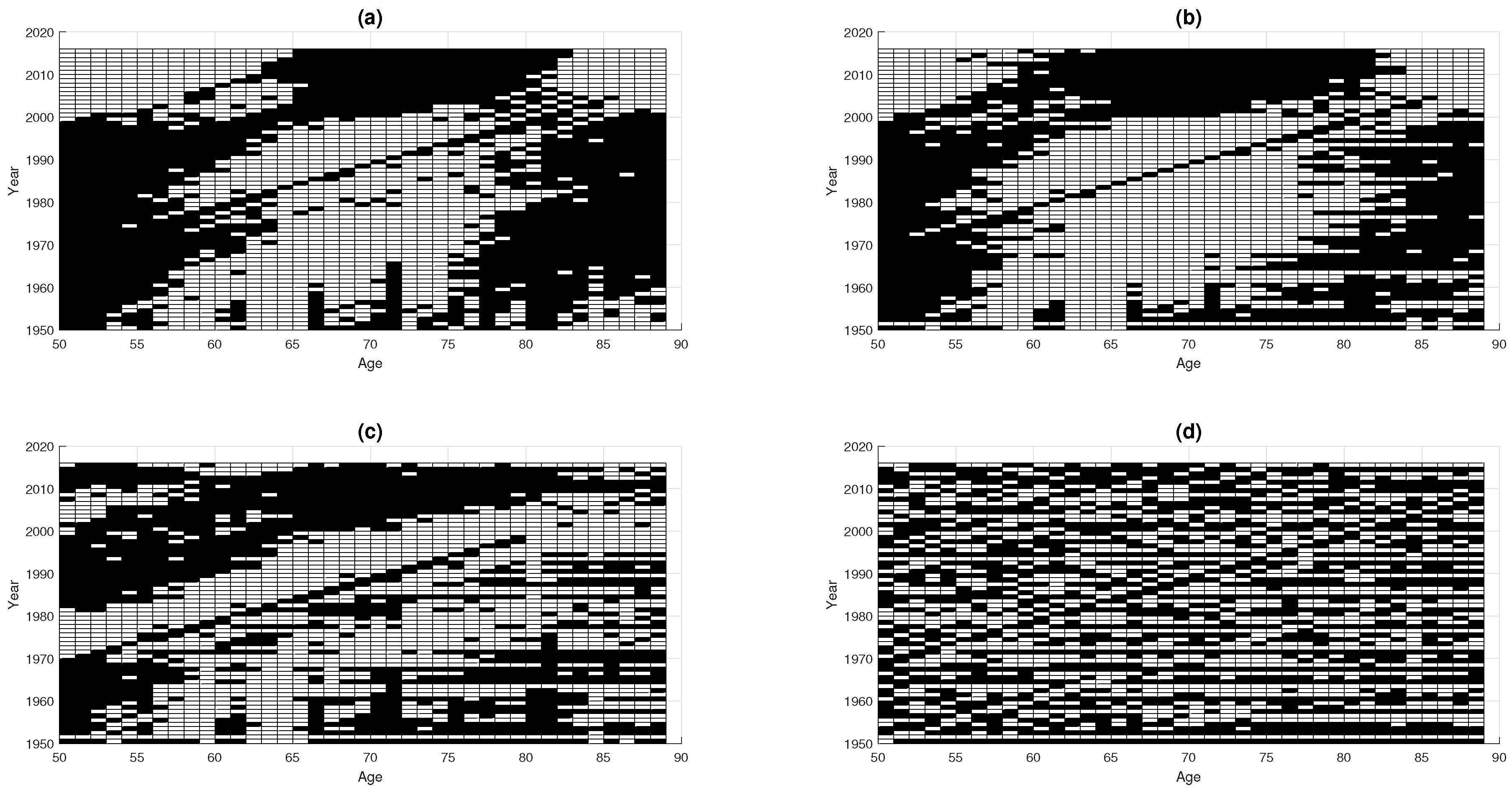
3.1. Data
3.2. Fit Quality and Residual Plots
- The average error (), which is a measure of overall bias, is calculated as:
- The absolute average error (), which measures the absolute size of the deviance, is calculated as:
- The standard deviation of error (), which is an indicator of large deviance, is calculated as:
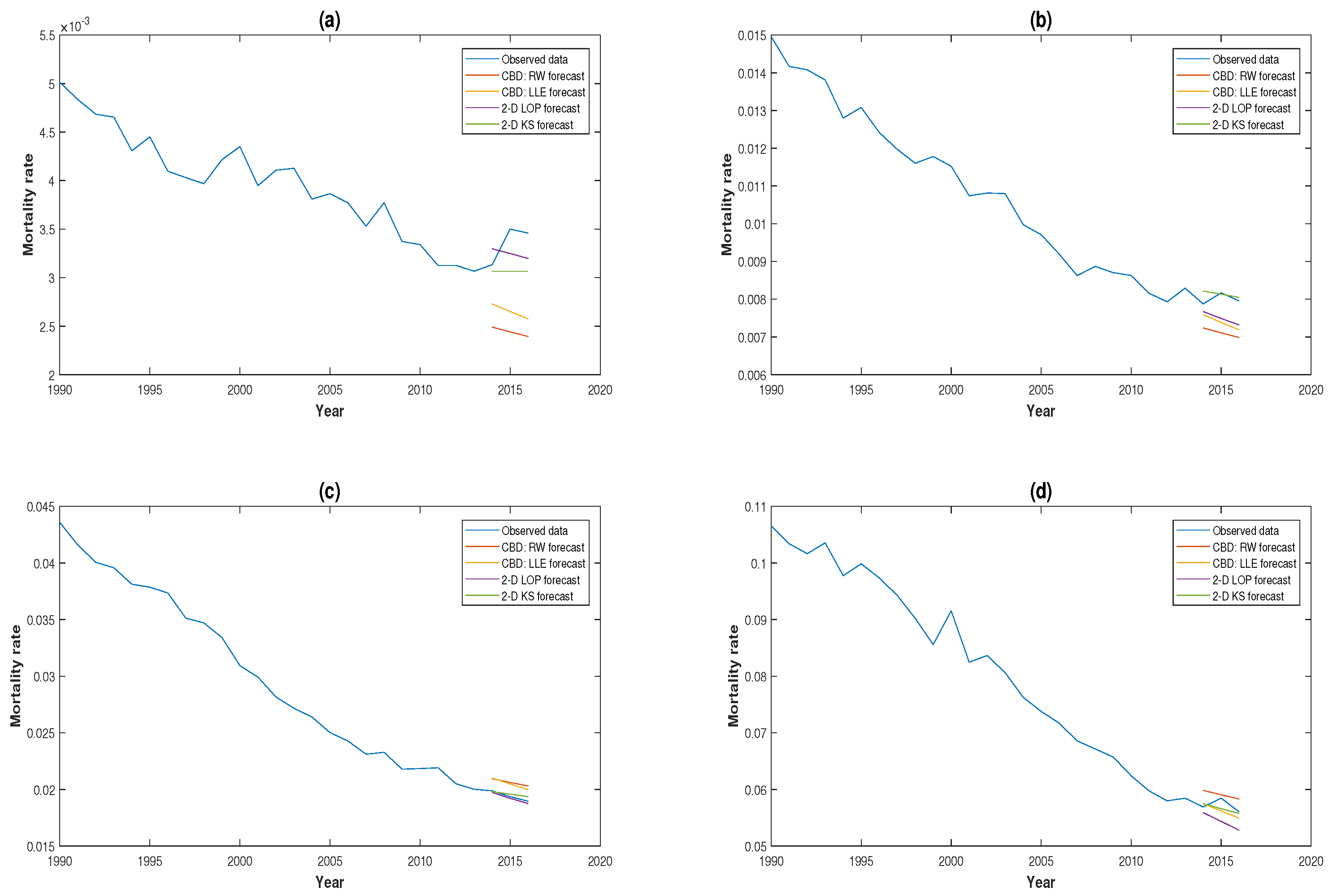
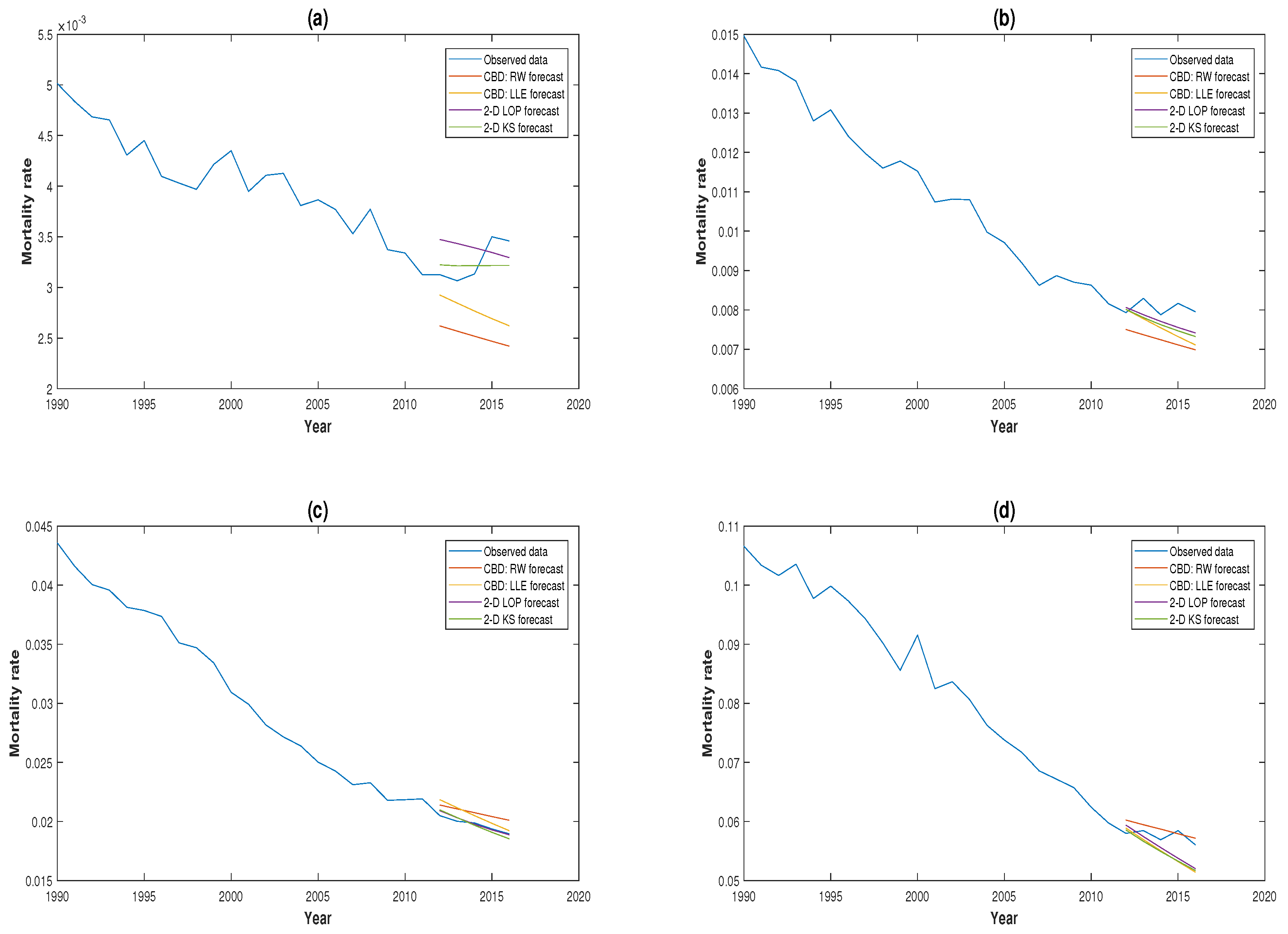
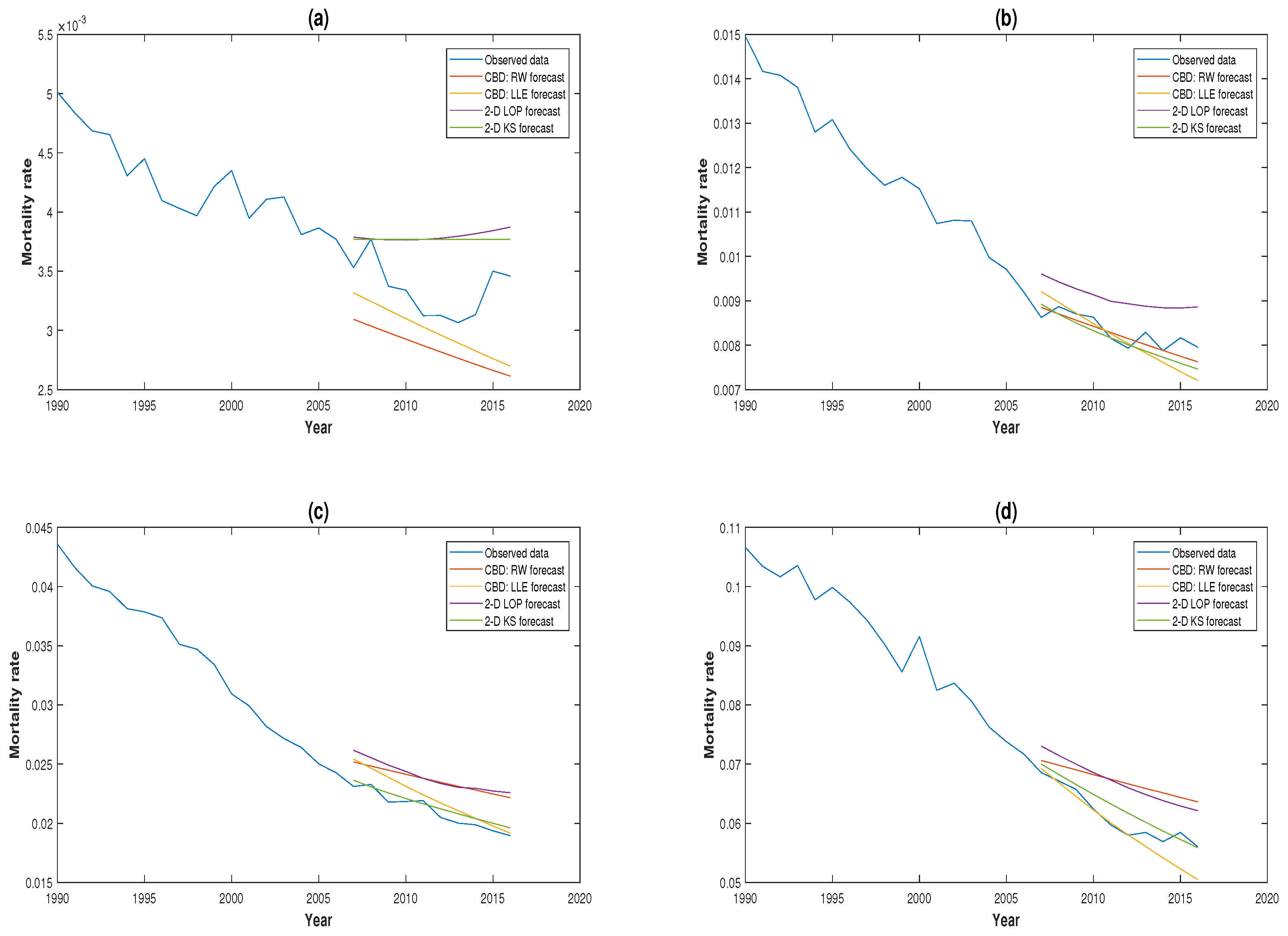
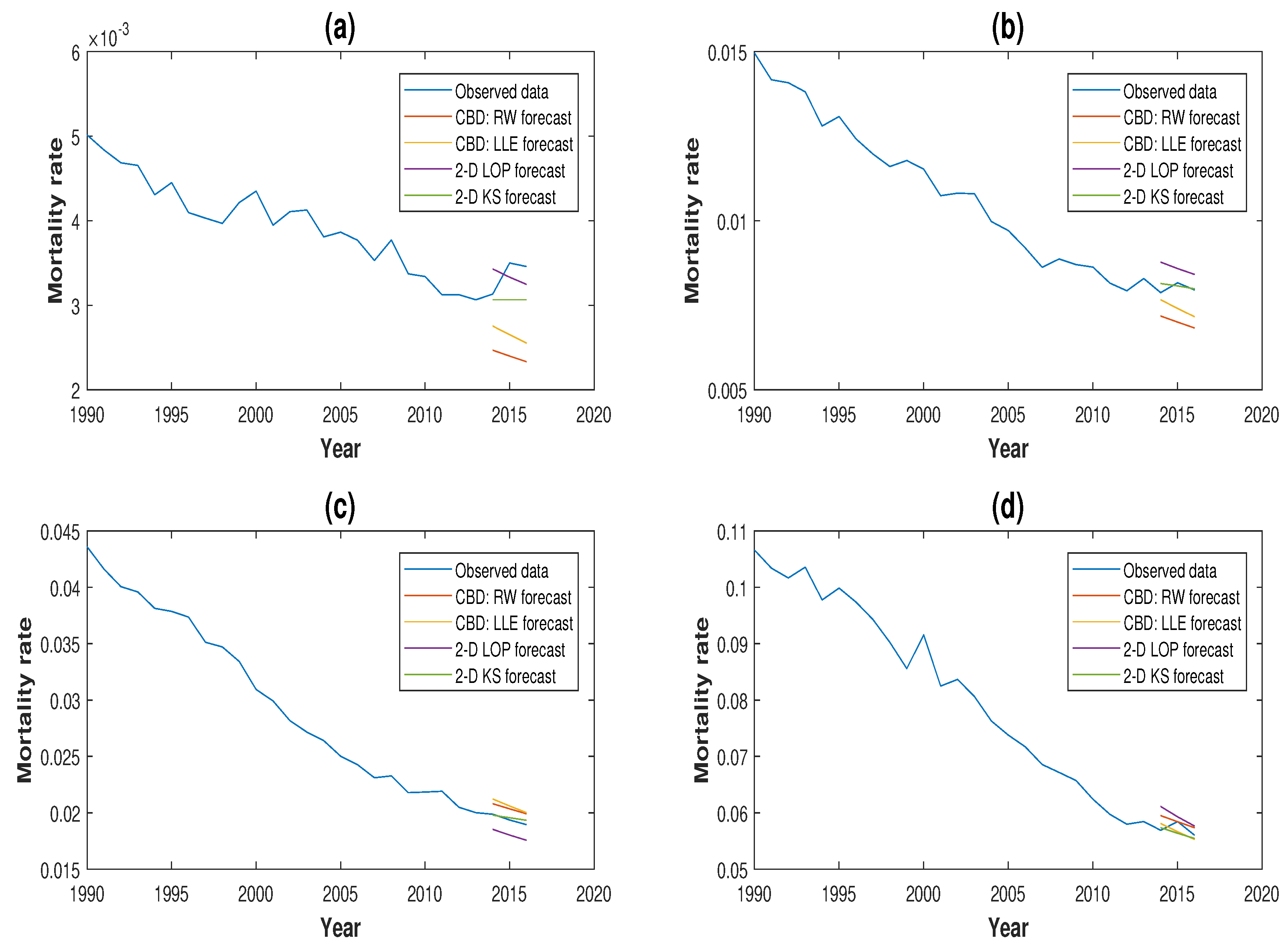
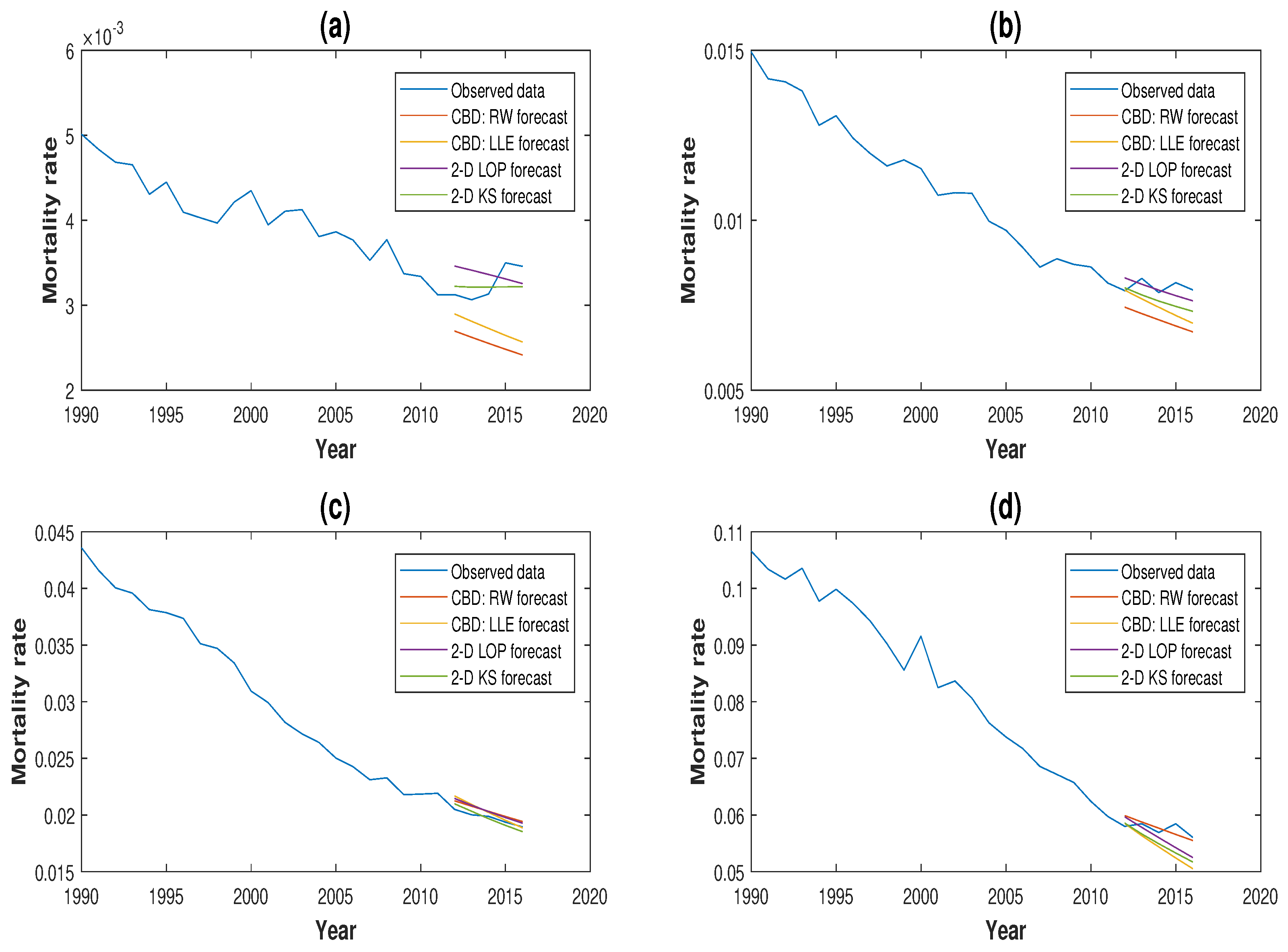
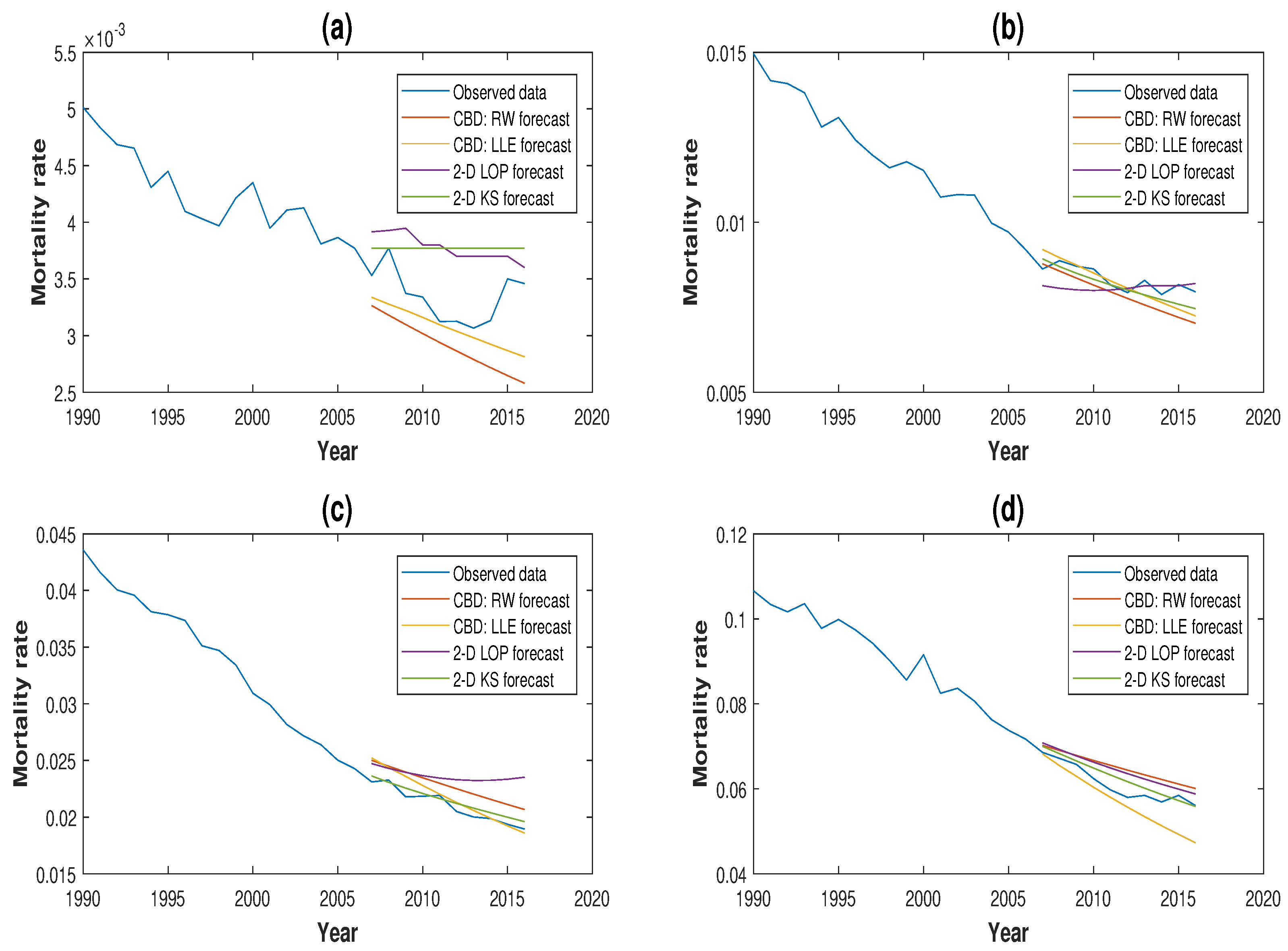
3.3. Comparison of Forecasting Performance
3.4. Robustness of Projections
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Booth, Heather, and Leonie Tickle. 2008. Mortality modelling and forecasting: A review of methods. Annals of Actuarial Science 3: 3–43. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson log-bilinear approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from England & Wales and the United States. North American Actuarial Journal 13: 1–35. [Google Scholar]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, and Marwa Khalaf-Allah. 2011. Mortality density forecasts: An analysis of six stochastic mortality models. Insurance: Mathematics and Economics 48: 355–67. [Google Scholar] [CrossRef]
- Currie, Iain D., Maria Durban, and Paul H. C. Eilers. 2004. Smoothing and forecasting mortality rates. Statistical Modeling 4: 279–98. [Google Scholar] [CrossRef]
- Denuit, Michel, and Anne-Cécile Goderniaux. 2005. Closing and projecting life tables using log-linear models. Bulletin of the Swiss Association of Actuaries 1: 29–48. [Google Scholar]
- Dickson, David C. M., Mary Hardy, and Howard R. Waters. 2009. Actuarial Mathematics for Life Contingent Risks. London: Cambridge University Press. [Google Scholar]
- Dokumentov, Alexander, and Rob J. Hyndman. 2014. Bivariate Data with Ridges: Two-Dimensional Smoothing of Mortality Rates. Working Paper Series; Melbourne: Monash University. [Google Scholar]
- Dowd, Kevin, Andrew J. G. Cairns, David Blake, Guy D. Coughlan, David Epstein, and Marwa Khalaf-Allah. 2010. Evaluating the goodness of fit of stochastic mortality models. Insurance: Mathematics and Economics 47: 255–65. [Google Scholar] [CrossRef]
- Gompertz, Benjamin. 1825. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society 115: 513–85. [Google Scholar] [CrossRef]
- Härdle, Wolfgang. 1990. Applied Nonparametric Regression. London: Cambridge University Press. [Google Scholar]
- Haberman, Steven, and Arthur Renshaw. 2009. On age-period-cohort parametric mortality rate projections. Insurance: Mathematics and Economics 45: 255–70. [Google Scholar] [CrossRef]
- Human Mortality Database. 2019. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: http://www.mortality.org (accessed on 22 February 2019).
- Hyndman, Rob J., and Md Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates a functional data approach. Computational Statistics & Data Analysis 51: 4942–56. [Google Scholar]
- Li, Han, Colin O’Hare, and Xibin Zhang. 2015. A semiparametric panel approach to mortality modelling. Insurance: Mathematics and Economics 61: 264–70. [Google Scholar]
- Li, Han, Colin O’Hare, and Farshid Vahid. 2016. Two-dimensional kernel smoothing of mortality surface: An evaluation of cohort strength. Journal of Forecasting 35: 553–63. [Google Scholar] [CrossRef]
- Li, Han, and Colin O’Hare. 2017. Semi-parametric extensions of the Cairns–Blake–Dowd model: A one-dimensional kernel smoothing approach. Insurance: Mathematics and Economics 77: 166–76. [Google Scholar] [CrossRef]
- Li, Han, Colin O’Hare, and Farshid Vahid. 2017. A flexible functional form approach to mortality modelling: Do we need additional cohort dummies? Journal of Forecasting 36: 357–67. [Google Scholar]
- Lee, Ronald D, and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–75. [Google Scholar] [CrossRef]
- Mádi-Nagy, Gergely. 2012. Polynomial bases on the numerical solution of the multivariate discrete moment problem. Annals Operations Research 200: 75–92. [Google Scholar] [CrossRef]
- O’Hare, Colin, and Youwei Li. 2012. Explaining young mortality. Insurance: Mathematics and Economics 50: 12–25. [Google Scholar] [CrossRef]
- Plat, Richard. 2009. On stochastic mortality modelling. Insurance: Mathematics and Economics 45: 393–404. [Google Scholar]
| 1 | For a summary of existing forecasting models, please see Booth and Tickle (2008). Mortality modelling and forecasting: A review of methods. Annals of Actuarial Science 3, 3–43. |
| 2 | For readers who want to read about the detailed derivation of the formula, please refer to: Dickson et al. (2009). Actuarial Mathematics for Life Contingent Risks. Cambridge University Press, London. |
| 3 | |
| 4 | |
| 5 | We have also considered the mortality experience of the U.S. and Luxembourg for the periods 1950–2016 and 1960–2014, respectively. The results are in line with the findings and conclusions in this paper. These additional results are available upon request. |
| CBD Model: MLE | CBD Model: LLE | 2D LOP Model | 2D KS Model | |
|---|---|---|---|---|
| 0.64 | 0.07 | 0.03 | ||
| 4.23 | 4.42 | 2.94 | 1.75 | |
| 5.73 | 5.52 | 3.63 | 2.34 |
| CBD Model: RW Forecast | CBD Model: LL Forecast | |||||
|---|---|---|---|---|---|---|
| Forecast horizon | ||||||
| 3 | 8.13 | 10.16 | 7.08 | 8.89 | ||
| 5 | 7.44 | 9.23 | 7.37 | 9.32 | ||
| 10 | 3.58 | 8.15 | 9.73 | 6.36 | 8.11 | |
| 2D LOP Model | 2D KS Model | |||||
|---|---|---|---|---|---|---|
| Forecast horizon | ||||||
| 3 | 4.71 | 5.62 | 2.39 | 3.14 | ||
| 5 | 4.54 | 5.69 | 4.53 | 5.53 | ||
| 10 | 8.87 | 9.02 | 10.25 | 1.97 | 3.80 | 5.06 |
| CBD Model: RW Forecast | CBD Model: LLE Forecast | |||||
|---|---|---|---|---|---|---|
| Forecast horizon | ||||||
| 3 | 8.34 | 10.80 | 7.11 | 8.73 | ||
| 5 | 8.06 | 10.42 | 7.04 | 9.10 | ||
| 10 | 7.42 | 8.97 | 6.94 | 9.52 | ||
| 2D LOP Model | 2D KS Model | |||||
|---|---|---|---|---|---|---|
| Forecast horizon | ||||||
| 3 | 3.70 | 4.50 | 2.39 | 3.14 | ||
| 5 | 4.64 | 5.76 | 4.53 | 5.53 | ||
| 10 | 5.25 | 7.06 | 9.98 | 1.97 | 3.80 | 5.06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; O’Hare, C. Mortality Forecasting: How Far Back Should We Look in Time? Risks 2019, 7, 22. https://doi.org/10.3390/risks7010022
Li H, O’Hare C. Mortality Forecasting: How Far Back Should We Look in Time? Risks. 2019; 7(1):22. https://doi.org/10.3390/risks7010022
Chicago/Turabian StyleLi, Han, and Colin O’Hare. 2019. "Mortality Forecasting: How Far Back Should We Look in Time?" Risks 7, no. 1: 22. https://doi.org/10.3390/risks7010022
APA StyleLi, H., & O’Hare, C. (2019). Mortality Forecasting: How Far Back Should We Look in Time? Risks, 7(1), 22. https://doi.org/10.3390/risks7010022





