1. Introduction
Many investment instruments are illiquid and costly to trade. This makes the corresponding optimal risk and performance management a highly complex task: When the investor is subject to a lower bound on net return, he/she is forced to reduce the total risk of his/her portfolio after a loss. In this case, he/she faces a tradeoff of either paying the transaction cost and deleveraging or keeping his/her current position in the illiquid instrument and hedging away some of the risk with more liquid instruments (such as, e.g., futures contracts). While hedging is an attractive solution because it allows one to economize the transaction costs, this solution is not perfect because it leaves the investor with the residual, unhedgeable risk and thus may expose him/her to further losses. How should an investor optimally exploit this tradeoff, and how do the corresponding optimal policies depend on the portfolio characteristics? The goal of this paper is to address these questions.
To this end, we consider a modified version of the
Merton (
1969,
1971) problem for a finite horizon investor (a portfolio manager) facing a lower bound on net return: the total return over the investment horizon needs to stay above a given threshold. The investor has access to three securities: a risk-free bond, a risky and illiquid alpha-generating asset (the asset) and a liquid futures contract, positively correlated with the asset. After experiencing a loss, investor’s effective risk aversion naturally increases, forcing him/her to reduce his/her risky positions and move into the risk-free bonds.
We perform our analysis in two steps. First, we study the “frictionless” problem without transaction costs. Second, we assume that transaction costs are small and use recent results in portfolio selection with small transaction costs (see
Kallsen and Muhle-Karbe 2017) to solve for the optimal portfolio in the case with frictions.
For simplicity, we assume that the investment opportunity set (captured by the expected returns, volatilities and correlations of all assets) is constant. As a result, the investor’s frictionless allocation problem across the asset and the futures contract is effectively static, determined by the short-term (instantaneous) mean-variance tradeoff. Thus, the only non-trivial part of the problem comes from determining the total amount of leverage (or, equivalently, exposure to risk) as a function of the investment horizon. We characterize this optimal risky exposure explicitly and study how it depends on various model parameters. Then, using the explicit solution of
Kallsen and Muhle-Karbe (
2017), we show that the optimal policy consists of keeping the asset position inside an explicitly given no-trade region around the target asset position in the frictionless model; we then study the behavior of this no-trade region.
3. Model
There is a risky asset (investment fund) whose price (net asset value)
follows a geometric Brownian motion process:
Here,
is a Brownian motion, and
is the futures price that also follows a geometric Brownian motion,
where
is a Brownian motion that is independent of
By definition,
measures the residual (unhedgeable) risk of the asset. We assume that the risky asset is illiquid and trading it requires paying a proportional cost of
per share of the asset. Because of this illiquidity, the residual risk captured by
will play a crucial role in the risk-liquidity tradeoff that we study below.
In addition to the risky investment opportunities (the asset and the futures contract), the agent in our model has a bank account that grows continuously at the risk-free rate
We assume that futures are traded at margin, and hence, changes in the futures price are immediately included in the bank account balance. Under this assumption, given the total notional exposure of
to the futures contract, the agents’ bank account evolves as:
where
is the cost of trading and rebalancing the illiquid asset, given by:
where
is the total variation of the number of shares process,
over the interval
1 Here,
is the number of shares of the risky asset in the agent’s portfolio, while
represents the amount of wealth invested in the fund. That is, the bank account grows at the rate
and the agent uses it to pay the transaction fees,
, whenever he/she changes the number of shares by
also, the fund value is transferred to/from the bank account whenever
Finally, the futures contract position is continuously marked to market, generating the term
in the bank account dynamics.
We assume that the agent has constant relative risk aversion preferences over terminal wealth:
given by the sum of the bank account value and the value of the illiquid asset; the agent maximizes the value function:
for some
under the terminal wealth constraint
with:
That is, his/her time
T wealth is allowed to be at most
percent below his/her initial wealth
The set of admissible strategies is defined as usual to be the set of progressively measurable processes
satisfying the square integrability condition:
as well as the nonnegative liquidation value constraint
almost surely for all
5. Approximately Optimal Strategies with Small Transaction Costs
In this section, we use the general results of
Kallsen and Muhle-Karbe (
2017) to derive approximately optimal trading strategies for the case with small transaction costs. Recall that we use
to denote the amount of wealth invested into the illiquid fund, so that the optimal number of shares in the fund for the frictionless case is given by
As
Kallsen and Muhle-Karbe (
2017) show, in this case, the approximate optimal strategy is characterized by a no-trading zone
around the frictionless optimal policy, so that the agent always keeps his/her total number of shares
of the illiquid asset inside this zone and trades towards the boundary of the zone every time when his/her position crosses the boundary. This policy is approximately optimal in the sense that the expected utility loss from following this policy is of the order of
The optimal half-width of the approximate no-trading zone,
is given by:
where
and
denote the realized quadratic variations of the trading strategy
and the fund value
, respectively. Furthermore,
is the effective risk tolerance of the agent.
We thus arrive at the following result.
Proposition 1. Let be the wealth process after transaction costs. The approximately optimal no-trading zone is given by:where:Here, is the optimal wealth process with transaction costs. The optimal strategy is to keep the number of shares inside the band, by minimally buying it when reaches the lower boundary and minimally selling when it reaches the upper boundary of the band. That is,where are the minimal nondecreasing processes that such that always stays inside the band (6). In particular, satisfy:When the number of illiquid asset shares, is inside the no-trading zone, the width of the zone is proportional to the hedging ratio, : Recall that, by Lemma 2, the optimal policy in the frictionless case is to keep the ratio between the number of fund shares,
, and the quotient
of the benchmark-adjusted wealth process,
to the fund value,
, at a constant level
given by the risk-return tradeoff of the fund,
normalized by the risk aversion
Proposition 1 shows that in the presence of transaction costs, the optimal policy is to keep the number of shares within a band around the quotient
. The width of this band is increasing in the transaction costs size
the larger the cost, the costlier it is to track the optimal position
because the latter is too volatile and moves too much with
and
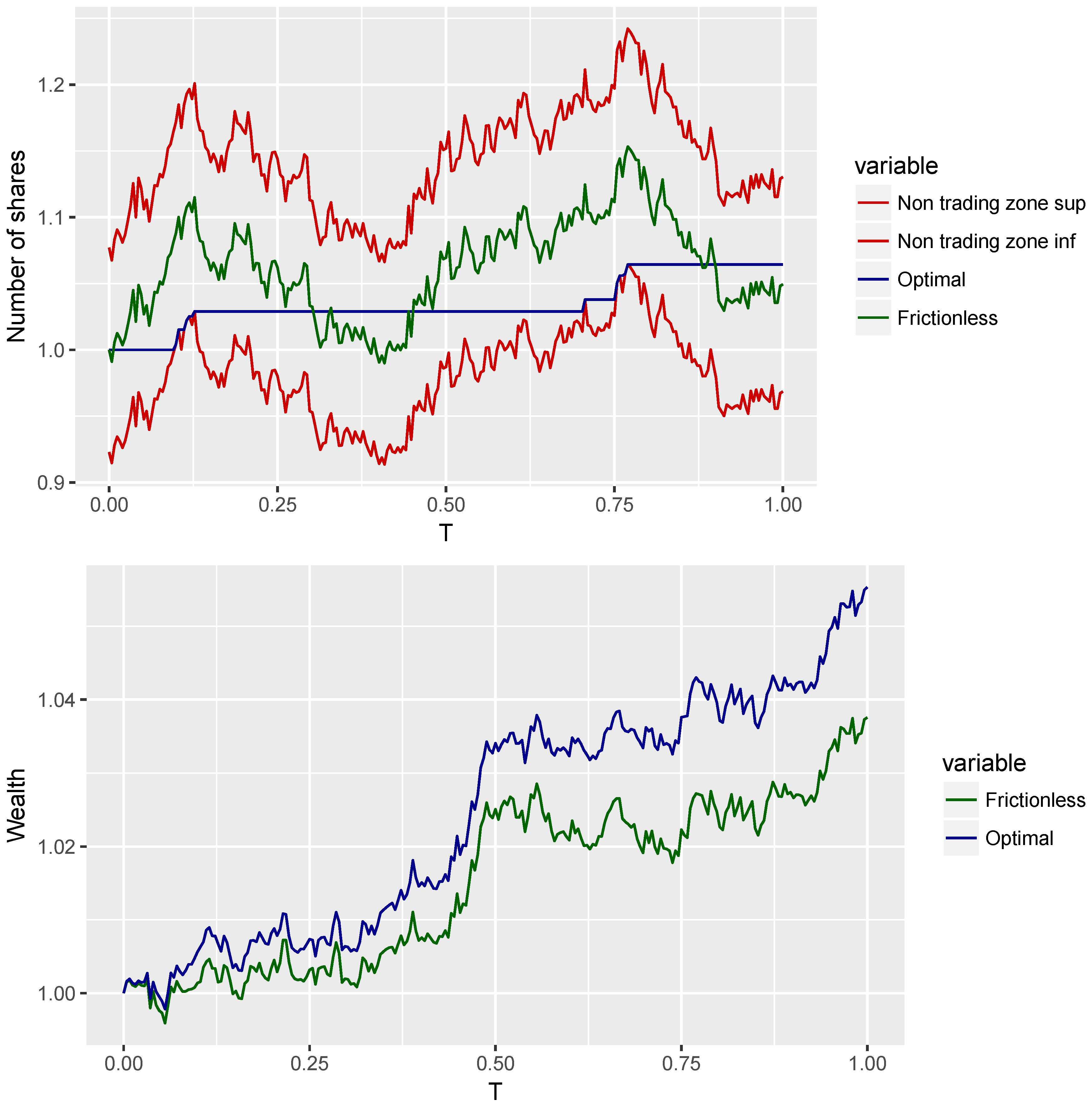
Figure 1 illustrates the inefficiency of frequent rebalancing: while following
of Lemma 2 would be optimal absent costs, in the presence of costs, it leads to significant losses, and the returns from following the strategy of Proposition 1 significantly dominate the returns from following the frictionless strategy, despite infrequent rebalancing.
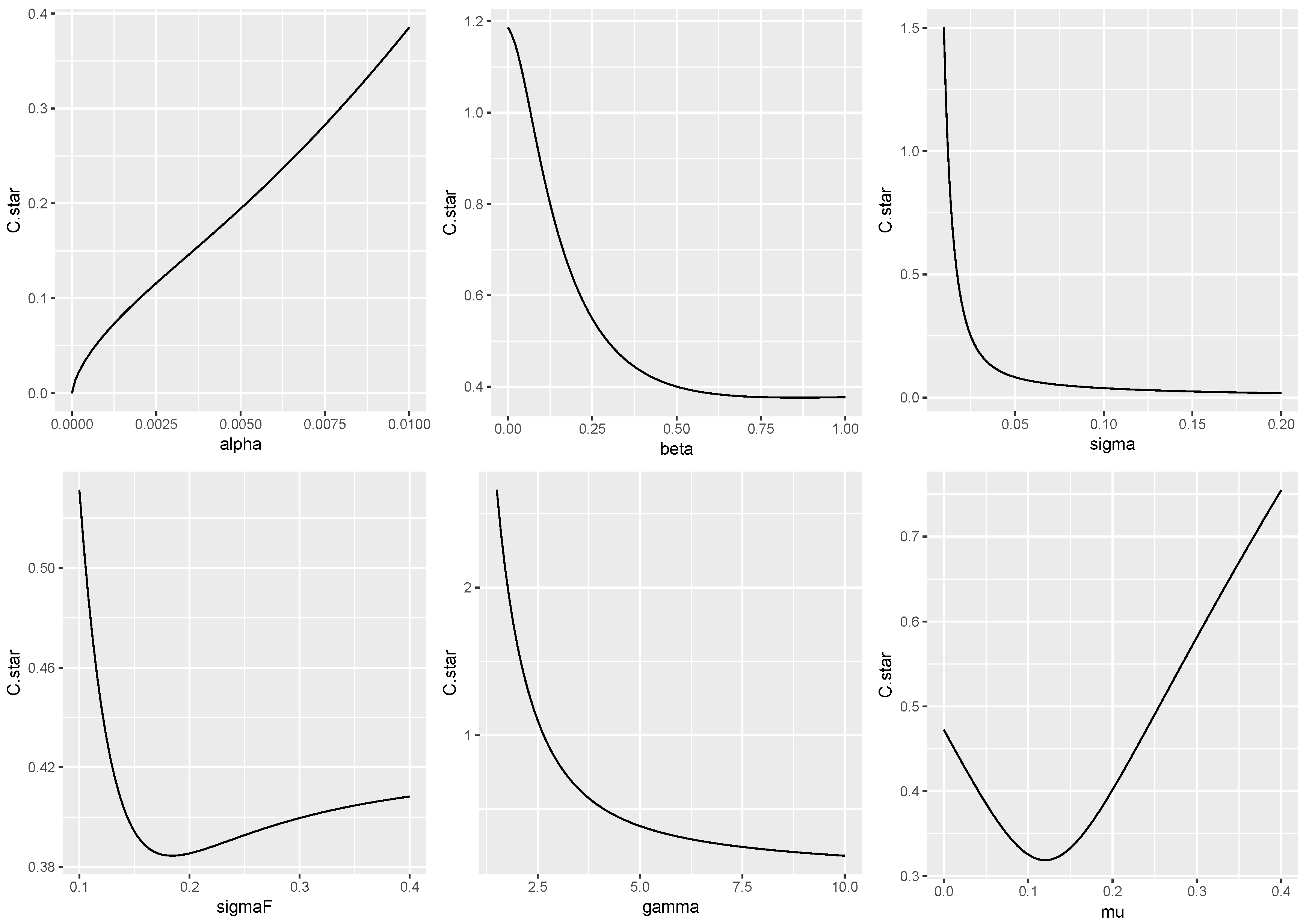
Our explicit expression for the width parameter of the no-trading zone, allows us to derive several interesting comparative statics results. The following result follows directly from the expression:
Proposition 2. The following is true:
If , then is monotone increasing in α and monotone decreasing in σ;
if and then is monotone decreasing in
If then is monotone decreasing in both β and ;
is monotone decreasing in μ for , and is monotone increasing in μ otherwise.
Proposition 2 and
Figure 2 show that
may exhibit complex behavior. First,
tends to be monotone increasing in
when the asset is good (with
large relative to risk,
), it is less expensive to hedge and stay exposed to
than to rebalance. Second, when risk aversion is higher, the agent finds it optimal to track the target portfolio as close as possible because the utility cost of an inefficient amount of risk taking is high; hence,
tends to be decreasing in
The effect of unhedgeable risk is similar: a larger
increases the utility cost of inefficient portfolio and hence triggers a more frequent rebalancing, implying that
is decreasing in
The effects of
and
(the parameters of the futures price process) are more subtle. For small values of
and
the risk-return tradeoff effect of the illiquid asset dominates: a larger
or a larger
makes it more costly to deviate from the target. However, when
is large, the ratio
is small, and hence, the liquid futures contract becomes a good substitute for the illiquid asset. Thus, it becomes less important to hold the efficient exposure to the illiquid asset, and the no-trade band widens.
The Response of the No-Trading Zone to Shocks
The following proposition follows by direct calculation.
Proposition 3. Inside the no-trade region, the wealth dynamics is given by:with:where s is the number of shares of the illiquid asset. Because the number of shares does not change inside the no-trading zone, the frictional wealth process deviates from its frictionless counterpart in Lemma 2. In particular, while the hedging ratio, is constant in the frictionless case, it exhibits a non-trivial behavior in the presence of frictions. The following is a direct consequence of Proposition 3 and Lemma 2:
Corollary 1. Inside the no-trading zone, given the illiquid asset position, the hedging ratio satisfies:Thus, the sensitivity of the hedging ratio to shocks is positive if and only if That is, when is high relative to , a negative shock to leads to a drop in the hedging ratio. By contrast, when is low, hedging substitutes for rebalancing: a negative shock to leads to a drop in the hedging ratio. Furthermore, the sensitivity of the hedging ratio to shocks is always positive. The intuition behind this result is straightforward: the response of to depends on the contribution of to total wealth (net of benchmark), When this contribution is large, its contribution to the numerator in dominates, and the hedging ratio responds positively to shocks to By contrast, when is low, barely responds to shocks to and hence, the denominator in dominates, making the hedging ratio respond negatively to shocks to
By Proposition 1, the width of the no-trading zone is proportional to . Thus, all results of Corollary 1 translate directly into analogous results for the no-trading zone.
Corollary 2. Inside the no-trading zone, given the illiquid asset position, the sensitivity of to shocks is positive if and only if That is, when is high relative to , a negative shock to narrows the no-trading zone. By contrast, when is low, a negative shock to leads to a widening of the no-trading zone. Furthermore, the sensitivity of the hedging ratio to shocks is always positive.
The intuition behind this result is similar to that for Corollary 1: when is large relative to it is less expensive for the agent to hedge rather then to sell. By contrast, when is small, the illiquid asset’s contribution is already so small that it is more efficient for the agent to sell.