Surrender Risk in the Context of the Quantitative Assessment of Participating Life Insurance Contracts under Solvency II
Abstract
1. Introduction
2. Regulatory Requirements on the Recognition of Policyholder Behavior
2.1. General Definitions of Solvency II
2.2. Reflection of Policyholder Behavior in Quantitative Assessments under Solvency II
- lapse up: a permanent increase of option exercise rates by ;
- lapse down: a permanent decrease of option exercise rates by , with the decrease not exceeding 20 percentage points;
- mass lapse: the instantaneous discontinuance of of the insurance policies.
3. Analysis Framework
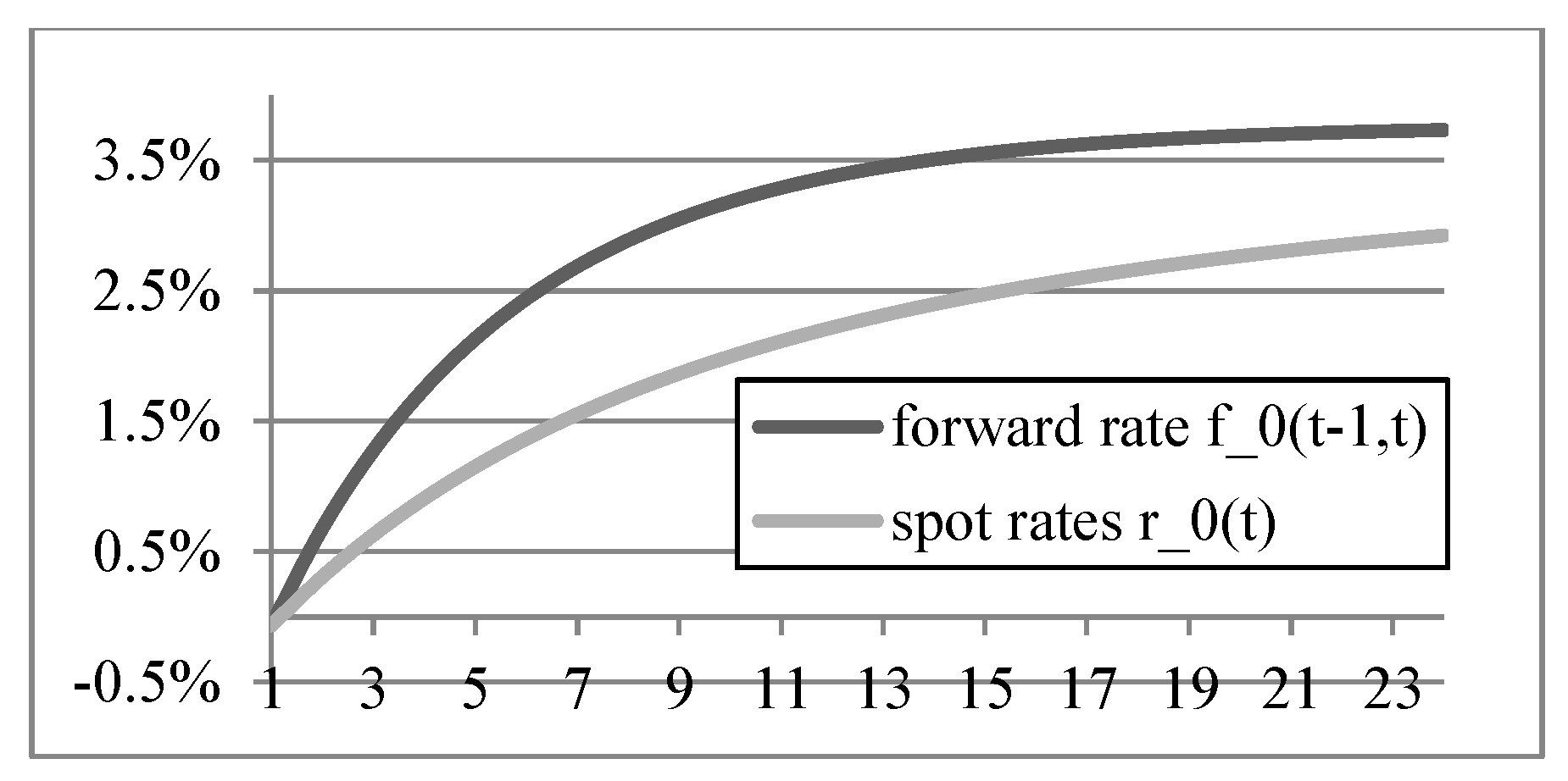
3.1. Financial Market Model
3.2. Liability Model
3.2.1. Premium Calculation and Reserving
3.2.2. Surplus Participation and Benefit Payments
- ongoing bonuses that are accumulated in an interest-bearing bonus reserve , i.e.,with ;
- terminal bonuses , allocated to the terminal bonus fund , that evolves according toPolicyholders do not have a claim on the Terminal Bonus Funds (TBF) until they are declared for payout in the next year. Funds may even be withdrawn from the TBF according to § 140 Insurance Supervision Law (VAG, Versicherungsaufsichtsgesetz) in case of adverse events ().
3.2.3. Liability Portfolio Development
3.3. Surrender Model
3.4. Cost Model
3.5. Asset Model
3.6. Surplus Distribution
3.6.1. Sources of Surplus
- investment surplus, representing the difference between investment return and guaranteed return :where the policyholders’ account value at the beginning of year t (after premium payment) is given by ;
- risk surplus, representing the difference regarding mortality:
- cost surplus, representing the difference between charges included in the premium and actual costs incurred:
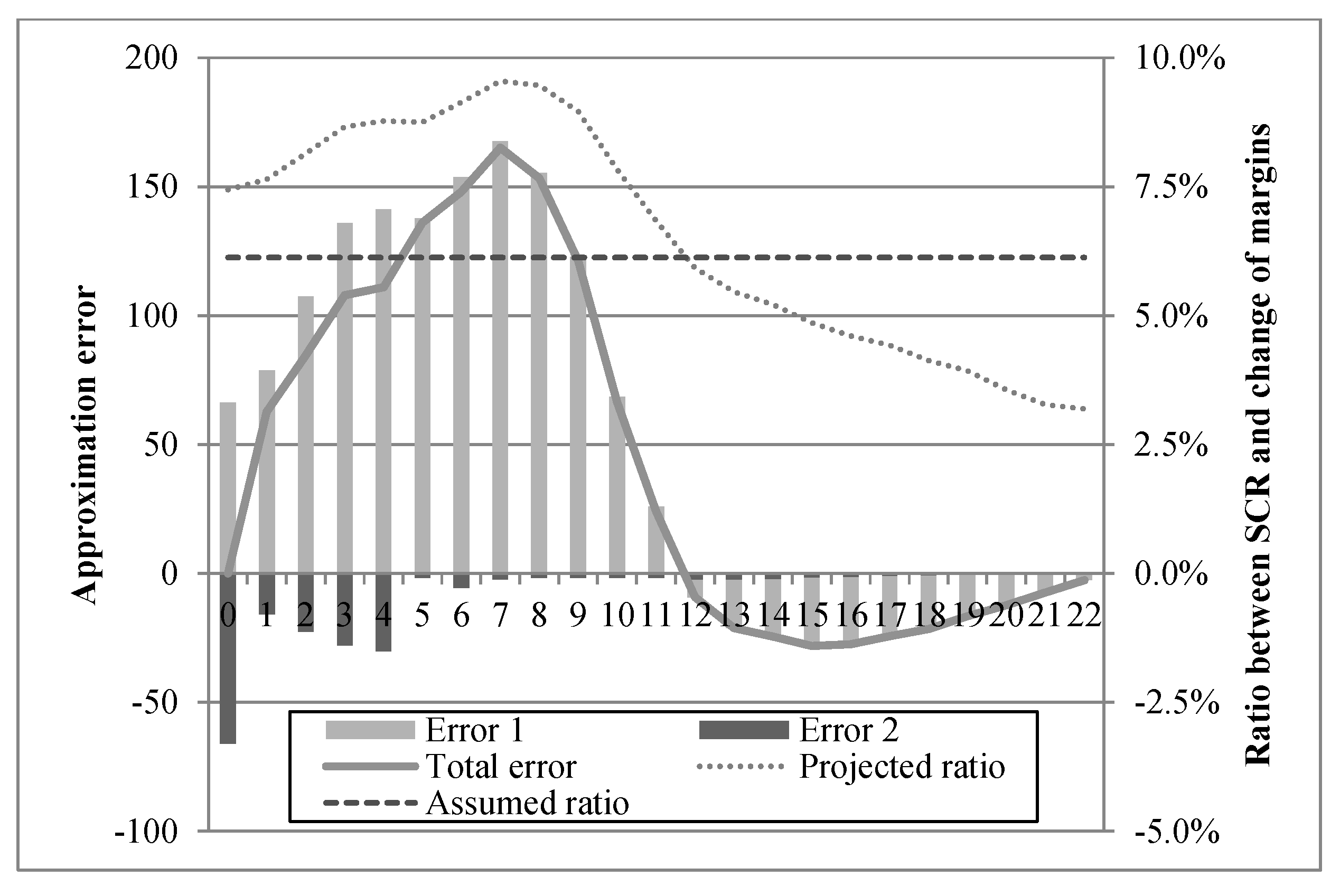
- surrender surplus, representing the surplus due to actual surrender, consisting of the net benefits to be paid to policyholders and the possible refunds received from the intermediary (with no surrender rates being included in the premium calculation):
3.6.2. Splitting of Surplus
3.6.3. Declaration of Surplus
3.6.4. Allocation of Surplus to Individual Policyholders
- Investment bonuses are distributed such that all policyholders receive the same total yield (sum of the guaranteed interest rate and the bonus rate ) on their account values. However, if investment bonuses are not sufficient for all policyholders to receive a total yield above their minimum guaranteed interest rate, bonus rates of cohorts with a lower guaranteed interest rate have to be reduced accordingly.
- Risk bonuses are allocated based on the capital at risk ().
- Other bonuses are allocated based on the premium .
3.7. Statutory Balance Sheet
3.8. Economic Balance Sheet
3.8.1. Base Case
- the BOF, which can be decomposed into the Present Value of Future Profits (PVFP) and the shareholders’ equity , i.e., ;
- the BEL, representing the insurer’s future obligations from the business in-force.
3.8.2. Allowance for Going Concern Reserve
3.8.3. Allowance for Surplus Funds
4. Numerical Results and Discussion
4.1. Model Assumptions
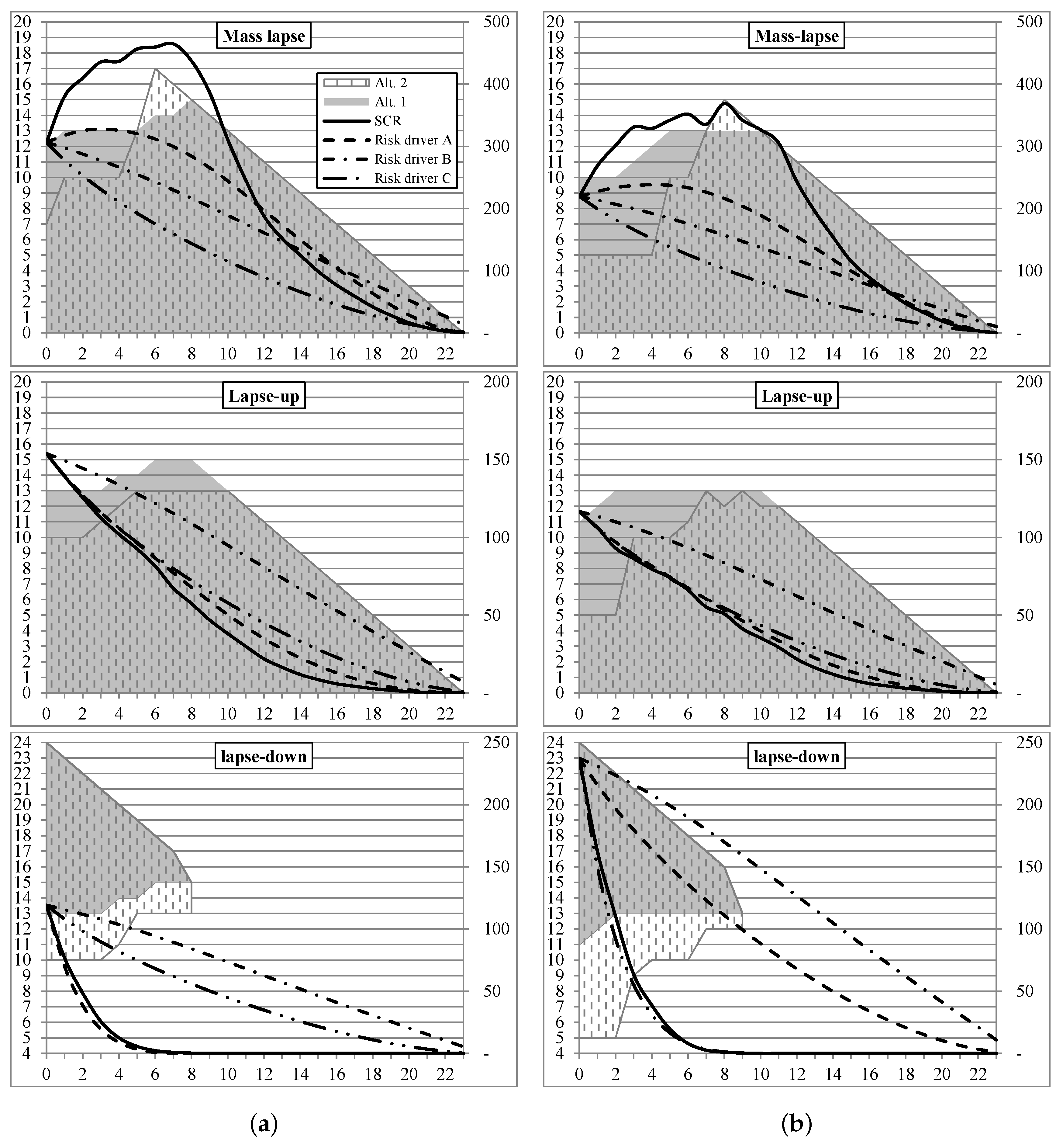
4.2. Surrender Risk in the Context of Solvency Capital Requirements
4.2.1. Segmentation Alternative 1: Change of
4.2.2. Segmentation Alternative 2: Change of BEL
- increase the stressed subset, starting with a stress of the HRG with the highest exposure and successively adding the HRG with the next highest exposure or
- start with a stress of the entire portfolio and successively eliminate the HRG with the lowest exposure.
- mass lapse/lapse up: we increase the number of stressed HRGs as long as SCR increases, starting with the youngest cohort (lowest technical interest rate and longest remaining duration);
- lapse down: we reduce the number of stressed HRGs as long as SCR increases, also starting with the youngest cohort.
4.2.3. Comparison and Conclusions
4.3. Surrender Risk in the Context of the Risk Margin
4.3.1. Explicit Projection of Future Solvency Capital Requirements
4.3.2. Approximation of Future Solvency Capital Requirements
Risk Driver A: Change of
Risk Driver B: Liabilities against Policyholders
Risk Driver C: Premium Income
4.3.3. Comparison
- Error 1: The approximation assumes a constant ratio between the (positive) change of margins and the resulting over time.
- Error 2: The positive change of margins used for the risk driver is based on segmentation alt. 1 and differs from the actual change of margins for the SCR projection which is based on segmentation alt. 2 (cf. Figure 1, grey highlighted area vs. patterned area).
4.3.4. Conclusions
4.4. The Impact of Lapse Stresses on Going Concern Reserve and Surplus Funds
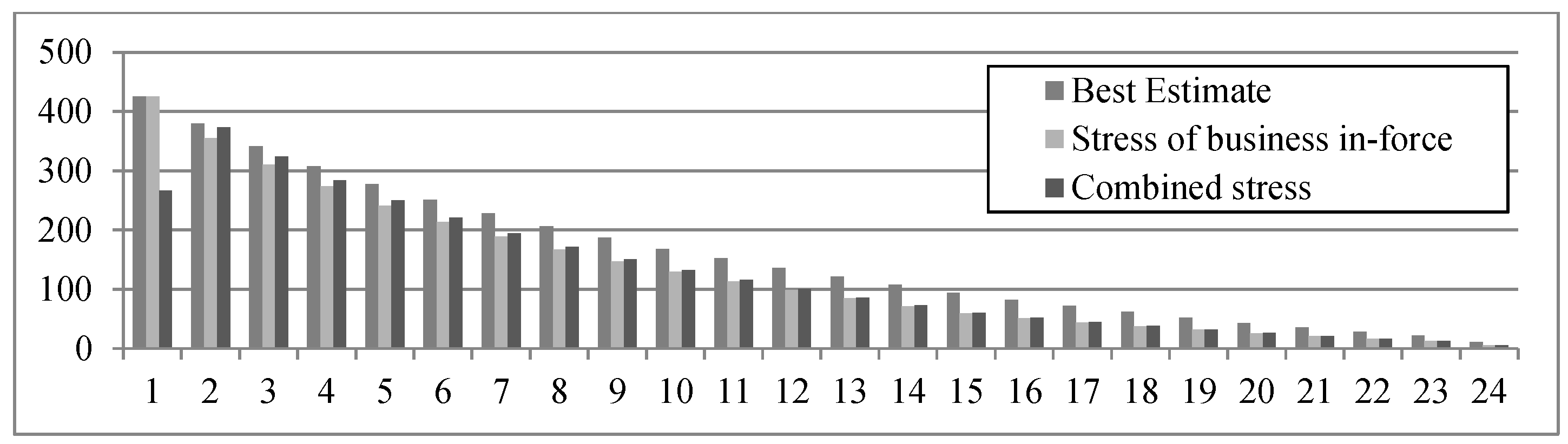
4.4.1. Going Concern Reserve
4.4.2. Surplus Funds
5. Conclusions
- Alt. 1 approximates the impact of a lapse stress on the BEL by the change of the guaranteed obligations (). The method allows for a simultaneous analysis of all contracts within a single projection. It is the methods currently applied by most life insurance companies in Germany.
- Alt. 2 represents a segmentation heuristic based on stochastic valuations. Contracts are classified into HRGs based on their expected lapse risk exposure. The HRGs are ranked based on a stand-alone assessment of their lapse risk. Based on this ranking, the actual cash flow projection model is repeatedly applied in order to identify the subset of stressed HRGs that results in the highest SCR.
Abbreviations
| Best Estimate of Guaranteed Obligations | |
| BEL | Best Estimate of Liabilities |
| BOF | Basic Own Funds |
| CE | Certainty Equivalent |
| CoC | Cost-of-Capital rate |
| ExC | Excess Capital |
| FDB | Future Discretionary Benefits |
| GCR | Going Concern Reserve |
| HRG | Homogeneous risk group |
| Mrg | Present Value of Margins |
| PVFP | Present Value of Future Profits |
| RfB | Reserve for Bonuses and Rebates (Rückstellung für Beitragsrückerstattung) |
| RM | Risk Margin |
| SCR | Solvency Capital Requirement |
| SF | Surplus Funds |
| TBF | Terminal Bonus Funds |
| TP | Technical Provisions |
| TVG | Time Value of Financial Guarantees |
| TVFOG | Time Value of Financial Options and Guarantees |
| TVO | Time Value of Financial Options |
| UGL | Unrealized Gains or Losses |
| VAG | Insurance Supervision Law (Versicherungsaufsichtsgesetz) |
Appendix A. Data from the German Life Insurance Market
| Year | Tariff | Cohort | Net Investment | Administration | Acquisition |
|---|---|---|---|---|---|
| Generation | Return a | Cost Rate a,c | Cost Rate a,d | ||
| 1987 | 0 | - | 7.58 % | 5.80 % | 5.50 % |
| 1988 | 0 | - | 7.32 % | 5.70 % | 5.50 % |
| 1989 | 0 | - | 7.05 % | 5.50 % | 5.50 % |
| 1990 | 0 | - | 6.78 % | 5.40 % | 5.50 % |
| 1991 | 0 | - | 7.44 % | 5.16 % | 5.50 % |
| 1992 | 0 | - | 7.39 % | 4.92 % | 5.50 % |
| 1993 | 0 | 24 | 7.59 % | 4.68 % | 5.50 % |
| 1994 | 0 | 23 | 7.15 % | 4.44 % | 5.50 % |
| 1995 | 1 | 22 | 7.37 % | 4.20 % | 5.50 % |
| 1996 | 1 | 21 | 7.37 % | 4.06 % | 5.52 % |
| 1997 | 1 | 20 | 7.46 % | 3.92 % | 5.54 % |
| 1998 | 1 | 19 | 7.57 % | 3.78 % | 5.56 % |
| 1999 | 1 | 18 | 7.58 % | 3.64 % | 5.58 % |
| 2000 | 1 | 17 | 7.51 % | 3.50 % | 5.60 % |
| 2001 | 2 | 16 | 6.12 % | 3.44 % | 5.60 % |
| 2002 | 2 | 15 | 4.68 % | 3.38 % | 5.60 % |
| 2003 | 2 | 14 | 5.05 % | 3.32 % | 5.60 % |
| 2004 | 3 | 13 | 4.90 % | 3.26 % | 5.60 % |
| 2005 | 3 | 12 | 5.18 % | 3.20 % | 5.60 % |
| 2006 | 3 | 11 | 4.82 % | 3.00 % | 4.90 % |
| 2007 | 4 | 10 | 4.65 % | 2.90 % | 5.20 % |
| 2008 | 4 | 9 | 3.54 % | 2.80 % | 4.90 % |
| 2009 | 4 | 8 | 4.18 % | 2.70 % | 5.20 % |
| 2010 | 4 | 7 | 4.27 % | 2.40 % | 5.10 % |
| 2011 | 4 | 6 | 4.13 % | 2.40 % | 5.00 % |
| 2012 | 5 | 5 | 4.01 % b | 2.40 % | 5.00 % |
| 2013 | 5 | 4 | 4.01 % b | 2.30 % | 5.10 % |
| 2014 | 5 | 3 | 3.91 % b | 2.20 % | 5.00 % |
| 2015 | 6 | 2 | 3.64 % b | 2.30 % | 4.90 % |
| 2016 | 6 | 1 | 3.35 % b | 2.30 % | 4.80 % |
References
- Albizzati, Marie-Odile, and Hélyette Geman. 1994. Interest rate risk management and valuation of the surrender option in life insurance policies. Journal of Risk and Insurance 61: 616–37. [Google Scholar] [CrossRef]
- Bacinello, Anna Rita. 2003. Fair valuation of a guaranteed life insurance participating contract embedding a surrender option. Journal of Risk and Insurance 70: 461–87. [Google Scholar] [CrossRef]
- BaFin. 2013. Jahresbericht der bundesanstalt für finanzdienstleistungsaufsicht. Bonn/Frankfurt: BaFin. [Google Scholar]
- BaFin. 2015. Interpretative decisions—Überschussfonds nach Art. 91 der Solvency-II-Richtlinie. Bonn/Frankfurt: BaFin. [Google Scholar]
- Bauer, Daniel, Rüdiger Kiesel, Alexander Kling, and Jochen Ruß. 2006. Risk-neutral valuation of participating life insurance contracts. Insurance: Mathematics and Economics 39: 171–83. [Google Scholar] [CrossRef]
- Berdin, Elia, Helmut Gründl, and Christian Kubitza. 2017. Rising interest rates, lapse risk, and the stability of life insurers. ICIR Working Paper Series. [Google Scholar] [CrossRef]
- Branger, Nicole, and Christian Schlag. 2004. Zinsderivate: Modelle und Bewertung. Berlin: Springer. [Google Scholar]
- Bundesbank. 2017. Zeitreihe BBK01.WZ3089: Aus der Zinsstruktur abgeleitete Renditen für Pfandbriefe mit jährlichen Kuponzahlungen / RLZ 12 Jahr(e)/Monatsendstand. Available online: https://www.bundesbank.de/Navigation/DE/Statistiken/Zeitreihen_Datenbanken/Geld_und_Kapitalmaerkte/geld_und_kapitalmaerkte_details_value_node.html?tsId=BBK01.WZ3089&listId=www_skms_it04b (accessed on 1 December 2017).
- Burkhart, Tobias, Andreas Reuß, and Hans-Joachim Zwiesler. 2015. Participating life insurance contracts under solvency ii: Inheritance effects and allowance for a going concern reserve. European Actuarial Journal 5: 203–44. [Google Scholar] [CrossRef]
- Burkhart, Tobias, Andreas Reuß, and Hans-Joachim Zwiesler. 2017. Allowance for surplus funds under solvency ii: Adequate reflection of risk sharing between policyholders and shareholders in a risk-based solvency framework? European Actuarial Journal 7: 51–88. [Google Scholar] [CrossRef]
- Campbell, Jason, Michael Chan, Kate Li, Louis Lombardi, Lucian Lombardi, Marianne Purushotham, and Anand Rao. 2014. Modeling of Policyholder Behavior for Life Insurance and Annuity products. Schaumburg: Society of Actuaries. [Google Scholar]
- CFO Forum. 2016. Market Consistent Embedded Value Principles. Available online: http://www.cfoforum.nl/downloads/CFO-Forum_MCEV_Principles_and_Guidance_April_2016.pdf (accessed on 1 December 2017).
- Christiansen, Marcus C., and Andreas Niemeyer. 2014. Fundamental definition of the solvency capital requirement in solvency II. Astin Bulletin 44: 501–33. [Google Scholar] [CrossRef]
- Clark, Dominic, Jeremy Kent, and Edward Morgan. 2013. Dynamic Policyholder Behaviour and Management Actions Survey Report. Seattle: Milliman Survey, October 3, 59 p. [Google Scholar]
- EIOPA. 2011. Report on the Fifth Quantitative Impact Study (QIS5) for Solvency II (EIOPA-TFQIS5-11/001). Frankfurt: EIOPA, March 14. [Google Scholar]
- EIOPA. 2015. Guidelines on the Valuation of Technical Provisions (EIOPA-BoS-14/166 EN). Frankfurt: EIOPA, February 2. [Google Scholar]
- Eling, Martin, and Michael Kochanski. 2013. Research on lapse in life insurance: what has been done and what needs to be done? The Journal of Risk Finance 14: 392–413. [Google Scholar] [CrossRef]
- European Commission. 2015. Commission Delegated Regulation (EU) 2015/35. Brussels: European Commission. [Google Scholar]
- European Union. 2009. Directive 2009/138/EC of the European Parliament and of the Council of 25 November 2009 on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance (Solvency II). OJ L 335, 17.12.2009. Brussels: European Union, pp. 1–155. [Google Scholar]
- Feodoria, Mark, and Till Förstemann. 2015. Lethal Lapses: How a Positive Interest Rate Shock Might Stress German Life Insurers. No. 12. Frankfurt: Deutsche Bundesbank. [Google Scholar]
- Führer, Christian, and Arnd Grimmer. 2010. Einführung in die lebensversicherungsmathematik, 2nd ed. Karlsruhe: Verl. Versicherungswirtschaft. [Google Scholar]
- Gatzert, Nadine. 2009. Implicit options in life insurance: An overview. Zeitschrift für Die Gesamte Versicherungswissenschaft 98: 141–64. [Google Scholar] [CrossRef]
- GDV. 2015. Säule I-Anleitung für einzelunternehmen—Eine zusammenfassung der säule I-anforderungen von Solvency II für einzelunternehmen. Berlin: GDV. [Google Scholar]
- GDV. 2017a. Fachkonzept branchensimulationsmodell. Berlin: GDV. [Google Scholar]
- GDV. 2017b. Statistisches Rundschreiben Nr. 0960/2017 (LV): Kennzahlen-mappe 2017—Die deutsche lebensversicherung. Berlin: GDV. [Google Scholar]
- Geneva Association. 2012. Surrenders in the Life Insurance Industry and Their Impact on Liquidity. Geneva: Geneva Association. [Google Scholar]
- Glasserman, Paul. 2010. Monte Carlo Methods in Financial Engineering. New York: Springer. [Google Scholar]
- Grosen, Anders, and Peter Løchte Jørgensen. 2000. Fair valuation of life insurance liabilities: The impact of interest rate guarantees, surrender options, and bonus policies. Insurance: Mathematics and Economics 26: 37–57. [Google Scholar] [CrossRef]
- Kling, Alexander, Frederik Ruez, and Jochen Ruß. 2014. The impact of policyholder behavior on pricing, hedging, and hedge efficiency of withdrawal benefit guarantees in variable annuities. European Actuarial Journal 4: 281–314. [Google Scholar] [CrossRef]
- Kochanski, Michael. 2010. Solvenzkapital für flv unter berücksichtigung von dynamischem storno. Zeitschrift für Die Gesamte Versicherungswissenschaft 99: 689–710. [Google Scholar] [CrossRef]
- Kuo, Weiyu, Chenghsien Tsai, and Wei-Kuang Chen. 2003. An empirical study on the lapse rate: The cointegration approach. Journal of Risk and Insurance 70: 489–508. [Google Scholar] [CrossRef]
- Oechslin, Joachim, Olivier Aubry, Matthias Aellig, Alexander Kappeli, Daniel Bronnimann, Arnaud Tandonnet, and Guillaume Valois. 2007. Replicating embedded options. Life & Pension Risk February 3: 47–52. [Google Scholar]
- Reuß, Andreas, Jochen Ruß, and Jochen Wieland. 2015. Participating life insurance contracts under risk based solvency frameworks: How to increase capital efficiency by product design. In Innovations in Quantitative Risk Management. Springer Proceedings in Mathematics & Statistics. Cham: Springer, vol. 99, pp. 185–208. [Google Scholar]
- Wolfsdorf, Kurt. 1997. Versicherungsmathematik: Teil 1: Personenversicherung. Stuttgart: Vieweg + Teubner Verlag. [Google Scholar]
| 1. | For an overview of the existing literature e.g., see Eling and Kochanski (2013) or Campbell et al. (2014). |
| 2. | For more details concerning the definition of SCR see Christiansen and Niemeyer (2014). |
| 3. | We do not address the allowance of ancillary own funds and eligibility restrictions under the Solvency II framework. Therefore, BOF coincide with Eligible Own Funds. |
| 4. | |
| 5. | See comments given by the German Insurance Association regarding the required segmentation (GDV 2015). |
| 6. | Please note that although this paper concentrates on the option to surrender a contract prior to maturity, those challenges apply to all types of options, e.g., annuitization or premium indexation options. |
| 7. | The actual valuation does not consider new business. However, assumptions regarding expected new business are required to determine the GCR. |
| 8. | For technical reasons, both death and surrender occur at the end of the year. |
| 9. | |
| 10. | The valuation does not include new business and acquisition costs are only relevant for the calculation of the GCR (see Section 3.8.2). |
| 11. | Please note that the part of the commission that has to be repaid in case of surrender is similar but not identical to the Zillmer receivable. |
| 12. | This management rule is in line with common practice but different from Burkhart et al. (2017). |
| 13. | Please note that since the offsetting of different surplus sources is limited to the case of negative investment surplus, it is generally possible to have a positive surplus participation despite a negative raw surplus . |
| 14. | For a more detailed description of the surplus allocation process see Burkhart et al. (2015). |
| 15. | Please note that the Market Consistent Embedded Value framework (CFO Forum 2016) defines the TVFOG from the shareholders’ perspective (based on the PVFP), but in our model framework both approaches result in the same value. |
| 16. | Please note that are not included in the cash flows used to determine BEL (cf. Equation (5)). |
| 17. | SF can easily be combined with the GCR via the ex-post approach. |
| 18. | The rather small value of TVO is in line with current observations from practical applications. |
| 19. | Please note that margins increase from cohorts 16 to 14, 13 to 11, and 10 to 6. |
| 20. | Please note that similar to alt. 1, applying the lapse stresses to the oldest cohort 24 does not change the BEL at all. |
| 21. | |
| 22. | The latter can be traced back to the asymmetry of the profit sharing process in Germany which is reflected in our Monte Carlo valuation framework. Additional surrenders of contracts with fairly high technical interest rates in alt. 1 may reduce losses related to investment returns below the technical interest rate in downside scenarios, but has a smaller impact in upside scenarios. Overall, this has a positive impact on the PVFP that exceeds the loss of future margins. Hence, despite losing additional margins in alt. 1, the insurer is better off due to reduced volume of minimum interest rate guarantees. |
| 23. | For the base case, SCRs and the respective segmentations at time correspond to the results presented in Section 4.2. |
| 24. | For further details regarding the joint impact of increasing interest rates and surrender rates on the insurer’s solvency, see Berdin et al. (2017). |
| 25. | Although the segmentation between alt. 1 and 2 only differs until year 7, error 2 can be observed throughout the projection. This is due to the fact that risk driver A does not allow for dynamic policyholder behavior which slightly affects the change of margin. |
| Assets | Liabilities |
|---|---|
| Tariff | Years of Sale | x | n | G | i | Mortality Table | |||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1987–1994 | 40 | 25 | € 20,000 | DAV 2008 T a | ||||
| 1 | 1995–2000 | 40 | 25 | € 20,000 | DAV 2008 T | ||||
| 2 | 2001–2003 | 40 | 25 | € 20,000 | DAV 2008 T | ||||
| 3 | 2004–2006 | 40 | 25 | € 20,000 | DAV 2008 T | ||||
| 4 | 2007–2011 | 40 | 25 | € 20,000 | DAV 2008 T | ||||
| 5 | 2012–2014 | 40 | 25 | € 20,000 | DAV 2008 T | ||||
| 6 | 2015–2016 | 40 | 25 | € 20,000 | DAV 2008 T | ||||
| 7 | since 2017 | 40 | 25 | € 20,000 | DAV 2008 T |
| Assets | Liabilities | ||
|---|---|---|---|
| 1895 | |||
| 988 | |||
| 7067 | |||
| 2546 | |||
| Contract Year m | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| Deterministic surrender rate |
| d | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 years | 10 years | 5 years |
| Scenario | ||||||
|---|---|---|---|---|---|---|
| Base case | ||||||
| Interest rate sensitivity |
| Base Case | Interest Rate Sensitivity | |||||||
|---|---|---|---|---|---|---|---|---|
| Assets | Liabilities | Assets | Liabilities | |||||
| BOF | 1236 | BOF | 21 | |||||
| BEL | BEL | |||||||
| 2382 | 3259 | |||||||
| 120 | 211 | |||||||
| 2262 | 3048 | |||||||
| () | () | |||||||
| k | Alt. 1: | Alt. 2: (Stand-Alone Stress) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass Lapse | Lapse Up | Lapse Down | Mass Lapse | Lapse Up | Lapse Down | ||||||
| 24 | −0.79 | - | - | - | −576 | (-) | 42 | (-) | - | (-) | |
| 23 | −1.27 | −0.23 | −0.01 | 0.01 | −576 | (−16.1) | 42 | (−0.5) | 1 | (0.5) | |
| 22 | −1.80 | −0.44 | −0.03 | 0.03 | −580 | (−41.5) | 43 | (−2.0) | 2 | (1.8) | |
| 21 | −2.01 | −0.55 | −0.04 | 0.04 | −560 | (−61.9) | 45 | (−4.0) | 6 | (3.7) | |
| 20 | −2.12 | −0.62 | −0.06 | 0.06 | −522 | (−76.4) | 49 | (−6.1) | 12 | (5.9) | |
| 19 | −2.15 | −0.65 | −0.07 | 0.07 | −463 | (−95.7) | 56 | (−9.0) | 22 | (9.1) | |
| 18 | −2.12 | −0.66 | −0.08 | 0.08 | −382 | (−110.2) | 65 | (−12.1) | 34 | (12.2) | |
| 17 | −2.05 | −0.65 | −0.09 | 0.09 | −280 | (−123.3) | 77 | (−15.2) | 50 | (15.8) | |
| 16 | −1.28 | −0.37 | −0.04 | 0.04 | −158 | (−91.3) | 93 | (−12.7) | 64 | (13.4) | |
| 15 | −1.14 | −0.32 | −0.03 | 0.03 | −72 | (−95.8) | 105 | (−14.5) | 79 | (15.4) | |
| 14 | −1.00 | −0.27 | −0.02 | 0.03 | 23 | (−98.7) | 119 | (−15.6) | 97 | (16.9) | |
| 13 | −0.28 | −0.00 | 0.04 | −0.05 | 124 | (−57.6) | 135 | (−7.9) | 106 | (8.9) | |
| 12 | −0.12 | 0.05 | 0.06 | −0.07 | 185 | (−53.0) | 142 | (−6.7) | 114 | (7.1) | |
| 11 | 0.02 | 0.10 | 0.07 | −0.09 | 243 | (−47.8) | 149 | (−5.2) | 119 | (5.3) | |
| 10 | 0.73 | 0.38 | 0.16 | −0.19 | 297 | (−5.1) | 154 | (5.0) | 113 | (−5.9) | |
| 9 | 0.85 | 0.42 | 0.18 | −0.21 | 304 | (−3.6) | 149 | (5.1) | 106 | (−6.1) | |
| 8 | 0.95 | 0.45 | 0.20 | −0.24 | 305 | (−1.6) | 144 | (5.4) | 100 | (−6.2) | |
| 7 | 1.05 | 0.48 | 0.22 | −0.26 | 306 | (−0.5) | 138 | (5.2) | 94 | (−5.4) | |
| 6 | 1.13 | 0.51 | 0.23 | −0.29 | 305 | (2.4) | 134 | (5.8) | 88 | (−5.8) | |
| 5 | 1.74 | 0.75 | 0.33 | −0.41 | 300 | (37.9) | 129 | (15.7) | 71 | (−16.8) | |
| 4 | 1.75 | 0.76 | 0.35 | −0.45 | 257 | (37.7) | 114 | (15.8) | 55 | (−17.2) | |
| 3 | 1.74 | 0.76 | 0.38 | −0.48 | 219 | (39.9) | 98 | (17.4) | 35 | (−19.2) | |
| 2 | 2.49 | 1.02 | 0.54 | −0.71 | 178 | (87.5) | 81 | (38.0) | −8 | (−43.9) | |
| 1 | 2.39 | 0.96 | 0.56 | -0.76 | 85 | (84.6) | 42 | (42.0) | −57 | (−49.3) | |
| Change of | Mass Lapse | Lapse Up | Lapse Down | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| All | Alt. 1 | Alt. 2 | All | Alt. 1 | Alt. 2 | All | Alt. 1 | Alt. 2 | |||
| BEL | −576 | 185 | 306 | 42 | 135 | 154 | −57 | 97 | 119 | ||
| 3842 | 5303 | 4207 | 2366 | 2542 | 2440 | −3057 | 183 | 64 | |||
| −3232 | −4645 | −3755 | −2115 | −2285 | −2210 | 2763 | −169 | −80 | |||
| −1186 | −473 | −146 | −209 | −122 | −76 | 237 | 83 | 135 | |||
| (3.5%) | (4.9%) | (2.3%) | (2.6%) | (0.8%) | (1.1%) | ||||||
| SCR Projection | SCR Approximation (In % of Explicit SCR Projection) | ||||||
|---|---|---|---|---|---|---|---|
| Risk Driver A | Risk Driver B | Risk Driver C | |||||
| (Base case) | |||||||
| Mass lapse | 324 | 266 | () | 233 | () | 161 | () |
| Lapse up | 66 | 74 | () | 117 | () | 81 | () |
| Lapse down | 17 | 16 | () | 91 | () | 63 | () |
| Lapse | 324 | 266 | () | 233 | () | 161 | () |
| (Interest rate sensitivity) | |||||||
| Mass lapse | 281 | 201 | () | 169 | () | 115 | () |
| Lapse up | 54 | 57 | () | 90 | () | 61 | () |
| Lapse down | 38 | 35 | () | 183 | () | 124 | () |
| Lapse | 283 | 202 | () | 183 | () | 124 | () |
| Scenario | Mass Lapse | Lapse Up | Lapse Down | Lapse | ||||
|---|---|---|---|---|---|---|---|---|
| Base case | 303 | () | 71 | () | 22 | () | 303 | () |
| Interest rate sensitivity | 283 | () | 57 | () | 49 | () | 284 | () |
| Assumptions Regarding GCR | BOF | Change of BOF in Case of | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Best Estimate | Mass Lapse | Lapse Up | Lapse Down | ||||||||
| GCR | Total | GCR | Total | GCR | Total | GCR | Total | ||||
| Best estimate | 3445 | 3520 | 0 | −493 | 0 | −208 | 0 | −132 | |||
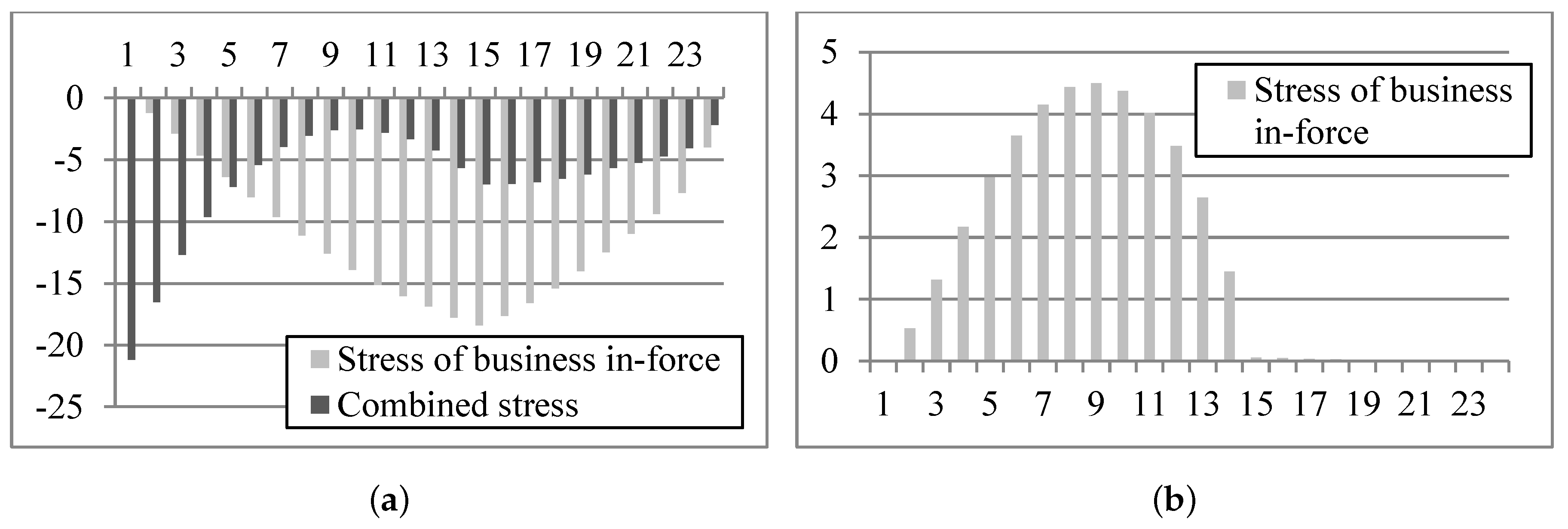
| Stress of business in-force | 3445 | 3520 | −556 | −825 | −184 | −342 | 32 | −115 | |||
| Combined stress | 3445 | 3520 | −632 | −878 | −118 | −284 | n/a | n/a | |||
| Calculation of Surplus Funds | BOF | Change of BOF | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Best Estimate | Mass Lapse | ||||||||
| SF | Total | SF | Total | SF | Total | ||||
| based on best estimate valuation | 3513 | 4749 | 3513 | 4452 | 0 | ||||
| without change of due to stress | 3513 | 4749 | 3543 | 4482 | |||||
| with change of due to stress | 3513 | 4749 | 3321 | 4260 | |||||
| (Terminal bonuses in year 1) | (411) | (633) | () | ||||||
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burkhart, T. Surrender Risk in the Context of the Quantitative Assessment of Participating Life Insurance Contracts under Solvency II. Risks 2018, 6, 66. https://doi.org/10.3390/risks6030066
Burkhart T. Surrender Risk in the Context of the Quantitative Assessment of Participating Life Insurance Contracts under Solvency II. Risks. 2018; 6(3):66. https://doi.org/10.3390/risks6030066
Chicago/Turabian StyleBurkhart, Tobias. 2018. "Surrender Risk in the Context of the Quantitative Assessment of Participating Life Insurance Contracts under Solvency II" Risks 6, no. 3: 66. https://doi.org/10.3390/risks6030066
APA StyleBurkhart, T. (2018). Surrender Risk in the Context of the Quantitative Assessment of Participating Life Insurance Contracts under Solvency II. Risks, 6(3), 66. https://doi.org/10.3390/risks6030066




