Abstract
Under state-dependent preferences, probabilities and units of scale of state-dependent utilities are not separately identified. In standard models, only their products matter to decisions. Separate identification has been studied under implicit actions by Drèze or under explicit actions and observations by Karni. This paper complements both approaches and relates them when conditional preferences for final outcomes are independent of actions and observations. That special case permits drastic technical simplification while remaining open to some natural extensions.
1. Introduction
This paper offers a modest contribution to the theme of separately identifying probabilities and utility scales in the expected-utility analysis of individual decisions under uncertainty with state-dependent preferences. For a background discussion, see the survey in Drèze and Rustichini (2004). The basic issue is that probabilities and state-dependent utility scales enter as products in expected utility calculations—hence they are not separately identified from observed decisions. Yet, there are situations where separate identification is highly desirable. For instance, it is often claimed that medical decisions should reflect the probabilities of the doctor and the utility of the patient.
In order to achieve separate identification, one can (sometimes) rely on expected utilities evaluated under alternative probabilities. How do alternative probabilities enter the model? There are two routes: (i) actions of the decision-maker affecting the likelihood of events (e.g., diet); and (ii) new information modifying the probabilities of given events (e.g., medical tests).
Route (i) carries the limitation of being applicable only to those events that are potentially subject to influence by the decision maker.1 It calls for a specification of the actions through which that influence is exercised, and their properties, such as: are these actions observable? Are they costly? Do they affect preferences, and if so how?
Route (ii) has potentially wider application; but its implementation requires evaluation of the probabilities with which specific information may become available. This may impose on the decision maker the unwieldy task of assessing the probabilities of occurrences that lie outside the decision problem at hand. The present paper avoids that difficulty by restricting attention to information with exogenous probabilities—coming from statistical sources, expert evaluations and the like. That does not exhaust the topic, but has the advantage of transparency.
Route (i) was followed for the first time (in so far as I know) in Drèze (1958)—my unpublished PhD dissertation, written under the precious guidance of William Vickrey. The complete model came out in Drèze (1987a), with a preview in French (Drèze 1961). In that model, actions are not observable, only their influence on state probabilities comes in. Observable actions appear in Karni (2011, 2013).
Route (ii) was introduced, and integrated with route (i), by Karni (2011), extending some of his earlier work; it is pursued by Karni (2013)—the most general treatment to date.
The papers by Drèze and Karni are technically demanding—the more so when the model and assumptions are very general. One motivation of the present paper is to provide a transparent analysis for a model that is less general—while retaining applicability to a meaningful set of circumstances. Two limitations are introduced: (i) actions are assumed observable; they may carry some cost or disutility; but they do not affect conditional preferences; this corresponds to the specification in Karni (2011), generalised to action-dependent preferences in Karni (2013); it carries the limitation that separate identification of probabilities and utility scales is obtained for the set of representations with action-independent conditional utility functions;2 (ii) information carries exogenous probabilities; again, this is generalised by Karni (2011, 2013).
Yet, I do not rely on constant utility bets as defined in Karni (2011) or strings of such bets as defined in Karni (2013). I rely instead on the less restrictive notion of pairs of bets with constant utility differences.3 This extension is important in many real situations—including life insurance, risky jobs, and so on—where the ranges of conditional utilities are unlikely to overlap.
Restrictive assumptions may sometimes be interpreted as characteristics of the class of decision problems under study (as with exogenous probabilities for information), sometimes as characteristics of preferences (as for constant utility bets), and sometimes either way (as for action-independent conditional preferences). Restricting attention to a class of decision problems entails no restriction on preferences. It is standard practice in decision theory where the models often cover decision problems that are not encountered in daily life (like betting on arbitrary events). However, one should remain conscious of the fact that representations derived from restrictive assumptions may admit alternatives.
The present paper illustrates how route (i) and route (ii) combine, in a simple additive manner, to generate the desired variation in probabilities—in a formal model that is developed as a natural extension of the standard model with state-independent preferences, namely the model of Savage (1954) then Anscombe and Aumann (1963). In particular, I rely exclusively on naturally observable choices.
The logic of the argument in this paper is straightforward. First, I extend the Savage–Anscombe–Aumann model to allow for state-dependent preferences, successively with a single action (Theorem 1), then with multiple actions (Corollary 1). Next, I introduce the new concept of “strong separability”, which characterizes situations where preferences over state-dependent utility gains are revealed invariant to the choice of action. This property opens the way towards separate identification of probabilities and state-dependent utility scales (Theorem 2). Next, I introduce observations and define “observational separability”, a parallel (Corollary 2) or complementary (Theorem 3) avenue towards separate identification. The respective contributions of routes (i) and (ii) are found to be of the same nature; they are measured by the rank of the matrix of state probabilities with which they are compatible—first separately, then jointly. This common nature is a useful explicitation—with the additional merit of being technically transparent.
A simple example may help intuition. A sailor plans to cross from Bermuda to the Azores on his way back to work in Portugal. Listening to weather forecasts, he hears that a major storm is building up on the Atlantic. If the storm heads north, it will cross the sailor’s route, with possibly severe implications, ranging from minor boat damages to dismasting. But perhaps the storm will head west and stay off the planned route. The ensuing developments (states) may be summarized as: (θ) no storm, safe crossing; (θ’) storm, minor damages; (θ”) storm, dismasting. With these three states, the sailor could associate subjective probabilities, as well as state-dependent utilities. To that end, he consults a decision theorist, who: (i) elicits his preferences over a set (B) of bets (b), with state-dependent monetary payoffs (z); but (ii) concludes that he cannot, on that basis, separately identify the sailor’s probabilities and state-dependent utility scales.
Besides immediate departure (a), the sailor has access to an alternative action, (a’): take on board a volunteer crew, whose assistance would reduce the risk of dismasting4, thereby modifying the relative probabilities of states (θ’, θ”). The sailor could also adopt the strategy (f) of postponing his choice between (a) and (a’) until hearing tomorrow’s weather forecast. That strategy involves new information, hence a new probability for (θ). Processing the implications of alternative actions or new information for the separate identification of probabilities and state-dependent utility scales is the subject matter of this paper. In my example, the decision theorist could achieve separate identification by combining the choice of action with the new information (as explained below).
The paper is organized as follows. Section 2 introduces basic concepts and notation. Analytical developments are then divided in two parts: Part I considers actions with no observations, and Part II combines actions and observations. Each part consists of an introduction and two sections: (i) a single action (Section 3 and Section 5); and (ii) multiple actions (Section 4 and Section 6). Section 7 concludes.
2. Basic Concepts and Notation
Starting from the Savage–Anscombe–Aumann framework, let:
Θ be a finite set of T states (θ, θ’…)5;
Z be a given set of outcomes (z, z’…) defined as probability distributions on a finite set of primary outcomes (money in the above example).
A bet b ∈ B is a mapping b: Θ → Z that assigns an outcome to every state.
In addition, let A be a finite set of M actions (a, a’…); and let a consequence c ∈ C: = Z × A × Θ be a triplet (z, a, θ), equivalently denoted (b, a, θ).
A decision d ∈ D is a pair (a, b) ∈ (A × B), or more generally a lottery l ∈ L: = Δ(D)6 over such pairs. A lottery involving a single action reduces to a bet.7,8
Starting from a bet b, to replace b(θ) by b’(θ) for some θ, I write bb’(θ).
Preferences (≿, ≽, ≈) are defined over lotteries. They throughout satisfy the von Neumann Morgenstern axioms:
(A.1) Weak Order: ≽ on L is complete and transitive.
(A.2) Independence: for all d, d’, d” in D and all α ∈ (0, 1], d ≽ d’ if and only if
αd + (1 − α)d” ≽ αd’ + (1 − α)d”.
(A.3) Continuity: for all d, d’, d” in D, if d ≻ d’ ≻ d”, then there exist
(α,β) ∈ (0, 1)2 such that αd + (1 − α)d” ≻ d’ ≻ βd + (1 − β)d”.
I also assume throughout:
(A.4) Non-triviality: for each a in A, there exist b, b’ in B such that (a, b) ≻ (a, b’).
Part I: Actions (No Observations)
This part complements the earlier work of Drèze (1961, 1987a) by (i) treating actions as observable, instead of implicit, choices; and by (ii) letting actions affect preferences directly in addition to via their impact on the likelihood of events. Still, conditional preferences for outcomes given a final state are assumed independent of actions.
3. Single Action: A = (a)
This section is an extension of Anscombe and Aumann (1963—hereafter AA) to state-dependent preferences. Beyond (A.1)–(A.4), AA use two assumptions: « conditional preferences » (their ‘monotonicity’) and « reversal of order ». I relax their conditional preferences to allow for state-dependence.
Definition 1.
(State-dependent conditional preferences):
b ≽ b’ given a and θ (b ≽a,θb’) iff, for some b* ∈ B, (a, b*b(θ))≽ (a, b*b’(θ))
(A.5) Conditional preferences: for all (a, θ, b, b’), if b ≽a,θ b’, then there does not exist b*’ such that (a, b*’b(θ))≺a,θ (a, b*’b’(θ)).
Under assumptions (A.1)–(A.5), the conditional preferences over bets can be represented by expected utilities of their outcomes.
Definition 2.
(Reversal of order): With a single given action, a lottery over decisions is a lottery over bets, hence is itself a bet. If it is a matter of indifference to the decision-maker that the random drawing takes place before or after the state is revealed, reversal of order holds.
With a single action, early information about the outcome of the bet is modeled as worthless, in this abstract model: no decision depends on that outcome.9 Hence the assumption that the drawing of the lottery choosing a bet may indifferently be drawn before or after observing the state:
(A.6) Reversal of order: every lottery l in L assigning probability 1 to action and probabilities μ (b/l) to elements of B is indifferent to the decision (a, (μ(b/l))).
Not surprisingly, probabilities and units of scale of conditional utilities are not separately identified, in this model; only their products are identified. I record this property by stating that probabilities and utilities are “jointly, but not separately, identified”.
Theorem 1.
(AA, as per Theorem 4.9 in Drèze and Rustichini (2004)).
Let A = (a). Under (A.1)–(A.6), there exists a family of probability measures π(θ/a) and a family of utility functions u(b, a, θ) such that
the probabilities and utilities are jointly, but not separately, identified.
(a, b) ≽ (a, b’) iff ∑θπ(θ/a).[u(b, a, θ) − u(b’, a, θ)] ≥ 0;
Thus, the model of this section places no numerical restrictions on admissible probabilities—as initially concluded by the decision theorist in my example…
4. Multiple Actions
With multiple actions, the developments under 3 can be repeated for each a ε A. However, assumption (A.5) for conditional preferences must be extended to actions.
(A.7) Extended conditional preferences: for all a in A and θ in Θ, if
(a, b*b(θ)) ≽ (a, b*b’(θ)), then there do not exist (a’, b*’) in (A × B) such that
(a’, b*’b(θ))≺ (a’, b*’b’(θ)).
That is, u(b, a, θ) and u(b, a’, θ) are positive linear transformations of each other, conditionally on θ. Since the units of scale of these utilities are undefined under Theorem 1, they may be chosen identical—with natural implications for probabilities—yielding an action-independent representation of conditional preferences. One then says that the functions {u(b, a, θ)}a∈A are related by a cardinal unit-comparable transformation (are ‘jointly cardinal’); and one obtains the following result:
Corollary 1.
Under (A.1)–(A.4) and (A.7), there exist a family of probability measures π(θ/a), a family of utility functions u(b, θ) and a function v(a) such that
where:
(a, b) ≽ (a’, b’) iff ∑θπ(θ/a)u(b, θ) + v(a) ≥ ∑θπ(θ/a’)u(b’, θ) + v(a’),
- -
- the probabilities and utilities are jointly, but not separately, identified;
- -
- the functions {u(b, θ)}θ in Θ and v(a) are jointly cardinal.
Remark 1.
In the representation (2), the action (a) does not appear as an argument of u(b, θ) in view of (A.7); but (2) does not rule out that v(a) = ∑θ v(a/θ), reflecting indeterminacy of the origins of the conditional utility functions.10
Multiple actions imply restrictions on relative units of scale of the state-dependent utilities. In Drèze (1987a), the analysis of these restrictions rests on the concept of equipotence,11 geared to (unobservable) actions for which v(a) = 0. In the model of this paper, I introduce instead the following central concept:
Definition 3.
(Strong separability):
Define ⊂ B × B as the set of pairs of bets (, ’) such that, for all a, a’ in A, the lottery l assigning equal probabilities to the decisions (a, ) and (a’, ’) is indifferent to the otherwise identical lottery l’ assigning equal probabilities to (a’, ) and (a, ’).
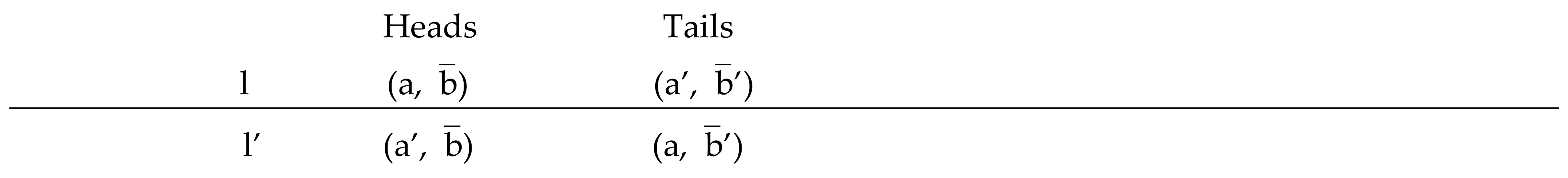
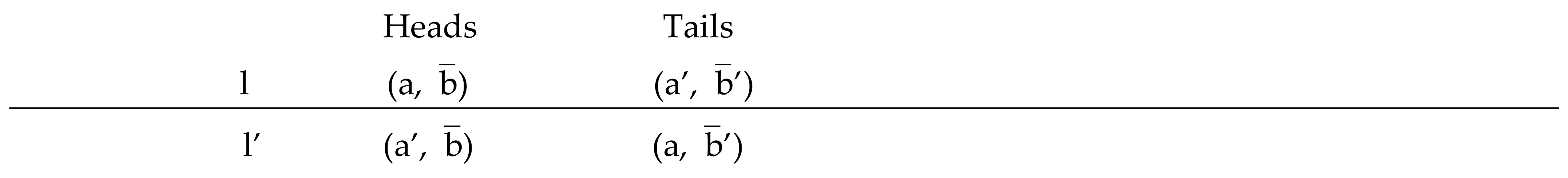
In view of Corollary 1, the bets (, ’) in are such that the expected utility gain
∑θπ(θ/a).[u(b, θ) − u(b’, θ)] is independent of a.12,13
If the set of actions A is so rich that there exist T linearly independent probability vectors π (θ/a), in other words, if the set of actions allows the decision-maker to affect the probability of every single state, then conditions (3) imply that the utility differences , are independent of θ—so that relative units of scale of state-dependent utilities are uniquely identified. Indeed, denoting by Π the T × T matrix of these probability vectors, and by τ the T × 1 vector of 1’s, we have: Π.τ = τ =Π−1.τ, so that
Π.[u(b, θ) − u(b’, θ)] = k.τ implies [u(b, θ) − u(b’, θ)] = kτ.
Definition 4.
(Strictness):
A pair of bets in is unique up to replacement of its coordinates by equivalent outcomes if there does not exist another pair (*, ) in with the property that *(θ) is indifferent to (θ) for some but not all θ’s.
The set is said to be strict if each of its constituent pairs is unique up to replacement of its coordinates by equivalent outcomes.
If is strict, it consists of pairs of bets with constant utility differences.14
Theorem 2.
If is strict, the probabilities and units of scale of utilities in Theorem 1 are separately identified in the set of representations with action-independent conditional utility functions.
Proof of Theorem 2.
Any state-dependent rescaling of the conditional utilities
In my example, no action affects the probability of θ (no storm) relative to the probability of θ’∪θ” (storm); but a’ (hosting a crew) entails relative probabilities for θ’ (no dismasting) versus θ” (dismasting) that are different from those entailed by a (sailing alone). Condition (3) then boils down to
That is, the utility difference between and ’ in B2 is the same under θ’ as under θ’’, thereby identifying the relative units of scale of the associated conditional utilities.
The concept of strong separability is thus meaningful, and elements of are readily identified. However, with three states and two actions, strictness is excluded.
Part II: Actions and Observations
Let E be a set of N mutually exclusive and collectively exhaustive observations Ei of given probabilities π(Ei) > 0. Treating π(Ei) as a primitive is restrictive (see Section 7), but natural in the case of statistical observations or official (e.g., weather) forecasts.
In my example, an observation corresponds to the report tomorrow about the path of the storm (west or north); that path is not influenced by the sailor’s actions; and the probabilities about tomorrow’s path come from the weather office—hence are given to the sailor.
A strategy is a function f ∈ F: E → D = A × B that assigns a decision to each observation16. I extend assumptions (A.1)–(A.4) and (A.7) from decisions or lotteries to strategies.
In Theorem 1 and Corollary 1, one may then replace π(θ/a) by ∑i π(Ei). π(θ/Ei, a).
With π(Ei) given, it is possible to construct, through randomization, a set E* of equiprobable observations Ei*. Thus, letting EN denote an observation such that π(Ei) ≥ π(EN) for all i, define Ei* as the product of Ei with a random drawing of probability π(EN)/π(Ei); then π(Ei*): = π(EN) > 0 for all i17.
A counterpart of strong separability is readily defined for E*. I do so in two steps: first under a given action a, then across actions. Indeed, the first step is of independent interest.
5. Single Action
As noted in Definition 2, with a single action, strategies reduce to bets.
Write b’b(E*i) for the bet b’ modified conditionally on E*I so as to coincide there with b.
Definition 5.
(Observational separability):
Let 2a be the set of pairs of bets (b, b’) such that (a, b’b(E*i)) ~ (a, b’b(E*j)) for all i,j.
The pairs of bets in 2a are readily seen to satisfy
∑θπ(θ/Ei*, a).[u(a, b’, θ) − u(a, b, θ)] is independent of i.
Applying to 2a the definition of strictness introduced above for 2, we obtain18:
Corollary 2.
If 2a is strict, the probabilities and the units of scale of state-dependent utilities in Theorem 1 are separately identified.
Corollary 3.
If 2a is strict, the origins of the state-dependent utilities in Theorem 1 are uniquely defined, up to a common additive constant.
In my example, assume for transparency that π(θ) = π(E1) = ½ with π(θ/E1) = 1. Then, condition (4) imposes that the gain in utility from replacing b’(θ) by b(θ) be the same as the gain in expected utility from replacing b’ by b on θ’∪θ”, under action a. The concept of observational separability is thus meaningful, and elements of 2a are readily identified. However, with three states and two observations, strictness is excluded.
Proof of Corollary 2.
If 2a is strict, the N × T matrix with elements π(θ/a, Ei*) owns a TxT (sub)matrix Πa of full rank T. Accordingly,
Πa.[u(b, a, θ) − u(b’, a, θ)] = kτ for some k > 0 and [u(b, a, θ) − u(b’, a, θ)] = kτ.
The relative units of scale of utilities are thus identified uniquely, entailing the same property for the probabilities. QED
Proof of Corollary 3.
Write u(b, a, θ) in Theorem 1 as cw(b, a, θ) + da (θ). Then: ∑θ[π(θ/a, Ei*) − π(θ/a, Ej*)]ya(θ) is independent of i and j. If Πa has full rank, this places T-1 constraints on da. QED
6. Multiple Actions
Definition 6.
(Global separability):
Let 2* be the set of pairs of bets (b*, b*’) ε ∩ a in A B2a that satisfy strong separability conditionally on Ei* for all Ei* in E*.
It is readily verified that every pair of bets in 2* satisfies
∑θπ(θ/Ei*, a).[u(b’, θ) − u(b, θ)] is independent of i and a.
Theorem 3.
If 2* is strict, the probabilities and units of scale in Theorem 2 are separately identified in the set of representations with action-independent conditional utility functions.
The proof of Theorem 3 is parallel to that of Corollary 2.
In my example, strategies call for deciding whether or not to host a crew after hearing tomorrow’s weather report. Preferences over strategies permit relating the units of scale of utility conditional on ‘no storm’ to the units of scale of expected utility conditional on ‘storm’—Equation (4). Also, preferences over actions permit relating the units of scale of utility conditional on ‘no dismasting’ to those conditional on ‘dismasting’—Equation (4). Accordingly, B2* is strict, and Theorem 3 applies. The complementarity between actions and observations towards separate identification of probabilities and utility scales stands out neatly.
Remark 2.
If 2* is not strict, but admits k < T − 1 degrees of freedom19, then the probabilities and units of scale of state-dependent utilities are only partly identified, with T − k − 1 remaining degrees of freedom.
7. Concluding Comments
First, we could conclude that 2* being strict is indeed a ‘strict’ condition, unlikely to be verified in many (most!) situations. My purpose is to elucidate the requirements underlying separate identification, not to assume them.
Yet, strictness of * is much less demanding than strictness of 2, or of 2a for some a. It will often be the case that observations impact probabilities in different domains than actions do—as my example clearly illustrates.20 There may exist specific interactions between observations and actions, reflected in the probabilities π(θ/a, Ei). With N potential observations and M actions, there is scope for NM conditional probability vectors, of which one could hope that T be linearly independent. Starting from the number of linearly independent probability vectors associated with actions in absence of observations, one may quantify the respective contributions of actions and observations to separate identification of probabilities and utility scales under action-independent utilities.
It is also important to note that this paper rests on observations with given (exogenous) probabilities.
That feature is used only in constructing the ‘equiprobable observations’ underlying conditions (4) and (5). It seems natural to conjecture that the analysis here could be extended to a model where equiprobable observations are based on subjective probabilities of primitive observations—as in Karni (2011, 2013). However, elicitation of these subjective probabilities is not immediate, because the observations affect the (action-dependent) subjective probabilities of the states.
Similarly, one would like to relax assumption (A.7) and allow for action-dependent conditional preferences, but the implication (3) of strong separability would then be lost. I have not found a reformulation of strong separability retaining implication (3). Whether that could be achieved without relying on constant-utility bets is an interesting open question.
Conflicts of Interest
The author declares no conflict of interest.
References
- Anscombe, Francis J., and Robert J. Aumann. 1963. A definition of subjective probabilities. Annals of Mathematical Statistics 34: 199–205. [Google Scholar] [CrossRef]
- Barberà, Salvador, Peter Hammond, and Christian Seidl. 2004. Handbook of Utility Theory. Dordrecht: Kluwer, vol. 2. [Google Scholar]
- Drèze, Jacques H. 1958. Individual Decision Making under Partially Controllable Uncertainty. Unpublished Ph.D. thesis, Columbia University, New York, NY, USA. [Google Scholar]
- Drèze, Jacques H. 1961. Les fondements logiques de l’utilité cardinale et de la probabilité subjective. In La Décision. Paris: Colloques Internationaux du CNRS, pp. 73–97. [Google Scholar]
- Drèze, Jacques H. 1987a. Decision theory with moral hazard and state-dependent preferences. Chapter 2 in Drèze (1987b). 23–89. [Google Scholar]
- Drèze, Jacques H. 1987b. Essays on Economic Decisions under Uncertainty. Cambridge: Cambridge University Press. [Google Scholar]
- Drèze, Jacques H., and Aldo Rustichini. 2004. State-dependent utility and decision theory. Chapter 16 in (Barberà et al. 2004). 839–92. [Google Scholar]
- Karni, Edi. 2011. A theory of Bayesian decision-making with action-dependent subjective probabilities. Economic Theory 48: 125–46. [Google Scholar] [CrossRef]
- Karni, Edi. 2013. Bayesian decision theory with action-dependent probabilities and risk attitudes. Economic Theory 53: 335–56. [Google Scholar] [CrossRef]
- Pope, Robin. 1983. The pre-outcome period and the utility of gambling, in Stigum and Wenstop (1983). [Google Scholar]
- Savage, Leonard J. 1954. The Foundations of Statistic. New York: Wiley. [Google Scholar]
- Stigum, B., and F. Wenston. 1983. Foundations of Utility and Risk Theory with Application. Dordrecht: Kluwer. [Google Scholar]
| 1 | Indeed, influence by others comes naturally under the heading of new information. |
| 2 | A comparable limitation is also present in the model of Savage (1954) where the probabilities and utilities are identified in the set of representations with state-independent utility functions. See further comments in Section 4 below. |
| 3 | Such pairs are mentioned in footnote 12 of Karni (2011). |
| 4 | Two men on board take turns supervising the course, whereas lone sailors must sleep part of the time… |
| 5 | “States” are labeled “effects” in Karni (2011, 2013). |
| 6 | Δ(D) is the set of probability distributions over D. |
| 7 | Indeed, ‘outcomes’ are themselves probability distributions. |
| 8 | In my example, there are three states and two actions. The decision theorist defines bets (b) with random monetary payoffs conditional on states (θ, θ’); he then observes the sailor’s preferences among such bets under action (a), that is, preferences among decisions (a,b), (a,b’)… and so on. |
| 9 | There are, of course, many real life situations where this property does not hold, because time elapses before the state obtains, and the decision maker may be adverse to “living under uncertainty”—a theme repeatedly explored by Robin Pope since 1983 (Pope 1983).manuscript |
| 10 | In the example, the presence of the volunteer crew may affect the pleasure of the crossing, hence the origins of the conditional utilities; but it may not affect the conditional betting preferences. |
| 11 | Two games are “equipotent” if lotteries among them verify reversal of order; see Section 6 in Drèze and Rustichini (2004). |
| 12 | The equal probabilities in Definition 3 are crucial: they entail irrelevance of states whose probabilities are identical under a and a’. The condition that l and l’ be ‘otherwise identical’ allows for equal probabilities lower than ½. |
| 13 | The property (3) holds for equipotent bets in Drèze (1987a), where in addition v(a) = 0. The step from equipotence to strong separability aims precisely at allowing for v(a) > 0. |
| 14 | This is a weaker property than “constant utilities”, as discussed in Drèze (1987a) and assumed in Karni (2011, 2013)—a condition that requires overlapping ranges for conditional utilities. |
| 15 | In my example, date 0 is today; date 1 is tomorrow, when a new weather report is issued; and date 2 is whenever the storm does (or would) cross the sailor’s route. There are two events at date 1 (‘west’ or ‘north’); the three final states at date 2 are unchanged. |
| 16 | This concept of strategy is used in Karni (2011). |
| 17 | The sum over i of π(Ei*) is thus less than 1—but that is immaterial, as noted in footnote 13 above, for pairs of strategies that are “otherwise identical”. |
| 18 | Note that strictness of 2a requires N ≥ T; see Section 7. |
| 19 | That is, the condition in Definition 4 that a bet be “unique up to replacement of its coordinates by equivalent outcomes” does not hold for k out of T coordinates. |
| 20 | In the example, strictness of 2* results from the combination of 2 constraints on probabilities—one coming from (3bis) (multiple actions), the other from (4) (observation). |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).