The Exponential Estimate of the Ultimate Ruin Probability for the Non-Homogeneous Renewal Risk Model

Abstract

In this work, the non-homogeneous risk model is considered. In such a model, claims and inter-arrival times are independent but possibly non-identically distributed. The easily verifiable conditions are found such that the ultimate ruin probability of the model satisfies the exponential estimate $exp\{-\varrho u\}$ for all values of the initial surplus $u⩾0$. Algorithms to estimate the positive constant $\varrho$ are also presented. In fact, these algorithms are the main contribution of this work. Sharpness of the derived inequalities is illustrated by several numerical examples.

1. Introduction

Insurance is a means of protection from random and untoward events, which can lead to significant financial losses. It is a method of risk management, that is used in order to hedge against a contingent loss risk. Risk theory came into being and was developed in order to provide a basis for the existence and significance of the insurance system. One of the most fundamental problems in risk theory is the ruin problem. It analyzes the behavior of a stochastic process, that represents the evolution of the capital of an insurance company. The objective is to estimate the ruin probability, so that the surplus at some time becomes negative. From an insurer’s point of view, the surplus can be defined as “initial surplus + premium income − claim payment”.

The simplest model, which describes the behavior of the insurer’s surplus with respect to time, is the discrete time risk model. It describes insurer’s capital level only in discrete time moments. Although this model is not very applicable in practice, it has been extensively investigated by many authors in theoretical results (see, for instance, Lefèvre and Loisel (2008); Leipus and Šiaulys (2011); Picard and Lefèvre (1997); Seal (1969); Tang (2004b); De Vylder and Goovaerts (1988)).

An extension of the discrete time risk model in the context of values of the insurer’s surplus at an arbitrary time moment is a classical risk model. Its development was begun at the beginning of the twentieth century by Lundberg and Cramér (see Cramér 1930; Cramér 1969; Lundberg 1903; Lundberg 1932; Rolski et al. 1999). They assumed that the special kind of counting process describes the number of appeared claims. In this model, the homogeneous Poisson process describes the number of claims until each time moment because of exponentially and identically distributed inter-arrival times between the consecutive claims. It is difficult to apply such a restriction of the classical risk model for real insurance activities. According to Dickson (2005), this model is a simplification of reality, however, this is a useful model, which can give some insight into the characteristics of an insurance operation.

A more general model is the renewal risk model, which was introduced by Anderson in 1957 (see Andersen 1957; Thorin 1974). In this case, it is supposed that the inter-arrival times between consecutive claims are independent and identically (but not necessarily exponentially) distributed, positive or non-negative (see, for instance, Tang (2004a)) random variables. After such improvement, the new model has become easier to use for real short-term insurance activities. However, from the mathematical point of view, the renewal risk model is more complicated due to the main part of the model being the so-called renewal counting process, whose behavior is quite different from the homogeneous Poisson process.

In the classical risk theory, all models discussed above divert our attention only to the case of homogeneous models. However, it is evident that the non-homogeneous models better reflect the real insurance activities compared to homogeneous models. Therefore, some authors extended the homogeneous renewal risk model into a non-homogeneous one in different ways. Some of them investigated non-homogeneous renewal risk models with independent, identically distributed claims and inter-arrival times, but mutual independence of these two sequences is no longer required (see, for instance, Albrecher and Teugels (2006); Li et al. (2010); Liu et al. (2017b)). Other authors worked with the claim sizes, which have a common distribution function and not necessarily identically distributed inter-arrival times (see Bernackaitė and Šiaulys 2015, 2017; Burnecki and Giuricich 2017; Mao et al. 2017). Other authors dealt with identically distributed claims and inter-arrival times, but there may be some kind of dependence between them (see Chen and Ng 2007; Huang et al. 2017; Constantinescu et al. 2016; Liu and Gao 2016; Li and Sendova 2015; Shen et al. 2016; Yang and Yuen 2016; Yang and Konstantinides 2015; Yang et al. 2014; Wang et al. 2013). Some authors consider models in which claim amounts are divided in several lines by supposing some dependence relations between these lines (see Fu and Ng 2017; Guo et al. 2017; Yang and Yuen 2016). In this work, we consider a non-homogeneous renewal risk model with independent, but not necessarily identically distributed claims and inter-arrival times like in articles by Andrulytė et al. (2015), Kievinaitė and Šiaulys (2018) and Răducan et al. (2015).

We say that the insurer’s surplus $R\left(t\right)$ varies according to a non-homogeneous renewal risk model, if equation

$$R\left(t\right)=u+pt-\sum _{\mathrm{I}=1}^{\mathsf{\Theta }\left(t\right)}{Z}_{\mathrm{I}}$$

holds for all $t⩾0$ with the insurer’s initial surplus $u⩾0$, a constant premium rate $p>0$, a sequence of independent, non-negative and possibly non-identically distributed claim amounts $\{Z_1,Z_2,\dots \}$ and the renewal counting process $\mathsf{\Theta }\left(t\right)$, that is generated by the inter-arrival times $\{{\theta }_1,{\theta }_2,\dots \}$, which form a sequence of independent, non-negative, not degenerated at zero and possibly non-identically distributed random variables. In addition, sequences $\{Z_1,Z_2,\dots \}$ and $\{{\theta }_1,{\theta }_2,\dots \}$ are supposed to be independent.

In the above definition, we say that the constant premium rate $p>0$ and two sequences of random variables $\{Z_1,Z_2,\dots \}$ and $\{{\theta }_1,{\theta }_2,\dots \}$ generate the non-homogeneous renewal risk model. If the generating claim amounts $Z_1,Z_2,\dots$ are identically distributed and the inter-arrival times ${\theta }_1,{\theta }_2,\dots$ are identically distributed, then the non-homogeneous model becomes the homogeneous one.

The central object of the renewal risk model is to investigate the probability that the insurer’s surplus $R\left(t\right)$ falls below zero at some particular time $t>0$. In this case, we say that the ruin occurs or, in other words, the insurer becomes unable to pay all the claims. This quantity may be defined as a probability of finite or infinite time ruin probability. Both of these quantities are very important for the insurance company, because the insurer can feel safer when the probability of ruin is low.

The probability of ruin until time moment T is called the finite time ruin probability and is defined by the equality

$$\psi \left(u,T\right)=\mathbb{P}\left(\underset{0⩽t⩽T}{min}R\left(t\right)<0\right)=\mathbb{P}\left(\underset{1⩽n⩽\mathsf{\Theta }\left(T\right)}{max}\left\{\sum _{k=1}^n\left(Z_k-p{\theta }_k\right)\right\}>u\right).$$

The infinite time or ultimate ruin probability is defined by equality

$$\psi \left(u\right)=\mathbb{P}\left(\underset{t⩾0}{inf}R\left(t\right)<0\right)=\mathbb{P}\left(\underset{n⩾1}{sup}\left\{\sum _{k=1}^n\left(Z_k-p{\theta }_k\right)\right\}>u\right).$$

The relationship between the finite time ruin probability and the ultimate ruin probability is shown by the formula$\underset{T\to \infty }{lim}\psi \left(u,T\right)=\psi \left(u\right).$

By denoting the ruin probability as a function of the initial surplus u, the effect of u for the ruin probability is analyzed. In practice, it is not necessary to know the exact values of the ruin probability. A good estimate of this quantity is sufficient for a risk assessment of an insurer’s business. An exponential bound for the ruin probability is usually called a Lundberg-type inequality. We further give the statement on the upper bound of the ultimate ruin probability $\psi \left(u\right)$ in the homogeneous renewal risk model.

Theorem 1.

Let the claims $\left\{Z_1,Z_2,\dots \right\}$ and the inter-arrival times $\left\{{\theta }_1,{\theta }_2,\dots \right\}$ form the homogeneous renewal risk model. Additionally, let the net profit condition $\mathbb{E}\left(Z_1-p{\theta }_1\right)<0$ hold and $\mathbb{E}{\mathrm{e}}^{h{Z}_1}<\infty$ for some positive h. Then, there exists a positive H such that

$$\psi \left(u\right)⩽{\mathrm{e}}^{-Hu}\mathit{for}\mathit{all}u⩾0.$$

(1)

If $\mathbb{E}{\mathrm{e}}^{R\left(Z_1-p{\theta }_1\right)}=1$ for some positive R, then we can take $H=R$ in estimate (1).

An exponential upper bound for the ruin probability with constant R is the well-known Lundberg’s inequality. Usually, the number R is unique and called the adjustment coefficient or Lundberg exponent. The Lundberg’s inequality can be proved in different ways. Some of the existing proofs can be found in Asmussen and Albrecher (2010); Embrechts et al. (1997) and Embrechts and Veraverbeke (1982). The most elegant way to prove this inequality is via a martingale approach, which was presented by Gerber (1973). On the other hand, it is sufficient to prove

$$\widehat{\psi }\left(u,N\right):=\mathbb{P}\left(\underset{1⩽n⩽N}{max}\left\{\sum _{k=1}^n\left(Z_k-p{\theta }_k\right)\right\}>u\right)⩽{\mathrm{e}}^{-Ru}$$

for all $N\in \mathbb{N}$, since we know relationship $\underset{N\to \infty }{lim}\widehat{\psi }(u,N)=\psi \left(u\right)$ (see, for instance, Mikosch (2009)). In addition, the Lundberg’s inequality can be proved using the exponential tail bound by Sgibnev (1997) for the random walk supremum and the inequality $\psi \left(0\right)<1$.

The main purpose of this work is to find easily verifiable conditions so that we could apply a similar Lundberg-type inequality in the non-homogeneous renewal risk model like in the homogeneous one. These assumptions would allow analysis of the model in more realistic cases of insurance. The main results of this paper extend and complement the results of other authors, who have considered the exponential estimate of the ruin probability in the non-homogeneous renewal risk model (see Andrulytė et al. 2015; Kievinaitė and Šiaulys 2018; Castañer et al. 2013; Grandell and Schmidli 2011; Liu et al. 2017a).

The net profit condition $\mathbb{E}\left(Z_1-p{\theta }_1\right)<0$ is the main condition in Theorem 1. If this condition is not satisfied in the homogeneous renewal risk model, then there is no estimate of the ruin probability, because $\psi \left(u\right)=1$ for each value of the initial surplus $u⩾0$. In the case of the non-homogeneous renewal risk model, the probability of ruin depends on the sequence of independent but possibly non-identically distributed random variables $\{Z_1-p{\theta }_1,Z_2-p{\theta }_2,\dots \}$. It is neither clear whether the requirement plays the role of the net profit condition in the non-homogeneous renewal risk model, nor whether it is the basis to get exponential upper bound for the probability of ruin. In articles by Andrulytė et al. (2015) and Kievinaitė and Šiaulys (2018), it is supposed that the “net profit condition” holds on average, i.e.,

$$\frac{1}{n}\sum _{k=1}^n\mathbb{E}(Z_k-p{\theta }_k)<0$$

for sufficiently large $n\in \mathbb{N}$. In these works, it is obtained that the above inequality together with other natural requirements imply that $\psi \left(u\right)⩽{\varrho }_{1}exp\{-{\varrho }_{2}u\}$, $u⩾0$, with some constants ${\varrho }_1>1$ and ${\varrho }_2>0$. In our case, we suppose that the “net profit condition” holds on maximum, i.e., $\mathbb{E}(Z_n-p{\theta }_n)<0$ for all $n\in \mathbb{N}$. The results below show that this stronger condition, together with suitable additional requirements, implies that the probability of ruin can be estimated by the smaller quantity $exp\{-\varrho u\}$ for some positive $\varrho$ and for all values of the initial surplus $u⩾0$. The main contribution of the paper are the algorithms to estimate this positive parameter $\varrho$.

The non-homogeneous renewal risk model can be rewritten as the random walk generated by a sequence of independent, but not necessarily identically distributed, random variables $\{Z_1-p{\theta }_1,Z_2-p{\theta }_2,\dots \}$. Many important results on such a walk in the multi-dimensional space can be found in the book by Menshikov et al. (2016). Our exponential estimates for the ruin probability, derived in this article, complement results of that book.

The rest of this paper is organized as follows. Our main results, which are related to the Lundberg-type inequality, are shown in Section 2. The proofs of theorems are presented in Section 3. Finally, in Section 4, we demonstrate some examples, which show the applicability of the theorems.

2. Results

In this section, three assertions are presented on the Lundberg-type inequalities for the ultimate ruin probability in the case of the non-homogeneous renewal risk model. The first assertion below shows that the Lundberg-type estimate for ruin probability holds, if the non-homogeneous model satisfies quite wide requirements. The second theorem supplements Theorem 2. In this theorem, the Lundberg-type inequality, as well as a way to calculate the constant in the exponent, is derived. In order to get that constant all requirements for the model should have expressive forms. The third theorem below is devoted to the sharpest Lundberg-type inequality for the non-homogeneous risk model. However, in general, for this we need to estimate infinitely many “adjustment coefficients”.

In all theorems below, due to traditional definition sequences of random variables, $\{Z_1,Z_2,\dots \}$ and $\{{\theta }_1,{\theta }_2,\dots \}$ should be independent. However, from the proofs in Chapter 3, it follows that Theorems 2–4 remain valid when the sequence $\{(Z_1,{\theta }_1),(Z_2,{\theta }_2),\dots \}$ consists of independent random vectors. If this condition holds, then we can suppose the random variables $Z_{\mathrm{I}}$ and ${\theta }_{\mathrm{I}}$ to be dependent in an arbitrary way for each index i.

Theorem 2.

Let us consider the non-homogeneous renewal risk model generated by a premium rate $p>0$, a sequence of independent, non-negative random claims $\{Z_1,Z_2,\dots \}$ and a sequence of independent, non-negative, not degenerate at zero random inter-arrival times $\{{\theta }_1,{\theta }_2,\dots \}$. Let the following three conditions be satisfied:

$$\begin{array}{cc}\left(\mathrm{i}\right)& \underset{k\in \mathbb{N}}{sup}\mathbb{E}(Z_k-p{\theta }_k)<0,\hfill \\ \left(\mathrm{ii}\right)& \underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{\gamma Z_k}<\infty \mathit{for}\mathit{some}\gamma >0,\hfill \\ \left(\mathrm{iii}\right)& \underset{x\to \infty }{lim}\underset{k\in \mathbb{N}}{sup}\mathbb{E}({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>x\right\}})=0.\hfill \end{array}$$

Then there is a positive constant ϱ such that $\psi \left(u\right)⩽{\mathrm{e}}^{-\varrho u}$ for all values of the initial surplus $u⩾0$.

As stated above, a similar possibility of the exponential estimate was considered by Andrulytė et al. (2015). The more general risk renewal model was investigated in that paper. More precisely, it was supposed that the model satisfies the net profit condition only on average. Naturally, under weaker conditions a rougher estimate of the ruin probability can be obtained.

Theorem 3.

Let us consider the non-homogeneous renewal risk model generated by a premium rate $p>0$, a sequence of independent, non-negative random claims $\{Z_1,Z_2,\dots \}$ and a sequence of independent, non-negative, not degenerate at zero random inter-arrival times $\{{\theta }_1,{\theta }_2,\dots \}$. In addition, let the following three conditions be satisfied for some constants $\alpha >0,\gamma >0,\beta ⩾0,\varkappa >0$ and $\epsilon ⩾0$:

$$\begin{array}{cc}\left(\mathrm{i}\right)& \underset{k\in \mathbb{N}}{sup}\mathbb{E}(Z_k-p{\theta }_k)⩽-\alpha ,\hfill \\ \left(\mathrm{ii}\right)& \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\mathrm{e}}^{\gamma (Z_k-p{\theta }_k)}1{\mathrm{I}}_{\{Z_k-p{\theta }_k>0\}}\right)⩽\beta ,\hfill \\ \left(\mathrm{iii}\right)& \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>\varkappa /p\right\}}\right)⩽\epsilon .\hfill \end{array}$$

If, for some $\delta =\delta (\alpha ,\beta ,\gamma ,\varkappa ,\epsilon ,p)\in (0,1/2]$,

$$\begin{array}{c}\hfill 2p\epsilon +\frac{\delta \gamma {\varkappa }^2}{2}+\frac{2\delta \beta }{\gamma }-\alpha ⩽0,\end{array}$$

(2)

then the ultimate ruin probability of the model satisfies exponential upper bound $\psi \left(u\right)⩽{\mathrm{e}}^{-\delta \gamma u}$ for all values of the initial surplus $u⩾0$.

Similar statement on the calculation of an upper exponential bound for the ruin probability was given by Kievinaitė and Šiaulys (2018). Authors of that paper also consider the more general risk renewal model satisfying net profit condition on average. Such a model can have subsequences of random variables with a positive drift. Therefore, the formulas derived there give more conservative upper bounds in comparison to formula of Theorem 3.

Theorem 4.

Let us consider the non-homogeneous renewal risk model generated by a premium rate $p>0$, a sequence of independent, non-negative random claims $\{Z_1,Z_2,\dots \}$ and a sequence of independent, non-negative, not degenerate at zero random inter-arrival times $\{{\theta }_1,{\theta }_2,\dots \}$. If all conditions of Theorem 2 are satisfied, then there exists an interval $(0,H]$ such that

$$\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}⩽1$$

for all $h\in (0,H]$, and

$$\psi \left(u\right)⩽\underset{h\in (0,H]}{inf}\left\{{\mathrm{e}}^{-hu}\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}\right\}$$

for all values of the initial surplus $u⩾0$.

Theorem 4 has the classical form of Lundberg’s inequality. Inequalities of such a form, for risk renewal models having the special structures, are proved by Castañer et al. (2013); Grandell and Schmidli (2011) and Liu et al. (2017a). It is evident that we need a more explicit expression for ${sup}_{k\in \mathbb{N}}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}$ to obtain sharp upper exponential bounds for the ruin probability. For example, if ${sup}_{k\in \mathbb{N}}\mathbb{E}(exp\left\{h(Z_k-p{\theta }_k\}\right)⩽\widehat{c}⩽1$ for $h\in [0,\widehat{H}]$, then the estimate of Theorem 4 implies $\psi \left(u\right)⩽\widehat{c}exp\{-\widehat{H}u\}$ for $u⩾0$.

3. Proofs

This section is devoted to the detailed proofs of all theorems, which are presented in Section 2. Proofs of all these theorems, related with inequality (8) below are provided. If we know that the non-homogeneous renewal risk model satisfies the net profit condition (on maximum) together with two natural related requirements (see Theorem 2), then we derive from (8) the theoretical possibility to have a Lundberg-type exponential bound for the ruin probability. If we know all constants restricting the requirements of the model (see Theorem 3), then, using a slightly different approach, we get from the same inequality an estimate for the parameter of the exponential bound. On the other hand, if the non-homogeneous model satisfies the suitable conditions, then, using the same method as in the proof of Theorem 2, we can obtain the bound of the ruin probability expressed by a supremum of certain exponential moments (see Theorem 4).

Proof of Theorem 2.

Let $\widehat{\psi }(u,N)$ be the ruin probability within moment of the N-th claim, where $u⩾0$ and $N\in \mathbb{N}$. We have

$$\begin{array}{ccc}\hfill \widehat{\psi }(u,N)& =\hfill & \hfill \mathbb{P}\left(\underset{1⩽n⩽N}{max}\left\{\sum _{k=1}^n\left(Z_k-p{\theta }_k\right)\right\}>u\right)\\ & =\hfill & \hfill \mathbb{P}\left(\bigcup _{n=1}^N\left\{\sum _{k=1}^n\left(Z_k-p{\theta }_k\right)>u\right\}\right).\end{array}$$

(3)

It is obvious that

$$\underset{N\to \infty }{lim}\widehat{\psi }(u,N)=\psi \left(u\right)\mathrm{for}\mathrm{all}u⩾0.$$

Consequently, it is sufficient to prove the inequality

$$\widehat{\psi }(u,k_1,k_2,\dots ,k_N):=\mathbb{P}\left(\underset{1⩽j⩽N}{max}\left\{\sum _{\mathrm{I}=1}^j\left(Z_{k_{\mathrm{I}}}-p{\theta }_{k_{\mathrm{I}}}\right)\right\}>u\right)⩽{\mathrm{e}}^{-\varrho u}$$

(4)

for some positive $\varrho$, for all $u⩾0$, for an arbitrary $N\in \mathbb{N}$ and for an arbitrary collection of different indices $\{k_1,k_2,\dots ,k_N\}$.

We will prove this inequality by using induction on N. Let ${\xi }_k=Z_k-p{\theta }_k$ for all $k\in \mathbb{N}$.

If $N=1$, then we derive by the exponential Chebyshev’s inequality that

$$\widehat{\psi }(u,k_1)=\mathbb{P}\left({\xi }_{k_1}>u\right)=\mathbb{P}\left({\mathrm{e}}^{h{\xi }_{k_1}}>{\mathrm{e}}^{hu}\right)⩽{\mathrm{e}}^{-hu}\mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}$$

(5)

for all $u⩾0$, for all $0<h⩽\gamma$ and for an arbitrary $k_1\in \mathbb{N}$.

If $0<h⩽\gamma$ and $y>0$, then we have

$$\begin{array}{ccc}\hfill \mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}& =\hfill & \hfill 1+h\mathbb{E}{\xi }_{k_1}+\mathbb{E}\left(\left({\mathrm{e}}^{h{\xi }_{k_1}}-1\right)1{\mathrm{I}}_{\left\{{\xi }_{k_1}<-y\right\}}\right)-h\mathbb{E}\left({\xi }_{k_1}1{\mathrm{I}}_{\left\{{\xi }_{k_1}<-y\right\}}\right)\\ & & \hfill +\mathbb{E}\left(\left({\mathrm{e}}^{h{\xi }_{k_1}}-h{\xi }_{k_1}-1\right)1{\mathrm{I}}_{\left\{-y⩽{\xi }_{k_1}⩽0\right\}}\right)\\ & & \hfill +\mathbb{E}\left(\left({\mathrm{e}}^{h{\xi }_{k_1}}-h{\xi }_{k_1}-1\right)1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right).\end{array}$$

(6)

In order to estimate the right side of (6), we use the following well-known inequalities:

$$\begin{array}{c}\hfill \left|{\mathrm{e}}^x-1\right|⩽\left|x\right|,x⩽0;|{\mathrm{e}}^x-x-1|⩽\frac{x^2}{2},x⩽0;|{\mathrm{e}}^x-x-1|⩽\frac{x^2}{2}{\mathrm{e}}^x,x⩾0.\end{array}$$

(7)

Using these inequalities, we derive

$$\begin{array}{ccc}\hfill \mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}& ⩽\hfill & \hfill 1+h\mathbb{E}{\xi }_{k_1}+2h\mathbb{E}\left(\left|{\xi }_{k_1}\right|1{\mathrm{I}}_{\left\{{\xi }_{k_1}<-y\right\}}\right)\\ & & \hfill +\frac{h^2}{2}\mathbb{E}\left({\xi }_{k_1}^{2}1{\mathrm{I}}_{\left\{-y⩽{\xi }_{k_1}⩽0\right\}}\right)\\ & & \hfill +\frac{h^2}{2}\mathbb{E}\left({\xi }_{k_1}^2{\mathrm{e}}^{h{\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)\end{array}$$

(8)

with $0<h⩽\gamma$ and $y>0$.

We observe that

$$\begin{array}{c}\mathbb{E}\left(\left|{\xi }_{k_1}\right|1{\mathrm{I}}_{\left\{{\xi }_{k_1}<-y\right\}}\right)=\mathbb{E}\left(\left(p{\theta }_{k_1}-Z_{k_1}\right)1{\mathrm{I}}_{\left\{p{\theta }_{k_1}>y+Z_{k_1}\right\}}\right)⩽p\mathbb{E}\left({\theta }_{k_1}1{\mathrm{I}}_{\left\{{\theta }_{k_1}>y/p\right\}}\right),\hfill \\ \mathbb{E}\left({\xi }_{k_1}^{2}1{\mathrm{I}}_{\left\{-y⩽{\xi }_{k_1}⩽0\right\}}\right)⩽y^2\hfill \end{array}$$

and

$$\mathbb{E}{\mathrm{e}}^{\gamma {\xi }_{k_1}}⩽\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{\gamma Z_k}=:c_1$$

with some constant $c_1=c_1\left(\gamma \right)$ due to condition (ii) of the theorem.

Thus, using the last estimate we derive that if $0<h⩽\gamma /2$, then

$$\begin{array}{cc}\hfill \mathbb{E}\left({\xi }_{k_1}^2{\mathrm{e}}^{h{\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)& ⩽c_2\mathbb{E}\left({\mathrm{e}}^{\gamma {\xi }_{k_1}/2}{\mathrm{e}}^{\gamma {\xi }_{k_1}/2}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)\hfill \\ & ⩽c_2\mathbb{E}{\mathrm{e}}^{\gamma {\xi }_{k_1}}⩽c_1{c}_2=:c_3\hfill \end{array}$$

where $c_2=c_2\left(\gamma \right)$ is a constant from inequality $x^2⩽c_2{\mathrm{e}}^{\gamma x/2},x⩾0.$

Therefore, substituting the obtained estimates into expression (8), we get that

$$\begin{array}{cc}\hfill \mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}& ⩽1+h\left(\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\xi }_k+2p\underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>y/p\right\}}\right)+\frac{h{y}^2}{2}+\frac{h{c}_3}{2}\right)\hfill \end{array}$$

for all $0<h⩽\gamma /2$ and $y>0$.

Choosing $y=1/\sqrt[4]{h}$, we derive that

$$\begin{array}{c}\hfill \mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}⩽1+h\left(\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\xi }_k+2p\underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>1/\left(p\sqrt[4]{h}\right)\right\}}\right)+\frac{\sqrt{h}}{2}+\frac{h{c}_3}{2}\right)\end{array}$$

(9)

for all $0<h⩽\gamma /2$.

This estimate and conditions (i), (iii) of the theorem imply that

$$\mathbb{E}{\mathrm{e}}^{\varrho {\xi }_{k_1}}⩽1$$

(10)

for some sufficiently small $0<\varrho ⩽\gamma /2$ and an arbitrary $k_1\in \mathbb{N}$.

Therefore, according to the inequality (5) we have that

$$\widehat{\psi }(u,k_1)=\mathbb{P}\left({\xi }_{k_1}>u\right)⩽{\mathrm{e}}^{-\varrho u}$$

for the same positive $\varrho$, for each $k_1\in \mathbb{N}$ and for all $u⩾0$.

Now suppose that estimate (4) is correct for $N=L⩾1$, i.e.,

$$\widehat{\psi }(u,k_1,k_2,\dots ,k_L)=\mathbb{P}\left(\underset{1⩽j⩽L}{max}\left\{\sum _{\mathrm{I}=1}^j{\xi }_{k_{\mathrm{I}}}\right\}>u\right)⩽{\mathrm{e}}^{-\varrho u}$$

(11)

for the above positive coefficient $\varrho$, for all $u⩾0$ and for an arbitrary collection of different indices $\{k_1,k_2,\dots ,k_L\}$.

We must derive that the estimate (4) holds for $N=L+1$. According to the inequality (10) and the assumption (11), we have that

$$\begin{array}{cc}\hfill \widehat{\psi }(u,k_1,k_2,\dots ,k_{L+1})& =\mathbb{P}\left(\underset{1⩽j⩽L+1}{max}\left\{\sum _{\mathrm{I}=1}^j{\xi }_{k_{\mathrm{I}}}\right\}>u\right)\hfill \\ & =\mathbb{P}\left(max\left\{{\xi }_{k_1},\underset{2⩽j⩽L+1}{max}\left\{{\xi }_{k_1}+\sum _{\mathrm{I}=2}^j{\xi }_{k_{\mathrm{I}}}\right\}\right\}>u\right)\hfill \\ & =\mathbb{P}\left({\xi }_{k_1}>u\right)+\mathbb{P}\left({\xi }_{k_1}+\underset{2⩽j⩽L+1}{max}\left\{\sum _{\mathrm{I}=2}^j{\xi }_{k_{\mathrm{I}}}\right\}>u,{\xi }_{k_1}⩽u\right)\hfill \\ & =\underset{\left(u,\infty \right)}{\int }\mathrm{d}{F}_{{\xi }_{k_1}}\left(x\right)+\underset{\left(-\infty ,u\right]}{\int }\mathbb{P}\left(\underset{2⩽j⩽L+1}{max}\left\{\sum _{\mathrm{I}=2}^j{\xi }_{k_{\mathrm{I}}}\right\}>u-x\right)\mathrm{d}{F}_{{\xi }_{k_1}}\left(x\right)\hfill \\ & ⩽\underset{\left(u,\infty \right)}{\int }{\mathrm{e}}^{-\varrho \left(u-x\right)}\mathrm{d}{F}_{{\xi }_{k_1}}\left(x\right)+\underset{\left(-\infty ,u\right]}{\int }{\mathrm{e}}^{-\varrho \left(u-x\right)}\mathrm{d}{F}_{{\xi }_{k_1}}\left(x\right)\hfill \\ & ={\mathrm{e}}^{-\varrho u}\mathbb{E}{\mathrm{e}}^{\varrho {\xi }_{k_1}}⩽{\mathrm{e}}^{-\varrho u}\hfill \end{array}$$

for an arbitrary collection of different indices $\{k_1,k_2,\dots ,k_{L+1}\}$ and for all $u⩾0$.

We see that estimate (4) holds for $N=L+1$ and, consequently, for all $N\in \mathbb{N}$ according to the induction. So, the desired inequality $\psi \left(u\right)⩽{\mathrm{e}}^{-\varrho u},u⩾0,$ holds as a direct consequence of estimate (4). The theorem is proved. ☐

Proof of Theorem 3.

Let $\widehat{\psi }(u,N)$ and $\widehat{\psi }(u,k_1,k_2,\dots ,k_N)$ be probabilities as respectively defined in (3) and (4). For each fixed $u⩾0$, $\widehat{\psi }(u,N)$ is not decreasing with respect to $N\in \mathbb{N}$ and tends to $\psi \left(u\right)$, when N tends to infinity. In addition,

$$\widehat{\psi }(u,N)⩽\underset{k_1,k_2,\dots ,k_N}{sup}\widehat{\psi }(u,k_1,k_2,\dots ,k_N)$$

where indices $k_1,k_2,\dots ,k_N\in \mathbb{N}$ and $k_1\ne k_2\ne \dots \ne k_N$.

Hence, for the proof of Theorem 3 it is sufficient to get that

$$\widehat{\psi }(u,k_1,k_2,\dots ,k_N)⩽{\mathrm{e}}^{-\delta \gamma u}$$

(12)

for suitable chosen $\delta >0$, for all $u⩾0$, for each $N\in \mathbb{N}$ and for an arbitrary collection of different indices $\{k_1,k_2,\dots ,k_N\}$.

We prove this inequality by using induction on N like in the proof of Theorem 2. Let ${\xi }_k=Z_k-p{\theta }_k$ for all $k\in \mathbb{N}$ as before.

If $N=1$, then we have estimate (5) and arrangement (6) for $\mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}$ with $k_1\in \mathbb{N}$, $0<h⩽\gamma$ and $y=\varkappa$.

Using inequalities (7), we derive that

$$\begin{array}{ccc}\hfill \mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}& ⩽\hfill & \hfill 1+h\mathbb{E}{\xi }_{k_1}+2h\mathbb{E}\left(\left|{\xi }_{k_1}\right|1{\mathrm{I}}_{\left\{{\xi }_{k_1}<-\varkappa \right\}}\right)\\ & & \hfill +\frac{h^2}{2}\mathbb{E}\left({\xi }_{k_1}^{2}1{\mathrm{I}}_{\left\{-\varkappa ⩽{\xi }_{k_1}⩽0\right\}}\right)\\ & & \hfill +\frac{h^2}{2}\mathbb{E}\left({\xi }_{k_1}^2{\mathrm{e}}^{h{\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)\end{array}$$

(13)

for an arbitrary $k_1\in \mathbb{N}$.

It is evident that

$$\mathbb{E}\left(\left|{\xi }_{k_1}\right|1{\mathrm{I}}_{\left\{{\xi }_{k_1}<-\varkappa \right\}}\right)=\mathbb{E}\left(\left(p{\theta }_{k_1}-Z_{k_1}\right)1{\mathrm{I}}_{\left\{p{\theta }_{k_1}>\varkappa +Z_{k_1}\right\}}\right)⩽p\mathbb{E}\left({\theta }_{k_1}1{\mathrm{I}}_{\left\{{\theta }_{k_1}>\varkappa /p\right\}}\right)$$

(14)

and

$$\mathbb{E}\left({\xi }_{k_1}^{2}1{\mathrm{I}}_{\left\{-\varkappa ⩽{\xi }_{k_1}⩽0\right\}}\right)⩽{\varkappa }^2$$

(15)

for an arbitrary positive $\varkappa$.

In addition, using theorem’s condition (ii) and inequality $x^2⩽{\mathrm{e}}^x,x⩾0,$ we derive that

$$\begin{array}{ccc}\hfill \mathbb{E}\left({\xi }_{k_1}^2{\mathrm{e}}^{h{\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)& =\hfill & \hfill \frac{4}{{\gamma }^2}\mathbb{E}\left({\left(\frac{\gamma {\xi }_{k_1}}{2}\right)}^2{\mathrm{e}}^{h{\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)\\ & ⩽\hfill & \hfill \frac{4}{{\gamma }^2}\mathbb{E}\left({\mathrm{e}}^{\gamma {\xi }_{k_1}/2}{\mathrm{e}}^{h{\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)\\ & ⩽\hfill & \hfill \frac{4}{{\gamma }^2}\mathbb{E}\left({\mathrm{e}}^{\gamma {\xi }_{k_1}}1{\mathrm{I}}_{\left\{{\xi }_{k_1}>0\right\}}\right)⩽\frac{4\beta }{{\gamma }^2},\end{array}$$

(16)

if $0<h⩽\gamma /2$.

By substituting the obtained estimates (14), (15), (16) into expression (13), we get that

$$\begin{array}{ccc}\hfill \mathbb{E}{\mathrm{e}}^{h{\xi }_{k_1}}& ⩽& 1+h\left(\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\xi }_k+2p\underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>\varkappa /p\right\}}\right)+\frac{h{\varkappa }^2}{2}+\frac{2h\beta }{{\gamma }^2}\right)\hfill \\ & ⩽& 1+h\left(-\alpha +2p\epsilon +\frac{h{\varkappa }^2}{2}+\frac{2h\beta }{{\gamma }^2}\right)\hfill \end{array}$$

for all $0<h⩽\gamma /2$ and for an arbitrary index $k_1\in \mathbb{N}$.

Let now $h=\delta \gamma$ with $0<\delta ⩽1/2$ satisfying condition (2). The last estimate implies that

$$\mathbb{E}{\mathrm{e}}^{\delta \gamma {\xi }_{k_1}}⩽1$$

for each $k_1\in \mathbb{N}$.

This together with (5) implies that

$$\widehat{\psi }(u,k_1)=\mathbb{P}\left({\xi }_{k_1}>u\right)⩽{\mathrm{e}}^{-\delta \gamma u}$$

for each $k_1\in \mathbb{N}$ and for all $u⩾0$.

The desired inequality (12) follows from the last two estimates and the induction procedure, which is presented in the proof of Theorem 2 with details. Theorem 3 is proved. ☐

Proof of Theorem 4.

Suppose that ${\xi }_k=Z_k-p{\theta }_k$ for each $k\in \mathbb{N}$, as usual. The conditions of the theorem and the estimate (9) imply the existence of an interval $(0,H]$ such that $\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h{\xi }_k}⩽1$ for each $h\in (0,H]$. This is the first assertion of the theorem.

According to estimate (5), we have that

$$\widehat{\psi }(u,k_1)=\mathbb{P}({\xi }_{k_1}>u)⩽{\mathrm{e}}^{-hu}\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h{\xi }_k}$$

for all $u⩾0$, for all $h\in (0,H]$ and for each $k_1\in \mathbb{N}$.

Using the same proof framework as in Theorem 2, we obtain

$$\widehat{\psi }(u,N)⩽{\mathrm{e}}^{-hu}\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h{\xi }_k}$$

for all $u⩾0$, $N\in \mathbb{N}$ and an arbitrary $h\in (0,H]$.

Consequently,

$$\psi \left(u\right)⩽{\mathrm{e}}^{-hu}\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h{\xi }_k}$$

for all $u⩾0$, $h\in (0,H]$. The second assertion of the theorem follows from this and the theorem is proved. ☐

4. Numerical Examples

In this section, we present two examples, which show the applicability of theorems, that are in Section 2. Using the Monte Carlo method, we simulate exact values of ruin probability $\psi$. We compare these obtained values with upper exponential bounds, which can be derived using the received theoretical results. In Example 1, we investigate the discrete time risk model of five seasons which is a direct generalization of the classical discrete time risk model comprehensively studied by Dickson (2005), see also references therein. As usual, the discrete time risk model describes the insurance business when the insurer calculates surplus at time moments at equal intervals. In Example 2, we consider the non-homogeneous model with complex distributions of claim amounts and inter-arrival times. We show that the corresponding exponential bound can be obtained even for such an unstable model. Naturally, in this case, Theorem 4 should be employed.

Example 1.

Suppose that the non-homogeneous renewal risk model generated by a premium rate $p=1$, a sequence of degenerated inter-arrival times ${\theta }_1={\theta }_2=\cdots =1$ and a sequence of independent random claims $\{Z_1,Z_2,\dots \}$ such that $Z_{5m+k}\stackrel{d}{=}{Z}_k$ for $m\in \mathbb{N}$, $k\in \{1,2,3,4,5\}$, and

$Z_k$	0	1	k
$\mathbb{P}$	$1-1/3k-1/3k^2$	$1/3k$	$1/3k^2$

for $k\in \{1,2,3,4,5\}$.

• First of all, we find rough estimate of ruin probability according to Theorem 3. After some calculations, we get that

  $$\begin{array}{c}\underset{k\in \mathbb{N}}{sup}\mathbb{E}(Z_k-p{\theta }_k)=\underset{k\in \mathbb{N}}{sup}\left(\frac{2}{3k}-1\right)=-\frac{1}{3},\hfill \\ \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\mathrm{e}}^{\gamma (Z_k-p{\theta }_k)}1{\mathrm{I}}_{\{Z_k-p{\theta }_k>0\}}\right)=max\left\{0,\frac{{\mathrm{e}}^{\gamma }}{12},\frac{{\mathrm{e}}^{2\gamma }}{27},\frac{{\mathrm{e}}^{3\gamma }}{48},\frac{{\mathrm{e}}^{4\gamma }}{75}\right\}=\frac{{\mathrm{e}}^{\gamma }}{12}\mathrm{for}\mathrm{all}\gamma \in \left(0,61/100\right],\hfill \\ \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>1\right\}}\right)=0.\hfill \end{array}$$
  According to the above estimates, we obtain that conditions of Theorem 3 hold with parameters $\alpha =1/3,\gamma =3/5,\beta ={\mathrm{e}}^{3/5}/12,\varkappa =1$ and $\epsilon =0$. Substituting the obtained constants into expression (2), we get that the last parameter $\delta \in \left(0,41/100\right]$. Choosing $\delta =2/5$, we get from the assertion of Theorem 3 that

  $$\psi \left(u\right)⩽{\psi }_1\left(u\right):={\mathrm{e}}^{-6u/25}$$

  for all non-negative values of the initial surplus u.
  The derived estimate is exponential but quite conservative. For instance, it follows from the obtained inequality that $\psi \left(u\right)⩽0.02$, if $u⩾17$.
• Now, we find more precise upper bound of ruin probability on the basis of the Theorem 4. All theorem’s conditions hold due to the derived above estimates and

  $$\begin{array}{cc}\hfill \underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{\gamma Z_k}& =max\left\{\frac{2{\mathrm{e}}^{\gamma }+1}{3},\frac{{\mathrm{e}}^{2\gamma }+2{\mathrm{e}}^{\gamma }+9}{12},\frac{{\mathrm{e}}^{3\gamma }+3{\mathrm{e}}^{\gamma }+23}{27},\frac{{\mathrm{e}}^{4\gamma }+4{\mathrm{e}}^{\gamma }+43}{48},\frac{{\mathrm{e}}^{5\gamma }+5{\mathrm{e}}^{\gamma }+69}{75}\right\}\hfill \\ & =\frac{2{\mathrm{e}}^{\gamma }+1}{3}\mathrm{for}\mathrm{all}\gamma \in \left(0,4/5\right].\hfill \end{array}$$
  For positive h, we have that

  $$\begin{array}{c}\hfill \underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}=max\left\{\frac{2{\mathrm{e}}^h+1}{3e^h},\frac{{\mathrm{e}}^{2h}+2{\mathrm{e}}^h+9}{12{\mathrm{e}}^h},\frac{{\mathrm{e}}^{3h}+3{\mathrm{e}}^h+23}{27{\mathrm{e}}^h},\frac{{\mathrm{e}}^{4h}+4{\mathrm{e}}^h+43}{48{\mathrm{e}}^h},\frac{{\mathrm{e}}^{5h}+5{\mathrm{e}}^h+69}{75{\mathrm{e}}^h}\right\}.\end{array}$$
  Consequently, $\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}⩽1$ for all $h\in (0,47/50]$, and Theorem 4 implies that

  $$\psi \left(u\right)⩽\underset{h\in (0,47/50]}{inf}\left\{{\mathrm{e}}^{-hu}\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}\right\}⩽{\psi }_2\left(u\right):={\mathrm{e}}^{-47u/50}$$

  for all values of the initial surplus $u⩾0$.
  The derived estimate is almost four times accurate with respect to the previous one. For instance, it follows from the obtained inequality that $\psi \left(u\right)⩽0.02$, if $u⩾5$.
• Finally, we use the Monte Carlo simulations to get approximate values of ruin probability $\psi \left(u\right)$. For this we use the fact that $\widehat{\psi }(u,N)\approx \psi \left(u\right)$ for fixed u and for sufficiently large N. We consider the case when $u\in \{0,1,2,\dots ,10\}$ and $N=1000$. For each u, we simulate ${10}^7$ trajectories of the renewal risk process with N random claims and we calculate how many times on average they fall below zero in order to get values of $\widehat{\psi }(u,N)$. According to the obtained values of ruin probability, we get that $\psi \left(u\right)⩽0.02$, even if the initial surplus is especially small, i.e., $u⩾1$.
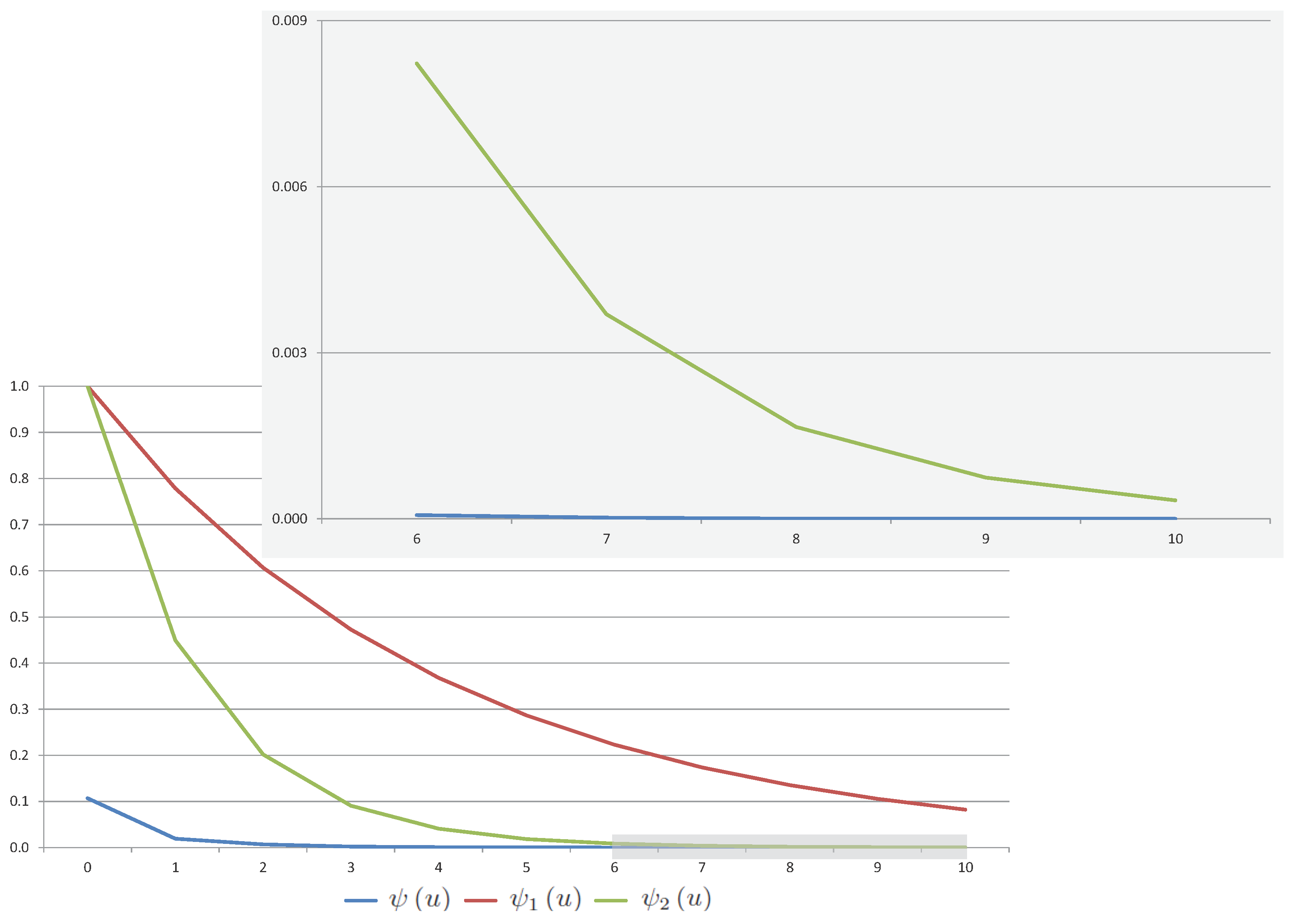
• After the above calculations, for $u\in \{0,1,2,\dots ,10\}$, we can compare approximate values of ruin probability $\psi \left(u\right)$ with their conservative estimate ${\psi }_1\left(u\right)$ and with their sharp estimate ${\psi }_2\left(u\right)$. All results are presented in

  Table 1. Values and estimates of ruin probability for model of Example 1.

  u	$\mathit{\psi }\left(\mathit{u}\right)$	${\mathit{\psi }}_1\left(\mathit{u}\right)$	${\mathit{\psi }}_2\left(\mathit{u}\right)$
  0	0.1069843	1.0000000	1.0000000
  1	0.0192021	0.7866279	0.3906278
  2	0.0068947	0.6187834	0.1525901
  3	0.0019112	0.4867523	0.0596059
  4	0.0006655	0.3828929	0.0232837
  5	0.0002378	0.3011942	0.0090953
  6	0.0000675	0.2369278	0.0035529
  7	0.0000217	0.1863740	0.0013878
  8	0.0000060	0.1466070	0.0005421
  9	0.0000014	0.1153251	0.0002118
  10	0.0000006	0.0907180	0.0000827

  and Figure 1. In fact, the conservative exponential upper bound ${\psi }_1$ is quite rough, but it is very easy to obtain an expression of this function using Theorem 3. The values of the sharp exponential upper bound ${\psi }_2$ are much closer to the simulated values of the ruin probability, however due to Theorem 4, more deeper analysis of the model elements is needed to obtain this bound. Values of $\psi \left(u\right)$, which are obtained by the Monte Carlo method, are sufficiently accurate, but such a procedure takes a lot of time and resources, because we need to generate a lot of process trajectories in order to get these values.

Example 2.

Suppose that the non-homogeneous renewal risk model is generated by a premium rate $p=11/10$, a sequence of independent random inter-arrival times $\{{\theta }_1,{\theta }_2,\dots \}$ and a sequence of independent random claims $\{Z_1,Z_2,\dots \}$. The random variable ${\theta }_k$ is distributed according to the Gamma law with the shape parameter k and the scale parameter $1/k$, while the random claim amount $Z_k$ is exponentially distributed with parameter $3+cosk$, i.e.,

$$\mathbb{P}({\theta }_k⩽x)=\frac{k^k}{\mathsf{\Gamma }\left(k\right)}\underset{0}{\overset{x}{\int }}{y}^{k-1}{\mathrm{e}}^{-ky}\mathrm{d}y,\mathbb{P}(Z_k⩽x)=\left(1-{\mathrm{e}}^{-(3+cosk)x}\right)1{\mathrm{I}}_{[0,\infty )}\left(x\right)$$

for each $k\in \mathbb{N}$. As it is already common, sequences $\{Z_1,Z_2,\dots \}$ and $\{{\theta }_1,{\theta }_2,\dots \}$ are supposed to be independent.

The presented model is more complex with respect to the model, which is described in Example 1, because all random variables in sequences $\{{\theta }_1,{\theta }_2,\dots \}$ and $\{Z_1,Z_2,\dots \}$ are non-identically distributed. We analyze this example step by step as in the previous one.

• Firstly, we start with the rough estimate of ruin probability, which can be derived using Theorem 3. In the case, we get that

  $$\begin{array}{c}\underset{k\in \mathbb{N}}{sup}\mathbb{E}(Z_k-p{\theta }_k)=\underset{k\in \mathbb{N}}{sup}\left(\frac{1}{3+cosk}-\frac{11}{10}\right)⩽-\frac{3}{5},\hfill \\ \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\theta }_{k}1{\mathrm{I}}_{\left\{{\theta }_k>4\right\}}\right)=\underset{k\in \mathbb{N}}{sup}\underset{4}{\overset{\infty }{\int }}x\frac{k^k{x}^{k-1}{\mathrm{e}}^{-kx}}{\mathsf{\Gamma }\left(k\right)}\mathrm{d}x=\underset{4}{\overset{\infty }{\int }}x{\mathrm{e}}^{-x}\mathrm{d}x=\frac{5}{{\mathrm{e}}^4}.\hfill \end{array}$$
  In addition, we have that

  $$\begin{array}{ccc}\hfill \mathbb{P}\left(Z_k-p{\theta }_k⩽x\right)& =& \underset{-\infty }{\overset{\infty }{\int }}\mathbb{P}\left(Z_k-\frac{11}{10}y⩽x\right)\mathrm{d}\mathbb{P}\left({\theta }_k⩽y\right)\hfill \\ & =& \frac{k^k}{\mathsf{\Gamma }\left(k\right)}\underset{0}{\overset{\infty }{\int }}\mathbb{P}\left(Z_k-\frac{11}{10}y⩽x\right)y^{k-1}{\mathrm{e}}^{-ky}\mathrm{d}y\hfill \\ & =& \frac{k^k}{\mathsf{\Gamma }\left(k\right)}\underset{0}{\overset{\infty }{\int }}\left(1-e^{-(3+cosk)(x+11y/10)}\right)1{\mathrm{I}}_{\left[0,\infty \right)}\left(x+\frac{11}{10}y\right)y^{k-1}{\mathrm{e}}^{-ky}\mathrm{d}y\hfill \\ & =& \frac{k^k}{\mathsf{\Gamma }\left(k\right)}\underset{max\left\{0,-10x/11\right\}}{\overset{\infty }{\int }}\left(1-e^{-(3+cosk)(x+11y/10)}\right)y^{k-1}{\mathrm{e}}^{-ky}\mathrm{d}y.\hfill \end{array}$$
  Since random values $Z_k$ and ${\theta }_k$ are absolutely continuous, so that random value $Z_k-p{\theta }_k$ has density, which for all $x⩾0$ has the following expression

  $$\begin{array}{c}\hfill f_{Z_k-p{\theta }_k}\left(x\right)=\frac{\left(3+cosk\right)k^k}{\mathsf{\Gamma }\left(k\right)}{\mathrm{e}}^{-\left(3+cosk\right)x}\underset{0}{\overset{\infty }{\int }}{y}^{k-1}{\mathrm{e}}^{-\left(k+33/10+11(cosk)/10\right)y}\mathrm{d}y.\end{array}$$
  Hence, we get that

  $$\begin{array}{ccc}\hfill \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left({\mathrm{e}}^{\gamma (Z_k-p{\theta }_k)}1{\mathrm{I}}_{\{Z_k-p{\theta }_k>0\}}\right)& =& \underset{k\in \mathbb{N}}{sup}\underset{0}{\overset{\infty }{\int }}{\mathrm{e}}^{\gamma x}{f}_{Z_k-p{\theta }_k}\left(x\right)\mathrm{d}x\hfill \\ & & =\underset{k\in \mathbb{N}}{sup}\left(\frac{\left(3+cosk\right)k^k}{\mathsf{\Gamma }\left(k\right)}\underset{0}{\overset{\infty }{\int }}{y}^{k-1}{\mathrm{e}}^{-\left(k+33/10+11(cosk)/10\right)y}\mathrm{d}y\underset{0}{\overset{\infty }{\int }}{\mathrm{e}}^{\left(\gamma -3-cosk\right)x}\mathrm{d}x\right)\hfill \\ & & ⩽\underset{k\in \mathbb{N}}{sup}\left(\frac{\left(3+cosk\right)k^k}{(3+cosk-\gamma )\mathsf{\Gamma }\left(k\right)}\underset{0}{\overset{\infty }{\int }}{y}^{k-1}{\mathrm{e}}^{-\left(k+22/10\right)y}\mathrm{d}y\right)\hfill \\ & & =\underset{k\in \mathbb{N}}{sup}\left(\frac{\left(3+cosk\right)k^k}{(3+cosk-\gamma )\mathsf{\Gamma }\left(k\right)}\frac{\mathsf{\Gamma }\left(k\right)}{{\left(k+\frac{11}{5}\right)}^k}\right)\hfill \\ & & ⩽\underset{k\in \mathbb{N}}{sup}\left(\frac{3+cosk}{3+cosk-\gamma }\right)\underset{k\in \mathbb{N}}{sup}{\left(\frac{k}{k+\frac{11}{5}}\right)}^k⩽\frac{5}{8\left(2-\gamma \right)}\mathrm{for}\mathrm{all}\gamma \in \left(0,2\right).\hfill \end{array}$$
  According to the derived estimates, conditions of Theorem 3 hold with such parameters $\alpha =3/5,\gamma =13/10,\beta =25/28,\varkappa =44/10$ and $\epsilon =5/{\mathrm{e}}^4$. Substituting the obtained constants into expression (2), we get that the parameter $\delta$ should be selected from the interval $\left(0,0.02855\right]$. If $\delta =7/250$, then Theorem 3 implies that

  $$\psi \left(u\right)⩽{\psi }_1\left(u\right):={\mathrm{e}}^{-91u/2500}$$

  for all $u⩾0$.
  The derived estimate is extremely conservative. For instance, it follows from the obtained inequality that $\psi \left(u\right)⩽0.02$, if $u⩾108$.
• We can use Theorem 4 to obtain the more sharper upper bound for the ruin probability. Conditions of this theorem are satisfied due to the above estimates and

  $$\begin{array}{c}\hfill \underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{\gamma Z_k}=\underset{k\in \mathbb{N}}{sup}\left(\frac{3+cosk}{3+cosk-\gamma }\right)⩽\frac{2}{2-\gamma }\mathrm{for}\mathrm{all}\gamma \in \left(0,2\right).\end{array}$$
  In addition, we have that

  $$\begin{array}{c}\hfill \underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}=\underset{k\in \mathbb{N}}{sup}\left(\frac{3+cosk}{3+cosk-h}\frac{1}{{\left(1+\frac{11h}{10k}\right)}^k}\right)⩽\frac{2}{2-h}\underset{k\in \mathbb{N}}{sup}\left(\frac{1}{{\left(1+\frac{11h}{10k}\right)}^k}\right)⩽1\end{array}$$

  for all $h\in \left(0,12/11\right]$.
  Accordingly, Theorem 4 together with the remark presented after this theorem imply that

  $$\psi \left(u\right)⩽\underset{h\in (0,12/11]}{inf}\left\{{\mathrm{e}}^{-hu}\underset{k\in \mathbb{N}}{sup}\mathbb{E}{\mathrm{e}}^{h(Z_k-p{\theta }_k)}\right\}⩽{\psi }_2\left(u\right):={\mathrm{e}}^{-12u/11}$$

  for all $u⩾0$.
  The derived estimate is exponential and almost 30 times more accurate than the previous one. For instance, it follows from the obtained inequality that $\psi \left(u\right)⩽0.02$, if $u⩾4$.
• After all these calculations, we again apply the Monte Carlo method in order to get approximate values of ruin probability $\psi \left(u\right)$ as in the previous example. We also analyze the same way, while $u\in \{0,1,2,\dots ,10\}$ and $N=1000$, and we simulate ${10}^7$ trajectories of the renewal risk process with N random claims and with N random inter-arrival times for each u. Although this example is sufficiently erratic, on the basis of the received values of ruin probability $\widehat{\psi }(u,N)\approx \psi \left(u\right)$, we get that $\psi \left(u\right)⩽0.02$, even if the initial surplus is relatively small, i.e., $u⩾2$.
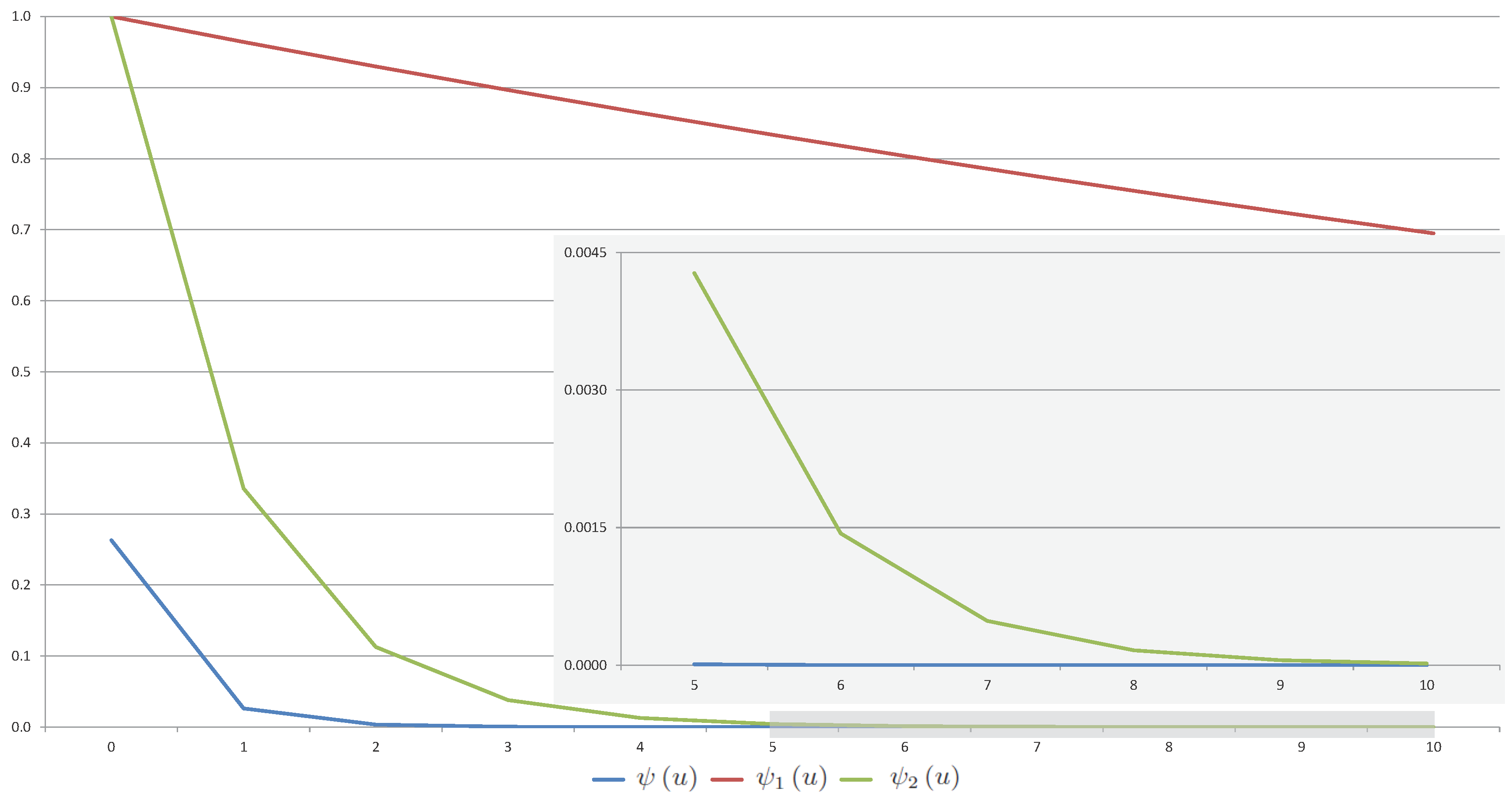
• Ultimately, we can make a comparison of approximate values of ruin probability $\psi \left(u\right)$ to their conservative exponential upper bound ${\psi }_1\left(u\right)$ and to their sharp exponential upper bound ${\psi }_2\left(u\right)$ for $u\in \{0,1,2,\dots ,10\}$. All results are presented in

  Table 2. Values and estimates of ruin probability for model of Example 2.

  u	$\mathit{\psi }\left(\mathit{u}\right)$	${\mathit{\psi }}_1\left(\mathit{u}\right)$	${\mathit{\psi }}_2\left(\mathit{u}\right)$
  0	0.2628618	1.0000000	1.0000000
  1	0.0262527	0.9642545	0.3359110
  2	0.0035110	0.9297868	0.1128362
  3	0.0005077	0.8965511	0.0379029
  4	0.0000739	0.8645034	0.0127320
  5	0.0000102	0.8336013	0.0042768
  6	0.0000015	0.8038039	0.0014366
  7	0.0000001	0.7750715	0.0004826
  8	0.0000000	0.7473662	0.0001621
  9	0.0000000	0.7206512	0.0000545
  10	0.0000000	0.6948912	0.0000183

  and Figure 2. Actually, the conservative estimate ${\psi }_1$ is too rough. The values of sharp estimate ${\psi }_2$ are more accurate than ${\psi }_1$. It should be noted that the Monte Carlo method takes even more time in this example than in Example 1, because we need to generate values of two random variables $Z_k$ and ${\theta }_k$, which are non-identically distributed for each $k=1,2,\dots ,N$.

5. Conclusions

Lundberg’s inequality or, in other words, an upper bound for the ultimate ruin probability, plays an important role in the homogeneous models. Although, in recent years, non-homogeneous models are considered in many papers, just a few of them contain exponential estimates of the ruin probability. Therefore, our primary goal is to establish conditions leading to a Lundberg-type inequality for a non-homogeneous renewal risk model, which is comparable to the analogous inequality for the homogeneous case. In this paper, three theorems are proved and two examples demonstrating their applicability are given. Theorem 2 guarantees the existence of some positive constant for an upper bound of the ultimate ruin probability. Theorems 3 and 4 demonstrate how that constant can be calculated. Note that Theorem 3 allows for a fast estimate of ruin probability. However, the large number of constants involved in the process makes it difficult to get an optimal estimate. A sharp exponential estimate can be obtained from Theorem 4. However, in this case, to get an explicit expression of an upper bound is an even more complicated process.