Multivariate Birnbaum-Saunders Distributions: Modelling and Applications
Abstract
1. Introduction and Literature Review
2. Univariate Birnbaum–Saunders Distributions
2.1. Genesis and Features of the Univariate BS Distribution
- (A1)
- , with .
- (A2)
- .
- (A3)
- , that is, follows a distribution with one degree of freedom.
2.2. Univariate Log-BS Distribution and BS Modelling
- (B1)
- , with , that is, a random variable with log-BS distribution can be obtained directly from a random variable with standard normal distribution.
- (B2)
- .
- (B3)
- , that is, follows a distribution with one degree of freedom.
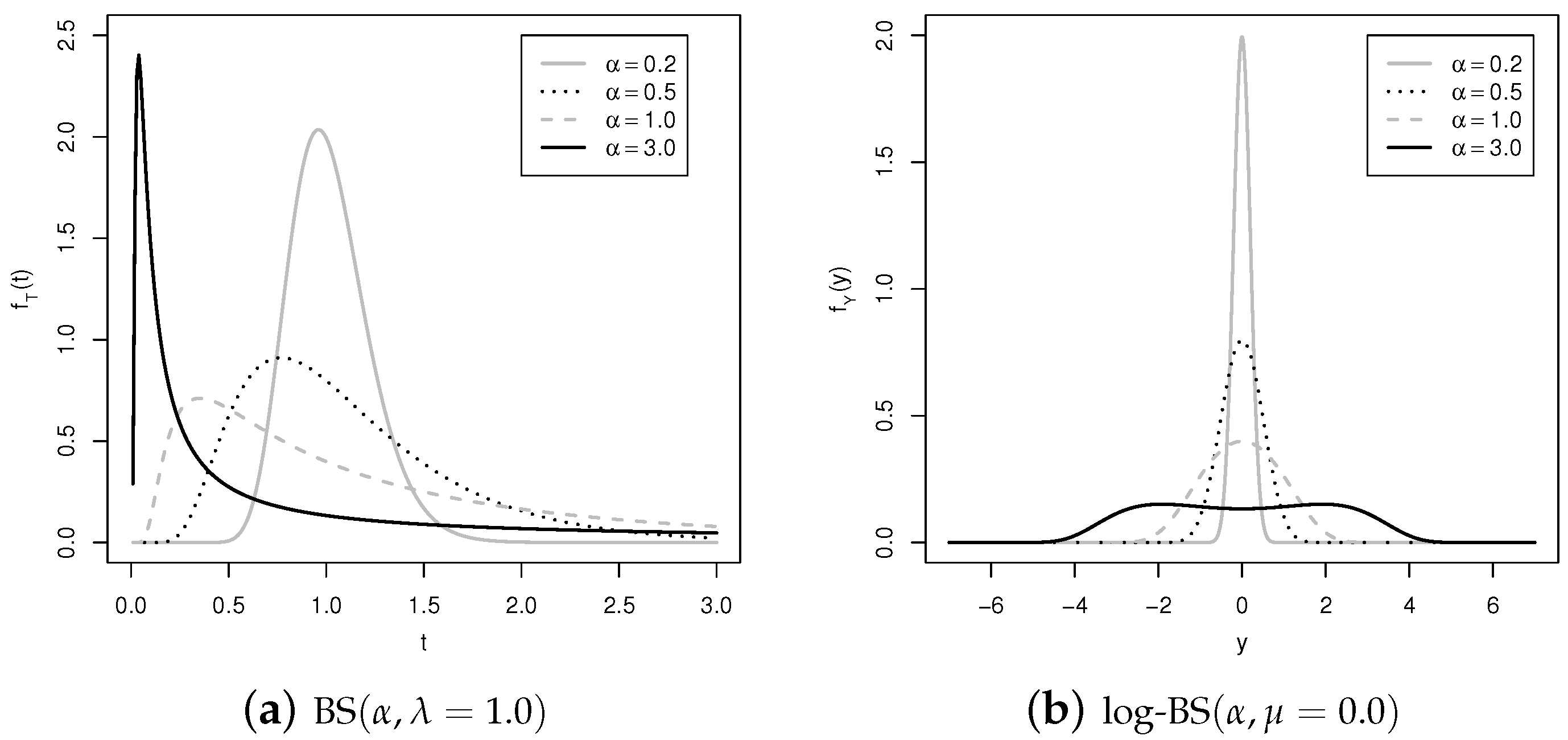
2.3. Illustration
3. Multivariate Birnbaum–Saunders Distributions
3.1. Multivariate Normal Distribution
3.2. Multivariate BS Distribution
- (C1)
- , with .
- (C2)
- , with .
- (C3)
- .
3.3. Multivariate Log-BS Distribution
- (D1)
- , where and
- (D2)
- , that is, a distribution with m degrees of freedom.
3.4. Mahalanobis Distance and Generation of Log-BS Random Vectors
| Algorithm 1 Generator of random vectors from multivariate log-BS distributions. |
|
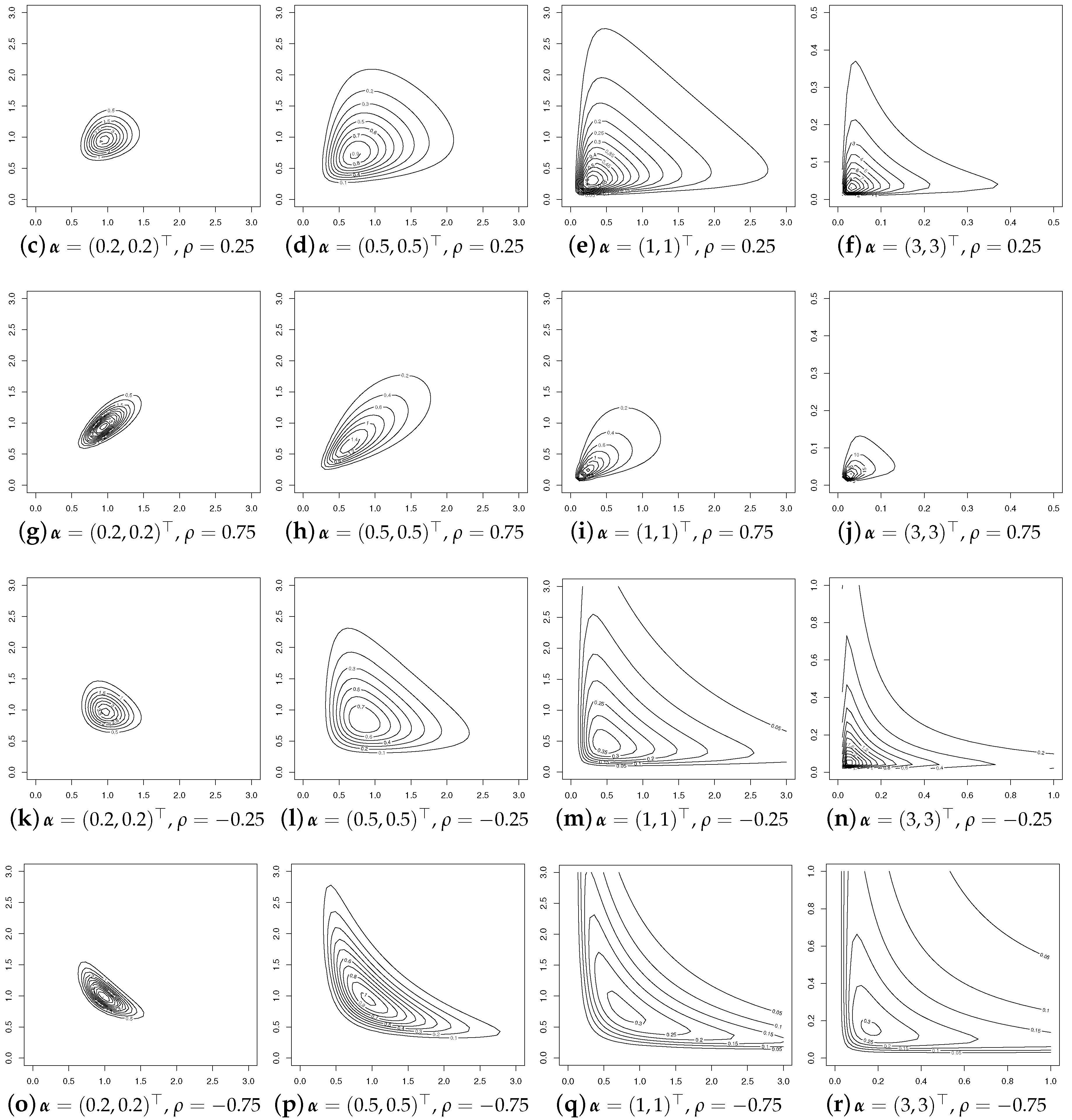
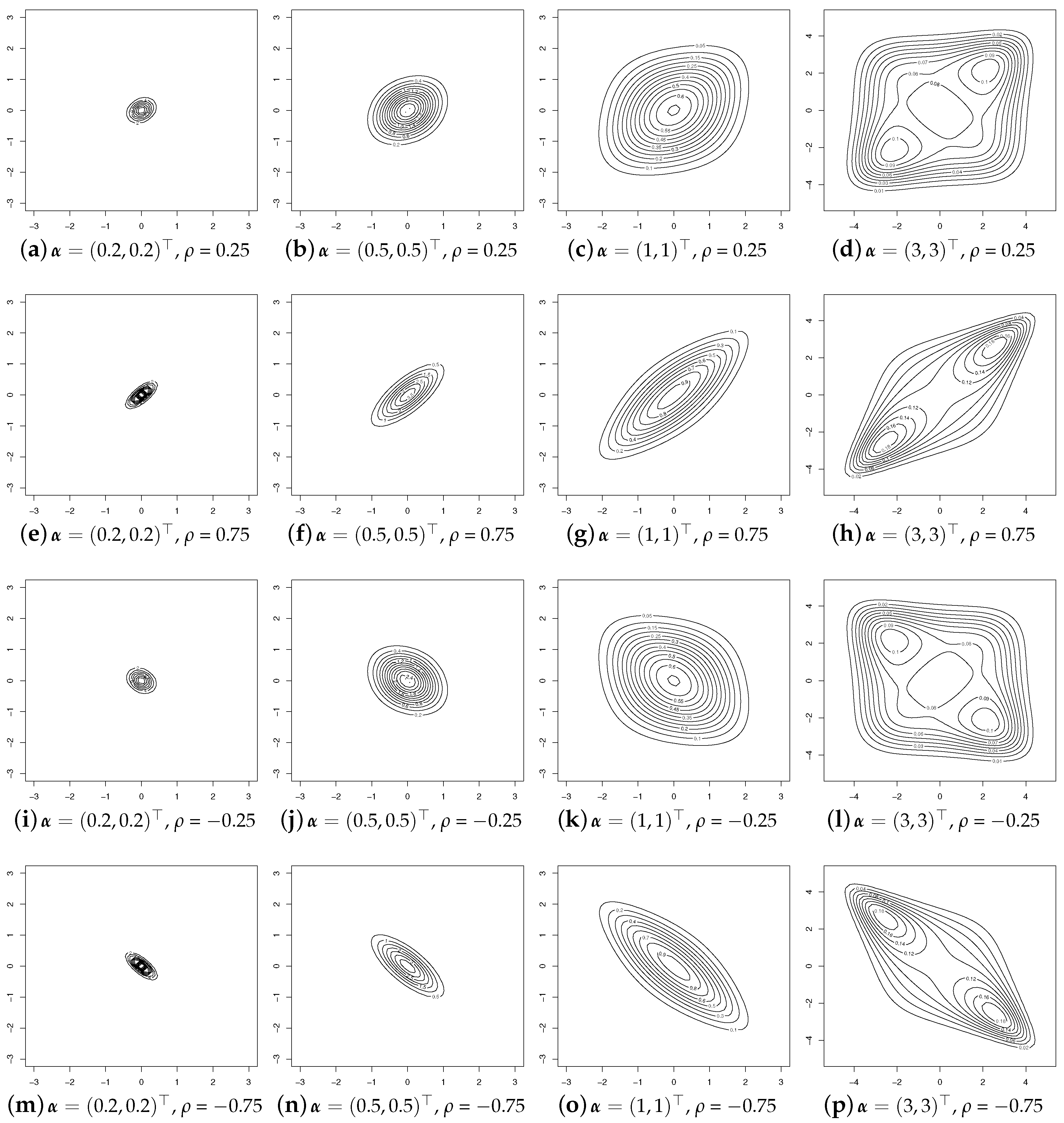
3.5. Illustration
4. Regression Modelling Based on Multivariate Birnbaum–Saunders Distributions
4.1. Formulation
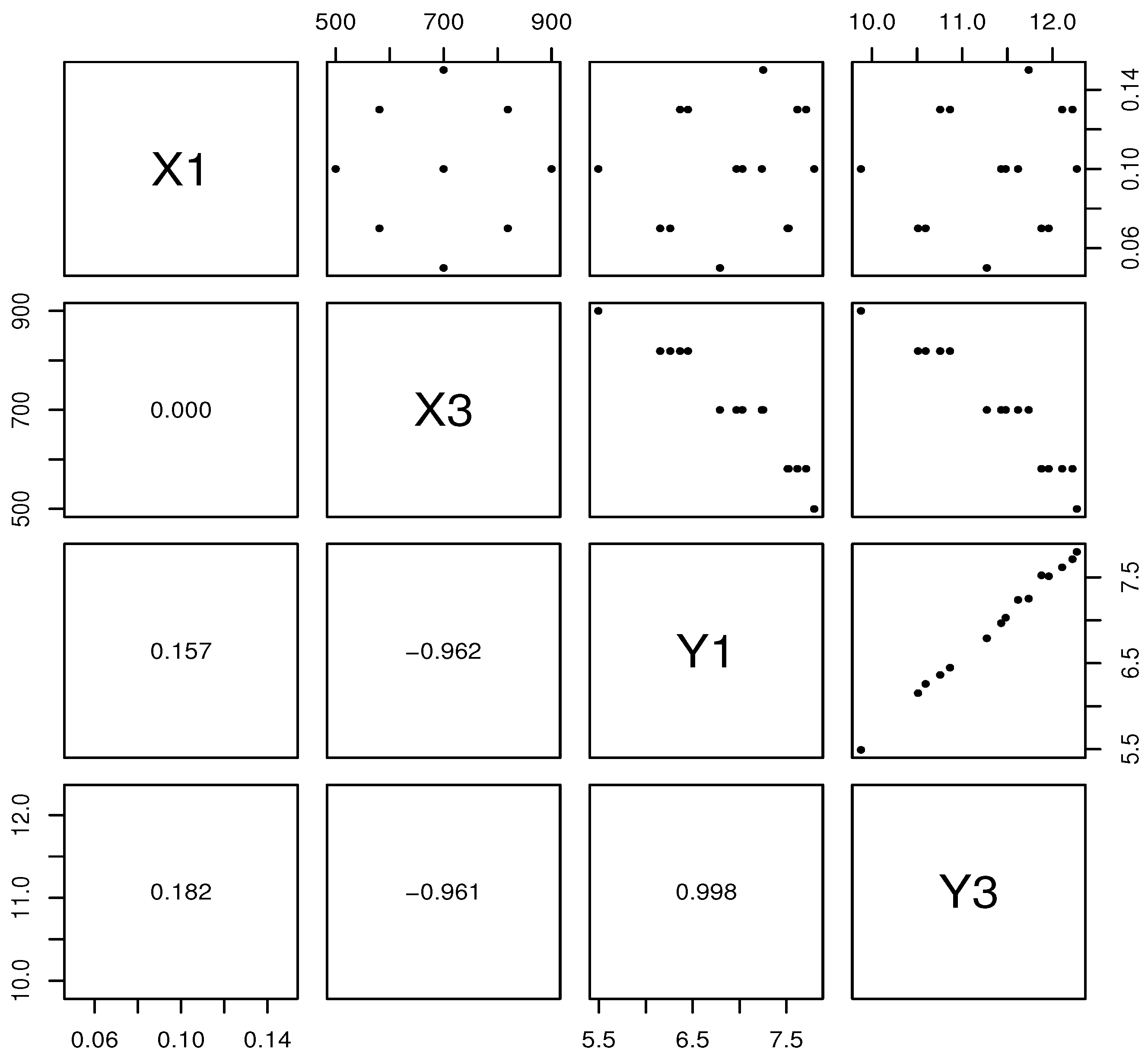
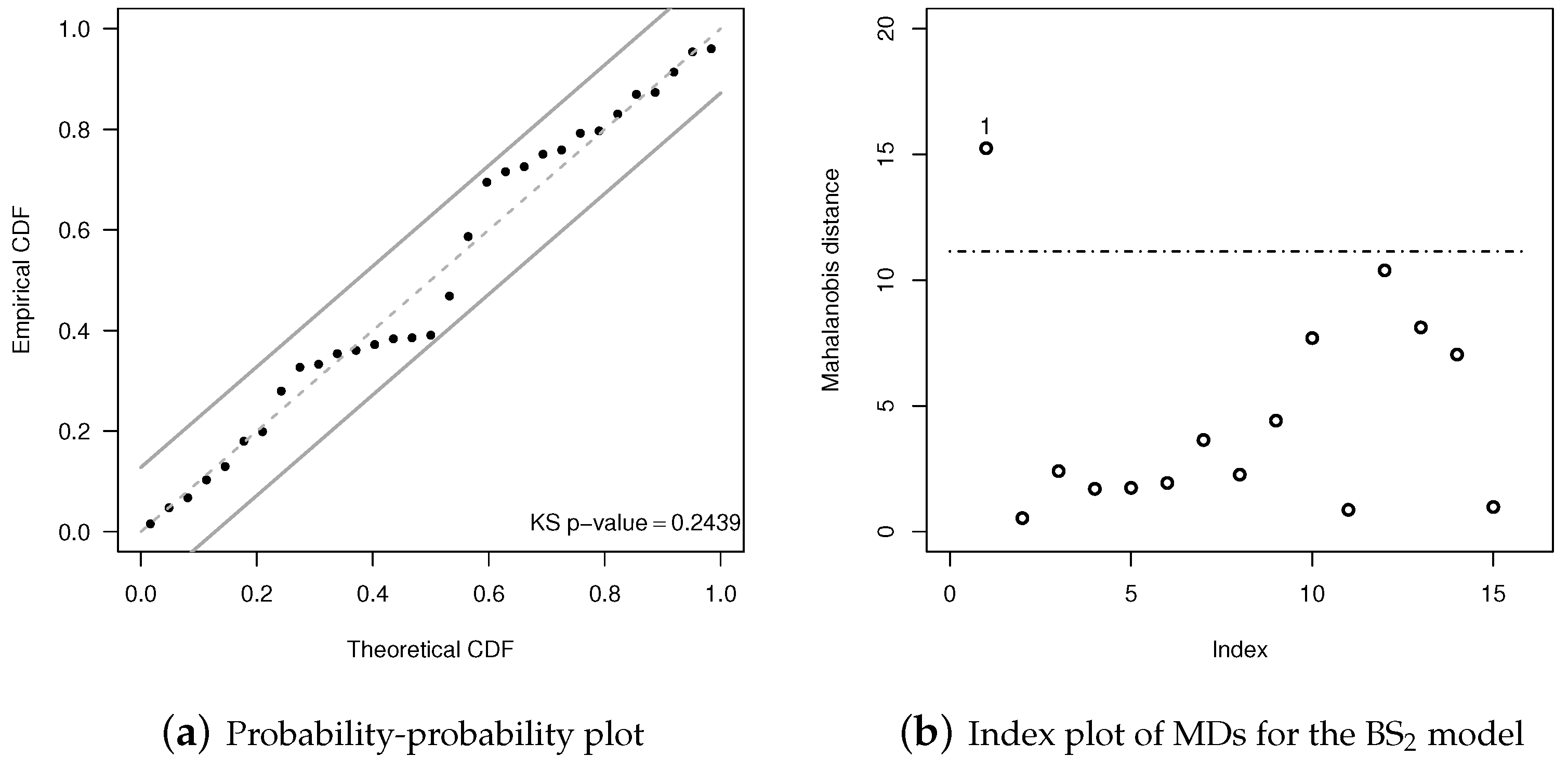
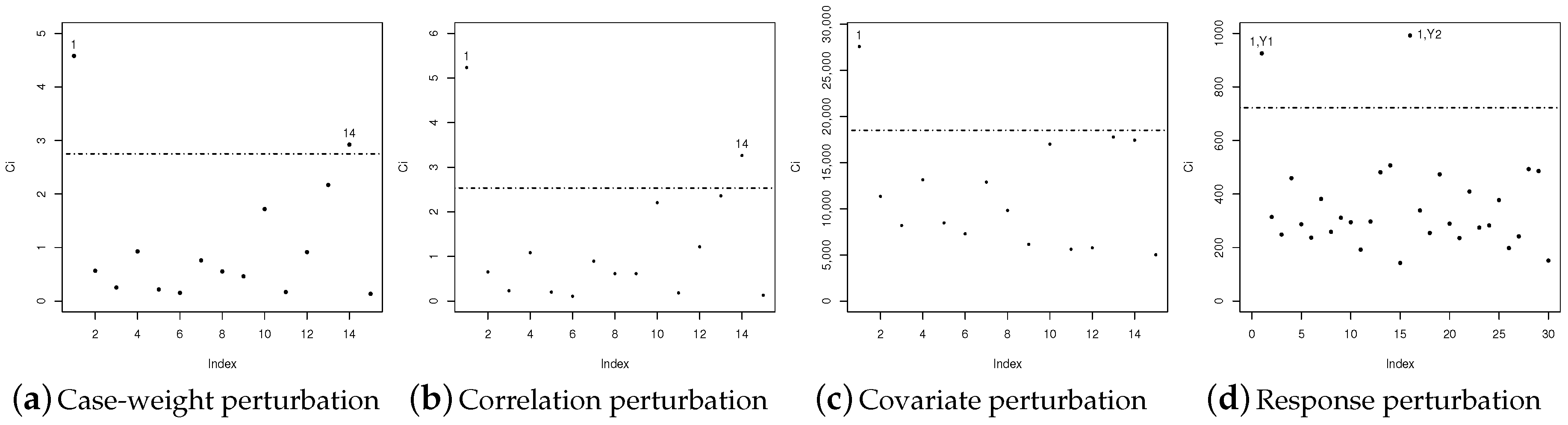
4.2. Illustration
| Algorithm 2 PP plots with acceptance bands for testing normality. |
|
5. Spatial Modelling Based on Multivariate BS Distributions
5.1. Formulation
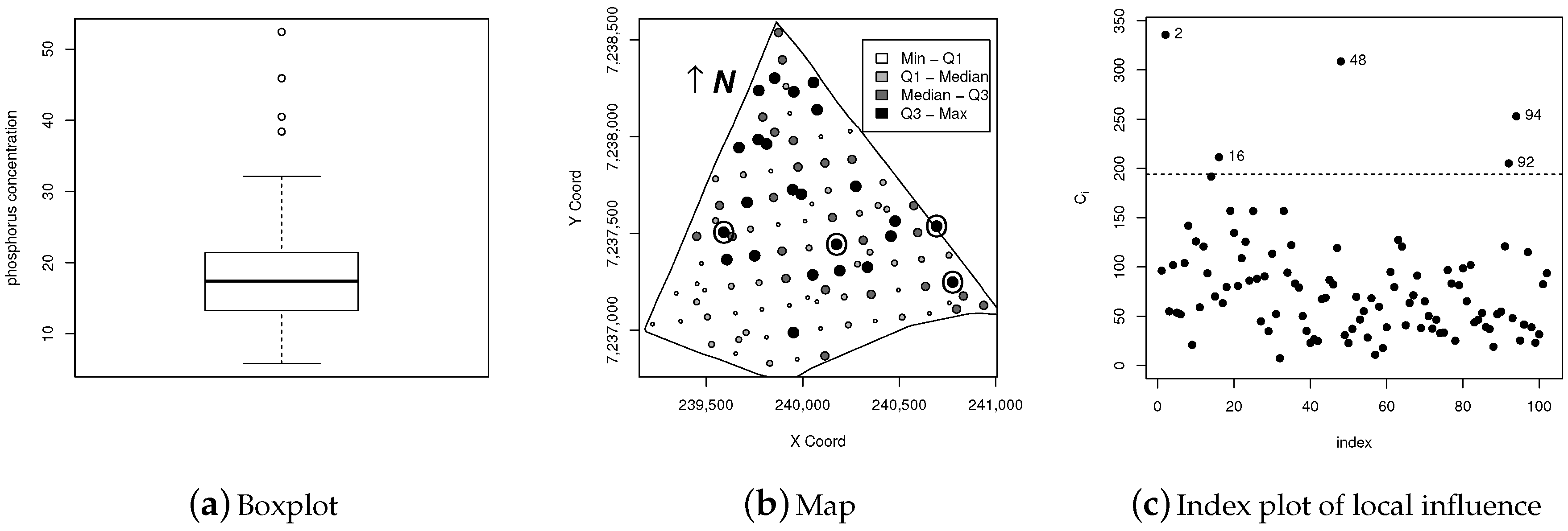
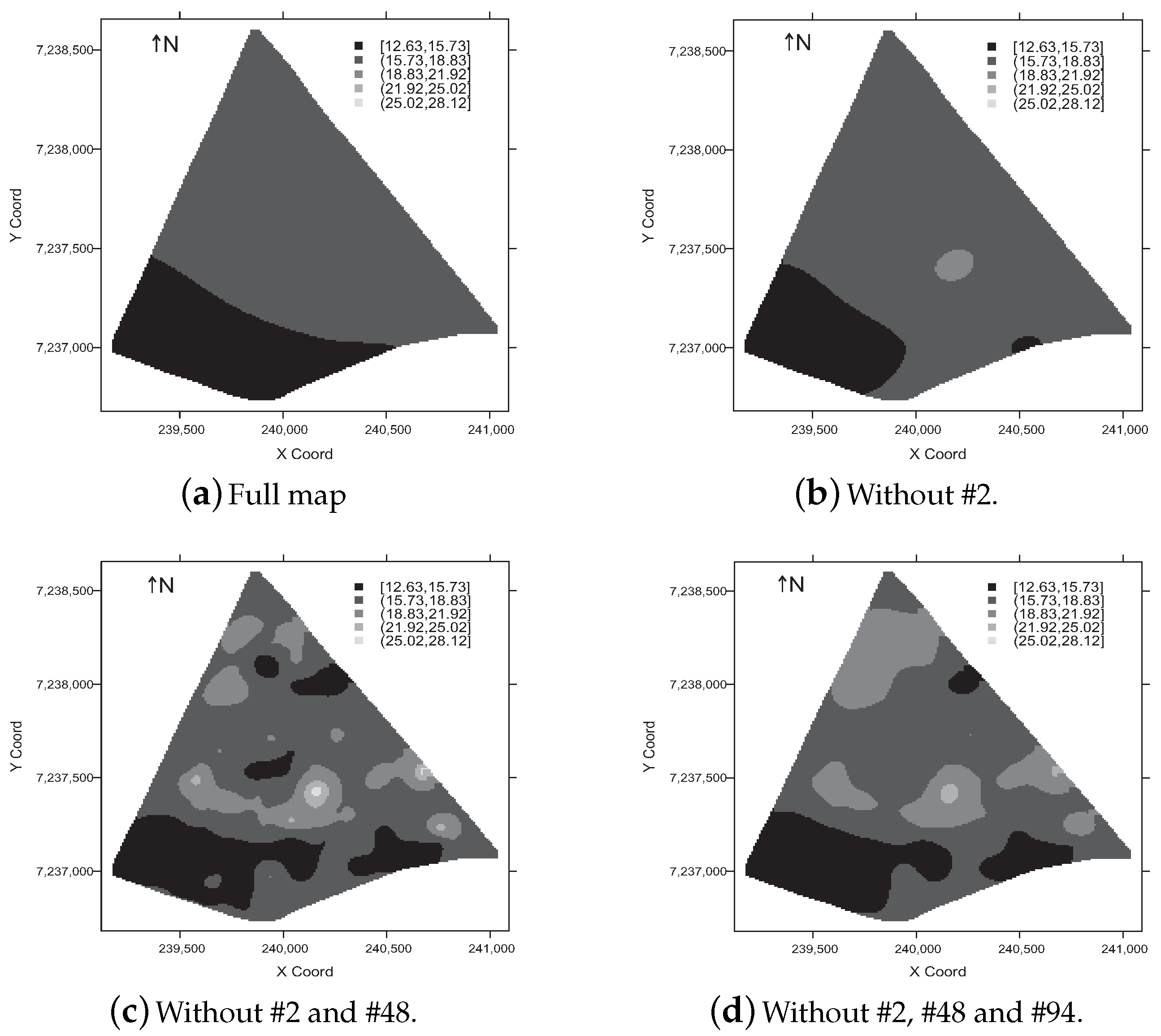
5.2. Illustration
6. Multivariate Birnbaum–Saunders Control Charts
6.1. Formulation
| Algorithm 3 Computation of BS control chart limits in Phase I. |
|
| Algorithm 4 Process monitoring using the multivariate BS chart in Phase II. |
|
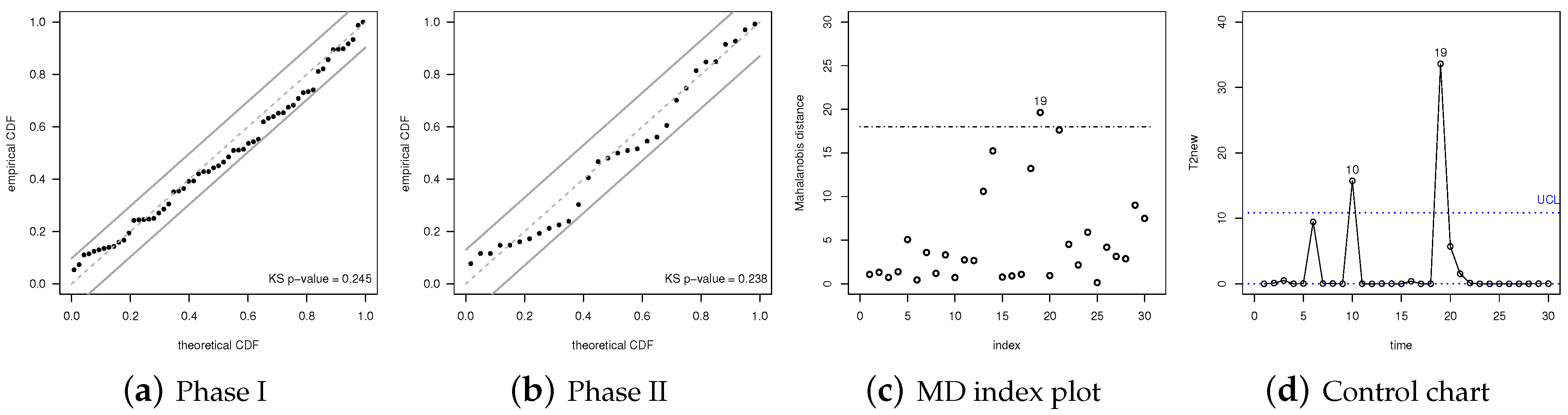
6.2. Illustration
7. Discussion, Conclusions and Future Research
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alt, Frank. 1985. Multivariate quality control. In The Encyclopedia of Statistical Sciences. Edited by S. Kotz, N. L. Johnson and C. Read. New York: Wiley, pp. 110–12. [Google Scholar]
- Anderson, James R., Ernest E. Hardy, John T. Roach, and Richard E. Witmer. 1976. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; Technical Report 964. Washington: US Government Printing Office.
- Athayde, Emilia. 2017. A characterization of the Birnbaum–Saunders distribution. REVSTAT Statistical Journal 15: 333–54. [Google Scholar]
- Athayde, Emilia, Assis Azevedo, Michelli Barros, and Víctor Leiva. 2018. Failure rate of Birnbaum–Saunders distributions: Shape, change-point, estimation and robustness. Brazilian Journal of Probability and Statistics. in press. [Google Scholar]
- Atkinson, Anthony C. 2009. Econometric applications of the forward search in regression: Robustness, diagnostics, and graphics. Econometric Reviews 28: 21–39. [Google Scholar] [CrossRef]
- Azevedo, Cecilia, Víctor Leiva, Emilia Athayde, and Narayanaswamy Balakrishnan. 2012. Shape and change point analyses of the Birnbaum–Saunders-t hazard rate and associated estimation. Computational Statistics and Data Analysis 56: 3887–97. [Google Scholar] [CrossRef]
- Balakrishnan, Narayanaswamy, Ramesh Gupta, Debasis Kundu, Víctor Leiva, and Antonio Sanhueza. 2011. On some mixture models based on the Birnbaum–Saunders distribution and associated inference. Journal of Statistical Planning and Inference 141: 2175–90. [Google Scholar] [CrossRef]
- Balakrishnan, Narayanaswamy, Víctor Leiva, Antonio Sanhueza, and Filidor Vilca. 2009. Estimation in the Birnbaum–Saunders distribution based on scale-mixture of normals and the EM-algorithm. Statistics and Operations Research Transactions 33: 171–92. [Google Scholar]
- Barros, Michelli, Víctor Leiva, Raydonal Ospina, and Aline Tsuyuguchi. 2014. Goodness-of-fit tests for the Birnbaum–Saunders distribution with censored reliability data. IEEE Transactions on Reliability 63: 543–54. [Google Scholar] [CrossRef]
- Bebbington, Mark, Chin-Diew Lai, and Ricardas Zitikis. 2008. A proof of the shape of the Birnbaum–Saunders hazard rate function. Mathematical Scientist 33: 49–56. [Google Scholar]
- Bhatti, Chad. 2010. The Birnbaum–Saunders autoregressive conditional duration model. Mathematics and Computers in Simulation 80: 2062–78. [Google Scholar] [CrossRef]
- Birnbaum, Zygmunt W., and Sam C. Saunders. 1969a. A new family of life distributions. Journal of Applied Probability 6: 319–27. [Google Scholar] [CrossRef]
- Birnbaum, Zygmunt W., and Sam C. Saunders. 1969b. Estimation for a family of life distributions with applications to fatigue. Journal of Applied Probability 6: 328–47. [Google Scholar] [CrossRef]
- Bourguignon, Marcelo, Jeremias Leão, Víctor Leiva, and Manoel Santos-Neto. 2017. The transmuted Birnbaum–Saunders distribution. REVSTAT Statistical Journal 15: 601–28. [Google Scholar]
- Caro-Lopera, Francisco, Víctor Leiva, and Narayanaswamy Balakrishnan. 2012. Connection between the Hadamard and matrix products with an application to matrix-variate Birnbaum–Saunders distributions. Journal of Multivariate Analysis 104: 126–39. [Google Scholar] [CrossRef]
- Chatterjee, Samprit, and Ali S. Hadi. 1988. Sensitivity Analysis in Linear Regression. New York: Wiley. [Google Scholar]
- CONAMA. 1998. Establishment of Primary Quality Guideline for PM10 That Regulates Environmental Alerts; Technical Report Decree 59. Santiago: The Ministry of Environment (CONAMA) of the Chilean Government.
- Cook, R. Dennis. 1987. Influence assessment. Journal of Applied Statistics 14: 117–31. [Google Scholar] [CrossRef]
- Cook, R. Dennis, and Sanford Weisberg. 1982. Residuals and Influence in Regression. London: Chapman and Hall. [Google Scholar]
- D’Agostino, Ralph B., and Michael A. Stephens. 1986. Goodness-of-Fit Techniques. New York: Marcel Dekker. [Google Scholar]
- Desmond, Anthony F., Gabriel A. Rodríguez-Yam, and Xuewen Lu. 2008. Estimation of parameters for a Birnbaum–Saunders regression model with censored data. Journal of Statistical Computation and Simulation 78: 983–97. [Google Scholar] [CrossRef]
- Desousa, Mario F., Helton Saulo, Víctor Leiva, and Paulo Scalco. 2018. On a tobit-Birnbaum–Saunders model with an application to antibody response to vaccine. Journal of Applied Statistics 45: 932–55. [Google Scholar] [CrossRef]
- Dupuis, Debbie J., and Joanna E. Mills. 1998. Robust estimation of the Birnbaum–Saunders distribution. IEEE Transactions on Reliability 1: 88–95. [Google Scholar] [CrossRef]
- Engle, Robert, and Jeffrey R. Russell. 1998. Autoregressive conditional duration: A new method for irregularly spaced transaction data. Econometrica 66: 1127–62. [Google Scholar] [CrossRef]
- Ferreira, Marta, M. Ivette Gomes, and Víctor Leiva. 2012. On an extreme value version of the Birnbaum–Saunders distribution. REVSTAT Statistical Journal 10: 181–210. [Google Scholar]
- Galea, Manuel, Víctor Leiva, and Gilberto A. Paula. 2004. Influence diagnostics in log-Birnbaum–Saunders regression models. Journal of Applied Statistics 31: 1049–64. [Google Scholar] [CrossRef]
- Garcia-Papani, Fabiana, Miguel A. Uribe-Opazo, Víctor Leiva, and Robert G. Aykroyd. 2017. Birnbaum-Saunders spatial modelling and diagnostics applied to agricultural engineering data. Stochastic Environmental Research and Risk Assessment 31: 105–24. [Google Scholar] [CrossRef]
- Hall, Peter. 2013. The Bootstrap and Edgeworth Expansion. New York: Springer. [Google Scholar]
- Hotelling, Harold. 1947. Multivariate Quality Control Illustrated by Air Testing of Sample Bombsights. In Techniques of Statistical Analysis. Edited by C. Eisenhart, M. W. Hastay and W. A. Wallis. New York: McGraw Hill, pp. 111–84. [Google Scholar]
- Ibacache-Pulgar, Germán, Gilberto A. Paula, and Manuel Galea. 2014. On influence diagnostics in elliptical multivariate regression models with equicorrelated random errors. Statistical Modelling 16: 14–21. [Google Scholar] [CrossRef]
- Jamalizadeh, Ahad, and Debasis Kundu. 2015. Multivariate Birnbaum–Saunders distribution based on multivariate skew-normal distribution. Journal of the Japan Statistical Society 45: 1–20. [Google Scholar] [CrossRef][Green Version]
- Johnson, Norman L., Samuel Kotz, and Narayanaswamy Balakrishnan. 1995. Continuous Univariate Distributions. New York: Wiley, vol. 2. [Google Scholar]
- Khosravi, Mohsen, Debasis Kundu, and Ahad Jamalizadeh. 2015. On bivariate and mixture of bivariate Birnbaum-Saunders distributions. Statistical Methodology 23: 1–17. [Google Scholar] [CrossRef]
- Kotz, Samuel, Víctor Leiva, and Antonio Sanhueza. 2010. Two new mixture models related to the inverse Gaussian distribution. Methodology and Computing in Applied Probability 12: 199–212. [Google Scholar] [CrossRef]
- Krippendorff, Klaus. 2004. Content Analysis: An Introduction to its Methodology. Thousand Oaks: Sage. [Google Scholar]
- Kundu, Debasis. 2015a. Bivariate log-Birnbaum-Saunders distribution. Statistics 49: 900–17. [Google Scholar] [CrossRef]
- Kundu, Debasis. 2015b. Bivariate sinh-normal distribution and a related model. Brazilian Journal of Probability and Statistics 20: 590–607. [Google Scholar] [CrossRef]
- Kundu, Debasis, Narayanaswamy Balakrishnan, and Ahad Jamalizadeh. 2010. Bivariate Birnbaum–Saunders distribution and associated inference. Journal of Multivariate Analysis 101: 113–25. [Google Scholar] [CrossRef]
- Kundu, Debasis, Narayanaswamy Balakrishnan, and Ahad Jamalizadeh. 2013. Generalized multivariate Birnbaum–Saunders distributions and related inferential issues. Journal of Multivariate Analysis 116: 230–44. [Google Scholar] [CrossRef]
- Kundu, Debasis, N. Kannan, and Narayanaswamy Balakrishnan. 2008. On the hazard function of Birnbaum–Saunders distribution and associated inference. Computational Statistics and Data Analysis 52: 2692–702. [Google Scholar] [CrossRef]
- Lange, Kenneth. 2001. Numerical Analysis for Statisticians. New York: Springer. [Google Scholar]
- Leão, Jeremias, Víctor Leiva, Helton Saulo, and Vera Tomazella. 2017. Birnbaum–Saunders frailty regression models: Diagnostics and application to medical data. Biometrical Journal 59: 291–314. [Google Scholar] [CrossRef] [PubMed]
- Leão, Jeremias, Víctor Leiva, Helton Saulo, and Vera Tomazella. 2018a. A survival model with Birnbaum–Saunders frailty for uncensored and censored cancer data. Brazilian Journal of Probability and Statistics. in press. [Google Scholar]
- Leão, Jeremias, Víctor Leiva, Helton Saulo, and Vera Tomazella. 2018b. Incorporation of frailties into a cure rate regression model and its diagnostics and application to melanoma data. Statistics in Medicine. under review. [Google Scholar]
- Leiva, Víctor. 2016. The Birnbaum–Saunders Distribution. New York: Academic Press. [Google Scholar]
- Leiva, Víctor, Emilia Athayde, Cecilia Azevedo, and Carolina Marchant. 2011. Modeling wind energy flux by a Birnbaum–Saunders distribution with unknown shift parameter. Journal of Applied Statistics 38: 2819–38. [Google Scholar] [CrossRef]
- Leiva, Víctor, Marta Ferreira, M. Ivette Gomes, and Camilo Lillo. 2016. Extreme value Birnbaum–Saunders regression models applied to environmental data. Stochastic Environmental Research and Risk Assessment 30: 1045–58. [Google Scholar] [CrossRef]
- Leiva, Víctor, Carolina Marchant, Fabrizio Ruggeri, and Helton Saulo. 2015. A criterion for environmental assessment using Birnbaum–Saunders attribute control charts. Environmetrics 26: 463–76. [Google Scholar] [CrossRef]
- Leiva, Víctor, Carolina Marchant, Helton Saulo, Muhammad Aslam, and Fernando Rojas. 2014. Capability indices for Birnbaum–Saunders processes applied to electronic and food industries. Journal of Applied Statistics 41: 1881–902. [Google Scholar] [CrossRef]
- Leiva, Víctor, M. Guadalupe Ponce, Carolina Marchant, and Oscar Bustos. 2012. Fatigue statistical distributions useful for modeling diameter and mortality of trees. Revista Colombiana de Estadística 35: 349–67. [Google Scholar]
- Leiva, Víctor, Edgardo Rojas, Manuel Galea, and Antonio Sanhueza. 2014. Diagnostics in Birnbaum–Saunders accelerated life models with an application to fatigue data. Applied Stochastic Models in Business and Industry 30: 115–31. [Google Scholar] [CrossRef]
- Leiva, Víctor, Fabrizio Ruggeri, Helton Saulo, and Juan F. Vivanco. 2017. A methodology based on the Birnbaum–Saunders distribution for reliability analysis applied to nano-materials. Reliability Engineering and System Safety 157: 192–201. [Google Scholar] [CrossRef]
- Leiva, Víctor, Antonio Sanhueza, and José M. Angulo. 2009. A length-biased version of the Birnbaum–Saunders distribution with application in water quality. Stochastic Environmental Research and Risk Assessment 23: 299–307. [Google Scholar] [CrossRef]
- Leiva, Víctor, Antonio Sanhueza, Samuel Kotz, and Nelson Araneda. 2010. A unified mixture model based on the inverse Gaussian distribution. Pakistan Journal of Statistics 26: 445–60. [Google Scholar]
- Leiva, Víctor, Antonio Sanhueza, Pranab K. Sen, and Gilberto A. Paula. 2008. Random number generators for the generalized Birnbaum–Saunders distribution. Journal of Statistical Computation and Simulation 78: 1105–18. [Google Scholar] [CrossRef]
- Leiva, Víctor, Manoel Santos-Neto, Francisco José A. Cysneiros, and Michelli Barros. 2014. Birnbaum–Saunders statistical modelling: A new approach. Statistical Modelling 14: 21–48. [Google Scholar] [CrossRef]
- Leiva, Víctor, Manoel Santos-Neto, Francisco José A. Cysneiros, and Michelli Barros. 2016. A methodology for stochastic inventory models based on a zero-adjusted Birnbaum–Saunders distribution. Applied Stochastic Models in Business and Industry 32: 74–89. [Google Scholar] [CrossRef]
- Leiva, Víctor, and Helton Saulo. 2017. Environmental applications based on Birnbaum–Saunders models. In Mathematical and Statistical Applications in Life Sciences and Engineering. Edited by A. Adhikari, M. Adhikari and Y. Chaubey. New York: Springer, pp. 283–304. [Google Scholar]
- Leiva, Víctor, Helton Saulo, Jeremias Leão, and Carolina Marchant. 2014. A family of autoregressive conditional duration models applied to financial data. Computational Statistics and Data Analysis 79: 175–91. [Google Scholar] [CrossRef]
- Leiva, Víctor, and Sam C. Saunders. 2015. Cumulative damage models. Wiley StatsRef: Statistics Reference Online 1: 1–10. [Google Scholar]
- Leiva, Víctor, Mauricio Tejo, Pierre Guiraud, Oliver Schmachtenberg, Patricio Orio, and Fernando Marmolejo-Ramos. 2015. Modeling neural activity with cumulative damage distributions. Biological Cybernetics 109: 421–33. [Google Scholar] [CrossRef] [PubMed]
- Leiva, Víctor, and Juan F. Vivanco. 2016. Fatigue models. Wiley StatsRef: Statistics Reference Online 1: 1–10. [Google Scholar]
- Lemonte, Artur J. 2011. Covariance matrix formula for Birnbaum–Saunders regression models. Journal of Statistical Computation and Simulation 81: 899–908. [Google Scholar] [CrossRef]
- Lemonte, Artur J., and Silvia L. P. Ferrari. 2011a. Signed likelihood ratio tests in the Birnbaum–Saunders regression model. Journal of Statistical Planning and Inference 141: 1031–40. [Google Scholar] [CrossRef]
- Lemonte, Artur J., and Silvia L. P. Ferrari. 2011b. Small-sample corrections for score tests in Birnbaum–Saunders regressions. Communications in Statistics: Theory and Methods 40: 232–43. [Google Scholar] [CrossRef]
- Lemonte, Artur J., Guillermo Martínez-Flores, and Germán Moreno-Arenas. 2015. Multivariate Birnbaum–Saunders distribution: Properties and associated inference. Journal of Statistical Computation and Simulation 85: 374–92. [Google Scholar] [CrossRef]
- Lemonte, Artur J., Alexandre Simas, and Francisco Cribari-Neto. 2008. Bootstrap-based improved estimators for the two-parameter Birnbaum–Saunders distribution. Journal of Statistical Computation and Simulation 78: 37–49. [Google Scholar] [CrossRef]
- Lemonte, Artur J. 2016. Robust inference for Birnbaum–Saunders regressions. Journal of Statistical Computation and Simulation 86: 611–22. [Google Scholar] [CrossRef]
- Lepadatu, Daniel, Abdessamad Kobi, Ridha Hambli, and Alain Barreau. 2005. Lifetime multiple response optimization of metal extrusion die. Proceedings of the Annual Reliability and Maintainability Symposium, Institute of Electrical and Electronics Engineers 1: 37–42. [Google Scholar]
- Lillo, Camilo, Víctor Leiva, Orietta Nicolis, and Robert G. Aykroyd. 2018. L-moments of the Birnbaum–Saunders distribution and its extreme value version: Estimation, goodness of fit and application to earthquake data. Journal of Applied Statistics 45: 187–209. [Google Scholar] [CrossRef]
- Lio, Yuhlong L., and Chanseok Park. 2008. A bootstrap control chart for Birnbaum–Saunders percentiles. Quality and Reliability Engineering International 24: 585–600. [Google Scholar] [CrossRef]
- Marchant, Carolina, Víctor Leiva, M. Fernanda Cavieres, and Antonio Sanhueza. 2013. Air contaminant statistical distributions with application to PM10 in Santiago, Chile. Reviews of Environmental Contamination and Toxicology 223: 1–31. [Google Scholar] [PubMed]
- Marchant, Carolina, Víctor Leiva, and Francisco José A. Cysneiros. 2016. A multivariate log-linear model for Birnbaum–Saunders distributions. IEEE Transactions on Reliability 65: 816–27. [Google Scholar] [CrossRef]
- Marchant, Carolina, Víctor Leiva, Francisco José A. Cysneiros, and Shuangzhe Liu. 2018. Robust multivariate control charts based on Birnbaum–Saunders distributions. Journal of Statistical Computation and Simulation 88: 182–202. [Google Scholar] [CrossRef]
- Marchant, Carolina, Víctor Leiva, Franciso José A. Cysneiros, and Juan F. Vivanco. 2016. Diagnostics in multivariate generalized Birnbaum–Saunders regression models. Journal of Applied Statistics 43: 2829–49. [Google Scholar] [CrossRef]
- MMA. 2011. Establishment of Primary Quality Guideline for Inhalable Fine Particulate Matter PM2.5; Technical Report Decree 12. Santiago: The Ministry of Environment of the Chilean Government.
- Nocedal, Jorge, and Stephen J. Wright. 1999. Numerical Optimization. New York: Springer. [Google Scholar]
- Osorio, Felipe, Gilberto A. Paula, and Manuel Galea. 2007. Assessment of local influence in elliptical linear models with longitudinal structure. Computational Statistics and Data Analysis 51: 4354–68. [Google Scholar] [CrossRef]
- Owen, William J. 2006. A new three-parameter extension to the Birnbaum–Saunders distribution. IEEE Transactions on Reliability 55: 475–79. [Google Scholar] [CrossRef]
- Owen, William J., and William J. Padgett. 1999. Accelerated test models for system strength based on Birnbaum–Saunders distribution. Lifetime Data Analysis 5: 133–47. [Google Scholar] [CrossRef] [PubMed]
- Owen, William J., and William J. Padgett. 2000. A Birnbaum–Saunderss accelerated life model. IEEE Transactions on Reliability 49: 224–29. [Google Scholar] [CrossRef]
- Paula, Gilberto A. 1993. Assessing local influence in restricted regression models. Communications in Statistics: Theory and Methods 16: 63–79. [Google Scholar] [CrossRef]
- Paula, Gilberto A., Víctor Leiva, Michelli Barros, and Shuangzhe Liu. 2012. Robust statistical modeling using the Birnbaum–Saunders-t distribution applied to insurance. Applied Stochastic Models in Business and Industry 28: 16–34. [Google Scholar] [CrossRef]
- R Core Team. 2016. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Rieck, James R. 2003. A comparison of two random number generators for the Birnbaum–Saunders distribution. Communications in Statistics: Theory and Methods 32: 929–34. [Google Scholar] [CrossRef]
- Rieck, James R., and Jerry R. Nedelman. 1991. A log-linear model for the Birnbaum–Saunders distribution. Technometrics 3: 51–60. [Google Scholar]
- Rojas, Fernando, Víctor Leiva, Peter Wanke, and Carolina Marchant. 2015. Optimization of contribution margins in food services by modeling independent component demand. Revista Colombiana de Estadística 38: 1–30. [Google Scholar] [CrossRef]
- Sánchez, Luis, Víctor Leiva, Francisco J. Caro-Lopera, and Franciso José A. Cysneiros. 2015. On matrix-variate Birnbaum-Saunders distributions and their estimation and application. Brazilian Journal of Probability and Statistics 29: 790–812. [Google Scholar] [CrossRef]
- Santana, Lucia, Filidor Vilca, and Víctor Leiva. 2011. Influence analysis in skew-Birnbaum–Saunders regression models and applications. Journal of Applied Statistics 38: 1633–49. [Google Scholar] [CrossRef]
- Santos-Neto, Manoel, Franciso José A. Cysneiros, Víctor Leiva, and S. Ejaz Ahmed. 2012. On new parameterizations of the Birnbaum–Saunders distribution. Pakistan Journal of Statistics 28: 1–26. [Google Scholar]
- Santos-Neto, Manoel, Franciso José A. Cysneiros, Víctor Leiva, and Michelli Barros. 2014. On new parameterizations of the Birnbaum–Saunders distribution and its moments, estimation and application. REVSTAT Statistical Journal 12: 247–72. [Google Scholar]
- Santos-Neto, Manoel, Franciso José A. Cysneiros, Víctor Leiva, and Michelli Barros. 2016. Reparameterized Birnbaum–Saunders regression models with varying precision. Electronic Journal of Statistics 10: 2825–55. [Google Scholar] [CrossRef]
- Saulo, Helton, J. Leão, Víctor Leiva, and Robert G. Aykroyd. 2018. Birnbaum-Saunders autoregressive conditional duration models applied to high-frequency financial data. Statistical Papers, 1–25. [Google Scholar] [CrossRef]
- Saulo, Helton, Víctor Leiva, Flavio A. Ziegelmann, and Carolina Marchant. 2013. A nonparametric method for estimating asymmetric densities based on skewed Birnbaum–Saunders distributions applied to environmental data. Stochastic Environmental Research and Risk Assessment 27: 1479–91. [Google Scholar] [CrossRef]
- Shewhart, Walter A. 1931. Economic Control of Quality of Manufactured Product. New York: D. Van Nostrand Company. [Google Scholar]
- Shi, Lei. 1997. Local influence in principal components analysis. Biometrika 84: 175–86. [Google Scholar] [CrossRef]
- Tsionas, Efthymios G. 2001. Bayesian inference in Birnbaum–Saunders regression. Communications in Statistics: Theory and Methods 30: 179–93. [Google Scholar] [CrossRef]
- Vilca, Filidor, Narayanaswamy Balakrishnan, and Camila Borelli Zeller. 2014. A robust extension of the bivariate Birnbaum–Saunders distribution and associated inference. Journal of Multivariate Analysis 124: 418–35. [Google Scholar] [CrossRef]
- Vilca, Filidor, Antonio Sanhueza, Víctor Leiva, and George Christakos. 2010. An extended Birnbaum–Saunders model and its application in the study of environmental quality in Santiago, Chile. Stochastic Environmental Research and Risk Assessment 24: 771–82. [Google Scholar] [CrossRef]
- Villegas, Cristian, Gilberto A. Paula, and Víctor Leiva. 2011. Birnbaum–Saunders mixed models for censored reliability data analysis. IEEE Transactions on Reliability 60: 748–58. [Google Scholar] [CrossRef]
- Volodin, Igor N., and Olga A. Dzhungurova. 2000. On limit distribution emerging in the generalized Birnbaum–Saunders model. Journal of Mathematical Science 99: 1348–66. [Google Scholar] [CrossRef]
- Wand, Matt P., John T. Ormerod, Simone A. Padoan, and Rudi Frühwirth. 2011. Mean field variational Bayes for elaborate distributions. Bayesian Analysis 6: 847–900. [Google Scholar] [CrossRef]
- Wang, Min, Chanseok Park, and Xiaoqian Sun. 2015. Simple robust parameter estimation for the Birnbaum–Saunders distribution. Journal of Statistical Distributions and Applications 2: 1–11. [Google Scholar] [CrossRef]
- Wang, Min, Jng Zhao, Xiaoqian Sun, and Chanseok Park. 2013. Robust explicit estimation of the two-parameter Birnbaum–Saunders distribution. Journal of Applied Statistics 40: 2259–74. [Google Scholar] [CrossRef]
- Wanke, Peter, and Víctor Leiva. 2015. Exploring the potential use of the Birnbaum–Saunders distribution in inventory management. Mathematical Problems in Engineering 2015: 827246. [Google Scholar] [CrossRef]
- Xia, Jianhong, Panlop Zeephongsekul, and David Packer. 2011. Spatial and temporal modelling of tourist movements using semi-Markov processes. Tourism Management 51: 844–51. [Google Scholar] [CrossRef]
- Xie, Feng-Chang, and Cheng Wei. 2007. Diagnostics analysis for log-Birnbaum–Saunders regression models. Computational Statistics and Data Analysis 51: 4692–96. [Google Scholar] [CrossRef]

| Parameter | ||||||
|---|---|---|---|---|---|---|
| ML estimate | 0.147407 | 10.897981 | 15.524423 | −0.005647 | −0.005930 | 0.972392 |
| Standard error | 0.014813 | 0.236175 | 0.235865 | 0.000333 | 0.000333 | 0.005219 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Removed case(s) | Matérn Order | GA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.997 | 2.807 | 0.134 | 0.020 | 177.940 | 1053.405 | - | - | ||
| None | (3.521) | (0.082) | (0.946) | (0.142) | (0.0000014) | (0.0000083) | |||
| [0.389] | [<0.001] | [0.444] | [0.444] | [<0.001] | [<0.001] | ||||
| 0.993 | 2.831 | 0.125 | 0.016 | 108.655 | 643.238 | 0.90 | 0.72 | ||
| #2 | (4.097) | (0.059) | (1.031) | (0.132) | (0.0000008) | (0.0000047) | |||
| [0.404] | [<0.001] | [0.452] | [0.452] | [<0.001] | [<0.001] | ||||
| 0.996 | 2.824 | 0.125 | 0.019 | 152.374 | 902.054 | 0.97 | 0.92 | ||
| #48 | (3.417) | (0.073) | (0.856) | (0.133) | (0.0000012) | (0.0000071) | |||
| [0.386] | [<0.001] | [0.442] | [0.443] | [<0.001] | [<0.001] | ||||
| 0.997 | 2.817 | 0.122 | 0.028 | 308.828 | 1235.312 | 0.84 | 0.69 | ||
| #94 | (3.417) | (0.073) | (0.856) | (0.133) | (0.0000012) | (0.0009092) | |||
| [0.374] | [<0.001] | [0.436] | [0.437] | [<0.001] | [<0.001] | ||||
| 0.991 | 2.845 | 0.071 | 0.060 | 81.052 | 243.156 | 0.65 | 0.31 | ||
| #2, #48 | (exponential) | (6.149) | (0.046) | (0.882) | (0.746) | (0.0000884) | (0.0002652) | ||
| [0.436] | [<0.001] | [0.468] | [0.469] | [<0.001] | [<0.001] | ||||
| 0.995 | 2.840 | 0.097 | 0.038 | 182.059 | 546.177 | 0.72 | 0.45 | ||
| #2, #94 | (exponential) | (3.308) | (0.063) | (0.644) | (0.254) | (0.0002974) | (0.0008922) | ||
| [0.382] | [<0.001] | [0.440] | [0.441] | [<0.001] | [<0.001] | ||||
| 0.994 | 2.834 | 0.114 | 0.024 | 144.768 | 856.737 | 0.80 | 0.60 | ||
| #48, #94 | (2.980) | (0.077) | (0.683) | (0.145) | (0.0000010) | (0.0000059) | |||
| [0.370] | [<0.001] | [0.434] | [0.435] | [<0.001] | [<0.001] | ||||
| 0.982 | 2.855 | 0.085 | 0.041 | 143.699 | 431.097 | 0.66 | 0.35 | ||
| #2, #48, #94 | (exponential) | (3.442) | (0.056) | (0.597) | (0.287) | (0.0002051) | (0.0006153) | ||
| [0.388] | [<0.001] | [0.444] | [0.443] | [<0.001] | [<0.001] |
| Model | AIC | BIC | ||
|---|---|---|---|---|
| BS | 28.224 | |||
| Gaussian | – |
| Evidence in Favour of | |
|---|---|
| <0 | Negative ( is accepted) |
| Weak | |
| Positive | |
| Strong | |
| ≥10 | Very strong |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aykroyd, R.G.; Leiva, V.; Marchant, C. Multivariate Birnbaum-Saunders Distributions: Modelling and Applications. Risks 2018, 6, 21. https://doi.org/10.3390/risks6010021
Aykroyd RG, Leiva V, Marchant C. Multivariate Birnbaum-Saunders Distributions: Modelling and Applications. Risks. 2018; 6(1):21. https://doi.org/10.3390/risks6010021
Chicago/Turabian StyleAykroyd, Robert G., Víctor Leiva, and Carolina Marchant. 2018. "Multivariate Birnbaum-Saunders Distributions: Modelling and Applications" Risks 6, no. 1: 21. https://doi.org/10.3390/risks6010021
APA StyleAykroyd, R. G., Leiva, V., & Marchant, C. (2018). Multivariate Birnbaum-Saunders Distributions: Modelling and Applications. Risks, 6(1), 21. https://doi.org/10.3390/risks6010021







