Longevity Risk Management and the Development of a Value-Based Longevity Index
Abstract
1. Introduction
2. Value-Based Longevity Index
3. Mortality Data Analysis
3.1. Drift of Mortality Intensity
3.2. Volatility of Mortality Intensity
3.3. Cohort Correlations
3.4. Principal Component Analysis
4. Mortality Model
4.1. Model Development
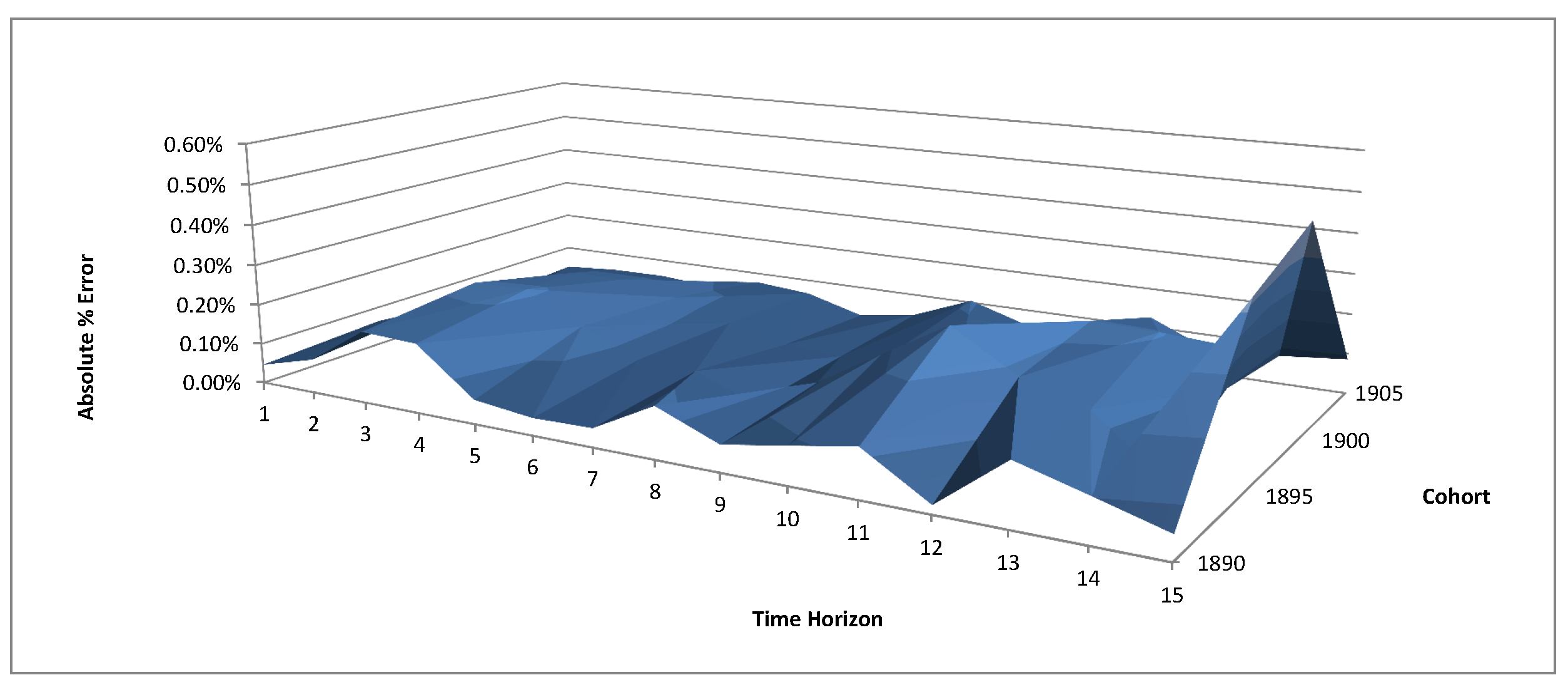
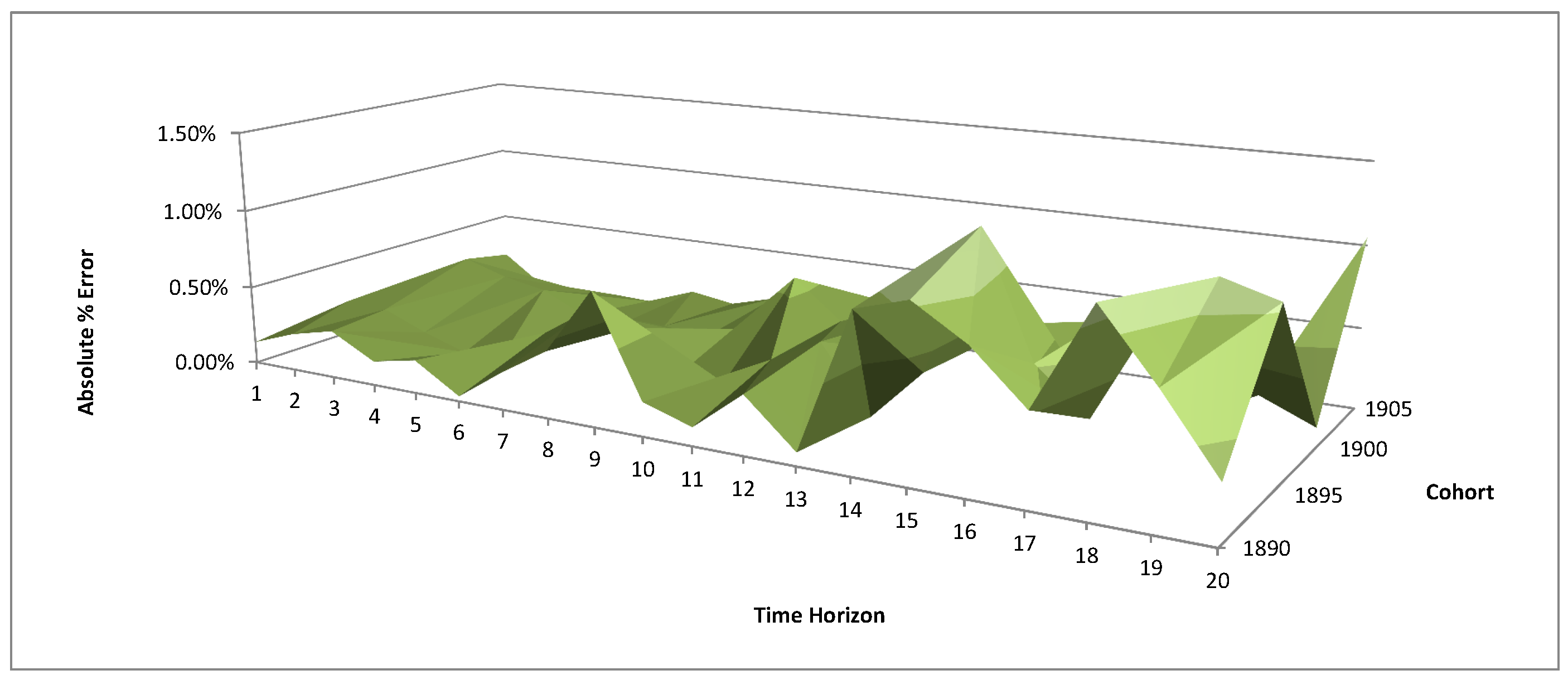
4.2. Calibration
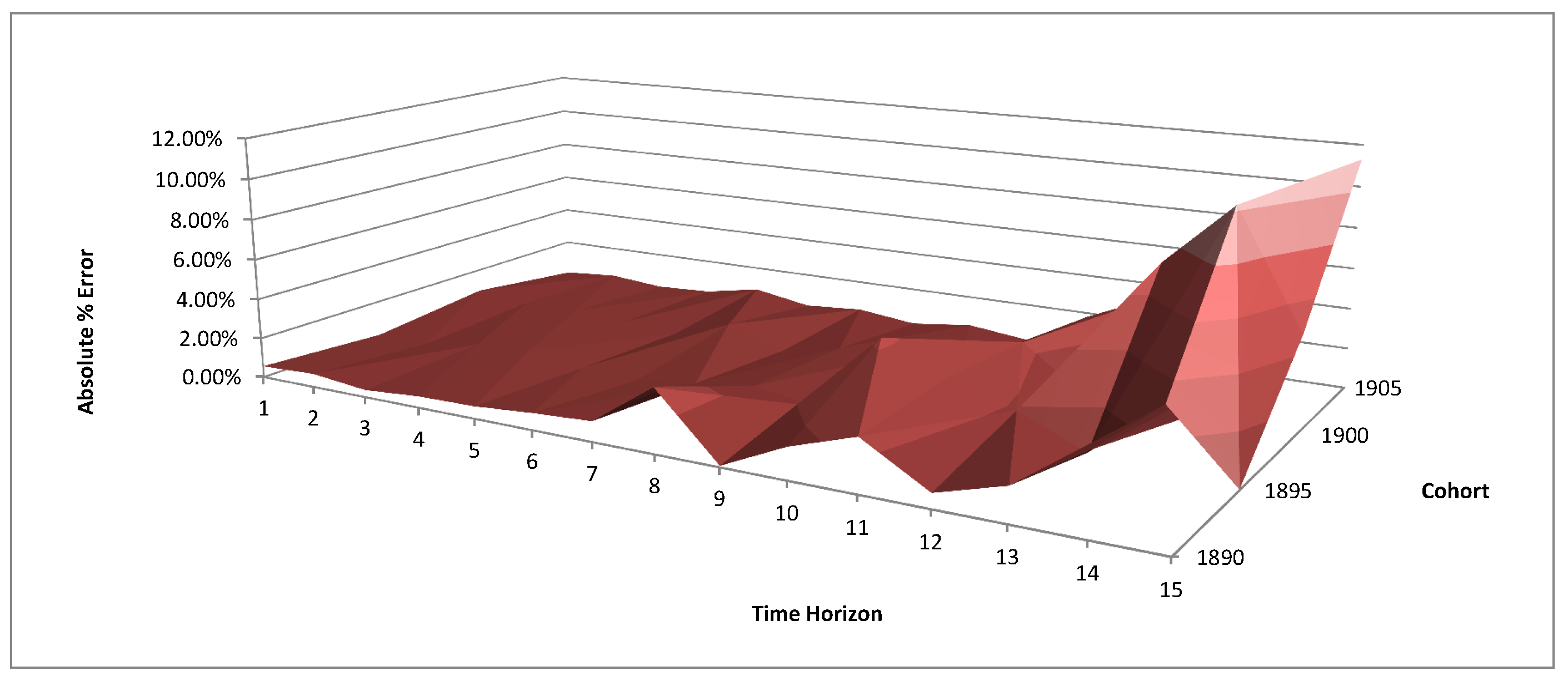
4.3. Calibration Results
5. Interest Rate Model
5.1. Vasicek Model
5.2. Data and Calibration
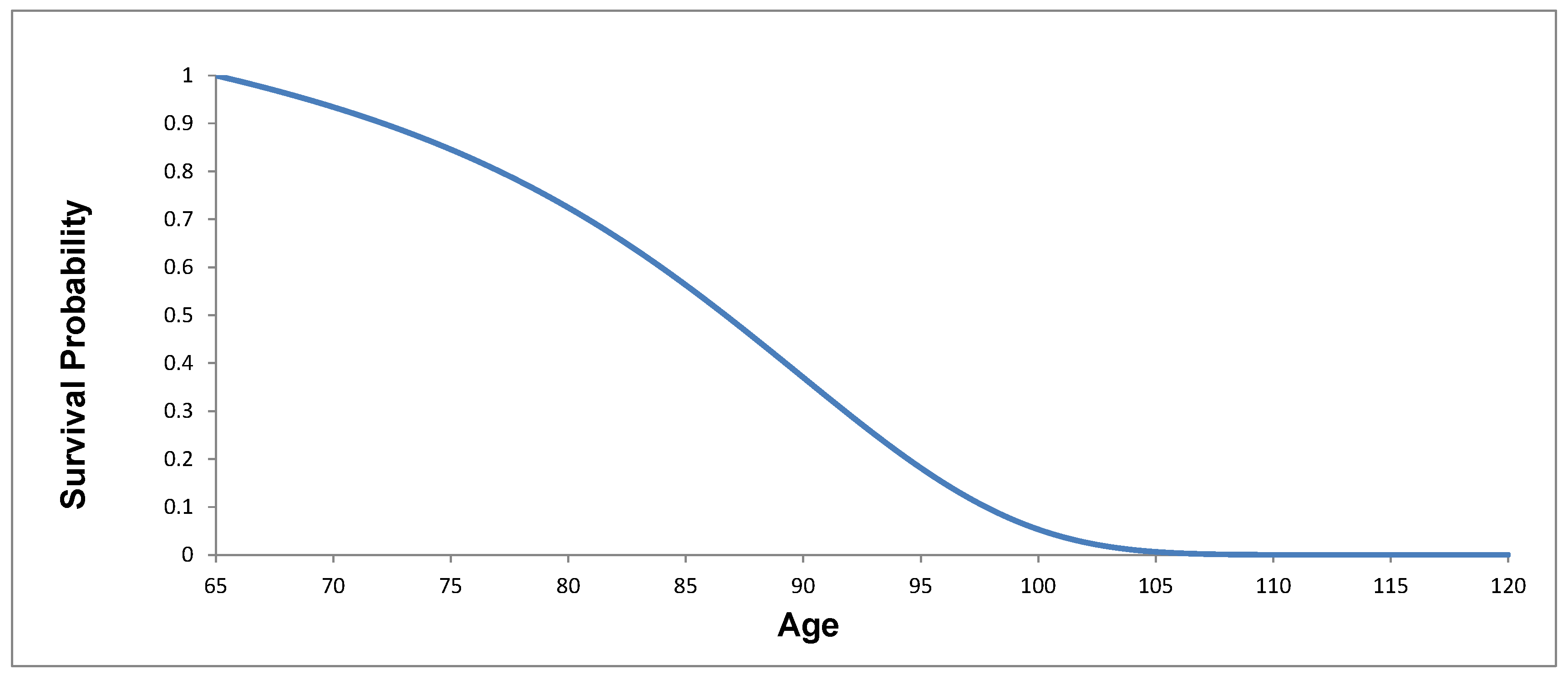
5.3. Calibration Results
6. Value-Based Longevity Index
6.1. Index Construction
6.2. Hedge Efficiency
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Biffis, Enrico. 2005. Affine processes for dynamic mortality and actuarial valuations. Insurance: Mathematics and Economics 37: 443–68. [Google Scholar] [CrossRef]
- Blackburn, Craig, Katja Hanewald, Michael Sherris, and Annamaria Olivieri. 2017. Longevity risk management and shareholder value for a life annuity business. ASTIN Bulletin 47: 43–77. [Google Scholar] [CrossRef]
- Blackburn, Craig, and Michael Sherris. 2013. Consistent dynamic affine mortality models for longevity risk applications. Insurance: Mathematics and Economics 53: 64–73. [Google Scholar] [CrossRef]
- Blackburn, Craig, and Michael Sherris. 2014. Forward mortality modelling of multiple populations. Paper present at the 49th Actuarial Research Conference, Santa Barbara CA, USA, July, 13–16. Unpublished manuscript. [Google Scholar]
- Blake, David, Anja De Waegenaere, Richard McMinn, and Theo Nijman. 2009. Longevity risk and capital markets: The 2008–2009 update. Pensions Institute Discussion Paper (PI-0907). Insurance: Mathematics and Economics. [Google Scholar] [CrossRef]
- Bolder, David Jamieson. 2001. Affine Term-Structure Models: Theory and Implementation. Bank of Canada Working Paper 2001–1015. Ottawa: Bank of Canada, October. [Google Scholar]
- Brigo, Damiano, and Fabio Mercurio. 2006. Interest Rate Models: Theory and Practice, 2nd ed.Berlin: Springer-Verlag. [Google Scholar]
- Cairns, Andrew J., Kevin Dowd, David Blake, and Guy D. Coughlan. 2014. Longevity hedge effectiveness: A decomposition. Quantitative Finance 14: 217–35. [Google Scholar] [CrossRef]
- Cairns, Andrew J., and Delme J. Pritchard. 2001. Stability of descriptive models for the term structure of interest rates with application to German market data. British Actuarial Journal 7: 467–507. [Google Scholar] [CrossRef]
- Coughlan, Guy, David Epstein, Alen Ong, Amit Sinha, Javier Hevia-Portocarrero, Emily Gingrich, Marwa Khalaf-Allah, and Praveen Joseph. 2007. Lifemetrics: A Toolkit for Measuing and Managing Longevity and Mortality Risks, Technical report. Available online: www.lifemetrics.com (accessed on 17 January 2017).
- Coughlan, Guy, Marwa Khalaf-Allah, Yijing Ye, Sumit Kumar, Andrew Cairns, David Blake, and Andrew Cairns. 2011. Longevity hedging 101: A framework for longevity basis risk analysis and hedge effectiveness. North American Actuarial Journal 15: 150–76. [Google Scholar] [CrossRef]
- Cox, John C., Jonathan E. Ingersoll, and Stephen A. Ross. 1985. A theory of the term structure of interest rates. Econometrica 53: 385–407. [Google Scholar] [CrossRef]
- Dahl, Mikkel. 2004. Stochastic mortality in life insurance: Market reserves and mortality-linked insurance contracts. Insurance: Mathematics and Economics 35: 113–36. [Google Scholar] [CrossRef]
- DeutscheBörse. 2012. Deutsche Börse Xpect Club Vita Indices: Longevity Risk of Specific Pensioner Groups. Technical Report. Frankfurt: Deutsche Börse Market Data. [Google Scholar]
- Duffie, Darrell, and Rui Kan. 1996. A yield-factor model of interet rates. Mathematical Finance 6: 379–406. [Google Scholar] [CrossRef]
- Guimaraes, Marco Antonio. 2005. Half-Life in Mean Reversion Processes. Rio de Janeiro: Pontificia Universidade Catolica. [Google Scholar]
- Jevtic, Petar, Elisa Luciano, and Elena Vigna. 2013. Mortality surface by means of continuous time cohort models. Insurance: Mathematics and Economics 53: 122–33. [Google Scholar] [CrossRef]
- LLMA. 2010. Technical Note: The S-Forward. Washington: Life & Longevity Markets Association, October. [Google Scholar]
- Loeys, Jan, Nikolaos Panigirtzoglou, and Ruy M. Ribeiro. 2007. Longevity: A Market in the Making. Technical Report. New York: J.P. Moragn Securities Ltd. [Google Scholar]
- Luciano, Elisa, and Elena Vigna. 2005. Non Mean Reverting Affine Processes for Stochastic Mortality. ICER Working Paper Series (4/05); Boston: ICER. [Google Scholar]
- Luciano, Elisa, and Elena Vigna. 2008. Mortality risk via affine stochastic intensities: Calibration and empirical relevance. Belgian Actuarial Bulletin 8: 5–16. [Google Scholar]
- Ngai, Andrew, and Michael Sherris. 2011. Longevity risk management for life and variable annuities: The effectiveness of static hedging using longevity bonds and derivatives. Insurance: Mathematics and Economics 49: 100–14. [Google Scholar] [CrossRef]
- Njenga, Carolyn N., and Sherris Michael. 2011. Longevity risk and the econometric analysis of mortality trends and volatility. Asia-Pacific Journal of Risk and Insurance 5: 22–73. [Google Scholar] [CrossRef]
- Schrager, David F. 2006. Affine stochastic mortality. Insurance: Mathematics and Economics 38: 81–97. [Google Scholar] [CrossRef]
- Sherris, Michael. 2009. AIPAR Longevity Index. Sydney: Australian Institute for Population Ageing Research, September. [Google Scholar]
- Sherris, Michael, and Samuel Wills. 2008. Financial innovation and the hedging of longevity risk. Asia-Pacific Journal of Risk and Insurance 3: 1–14. [Google Scholar] [CrossRef]
- Vasicek, Oldrich. 1977. An equilibrium characterization of the term structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- Wadsworth, Michael. 2005. The Pension Annuity Market: Further Research Into Supply and Constraints. Technical Report. London: Association of British Insurers. [Google Scholar]
| 1 | The first index-based hedge, q-forward based on J.P. Morgan’s LifeMetrics longevity index, was executed in January 2008 by the U.K. pension insurer Lucida. The first indemnity-based longevity swap was entered in July 2008 by Canada Life with J.P. Morgan as the counterparty. |
| 2 | We do so in order to keep the model tractable. Calibration results show that the two-factor model fits the observed survival probabilities well. |
| 3 | We drop the cohort index i for the ease of exposition. |
| 4 | See Brigo and Mercurio (2006) for the detailed proof. |
| 5 | Ninety five percent is the lowest correlation level calibrated by the two-factor model of Jevtic et al. (2013). However, this is a rough, but conservative, estimate of the fitting errors of the correlations resulting from their model. |
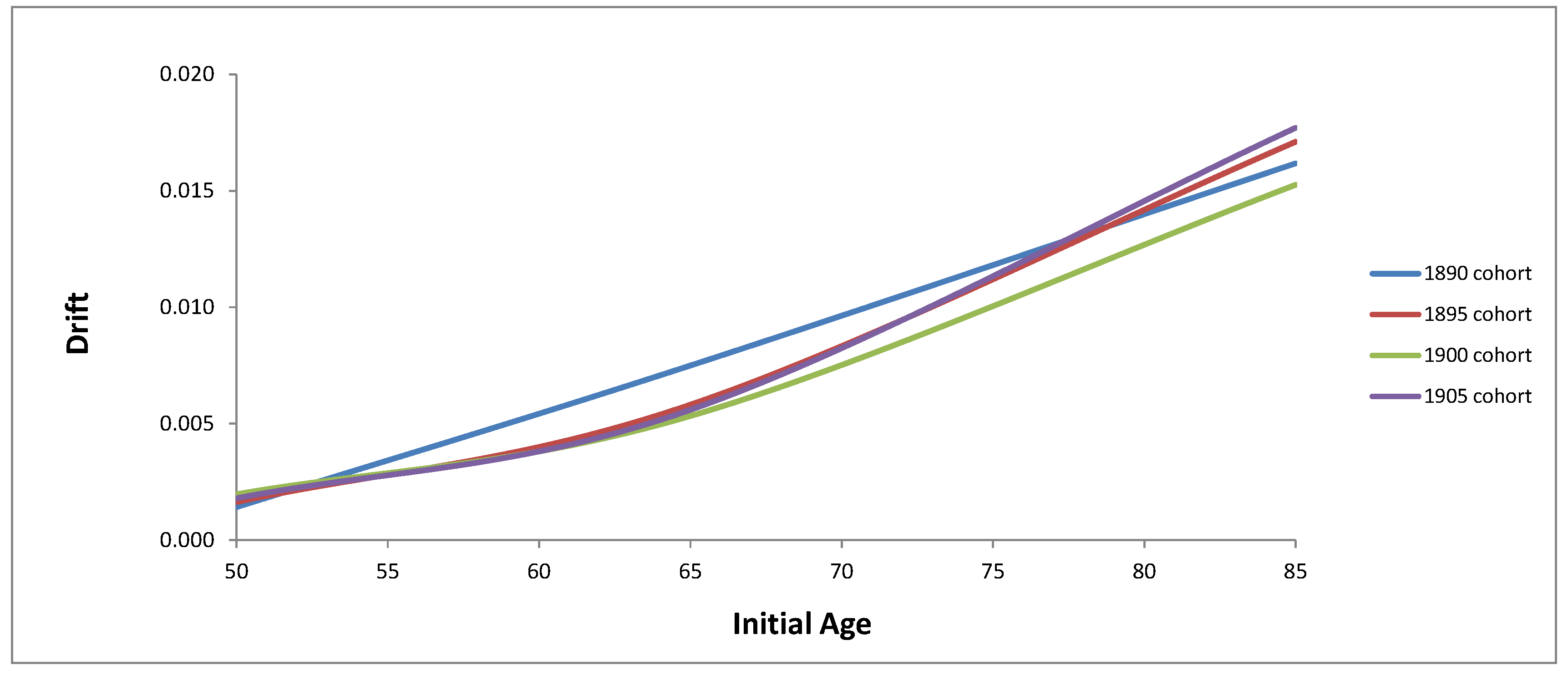
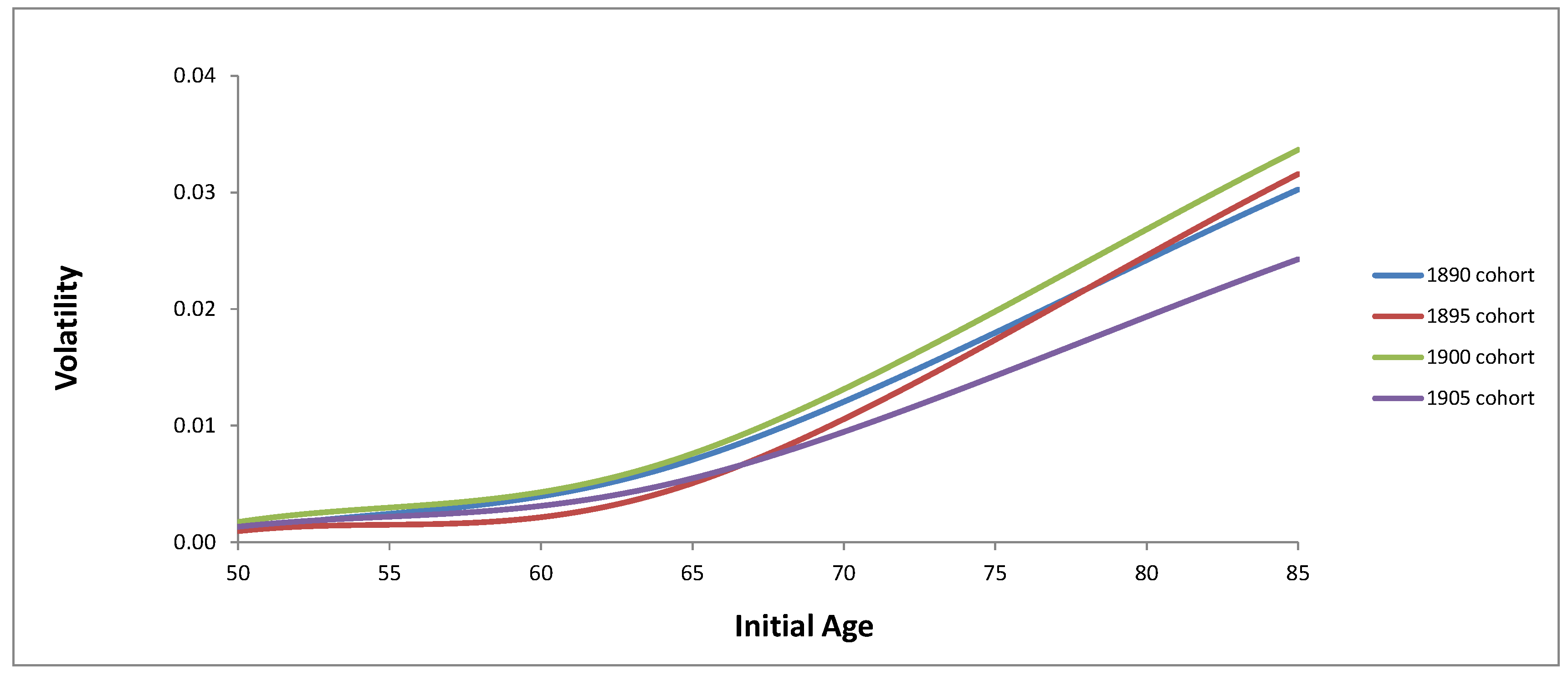


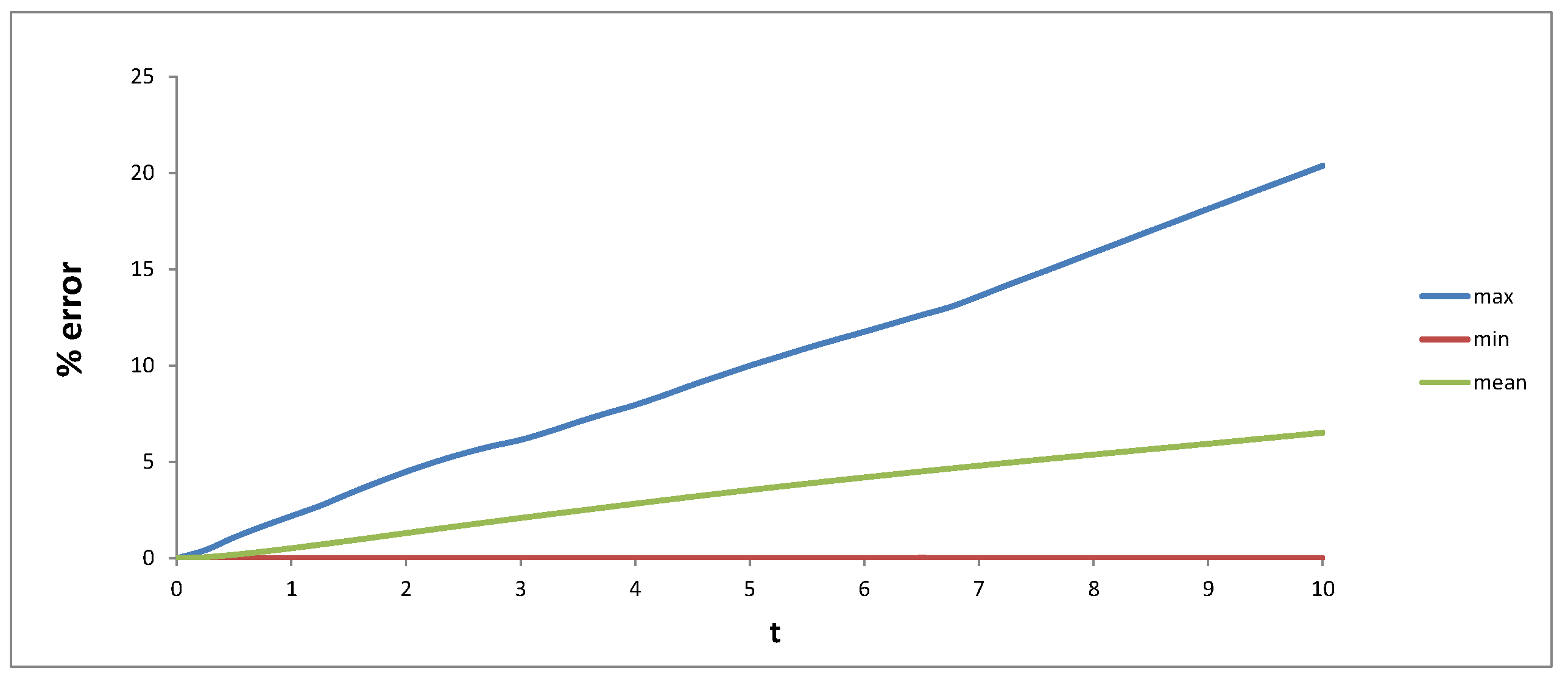

| Initial Age | 1890 | 1895 | 1900 | 1905 |
|---|---|---|---|---|
| 50 | 0.001425 | 0.001639 | 0.001977 | 0.001800 |
| 65 | 0.007501 | 0.005820 | 0.005335 | 0.005601 |
| 85 | 0.016177 | 0.017104 | 0.015258 | 0.017705 |
| Initial Age | 1890 | 1895 | 1900 | 1905 |
|---|---|---|---|---|
| 50 | 0.001031 | 0.000965 | 0.001748 | 0.001343 |
| 65 | 0.007080 | 0.005082 | 0.007610 | 0.005494 |
| 85 | 0.030253 | 0.031574 | 0.033655 | 0.024272 |
| Calendar Time 1955 | ||||
|---|---|---|---|---|
| Cohort | 1890 | 1895 | 1900 | 1905 |
| 1890 | 1.0000 | |||
| 1895 | 0.6124 | 1.0000 | ||
| 1900 | 0.5157 | 0.4758 | 1.0000 | |
| 1905 | 0.4271 | 0.1857 | 0.5568 | 1.0000 |
| Calendar Time 1960 | ||||
| 1890 | 1.0000 | |||
| 1895 | 0.4707 | 1.0000 | ||
| 1900 | 0.1489 | 0.2728 | 1.0000 | |
| 1905 | 0.2103 | 0.1968 | 0.0949 | 1.0000 |
| Calendar Time 1965 | ||||
| 1890 | 1.0000 | |||
| 1895 | 0.6583 | 1.0000 | ||
| 1900 | 0.2881 | 0.4585 | 1.0000 | |
| 1905 | 0.4376 | 0.4899 | 0.5200 | 1.0000 |
| Calendar Time 1970 | ||||
| 1890 | 1.0000 | |||
| 1895 | 0.4468 | 1.0000 | ||
| 1900 | 0.3600 | 0.4117 | 1.0000 | |
| 1905 | 0.2401 | 0.7432 | 0.6260 | 1.0000 |
| Cohort | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1890 | 0.0032 | 0.0002 | 0.7660 | 0.0091 | 0.0305 | 0.1805 | 0.0091 | 0.0305 | 0.1805 |
| 1895 | 0.0011 | −0.0001 | 0.9999 | 0.0080 | 0.0326 | 0.1490 | 0.0080 | 0.0326 | 0.1490 |
| 1900 | 0.0151 | 0.0017 | 0.9999 | 0.0079 | 0.0375 | 0.1442 | 0.0079 | 0.0375 | 0.1442 |
| 1905 | 0.0031 | −0.0041 | 0.8377 | 0.0074 | 0.0344 | 0.1465 | 0.0074 | 0.0344 | 0.1465 |
| a | b | c | d |
|---|---|---|---|
| 0.2280 | −0.0037 | −10.3270 | 0.0343 |
| Cohort | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1890 | 0.0721 | −0.0001 | 0.7306 | −0.0068 | −0.0145 | 0.0227 | 0.0157 | 0.0460 | 0.1528 |
| 1895 | 0.0632 | −0.0073 | 0.8710 | −0.0368 | −0.0292 | −0.0343 | 0.0444 | 0.0607 | 0.1844 |
| 1900 | 0.0598 | 0.0000 | 0.9767 | −0.0241 | −0.0045 | −0.0255 | 0.0321 | 0.0449 | 0.1815 |
| 1905 | 0.0817 | −0.0000 | 0.8482 | −0.0072 | 0.0106 | −0.0011 | 0.0146 | 0.0256 | 0.1409 |
| Calendar Time 1955 | ||||
|---|---|---|---|---|
| Cohort | 1890 | 1895 | 1900 | 1905 |
| 1890 | 1.0000 | |||
| 1895 | 0.4710 | 1.0000 | ||
| 1900 | 0.3427 | 0.4019 | 1.0000 | |
| 1905 | 0.5471 | 0.6195 | 0.5193 | 1.0000 |
| Calendar Time 1960 | ||||
| 1890 | 1.0000 | |||
| 1895 | −0.1862 | 1.0000 | ||
| 1900 | 0.3584 | −0.1156 | 1.0000 | |
| 1905 | 0.6125 | −0.2554 | 0.5283 | 1.0000 |
| Calendar Time 1965 | ||||
| 1890 | 1.0000 | |||
| 1895 | 0.2348 | 1.0000 | ||
| 1900 | 0.6964 | 0.2709 | 1.0000 | |
| 1905 | 0.8403 | 0.2587 | 0.7707 | 1.0000 |
| Calendar Time 1970 | ||||
| 1890 | 1.0000 | |||
| 1895 | 0.4367 | 1.0000 | ||
| 1900 | 0.7740 | 0.4174 | 1.0000 | |
| 1905 | 0.9324 | 0.4593 | 0.8174 | 1.0000 |
| Calendar Time 1955 | |||
|---|---|---|---|
| Cohort | 1890 | 1895 | B |
| 1895 | 0 | ||
| 1900 | 0 | 0 | |
| 1905 | 0 | 0 | 0 |
| Calendar Time 1960 | |||
| 1895 | 0.0484 | ||
| 1900 | 0 | 0 | |
| 1905 | 0 | 0 | 0 |
| Calendar Time 1965 | |||
| 1895 | 0.0026 | ||
| 1900 | 0 | 0 | |
| 1905 | 0 | 0 | 0 |
| Calendar Time 1970 | |||
| 1895 | 0 | ||
| 1900 | 0 | 0.0391 | |
| 1905 | 0 | 0 | 0 |
| Inputs | k | ||
|---|---|---|---|
| Initial Value | 0.1386 | 0.0542 | 0.0009 |
| Upper Bound | 2.7726 | 0.0660 | 0.0043 |
| Lower Bound | 0.0693 | 0.0375 | 0.0002 |
| Portfolio Size | 200 | 1000 | 100,00 |
| Index Swap | 12.60% | 63.23% | 95.73% |
| s-Forward | 11.45% | 52.31% | 68.61% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Sherris, M. Longevity Risk Management and the Development of a Value-Based Longevity Index. Risks 2018, 6, 10. https://doi.org/10.3390/risks6010010
Chang Y, Sherris M. Longevity Risk Management and the Development of a Value-Based Longevity Index. Risks. 2018; 6(1):10. https://doi.org/10.3390/risks6010010
Chicago/Turabian StyleChang, Yang, and Michael Sherris. 2018. "Longevity Risk Management and the Development of a Value-Based Longevity Index" Risks 6, no. 1: 10. https://doi.org/10.3390/risks6010010
APA StyleChang, Y., & Sherris, M. (2018). Longevity Risk Management and the Development of a Value-Based Longevity Index. Risks, 6(1), 10. https://doi.org/10.3390/risks6010010





