Actuarial Applications and Estimation of Extended CreditRisk+
Abstract
:1. Introduction
2. An Alternative Stochastic Mortality Model
2.1. Basic Definitions and Notation
2.2. Some Classical Stochastic Mortality Models
2.3. An Additive Stochastic Mortality Model
3. Parameter Estimation
3.1. Estimation via Maximum Likelihood
3.2. Estimation via a Maximum a Posteriori Approach
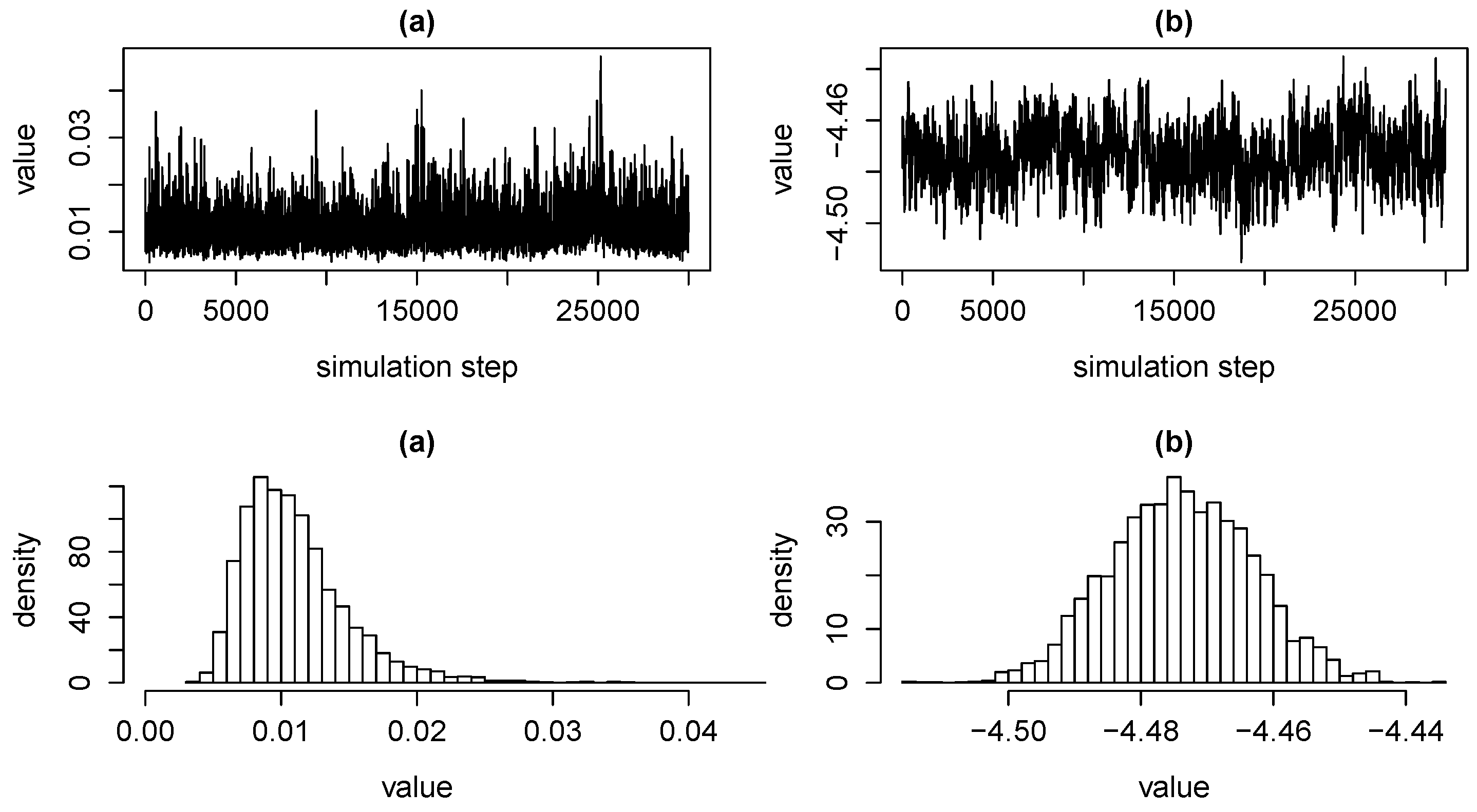
3.3. Estimation via MCMC
3.4. Estimation via Matching of Moments
4. Applications
4.1. Prediction of Underlying Death Causes
4.2. Forecasting Death Probabilities
5. A Link to the Extended CreditRisk Model and Applications
5.1. The ECRP Model
- (a)
- For applications in the context of internal models we may set as the best estimate liability, i.e., discounted future cash flows, of policyholder i at the end of the period. Thus, when using stochastic discount factors or contracts with optionality, for example, portfolio quantities may be stochastic.
- (b)
- In the context of portfolio payment analysis we may set as the payments (such as annuities) to i over the next period. We may include premiums in a second dimension in order to get joint distributions of premiums and payments.
- (c)
- For applications in the context of mortality estimation and projection we set .
- (d)
- Using discretisation which preserves expectations (termed as stochastic rounding in (Schmock 2017, section 6.2.2), we may assume to be -valued .
- (a)
- Consider independent random common risk factors which have a gamma distribution with mean and variance , i.e., with shape and inverse scale parameter . Also the degenerate case with for is allowed. Corresponding weights for every policyholder . Risk index zero represents idiosyncratic risk and we require .
- (b)
- Deaths are independent from one another, as well as all other random variables and, for all , they are Poisson distributed with intensity , i.e.,
- (c)
- Given risk factors, deaths are independent and, for every policyholder and , they are Poisson distributed with random intensity , i.e.,for all .
- (d)
- For every policyholder , the total number of deaths is split up additively according to risk factors as . Thus, by model construction, .
5.2. Application I: Mortality Risk, Longevity Risk and Solvency II Application
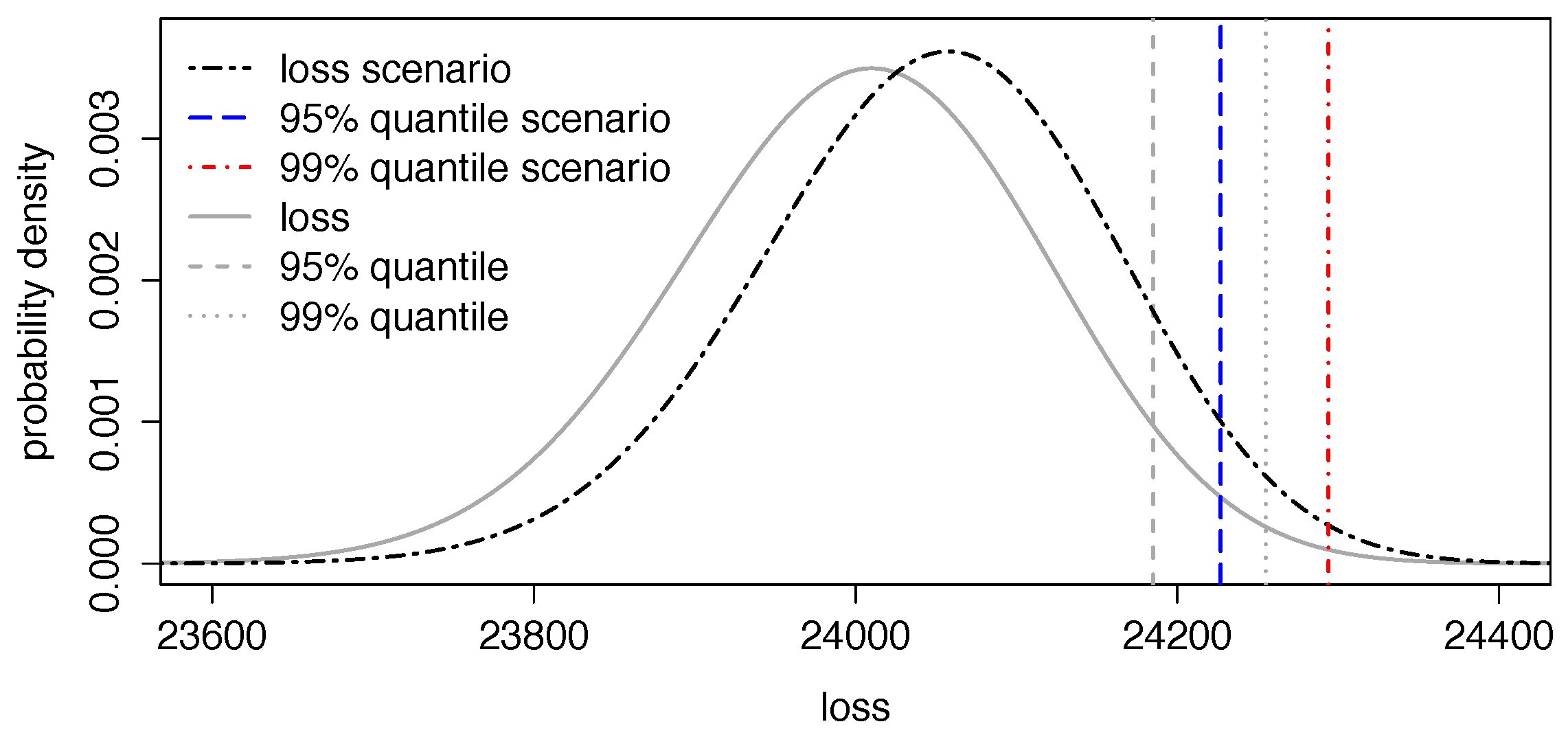
5.3. Application II: Impact of Certain Health Scenarios in Portfolios
5.4. Application III: Forecasting Central Death Rates and Comparison With the Lee–Carter Model
5.5. Considered Risks
5.6. Generalised and Alternative Models
6. Model Validation and Model Selection
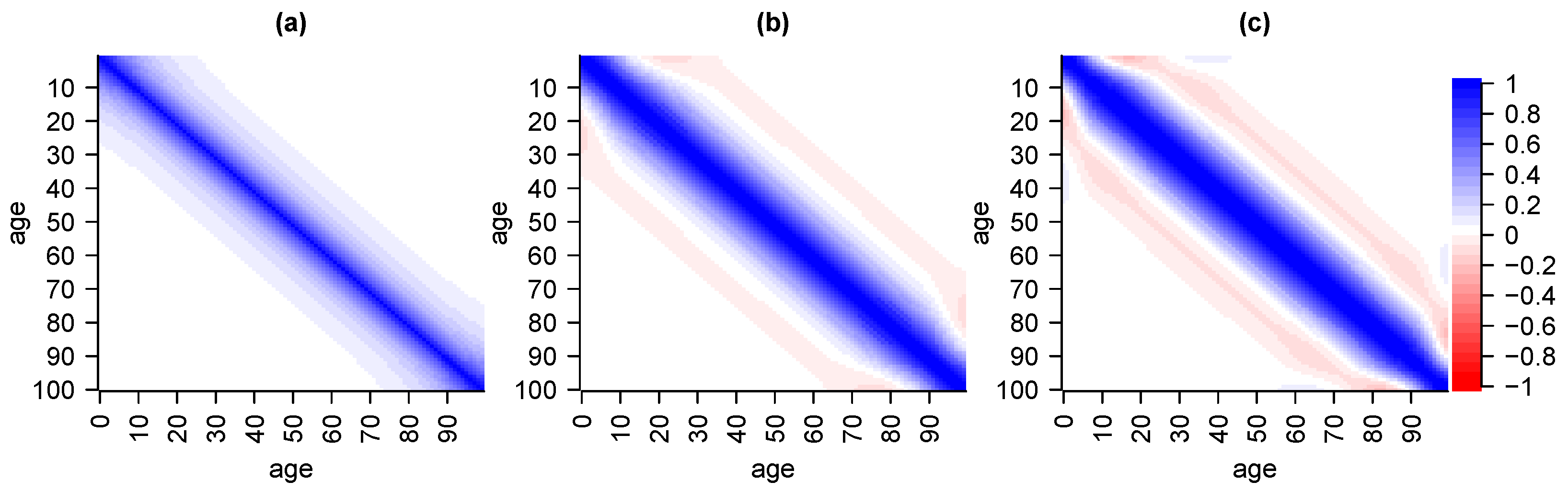
6.1. Validation via Cross-Covariance
6.2. Validation via Independence
6.3. Validation via Serial Correlation
6.4. Validation via Risk Factor Realisations
6.5. Model Selection
7. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alai, Daniel H., Séverine Arnold, and Michael Sherris. 2015. Modelling cause-of-death mortality and the impact of cause-elimination. Annals of Actuarial Science 9: 167–86. [Google Scholar] [CrossRef]
- Barbour, Andrew D., Lars Holst, and Svante Janson. 1992. Poisson Approximation. Oxford Studies in Probability. Oxford: Oxford University Press, vol. 2. [Google Scholar]
- Booth, Heather, and Leonie Tickle. 2008. Mortality modelling and forecasting: A review of methods. Annals of Actuarial Science 3: 3–43. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Chaudhry, M. Aslam, and Syed M. Zubair. 2001. On a Class of Incomplete Gamma Functions with Applications. Abingdon: Taylor & Francis. [Google Scholar]
- Credit Suisse First Boston. 1997. Creditrisk+: A Credit Risk Management Framework. Technical Report. New York: CSFB. [Google Scholar]
- Fung, Man Chung, Gareth W. Peters, and Pavel V. Shevchenko. 2017. A unified approach to mortality modelling using state-space framework: Characterization, identification, estimation and forecasting. To appear in Annals of Actuarial Science. [Google Scholar]
- Fung, Man Chung, Gareth W. Peters, and Pavel V. Shevchenko. A state-space estimation of the Lee–Carter mortality model and implications for annuity pricing pp. 952–58. Paper presented at 21st International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand (MODSIM2015), Broadbeach, Australia, 29 November–4 2015; Edited by T. Weber, M.J. McPhee and R.S. Anderssen. pp. 952–58. [Google Scholar]
- Gamerman, Dani, and Hedibert F. Lopes. 2006. Markov chain Monte Carlo: Stochastic Simulation for Bayesian Inference, 2nd ed. Texts in Statistical Science Series; Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Gerhold, Stefan, Uwe Schmock, and Richard Warnung. 2010. A generalization of Panjer’s recursion and numerically stable risk aggregation. Finance and Stochastics 14: 81–128. [Google Scholar] [CrossRef]
- Giese, Gotz. 2003. Enhancing CreditRisk+. Risk 16: 73–77. [Google Scholar]
- Gilks, Walter R., Sylvia Richardson, and David Spiegelhalter. 1995. Markov Chain Monte Carlo in Practice. Boca Raton: Chapman & Hall/CRC Interdisciplinary Statistics, Taylor & Francis. [Google Scholar]
- Godfrey, Leslie G. 1978. Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables. Econometrica 46: 1293–301. [Google Scholar] [CrossRef]
- Grzenda, Wioletta, and Wieslaw Zieba. 2008. Conditional central limit theorem. International Mathematical Forum 3: 1521–28. [Google Scholar]
- Haaf, Hermann, Oliver Reiss, and John Schoenmakers. 2004. Numerically stable computation of CreditRisk+. In CreditRisk+ in the Banking Industry. Edited by Matthias Gundlach and Frank Lehrbass. Berlin: Springer Finance, pp. 69–77. [Google Scholar]
- Kainhofer, Reinhold, Martin Predota, and Uwe Schmock. 2006. The new Austrian annuity valuation table AVÖ 2005R. Mitteilungen der Aktuarvereinigung Österreichs 13: 55–135. [Google Scholar]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Lehmann, Erich L., and Joseph P. Romano. 2005. Testing Statistical Hypotheses, 3rd ed. Springer Texts in Statistics. Berlin: Springer-Verlag. [Google Scholar]
- Li, Johnny Siu-Hang, and Mary R. Hardy. 2011. Measuring basis risk in longevity hedges. North American Actuarial Journal 15: 177–200. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton Series in Finance; Princeton: Princeton University Press. [Google Scholar]
- Pasdika, Ulrich, and Jürgen Wolff. Coping with longvity: The new German annuity valuation table DAV 2004 R. Paper presented at the Living to 100 and beyond Symposium, Orlando, FL, USA, 12–14 January 2005. [Google Scholar]
- Pitacco, Ermanno, Michel Denuit, and Steven Haberman. 2009. Modelling Dynamics for Pensions and Annuity Business. Oxford: Oxford University Press. [Google Scholar]
- Qi, Feng, Run-Qing Cui, Chao-Ping Chen, and Bai-Ni Guo. 2005. Some completely monotonic functions involving polygamma functions and an application. Journal of Mathematical Analysis and Applications 310: 303–8. [Google Scholar] [CrossRef]
- R Core Team. 2013. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Robert, Christian P., and George Casella. 2004. Monte Carlo Statistical Methods, 2nd ed. Springer Texts in Statistics. New York: Springer-Verlag. [Google Scholar]
- Roberts, Gareth O., Andrew Gelman, and Walter R. Gilks. 1997. Weak convergence and optimal scaling of random walk Metropolis algorithms. The Annals of Applied Probability 7: 110–20. [Google Scholar] [CrossRef]
- Schmock, Uwe. 1999. Estimating the value of the WinCAT coupons of the Winterthur insurance convertible bond: A study of the model risk. Astin Bulletin 29: 101–63. [Google Scholar] [CrossRef]
- Schmock, Uwe. Modelling Dependent Credit Risks with Extensions of Credit Risk+ and Application to Operational Risk. Lecture Notes, Version March 28, 2017. Available online: http://www.fam.tuwien.ac.at/~schmock/notes/ExtensionsCreditRiskPlus.pdf (accessed on 28 March 2017).
- Shevchenko, Pavel V., Jonas Hirz, and Uwe Schmock. Forecasting leading death causes in Australia using extended CreditRisk+. Paper presented at 21st International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand (MODSIM2015), Broadbeach, Australia, 29 November–4 December 2015; Edited by T. Weber, M. J. McPhee and R. S. Anderssen. pp. 966–72. [Google Scholar]
- Shevchenko, Pavel V. 2011. Modelling Operational Risk Using Bayesian Inference. Berlin: Springer-Verlag. [Google Scholar]
- Sundt, Bjørn. 1999. On multivariate Panjer recursions. Astin Bulletin 29: 29–45. [Google Scholar] [CrossRef]
- Tierney, Luke. 1994. Markov chains for exploring posterior distributions. The Annals of Statistics 22: 1701–62. [Google Scholar] [CrossRef]
- Todesfallrisiko, DAV-Unterarbeitsgruppe. 2009. Herleitung der Sterbetafel DAV 2008 T für Lebensversicherungen mit Todesfallcharakter. Blätter der DGVFM 30: 189–224. (In German). [Google Scholar] [CrossRef]
- Vellaisamy, P., and B. Chaudhuri. 1996. Poisson and compound Poisson approximations for random sums of random variables. Journal of Applied Probability 33: 127–37. [Google Scholar] [CrossRef]
- Wilmoth, John R. 1995. Are mortality projections always more pessimistic when disaggregated by cause of death? Mathematical Population Studies 5: 293–319. [Google Scholar] [CrossRef] [PubMed]
- Zeileis, Achim, and Torsten Hothorn. 2002. Diagnostic checking in regression relationships. R News 2: 7–10. [Google Scholar]
| 1. | https://eiopa.europa.eu/regulation-supervision/insurance/solvency-ii, accessed on March 28, 2017. |
| 2. | http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3101.0Jun%202013?OpenDocument, accessed on May 10, 2016. |
| 3. | http://www.aihw.gov.au/deaths/aihw-deaths-data/#nmd, accessed on May 10, 2016. |
| 4. | |
| 5. |


| Death Cause | Factor | Death Cause | Factor | Death Cause | Factor | Death Cause | |
|---|---|---|---|---|---|---|---|
| infectious | 1.25 | neoplasms | 1.00 | endocrine | 1.01 | mental | 0.78 |
| nervous | 1.20 | circulatory | 1.00 | respiratory | 0.91 | digestive | 1.05 |
| genitourinary | 1.14 | external | 1.06 | not elsewhere | 1.00 |
| MM | Appr. | Mean | 5% | 95% | Stdev. | |
|---|---|---|---|---|---|---|
| infectious | 0.1932 | 0.0787 | 0.0812 | 0.0583 | 0.1063 | 0.0147 |
| neoplasms | 0.0198 | 0.0148 | 0.0173 | 0.0100 | 0.0200 | 0.0029 |
| mental | 0.1502 | 0.1357 | 0.1591 | 0.1200 | 0.2052 | 0.0265 |
| circulatory | 0.0377 | 0.0243 | 0.0300 | 0.0224 | 0.0387 | 0.0053 |
| respiratory | 0.0712 | 0.0612 | 0.0670 | 0.0510 | 0.0866 | 0.0110 |
| external | 0.1044 | 0.0912 | 0.1049 | 0.0787 | 0.1353 | 0.0176 |
| 2011, Male | 2031, Male | 2011, Female | 2031, Female | |
|---|---|---|---|---|
| neoplasms | 0.327 | 0.385 | 0.263 | 0.295 |
| circulatory | 0.324 | 0.169 | 0.340 | 0.145 |
| respiratory | 0.106 | 0.090 | 0.101 | 0.129 |
| endocrine | 0.047 | 0.073 | 0.053 | 0.071 |
| nervous | 0.044 | 0.058 | 0.054 | 0.080 |
| infectious | 0.015 | 0.020 | 0.015 | 0.019 |
| mental | 0.042 | 0.115 | 0.063 | 0.168 |
| Age in 2013 | 0 (Newborn) | 20 | 40 | 60 | 80 |
|---|---|---|---|---|---|
| male | |||||
| female |
| Quantiles | Speed | Accuracy | |||||
|---|---|---|---|---|---|---|---|
| 1% | 10% | 50% | 90% | 99% | |||
| Bernoulli (MC), | 450 | 472 | 500 | 528 | 552 | s | |
| Poisson (ECRP), | 449 | 471 | 500 | 529 | 553 | s | |
| Bernoulli (MC), | 202 | 310 | 483 | 711 | 936 | s | |
| Poisson (ECRP), | 204 | 309 | 483 | 712 | 944 | s | ≤0.0500 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirz, J.; Schmock, U.; Shevchenko, P.V. Actuarial Applications and Estimation of Extended CreditRisk+. Risks 2017, 5, 23. https://doi.org/10.3390/risks5020023
Hirz J, Schmock U, Shevchenko PV. Actuarial Applications and Estimation of Extended CreditRisk+. Risks. 2017; 5(2):23. https://doi.org/10.3390/risks5020023
Chicago/Turabian StyleHirz, Jonas, Uwe Schmock, and Pavel V. Shevchenko. 2017. "Actuarial Applications and Estimation of Extended CreditRisk+" Risks 5, no. 2: 23. https://doi.org/10.3390/risks5020023
APA StyleHirz, J., Schmock, U., & Shevchenko, P. V. (2017). Actuarial Applications and Estimation of Extended CreditRisk+. Risks, 5(2), 23. https://doi.org/10.3390/risks5020023






