Context Moderates Priming Effects on Financial Risk Taking

Abstract

Previous research has shown that risk preferences are sensitive to the financial domain in which they are framed. In the present paper, we explore whether the effect of negative priming on risk taking is moderated by financial context. A total of 120 participants completed questionnaires, where risky choices were framed in six different financial scenarios. Half of the participants were allocated to a negative priming condition. Negative priming reduced risk-seeking behaviour compared to a neutral condition. However, this effect was confined to non-experiential scenarios (i.e., gamble to win, possibility to lose), and not to ‘real world’ financial products (e.g., pension provision). The results call into question the generalisability of priming effects on different financial contexts.

1. Introduction

A consistent finding from behavioural sciences is that human preferences, rather than being stable and inherent in individuals, are heavily influenced by contextual factors such as the available choice options [1,2]. For example, the preference reversal phenomenon suggests that no stable pattern of preference underlies even basic choices: There is some degree of inconsistency when participants make trade-offs between lotteries with different probabilities and values [3]. Previous research has also suggested that decisions can be conceptualised as the result of an integration of influences derived from both the description (specified probability) and experience (pre-experimental beliefs about event frequencies) of risks. Therefore, the construction of risk preferences is also influenced by the accessibility of events in memory [4,5]. Preferences have also been shown to be driven by processes that are independent from inferences (e.g., familiarity) [6], the latter being more frequently hypothesised as the main factor underlying human preferences [7,8]. Indeed, phenomena such as ‘choice blindness’ suggest that people may not be even aware of the reasons informing their choices [9,10]. Thus, it can be argued that context effects often prompt complex mental states in risk taking, which result in choice patterns that can violate normative assumptions about stable and generalisable risk attitudes. For instance, Vlaev and his colleagues examined whether risk preferences are stable for different financial scenarios and found that not to be the case: Valence and complexity of the financial product at hand influenced participants’ decision-making [2]. Importantly, people made consistent choices within financial domains (e.g., positive scenarios such as salary and negative ones such as gamble to lose), but not particularly so across them.

Previous research has also investigated the influence of priming, which has been defined as recent context-activating complex mental states [11], on risk preferences. For example, priming has been shown to influence decision-making through changes in affective state or mood. The direction of the influence of priming on risk preferences depends on the valence of the affective state that is primed. For instance, it has been shown that priming negative affect associated with a target item can increase its perceived risk whilst lowering its perceived benefits [12]; the opposite pattern has been observed for positive affect [6,13,14]. Relatedly, other findings show that positive mood is associated with more risk taking [15]: Participants in a positive mood tend to report higher subjective probabilities for positive events and lower probabilities for negative events. These findings have been explained by the mood congruency hypothesis, which posits that information retrieval is influenced by the current affective state; thus, mood-congruent memories are more likely to be retrieved than mood-incongruent ones, which in turn impacts people’s decision-making as memory is hypothesised to drive judgment and decision-making [4].

However, it can be proposed that, overall, inconsistent findings have been observed in regard to the relationship between valence priming and risk taking [16,17]. Some results have showed that positive affect is associated with more risk seeking, whilst other studies have suggested that positive mood can reduce risk seeking [16,18]. Investigations about the effects of negative priming on risk taking are less numerous. Erb and colleagues exposed participants to lists of words in order to prime risk attitudes [11]. During the priming task, one group of participants rated the frequency of occurrence of some adjectives, which negatively depicted risk-seeking behaviour (e.g., as “thoughtless”) and positively depicted risk-avoidant behaviour (e.g., as “responsible)—together with some distractor adjectives (e.g., “colourful”). Participants in this condition, where risk taking was negatively primed, displayed reduced risk-seeking behaviour.

One avenue that could be explored in order to explain some of the above inconsistencies is the investigation of the domain in which a decision is elicited. For instance, Vlaev and colleagues showed that risk preferences were influenced not only by the valence of a financial product under consideration, but also by its complexity [2]. This finding suggests that people may adopt different decision strategies as a function of context, potentially reflecting different levels of processing (e.g., intuition versus reasoning) [19]. Thus, the impact of priming effects might differ depending on the financial context. For instance, it could be argued that contexts that attract shallower and intuition-driven processing might be more vulnerable to priming effects, as they are less likely to be shielded by effortful and analytical processing. On the other hand, it could also be argued that in complex decision-making contexts, it is actually ‘hot’ (intuition-like) cognition that prevails, and more automatic strategies—more vulnerable to priming effects—are implemented [20]. To summarise, it could be argued that people may interpret the risk in a different manner depending on the domain in which it is framed.

In light of the above research, it is yet unknown whether affect priming and contextual domains interact in determining financial risk taking. Relatedly, it is yet to be examined whether negative priming impacts financial decision-making regardless of the product under consideration. Answering these questions might contribute to the literature on financial risk taking in different ways. First, if priming effects are moderated by financial context, sustaining the stability of risk preferences becomes even more arduous. Second, the results will shed more light on the debate between ‘hot’ (intuition) and ‘cold’ (reasoning) cognition [20]—and on the interplay between processing depth and risk preferences. Finally, a systematic investigation of the effects of priming on risky decision-making in different financial scenarios is still missing. None of the published studies addresses those issues satisfactorily. For example, although Erb and colleagues examined the influence of priming on different contexts of risky decision-making [11], these were confined mainly to non-financial scenarios (e.g., holiday travel, betting on horses and buying a car). Moreover, Moore and Chater showed that for gambles to win, positive mood is associated with higher risk-seeking behaviour (Experiment 1); however, their investigation examined only one financial context [21]. The same limitation applies to a more recent study on priming, which included only investments as the financial domain under scrutiny [22]. Finally, the research by Isen and colleagues mostly involved the analysis of hypothetical gambles to win or to lose, and thus did not systematically examine the effects of priming on different financial products [17].

The Present Experiment

Participants were asked to fill in a questionnaire, which either had no background (neutral condition) or was printed on a picture of a dark tornado (negative priming condition). We used negative priming only as (a) the effects of negative priming are generally less explored in the study of financial risk taking and (b) negative events usually evoke greater immediate response than positive ones—for a review, see [23].

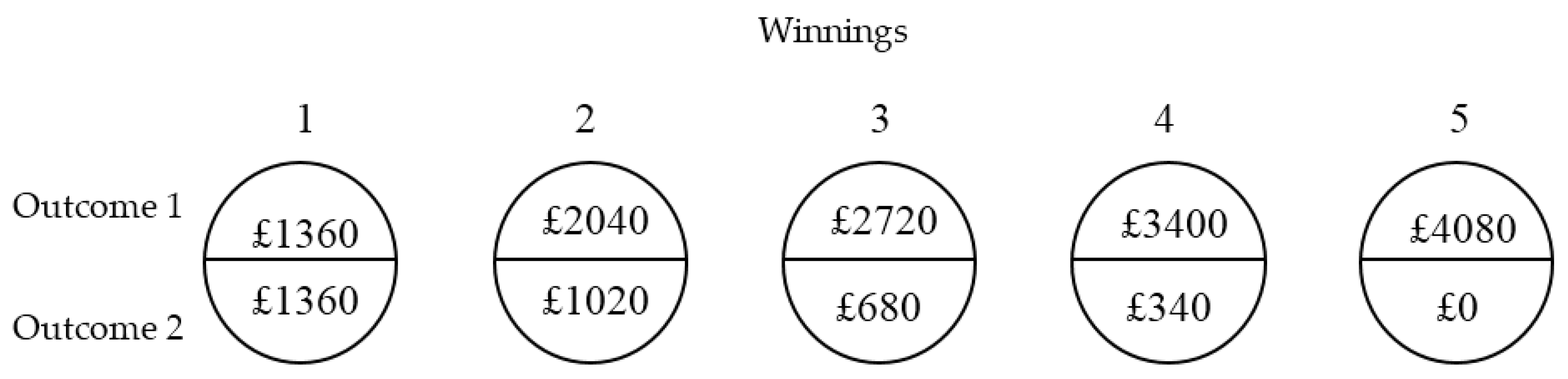
As a measure of risk seeking, we used a self-report and a variance-based hypothetical measure (see Appendix A). In this test, participants had to choose between five different options [24]. Each option had two potential outcomes, both equally likely to happen. The five options differed only according to the difference between the two amounts in each outcome. The two amounts in the first option (Option 1) always had a difference of zero; this difference increased linearly from Options 2 to 5, where the difference between the two potential outcomes was the largest (see Section 4.3 for further detail).

The hypothetical decision-making situations were framed as six different financial contexts. In this respect, we would like to stress that we made sure that there were analogous real financial products on the market. The frames we utilised were monetary gambles (i.e., gamble to win or to lose), insurance, pension provision, investment, and job salary (see Appendix A).

It is important to notice that the same risky questions were asked within each of the six different financial contexts; hence, the description of the problem was the only factor that could affect participants’ risk preferences—apart from the priming condition. Thus, the present study used a 2 (between: priming) × 6 (within: financial domain) mixed design. Finally, we controlled for absolute wealth by offering similar amounts across the different financial scenarios (see Section 4 below for further details regarding methodology).

2. Results

Irrespectively of financial context and priming condition, participants exhibited relatively low levels of risk-seeking behaviour. Almost two out of three of all the choices (62.5%) were for Options 1 and 2—and only 10.4% for Option 5 (the riskiest option). Over a fourth of choices (27.1%) were for Options 3 and 4.

The distributions of the six measures—i.e., risk-seeking preferences in each financial context—were inspected. Large deviations from normality were noted; for example, Pension (skewness, s = 1.1), Salary (s = 1.0) and Gamble to lose (s = 0.9) were positively skewed. Gamble to win (kurtosis, k = −1.4) and Insurance (k = −1.2) were platykurtic (SE for skewness was equal to 0.2; for kurtosis, it was 0.4). Considering that the normality assumption was not met and that participants provided one rating only for each scenario, non-parametric statistical analyses were run. In any case, the same results were obtained when the corresponding parametric analyses were run.

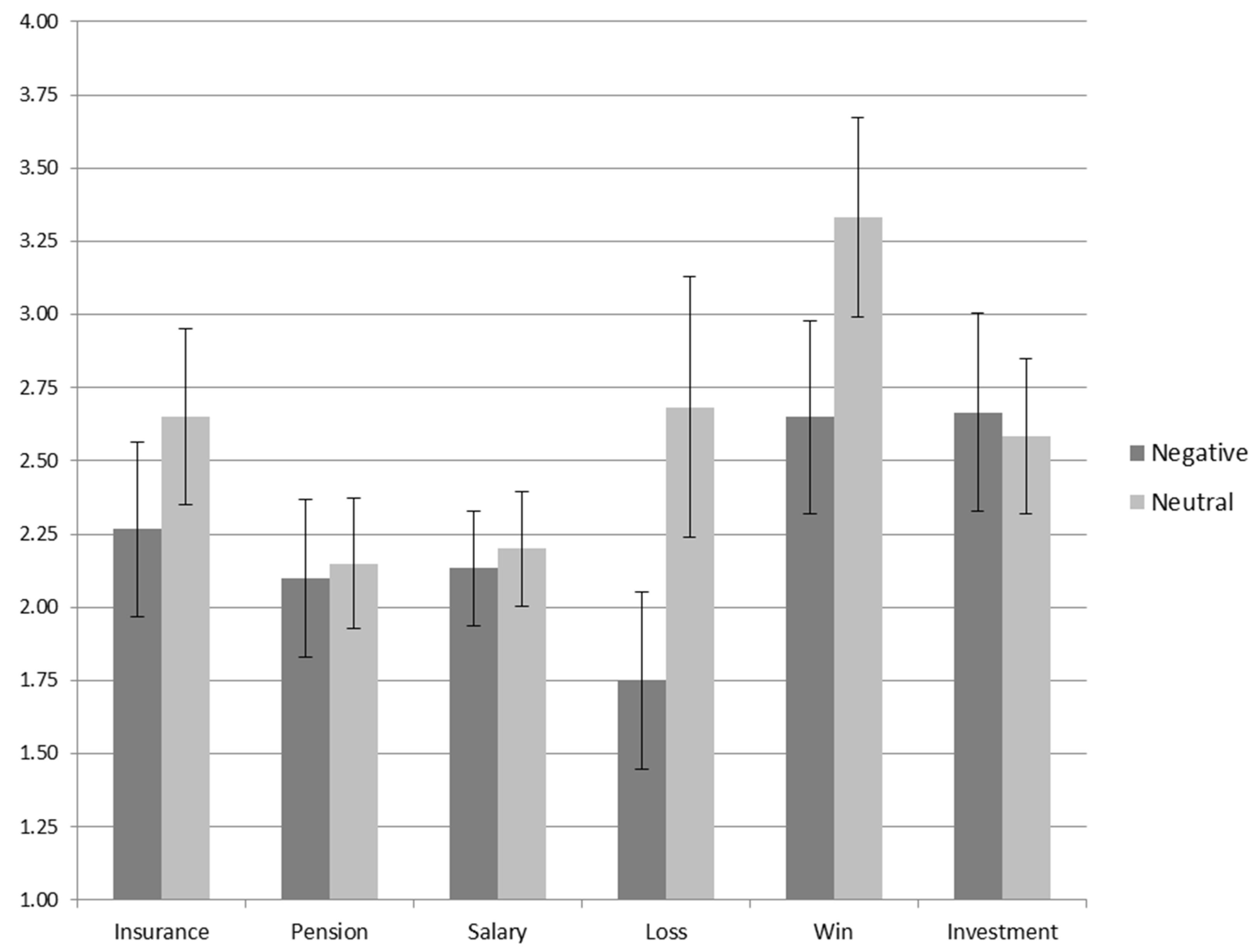
Overall, negative priming influenced the total amount of risk taken (see Figure 1 below); participants in the negative priming condition (Mean rank = 51.5) took significantly less risk than participants in the neutral condition (Mean rank = 69.5), U (N = 120) = 2342.0, z = 2.9, p = 0.004, r = 0.24.

Also, the financial context affected the amount of risk taken, regardless of priming, χ² (5) = 49.2, p < 0.001 (Friedman test). Regardless of the priming condition, Gamble to lose (Mean rank = 2.9) attracted the safest choices, while Gamble to win (Mean rank = 4.2) attracted the riskiest decision-making. In order to examine priming effects on risk taking depending on the financial scenario, separate Mann-Whitney U tests were run on each of the six domains, and p-values were adjusted according to the Bonferroni correction (the between-subjects factor was priming, negative vs. neutral). Of the six scenarios, only two provided a significant main effect of priming and they were Gamble to lose (U (N = 120) = 2313.0, z = 2.9, p = 0.018, r = 0.27) and Gamble to win (U (N = 120) = 2288.0, z = 2.6, p = 0.048, r = 0.24). The effect of priming in the remaining four domains was not significant (all p-values > 0.35). In the Gamble to win and lose scenarios, negatively primed participants (Mean rank = 52.4 and Mean rank = 51.9, respectively) took significantly less risk than participants in the neutral condition (Mean rank = 68.6 and Mean rank = 69.1, respectively).

3. Discussion

In the present study, priming effects were observed, as participants exposed to negative priming were less likely to take risky decisions (see also [25]). Interestingly, this negative priming effect was confined to simple and non-experiential financial scenarios (i.e., gambling to win or to lose). Compared to financial products such as pension provision or insurance, it can be argued that simple monetary gambles may represent a different (possibly simplified) version of the choices people take for real financial products. A potential explanation of the above difference could be as follows: People may understand (conceptualise) the financial risk differently in each decision-making domain. It is plausible that the respondents’ risky behaviour is informed by aspects of the interface with which they are dealing, rather than underlying decision-making processes. Specifically, it could be argued that people’s experiences of events “leak” into decisions even when risk information is explicitly provided—an integration of experience and description of risks on preferences [5]. A consequence of this view is that people do not have stable underlying preferences for risk; instead, context and experience determine preferences even when the utilities (risk and reward) of alternative options are known [4,5].

Already, previous results questioned the assumption that monetary gambles are a methodology that accurately measures people’s risk preferences across financial domains [2,4,26]. Simpler situations such as gambling scenarios might induce different decision-making processes than real financial scenarios. The results of the present study suggest that people are more largely affected by situational factors (e.g., affective activation) when gambles to win or to lose are presented, rather than financial products.

These results are somewhat in line with those of Gilad and Kliger [22]. In their study, professionals (commercial bank investment advisors and accountants in Certified Public Accounting firms) were more affected by priming; the authors argued that professionals may use more intuitive—and less analytic—decision-making, which made them more vulnerable to priming biases. Here, we suggest that less analytical strategies were employed for hypothetical monetary gambles (i.e., possibility to lose, gamble to win), due to their non-experiential nature. When ‘real world’ financial domains were under consideration, the cognitive system might have been engaged to a higher extent; consequently, the higher level of processing hampered the effect of priming. It could be argued that when people make decisions about gambles to win or gambles to lose, they just need to process the variance in the payoffs—and somehow test their feelings of how lucky they feel at the moment. These are vulnerable to priming effects, and the negative affect induced by the manipulation might have somehow influenced the predictions on which region the pointer will be more likely to fall. On the other hand, when participants approach say, an investment scenario, they may engage to a higher analytic extent—and they may consider information not explicitly provided in the description (e.g., condition of the current financial system, previous experience and/or knowledge of financial products etc.); this processing in turn shifts the internal debate to an arena where ‘cold’ cognition may be called into play. Real financial contexts may also induce people to retrieve more context-dependent information, and beliefs. This “intrusion” of more complex memories and beliefs favours the use of analytic strategies as compared to the shallower cognitive tools used when the situation at hand refers to hypothetical gambles, which are more susceptible to priming effects.

4. Materials and Methods

4.1. Participants

A total of 120 respondents (59 females) took part in the gamble test; participants’ age ranged from 18 to 38 (M = 23.2, SD = 4.7). Participants were recruited from two UK based universities. The respondents received course credits in exchange for their participation. Sixty participants were randomly assigned to either priming condition. The allocation of females and males to either priming condition was counterbalanced, as 31 females and 29 males were assigned to the negative priming condition. All participants gave their informed consent for inclusion before they took part in the study. The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethics Committee of City University London (2013).

4.2. Design

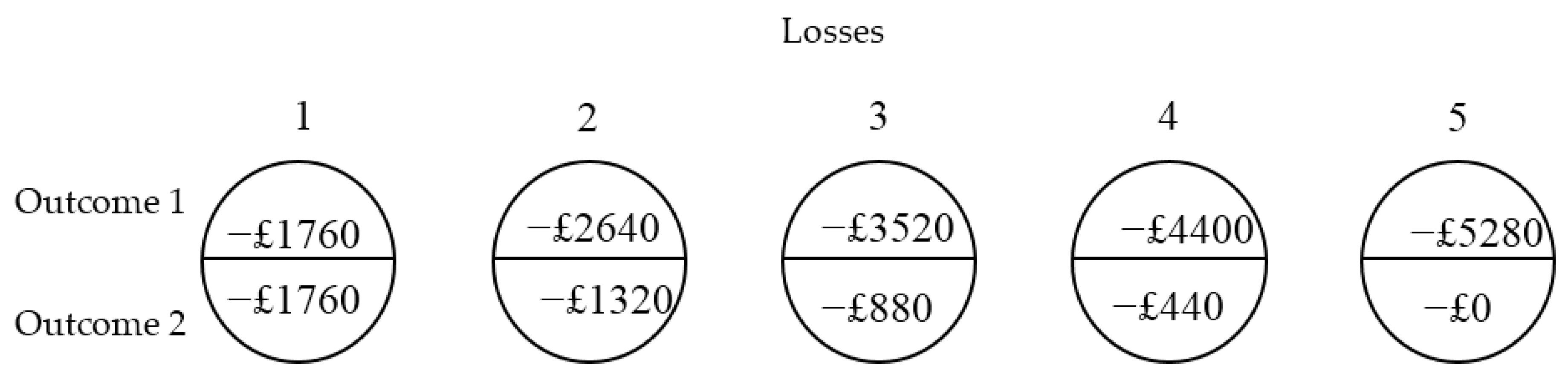
Our study was designed as a survey (questionnaire); each participant had to make a choice for each of the six financial products. In each context, participants had to choose between five different options with binary outcomes. Each option was represented as a pie-chart, equally split into an upper and lower area—these representing the equal chance of each of the two outcomes to happen. The monetary amounts for the two outcomes of Option 1 were always the same. For Option 2, the amount in the upper region was greater than the amount in the lower region, and this difference increased linearly all the way to Option 5. Hence, Option 1 represented the certain option—participants knew what the outcome was going to be. Option 5 represented the riskiest option, as the difference between the two outcomes was the largest. The ratio between the upper and lower region amounts was the same across scenarios, i.e., 1, 2, 4, 10 for Options 1 to 4, respectively. This was achieved by increasing the upper region amounts by a constant amount (e.g., £680) from Option 1 to 5, while decreasing the lower region amounts by half that amount (e.g., £340).

Hence, participants who were least risk seeking were expected to choose Option 1, which represented a sure amount that chance could not alter. A more risk-seeking person was instead expected to choose one between Options 2 to 5—the last representing the riskiest option within the choice set. Hence, the indicator of risk seeking behaviour was an ordinal measurement, each determined by a single choice within each scenario. Note that the present measure refers mostly to risk seeking behaviour, and no real measurement of risk aversion can be inferred.

As participants were handed questionnaires within booklets, four randomly pre-defined were determined—so that each scenario was presented in four different order positions across participants. The four orders were: (1) Win, Investment, Salary, Pension, Loss and Insurance; (2) Insurance, Loss, Pension, Salary, Investment and Win; (3) Insurance, Pension, Salary, Loss, Win, and Investment; and (4) Salary, Investment, Insurance, Win, Pension, and Loss. This strategy ensured that the influence of sequential effects was minimised.

4.3. Materials

Priming was manipulated by changing the questionnaire background between the two conditions [27]. In the neutral condition, no background picture was provided, as the questionnaire was printed on regular white paper. In the negative priming condition, the questionnaire had a picture of dark tornado as its background—for a similar priming procedure, see [28]. This picture was selected from the International Affective Picture System database (IAPS), [29]—and was characterised by a low valence rating (3.4, on a scale ranging from 1 to 9, 9 being the most positive) and high arousal (6.7 on a scale from 1 to 9, 9 being the most arousing).

As previously mentioned, in each scenario participants were required to make a choice between five different binary options, the two outcomes of each being equally likely; this measure was firstly used by [24]. Risk preferences were measured as the choice made in each domain—the higher the corresponding number of the chosen option, the more risk-seeking the choice. More specifically, level of risk was represented as the variance of expected payoff (EV). Taking the gamble to win domain as an example, the most risk-averse participants would sacrifice EV to avoid variance, choosing Option 1. Intermediate risk preference levels were represented by Options 2, 3, and 4. Risk-neutral or risk-seeking participants would choose Option 5—maximising EV in the domain of gambles to win. Indeed, along with risk, also Expected Value (EV) increased linearly across the Options; that is, choosing the riskiest option would have maximised EV for each trial. The only exception was gamble to lose, where each amount represented disutility. For this reason, it can be put forward that this paradigm did not allow us to test the predictions of Prospect Theory [30]. Specifically, the proposed method does not aim to test the four-fold pattern of risk preferences (based on abstract monetary gambles) predicted by Prospect Theory. Also note that, in absolute terms, the payoffs differed across the domains; for instance, the highest payoff in the gamble to win domain was £4080, whilst it was £4320 in the investment domain. Nonetheless, as previously mentioned, the ratio of the two different payoffs for Options 1 to 4 was the same across the different scenarios.

4.4. Procedure

Participants received a booklet, which included the six financial scenarios—each with a specific introduction and the options to choose from (see Appendix A). A general introduction explained that the current study was run so to improve the presentation of financial information, and its aim was to find out how people make risky decisions. It was also stressed that participants had to make a choice as if they were taking that decision for real. Participants indicated their choice for each of the six scenarios by circling the preferred option.