An Optimal Three-Way Stable and Monotonic Spectrum of Bounds on Quantiles: A Spectrum of Coherent Measures of Financial Risk and Economic Inequality
Abstract
:1. Introduction
A very serious shortcoming of VaR, in addition, is that it provides no handle on the extent of the losses that might be suffered beyond the threshold amount indicated by this measure. It is incapable of distinguishing between situations where losses that are worse may be deemed only a little bit worse, and those where they could well be overwhelming. Indeed, it merely provides a lowest bound for losses in the tail of the loss distribution and has a bias toward optimism instead of the conservatism that ought to prevail in risk management.
- (I)
- The common risk measures and are in the spectrum: and ; thus, interpolates between and for and extrapolates from and on towards higher degrees of risk sensitivity for . Details on this can be found in Section 5.1.
- (II)
- The risk measure is coherent for each and each , but it is not coherent for any and any . Thus, is the smallest value of the sensitivity index for which the risk measure is coherent. One may also say that for the risk measure inherits the coherence of , and for it inherits the lack of coherence of . For details, see Section 5.3.
- (III)
- is three-way stable and monotonic: in , in , and in X. Moreover, as stated in Theorem 3.4 and Proposition 3.5, is nondecreasing in X with respect to the stochastic dominance of any order ; but, this monotonicity property breaks down for the stochastic dominance of any order . Thus, the sensitivity index α is in a one-to-one correspondence with the highest order of the stochastic dominance respected by .
- *
- In Section 2, the three-way stability and monotonicity, as well as other useful properties, of the spectrum of upper bounds on tail probabilities are established.
- *
- In Section 3, the corresponding properties of the spectrum of risk measures are presented, as well as other useful properties.
- *
- The matters of effective computation of and , as well as optimization of with respect to X, are considered in Section 4.
- *
- An extensive discussion of results is presented in Section 5, particularly in relation with existing literature.
- *
- Concluding remarks are collected in Section 6.
- *
- The necessary proofs are given in Appendix A.
2. An Optimal Three-Way Stable and Three-Way Monotonic Spectrum of Upper Bounds on Tail Probabilities
- (i)
- is nonincreasing in .
- (ii)
- If and , then for all .
- (iii)
- If and for all real , then for all .
- (iv)
- If and , then as and as , so that for all .
- (v)
- If and for some real , then as and as , so that for all .
- (i)
- For all , one has
- (ii)
- For all , one has .
- (iii)
- The function is continuous and convex if ; we use the conventions and for all real ; concerning the continuity of functions with values in the set , we use the natural topology on this set. Also, the function is continuous and convex, with the convention .
- (iv)
- If , then the function is continuous.
- (v)
- The function is left-continuous.
- (vi)
- is nondecreasing in , and for all .
- (vii)
- If , then ; even for , it is of course possible that , in which case for all real x.
- (viii)
- , and if and only if .
- (ix)
- .
- (x)
- for all .
- (xi)
- If , then is strictly decreasing in .
- (i)
- (ii)
- Model-independence:
- depends on the r.v. X only through the distribution of X.
- Monotonicity in X:
- is nondecreasing with respect to the stochastic dominance of order : for any r.v. Y such that , one has . Therefore, is nondecreasing with respect to the stochastic dominance of any order ; in particular, for any r.v. Y such that , one has .
- Monotonicity in α:
- is nondecreasing in .
- Monotonicity in x:
- is nonincreasing in .
- Values:
- takes only values in the interval .
- α-concavity in x:
- is convex in x if , and is concave in x if .
- Stability in x:
- is continuous in x at any point – except the point when .
- Stability in α:
- Suppose that a sequence is as in Proposition 2.3. Then .
- Stability in X:
- Suppose that and a sequence is as in Proposition 2.4. Then .
- Translation invariance:
- for all real c.
- Consistency:
- for all real c; that is, if the r.v. X is the constant c, then all the tail probability bounds precisely equal the true tail probability .
- Positive homogeneity:
- for all real .
3. An Optimal Three-Way Stable and Three-Way Monotonic Spectrum of Upper Bounds on Quantiles
- (i)
- .
- (ii)
- If then .
- (iii)
- .
- (iv)
- .
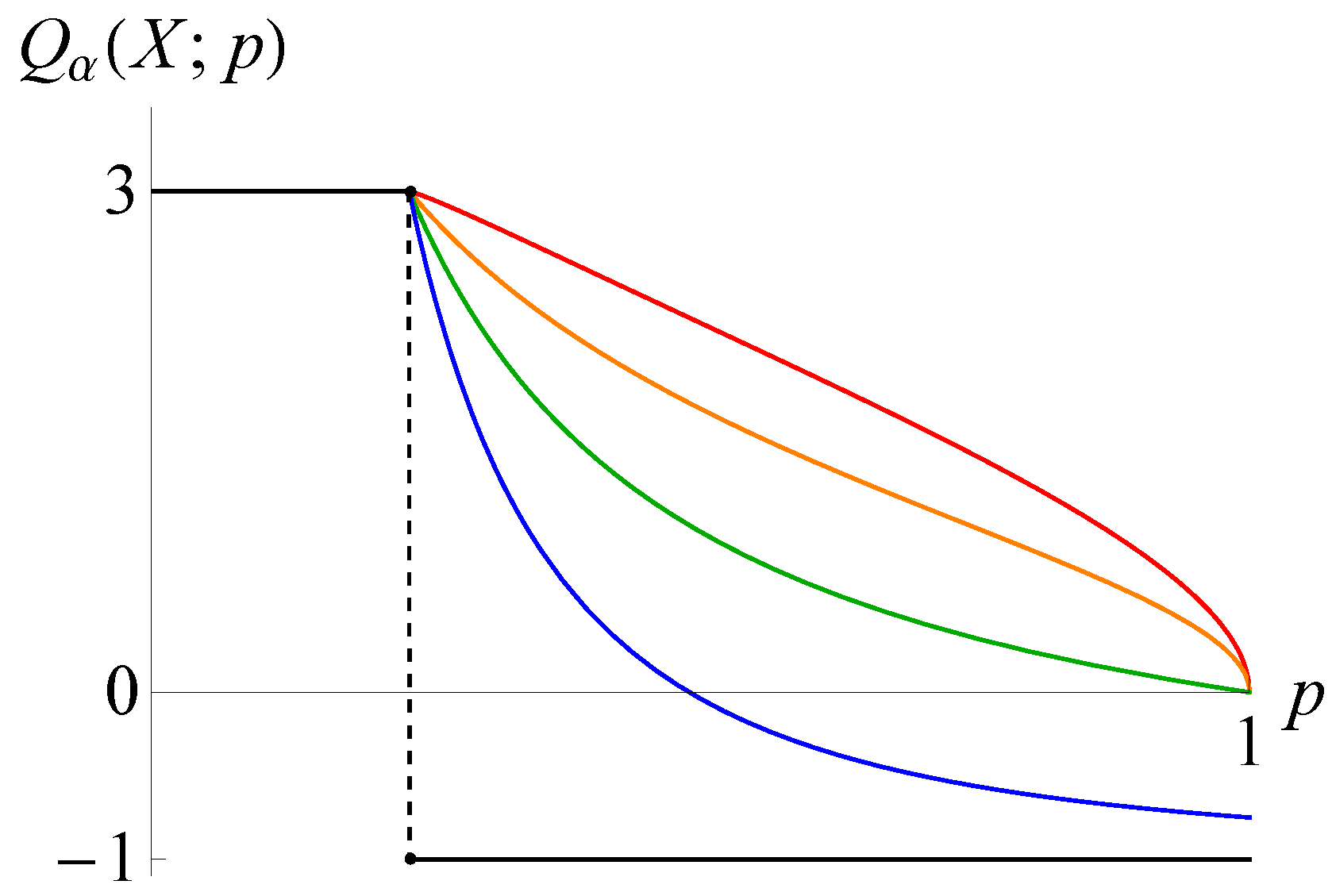
- (v)
- If , then the functionis the unique inverse to the continuous strictly decreasing functionTherefore, the function (3.6), too, is continuous and strictly decreasing.
- (vi)
- If , then for any , one has .
- (vii)
- If , then .
- Model-independence:
- depends on the r.v. X only through the distribution of X.
- Monotonicity in X:
- is nondecreasing with respect to the stochastic dominance of order : for any r.v. Y such that , one has . Therefore, is nondecreasing with respect to the stochastic dominance of any order ; in particular, for any r.v. Y such that , one has .
- Monotonicity in α:
- is nondecreasing in .
- Monotonicity in p:
- is nonincreasing in , and is strictly decreasing in if .
- Finiteness:
- takes only (finite) real values.
- Concavity in or in :
- is concave in if , and is concave in .
- Stability in p:
- is continuous in if .
- Stability in X:
- Suppose that and a sequence is as in Proposition 2.4. Then .
- Stability in α:
- Suppose that and a sequence is as in Proposition 2.3. Then .
- Translation invariance:
- for all real c.
- Consistency:
- for all real c; that is, if the r.v. X is the constant c, then all of the quantile bounds equal c.
- Positive sensitivity:
- Suppose here that . If at that , then for all ; if, moreover, , then .
- Positive homogeneity:
- for all real .
- Subadditivity:
- is subadditive in X if ; that is, for any other r.v. Y (defined on the same probability space as X) one has:
- Convexity:
- is convex in X if ; that is, for any other r.v. Y (defined on the same probability space as X) and any one has
4. Computation of the Tail Probability and Quantile Bounds
4.1. Computation of
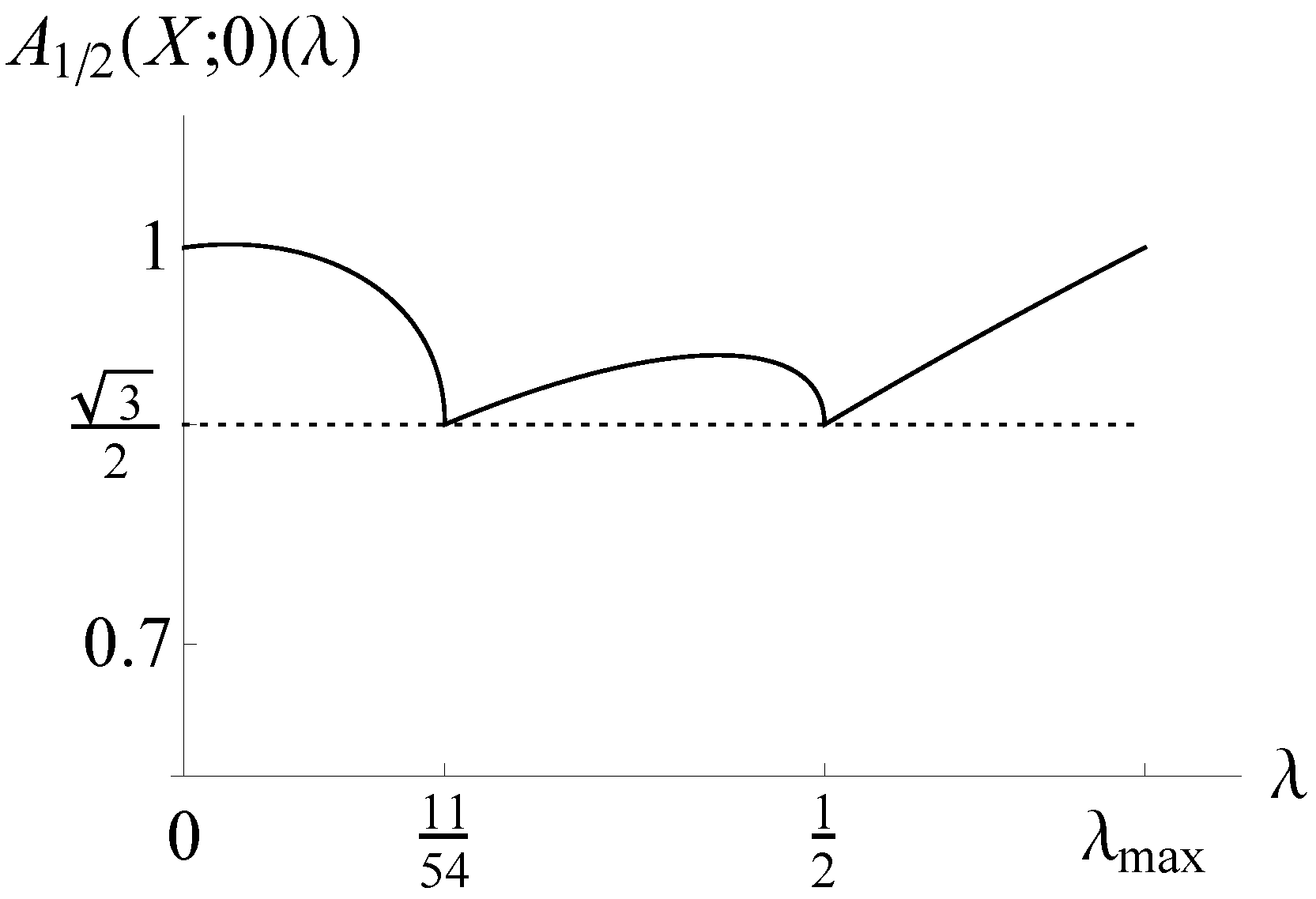
4.2. Computation of
- (i)
- (ii)
- (i)
- If , then is convex in the pair .
- (ii)
- If , then is strictly convex in .
- (iii)
- is strictly convex in , unless for some .
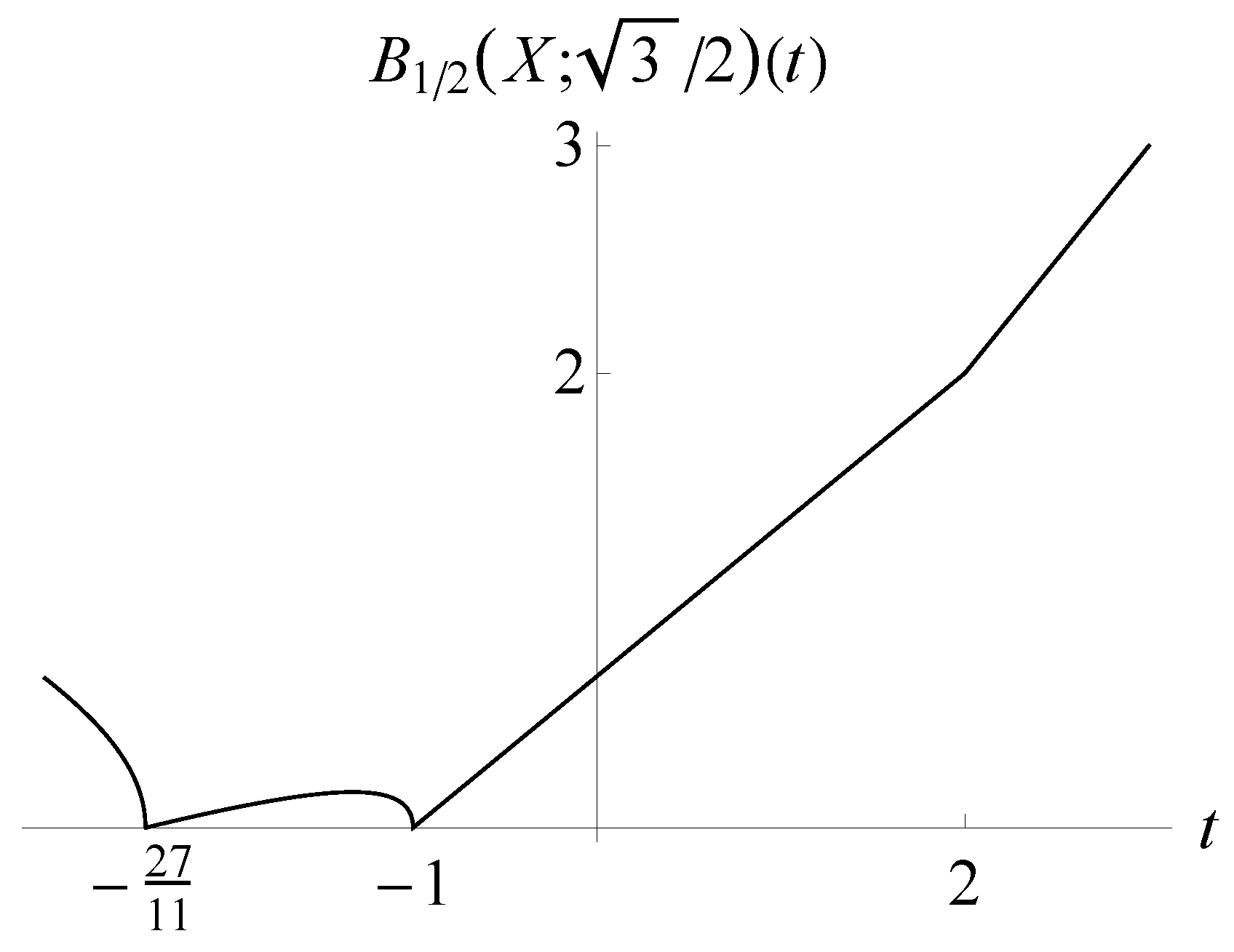
4.3. Optimization of the Risk Measures with Respect to X
4.4. Additional Remarks on the Computation and Optimization
5. Implications for Risk Assessment in Finance and Inequality Modeling in Economics
5.1. The Spectrum Contains and .
5.2. The Spectrum Parameter α as a Risk Sensitivity Index
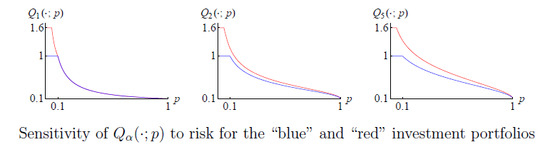
- (i)
- one of the portfolios is clearly riskier than the other;
- (ii)
- this distinction is sensed (to varying degrees, depending on α) by all the risk measures with ;
- (iii)
- yet, the values of are the same for both portfolios.
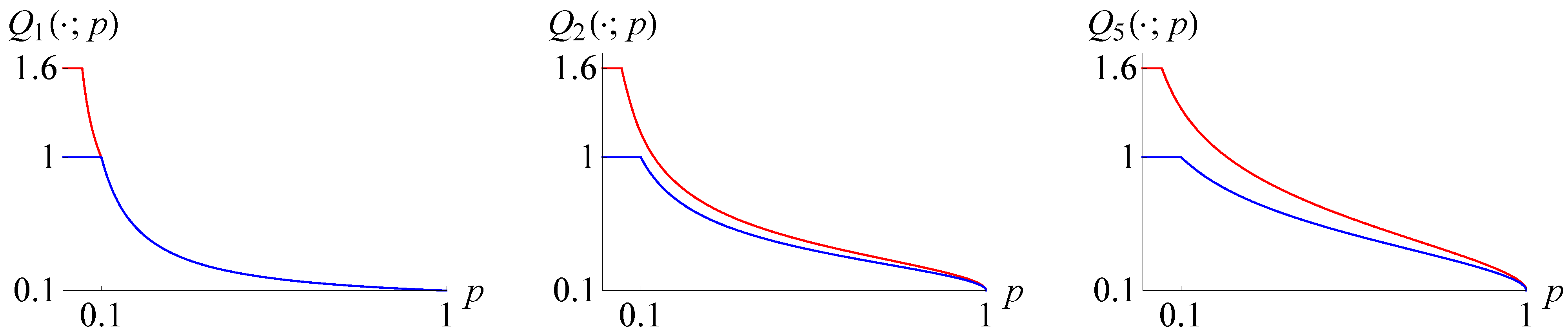
5.3. Coherent and Non-Coherent Measures of Risk
5.4. Other Terminology Used in the Literature for Some of the Listed Properties of
5.5. Gini-Type Mean Differences and Related Risk Measures
5.6. A Lorentz-Type Parametric Family of Risk Measures
5.7. Spectral Risk Measures
5.8. Risk Measures Reinterpreted as Measures of Economic Inequality
5.9. “Explicit” Expressions of
6. Conclusions
- and are three-way monotonic and three-way stable – in α, p, and X.
- The monotonicity in X is graded continuously in α, resulting in varying, controllable degrees of sensitivity of and to financial risk/economic inequality.
- is the tail-function of a certain probability distribution.
- is a -percentile of that probability distribution.
- For small enough values of p, the quantile bounds are close enough to the corresponding true quantiles , provided that the right tail of the distribution of X is light enough and regular enough, depending on α.
- In the case when the loss X is modeled as a normal r.v., the use of the risk measures reduces, to an extent, to using the Markowitz mean-variance risk-assessment paradigm – but with a varying weight of the standard deviation, depending on the risk sensitivity parameter α.
- and are solutions to mutually dual optimizations problems, which can be comparatively easily incorporated into more specialized optimization problems, with additional restrictions on the r.v. X.
- and are effectively computable.
- Even when the corresponding minimizer is not identified quite perfectly, one still obtains an upper bound on the risk/inequality measures or .
- The quantile bounds with constitute a spectrum of coherent measures of financial risk and economic inequality.
- The r.v.’s X of which the measures and are taken are allowed to take values of both signs. In particular, if, in a context of economic inequality, X is interpreted as the net amount of assets belonging to a randomly chosen economic unit, then a negative value of X corresponds to a unit with more liabilities than paid-for assets. Similarly, if X denotes the loss on a financial investment, then a negative value of X will obtain when there actually is a net gain.
Acknowledgment
Appendix
A. Proofs
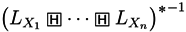 given in the course of the discussion in [23] following Corollary 2.2 therein. However, a direct proof, similar to the one above for , can be based on the observation that is convex in the pair . Since is obviously linear in , the convexity of in means precisely that for any natural number n, any r.v.’s , any positive real numbers , and any positive real numbers with , one has the inequality , where and ; but the latter inequality can be rewritten as an instance of Hölder’s inequality: , where and (so that ). (In particular, it follows that is convex in t, which is useful when is computed by Formula (3.8).)
given in the course of the discussion in [23] following Corollary 2.2 therein. However, a direct proof, similar to the one above for , can be based on the observation that is convex in the pair . Since is obviously linear in , the convexity of in means precisely that for any natural number n, any r.v.’s , any positive real numbers , and any positive real numbers with , one has the inequality , where and ; but the latter inequality can be rewritten as an instance of Hölder’s inequality: , where and (so that ). (In particular, it follows that is convex in t, which is useful when is computed by Formula (3.8).)Conflicts of Interest
References
- P. Artzner, F. Delbaen, J.-M. Eber, and D. Heath. “Coherent measures of risk.” Math. Financ. 9 (1999): 203–228. [Google Scholar] [CrossRef]
- R.T. Rockafellar, and S. Uryasev. “Conditional value at risk for general loss distributions.” J. Bank. Financ. 26 (2002): 1443–1471. [Google Scholar] [CrossRef]
- R.T. Rockafellar, and S. Uryasev. “Optimization of conditional value at risk.” J. Risk 2 (2000): 21–41. [Google Scholar]
- H. Grootveld, and W.G. Hallerbach. Upgrading value at risk from diagnostic metric to decision variable: A wise thing to do? In Risk Measures in the 21st Century. Hoboken, NJ, USA: Wiley, 2004, pp. 33–50. [Google Scholar]
- I. Pinelis. “Optimal tail comparison based on comparison of moments.” In High Dimensional Probability (Oberwolfach, 1996). Basel, Switzerland: Birkhäuser, 1998, Volume 43, pp. 297–314. [Google Scholar]
- I. Pinelis. “On the Bennett-Hoeffding Inequality.” 2009. Available online: http://arxiv.org/abs/0902.4058 (accessed on 24 February 2009).
- I. Pinelis. “On the Bennett–Hoeffding inequality.” Annales de l’Institut Henri Poincaré, Probabilités et Statistiques 50 (2014): 15–27. [Google Scholar] [CrossRef]
- I. Pinelis. “An Optimal Three-Way Stable and Monotonic Spectrum of Bounds On Quantiles: A Spectrum of Coherent Measures of Financial Risk and Economic Inequality, Version 1.” 2013. Available online: http://arxiv.org/abs/1310.6025 (accessed on 24 October 2013).
- I. Pinelis. “Fractional sums and integrals of r-concave tails and applications to comparison probability inequalities.” In Advances in Stochastic Inequalities (Atlanta, GA, 1997). Providence, RI, USA: American Mathematical Society, 1999, Volume 234, pp. 149–168. [Google Scholar]
- I. Pinelis. “Binomial upper bounds on generalized moments and tail probabilities of (super)martingales with differences bounded from above.” In High Dimensional Probability. Beachwood, OH, USA: Institute of Mathematical Statistics, 2006, Volume 51, pp. 33–52. [Google Scholar]
- M.L. Eaton. “A probability inequality for linear combinations of bounded random variables.” Ann. Statist. 2 (1974): 609–613. [Google Scholar] [CrossRef]
- J.-M. Dufour, and M. Hallin. “Improved Eaton bounds for linear combinations of bounded random variables, with statistical applications.” J. Am. Stat. Assoc. 88 (1993): 1026–1033. [Google Scholar] [CrossRef]
- I. Pinelis. “Extremal probabilistic problems and Hotelling’s T2 test under symmetry condition.” 1991. Available online: http://arxiv.org/abs/math/0701806 (accessed on 31 January 2007).
- I. Pinelis. “Extremal probabilistic problems and Hotelling’s T2 test under a symmetry condition.” Ann. Stat. 22 (1994): 357–368. [Google Scholar] [CrossRef]
- P. Billingsley. Convergence of Probability Measures. New York, NY, USA: John Wiley & Sons Inc., 1968. [Google Scholar]
- M. Shaked, and J.G. Shanthikumar. Stochastic Orders. New York, NY, USA: Springer Series in Statistics; Springer, 2007. [Google Scholar]
- P.C. Fishburn. “Continua of stochastic dominance relations for unbounded probability distributions.” J. Math. Econ. 7 (1980): 271–285. [Google Scholar] [CrossRef]
- P.C. Fishburn. “Continua of stochastic dominance relations for bounded probability distributions.” J. Math. Econ. 3 (1976): 295–311. [Google Scholar] [CrossRef]
- A.B. Atkinson. “More on the measurement of inequality.” J. Econ. Inequal. 6 (2008): 277–283. [Google Scholar] [CrossRef]
- P. Muliere, and M. Scarsini. “A note on stochastic dominance and inequality measures.” J. Econ. Theory 49 (1989): 314–323. [Google Scholar] [CrossRef]
- S. Ortobelli, S.T. Rachev, H. Shalit, and F.J. Fabozzi. “The Theory of Orderings and Risk Probability Functionals.” 2006. Available online: http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&ved=0CDIQFjAA&url=http (accessed on 15 July 2013).
- S. Ortobelli, S.T. Rachev, H. Shalit, and F.J. Fabozzi. “Orderings and probability functionals consistent with preferences.” Appl. Math. Financ. 16 (2009): 81–102. [Google Scholar] [CrossRef]
- I. Pinelis. “(Quasi)additivity Properties of the Legendre–Fenchel Transform and Its Inverse, with Applications in Probability.” 2013. Available online: http://arxiv.org/abs/1305.1860 (accessed on 5 June 2013).
- E. Rio. Personal Communication, 2013.
- E. De Giorgi. “Reward-risk portfolio selection and stochastic dominance.” J. Bank. Financ. 29 (2005): 895–926. [Google Scholar] [CrossRef]
- G.C. Pflug. “Some remarks on the value at risk and the conditional value at risk.” In Probabilistic Constrained Optimization. Dordrecht, The Netherlands: Kluwer Academic Publishers, 2000, Volume 49, pp. 272–281. [Google Scholar]
- R.M. Corless, G.H. Gonnet, D.E.G. Hare, D.J. Jeffrey, and D.E. Knuth. “On the Lambert W function.” Adv. Comput. Math. 5 (1996): 329–359. [Google Scholar] [CrossRef]
- I. Pinelis. “Positive-part moments via the Fourier–Laplace transform.” J. Theor. Probab. 24 (2011): 409–421. [Google Scholar] [CrossRef]
- A. Kibzun, and A. Chernobrovov. “Equivalence of the problems with quantile and integral quantile criteria.” Autom. Remote Control 74 (2013): 225–239. [Google Scholar] [CrossRef]
- C. Acerbi, and D. Tasche. “Expected shortfall: A natural coherent alternative to value at risk.” Econ. Notes 31 (2002): 379–388. [Google Scholar] [CrossRef]
- S.T. Rachev, S. Stoyanov, and F.J. Fabozzi. Advanced Stochastic Models, Risk Assessment, and Portfolio Optimization: The Ideal Risk, Uncertainty, and Performance Measures. Hoboken, NJ, USA: John Wiley, 2007. [Google Scholar]
- R.H. Litzenberger, and D.M. Modest. “Crisis and non-crisis risk in financial markets: A unified approach to risk management.” In The Known, the Unknown, and Unknowable in Financial Risk Management. Princeton, NJ, USA: Princeton University Press, 2008, pp. 74–102. [Google Scholar]
- H. Mausser, and D. Rosen. “Efficient risk/return frontiers for credit risk.” Algo Res. Q. 2 (1999): 35–47. [Google Scholar]
- F. Bassi, P. Embrechts, and M. Kafetzaki. “Risk management and quantile estimation.” In A Practical Guide to Heavy Tails (Santa Barbara, CA, 1995). Boston, MA, USA: Birkhäuser Boston, 1998, pp. 111–130. [Google Scholar]
- P. Embrechts, C. Klüppelberg, and T. Mikosch. Modelling Extremal Events for Insurance and Finance. New York, NY, USA: Springer, 1997. [Google Scholar]
- P.C. Fishburn. “Mean-risk analysis with risk associated with below-target returns.” Am. Econ. Rev. 67 (1977): 116–126. [Google Scholar]
- J.A. Clarkson. “Uniformly convex spaces.” Trans. Amer. Math. Soc. 40 (1936): 396–414. [Google Scholar] [CrossRef]
- M. Frittelli, and E.R. Gianin. “Dynamic convex risk measures.” In Risk Measures in the 21st Century. Hoboken, NJ, USA: Wiley, 2004, pp. 227–248. [Google Scholar]
- M.E. Yaari. “The dual theory of choice under risk.” Econometrica 55 (1987): 95–115. [Google Scholar] [CrossRef]
- S. Yitzhaki. “Stochastic dominance, mean variance, and Gini’s mean difference.” Am. Econ. Rev. 72 (1982): 178–185. [Google Scholar]
- A. Cillo, and P. Delquie. “Mean-risk analysis with enhanced behavioral content.” Eur. J. Oper. Res. 239 (2014): 764–775. [Google Scholar] [CrossRef]
- P. Delquie, and A. Cillo. “Disappointment without prior expectation: A unifying perspective on decision under risk.” J. Risk Uncertain. 33 (2006): 197–215. [Google Scholar] [CrossRef]
- M.J. Machina. “Expected utility analysis without the independence axiom.” Econometrica 50 (1982): 277–323. [Google Scholar] [CrossRef]
- R.T. Rockafellar, S. Uryasev, and M. Zabarankin. “Generalized deviations in risk analysis.” Financ. Stoch. 10 (2006): 51–74. [Google Scholar] [CrossRef]
- R. Mansini, W. Ogryczak, and M.G. Speranza. “LP solvable models for portfolio optimization: A classification and computational comparison.” IMA J. Manag. Math. 14 (2003): 187–220. [Google Scholar] [CrossRef]
- W. Ogryczak, and A. Ruszczyński. “On consistency of stochastic dominance and mean-semideviation models.” Math. Program. 89 (2001): 217–232. [Google Scholar] [CrossRef]
- S. Ortobelli, S.T. Rachev, H. Shalit, and F.J. Fabozzi. “Risk Probability Functionals and Probability Metrics Applied To Portfolio Theory.” 2007. Available online: http://www.pstat.ucsb.edu/research/papers/2006mid/view.pdf (accessed on 15 July 2013).
- W. Ogryczak, and A. Ruszczyński. “Dual stochastic dominance and related mean-risk models.” SIAM J. Optim. 13 (2002): 60–78. [Google Scholar] [CrossRef]
- A. Kibzun, and E.A. Kuznetsov. “Comparison of VaR and CVaR criteria.” Autom.Remote Control 64 (2003): 1154–1164. [Google Scholar] [CrossRef]
- A.B. Atkinson. “On the measurement of inequality.” J. Econom. Theory 2 (1970): 244–263. [Google Scholar] [CrossRef]
- C. Acerbi. “Spectral measures of risk: A coherent representation of subjective risk aversion.” J. Bank. Financ. 26 (2002): 1505–1518. [Google Scholar] [CrossRef]
- R. Giacometti, and S. Ortobelli. “Risk measures for asset allocation models.” In Risk Measures in the 21st Century. Hoboken, NJ, USA: Wiley, 2004, pp. 69–86. [Google Scholar]
- A.D. Roy. “Safety first and the holding of assets.” Econometrica 20 (1952): 431–449. [Google Scholar] [CrossRef]
- I. Pinelis. “Exact inequalities for sums of asymmetric random variables, with applications.” Probab. Theory Relat. Fields 139 (2007): 605–635. [Google Scholar] [CrossRef]
- I. Pinelis. “A Necessary and Sufficient Condition on the Stability of the Infimum of Convex Functions.” 2013. Available online: http://arxiv.org/abs/1307.3806 (accessed on 7 August 2013).
- R.T. Rockafellar. Convex Analysis. Princeton Landmarks in Mathematics; Princeton, NJ, USA: Princeton University Press, 1997, Reprint of the 1970 original, Princeton Paperbacks. [Google Scholar]
- E. Rio. “English translation of the monograph Théorie asymptotique des processus aléatoires faiblement dépendants (2000) by E. Rio.” 2012, Work in Progress. [Google Scholar]
- E. Rio. “Local invariance principles and their application to density estimation.” Probab. Theory Relat. Fields 98 (1994): 21–45. [Google Scholar] [CrossRef]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinelis, I. An Optimal Three-Way Stable and Monotonic Spectrum of Bounds on Quantiles: A Spectrum of Coherent Measures of Financial Risk and Economic Inequality. Risks 2014, 2, 349-392. https://doi.org/10.3390/risks2030349
Pinelis I. An Optimal Three-Way Stable and Monotonic Spectrum of Bounds on Quantiles: A Spectrum of Coherent Measures of Financial Risk and Economic Inequality. Risks. 2014; 2(3):349-392. https://doi.org/10.3390/risks2030349
Chicago/Turabian StylePinelis, Iosif. 2014. "An Optimal Three-Way Stable and Monotonic Spectrum of Bounds on Quantiles: A Spectrum of Coherent Measures of Financial Risk and Economic Inequality" Risks 2, no. 3: 349-392. https://doi.org/10.3390/risks2030349
APA StylePinelis, I. (2014). An Optimal Three-Way Stable and Monotonic Spectrum of Bounds on Quantiles: A Spectrum of Coherent Measures of Financial Risk and Economic Inequality. Risks, 2(3), 349-392. https://doi.org/10.3390/risks2030349