Model Risk in Portfolio Optimization
Abstract
:1. Introduction
2. General Definitions
- (i)
- Mean-variance optimization: the investor is assumed to maximizewhere is a given risk aversion parameter. The solution of Equation (1) in the unconstrained case can be calculated using first order conditions and is given byIn the case of linear constraints we set , where is a matrix of rank k and . The solution of Equation (1) can be calculated using the method of Lagrange and is given by
- (ii)
- Minimum variance: the investor is assumed to maximize the following utility functionConsider the following linear equality constraints , where is a matrix of rank k, and . In this problem we are looking for the portfolio with minimal variance satisfying linear constraints and having expected return equal to . The optimal portfolio can be calculated using the method of Lagrange and is given bywhere and . In this example note that the set of admissible strategies also depends on the distribution of the random returns through the mean vector μ.
- (iii)
- Equal contributions to risk: the investor is assumed to maximizewhere denotes the contribution of asset i to the total portfolio variance. This means that the investor looks for a portfolio with risk contributions as close to each other as possible with respect to the Euclidean distance. Typically, constraints as in (ii) are chosen.
- (iv)
- Maximum diversification: the investor is assumed to maximizewhere is the i-th element on the diagonal of Σ. This means that the investor maximizes the benefits of diversification. Typically, constraints as in (ii) are chosen.
3. Analysis of the Loss Function in the Mean-Variance Case
- (i)
- for and being the n-dimensional zero vector and identity matrix, respectively;
- (ii)
- W is an almost surely positive random variable, independent of , satisfying ; and
- (iii)
- is a non-singular matrix such that .
- (i)
- ,
- (ii)
- , and for all .
- (i)
- Multivariate Gauss: set .
- (ii)
- 2-points mixture: let W be discrete and take positive values and with probabilities and . The condition implies and . This is a regime switching model with 2 variance regimes characterized by and .
- (iii)
- Multivariate Student-t: let , where and denotes the inverse gamma distribution. The scaling is chosen so that . Then, for all , the random vector has a multivariate Student-t distribution with ν degrees of freedom, mean vector μ and covariance matrix Σ.
- (i)
- Conditional on W we havewhere denotes the Wishart distribution. Moreover, and are conditionally independent given W. See Appendix 2 for more details.
- (ii)
- For the sample covariance matrix is almost surely positive definite and exists almost surely. See Appendix 2 for more details.
- (iii)
- For any we have , , and . This means that , and are unbiased estimators for μ, Σ and , respectively.
- (i)
- Jensen’s inequality implies . Hence forsee also Proposition 1. This lower bound is strictly positive in the non-Gaussian case.
- (ii)
- If we fix the number of assets n and let we obtainIn particular, in the multivariate Gaussian, case we have as , see Example 2(i).
- (iii)
- For and we getThis asymptotic analysis corresponds to large number of risky assets n and comparable sample size m. This limit is considered in El Karoui [29,30] to obtain asymptotic results on model uncertainty in a problem with constraints. The same limit is also considered in Ledoit and Wolf [35] to study asymptotic properties of the spectrum of . In this paper, we have an explicit characterization of model uncertainty for finite n and m. Note that for we obtain the same limit as in (ii), and for we have .
- (iv)
- Note that the loss function depends on the unobservable distribution of W, true mean vector μ and true covariance matrix Σ.
- (i)
- multivariate Gauss:
- (ii)
- 2-points mixture:where and ;
- (iii)
- multivariate Student-t:where .
- (i)
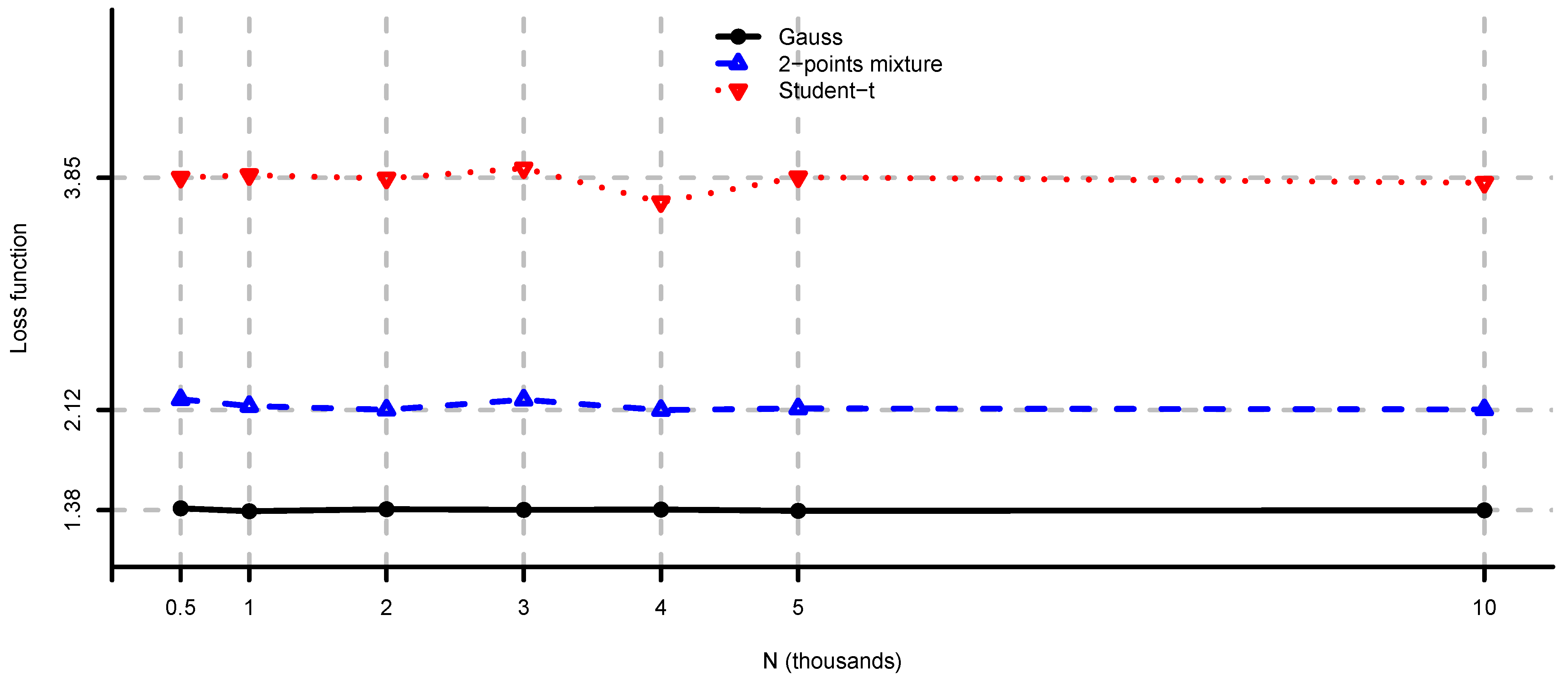
- In the 2-points mixture model we have for or , and for . The more we increase the difference between the two variance regimes (i.e., by considering or ), the greater the average negative effect of model risk. If we decrease the difference (by considering ), then the loss function becomes closer to the Gaussian case.
- (ii)
- In the multivariate Student-t model we have for , and for . This means, by making the marginals “less normal” (i.e., by considering ), we increase the average negative effect of model risk.
4. Adjusting for Model Risk
- (i)
- is the diagonal matrix of eigenvalues (also called eigenvariances in this context) of Σ, which satisfy ; and
- (ii)
- T is an orthogonal matrix with columns being the eigenvectors (also called eigenportfolios) of Σ corresponding to , respectively.
- (i)
- is a simple proportional scaling type estimator. The unconstrained mean-variance portfolio constructed using is given by
- (ii)
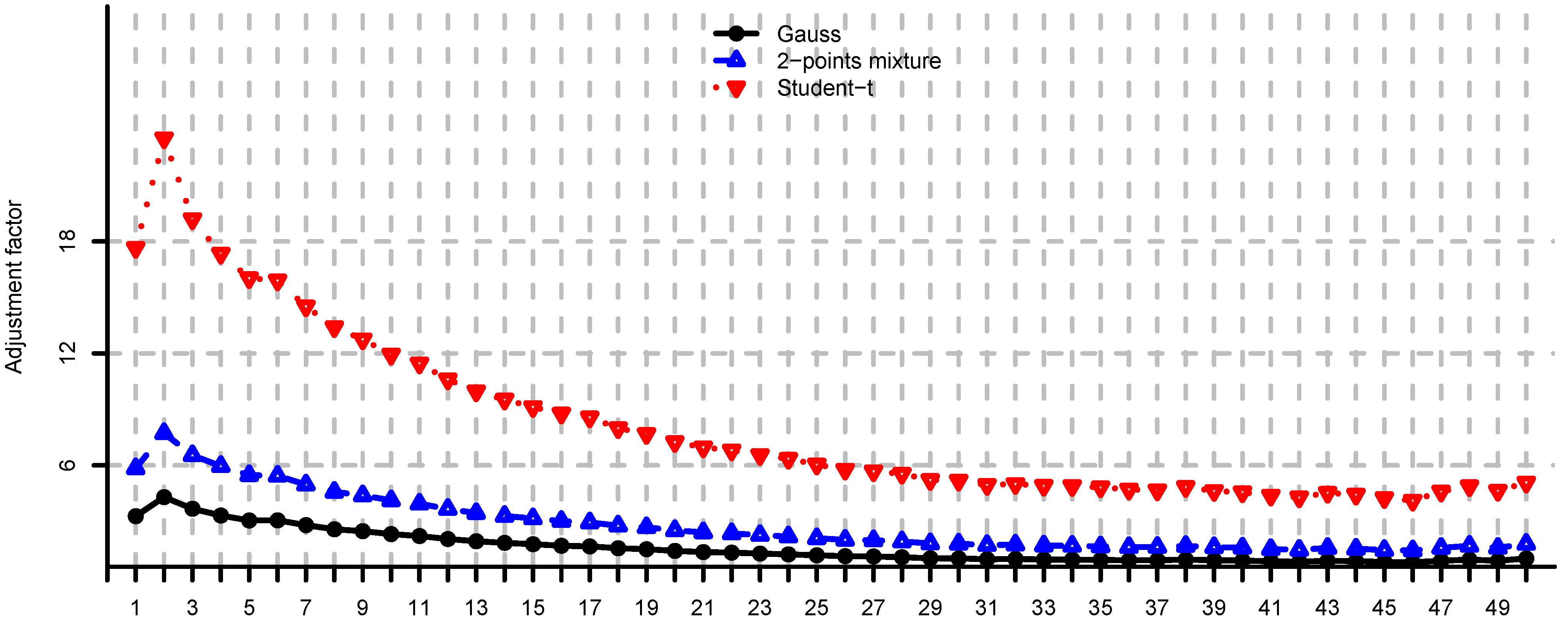
- In general, adjustment factors (7) are unobservable since they depend on the unknown distribution of W. Note that, by Remark 8(i) we havewith equality in the multivariate Gaussian case.
- (i)
- independent of ,
- (ii)
- almost surely and integrable, and
- (iii)
- .
5. Case Studies
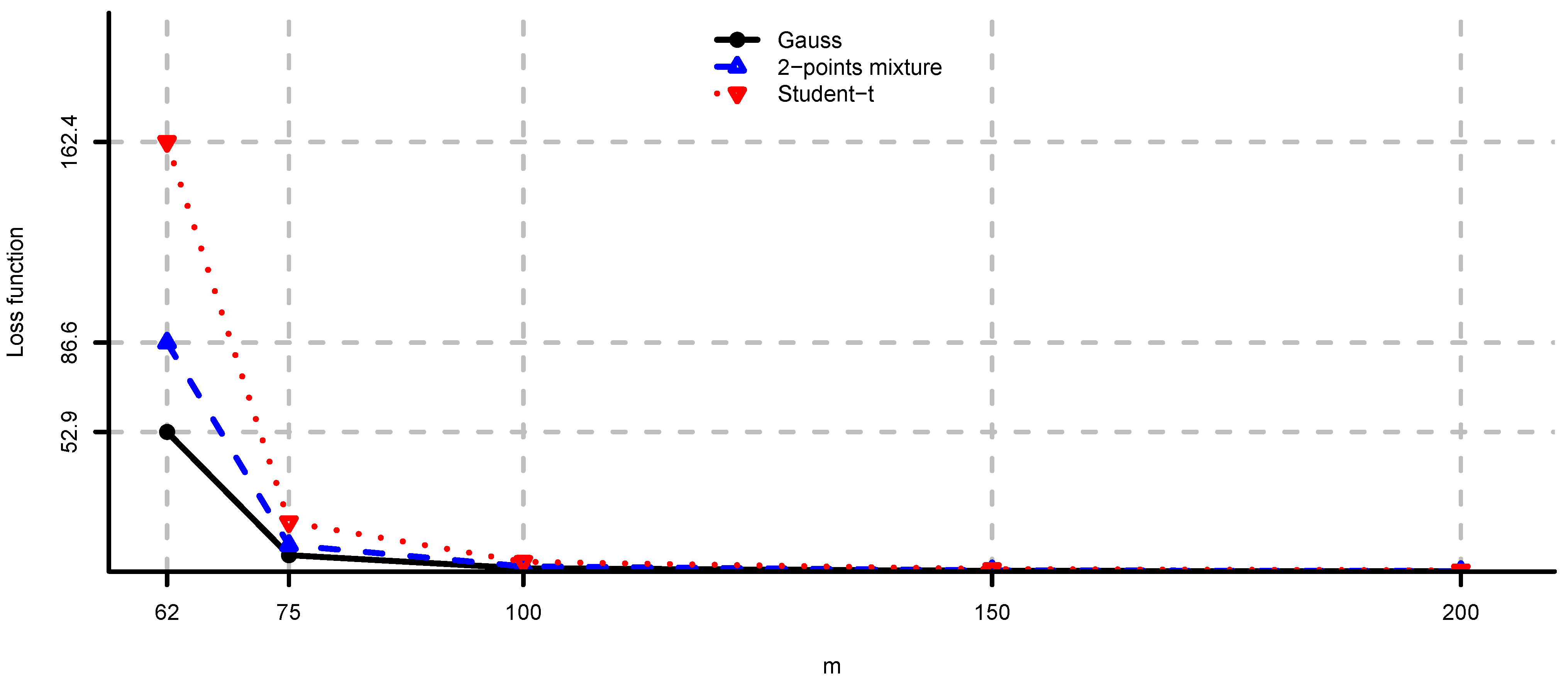
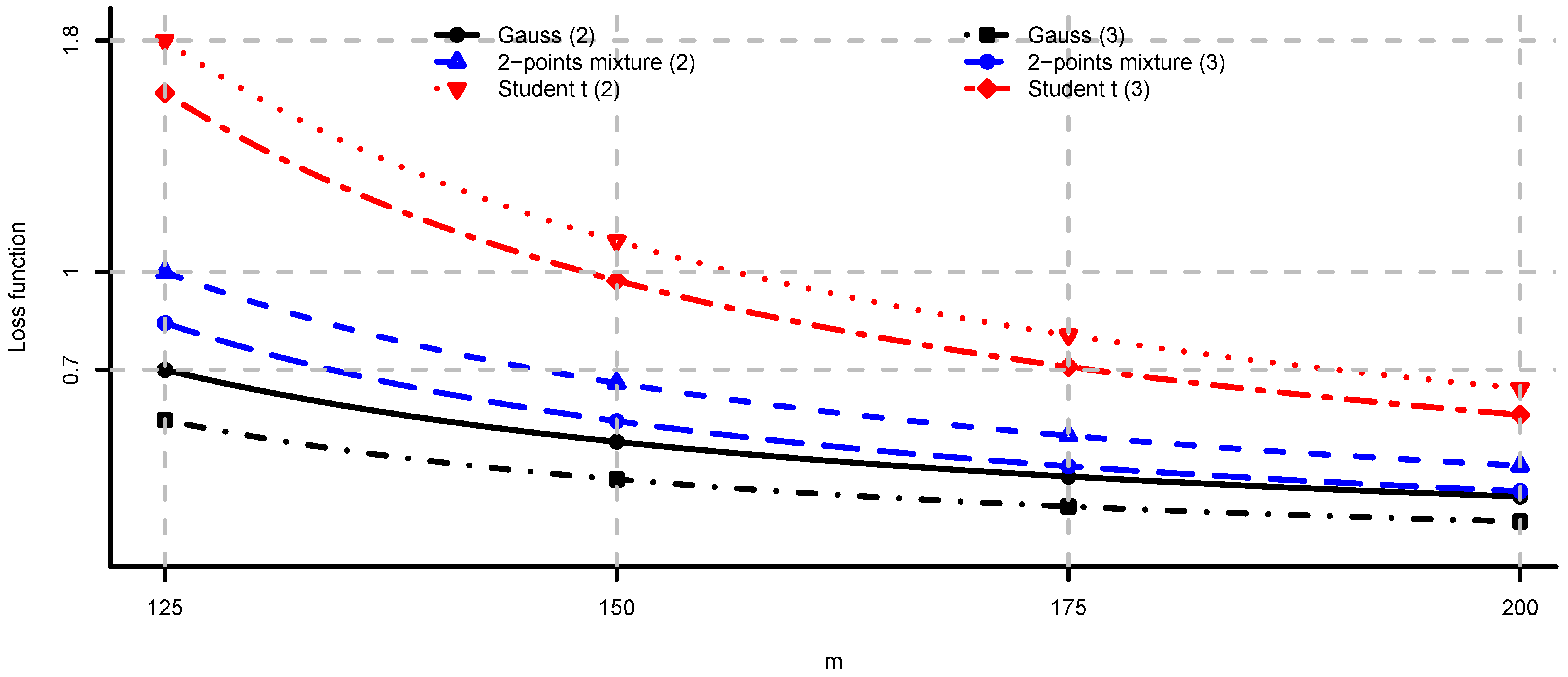
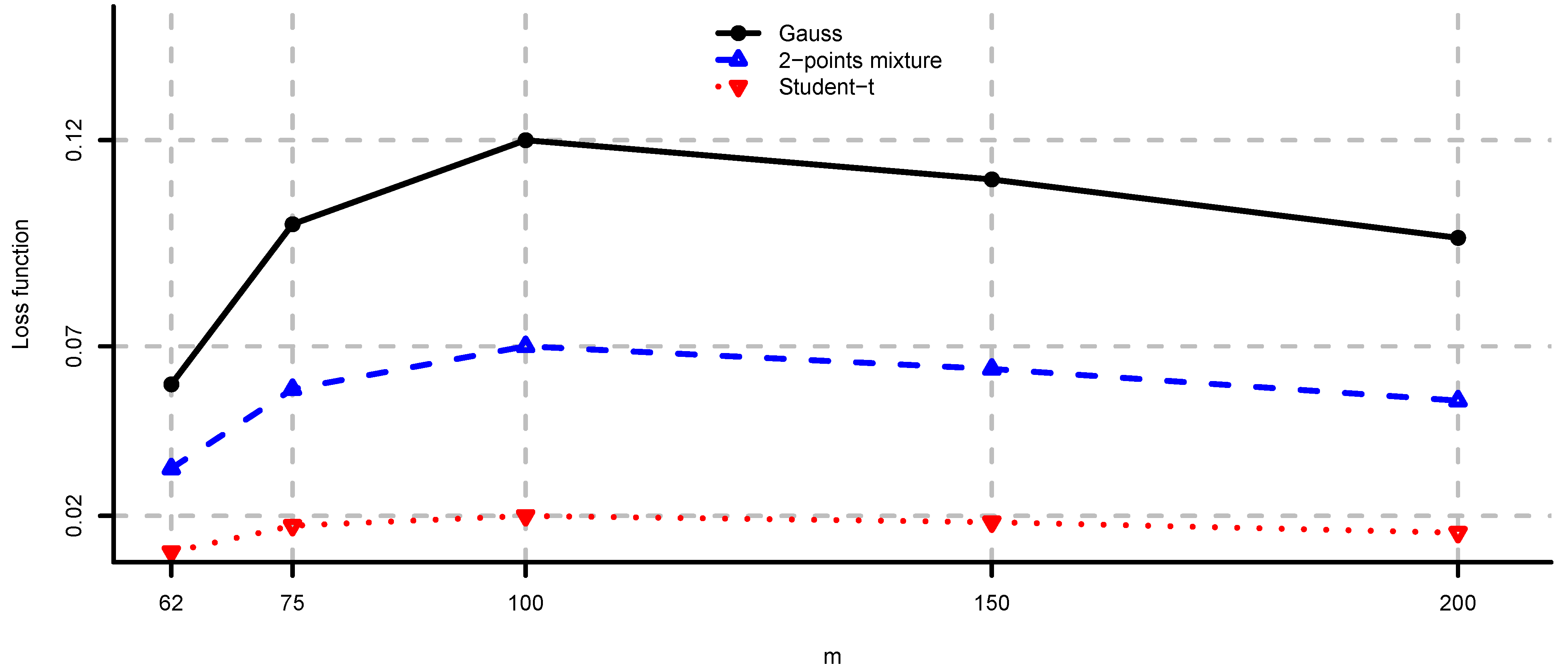
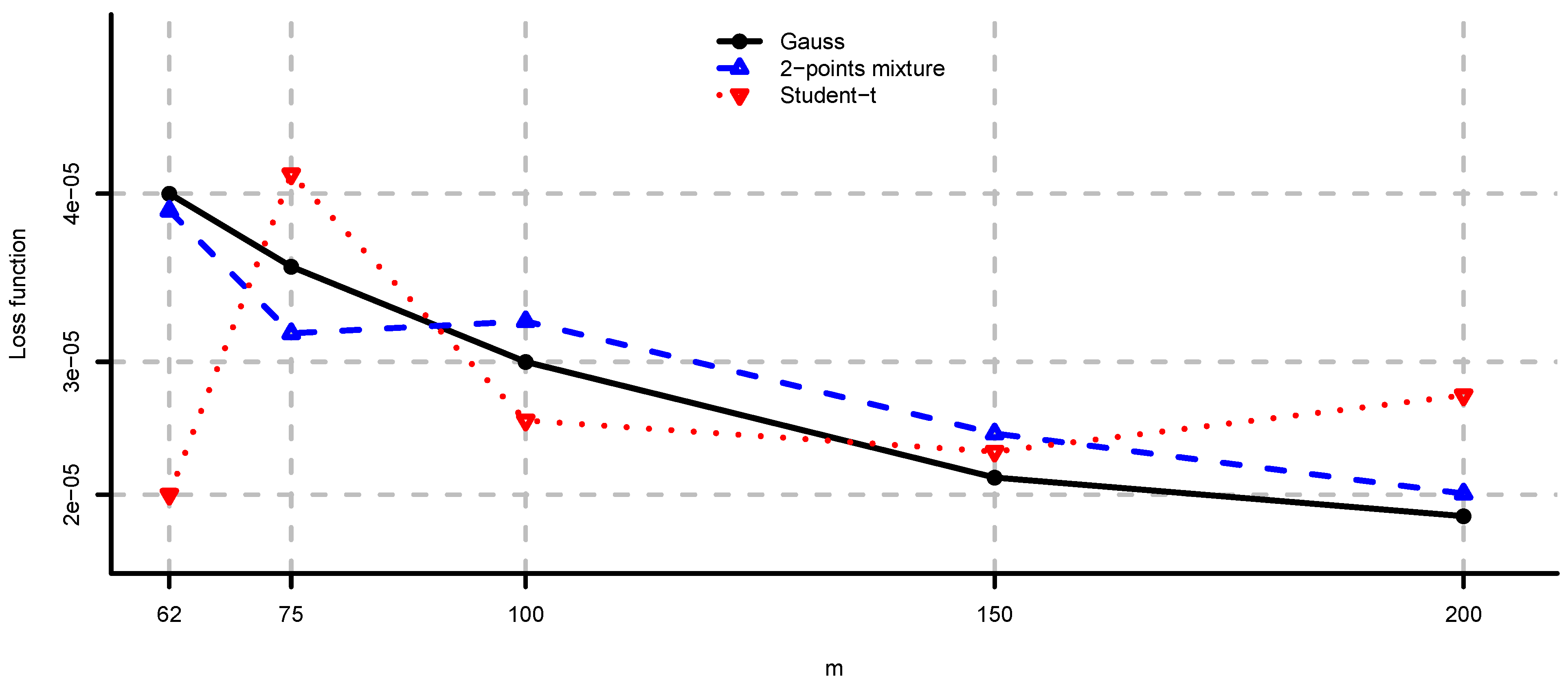
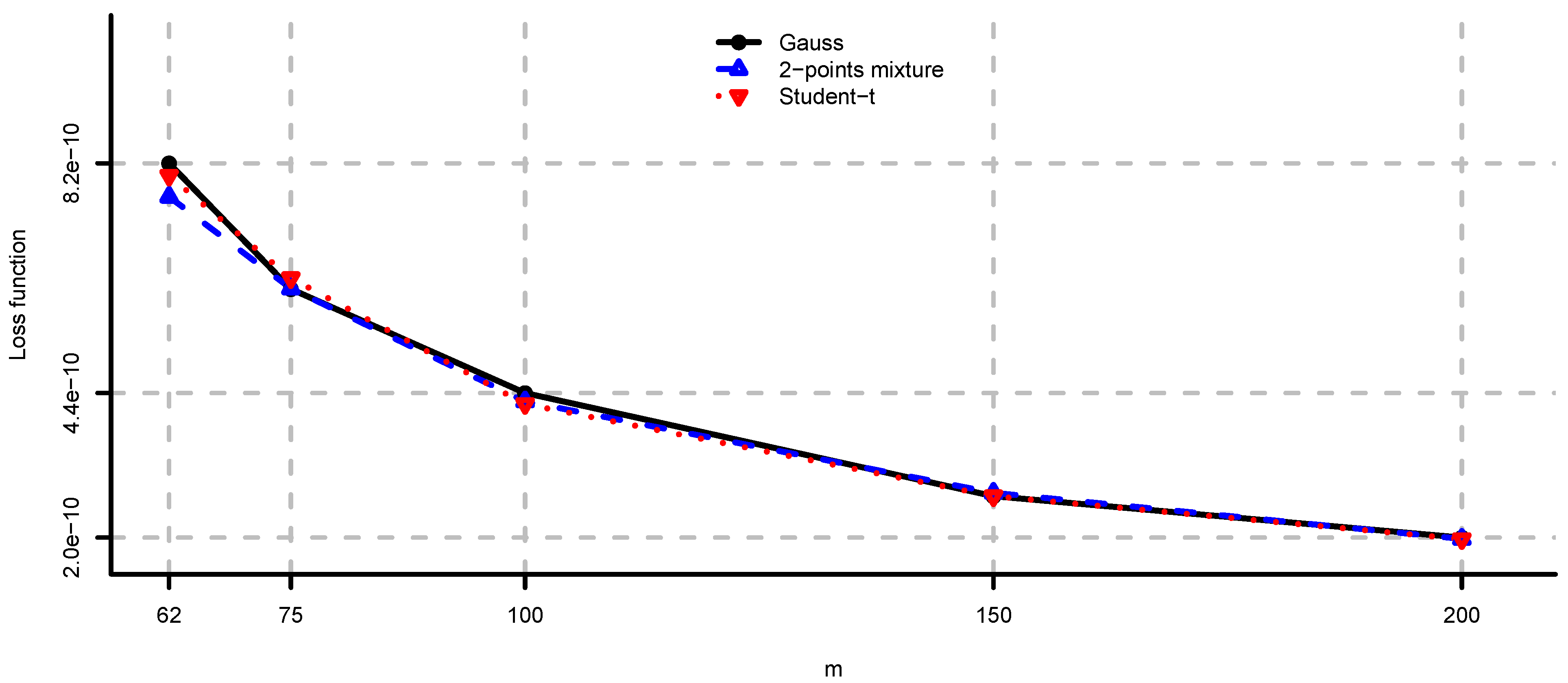
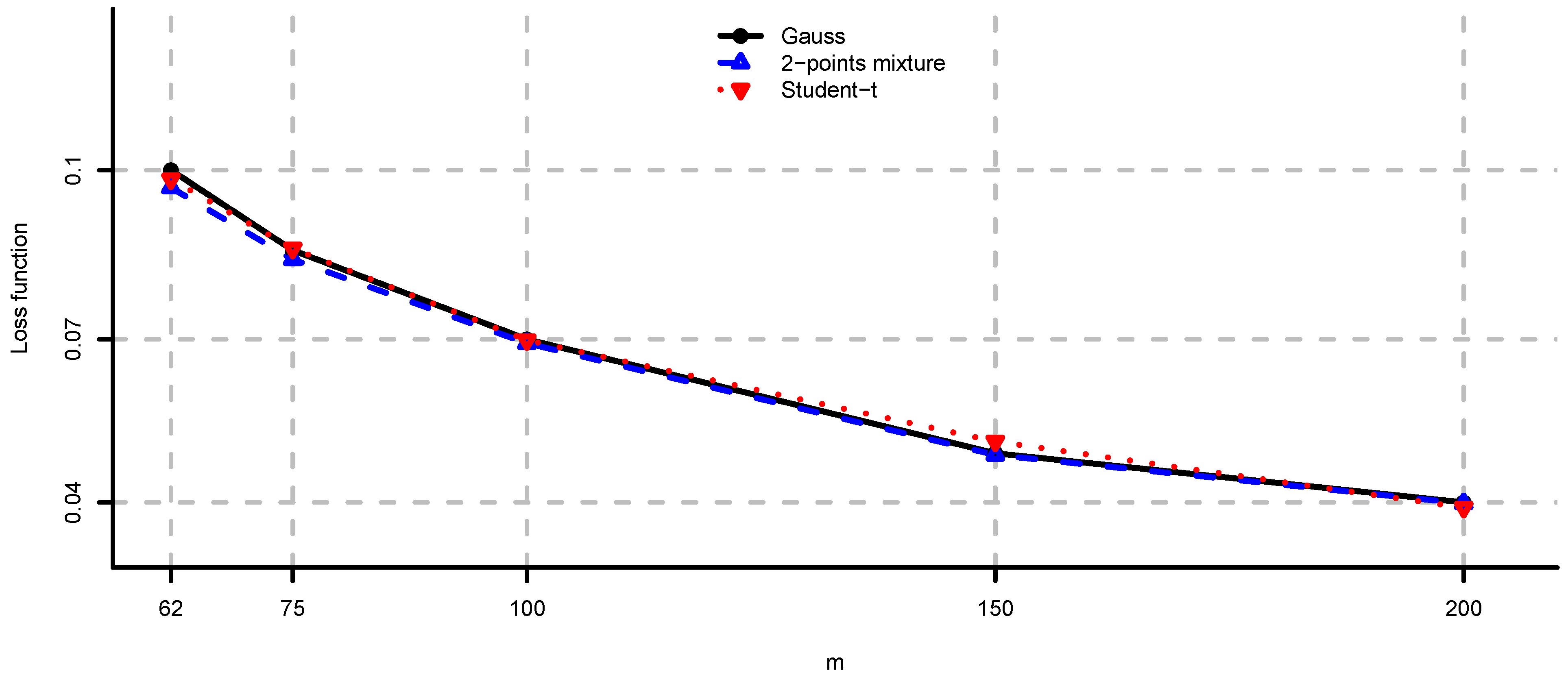
5.1. Simulated Observations
- (i)
- Unconstrained mean-variance: and . We set for the risk aversion parameter.
- (ii)
- Long only fully invested minimum variance: and .
- (iii)
- Long only fully invested equal contributions to risk: and as in (ii).
- (iv)
- Long only fully invested maximum diversification: and as in (ii).
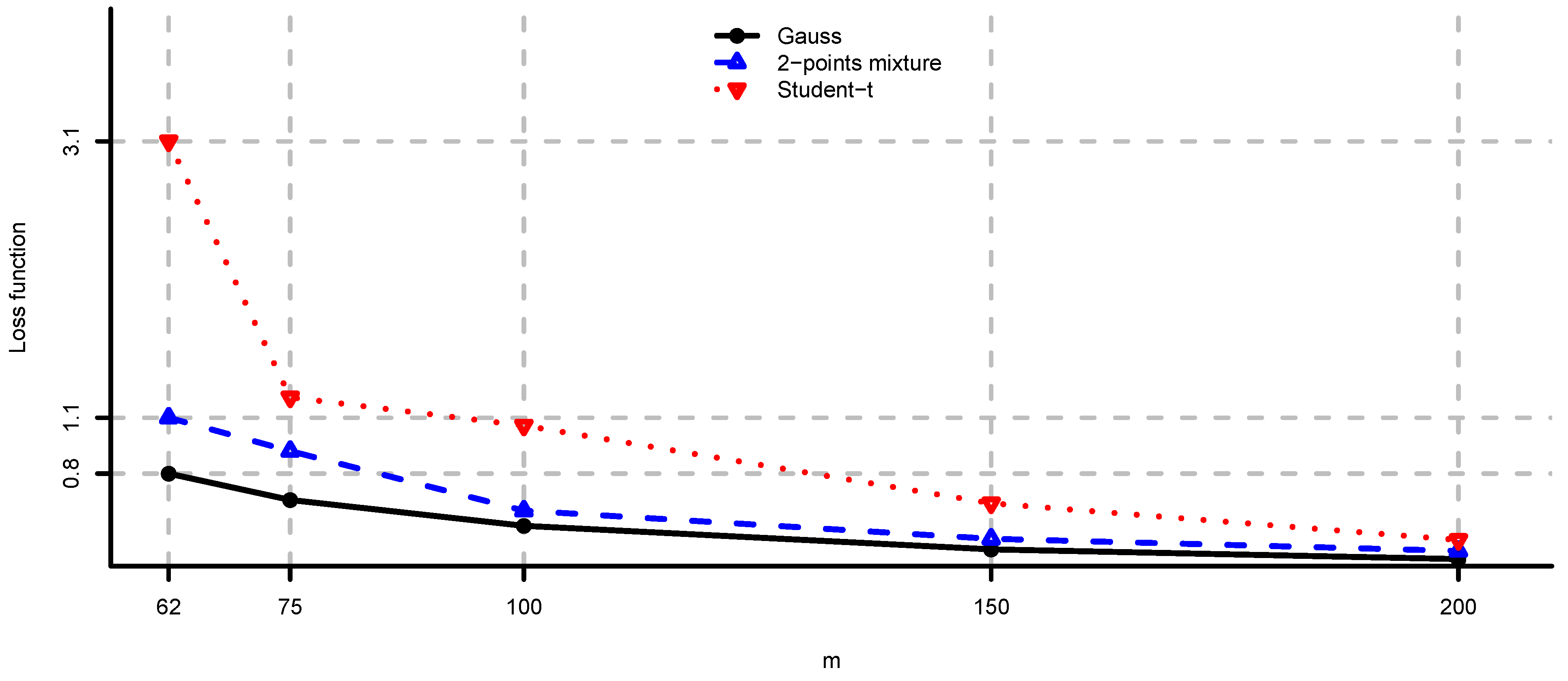
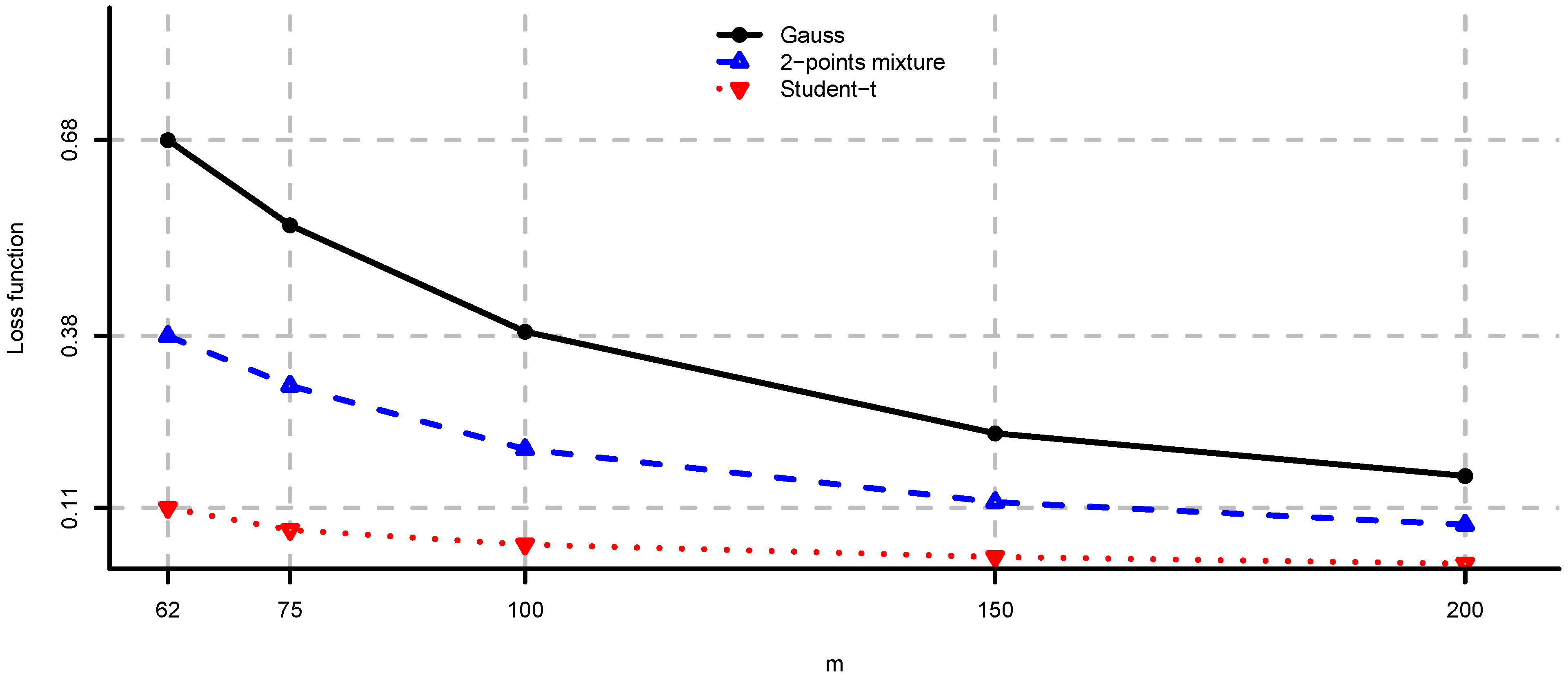
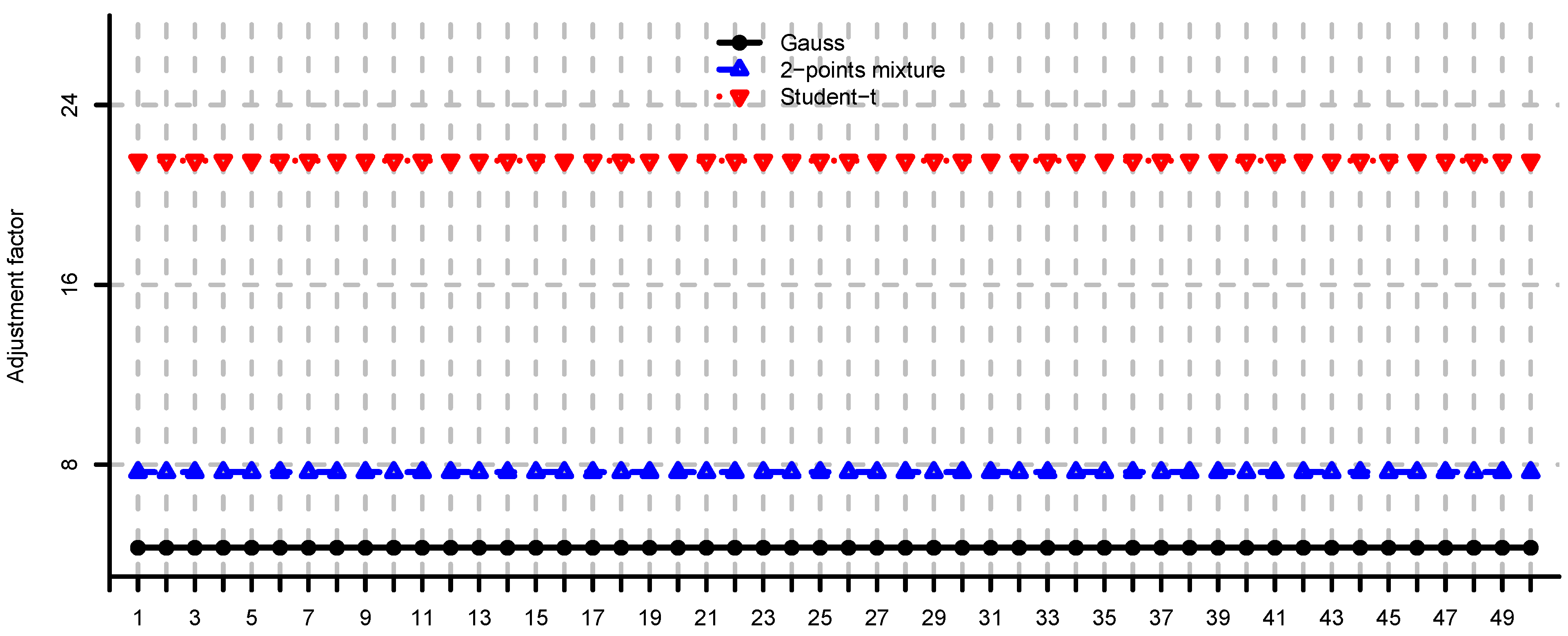
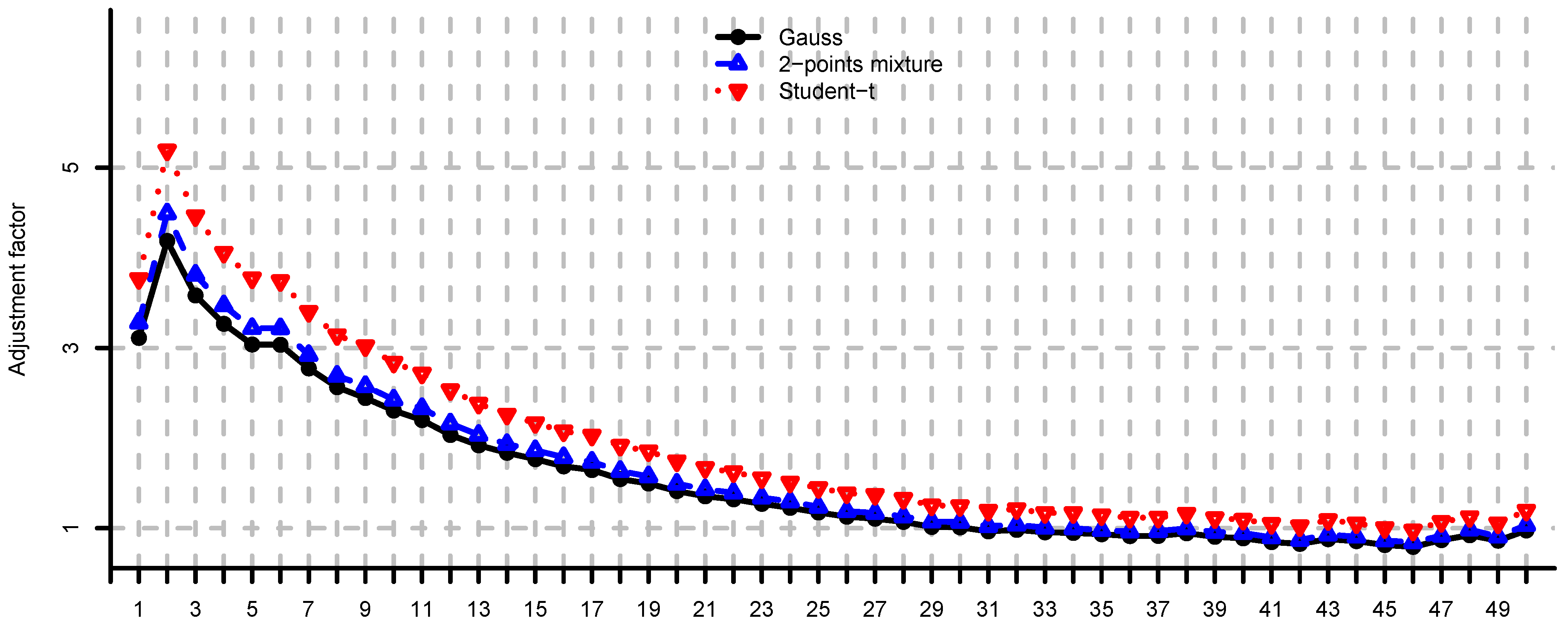
5.2. Large-Cap U.S. Equity Portfolios
- (i)
- The classical mean-variance portfolio based on the sample estimators and .
- (ii)
- Portfolio based on the estimators and , where is determined by Equation (7) under a multivariate Gaussian model.
- (iii)
- As in (ii), where is determined by Equation (7) under a multivariate Student-t model.
- (iv)
- Portfolio based on the estimators and , where are determined numerically by Equation (12) under a multivariate Gaussian model.
- (v)
- As in (iv), where are determined numerically by Equation (12) under a multivariate Student-t model.
| Return Annualized | Volatility Annualized | Sharpe Ratio | Maximum Drawdown | Average Turnover | Average Diversification | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (i) | (ii) | (iii) | (i) | (ii) | (iii) | (i) | (ii) | (iii) | (i) | (ii) | (iii) | (i) | (ii) | (iii) | (i) | (ii) | (iii) | |
| All | 7.63 | 8.03 | 8.66 | 15.06 | 15.01 | 15.00 | 0.51 | 0.53 | 0.58 | 47.80 | 47.16 | 45.31 | 13.38 | 12.78 | 12.25 | 10.05 | 10.10 | 10.15 |
| 2011 | 10.85 | 11.85 | 12.01 | 14.09 | 13.97 | 13.88 | 0.77 | 0.85 | 0.87 | 10.04 | 9.58 | 9.75 | 13.75 | 12.95 | 12.31 | 8.87 | 8.98 | 9.05 |
| 2010 | 9.13 | 9.26 | 8.90 | 11.12 | 10.97 | 10.86 | 0.82 | 0.84 | 0.82 | 7.63 | 7.35 | 7.33 | 10.39 | 9.94 | 9.80 | 7.74 | 7.88 | 8.05 |
| 2009 | 22.10 | 21.35 | 24.27 | 17.94 | 18.05 | 18.19 | 1.23 | 1.18 | 1.33 | 19.56 | 20.06 | 18.83 | 10.84 | 10.69 | 10.28 | 9.66 | 9.57 | 9.54 |
| 2008 | −27.67 | −26.57 | −25.93 | 28.82 | 28.74 | 28.91 | neg | neg | neg | 39.68 | 38.59 | 38.05 | 12.95 | 12.31 | 11.60 | 8.03 | 7.97 | 7.94 |
| 2007 | 10.29 | 10.06 | 10.72 | 11.33 | 11.23 | 11.09 | 0.91 | 0.90 | 0.97 | 7.05 | 6.87 | 6.70 | 14.27 | 13.27 | 12.80 | 8.39 | 8.34 | 8.38 |
| 2006 | 9.30 | 10.04 | 10.91 | 8.05 | 7.96 | 7.89 | 1.16 | 1.26 | 1.38 | 5.93 | 5.37 | 4.78 | 15.06 | 13.62 | 12.40 | 8.43 | 8.23 | 8.03 |
| 2005 | 1.66 | 2.02 | 1.94 | 9.59 | 9.51 | 9.41 | 0.17 | 0.21 | 0.21 | 7.29 | 6.79 | 6.62 | 15.75 | 15.16 | 14.48 | 9.38 | 9.47 | 9.53 |
| 2004 | 9.17 | 9.76 | 10.38 | 9.45 | 9.35 | 9.26 | 0.97 | 1.04 | 1.12 | 7.68 | 7.18 | 6.79 | 14.28 | 13.50 | 12.59 | 8.52 | 8.68 | 8.86 |
| 2003 | 20.49 | 21.05 | 21.44 | 12.16 | 12.10 | 12.07 | 1.69 | 1.74 | 1.78 | 8.57 | 8.59 | 8.80 | 13.03 | 12.64 | 12.05 | 9.24 | 9.20 | 9.15 |
| 2002 | −13.33 | −13.29 | −12.20 | 18.12 | 18.25 | 18.26 | neg | neg | neg | 27.35 | 27.56 | 27.19 | 12.33 | 12.05 | 11.74 | 9.39 | 9.52 | 9.56 |
| 2001 | −7.23 | −6.52 | −5.41 | 13.97 | 13.89 | 13.94 | neg | neg | neg | 16.49 | 16.20 | 16.00 | 13.93 | 13.45 | 13.14 | 11.85 | 11.93 | 12.02 |
| 2000 | 6.64 | 6.29 | 6.83 | 17.99 | 17.99 | 18.01 | 0.37 | 0.35 | 0.38 | 22.37 | 22.42 | 22.34 | 14.70 | 14.49 | 13.95 | 12.80 | 12.94 | 13.00 |
| 1999 | −2.76 | −1.62 | −0.41 | 15.32 | 15.30 | 15.25 | neg | neg | neg | 15.12 | 14.52 | 14.01 | 14.45 | 13.77 | 13.47 | 12.00 | 12.16 | 12.35 |
| 1998 | 18.57 | 19.22 | 19.09 | 17.63 | 17.57 | 17.61 | 1.05 | 1.09 | 1.08 | 17.41 | 17.57 | 17.88 | 13.82 | 13.53 | 13.35 | 11.09 | 10.99 | 10.92 |
| 1997 | 26.78 | 26.58 | 26.09 | 15.91 | 15.76 | 15.59 | 1.68 | 1.69 | 1.67 | 8.05 | 8.07 | 8.13 | 12.54 | 11.82 | 11.12 | 11.32 | 11.31 | 11.25 |
| 1996 | 18.62 | 19.32 | 20.01 | 12.01 | 11.94 | 11.88 | 1.55 | 1.62 | 1.68 | 7.33 | 7.13 | 7.17 | 14.93 | 14.22 | 13.70 | 12.03 | 12.33 | 12.61 |
| 1995 | 17.80 | 18.60 | 19.35 | 7.76 | 7.60 | 7.47 | 2.29 | 2.45 | 2.59 | 3.77 | 3.72 | 3.78 | 9.72 | 9.26 | 8.83 | 12.92 | 13.15 | 13.40 |
| Return annualized | Volatility annualized | Sharpe ratio | Maximum drawdown | Average turnover | Average diversification | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (i) | (iv) | (v) | (i) | (iv) | (v) | (i) | (iv) | (v) | (i) | (iv) | (v) | (i) | (iv) | (v) | (i) | (iv) | (v) | |
| All | 7.63 | 7.64 | 9.34 | 15.06 | 14.74 | 14.55 | 0.51 | 0.52 | 0.64 | 47.80 | 45.43 | 41.17 | 13.38 | 11.40 | 9.55 | 10.05 | 11.78 | 12.13 |
| 2011 | 10.85 | 11.46 | 13.43 | 14.09 | 13.95 | 13.35 | 0.77 | 0.82 | 1.01 | 10.04 | 10.10 | 9.65 | 13.75 | 11.63 | 8.65 | 8.87 | 10.19 | 10.64 |
| 2010 | 9.13 | 9.42 | 7.85 | 11.12 | 10.83 | 10.43 | 0.82 | 0.87 | 0.75 | 7.63 | 7.09 | 6.83 | 10.39 | 9.34 | 8.34 | 7.74 | 8.26 | 8.32 |
| 2009 | 22.10 | 17.63 | 18.27 | 17.94 | 16.48 | 16.00 | 1.23 | 1.07 | 1.14 | 19.56 | 19.49 | 19.72 | 10.84 | 8.77 | 7.83 | 9.66 | 10.94 | 10.13 |
| 2008 | −27.67 | −25.08 | −20.81 | 28.82 | 28.09 | 28.06 | neg | neg | neg | 39.68 | 37.17 | 33.29 | 12.95 | 11.06 | 10.74 | 8.03 | 9.05 | 8.48 |
| 2007 | 10.29 | 11.40 | 13.34 | 11.33 | 11.23 | 10.77 | 0.91 | 1.02 | 1.24 | 7.05 | 6.67 | 5.60 | 14.27 | 12.58 | 9.21 | 8.39 | 9.82 | 9.91 |
| 2006 | 9.30 | 9.41 | 12.84 | 8.05 | 7.98 | 7.80 | 1.16 | 1.18 | 1.65 | 5.93 | 6.12 | 4.26 | 15.06 | 12.41 | 9.22 | 8.43 | 11.00 | 11.12 |
| 2005 | 1.66 | 2.60 | 0.69 | 9.59 | 9.55 | 9.28 | 0.17 | 0.27 | 0.07 | 7.29 | 6.80 | 7.42 | 15.75 | 13.71 | 11.14 | 9.38 | 11.37 | 11.87 |
| 2004 | 9.17 | 9.63 | 10.66 | 9.45 | 9.39 | 9.10 | 0.97 | 1.03 | 1.17 | 7.68 | 7.27 | 6.63 | 14.28 | 12.32 | 9.32 | 8.52 | 10.48 | 11.45 |
| 2003 | 20.49 | 20.85 | 22.23 | 12.16 | 11.98 | 11.90 | 1.69 | 1.74 | 1.87 | 8.57 | 7.95 | 8.03 | 13.03 | 11.12 | 9.81 | 9.24 | 10.07 | 9.54 |
| 2002 | −13.33 | −15.84 | −15.64 | 18.12 | 17.72 | 18.16 | neg | neg | neg | 27.35 | 28.48 | 29.53 | 12.33 | 10.59 | 9.98 | 9.39 | 9.95 | 10.26 |
| 2001 | −7.23 | −10.55 | −5.53 | 13.97 | 13.75 | 13.67 | neg | neg | neg | 16.49 | 17.88 | 15.71 | 13.93 | 10.92 | 9.44 | 11.85 | 13.61 | 14.53 |
| 2000 | 6.64 | 8.22 | 11.63 | 17.99 | 17.71 | 17.74 | 0.37 | 0.46 | 0.66 | 22.37 | 21.88 | 21.99 | 14.70 | 12.09 | 10.29 | 12.80 | 16.04 | 17.02 |
| 1999 | −2.76 | −0.29 | 4.73 | 15.32 | 14.97 | 14.79 | neg | neg | 0.32 | 15.12 | 13.74 | 10.51 | 14.45 | 11.69 | 9.65 | 12.00 | 14.46 | 14.84 |
| 1998 | 18.57 | 16.90 | 15.64 | 17.63 | 17.57 | 17.45 | 1.05 | 0.96 | 0.90 | 17.41 | 18.08 | 18.41 | 13.82 | 12.30 | 11.17 | 11.09 | 12.08 | 11.89 |
| 1997 | 26.78 | 26.78 | 27.04 | 15.91 | 15.78 | 15.10 | 1.68 | 1.70 | 1.79 | 8.05 | 7.86 | 7.87 | 12.54 | 10.87 | 8.82 | 11.32 | 12.65 | 12.57 |
| 1996 | 18.62 | 18.54 | 22.43 | 12.01 | 12.03 | 11.77 | 1.55 | 1.54 | 1.91 | 7.33 | 6.94 | 7.78 | 14.93 | 13.33 | 11.13 | 12.03 | 15.06 | 16.62 |
| 1995 | 17.80 | 19.73 | 20.95 | 7.76 | 7.73 | 7.10 | 2.29 | 2.55 | 2.95 | 3.77 | 3.62 | 4.05 | 9.72 | 8.49 | 6.94 | 12.92 | 16.74 | 19.58 |
Author Contributions
Appendix
1. Proofs
1.1. Proof of Proposition 1
1.2. Proof of Theorem 2
1.3. Proof of Corollary 1
- (i)
- Multivariate Gauss: the statement follows directly setting .
- (ii)
- 2-points mixture: set , where and . Then, and .
- (iii)
- Multivariate Student-t: set . Then, , .
1.4. Proof of Corollary 2
1.5. Proof of Proposition 3
1.6. Proof of Theorem 4
1.7. Proof of Theorem 5
2. Wishart Distribution
- (i)
- ; and
- (ii)
- ;
3. Equity Universe for Case Studies
| Nr. | Company | Bloomberg Ticker | Industry Sector |
|---|---|---|---|
| 1 | Wells Fargo & Company | WFC US Equity | financials |
| 2 | JP Morgan Chase & Co. | JPM US Equity | financials |
| 3 | Citigroup, Inc. | C US Equity | financials |
| 4 | Bank of America Corporation | BAC US Equity | financials |
| 5 | American Express Company | AXP US Equity | financials |
| 6 | American International Group | AIG US Equity | financials |
| 7 | PNC Financial Services Group | PNC US Equity | financials |
| 8 | General Electric Company | GE US Equity | industrials |
| 9 | United Technologies Corporation | UTX US Equity | industrials |
| 10 | 3M Company | MMM US Equity | industrials |
| 11 | Caterpillar, Inc. | CAT US Equity | industrials |
| 12 | Boeing Company | BA US Equity | industrials |
| 13 | Union Pacific Corporation | UNP US Equity | industrials |
| 14 | Honeywell International | HON US Equity | industrials |
| 15 | Wal-Mart Stores, Inc. | WMT US Equity | consumer staples |
| 16 | McDonald’s Corporation | MCD US Equity | consumer discretionary |
| 17 | Comcast Corporation | CMCSA US Equity | consumer discretionary |
| 18 | Walt Disney Company | DIS US Equity | consumer discretionary |
| 19 | Home Depot, Inc. | HD US Equity | consumer discretionary |
| 20 | CVS Caremark Corporation | CVS US Equity | consumer staples |
| 21 | Costco Wholesale Corporation | COST US Equity | consumer staples |
| 22 | Apple Inc. | AAPL US Equity | information technology |
| 23 | Microsoft Corporation | MSFT US Equity | information technology |
| 24 | International Business Machines (IBM) | IBM US Equity | information technology |
| 25 | Oracle Corporation | ORCL US Equity | information technology |
| 26 | Intel Corporation | INTC US Equity | information technology |
| 27 | Hewlett-Packard Company | HPQ US Equity | information technology |
| 28 | EMC Corporation Common | EMC US Equity | information technology |
| 29 | Exxon Mobil Corporation | XOM US Equity | energy |
| 30 | Chevron Corporation Common | CVX US Equity | energy |
| 31 | Schlumberger N.V. | SLB US Equity | energy |
| 32 | ConocoPhillips | COP US Equity | energy |
| 33 | Occidental Petroleum | OXY US Equity | energy |
| 34 | Anadarko Petroleum | APC US Equity | energy |
| 35 | Apache Corporation | APA US Equity | energy |
| 36 | Procter & Gamble Company | PG US Equity | consumer staples |
| 37 | Coca-Cola Company | KO US Equity | consumer staples |
| 38 | Pepsico, Inc. | PEP US Equity | consumer staples |
| 39 | Altria Group, Inc. | MO US Equity | consumer staples |
| 40 | Colgate-Palmolive Company | CL US Equity | consumer staples |
| 41 | Ford Motor Company | F US Equity | consumer discretionary |
| 42 | Nike, Inc. | NKE US Equity | consumer discretionary |
| 43 | Kimberly-Clark Corporation | KMB US Equity | consumer staples |
| 44 | Johnson & Johnson | JNJ US Equity | health care |
| 45 | Pfizer, Inc. Common Stock | PFE US Equity | health care |
| 46 | Merck & Company, Inc. | MRK US Equity | health care |
| 47 | Abbott Laboratories | ABT US Equity | health care |
| 48 | Bristol-Myers Squibb Company | BMY US Equity | health care |
| 49 | Amgen Inc. | AMGN US Equity | health care |
| 50 | UnitedHealth Group | UNH US Equity | health care |
Conflicts of Interest
References
- H.M. Markowitz. “Mean-variance analysis in portfolio choice and capital markets.” J. Financ. 7 (1952): 77–91. [Google Scholar]
- R. Michaud. “The Markowitz optimization enigma: Is "optimized" optimal? ” Financ. Anal. J. 45 (1989): 31–42. [Google Scholar] [CrossRef]
- B. Litterman. Modern Investment Management: An Equilibrium Approach. New York, NY, USA: Wiley, 2003. [Google Scholar]
- A. Meucci. Risk and Asset Allocation. Berlin, Germany: Springer, 2007. [Google Scholar]
- Y. Choueifaty, and Y. Coignard. “Toward maximum diversification.” J. Portf. Manag. 35 (2008): 40–51. [Google Scholar] [CrossRef]
- S. Maillard, T. Roncalli, and J. Teiletche. “The properties of equally weighted risk contribution portfolios.” J. Portf. Manag. 36 (2010): 60–70. [Google Scholar] [CrossRef]
- R. Clarke, H. de Silva, and S. Thorley. “Risk parity, maximum diversification, and minimum variance: An analytic perspective.” J. Portf. Manag. 39 (2013): 39–53. [Google Scholar] [CrossRef]
- S.J. Brown. “Optimal portfolio choice under uncertainty: A Bayesian approach.” Ph.D. Thesis, University of Chicago, Chicago, IL, USA, 1976. [Google Scholar]
- S.J. Brown. “The portfolio choice problem: Comparison of certainty equivalence and optimal Bayes portfolios.” Commun. Stat. Simul. Comput. 7 (1978): 321–334. [Google Scholar] [CrossRef]
- R.W. Klein, and V.S. Bawa. “The effect of estimation risk on optimal portfolio choice.” J. Financ. Econ. 3 (1976): 215–231. [Google Scholar] [CrossRef]
- S. Kandel, and R.F. Stambaugh. “On the predictability of stock returns: An asset-allocation perspective.” J. Financ. 51 (1996): 385–424. [Google Scholar] [CrossRef]
- N. Barberis. “Investing for the long run when returns are predictable.” J. Financ. 55 (2000): 225–264. [Google Scholar] [CrossRef]
- L. Pástor. “Portfolio selection and asset pricing models.” J. Financ. 55 (2000): 179–223. [Google Scholar] [CrossRef]
- L. Pástor, and R.F. Stambaugh. “Comparing asset pricing models: An investment perspective.” J. Financ. Econ. 56 (2000): 335–381. [Google Scholar] [CrossRef]
- L. Xia. “Learning about predictability: The effect of parameter uncertainty on dynamic asset allocation.” J. Financ. 56 (2001): 205–246. [Google Scholar] [CrossRef]
- J. Tu, and G. Zhou. “Data-generating process uncertainty: What difference does it make in portfolio decisions? ” J. Financ. Econ. 72 (2004): 385–421. [Google Scholar] [CrossRef]
- J.D. Jobson, B. Korkie, and V. Ratti. “Improved Estimation for Markowitz Portfolios Using James-Stein Type Estimators.” In Proceedings of Business and Economics Statistics Section. Boston, MA, USA: American Statistical Association, 1979, Volume 41, pp. 279–284. [Google Scholar]
- P. Jorion. “Bayes-Stein estimation for portfolio analysis.” J. Financ. Quant. Anal. 21 (1986): 279–292. [Google Scholar] [CrossRef]
- P.A. Frost, and J.E. Savarino. “An empirical Bayes approach to efficient portfolio selection.” J. Financ. Quant. Anal. 21 (1986): 293–305. [Google Scholar] [CrossRef]
- J.R. Ter Horst, F.A. de Roon, and B.J.M. Werker. “An Alternative Approach to Estimation Risk.” 2004. Available online: http://citeseerx.ist.psu.edu (accessed on 9 September 2013).
- R. Kan, and G. Zhou. “Portfolio choice with parameter uncertainty.” J. Financ. Quant. Anal. 42 (2007): 621–656. [Google Scholar] [CrossRef]
- J.D. Jobson, and B. Korkie. “Estimation for Markowitz efficient portfolios.” J. Am. Stat. Assoc. 75 (1980): 544–554. [Google Scholar] [CrossRef]
- H. Mori. “Finite sample properties of estimators for the optimal portfolio weights.” Jpn. Stat. Soc. 34 (2004): 27–46. [Google Scholar] [CrossRef]
- I. Kondor, S. Pafka, and G. Nagy. “Noise sensitivity of portfolio selection under various risk measures.” J. Bank. Financ. 31 (2007): 1545–1573. [Google Scholar] [CrossRef]
- Y. Simaan. “The opportunity cost of mean-variance choice under estimation risk.” Eur. J. Oper. Res. 234 (2014): 382–391. [Google Scholar] [CrossRef]
- O. Ledoit, and M. Wolf. “A well conditioned estimator for large dimensional covariance matrices.” J. Multivar. Anal. 88 (2004): 365–411. [Google Scholar] [CrossRef]
- V. DeMiguel, J. Nogales, and R. Uppal. “A generalized approach to portfolio optimization: Improving performance by constraining portfolio norms.” Manag. Sci. 55 (2009): 798–812. [Google Scholar] [CrossRef]
- X. Zhou, D. Malioutov, F.J. Fabozzi, and S.T. Rachev. “Smooth monotone covariance for elliptical distributions and applications in finance.” Quant. Financ., 2014, in press. [Google Scholar] [CrossRef]
- N. El Karoui. “High-dimensionality effects in the Markowitz problem and other quadratic programs with linear constraints: Risk underestimation.” Ann. Stat. 38 (2009): 3487–3566. [Google Scholar] [CrossRef]
- N. El Karoui. “On the Realized Risk of High-Dimensional Markowitz Portfolios.” 2010. Available online: http://stat-reports.lib.berkeley.edu/accessPages/784.html (accessed on 17 September 2013).
- D. Goldfarb, and G. Iyengar. “Robust portfolio selection problems.” Math. Oper. Res. 28 (2003): 1–38. [Google Scholar] [CrossRef]
- A.J. McNeil, R. Frey, and P. Embrechts. Quantitative Risk Management. Princeton, NJ, USA: Princeton University Press, 2005. [Google Scholar]
- I. Johnstone. “On the distribution of the largest eigenvalue in principal components analysis.” Ann. Stat. 29 (2001): 295–327. [Google Scholar] [CrossRef]
- N. El Karoui. “Spectrum estimation for large dimensional covariance matrices using random matrix theory.” Ann. Stat. 36 (2008): 2757–2790. [Google Scholar] [CrossRef]
- O. Ledoit, and M. Wolf. “Nonlinear shrinkage estimation of large-dimensional covariance matrices.” Ann. Stat. 40 (2012): 1024–1060. [Google Scholar] [CrossRef]
- V.A. Marchenko, and L.A. Pastur. “Distribution of eigenvalues for some sets of random matrices.” Mat. Sb. 72 (1967): 507–536. [Google Scholar]
- G. Papp, S. Pafka, M.A. Nowak, and I. Kondor. “Random matrix filtering in portfolio optimization.” Acta Phys. Pol. B 36 (2005): 2757–2765. [Google Scholar]
- J. Menchero, J. Wang, and D.J. Orr. “Eigen-adjusted covariance matrices.” 2011, SSRN:1915318. [Google Scholar]
- P.G. Shepard. “Second order risk.” 2009, arXiv:0908.2455. [Google Scholar]
- D. De Giovanni, S. Ortobelli, and S. Rachev. “Delta hedging strategies comparison.” Eur. J. Oper. Res. 185 (2008): 1615–1631. [Google Scholar] [CrossRef]
- E. Pantaleo, M. Tumminello, F. Lillo, and R.N. Mantegna. “When do improved covariance matrix estimators enhance portfolio optimization? An empirical comparative study of nine estimators.” Quant. Financ. 11 (2011): 1067–1080. [Google Scholar] [CrossRef]
- K.V. Mardia, J.T. Kent, and J.M. Bibby. Multivariate Analysis. San Diego, CA, USA: Academic Press, 1979. [Google Scholar]
- L.R. Haff. “An identity for the Wishart distribution with applications.” J. Multivar. Anal. 9 (1979): 531–544. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanovits, D.; Schubiger, U.; Wüthrich, M.V. Model Risk in Portfolio Optimization. Risks 2014, 2, 315-348. https://doi.org/10.3390/risks2030315
Stefanovits D, Schubiger U, Wüthrich MV. Model Risk in Portfolio Optimization. Risks. 2014; 2(3):315-348. https://doi.org/10.3390/risks2030315
Chicago/Turabian StyleStefanovits, David, Urs Schubiger, and Mario V. Wüthrich. 2014. "Model Risk in Portfolio Optimization" Risks 2, no. 3: 315-348. https://doi.org/10.3390/risks2030315
APA StyleStefanovits, D., Schubiger, U., & Wüthrich, M. V. (2014). Model Risk in Portfolio Optimization. Risks, 2(3), 315-348. https://doi.org/10.3390/risks2030315




