Tail Risk in Commercial Property Insurance

Abstract

We present some new evidence on the tail distribution of commercial property losses based on a recently constructed dataset on large commercial risks. The dataset is based on contributions from Lloyd’s of London syndicates, and provides information on over three thousand claims occurred during the period 2000–2012, including detailed information on exposures. We use occupancy characteristics to compare the tail risk profiles of different commercial property exposures, and find evidence of substantial heterogeneity in tail behavior. The results demonstrate the benefits of aggregating granular information on both claims and exposures from different data sources, and provide warning against the use of reserving and capital modeling approaches that are not robust to heavy tails.

1. Introduction

Property and business interruption risks represent roughly a third,1 or USD 175 billion, of direct insurance premiums written in commercial insurance lines worldwide (see [1]). The latter also include liability insurance, commercial auto insurance, and specialty lines such as off-shore energy and workers’ compensation.2 Property insurance typically includes fire insurance, which offers protection against fire and lightning, but may also provide additional cover against natural and social perils such as wind, flood, and vandalism. Business interruption is a complementary insurance covering the expenses and losses incurred when business is interrupted and damages are being repaired. The demand for commercial property insurance is dominated by medium and large corporations that need to insure complex, high severity risks. The largest property insurance markets in the world are the US3 and the UK.4

Despite their relevance for the corporate sector and (re)insurers operating in commercial insurance lines, large commercial property risks are poorly understood. This is due to the limited public information available on property losses and exposures, the heterogeneity of risk characteristics of insured values, and the complex relation between hazard events and realized losses, as small events may often precipitate major disasters. These factors make it difficult for insurers to build reliable statistical claims information, whereas companies that have larger insurance portfolios and more sophisticated claims reporting systems have no incentive to disclose information for competitive reasons. The literature on the subject is scant. The few methodological contributions available emphasize the challenges of pricing high layers of exposure, and offer insights into the blending of exposure and experience rating (see [2,3,4]). As a result, the insurance industry is overly reliant on underwriters’ judgment and recent claims history, and finds it difficult to properly understand the true risk that it is taking on. On the demand side, the excessive weight placed on reported claims and the variability of pricing schedules across exposures result in a considerable degree of price volatility, which makes it challenging for corporates to budget for insurance purchases on a systematic basis.5

In this paper, we shed some light on the tail distribution of commercial property risks by using a recently constructed dataset on large commercial risks. This new data source is based on information collected from two leading Lloyd’s syndicates writing a total of GBP 2.67bn gross premiums across all lines of business in 2012, a figure representing around 10% of Lloyd’s gross premiums that year. As Lloyd’s is predominantly a subscription market, the claims information provided by the two syndicates allows us to encompass a substantially larger fraction of business transacted, making the dataset representative of the business written in the London market.6

To measure the tail risk of commercial property exposures, we use a parsimonious model based on approximating the tail behavior of the claims with a power law. In particular, we estimate the tail index, a parameter describing how fast the tail of a power law decays: the lower the tail index, the greater the probability mass in the tails. To ensure robustness relative to small sample bias, heterogeneity, and dependence of the claims considered, we resort to the log-log rank-size method, as presented by Gabaix and Ibragimov [6], and discussed more in detail in Section 3 below. As a robustness check, we also apply the method of Huisman et al. [7], which is designed to address small sample issues (see Section 3.3 for a review of alternative approaches). Estimation of the tail index offers immediate insights for pricing, reserving, and capital modeling exercises. In particular, the value of the tail index is in one-to-one correspondence with the maximal order of finite (centered) moments of the risks considered. For example, the skewness only exists for values of the tail index strictly larger than three; the variance only exists for values strictly larger than two; and the mean only exists for values strictly larger than one (e.g., [8,9]). The tail index can be regarded as being infinite for Normal distributions, as the tail decay is faster than exponential, and moments of an arbitrary order are then finite. In our data, we find that commercial property risks are significantly heavy tailed. For several rating factor configurations, the hypothesis of existence of the variance can be rejected at the 5% significance level. For some important classes of risk, even the hypothesis of existence of the mean can be rejected.7

Existence of a finite variance is essential for the application of standard statistical methods, such as least squares methods. It is also crucial for reserving methods based on risk margins proportional to the standard deviation of the claims,8 meaning that such methods are inappropriate for liabilities modeled by extrapolating available claims information far into the tails. Existence of a finite mean is important for capital modeling and quantile-based risk measures, such as Value at Risk (VaR) in the Solvency II framework. In particular, coherence of VaR as a risk measure in the sense of Artzner et al. [13] may be violated, meaning that the diversification benefits on which a subscription market like Lloyd’s is based may be limited for some classes of commercial property risks. As an example, denote by the random variable $Z_{(w_1,\dots ,w_n)}:={\sum }_{i=1}^n{w}_i{X}_i$ the risk exposure resulting from retaining fractions $w_1,\dots ,w_n$ (with $w_i\in [0,1]$, $i=1,\dots ,n$) of i.i.d. risks $X_1,\dots ,X_n$. If the risks belong to the class of stable distributions with tail index α, for example, it can be shown that $Va{R}_q\left(Z_{(1,0,\dots ,0)}\right)<Va{R}_q\left(Z_{(1/n,\dots ,1/n)}\right)$ for tail probability parameter $q\in (0,1/2)$ and tail index value $\alpha \in (0,1)$ (see [14,15]). Regulators should therefore be aware of the risk concentration incentives that may arise from commercial property exposures. Similarly, (re)insurers should tread carefully with high layers of exposure in that space, as internal capital charges may underestimate the true risk being taken on.

On the methodological side, we need to deal with potential issues arising from the structure of the data. Although our dataset is large relative to extant data sources,9 we are still faced with small sample estimation challenges, in particular when conditioning on relevant rating factors. Moreover, the observed losses may have a dependence structure induced by the underwriting strategies pursued by the syndicates during the sampling period. We address these issues by using the log-log rank-size regression method with the optimal rank shift indicated by Gabaix and Ibragimov [6]. As demonstrated by these authors, their adjustment optimally reduces the bias arising in small samples, and delivers estimates robust to the presence of heterogeneity and dependency in the data, including common factors. For comparison, we pair this method with the popular Hill [17] estimator, and the weighted-Hill estimator of Huisman et al. [7], which was specifically designed to address small sample issues. The results allow us to reject the hypothesis of existence of first or second moments at a good significance level in some interesting cases. Finally, we explore the relative contribution of different rating factors to tail risk, by expressing the tail index as a deterministic function of relevant covariates, and adopting a regression approach in line with Beirlant et al. [18], Beirlant and Goegebeur [19], and Wang and Tsai [20].

The paper is organized as follows. In the next section, we provide details on the dataset. In Section 3, we outline the statistical methodologies used. In Section 4, we provide tail estimation results for some configurations of exposure characteristics. Section 5 concludes, offering recommendations for future research.

2. Data

The Imperial-IICI dataset contains claim and exposure information obtained from two leading syndicates of Lloyd’s of London. As the latter is a subscription market, the data span business written by a number of other syndicates. Granular information on claims and exposures was obtained from brokers’ submissions. These are documents informing the ‘lead’ underwriter of any claims occurring under a policy; the information is then shared with the market, in order to allocate the losses to each ‘follower’, depending on the individual retentions of the syndicates that co-insured the risk underwritten by the ‘lead’. Brokers’ submissions are fundamental in our analysis, as they allow us to determine claims from the ground up (FGU). It is in general very difficult to recover FGU claims from the losses incurred by individual syndicates, due to the complex layering and coinsurance arrangements characterizing large commercial property insurance. All data were anonymized and aggregated by using fictitious claims and policy identifiers. Internal validation of the data was carried out by looking at individual claims narratives and policy schedules, which are documents listing the asset values insured under a policy. External macro-validation was carried out by using data from fire protection agencies as compiled by ISO Verisk.10

The Imperial-IICI FGU claims provide aggregate information on indemnities for physical damage and business interruption, as well as claims assessment and settlement fees. Both claims and exposures are expressed in 2012 USD terms;11 the normalization is obtained by trending claims and exposures at an average rate of 2.5% per annum across the two syndicates. An example of data record is presented in Table 1. The record reports location information, and classifies the risk type according to the Lloyd’s risk codes (a selection of these codes is presented in Table 2). The claim can be further understood by using occupancy type information, which has three levels of increasing granularity. The first one broadly classifies exposures into commercial (e.g., offices, banks, stores), manufacturing (e.g., utilities, food processors, mines), and residential property (e.g., hotels, hospitals). The second level provides some more detail according to the definitions reported in Table 3, allowing one to distinguish, for example, a hotel from a hospital, or metals from food producers. The third occupancy level offers a more granular view of the exposures, distinguishing for example between large vs. small hotels, heavy vs. light fabrication infrastructure, and food & drugs vs. chemicals vs. metal & minerals processing plants. Finally, occupancy information is complemented by the claim narrative, which may also provide some indications on the hazard event (e.g., burst of waterpipe, electrical failure, fire from hotel restaurant).

Table 4 gives an idea of the geographical distribution of the losses. Although the dataset has global scope, the largest subsample is represented by North American data. The Worldwide data class is currently being analyzed at a deeper level, and might result in the allocation of claims to more precise locations in the future. In Figure 1, we give an idea of the claim counts and average FGU losses in excess of different thresholds. Information on claim counts by year and occcupancy level 2 information is reported in Table 5.

Table 1. Example of data record, with three levels of occupancy information.

Region	Country	Risk Code	Occupancy 1	Occupancy 2	Occupancy 3
NoA	US	P2	RE	R	51
		(Physical damage; primary layer property; USA; excluding binders)	(residential)	(residential)	(Large Hotels)

Table 1. Example of data record, with three levels of occupancy information.

Region	Country	Risk Code	Occupancy 1	Occupancy 2	Occupancy 3
NoA	US	P2	RE	R	51
		(Physical damage; primary layer property; USA; excluding binders)	(residential)	(residential)	(Large Hotels)

Table 2. Selection of Lloyd’s risk codes with relevant definitions.

Risk Code	Definition
B2	Physical damage; private property; USA; binder
B3	Physical damage; commercial property; USA; binder
B4	Physical damage; private property; excluding USA; binder
B5	Physical damage; commercial property; excluding USA; binder
P2	Physical damage; primary layer property; USA; excluding binders
P3	Physical damage; primary layer property; excluding USA; excluding binders
P4	Physical damage; full value of property; USA; excluding binders
P5	Physical damage; full value of property; excluding USA; excluding binders
P6	Physical damage; excess layer property; USA; excluding binders
P7	Physical damage; excess layer property; excluding USA; excluding binders
PG	Operational power generation, transmission, and utilities; excluding construction

Table 2. Selection of Lloyd’s risk codes with relevant definitions.

Risk Code	Definition
B2	Physical damage; private property; USA; binder
B3	Physical damage; commercial property; USA; binder
B4	Physical damage; private property; excluding USA; binder
B5	Physical damage; commercial property; excluding USA; binder
P2	Physical damage; primary layer property; USA; excluding binders
P3	Physical damage; primary layer property; excluding USA; excluding binders
P4	Physical damage; full value of property; USA; excluding binders
P5	Physical damage; full value of property; excluding USA; excluding binders
P6	Physical damage; excess layer property; USA; excluding binders
P7	Physical damage; excess layer property; excluding USA; excluding binders
PG	Operational power generation, transmission, and utilities; excluding construction

Table 3. Occupancy Level 2 definitions.

Code	Definition	Code	Definition
A	Miscellaneous	Q	Offices/Banks
B	Manufacturers/Processors	R	Residential
C	Chemicals/Pharmaceuticals	T	Transport
D	Bridges/Dams/Tunnels/Piers	U	Utilities
E	Conglomerates	V	Telecoms and Data Processing
F	Food	W	Woodworkers (Sawmills, Papermills)
G	Grain	X	Onshore Crude
H	General Mercantile/Shops	Y	Onshore GasPlants
J	Mines	Z	Onshore Construction
K	Crops	2	Hospital/Health care centres
L	Auto	4	Semiconductor/Fabs
M	Metals	5	Motor Manufaturers
O	Municipal Property	6	Warehouses
P	Energy (Oil Refineries/Petrochemicals)

Table 3. Occupancy Level 2 definitions.

Code	Definition	Code	Definition
A	Miscellaneous	Q	Offices/Banks
B	Manufacturers/Processors	R	Residential
C	Chemicals/Pharmaceuticals	T	Transport
D	Bridges/Dams/Tunnels/Piers	U	Utilities
E	Conglomerates	V	Telecoms and Data Processing
F	Food	W	Woodworkers (Sawmills, Papermills)
G	Grain	X	Onshore Crude
H	General Mercantile/Shops	Y	Onshore GasPlants
J	Mines	Z	Onshore Construction
K	Crops	2	Hospital/Health care centres
L	Auto	4	Semiconductor/Fabs
M	Metals	5	Motor Manufaturers
O	Municipal Property	6	Warehouses
P	Energy (Oil Refineries/Petrochemicals)

Table 4. Claim counts and regional breakdown.

Lloyd’s Code	Description
AF	Africa	22
AS	Asia - Pacific	54
CA	Central Asia	21
EU	Europe	78
LA	Latin America - Carribean	78
ME	Middle East	13
NA	North America	1576
OC	Oceania	71
WW	World Wide	1258
	Total	3171

Table 4. Claim counts and regional breakdown.

Lloyd’s Code	Description
AF	Africa	22
AS	Asia - Pacific	54
CA	Central Asia	21
EU	Europe	78
LA	Latin America - Carribean	78
ME	Middle East	13
NA	North America	1576
OC	Oceania	71
WW	World Wide	1258
	Total	3171

Figure 1. Claims breakdown by Occupancy Level 1 and by excess FGU above different thresholds.

Figure 1. Claims breakdown by Occupancy Level 1 and by excess FGU above different thresholds.

Table 5. Claim counts by year and occupancy: Residential (RE), Commercial (CO), Manufacturing (MA).

Years	RE	CO	MA
2000	5	116	69
2001	20	110	58
2002	17	97	92
2003	69	105	138
2004	41	96	112
2005	12	129	89
2006	22	74	55
2007	143	105	153
2008	51	76	100
2009	154	55	83
2010	110	97	108
2011	23	60	51
2012	2	4	0
Total	669	1124	1108

Table 5. Claim counts by year and occupancy: Residential (RE), Commercial (CO), Manufacturing (MA).

Years	RE	CO	MA
2000	5	116	69
2001	20	110	58
2002	17	97	92
2003	69	105	138
2004	41	96	112
2005	12	129	89
2006	22	74	55
2007	143	105	153
2008	51	76	100
2009	154	55	83
2010	110	97	108
2011	23	60	51
2012	2	4	0
Total	669	1124	1108

3. Methodology

We use a simple yet effective method to estimate the tail index, which relies on the log-log rank-size (LLRS) OLS regression. The method is severely biased in small samples and has often been applied with an incorrect formulation for the standard errors. We apply the optimal bias correction and the correct formula for the standard errors indicated by Gabaix and Ibragimov [6]. Application of the method with an optimal ranks shift is very robust to heterogeneity and dependence of the data, including common factor structures. For comparison, we pair the method with the popular Hill estimator, which suffers from significant bias in small samples, and with the weighted Hill estimator developed by Huisman et al. [7] to deal with small sample issues. Readers interested in the empirical results may skip the next sections and go directly to Section 4.

3.1. Hill Estimator.

Hill [17] proposed a simple method for estimating the tail index from a sequence of i.i.d. observations. Let $l\left(i\right)$ denote the i-th order statistic of losses, such that $l\left(i\right)\ge l(i-1)$ for $i=2,\dots ,n$, with n the size of the sample. Let us focus on the losses in excess of the k-th order statistic, and assume a conditional Pareto distribution for the random loss L in excess of the threshold $l\left(k\right)$. We have

$${\mathbb{P}}_k(L>z)=C{z}^{-\alpha \left(k\right)},$$

where $\alpha \left(k\right):=\gamma {\left(k\right)}^{-1}$ is the tail index and C a positive constant. The Hill estimator for the parameter $\gamma \left(k\right)$ is the maximum likelihood estimator

$$\widehat{\gamma }\left(k\right)=\frac{1}{k}\sum _{i=1}^{k}ln\left(\frac{l(n-i+1)}{l(n-k)}\right).$$

(1)

The standard error for the Hill estimate of the tail index, $\widehat{\alpha }\left(k\right)$, is $\mathsf{s}.\mathsf{e}{.}_{Hill}=\widehat{\alpha }\left(k\right)/\sqrt{k}$. To understand the bias affecting Equation (1) in small samples, consider the class of distribution functions (see [21,22]):

$${\mathbb{P}}_k(L\le z)=1-a{z}^{-\alpha }(1+b{z}^{-\beta }),$$

for positive parameters $\alpha ,\beta$, and real $a,b$ (the case $a=1$ and $b=0$ corresponding to a Pareto distribution). Dacorogna et al. [22] showed that the above is the second order expansion of the cumulative distribution function of a vast class of heavy tailed distributions, and provided the following approximations for the expected value and variance of the estimator $\widehat{\gamma }\left(k\right)$ in Equation (1):

$$E\left(\widehat{\gamma }\left(k\right)\right)\cong \frac{1}{\alpha }-\frac{b\beta }{\alpha (\alpha +\beta )}{a}^{\frac{-\beta }{\alpha }}{\left(\frac{k}{n}\right)}^{\frac{\beta }{\alpha }}Var\left(\widehat{\gamma }\left(k\right)\right)\cong \frac{1}{k{\alpha }^2},$$

(2)

for $n,k$ and $l\left(k\right)$ going to infinity. The above show how the choice of threshold $l\left(k\right)$ introduces an important trade-off between bias and efficiency.

3.2. LLRS Regression

A popular alternative to more complex estimators for the tail index is to run the OLS regression

$$ln(i-\eta )=a-blnl\left(i\right),$$

with $i=1,\dots ,k$. The tail index is given by the OLS estimator $\widehat{b}$. The procedure is typically applied with $\eta =0$, hence the name LLRS. Unfortunately, this approach is strongly biased in small samples, as can be seen from the following asymptotic expansions for the OLS estimator $\widehat{b}(\eta ,k)$ (see [6]):

$$E\left(\frac{\widehat{b}(\eta ,k)}{\alpha }-1\right)=\frac{(2\eta -1){ln}^{2}k}{4k}+o\left(\frac{{ln}^{2}k}{k}\right),$$

$$\frac{\widehat{b}(\eta ,k)}{\alpha }=1+\sqrt{\frac{2}{k}}\mathcal{N}(0,1)+O_P\left(\frac{{ln}^{2}k}{k}\right),$$

where $\mathcal{N}(0,1)$ denotes a standard Normal random variable. When using the LLRS method, one should therefore apply the optimal rank shift $\eta =1/2$. We will refer to this case as the LLRS-1/2 method. The relevant standard error of the OLS estimator of the slope coefficient $\widehat{b}(1/2,k)$ is then given by $\mathsf{s}.\mathsf{e}{.}_{LLRS}=\widehat{b}(1/2,k)\sqrt{2/k}$; again, we refer to Gabaix and Ibragimov [6] for a discussion of this result.

3.3. Alternative Methodologies

There are several alternative methods to estimate the tail index or its inverse.12 As a robustness check, we consider the method proposed by Huisman et al. [7] to deal with small samples, and the bias-efficiency trade-off formalized in Equation (2). Huisman et al. [7] note that, for small enough k, the bias can be approximated by a linear function, suggesting the use of the regression

$$\gamma \left(k\right)={\beta }_0+{\beta }_{1}k+\epsilon \left(k\right).$$

(3)

They then compute Hill estimates for different values of $k=1,\dots ,\overline{k}$, where the upper bound $\overline{k}$ is the largest value for which the linear approximation of $\gamma \left(k\right)$ holds, and use the resulting vector of $\widehat{\gamma }\left(k\right)$’s to estimate the parameters of (3). As k goes to zero, the intercept in (3) provides an unbiased estimate of the parameter γ. Note that ${\beta }_0$ and ${\beta }_1$ cannot be estimated by OLS for two reasons. First, from Equation (1) we see that the variance of $\widehat{\gamma }\left(k\right)$ depends on k, and hence the error term $\epsilon \left(k\right)$ is heteroskedastic. Second, for all $i,j\in \{1,\dots ,\overline{\kappa }\}$, the estimators $\gamma \left(i\right)$ and $\gamma \left(j\right)$ are correlated. Huisman et al. [7] therefore use Weighted Least Squares (WLS) combined with an appropriate method to compute the standard errors to deal with the overlapping data problem. They obtain the following weighted Hill estimator,

$${\gamma }_w\left(\kappa \right)=\sum _{k=1}^{\overline{\kappa }}w\left(k\right)\gamma \left(k\right),$$

(4)

where we refer to Huisman et al. [7] for details on the weights $w\left(k\right)$.

4. Empirical Evidence

In this section we provide tail index estimates for the subset of the Imperial-IICI dataset covering commercial property claims and exposures.13 Let us first provide a comparison of the two estimation methods outlined in Section 3.1–Section 3.2 by looking at property exposures classified as RE (residential) according to Occupancy Information Level 1. These include hotels, condos, and municipal property such as council houses, universities, and colleges. 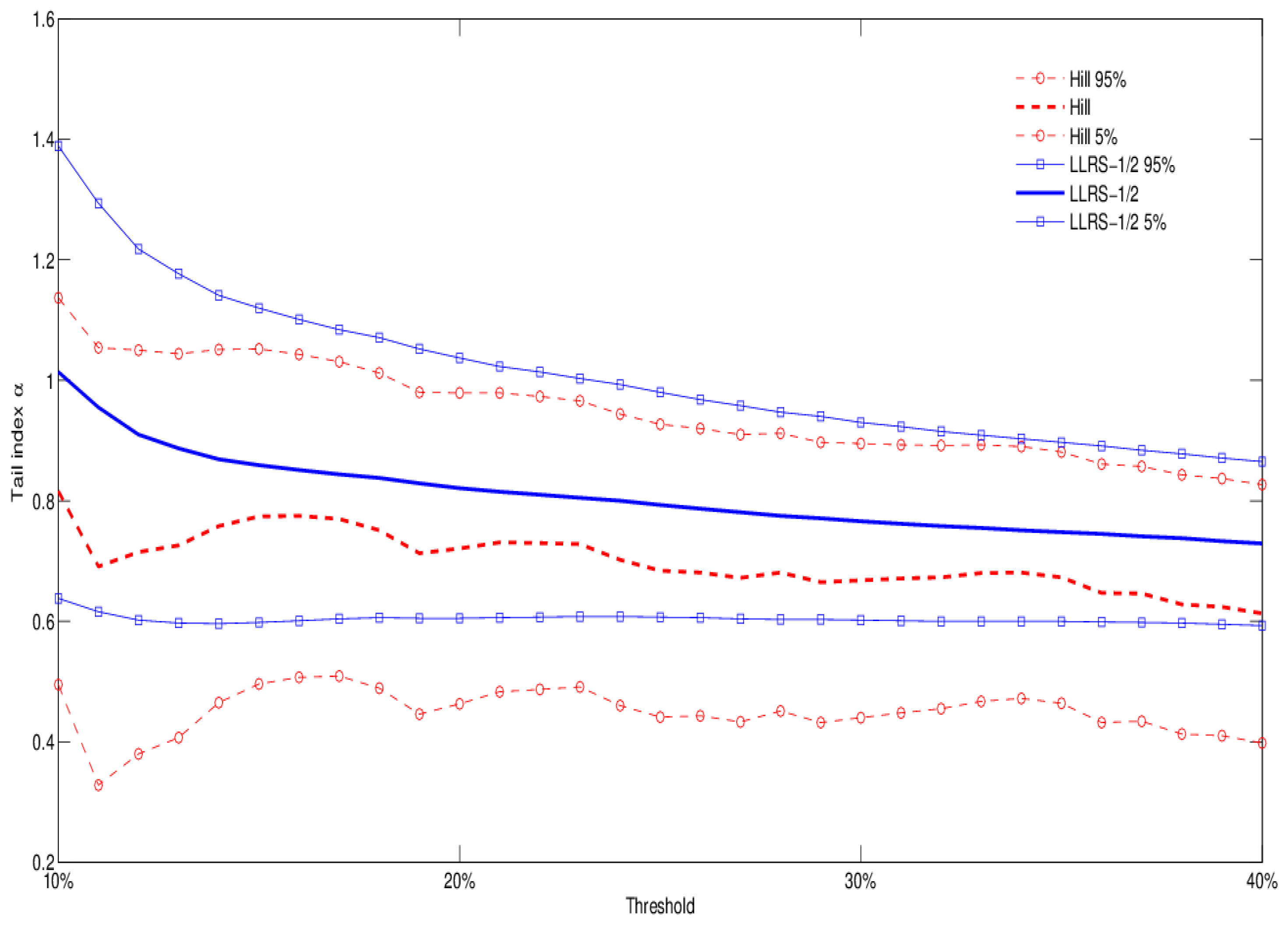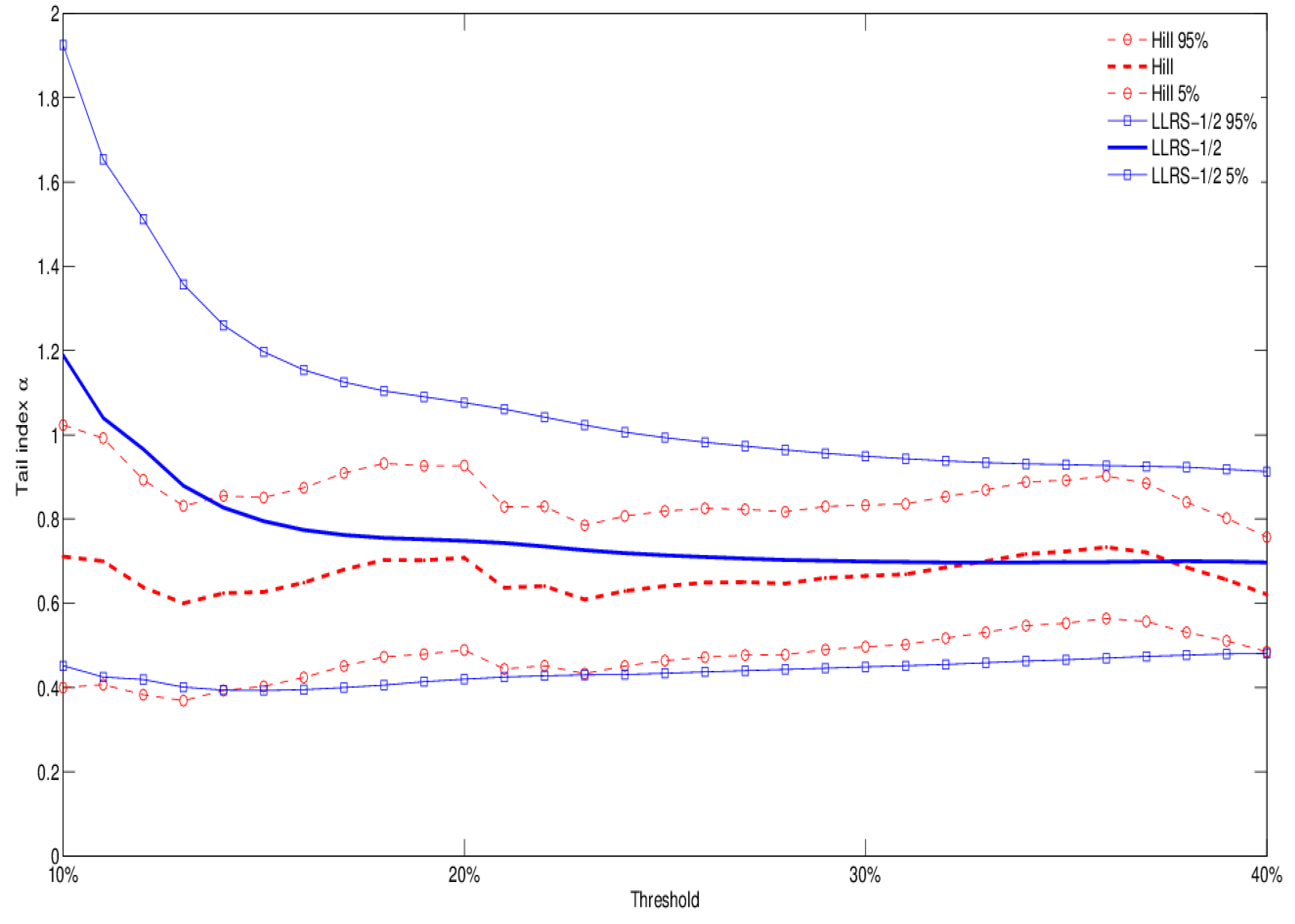Figure 2 reports tail index estimates and 90% confidence bands for the Hill and LLRS-1/2 methods. Estimates are based on subsamples obtained by considering between 10% and 40% of the largest losses. The results suggest considerable heaviness of the tail distribution: both estimation methods indicate a tail index close to one; the existence of a finite variance can be rejected at the 5% significance level.

Figure 2. Tail index estimates and 90% confidence bands for Occupancy Level 1 RE (residential): comparison of Hill and LLRS-1/2 regression methods for different estimation thresholds (from 10-th to 40-th percentile of the data).

Figure 2. Tail index estimates and 90% confidence bands for Occupancy Level 1 RE (residential): comparison of Hill and LLRS-1/2 regression methods for different estimation thresholds (from 10-th to 40-th percentile of the data).

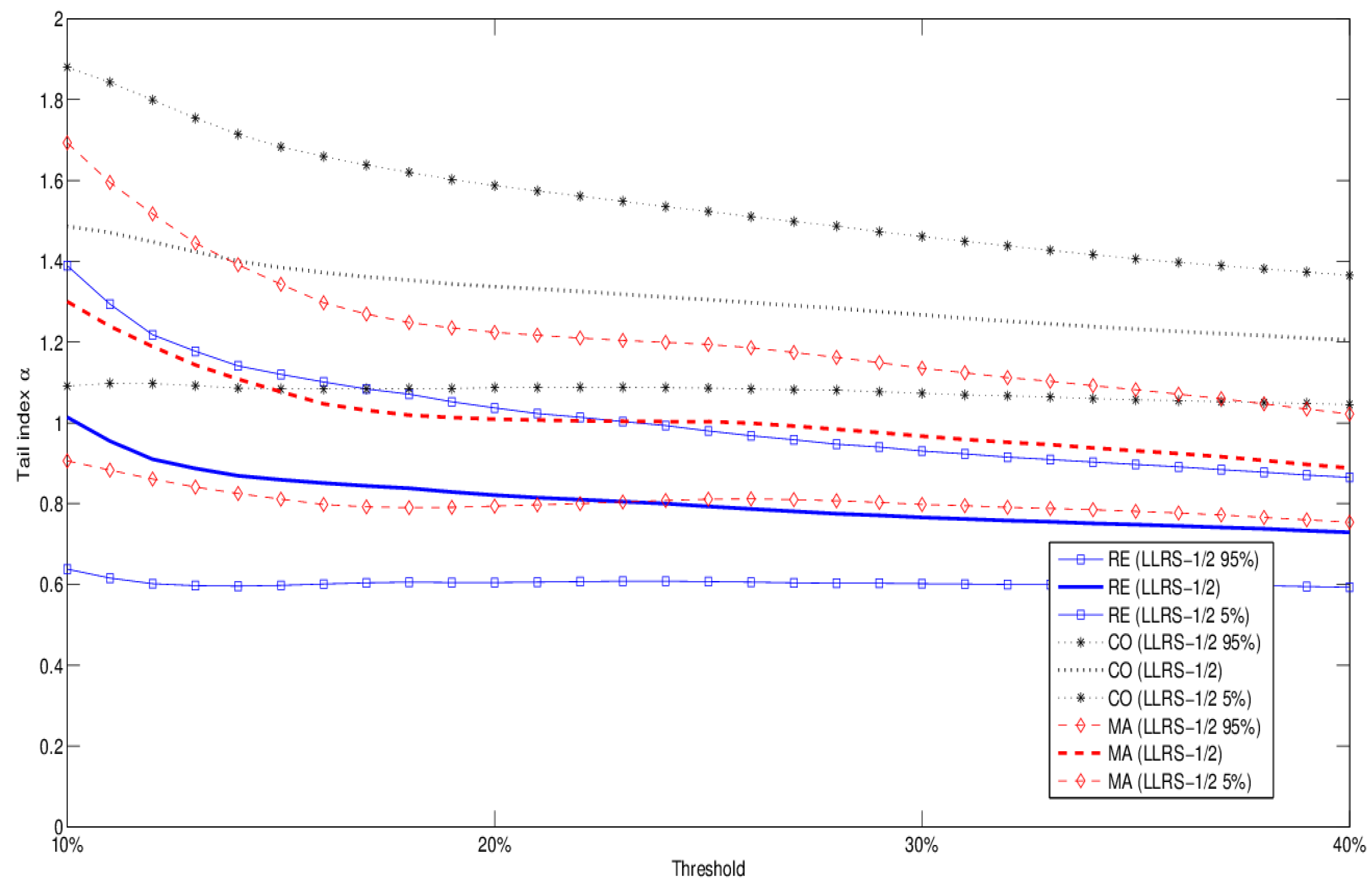
To demonstrate the importance of occupancy type, we then compare the tail behavior of Occupancy Information Level 1 types RE (residential), CO (commercial), and MA (manufacturing). Figure 3 depicts the results obtained with the LLRS-1/2 method. They indicate considerable variation in tail behavior across occupancy types. Based on our data, in particular, all types have tail indices lower than two at the 95% confidence level; commercial losses have the highest tail index estimates, residential losses the lowest, whereas manufacturing claims are somewhere in the middle. Although losses in our dataset are on average substantially larger for manufacturing than residential exposures, the results suggest that the latter may be more dangerous from a distributional perspective. We must bear in mind, however, that residential exposures are underrepresented in our dataset, as shown for example in Figure 1. As a robustness check, in Table 6 we report the results obtained by applying the method of Huisman et al. [7] to the three occupancy types. The results show broad agreement with the LLRS-1/2 method, in particular for MA and CO exposures.

Figure 3. Tail index estimates and 90% confidence bands (LLRS-1/2 regression method) for all Occupancy Level 1 types (CO, MA, RE).

Figure 3. Tail index estimates and 90% confidence bands (LLRS-1/2 regression method) for all Occupancy Level 1 types (CO, MA, RE).

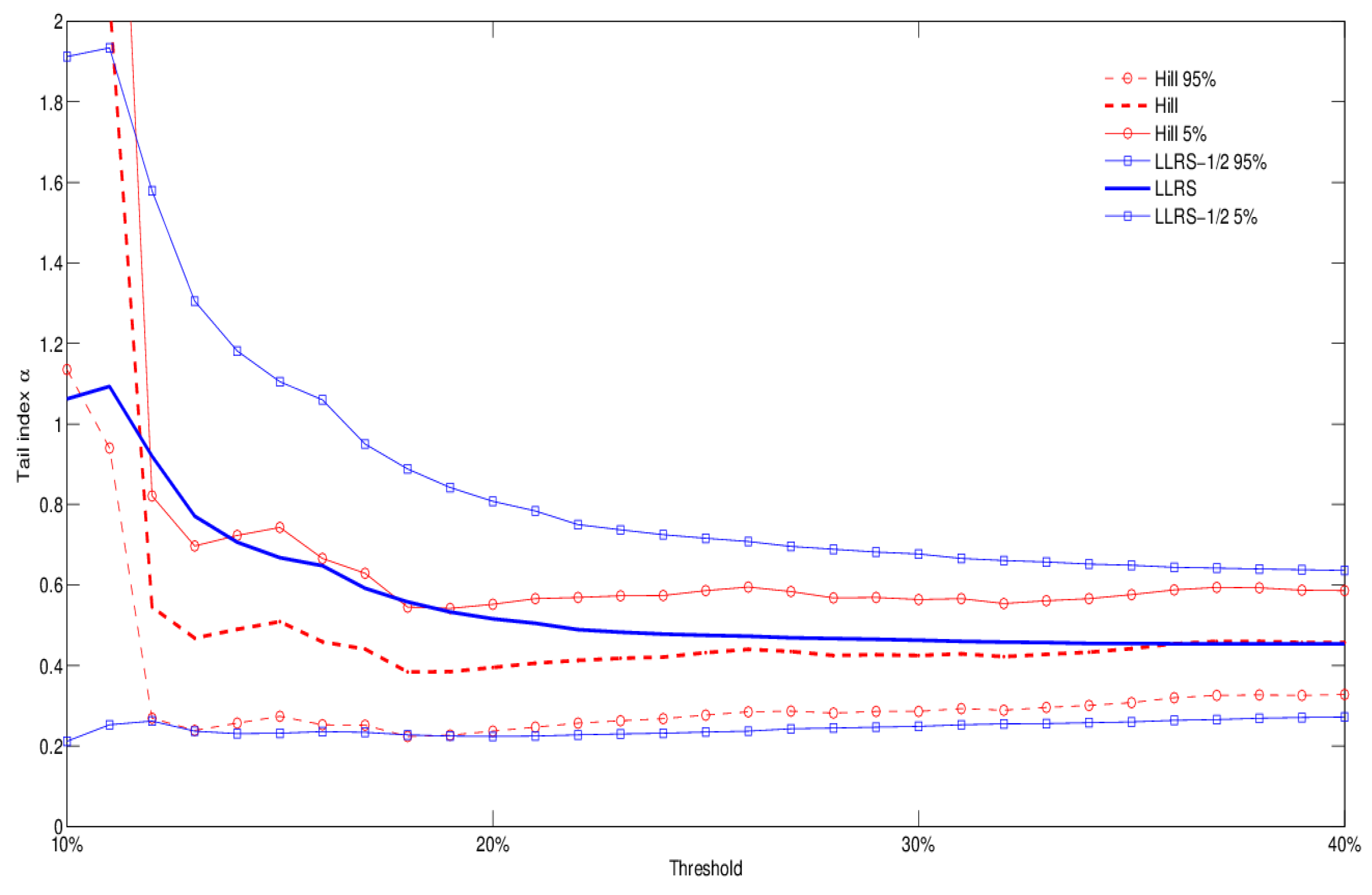
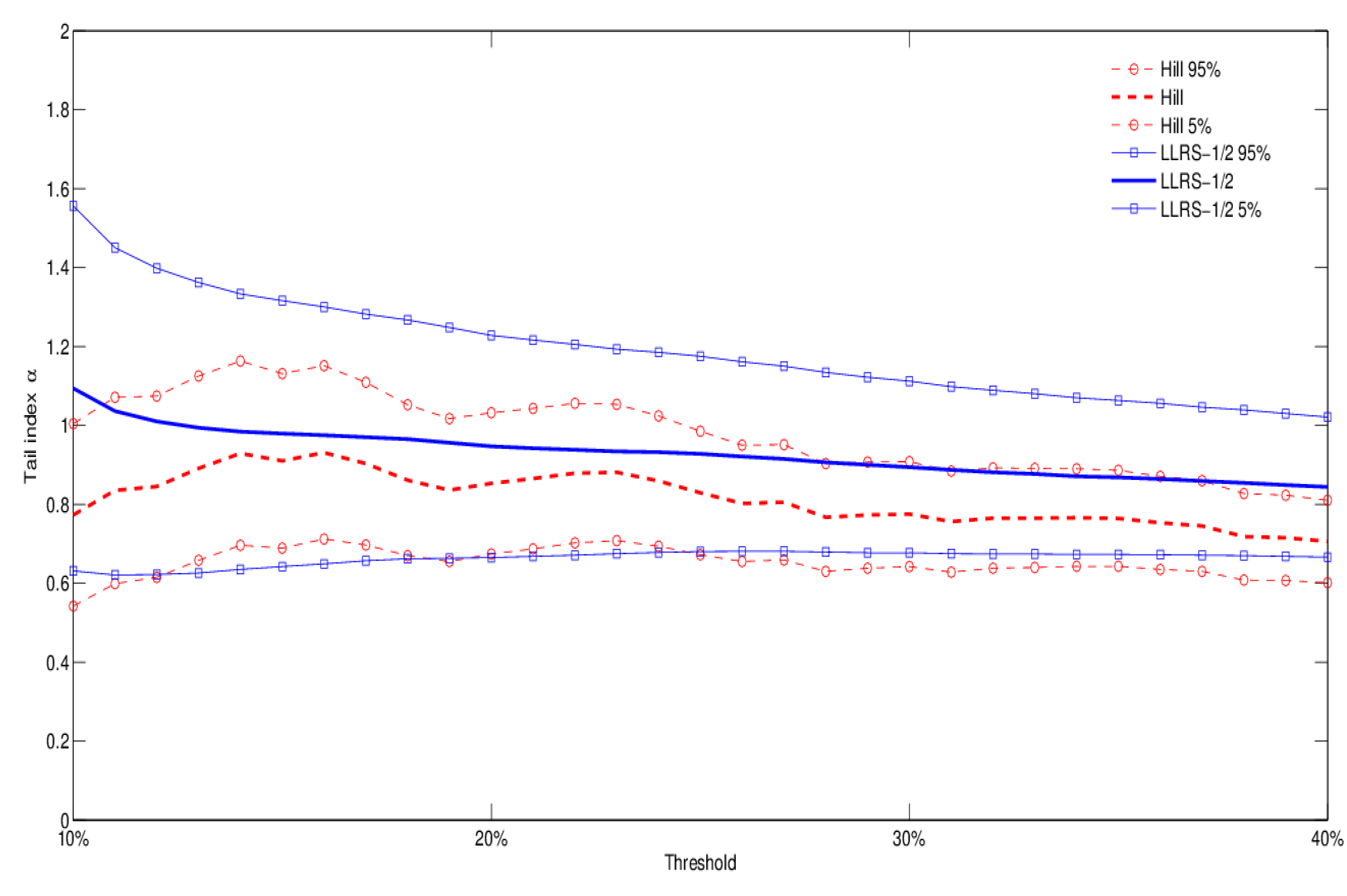
The use of Occupancy Information Level 3 gives us the opportunity to explore variations in tail behavior within a specific occupancy class. Let us consider RE (residential) exposures, for example, and distinguish between Large Hotels and Dwellings, the latter including condos, housing associations, and institutional housing. Figure 4 and Figure 5 show that the second type of exposures is lighter tailed than Large Hotels. We report results for both the Hill and LLRS-1/2 estimation methods, which provide similar implications. It is well known that hotel exposures have different risk profiles, depending for example on the presence of a restaurant (increasing the risk of fire), and may be more or less risky than condos and apartment complexes. Although the dataset does not allow us to explore this dimension at the moment (including the presence of sprinklers), our results suggest that the Large Hotels occupancy class may subsume the presence of serious sources of risk (such as restaurants), thus explaining the lighter tail behavior of Dwellings. Finally, in Figure 6 we report the tail index estimates for the case of aggregate Occupancy Level 2 types C (chemicals), J (metals), and M (mines). Again, the results show considerable tail heaviness, which is comparable to Dwellings, but lighter than Large Hotels across different thresholds and estimation methods.

Table 6. Comparison of estimates and 90% confidence bands for the Hill estimator given in Equation (1), for the LLRS-1/2 estimator obtained from the OLS estimate $\widehat{d}$ of the regression $lnl\left(i\right)=c-dln(i-1/2)$, and for the weighted Hill estimator ${\widehat{\gamma }}_w$ given in Equation (4). Occupancy Level 1 data: RE (residential), CO (commercial), and MA (manufacturing).

		RE			CO			MA
Obs.	5%	${\widehat{\gamma }}_{Hill}$	95%	5%	${\widehat{\gamma }}_{Hill}$	95%	5%	${\widehat{\gamma }}_{Hill}$	95%
10%	0.905	1.225	1.546	0.593	0.731	0.868	0.829	1.055	1.281
15%	1.014	1.292	1.570	0.676	0.798	0.920	1.006	1.219	1.432
20%	1.129	1.388	1.646	0.703	0.811	0.918	0.877	1.032	1.188
25%	1.219	1.463	1.706	0.759	0.861	0.963	0.899	1.039	1.180
30%	1.271	1.498	1.725	0.820	0.919	1.018	1.084	1.237	1.389
35%	1.278	1.486	1.695	0.840	0.933	1.027	1.155	1.304	1.453
40%	1.417	1.632	1.846	0.881	0.972	1.063	1.322	1.480	1.638
Obs.	5%	${\widehat{\gamma }}_{LLRS-1/2}$	95%	5%	${\widehat{\gamma }}_{LLRS-1/2}$	95%	5%	${\widehat{\gamma }}_{LLRS-1/2}$	95%
10%	0.572	0.908	1.244	0.486	0.662	0.838	0.493	0.707	0.920
15%	0.745	1.071	1.396	0.556	0.709	0.863	0.639	0.848	1.057
20%	0.840	1.140	1.440	0.598	0.736	0.873	0.723	0.919	1.115
25%	0.912	1.193	1.473	0.629	0.755	0.881	0.760	0.939	1.119
30%	0.976	1.242	1.509	0.658	0.777	0.895	0.809	0.980	1.150
35%	1.024	1.278	1.531	0.685	0.798	0.911	0.855	1.019	1.184
40%	1.070	1.314	1.559	0.708	0.816	0.924	0.906	1.067	1.228
Obs.	5%	${\widehat{\gamma }}_w$	95%	5%	${\widehat{\gamma }}_w$	95%	5%	${\widehat{\gamma }}_w$	95%
10%	0.328	0.436	0.544	0.61	0.657	0.704	0.493	0.707	0.92
15%	0.5	0.656	0.813	0.544	0.586	0.628	0.639	0.848	1.057
20%	0.691	0.883	1.075	0.596	0.639	0.683	0.723	0.919	1.115
25%	0.793	0.986	1.18	0.623	0.668	0.713	0.76	0.939	1.119
30%	0.836	1.024	1.212	0.617	0.664	0.71	0.809	0.98	1.15
35%	0.906	1.088	1.269	0.618	0.665	0.712	0.855	1.019	1.184
40%	0.91	1.092	1.275	0.635	0.681	0.727	0.906	1.067	1.228

Table 6. Comparison of estimates and 90% confidence bands for the Hill estimator given in Equation (1), for the LLRS-1/2 estimator obtained from the OLS estimate $\widehat{d}$ of the regression $lnl\left(i\right)=c-dln(i-1/2)$, and for the weighted Hill estimator ${\widehat{\gamma }}_w$ given in Equation (4). Occupancy Level 1 data: RE (residential), CO (commercial), and MA (manufacturing).

		RE			CO			MA
Obs.	5%	${\widehat{\gamma }}_{Hill}$	95%	5%	${\widehat{\gamma }}_{Hill}$	95%	5%	${\widehat{\gamma }}_{Hill}$	95%
10%	0.905	1.225	1.546	0.593	0.731	0.868	0.829	1.055	1.281
15%	1.014	1.292	1.570	0.676	0.798	0.920	1.006	1.219	1.432
20%	1.129	1.388	1.646	0.703	0.811	0.918	0.877	1.032	1.188
25%	1.219	1.463	1.706	0.759	0.861	0.963	0.899	1.039	1.180
30%	1.271	1.498	1.725	0.820	0.919	1.018	1.084	1.237	1.389
35%	1.278	1.486	1.695	0.840	0.933	1.027	1.155	1.304	1.453
40%	1.417	1.632	1.846	0.881	0.972	1.063	1.322	1.480	1.638
Obs.	5%	${\widehat{\gamma }}_{LLRS-1/2}$	95%	5%	${\widehat{\gamma }}_{LLRS-1/2}$	95%	5%	${\widehat{\gamma }}_{LLRS-1/2}$	95%
10%	0.572	0.908	1.244	0.486	0.662	0.838	0.493	0.707	0.920
15%	0.745	1.071	1.396	0.556	0.709	0.863	0.639	0.848	1.057
20%	0.840	1.140	1.440	0.598	0.736	0.873	0.723	0.919	1.115
25%	0.912	1.193	1.473	0.629	0.755	0.881	0.760	0.939	1.119
30%	0.976	1.242	1.509	0.658	0.777	0.895	0.809	0.980	1.150
35%	1.024	1.278	1.531	0.685	0.798	0.911	0.855	1.019	1.184
40%	1.070	1.314	1.559	0.708	0.816	0.924	0.906	1.067	1.228
Obs.	5%	${\widehat{\gamma }}_w$	95%	5%	${\widehat{\gamma }}_w$	95%	5%	${\widehat{\gamma }}_w$	95%
10%	0.328	0.436	0.544	0.61	0.657	0.704	0.493	0.707	0.92
15%	0.5	0.656	0.813	0.544	0.586	0.628	0.639	0.848	1.057
20%	0.691	0.883	1.075	0.596	0.639	0.683	0.723	0.919	1.115
25%	0.793	0.986	1.18	0.623	0.668	0.713	0.76	0.939	1.119
30%	0.836	1.024	1.212	0.617	0.664	0.71	0.809	0.98	1.15
35%	0.906	1.088	1.269	0.618	0.665	0.712	0.855	1.019	1.184
40%	0.91	1.092	1.275	0.635	0.681	0.727	0.906	1.067	1.228

Figure 4. Occupancy level 3 type “Large Hotel”: tail index estimation (both Hill and LLRS-1/2 regression methods), with 90% confidence bands.

Figure 4. Occupancy level 3 type “Large Hotel”: tail index estimation (both Hill and LLRS-1/2 regression methods), with 90% confidence bands.

Figure 5. Occupancy level 3 types corresponding to dwellings (single family and multi family), institutional housing, condos, housing associations, : tail index estimation (both Hill and LLRS-1/2 regression methods), with 90% confidence band.

Figure 5. Occupancy level 3 types corresponding to dwellings (single family and multi family), institutional housing, condos, housing associations, : tail index estimation (both Hill and LLRS-1/2 regression methods), with 90% confidence band.

Figure 6. Occupancy level 2 types C (chemicals), J (metals), and M (mines) aggregated: tail index estimation (both Hill and LLRS-1/2 regression methods), with 90% confidence band.

Figure 6. Occupancy level 2 types C (chemicals), J (metals), and M (mines) aggregated: tail index estimation (both Hill and LLRS-1/2 regression methods), with 90% confidence band.

A more robust way of comparing the tail characteristics of different occupancy types is to regress the tail index on a number of relevant covariates (or rating factors). Following Beirlant et al. [18], Beirlant and Goegebeur [19], and Wang and Tsai [20], we assume that the tail index can be expressed as a deterministic function of rating factors, which in the examples below are represented by occupancy types, but more generally could include Total Insurable Value (TIV) bands and/or locations. Using the notation of (3.1), we assume

$${\mathbb{P}}_k(L>z|X)=C(z;X)z^{-\tilde{\alpha }(X;k)},$$

(5)

where $X={(X_1,\dots ,X_p)}^{\prime }$ is a vector of covariates, and the tail index is assumed to take the form $\tilde{\alpha }(X;k)=exp\left({\theta }^{\prime }X\right)$. We estimate the exponential regression coefficient $\theta \in {\mathbb{R}}^p$ by using the approximate maximum likelihood estimator of Wang and Tsai [20], as well as their methodology to select the optimal threshold k.

The approach can be used to quantify the relative contribution to tail risk of different property characteristics. We provide an example using as covariates dummy variables for Occupancy Level 1 classes RE, CO, and MA. Assuming that the Imperial-IICI dataset is representative of a diversified portfolio of commercial property risks insured in the London market, one can use the results reported in Table 7 to suggest that on average occupancy MA provides a positive contribution to portfolio tail risk, while occupancy types RE and CO provide a negative contribution. These results should be interpreted bearing mind that MA exposures are overrepresented in our sample, and associated with higher excess loss severity (see Figure 1).

Table 7. Tail regression results for the exponential model $\tilde{\alpha }=exp\left({\theta }^{\prime }X\right)$. The vector of covariates, $X={(X_1,X_2,X_3)}^{\prime }$, includes Occupancy Level 1 indicators for classes RE (residential), CO (commercial), and MA (manfacturing). The corresponding estimated loadings are indicated by $\widehat{\theta }={({\widehat{\theta }}_1,{\widehat{\theta }}_2,{\widehat{\theta }}_3)}^{\prime }$. Following Wang and Tsai [20], the optimal sample fraction corresponds to 10% of the largest losses in the entire dataset. We set ${\widehat{\alpha }}_i:=exp\left({\widehat{\theta }}_i\right)$ for the tail index estimate resulting from considering only the loading estimate ${\widehat{\theta }}_i$ pertaining to each individual occupancy type.

	5%	${\widehat{\theta }}_i$	95%	${\widehat{\alpha }}_i$
CO	0.177	0.196	0.215	1.217
RE	0.070	0.082	0.093	1.085
MA	−0.032	−0.019	−0.006	0.981

Table 7. Tail regression results for the exponential model $\tilde{\alpha }=exp\left({\theta }^{\prime }X\right)$. The vector of covariates, $X={(X_1,X_2,X_3)}^{\prime }$, includes Occupancy Level 1 indicators for classes RE (residential), CO (commercial), and MA (manfacturing). The corresponding estimated loadings are indicated by $\widehat{\theta }={({\widehat{\theta }}_1,{\widehat{\theta }}_2,{\widehat{\theta }}_3)}^{\prime }$. Following Wang and Tsai [20], the optimal sample fraction corresponds to 10% of the largest losses in the entire dataset. We set ${\widehat{\alpha }}_i:=exp\left({\widehat{\theta }}_i\right)$ for the tail index estimate resulting from considering only the loading estimate ${\widehat{\theta }}_i$ pertaining to each individual occupancy type.

	5%	${\widehat{\theta }}_i$	95%	${\widehat{\alpha }}_i$
CO	0.177	0.196	0.215	1.217
RE	0.070	0.082	0.093	1.085
MA	−0.032	−0.019	−0.006	0.981

5. Conclusions

In this article we have provided some new evidence on the tail behavior of commercial property losses. Using a new dataset based on London market claim and exposure information, we have provided tail estimates for different occupancy types, finding considerable variability of tail behavior across exposures. The results suggest significant heaviness of the tails, in particular for residential and manufacturing property exposures. We have also demonstrated the gains in estimation precision delivered by aggregating information collected from several data sources. The matching of reliable exposure information to observed claims is crucial to develop a sound statistical basis that can inform decision makers in pricing, reserving, and capital modeling exercises. Our findings represent a first step towards a better understanding of the statistical characteristics of large commercial risks, and towards the development of risk models that are less reliant on subjective assumptions driven by limited claims experience.