Survival Analysis for Credit Risk: A Dynamic Approach for Basel IRB Compliance
Abstract
1. Introduction
- Granular Risk Profiling: It enables the evaluation of credit risk at the level of individual loans or borrower segments.
- Dynamic Monitoring: Time-based risk assessment supports early detection of deteriorating credit quality.
- Strategic Insights: Outputs from survival models inform pricing, capital provisioning, and portfolio allocation decisions.
- Regulatory Alignment: The methodology supports key requirements of the IRB approach within the Basel framework (BCBS 2011).
2. Literature Review
3. Survival Analysis
3.1. Setup and Notation
- Age of a loan t: The duration (in years) from the origination date until default or the end of the observation period, where .
- Loan at age t: Denoted as .
- Maturity of a loan M: The time at which the loan is contractually scheduled to end.
- Remaining lifetime of a loan : The time left until default or maturity, satisfying .
- At the loan’s origination (), we have .
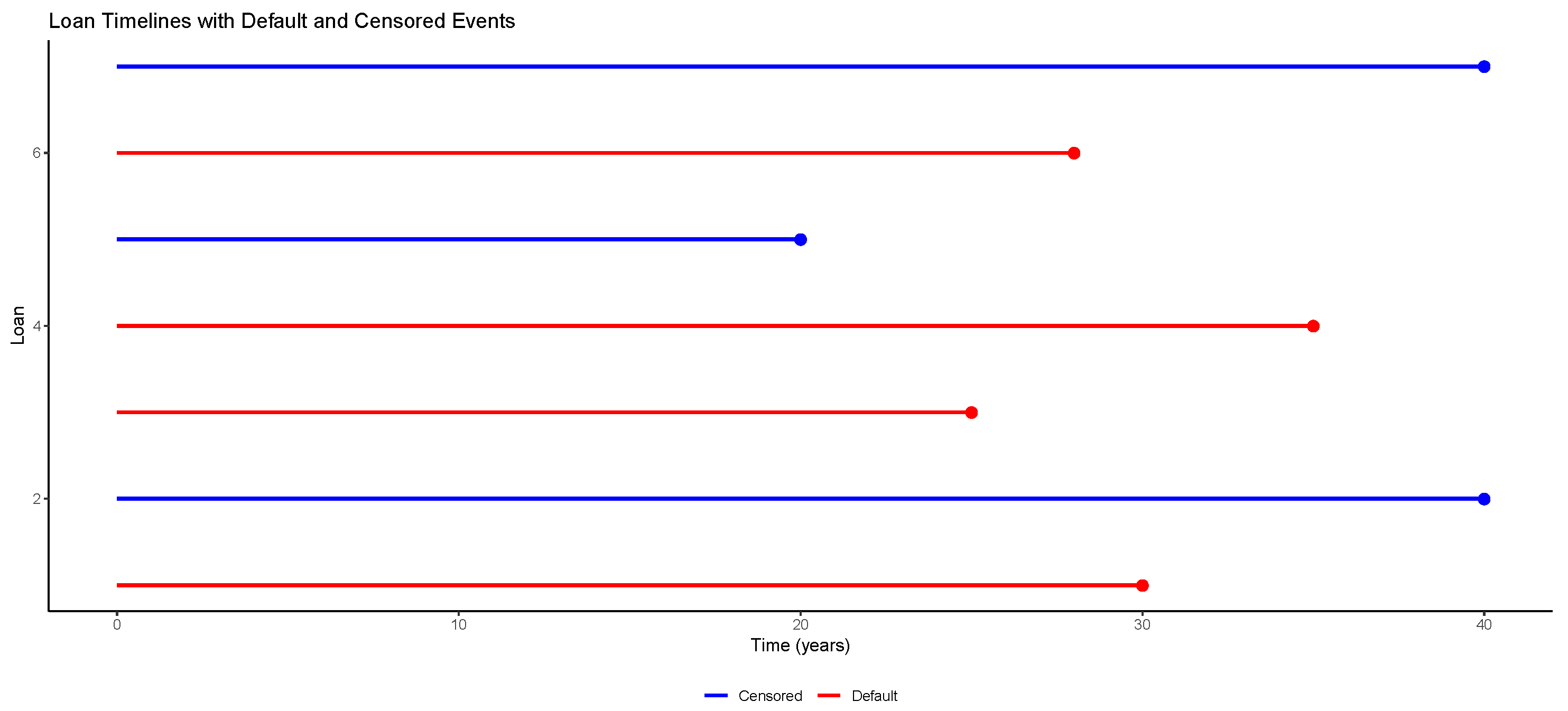
3.2. Censoring
3.3. Survival Table
- : number of loans at risk at the beginning of interval ;
- : number of defaults observed in ;
- : number of censored observations in .
4. Empirical Application
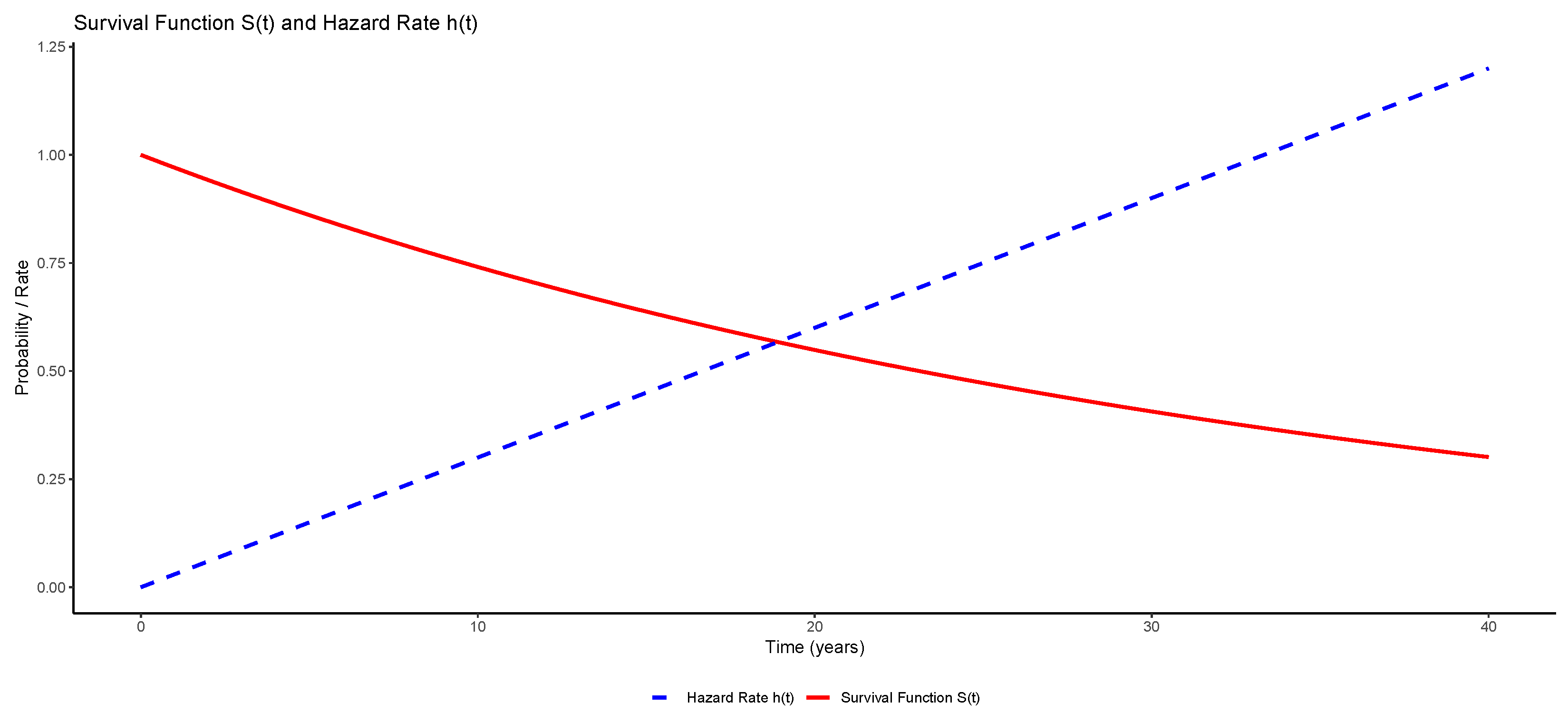
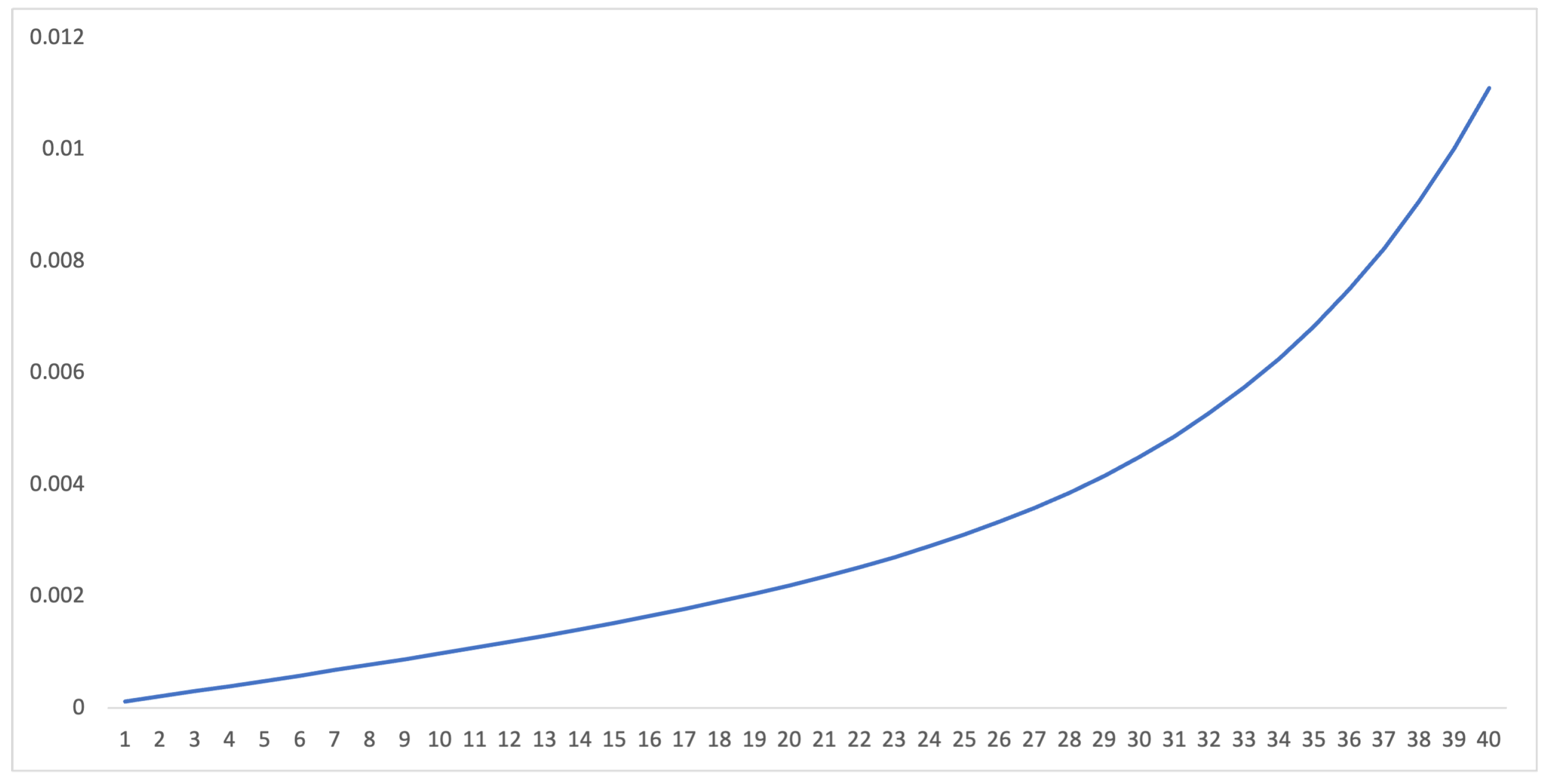
4.1. Hazard Functions
4.2. Default Probabilities
4.3. Loss Given Default
- Decreasing: .
- Increasing then Decreasing: for , for .
- Constant: .
- Increasing: .
4.4. Loss Process
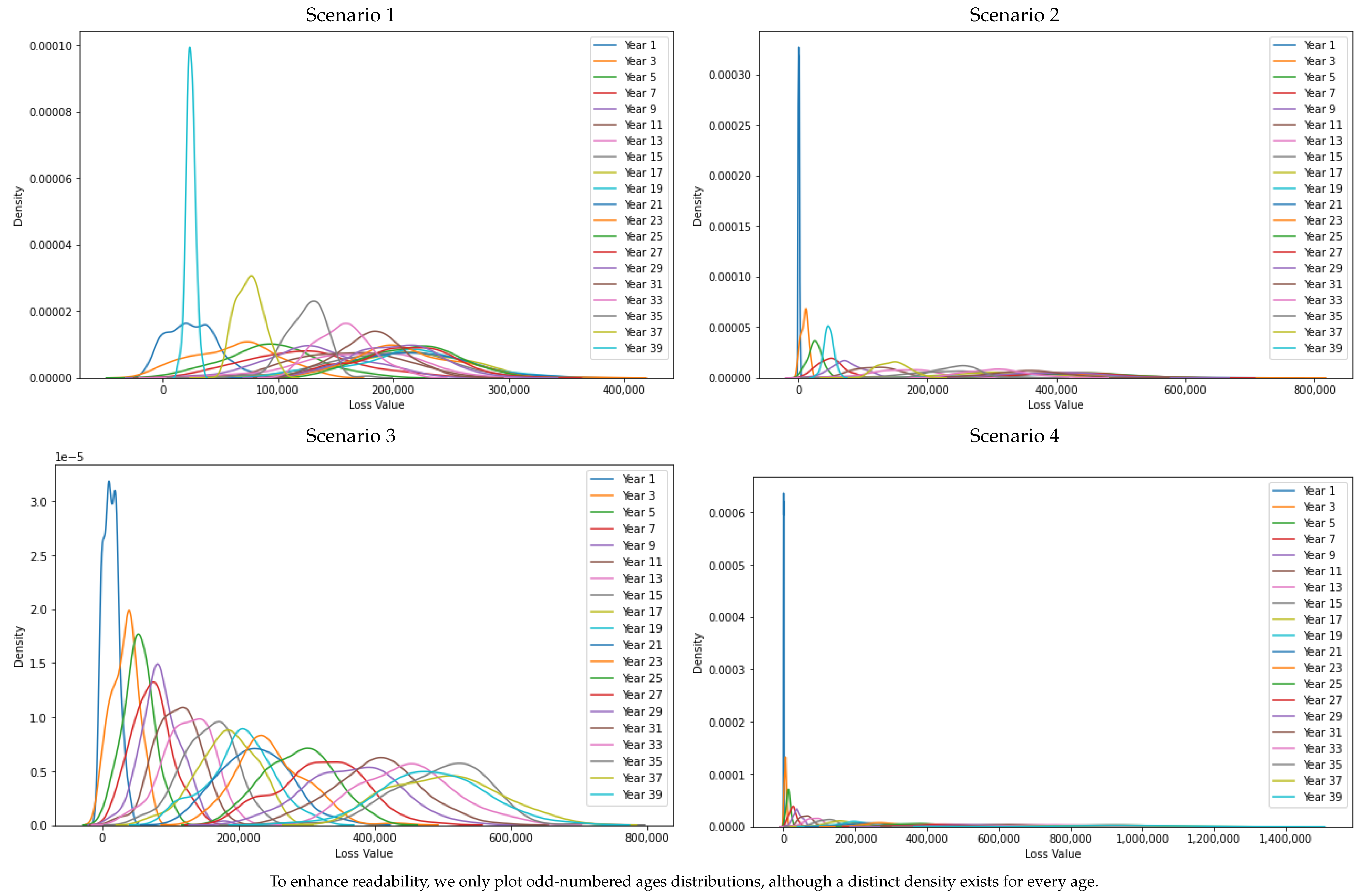
4.5. Computing Risk Measures
5. Managerial and Policy Implications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdalla, Hemn Barzan, Yulia Kumar, Jose Marchena, Stephany Guzman, Ardalan Awlla, Mehdi Gheisari, and Maryam Cheraghy. 2025. The future of artificial intelligence in the face of data scarcity. Computers, Materials & Continua 84: 1–27. [Google Scholar] [CrossRef]
- Baesens, Bart, Tony Van Gestel, Maria Stepanova, Dirk Van den Poel, and Jan Vanthienen. 2005. Neural network survival analysis for personal loan data. Journal of the Operational Research Society 56: 1089–98. [Google Scholar] [CrossRef]
- Banasik, John, Jonathan N. Crook, and Lyn C. Thomas. 1999. Not if but when will borrowers default. Journal of the Operational Research Society 50: 1185–90. [Google Scholar] [CrossRef]
- BCBS. 2011. Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems Revised Version June 2011. Basel: Basel Committee on Banking Supervision. [Google Scholar]
- BIS. 2006. Basel II: International Convergence of Capital Measurement and Capital Standards: A Revised Framework-Comprehensive Version. Bank for International Settlements. Available online: https://www.bis.org/publ/bcbs128.htm (accessed on 1 August 2025).
- Bo, Wang. 2024. The impact of macroeconomic factors on credit risk management in developing country banks: An analysis based on basel III. Financial Engineering and Risk Management 7: 97–105. [Google Scholar] [CrossRef]
- Borisov, Vadim, Tobias Leemann, Kathrin Seßler, Johannes Haug, Martin Pawelczyk, and Gjergji Kasneci. 2022. Deep neural networks and tabular data: A survey. IEEE Transactions on Neural Networks and Learning Systems 35: 7499–519. [Google Scholar] [CrossRef]
- Brier, Glenn W. 1950. Verification of forecasts expressed in terms of probability. Monthly Weather Review 78: 1–3. [Google Scholar] [CrossRef]
- Charpignon, Marie-Laure, Enguerrand Horel, and Flora Tixier. 2014. Prediction of Consumer Credit Risk. Stanford: Standford University. [Google Scholar]
- Crosbie, Peter, and Jeff Bohn. 2003. Modeling Default Risk: Modeling Methodology. San Francisco: KMV Corporation. [Google Scholar]
- Derbali, Abdelkader. 2018. How the Default Probability Is Defined by the Creditrisk+ Model? Available online: https://hal.science/hal-01696011v1 (accessed on 1 August 2025).
- Dickson, David C. M., Mary Hardy, Mary R. Hardy, and Howard R. Waters. 2013. Actuarial Mathematics for Life Contingent Risks. Cambridge: Cambridge University Press. [Google Scholar]
- Djeundje, Viani Biatat, and Jonathan Crook. 2019. Dynamic survival models with varying coefficients for credit risks. European Journal of Operational Research 275: 319–33. [Google Scholar] [CrossRef]
- Erkkilä, Rami. 2025. Interpretable machine learning for credit risk predictions. Economic Review 105: 315–20. [Google Scholar]
- Fejza, Doris, Dritan Nace, and Orjada Kulla. 2022. The credit risk problem—A developing country case study. Risks 10: 146. [Google Scholar] [CrossRef]
- Gompertz, Benjamin. 1825. Xxiv. on the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. in a letter to francis baily, esq. frs &c. Philosophical Transactions of the Royal Society of London 115: 513–83. [Google Scholar]
- Hassan, M. Kabir, Jennifer Brodmann, Blake Rayfield, and Makeen Huda. 2018. Modeling credit risk in credit unions using survival analysis. International Journal of Bank Marketing 36: 482–95. [Google Scholar] [CrossRef]
- Hernes, Marcin, Jędrzej Adaszyński, and Piotr Tutak. 2023. Credit risk modeling using interpreted xgboost. European Management Studies 21: 46–70. [Google Scholar] [CrossRef]
- Huang, Haonan, Jing Li, Chundan Zheng, Sikang Chen, Xuanyin Wang, and Xingyan Chen. 2025. Advanced default risk prediction in small and medum-sized enterprises using large language models. Applied Sciences 15: 2733. [Google Scholar] [CrossRef]
- Hurlin, Christophe, and Christophe Pérignon. 2023. Machine Learning and Irb Capital Requirements: Advantages, Risks, and Recommendations. Jouy-en-Josas: HEC Paris. Available online: https://ideas.repec.org/p/ebg/heccah/1480.html (accessed on 1 August 2025).
- Kakadiya, Rushikesh, Tarannum Khan, Anjali Diwan, and Rajesh Mahadeva. 2024. Transformer models for predicting bank loan defaults a next-generation risk management. Paper presented at 2024 IEEE 6th International Conference on Cybernetics, Cognition and Machine Learning Applications (ICCCMLA), Hamburg, Germany, October 19–20; pp. 26–31. [Google Scholar]
- Kaplan, Edward L., and Paul Meier. 1958. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association 53: 457–81. [Google Scholar] [CrossRef]
- Kleinbaum, David G., and Mitchel Klein. 2012a. Survival Analysis: A Self-Learning Text. Berlin and Heidelberg: Springer. [Google Scholar]
- Kleinbaum, David G., and Mitchel Klein. 2012b. Survival Analysis. Statistics for Biology and Health, 3rd ed. New York: Springer. [Google Scholar]
- Kragh Jørgensen, Rasmus Rask, Faartoft Jonas Jensen, Tarec El-Galaly, Martin Bøgsted, Rasmus Froberg Brøndum, Mikkel Runason Simonsen, and Lasse Hjort Jakobsen. 2025. Development of time to event prediction models using federated learning. BMC Medical Research Methodology 25: 143. [Google Scholar] [CrossRef]
- Leo, Martin, Suneel Sharma, and Koilakuntla Maddulety. 2019. Machine learning in banking risk management: A literature review. Risks 7: 29. [Google Scholar] [CrossRef]
- Mahbobi, Mohammad, Salman Kimiagari, and Marriappan Vasudevan. 2023. Credit risk classification: An integrated predictive accuracy algorithm using artificial and deep neural networks. Annals of Operations Research 330: 609–37. [Google Scholar] [CrossRef]
- Makeham, William Matthew. 1860. On the law of mortality and the construction of annuity tables. Journal of the Institute of Actuaries 8: 301–10. [Google Scholar] [CrossRef]
- McDonald, Ross A., Ania Matuszyk, and Lyn C. Thomas. 2010. Application of survival analysis to cash flow modelling for mortgage products. OR Insight 23: 1–14. [Google Scholar] [CrossRef]
- Micocci, Marco. 2000. MARC: An actuarial model for credit risk. Paper presented at ASTIN Colloquium 2000, Porto Cervo, Italy, September 17–20, vol. 31. [Google Scholar]
- Poudel, Ravi Prakash Sharma. 2013. Macroeconomic determinants of credit risk in nepalese banking industry. Paper presented at 21st International Business Research Conference, Toronto, ON, Canada, June 10–11; pp. 10–11. [Google Scholar]
- Rocha, Cristina, and Ana Luísa Papoila. 2009. Análise de Sobrevivência. Portugal: Sociedade Portuguesa de Estatística. [Google Scholar]
- Sharma, Alok Kumar, Li-Hua Li, and Ramli Ahmad. 2022. Default risk prediction using random forest and xgboosting classifier. In 2021 International Conference on Security and Information Technologies with AI, Internet Computing and Big-data Applications. Berlin and Heidelberg: Springer, pp. 91–101. [Google Scholar]
- Siphuma, Elekanyani, and Terence van Zyl. 2025. Enhancing credit risk assessment through transformer-based machine learning models. In Artificial Intelligence Research. SACAIR 2024. Communications in Computer and Information Science. Edited by Aurona Gerber, Jacques Maritz and Anban W. Pillay. Berlin and Heidelberg: Springer, vol. 2326. [Google Scholar]
- Smith, Peter J. 2017. Analysis of Failure and Survival Data. Boca Raton: CRC Press. [Google Scholar]
- Stepanova, Maria, and Lyn Thomas. 2002. Survival analysis methods for personal loan data. Operations Research 50: 277–89. [Google Scholar] [CrossRef]
- Steyerberg, Ewout W., Andrew J. Vickers, Nancy R. Cook, Thomas Gerds, Mithat Gonen, Nancy Obuchowski, Michael J. Pencina, and Michael W. Kattan. 2010. Assessing the performance of prediction models: A framework for traditional and novel measures. Epidemiology 21: 128–38. [Google Scholar] [CrossRef] [PubMed]
- Suisse Credit. 1997. Creditrisk+, A Credit Risk Management Framework. London: Credit Suisse Financial Products. [Google Scholar]
- Zhang, Dongfang, Basu Bhandari, and Dennis Black. 2021. Covariate selection for mortgage default analysis using survival models. Journal of Mathematical Finance 11: 218–33. [Google Scholar] [CrossRef]
- Zokirjonov, Mukhammadsodik. 2018. Methodology of creditmetrics for credit risk assessment. International Finance and Accounting 2018: 135. [Google Scholar]
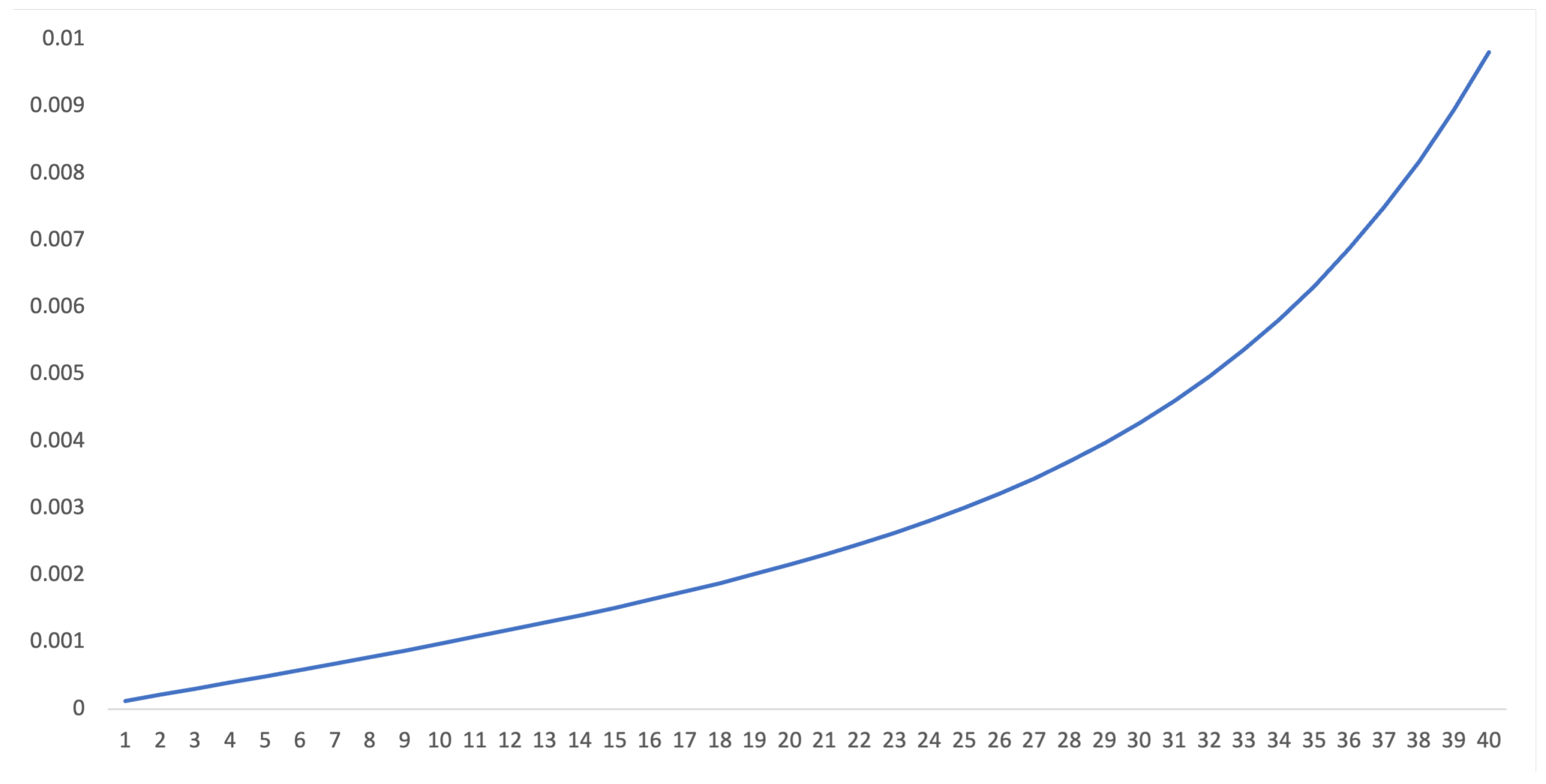
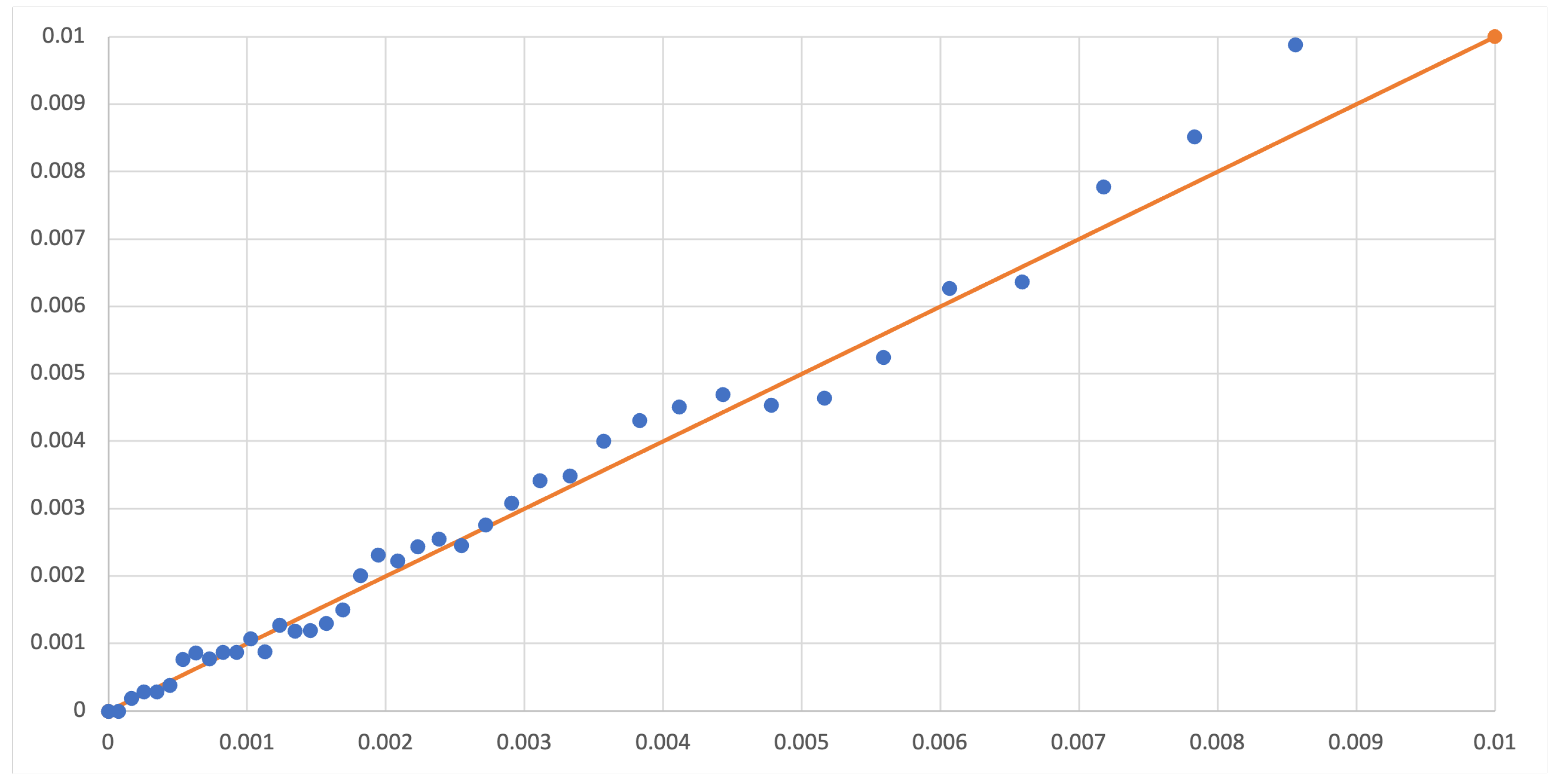
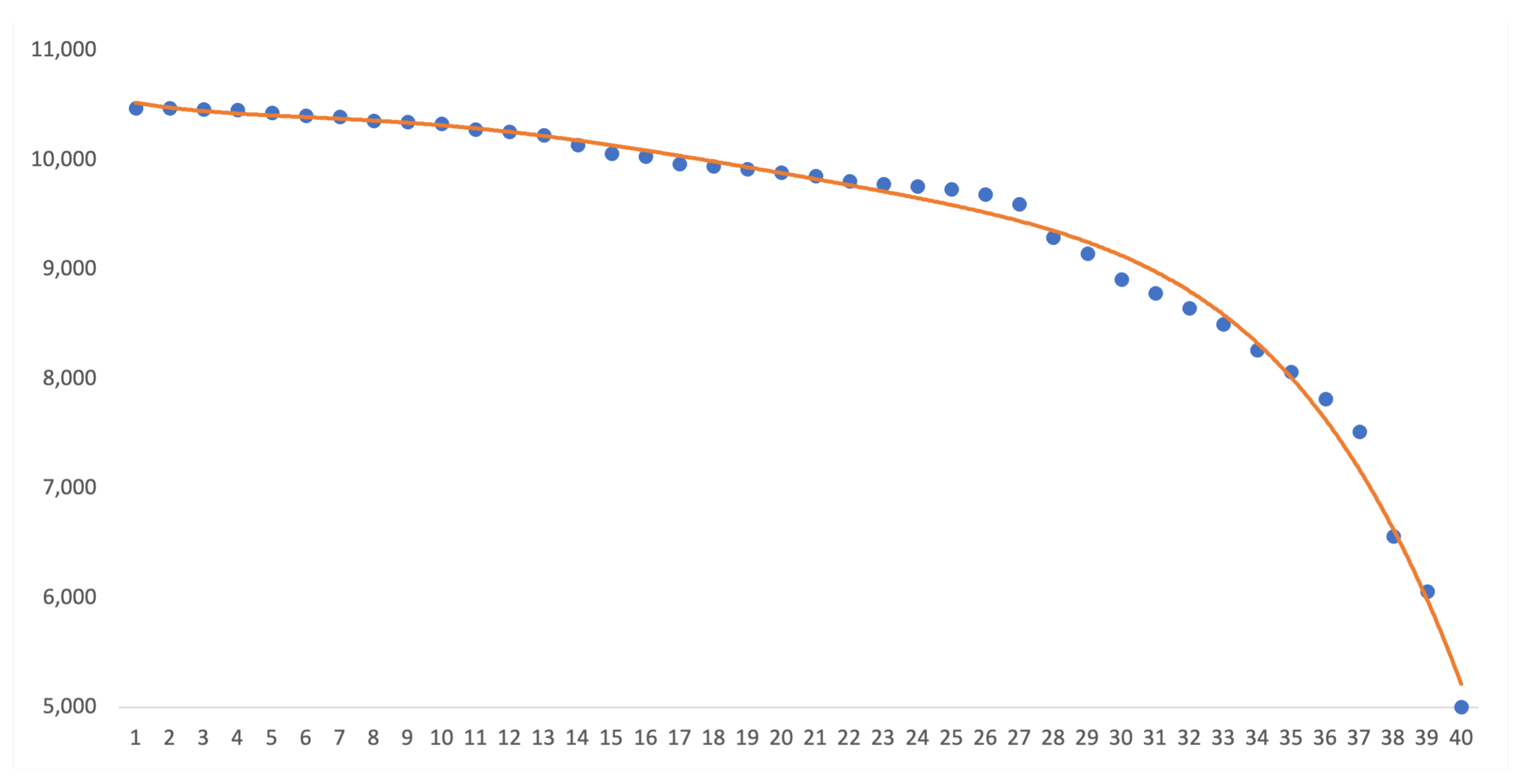
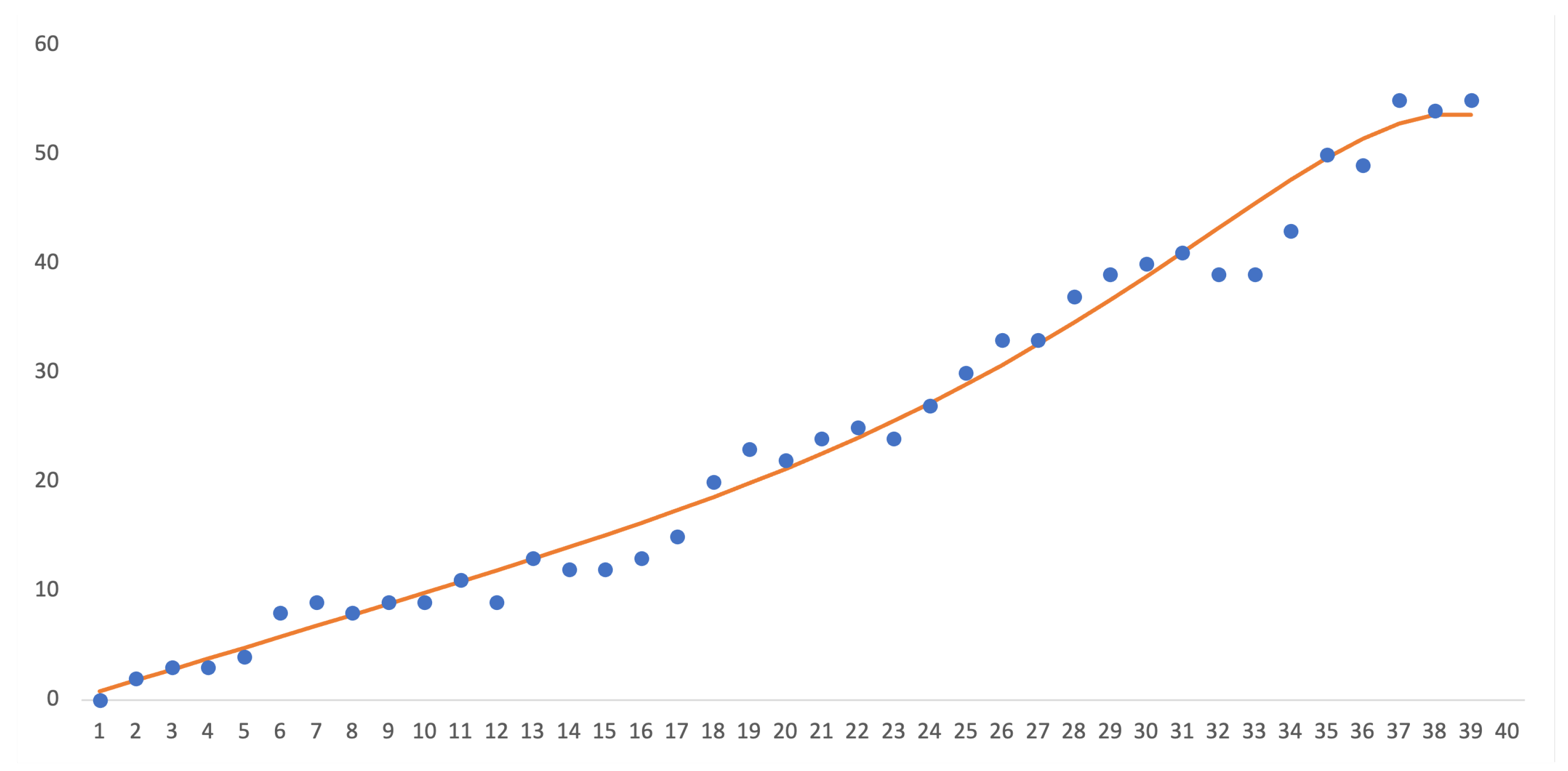
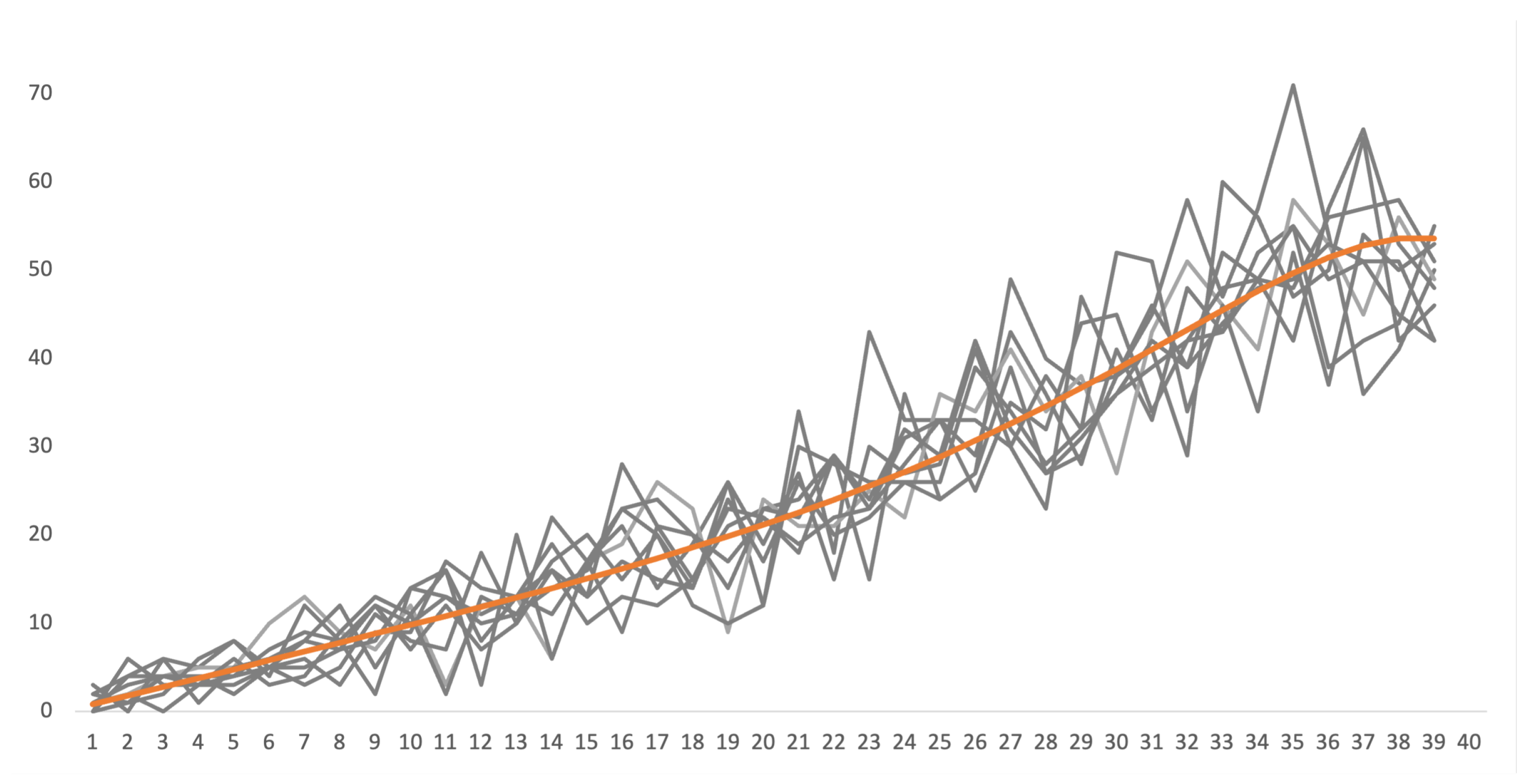
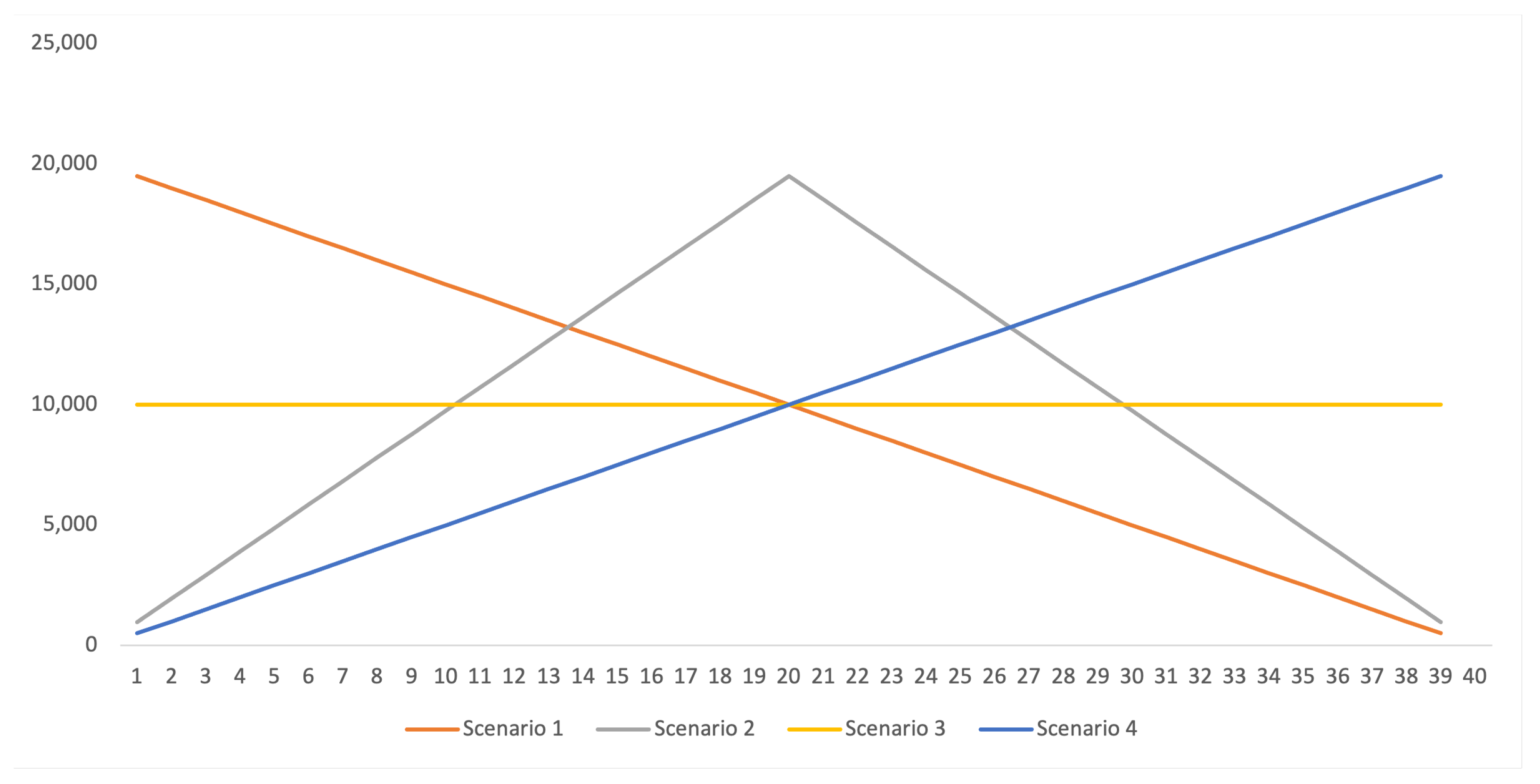
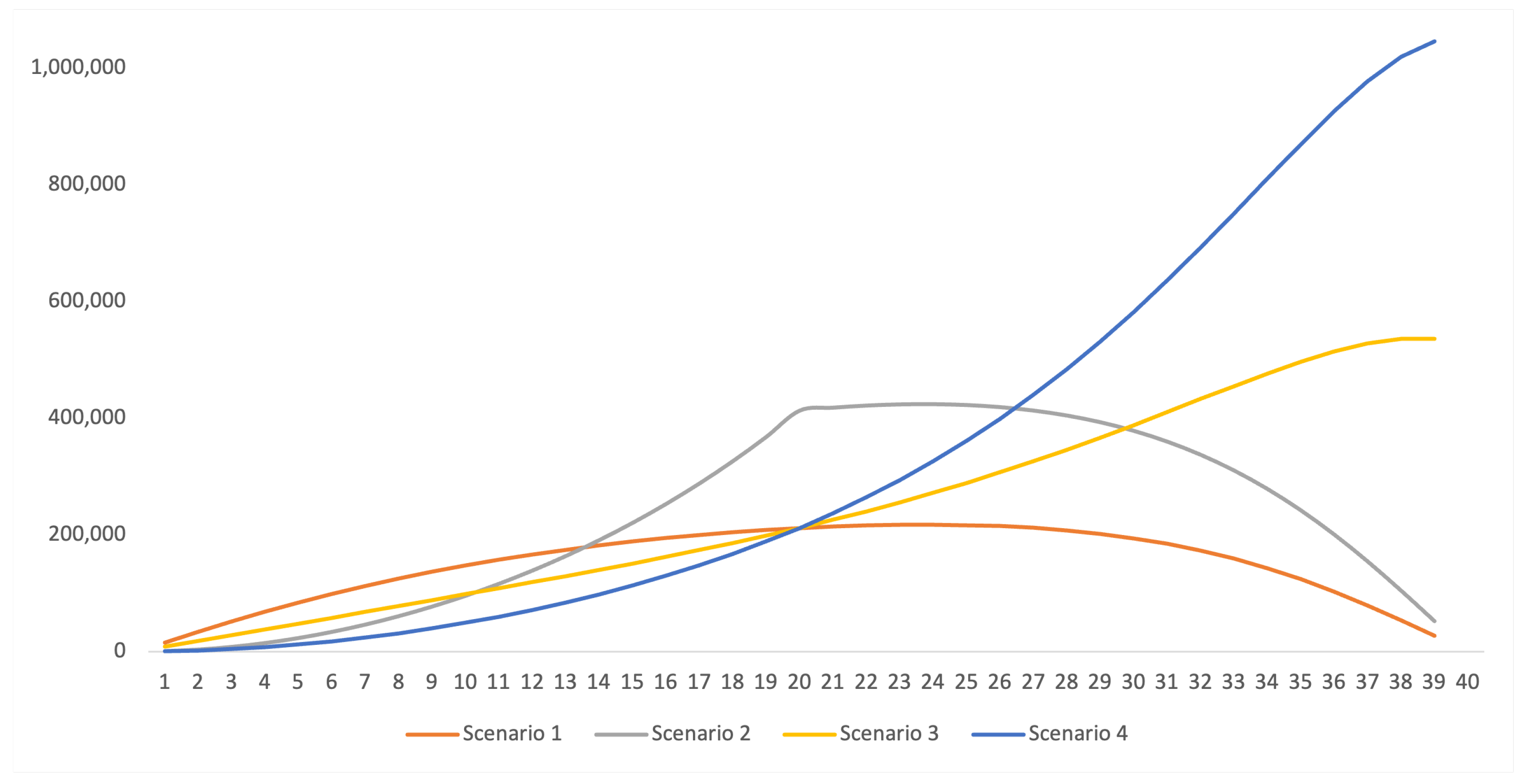
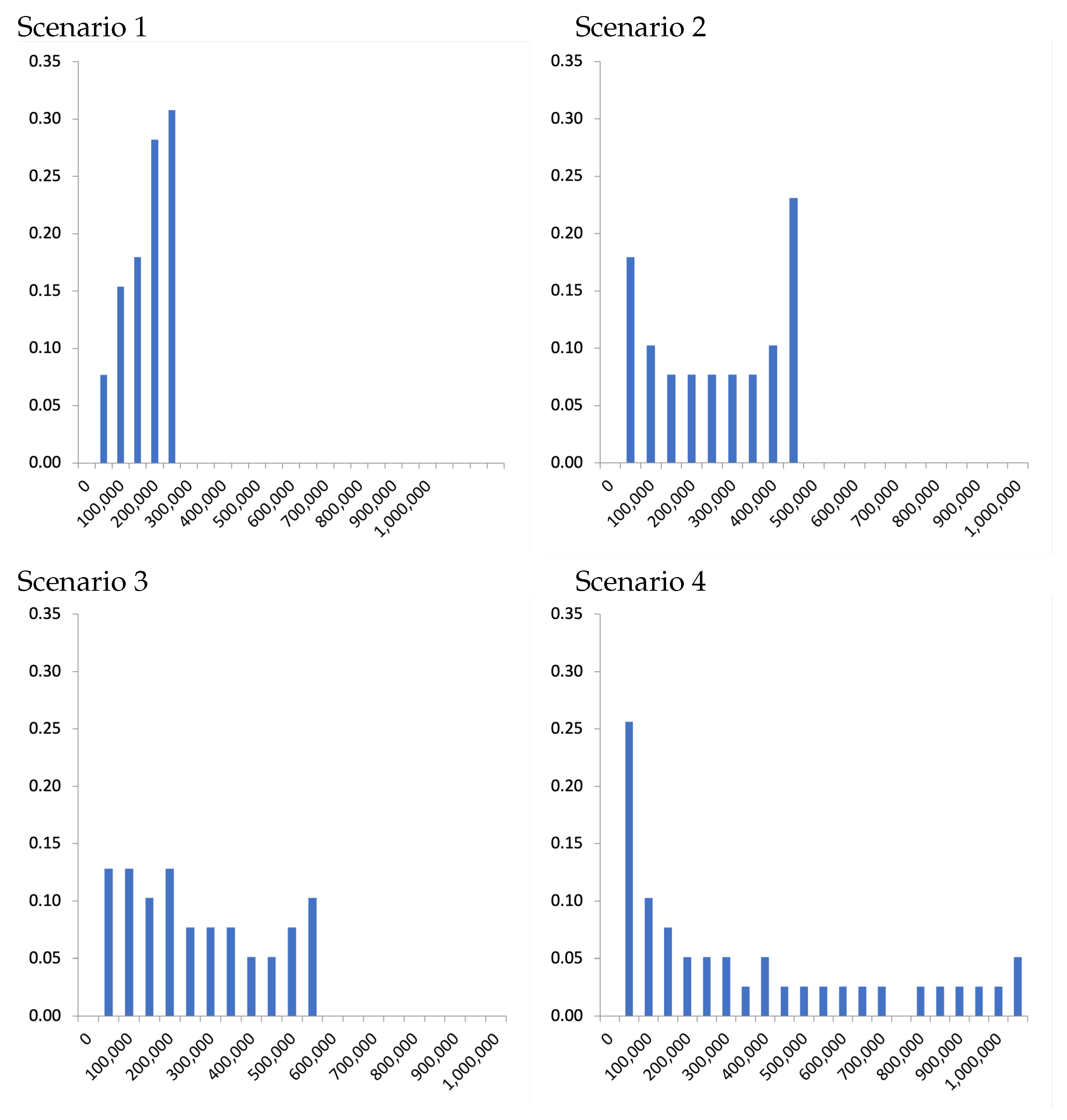
| Age | Interval | ||||||
|---|---|---|---|---|---|---|---|
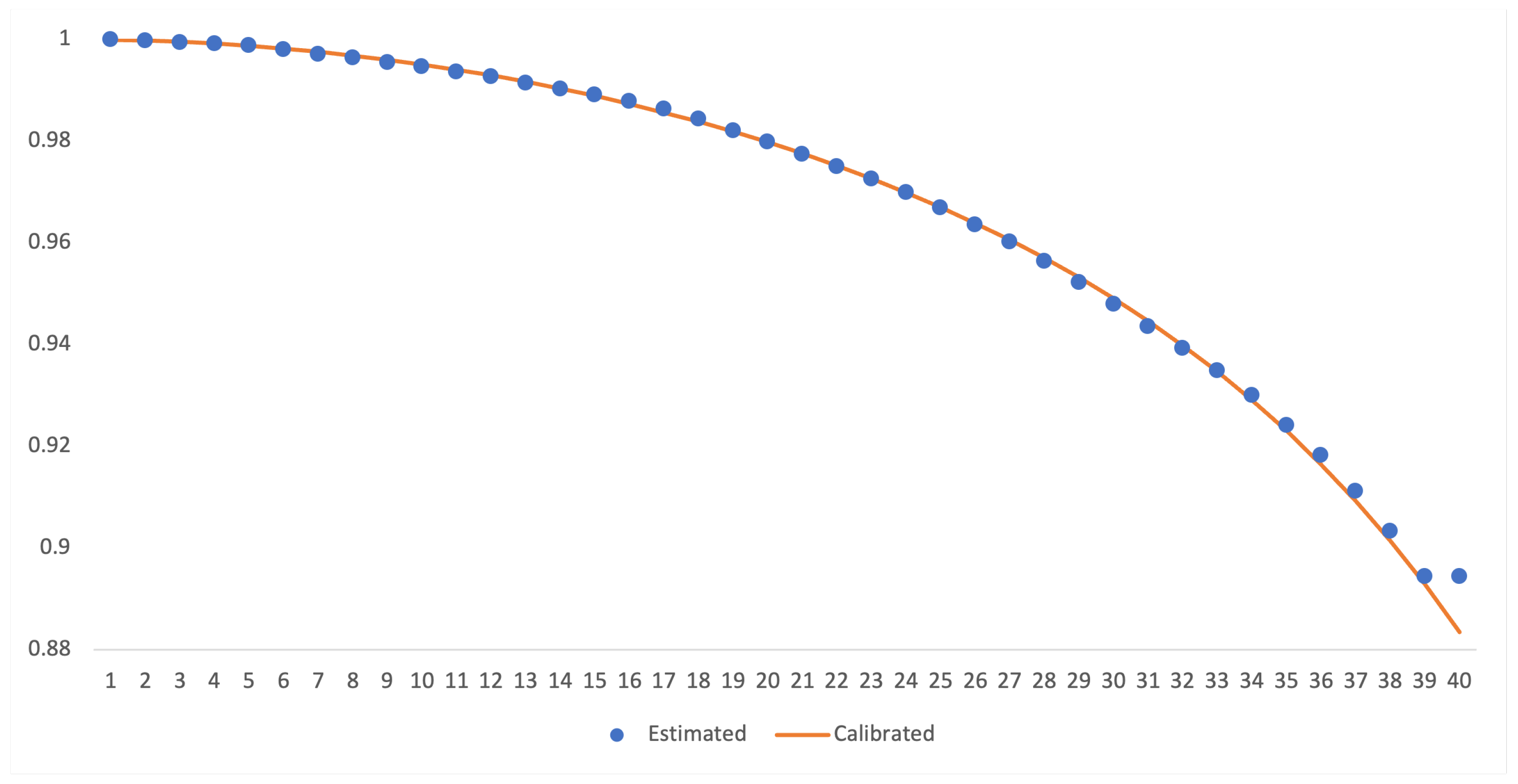
| 1 | [0, 1) | 0 | 0 | 10,479 | 0.000000 | 1.000000 | 1.000000 |
| 2 | [1, 2) | 2 | 12 | 10,479 | 0.000191 | 0.999809 | 0.999809 |
| 3 | [2, 3) | 3 | 0 | 10,465 | 0.000287 | 0.999713 | 0.999522 |
| 4 | [3, 4) | 3 | 25 | 10,462 | 0.000287 | 0.999713 | 0.999235 |
| 5 | [4, 5) | 4 | 23 | 10,434 | 0.000384 | 0.999616 | 0.998852 |
| 6 | [5, 6) | 8 | 3 | 10,407 | 0.000769 | 0.999231 | 0.998084 |
| 7 | [6, 7) | 9 | 23 | 10,396 | 0.000867 | 0.999133 | 0.997219 |
| 8 | [7, 8) | 8 | 4 | 10,364 | 0.000772 | 0.999228 | 0.996449 |
| 9 | [8, 9) | 9 | 7 | 10,352 | 0.000870 | 0.999130 | 0.995583 |
| 10 | [9, 10) | 9 | 43 | 10,336 | 0.000873 | 0.999127 | 0.994714 |
| 11 | [10, 11) | 11 | 10 | 10,284 | 0.001070 | 0.998930 | 0.993649 |
| 12 | [11, 12) | 9 | 24 | 10,263 | 0.000878 | 0.999122 | 0.992777 |
| 13 | [12, 13) | 13 | 77 | 10,230 | 0.001276 | 0.998724 | 0.991511 |
| 14 | [13, 14) | 12 | 67 | 10,140 | 0.001187 | 0.998813 | 0.990333 |
| 15 | [14, 15) | 12 | 13 | 10,061 | 0.001193 | 0.998807 | 0.989151 |
| 16 | [15, 16) | 13 | 56 | 10,036 | 0.001299 | 0.998701 | 0.987866 |
| 17 | [16, 17) | 15 | 5 | 9967 | 0.001505 | 0.998495 | 0.986379 |
| 18 | [17, 18) | 20 | 7 | 9947 | 0.002011 | 0.997989 | 0.984395 |
| 19 | [18, 19) | 23 | 8 | 9920 | 0.002319 | 0.997681 | 0.982112 |
| 20 | [19, 20) | 22 | 9 | 9889 | 0.002226 | 0.997774 | 0.979926 |
| 21 | [20, 21) | 24 | 23 | 9858 | 0.002437 | 0.997563 | 0.977538 |
| 22 | [21, 22) | 25 | 0 | 9811 | 0.002548 | 0.997452 | 0.975047 |
| 23 | [22, 23) | 24 | 0 | 9786 | 0.002452 | 0.997548 | 0.972656 |
| 24 | [23, 24) | 27 | 0 | 9762 | 0.002766 | 0.997234 | 0.969965 |
| 25 | [24, 25) | 30 | 15 | 9735 | 0.003084 | 0.996916 | 0.966974 |
| 26 | [25, 26) | 33 | 56 | 9690 | 0.003415 | 0.996585 | 0.963671 |
| 27 | [26, 27) | 33 | 275 | 9601 | 0.003487 | 0.996513 | 0.960311 |
| 28 | [27, 28) | 37 | 106 | 9293 | 0.004004 | 0.995996 | 0.956465 |
| 29 | [28, 29) | 39 | 200 | 9150 | 0.004309 | 0.995691 | 0.952344 |
| 30 | [29, 30) | 40 | 85 | 8911 | 0.004510 | 0.995490 | 0.948048 |
| 31 | [30, 31) | 41 | 98 | 8786 | 0.004693 | 0.995307 | 0.943599 |
| 32 | [31, 32) | 39 | 104 | 8647 | 0.004538 | 0.995462 | 0.939318 |
| 33 | [32, 33) | 39 | 198 | 8504 | 0.004640 | 0.995360 | 0.934959 |
| 34 | [33, 34) | 43 | 155 | 8267 | 0.005251 | 0.994749 | 0.930050 |
| 35 | [34, 35) | 50 | 200 | 8069 | 0.006274 | 0.993726 | 0.924215 |
| 36 | [35, 36) | 49 | 250 | 7819 | 0.006369 | 0.993631 | 0.918329 |
| 37 | [36, 37) | 55 | 900 | 7520 | 0.007779 | 0.992221 | 0.911185 |
| 38 | [37, 38) | 54 | 450 | 6565 | 0.008517 | 0.991483 | 0.903424 |
| 39 | [38, 39) | 55 | 1000 | 6061 | 0.009890 | 0.990110 | 0.894489 |
| 40 | [39, 40) | 0 | 5006 | 5006 | 0.000000 | 1.000000 | 0.894489 |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
|---|---|---|---|---|
| VaR | ||||
| 95% | 216,647.65 | 422,462.92 | 528,868.31 | 981,093.91 |
| 99% | 217,283.22 | 423,702.27 | 536,135.02 | 1,035,259.28 |
| ES | ||||
| 95% | 217,260.50 | 423,657.97 | 536,130.62 | 1,032,050.98 |
| 99% | 217,355.16 | 423,842.57 | 536,148.96 | 1,045,418.92 |
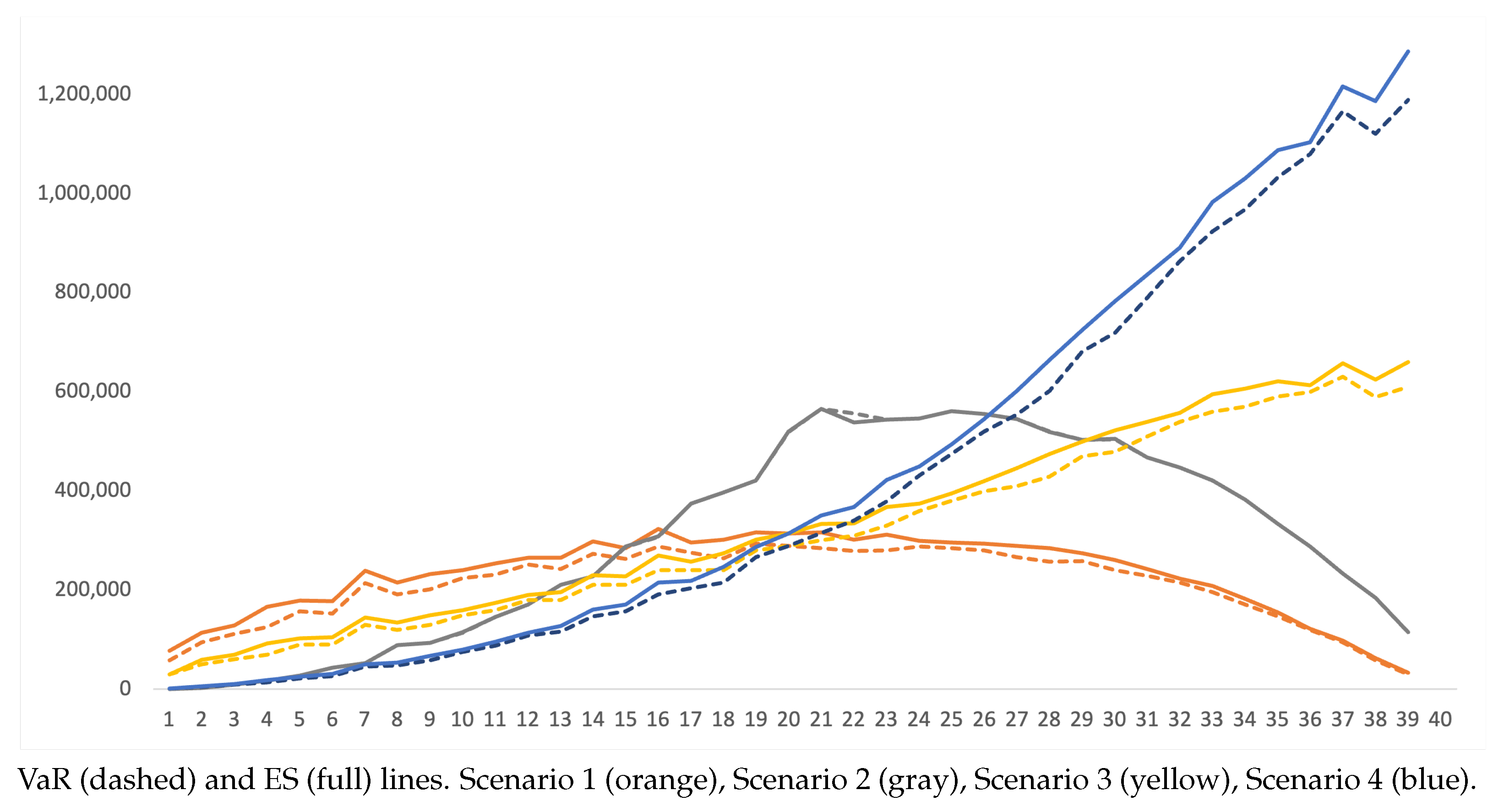
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | VaR 95 | ES 95 | VaR 99 | ES 99 | VaR 95 | ES 95 | VaR 99 | ES 99 | VaR 95 | ES 95 | VaR 99 | ES 99 | VaR 95 | ES 95 | VaR 99 | ES 99 |
| 1 | 58,500 | 78,000 | 78,000 | 78,500 | 2925 | 2925 | 2925 | 2925 | 30,000 | 30,500 | 40,000 | 40,500 | 1500 | 2000 | 2050 | 2150 |
| 2 | 95,000 | 114,000 | 114,000 | 114,500 | 9750 | 9750 | 9750 | 9750 | 50,000 | 60,000 | 60,500 | 70,000 | 5000 | 6000 | 6500 | 7000 |
| 3 | 111,925 | 129,500 | 129,500 | 129,550 | 17,696 | 17,843 | 17,843 | 20,475 | 60,500 | 70,000 | 72,500 | 75,000 | 9075 | 10,500 | 11,000 | 12,500 |
| 4 | 126,000 | 166,500 | 162,180 | 180,000 | 27,300 | 27,300 | 27,300 | 28,080 | 70,000 | 92,500 | 90,100 | 100,000 | 14,000 | 18,500 | 18,020 | 20,000 |
| 5 | 157,500 | 179,375 | 175,175 | 192,500 | 43,875 | 43,875 | 43,875 | 44,363 | 90,000 | 102,500 | 100,100 | 110,000 | 22,500 | 25,625 | 25,025 | 27,500 |
| 6 | 153,000 | 178,500 | 170,340 | 204,000 | 52,650 | 52,650 | 52,650 | 52,650 | 90,000 | 105,000 | 100,200 | 120,000 | 27,000 | 31,500 | 30,060 | 36,000 |
| 7 | 214,500 | 239,250 | 231,165 | 247,500 | 88,725 | 88,725 | 88,725 | 88,725 | 130,000 | 145,000 | 140,100 | 150,000 | 45,500 | 50,750 | 49,035 | 52,500 |
| 8 | 192,000 | 216,000 | 224,000 | 255,000 | 93,600 | 93,600 | 93,600 | 94,380 | 120,000 | 135,000 | 140,000 | 145,000 | 48,000 | 54,000 | 56,000 | 57,500 |
| 9 | 202,275 | 232,500 | 232,965 | 279,000 | 114,514 | 114,953 | 114,953 | 122,850 | 130,500 | 150,000 | 150,300 | 180,000 | 58,725 | 67,500 | 67,635 | 81,000 |
| 10 | 225,000 | 240,000 | 245,000 | 250,000 | 146,250 | 146,250 | 146,250 | 146,250 | 150,000 | 160,000 | 165,000 | 170,000 | 75,000 | 80,000 | 80,000 | 90,000 |
| 11 | 232,000 | 253,750 | 246,790 | 275,500 | 171,600 | 171,600 | 171,600 | 171,600 | 160,000 | 175,000 | 170,200 | 190,000 | 88,000 | 96,250 | 93,610 | 104,500 |
| 12 | 252,000 | 266,000 | 266,500 | 266,750 | 210,600 | 210,600 | 210,600 | 211,770 | 180,000 | 190,000 | 195,000 | 200,000 | 108,000 | 114,000 | 123,000 | 150,000 |
| 13 | 243,000 | 265,500 | 270,000 | 275,000 | 228,150 | 228,150 | 228,150 | 228,150 | 180,000 | 196,667 | 200,000 | 240,000 | 117,000 | 127,833 | 130,000 | 160,000 |
| 14 | 273,650 | 299,000 | 286,650 | 351,000 | 287,333 | 288,015 | 288,015 | 300,300 | 210,500 | 230,000 | 220,500 | 270,000 | 147,350 | 161,000 | 154,350 | 189,000 |
| 15 | 263,125 | 285,000 | 287,625 | 300,000 | 307,856 | 308,588 | 308,588 | 321,750 | 210,500 | 228,000 | 230,100 | 240,000 | 157,875 | 171,000 | 172,575 | 180,000 |
| 16 | 288,000 | 324,000 | 336,120 | 348,000 | 374,400 | 374,400 | 374,400 | 375,960 | 240,000 | 270,000 | 280,100 | 290,000 | 192,000 | 216,000 | 224,080 | 232,000 |
| 17 | 276,000 | 296,125 | 299,000 | 305,000 | 397,800 | 397,800 | 397,800 | 397,800 | 240,000 | 257,500 | 260,000 | 270,000 | 204,000 | 218,875 | 221,000 | 235,000 |
| 18 | 264,000 | 302,500 | 308,110 | 319,000 | 421,200 | 421,200 | 421,200 | 424,710 | 240,000 | 275,000 | 280,100 | 290,000 | 216,000 | 247,500 | 252,090 | 261,000 |
| 19 | 294,525 | 317,100 | 325,605 | 336,000 | 519,626 | 520,553 | 520,553 | 537,225 | 280,500 | 302,000 | 310,100 | 320,000 | 266,475 | 286,900 | 294,595 | 304,000 |
| 20 | 290,000 | 315,000 | 310,400 | 350,000 | 565,500 | 565,500 | 565,500 | 567,450 | 290,000 | 315,000 | 310,400 | 350,000 | 290,000 | 315,000 | 310,400 | 350,000 |
| 21 | 285,475 | 317,300 | 323,190 | 342,000 | 556,676 | 539,078 | 539,078 | 557,603 | 300,500 | 334,000 | 340,200 | 360,000 | 315,525 | 350,700 | 357,210 | 378,000 |
| 22 | 279,000 | 301,500 | 297,090 | 306,000 | 544,050 | 544,050 | 544,050 | 544,050 | 310,000 | 335,000 | 330,100 | 340,000 | 341,000 | 368,500 | 363,110 | 374,000 |
| 23 | 280,500 | 312,375 | 298,180 | 365,500 | 546,975 | 546,975 | 546,975 | 546,975 | 330,000 | 367,500 | 350,800 | 430,000 | 379,500 | 422,625 | 403,420 | 494,500 |
| 24 | 288,000 | 300,000 | 304,000 | 335,000 | 561,600 | 561,600 | 561,600 | 563,160 | 360,000 | 375,000 | 380,000 | 390,000 | 432,000 | 450,000 | 456,000 | 500,000 |
| 25 | 285,000 | 296,250 | 292,575 | 300,000 | 555,750 | 555,750 | 555,750 | 555,750 | 380,000 | 395,000 | 390,100 | 400,000 | 475,000 | 493,750 | 487,625 | 500,000 |
| 26 | 280,000 | 294,000 | 294,070 | 301,000 | 546,000 | 546,000 | 546,000 | 547,365 | 400,000 | 420,000 | 420,100 | 430,000 | 520,000 | 546,000 | 546,130 | 559,000 |
| 27 | 266,825 | 289,900 | 292,760 | 318,500 | 520,309 | 519,675 | 508,268 | 508,268 | 410,500 | 446,000 | 450,400 | 490,000 | 554,175 | 602,100 | 608,040 | 661,500 |
| 28 | 258,000 | 285,000 | 294,120 | 306,000 | 503,100 | 503,100 | 503,100 | 504,270 | 430,000 | 475,000 | 490,200 | 510,000 | 602,000 | 665,000 | 686,280 | 714,000 |
| 29 | 258,775 | 275,000 | 280,665 | 297,000 | 504,611 | 505,148 | 505,148 | 514,800 | 470,500 | 500,000 | 510,300 | 540,000 | 682,225 | 725,000 | 739,935 | 783,000 |
| 30 | 240,000 | 261,250 | 260,100 | 270,000 | 468,000 | 468,000 | 468,000 | 470,925 | 480,000 | 522,500 | 520,200 | 540,000 | 720,000 | 783,750 | 780,300 | 810,000 |
| 31 | 229,500 | 243,000 | 238,725 | 261,000 | 447,525 | 447,525 | 447,525 | 448,403 | 510,000 | 540,000 | 530,500 | 580,000 | 790,500 | 837,000 | 822,275 | 899,000 |
| 32 | 216,000 | 223,000 | 220,120 | 232,000 | 421,200 | 421,200 | 414,180 | 421,200 | 540,000 | 557,500 | 550,300 | 580,000 | 864,000 | 892,000 | 880,480 | 928,000 |
| 33 | 196,175 | 208,600 | 210,070 | 217,000 | 382,541 | 382,883 | 382,883 | 390,390 | 560,500 | 596,000 | 600,200 | 620,000 | 924,825 | 983,400 | 990,330 | 1,023,000 |
| 34 | 171,000 | 182,000 | 177,180 | 195,000 | 333,450 | 333,450 | 328,185 | 333,450 | 570,000 | 606,667 | 590,600 | 650,000 | 969,000 | 1,031,333 | 1,004,020 | 1,105,000 |
| 35 | 147,625 | 155,500 | 150,275 | 177,500 | 287,869 | 288,113 | 283,238 | 288,113 | 590,500 | 622,000 | 601,100 | 710,000 | 1,033,375 | 1,088,500 | 1,051,925 | 1,242,500 |
| 36 | 120,000 | 122,667 | 122,020 | 124,000 | 234,000 | 234,000 | 234,000 | 234,000 | 600,000 | 613,333 | 610,100 | 620,000 | 1,080,000 | 1,104,000 | 1,098,180 | 1,116,000 |
| 37 | 94,575 | 98,700 | 99,045 | 103,500 | 184,421 | 184,568 | 184,568 | 187,493 | 630,500 | 658,000 | 660,300 | 690,000 | 1,166,425 | 1,217,300 | 1,221,555 | 1,276,500 |
| 38 | 59,000 | 62,500 | 62,050 | 67,000 | 115,050 | 115,050 | 115,050 | 115,245 | 590,000 | 625,000 | 620,500 | 670,000 | 1,121,000 | 1,187,500 | 1,178,950 | 1,273,000 |
| 39 | 30,500 | 33,000 | 34,000 | 34,000 | 59,475 | 59,475 | 59,475 | 59,475 | 610,000 | 660,000 | 680,000 | 690,000 | 1,189,500 | 1,287,000 | 1,326,000 | 1,357,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dala, F.L.; Esquível, M.L.; Gaspar, R.M. Survival Analysis for Credit Risk: A Dynamic Approach for Basel IRB Compliance. Risks 2025, 13, 155. https://doi.org/10.3390/risks13080155
Dala FL, Esquível ML, Gaspar RM. Survival Analysis for Credit Risk: A Dynamic Approach for Basel IRB Compliance. Risks. 2025; 13(8):155. https://doi.org/10.3390/risks13080155
Chicago/Turabian StyleDala, Fernando L., Manuel L. Esquível, and Raquel M. Gaspar. 2025. "Survival Analysis for Credit Risk: A Dynamic Approach for Basel IRB Compliance" Risks 13, no. 8: 155. https://doi.org/10.3390/risks13080155
APA StyleDala, F. L., Esquível, M. L., & Gaspar, R. M. (2025). Survival Analysis for Credit Risk: A Dynamic Approach for Basel IRB Compliance. Risks, 13(8), 155. https://doi.org/10.3390/risks13080155






