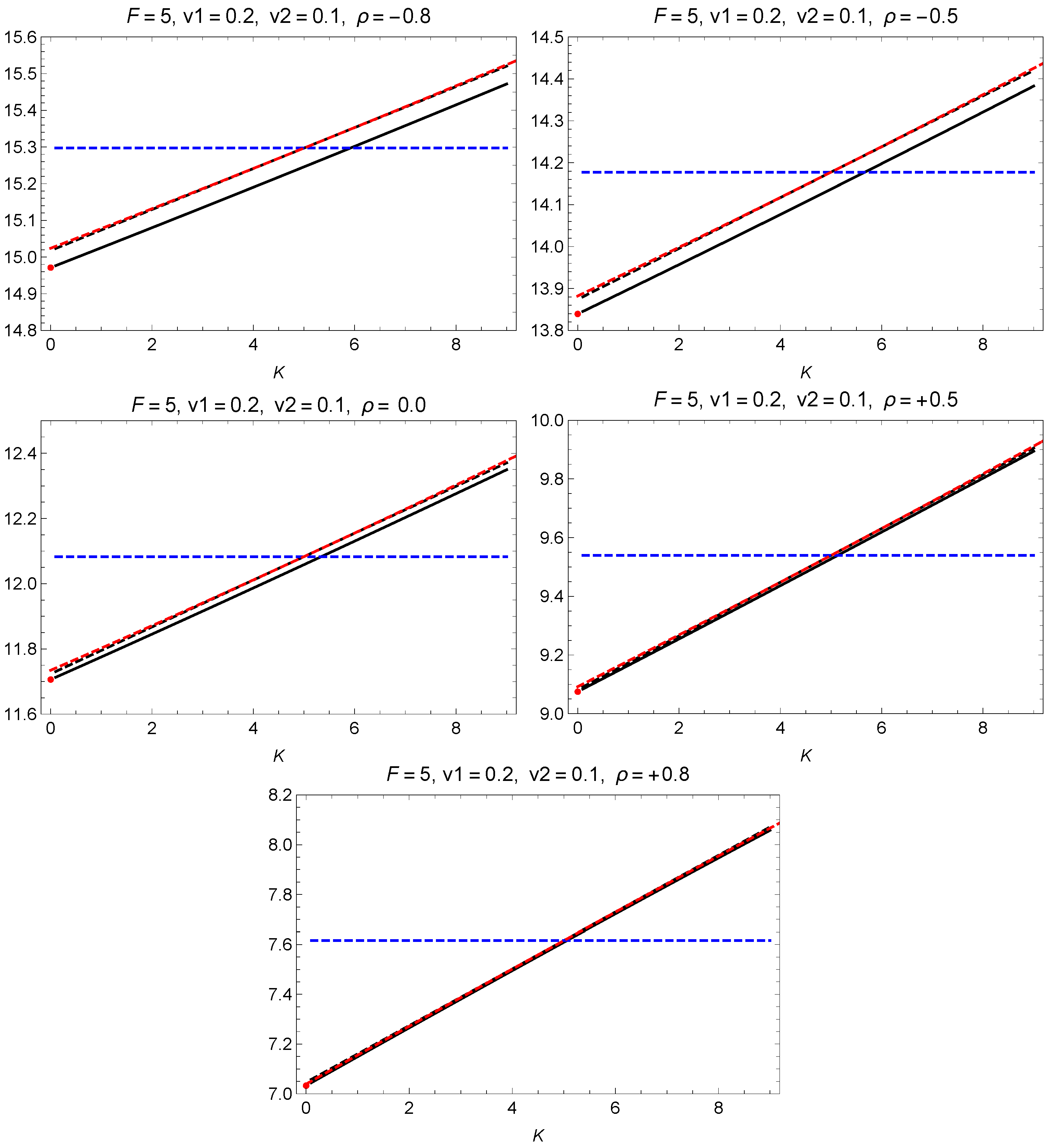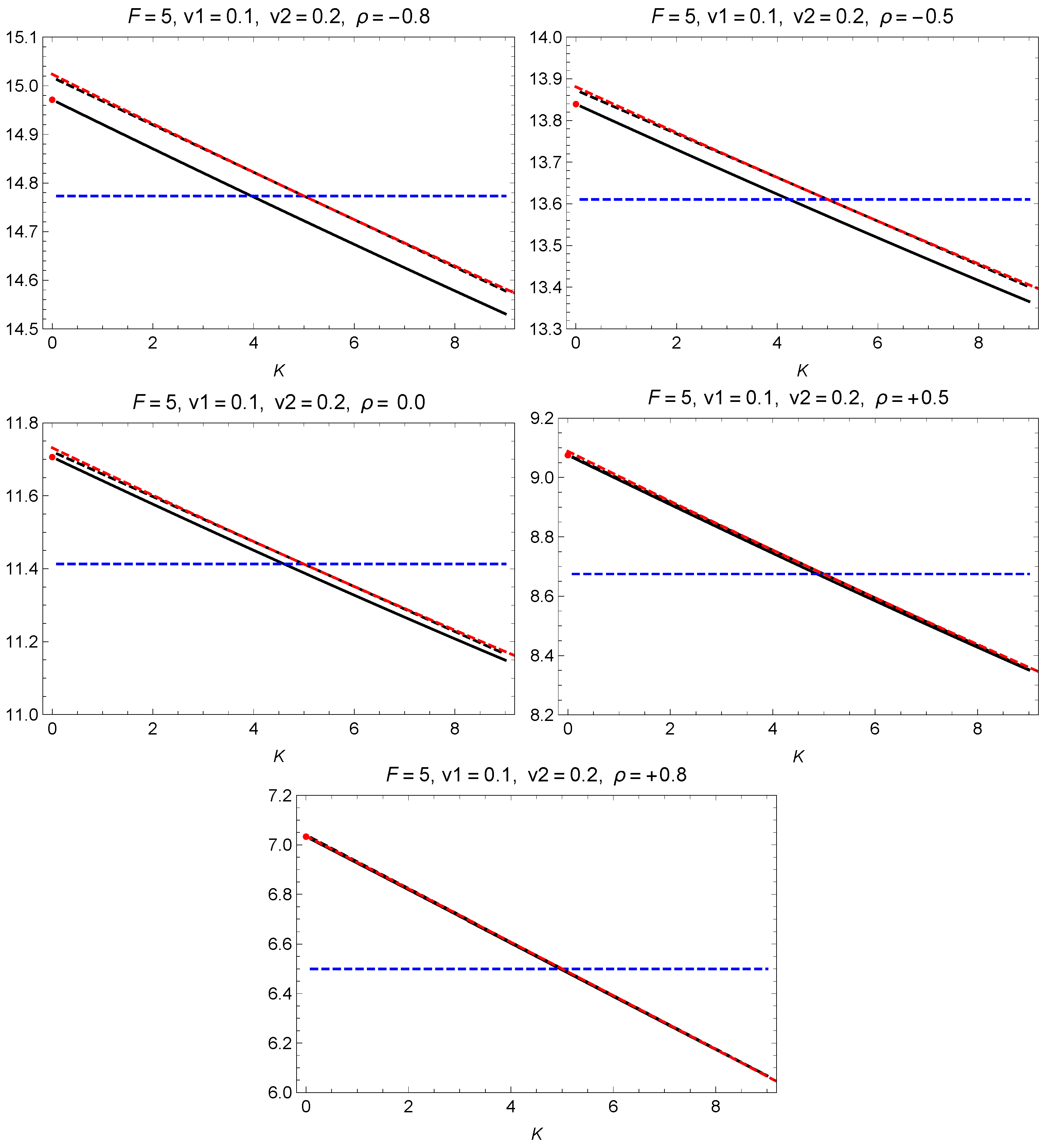Smile-Consistent Spread Skew

Abstract

We study the shape of the Bachelier-implied volatility of a spread option on two assets following correlated local volatility models. This includes the limiting case of spread options on two correlated Black–Scholes (BS) assets. We give an analytical result for the at-the-money (ATM) skew of the spread-implied volatility, which depends only on the components’ ATM volatilities and skews. We also compute the ATM convexity of the implied spread option for the case when the assets follow correlated BS models. The results are extracted from the short-maturity asymptotics for basket options obtained previously by Avellaneda, Boyer-Olson, Busca and Friz and, thus, become exact in the short-maturity limit. Numerical testing of the short-maturity analytical results under the Black–Scholes model and in a local volatility model show good agreement for strikes sufficiently close to the ATM point. Numerical experiments suggest that a linear approximation for the spread Bachelier volatility constructed from the ATM spread volatility and skew gives a good approximation for the spread volatility for highly correlated assets.

1. Introduction

Spread options are popular derivatives in the commodity markets. The European spread options on two assets have a payoff in the form ${\left[\theta (S_1\left(T\right)-S_2\left(T\right)-K)\right]}^{+}$, where $\theta =\pm 1$ corresponds to call/put spread options. See Carmona and Durrleman (2003) for an overview with discussions of their practical applications.

Several approximations and numerical methods have been proposed for their pricing under various assumptions for the distributional properties of the underlying assets ($S_i\left(t\right),i=1,2$). We summarize briefly a few of these methods below, distinguishing between methods that assume correlated log-normally distributed assets and methods that allow for components’ smiles.

The simplest setting assumes that $S_i\left(t\right),i=1,2$ are correlated log-normals. This arises, for example, when the underlying assets are assumed to follow correlated geometric Brownian motions (2 GBMs). Several pricing formulae have been proposed for this case. The simplest approach is the Kirk approximation (Kirk 1995), which assumes that the spread follows a displaced log-normal distribution. Shimko (1994) uses the Bachelier model for the spread and applies a correction, which approximates the true distribution of the spread using the Edgeworth expansion in terms of its skewness and kurtosis, following the Jarrow–Rudd approach. The Shimko approach has been extended to spread options on three assets by Schaefer (Schaefer 2002).

An analytical approximation for spread options’ prices was presented by Carmona and Durrleman (2003), which also gave constraining bounds. Bjerksund and Stensland (2014) proposed an equivalent result and a simpler approximation with a good numerical performance. A good overview of existing analytical methods for pricing spread options on correlated log-normal assets is given by Deng et al. (2008). They also presented an analytical approximation based on an approximation for the optimal exercise boundary, see also Galeeva and Wang (2024). The Kirk approximation has been extended to spread options on three assets in Alos et al. (2011), who also studied the short-maturity limit of these options using asymptotic methods (Avellaneda et al. 2003, 2002; Bayer and Laurence 2004). Liquidity risk effects in pricing spread options have been considered by Pirvu and Yazdanian (2015) and Pirvu and Zhang (2024).

In relaxing the log-normal assumption for the underlying assets ($S_{1,2}\left(T\right)$), several methods have been proposed for pricing spread options. Alexander and Scourse (2004) assume that the components have a bivariate log-normal mixture distribution. If the joint characteristic function of $(S_1\left(T\right),S_2\left(T\right))$ is known, Caldana and Fusai (2013) reduce the spread-pricing problem to the evaluation of one-dimensional integrals. Their method was extended to spread options on multiple assets by Pellegrino (2016). Copula-based methods have been discussed by Herath et al. (2011) and Berton and Mercuri (2024).

In financial practice, the prices of spread options are often quoted in terms of the Bachelier volatility. The Bachelier volatility is appropriate for this case, as the underlying of the spread options can take either sign. As an illustration, we show in Figure 1 the Bachelier implied volatilities of exchange-traded 1-month Calendar Spread Options (CSOs) on WTI crude oil futures, obtained from settlement prices on 12 March 2025 from the CME Group.1 The 1-month CSO payoff is linked to the difference ($F_i\left(T\right)-F_{i+1}\left(T\right)$) between consecutive futures contracts at maturity.

In the spread options literature, the focus has been on computing the prices of these options. We show, here, that there are advantages to working instead with the Bachelier implied volatility of the spread options, which is more tractable in certain respects. Specifically, assuming that the underlying assets follow correlated local volatility models, we show that the expansion of the spread-implied volatility around the at-the-money strike is simply related to the corresponding expansion of the single-asset-implied volatilities in log-moneyness. This is important for spread options on assets with implied volatility smiles, as it gives a simple way to include smile effects in pricing the spread option.

We assume that the assets follow correlated local volatility models. The local volatility model (Dupire 1994; Gatheral 2006) is the simplest dynamic model, which is consistent with observed implied volatility smiles for each underlying asset. From this point of view, our modeling choice is parsimonious. However, we note that more complex models are available: Piterbarg (2006) and Hagan et al. (2020) include stochastic volatility in pricing spread options. The local correlation model used for basket options, see, for example, Guyon and Henry-Labordere (2014) (Chapter 12), can also be applied for spread options. Jump-diffusion models could also be considered. All these models would introduce additional parameters, which require calibration. On the other hand, under the model assumed here, we derive analytical approximations for spread options, which depend only on observable parameters for the underlying assets, and their correlation.

Specifically, we assume that the asset prices follow the process

$$\begin{array}{c}\hfill {\displaystyle \frac{d{S}_i\left(t\right)}{S_i\left(t\right)}}={\sigma }_i\left(S_i\right)d{W}_t^{\left(i\right)}+rdt,\mathrm{corr}(d{W}_t^{\left(1\right)},d{W}_t^{\left(2\right)})=\rho ,S_i\left(0\right)=S_{i,0}.\end{array}$$

(1)

This formulation of the local volatility model is appropriate for cases when the asset prices ($S_i$) are strictly positive, as in equities, FX, and certain futures on positive definite assets. For this case, it is natural to quote implied volatilities as Black–Scholes (log-normal) volatilities.

We use short-maturity asymptotic methods to derive the ATM level and skew of the Bachelier-implied volatility of the spread option. The main result is stated in Proposition 1. An analytical result for the spread convexity is given in Proposition 2 for the case of spread options on log-normally distributed assets. The method of the proof is similar to that used in Pirjol (2023) to extract the ATM skew of a basket option from the short-maturity asymptotic results for basket options in Avellaneda et al. (2002). The result is also similar in spirit to those in Durrleman and El Karoui (2007), which gave analytical results for the ATM volatility, skew, and convexity of FX spread options.

For certain applications, it is convenient to relax the positivity assumption for the $S_i$ asset prices, for example, when these assets are interest rates. The model (1) must be modified by replacing $S_i{\sigma }_i\left(S_i\right)\mapsto {\sigma }_{N,i}\left(S_i\right)$.2 For this case, it is natural to express the ATM spread volatility and skew in terms of the Bachelier ATM volatility and skews of the individual names. The result is given in Proposition 3 and reproduces the result of Piterbarg (2006).

The theoretical predictions for the spread-implied volatility are tested in Section 3 for spread options on log-normally distributed assets, compared with direct spread-option pricing by numerical integration. Similar tests are presented in Section 4 for spread options on two assets with an implied volatility smile, by comparing with a Monte Carlo simulation.

2. Spread Options’ Bachelier-Implied Volatility

Consider spread options on the spread between two assets ($S_i\left(t\right)$), which follow correlated local volatility models with local volatility functions (${\sigma }_i\left(S\right)$):

$$\begin{array}{c}\hfill {\displaystyle \frac{d{S}_i\left(t\right)}{S_i\left(t\right)}}={\sigma }_i\left(S_i\right)d{W}_t^{\left(i\right)}+rdt,\mathrm{corr}(d{W}_t^{\left(1\right)},d{W}_t^{\left(2\right)})=\rho .\end{array}$$

(2)

The initial conditions are $S_i\left(0\right)=S_{i,0}$.

We consider spread options on these two assets. The call and put spread options have prices

$$C_s(K,T)=e^{-rT}\mathbb{E}\left[{(S_1\left(T\right)-S_2\left(T\right)-K)}^{+}\right]$$

(3)

$$P_s(K,T)=e^{-rT}\mathbb{E}\left[{(K-S_1\left(T\right)+S_2\left(T\right))}^{+}\right].$$

(4)

The underlying for spread options is the spread $s\left(t\right)=S_1\left(t\right)-S_2\left(t\right)$, which can take either sign. Therefore, the appropriate volatility quotation is in terms of the Bachelier-implied volatility.

Recall the Bachelier call option pricing formula for the (undiscounted) price of an option on an asset with forward price $\mathbb{E}\left[S\right(T\left)\right]=F$:

$$C_B(K,T;F,{\sigma }_N)=\mathbb{E}\left[{(S_T-K)}^{+}\right]=(F-K)\Phi \left({\displaystyle \frac{F-K}{{\sigma }_N\sqrt{T}}}\right)+{\displaystyle \frac{{\sigma }_N\sqrt{T}}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2{\sigma }_N^{2}T}}{(K-F)}^2},$$

(5)

where ${\sigma }_N$ is the so-called normal or Bachelier-implied volatility. The Bachelier price depends only on $y=K-F$ and $v={\sigma }_N\sqrt{T}$.

The Bachelier-implied volatility of a spread option (${\sigma }_s(K,T)$) is defined in terms of the spread option price ($C_s(K,T)$) as

$$C_s(K,T)=e^{-rT}{C}_B(K,T;F_s,{\sigma }_s(K,T)),$$

(6)

where $F_s=F_1-F_2$ is the forward spread, expressed in terms of the forwards of the two spread components ($F_i=\mathbb{E}\left[S_i\left(T\right)\right]=S_{i,0}{e}^{rT}$).

One unusual feature of the Bachelier-implied volatility is that it is bounded from above, in contrast to the usual Black–Scholes (log-normal)-implied volatility, which may take arbitrarily high values. As $\sigma$ increases, the Bachelier price (5) increases monotonically and can exceed the Merton bound ($C(K,T)<F$). This bound holds only if an explicit upper bound on $\sigma$ is enforced. However, this is not expected to be an issue for spread options for which there is no analog of the Merton upper bound on prices.

The implied volatility of the spread option (${\sigma }_s(K,T)$) is expanded around the ATM point as follows (we drop the dependence on T for simplicity):

$${\sigma }_s(K,T)={\sigma }_s+s_s(K-F_s)+{\displaystyle \frac{1}{2}}{\kappa }_s{(K-F_s)}^2+O\left({(K-F_s)}^3\right),$$

(7)

where the ATM spread option volatility is ${\sigma }_s:={\sigma }_s(F_s,T)$, and the higher-order coefficients are the ATM spread skew ($s_s$) and convexity (${\kappa }_s$).

Assume that the Black–Scholes (log-normal)-implied volatilities of the single-name options on $S_{1,2}$ are known. This is the case for equities, FX, and futures, which can take only positive values. The analogous result for the case when the single-name Bachelier implied volatilities are known is given below in Proposition 3.

Denote ${\sigma }_{\mathrm{BS}}^{\left(i\right)}(x,T)$ as the implied volatility of an option on asset $i=1,2$ with log-moneyness $x=\log (K/F_i\left(T\right))$. The first two terms in the expansion of ${\sigma }_{\mathrm{BS}}^{\left(i\right)}(x,T)$ in powers of log-moneyness give the ATM level and skew of the asset’s implied volatility.

$$\begin{array}{c}\hfill {\sigma }_{\mathrm{BS}}^{\left(i\right)}(x,T)={\sigma }_i\left(T\right)+s_i\left(T\right)x+{\displaystyle \frac{1}{2}}{k}_i\left(T\right)x^2+O\left(x^3\right).\end{array}$$

(8)

The following result gives the short-maturity asymptotics for the ATM spread volatility (${\sigma }_s$) and skew ($s_s$) in terms of the single-name parameters (${\sigma }_i,s_i$) and the correlation ($\rho$). Recall that the ATM point for the spread option corresponds to strike $K=F_s=F_1-F_2$. Since we work in the short-maturity limit, all maturity T dependence disappears, and we drop, for simplicity, the maturity argument (T) in all the quantities involved.

Proposition 1.

Assume that the two assets ($S_i\left(t\right)$) follow correlated local volatility models (1). The implied spread parameters (${\sigma }_s,s_s$) are expressed in terms of the components’ Black–Scholes-implied volatilities and skews (${\sigma }_i,s_i,i=1,2$), defined as in (8), as follows:

The ATM-implied Bachelier volatility of the spread option is

$${\sigma }_s^2=F_1^2{\sigma }_1^2+F_2^2{\sigma }_2^2-2\rho F_1{F}_2{\sigma }_1{\sigma }_2.$$

(9)

The ATM skew of the spread-implied volatility is

$$s_s={\displaystyle \frac{1}{2{\sigma }_s^3}}\left(s_{BS}+s_s\right),$$

(10)

where

$$\begin{array}{cc}\hfill s_{BS}& =(F_1^3{\sigma }_1^4-F_2^3{\sigma }_2^4)-2\rho F_1{F}_2{\sigma }_1{\sigma }_2(F_1{\sigma }_1^2-F_2{\sigma }_2^2)-{\rho }^2{F}_1{F}_2{\sigma }_1^2{\sigma }_2^2(F_1-F_2)\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill s_s& =2F_1{\sigma }_1{(F_1{\sigma }_1-\rho F_2{\sigma }_2)}^2{s}_1-2F_2{\sigma }_2{(F_1{\sigma }_1\rho -F_2{\sigma }_2)}^2{s}_2.\hfill \end{array}$$

(12)

Proof. 

The proof is given in Appendix B. □

Remark 1.

Assume that the two assets follow correlated Black–Scholes models ($s_i=0$). In the limiting case of assets with the same forward price ($F_1=F_2=F$), the ATM spread level and skew become

$${\sigma }_s^2=F^2({\sigma }_1^2+{\sigma }_2^2-2\rho {\sigma }_1{\sigma }_2),s_s={\displaystyle \frac{1}{2{\sigma }_s}}({\sigma }_1^2-{\sigma }_2^2).$$

(13)

The ATM skew vanishes at the equal volatility limit, regardless of the correlation.

The result of Proposition 1 is easily extended also to the ATM convexity of the implied spread volatility. This results in lengthy formulae, so we give, here, only the result for the spread option on correlated Black–Scholes assets.

Proposition 2.

The convexity of the Bachelier spread option implied volatility in the Black–Scholes model has the form

$${\kappa }_s={\displaystyle \frac{1}{6{\sigma }_s^{7}D}}\sum _{k=0}^5{c}_k{\rho }^k,D:=F_1^2{\sigma }_1+F_2^2{\sigma }_2-\rho F_1{F}_2({\sigma }_1+{\sigma }_2).$$

(14)

where the coefficients $c_k$ are given in Appendix C.

Spread Options on Assets Described by Bachelier Volatility

In some cases, the individual assets ($S_{1,2}$) can take either sign. This can happen, for example, with spread options on interest rates. For this case, the appropriate implied volatility for single-name options is the Bachelier (normal)-implied volatility. Denote the single-name Bachelier-implied volatilities as ${\sigma }_{\mathrm{N}}^{\left(i\right)}\left(x\right)$. They are expanded in powers of the differences ($x=K-F_i$) as

$${\sigma }_{\mathrm{N}}^{\left(i\right)}\left(x\right)={\sigma }_{N,i}+s_{N,i}x+O\left(x^2\right),i=1,2$$

(15)

with ${\sigma }_{N,i}$ and $s_{N,i}$ as the ATM level and skew of the Bachelier-implied volatility.

The following result gives the ATM Bachelier level and skew of the implied spread volatility, expressed in terms of ${\sigma }_{N,i}$ and $s_{N,i}$.

Proposition 3.

Assume that the Bachelier single-name ATM volatilities (${\sigma }_{N,i}$) and skews ($s_{N,i}$) are given.

Then, the ATM spread Bachelier volatility is

$${\sigma }_s^2={\sigma }_{N,1}^2+{\sigma }_{N,2}^2-2\rho {\sigma }_{N,1}{\sigma }_{N,2}.$$

(16)

The ATM skew of the spread-implied volatility is

$$s_s\left(\rho \right)={\displaystyle \frac{1}{{\sigma }_s^3}}\left({\sigma }_{N,1}{({\sigma }_{N,1}-\rho {\sigma }_{N,2})}^2{s}_{N,1}-{\sigma }_{N,2}{({\sigma }_{N,2}-\rho {\sigma }_{N,1})}^2{s}_{N,2}\right).$$

(17)

Proof. 

The proof is a simple modification of the proof of Proposition 1 and is omitted. □

Remark 2.

Results (16) and (17) can be recovered from Proposition 6.2 in Piterbarg (2006) by taking the local volatility limit in that result—by setting the stochastic volatility factor $z\left(t\right)\to 1$. The relation between the notations of Piterbarg (2006) and those used here is

$$p_i\mapsto {\sigma }_{N,i},q_i\mapsto 2s_{N,i}$$

(18)

and is analogous for the spread quantities ($p\mapsto {\sigma }_s,q\mapsto 2s_s$). Substituting $p_i$ and $q_i$ into the expressions for p and q in Piterbarg (2006) yields the same results as (16) and (17).

In the limiting case, when the two assets follow Bachelier models and, thus, have vanishing skews ($s_{N,1}=s_{N,2}=0$), the spread skew also vanishes. This is intuitively clear, since the difference of two normally distributed random variables is also normally distributed.

3. Numerical Tests in the Black–Scholes Model

We present, in this section, a few numerical tests for the predictions of this paper, considering spread options on two correlated Black–Scholes assets. The valuation of the spread options for this case can be performed numerically by integration over the bivariate normal distribution. For convenience, we summarize the relevant formulae in the Appendix A.

Test 1. Correlation dependence. In the first test, we compare the short-maturity predictions for the ATM level and skew of the spread-implied volatility against exact numerical evaluations by varying the correlation ($\rho$) at fixed $F_i,{\sigma }_i$.

Consider a spread option on two Black–Scholes assets with parameters

$$F_1=55,F_2=50,{\sigma }_1=0.2,{\sigma }_1=0.1,T=1.$$

(19)

The short-maturity spread ATM volatility and skew given in (9) and (10) are shown as the solid curves in Figure 2 as functions of the correlation $\rho \in [0,1]$. The left plot shows the ATM Bachelier spread volatility from the short-maturity result (9) (solid curve) and from a numerical evaluation of the spread option (red dots) by numerical integration over the bivariate joint distribution. The right plot shows the ATM spread skew, evaluated by central finite differences ($s_{s,ATM}={\displaystyle \frac{1}{2\Delta }}({\sigma }_s(F_s+\Delta ,T)-{\sigma }_s(F_s-\Delta ,T))$) with $\Delta =0.01$.

In a previous paper Pirjol (2023), we showed that the ATM skew of a basket of correlated Black–Scholes assets is non-negative in the short-maturity limit for any volatilities and correlation structure. From (10), we see that this does not hold for the ATM skew of a spread option. As ${\sigma }_1\to 0$, the term $s_{BS}$ becomes negative and approaches $-F_2^3{\sigma }_2^2<0$. This shows that for ${\sigma }_1$ values sufficiently low, the ATM spread skew may become negative in the BS model.

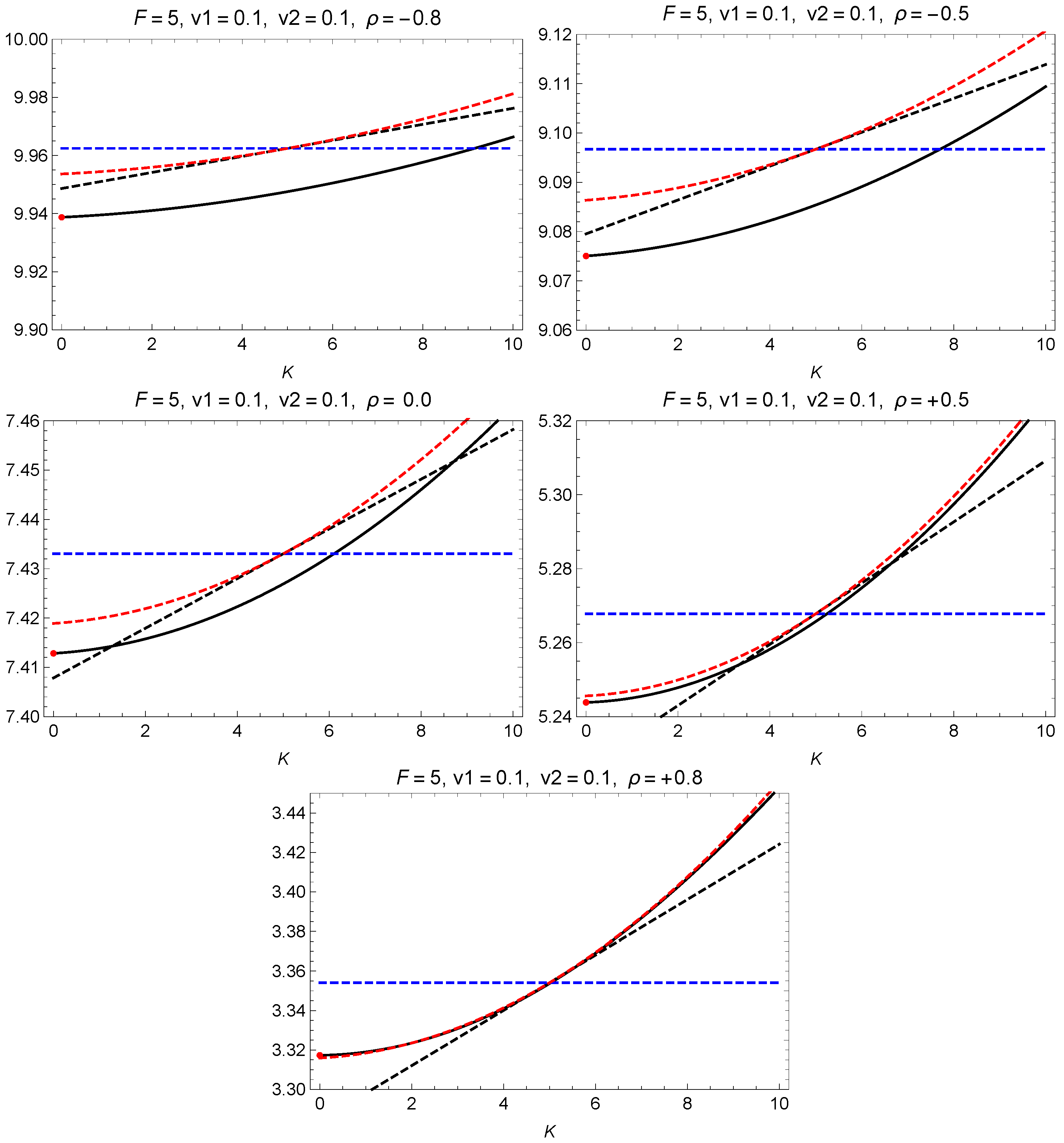
Test 2. Strike dependence. In the second test, we compare the exact Bachelier spread-implied volatility (${\sigma }_s\left(K\right)$) obtained by numerical integration against the short-maturity asymptotic result, constructed using the ATM level and skew given by Proposition 1 and the convexity from Proposition 2.

Using the analytical predictions for the ATM spread volatility, skew, and convexity (${\sigma }_s$, $s_s$, and ${\kappa }_s$), we can construct a linear and a quadratic approximation for the spread volatility, defined as

$$\begin{array}{cc}\hfill {\sigma }_s^{\mathrm{lin}}\left(K\right)& :={\sigma }_s+s_s(K-F_s),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\sigma }_s^{\mathrm{quad}}\left(K\right)& :={\sigma }_s+s_s(K-F_s)+{\displaystyle \frac{1}{2}}{\kappa }_s{(K-F_s)}^2.\hfill \end{array}$$

(21)

These parameters are given explicitly in terms of the Black–Scholes parameters of the underlyings by Proposition 1 (with $s_i=0$) and by Proposition 2.

Assume the same forward prices for the two assets as in the previous test $F_1=55$, $F_2=50$, which corresponds to a spread forward of $F_s=F_1-F_2=5$.

We consider several scenarios:

Scenario (i): The two assets have the same volatility ($v_1=v_2=0.1$). The total spread Bachelier volatility (${\sigma }_s\left(K\right)\sqrt{T}$) is shown in Figure 3 as the solid black curve for several choices of the correlation.

Scenario (ii): The two assets have different volatilities ($v_1=0.2$ and $v_2=0.1$). The total spread Bachelier volatility (${\sigma }_s\left(K\right)\sqrt{T}$) is shown in Figure 4 as the solid black curves for several choices of the correlation.

Scenario (iii): The same as in (i) and (ii) but with $v_1=0.1$ and $v_2=0.2$. The total spread Bachelier volatility (${\sigma }_s\left(K\right)\sqrt{T}$) is shown in Figure 5 as solid black curves for several choices of the correlation. For this scenario, the ATM spread skew is negative.

The spread option prices with zero strike ($K=0$) are known exactly in the Black–Scholes model from the Margrabe formula (Margrabe 1978):

$$\begin{array}{cc}\hfill C_M\left(T\right)& =e^{-rT}\mathbb{E}\left[{(S_1\left(T\right)-S_2\left(T\right))}^{+}\right]\hfill \\ \hfill & =S_{1,0}\Phi \left({\displaystyle \frac{-\log (S_{2,0}/S_{1,0})}{{\sigma }_M\sqrt{T}}}+{\displaystyle \frac{1}{2}}{\sigma }_M\sqrt{T}\right)-S_{2,0}\Phi \left({\displaystyle \frac{-\log (S_{2,0}/S_{1,0})}{{\sigma }_M\sqrt{T}}}-{\displaystyle \frac{1}{2}}{\sigma }_M\sqrt{T}\right),\hfill \end{array}$$

(22)

with ${\sigma }_M^2:={\sigma }_1^2+{\sigma }_2^2-2\rho {\sigma }_1{\sigma }_2$.

For each scenario, the red dot shows the exactly known value of the spread volatility (${\sigma }_s\left(0\right)$) from the Margrabe formula (22). Agreement with this value is a test for the quality of the numerical integration over the bivariate normal distribution used to obtain ${\sigma }_s\left(K\right)$, shown as the solid black curve.

The linear approximation (20) is shown as the black dashed line and the quadratic approximation as the red dashed curve. The horizontal dashed blue line shows the ATM spread volatility (${\sigma }_s$). The linear and quadratic approximations reproduce well the trend of the actual spread volatility around the ATM point, although there is a gap, which is due to subleading $O\left(T\right)$ corrections. The agreement of the linear and quadratic approximations with the numerical valuation improves markedly for large positive correlations for all the scenarios considered.

Test 3. Option maturity sensitivity tests. We present, here, tests for the accuracy of the asymptotic result for the Bachelier volatility of the spread options for several option maturities (T). The tests use the same parameters as above: $F_1=55$ and $F_2=50$, with ${\sigma }_i$ corresponding to scenarios (ii) and (iii). We compare the exact spread volatility computed by numerical integration with the asymptotic result.

The results are shown in

Table 1. Maturity dependence test. Scenario (ii). The table shows the exact Bachelier-implied volatility of a spread option with parameters $F_1=55$, $F_2=50$, and ${\sigma }_i,\rho$, as shown for several maturities (T). The second row shows the relative error with respect to the asymptotic prediction (shown in the last row).

	${\mathit{\sigma }}_1=0.2,{\mathit{\sigma }}_2=0.1$
$\mathit{T}/\mathit{\rho }$	$-\mathbf{0.8}$	$-\mathbf{0.5}$	0	0.5	0.8
0.1	15.2919	14.1734	12.0805	9.5382	7.6151
	−0.034%	−0.028%	−0.020%	−0.013%	−0.008%
0.2	15.2868	14.1693	12.0781	9.5370	7.6145
	−0.067%	−0.057%	−0.040%	−0.025%	−0.017%
0.5	15.2714	14.1572	12.0707	9.5334	7.6125
	−0.168%	−0.143%	−0.101%	−0.062%	−0.043%
1.0	15.2458	14.1370	12.0584	9.5275	7.6093
	−0.335%	−0.285%	−0.203%	−0.125%	−0.085%
asympt.	15.2971	14.1774	12.0830	9.5394	7.6158

and

Table 2. Maturity dependence test. Scenario (iii). Same as Table 1.

	${\mathit{\sigma }}_1=0.1,{\mathit{\sigma }}_2=0.2$
$\mathit{T}/\mathit{\rho }$	$-\mathbf{0.8}$	$-\mathbf{0.5}$	0	0.5	0.8
0.1	14.7682	13.6066	11.4103	8.6736	6.4996
	−0.035%	−0.030%	−0.021%	−0.012%	−0.006%
0.2	14.7631	13.6026	11.4079	8.6725	6.4992
	−0.069%	−0.059%	−0.042%	−0.025%	−0.013%
0.5	14.7477	13.5905	11.4007	8.6693	6.4979
	−0.173%	−0.148%	−0.105%	−0.062%	−0.032%
1.0	14.7223	13.5705	11.3886	8.6639	6.4958
	−0.345%	−0.295%	−0.211%	−0.124%	−0.064%
asympt.	14.7733	13.6107	11.4127	8.6747	6.500

. The tables show the exact Bachelier-implied volatility of an ATM spread option ($K=F_s=5$) obtained by numerical integration, and the analytical asymptotic result, for several maturities. The two tables correspond to scenarios (ii) and (iii), which have higher volatility than scenario (i) and are, thus, more conservative. The second row for each maturity shows the relative error of the asymptotic result. In all the cases considered with maturity T up to 1 year, the relative error of the asymptotic result is less than 0.4%. The error is much smaller for large and positive correlations ($\rho >0.5$), which is often relevant in practical applications of spread options on futures contracts.

Test 4. Spread option pricing tests. We also give performance tests of the linear approximation (20) for pricing spread options. For this test, we use the same parameters as those in Bjerksund and Stensland (2014). Consider a spread option on two assets with maturity $T=1$. The spot prices, volatilities, and dividend yields of the two assets are

$$S_{1,0}=110,S_{2,0}=100,{\sigma }_1=10\%,{\sigma }_2=15\%,,q_1=3\%,q_2=2\%.$$

(23)

The short rate is $r=5\%$. The forward prices are

$$F_1=110e^{(0.05-0.03)·1}=112.222,F_2=100e^{(0.05-0.02)·1}=103.045.$$

(24)

Table 3. Numerical tests for spread options with parameters (23), as in Bjerksund and Stensland (2014). The first row shows the result of the numerical integration and the second row the result from the linear approximation for the spread Bachelier volatility. The third row is the relative error of the linear approximation. For $K=0$, the fourth row shows the exact result from the Margrabe formula.

$\mathit{\rho }$	$-1$	$-0.5$	0	0.3	0.8	1.0
$\mathit{K}$
−20	29.6562	28.9951	28.3814	28.0704	27.7704	27.7541
	29.6556	28.9817	28.3611	28.0515	27.7673	27.7542
	−0.002%	−0.046%	−0.071%	−0.067%	−0.011%	0.001%
−10	21.8686	20.9052	19.8891	19.2703	18.3814	18.2442
	21.8797	20.9031	19.8759	19.2529	18.3728	18.2472
	0.051%	−0.010%	−0.066%	−0.090%	−0.047%	0.016%
0	15.1331	13.9181	12.5238	11.5619	9.6328	8.8215
	15.1554	13.9298	12.5260	11.5588	9.6250	8.8356
	0.147%	0.084%	0.017%	-0.027%	-0.080%	0.159%
Margrabe	15.1330	13.9180	12.5237	11.5618	9.6325	8.8215
5	12.244	10.9564	9.4455	8.3676	5.9672	4.4545
	12.2695	10.9725	9.4535	8.3713	5.9654	4.4645
	0.208%	0.147%	0.085%	0.045%	−0.030%	0.225%
15	7.5217	6.2423	4.7446	3.6799	1.3426	0.0493
	7.5463	6.2572	4.7508	3.6814	1.3374	0.0588
	0.327%	0.239%	0.131%	0.040%	−0.386%	19.54%

shows the exact (first row) and linear approximation (second row) results for the spread option prices with several strikes and correlations. The third row shows the relative error of the linear approximation. For $K=0$, we also show the exact result from the Margrabe formula as a check on the exact evaluation by numerical integration.

The relative error of the linear approximation is less than 1% in almost all the cases (except for $\rho =1.0$ and $K=15$, which have larger errors due to the low option prices). This suggests that the linear approximation could be useful for fast spread option valuation when the desired accuracy is below the 1% level.

4. Numerical Tests for Spread Options on Assets with Smiles

This section presents the numerical tests of our predictions for spread options on assets with non-zero skew. For this test, we assume that the underlyings follow correlated local volatility models ($d{S}_t=S_t\sigma \left(S_t\right)d{W}_t$) with local volatility

$$\sigma \left(S\right)={\sigma }_0\sqrt{1+2\rho \zeta +{\zeta }^2},\zeta ={\displaystyle \frac{\omega }{{\sigma }_0}}\log (S/S_0).$$

(25)

The function $\sigma \left(S\right)$ is the short-maturity limit of the local volatility of the log-normal SABR model (Hagan et al. 2014) with spot volatility $\sigma$, vol-of-vol $\omega$, and correlation $\rho$. The short-maturity asymptotic volatility of this local volatility model coincides with the short-maturity limit of the implied volatility in the stochastic SABR model (Hagan et al. 2002)

$$\underset{T\to 0}{\lim }{\sigma }_{BS}(K,T)=:{\sigma }_{BS,SABR}\left(K\right)={\sigma }_0{\displaystyle \frac{\zeta }{D\left(\zeta \right)}},$$

(26)

with $D\left(\zeta \right)=\log {\displaystyle \frac{\sqrt{1+2\rho \zeta +{\zeta }^2}+\rho +\zeta }{1+\rho }}$. The ATM-implied volatility level and skew in this model are

$${\sigma }_{ATM}={\sigma }_0,s_E={\displaystyle \frac{1}{2}}\rho \omega .$$

(27)

Numerical tests. For the numerical tests, we choose the parameters $S_{0,i}$, ${\sigma }_{0,i}$, and ${\omega }_i,{\rho }_i$, as in

Table 4. Model parameters of the spread components for the local volatility test.

Parameter	Component 1	Component 2
$S_{0,i}$	55	50
${\sigma }_{0,i}$	0.1	0.1
${\omega }_i$	1.0	1.0
${\rho }_i$	−0.75	−0.3

. The risk-free interest rate is $r=0$. The spot volatility values (${\sigma }_{i,0}$) correspond to those in Scenario (i) for the Black–Scholes testing.

Figure 6 shows the BS-implied volatility of the options on the two spread components obtained by MC simulation with $N_{MC}={10}^5$ paths (red) for maturity $T=0.1$, compared with the short-maturity asymptotics (26) (black). The dashed line is a linear approximation with coefficients given by (27)

$${\sigma }_{lin}\left(K\right)={\sigma }_0+s_E\log {\displaystyle \frac{K}{F_s}}.$$

(28)

Consider, now, a spread call option with payoff $\max (S_1\left(T\right)-S_2\left(T\right)-K,0)$, where $S_{1,2}\left(t\right)$ follow correlated local volatility models with $\sigma (·)$ in (25) and correlation ${\rho }_{12}$. We computed the Bachelier-implied volatility of the spread option by MC simulation with $N_{MC}={10}^5$ paths and $n=200$ time steps. The option maturity is $T=0.1$ years.

The ATM spread skew can be estimated by MC simulation using the exact relation

$$s_s\left(T\right):={\displaystyle \frac{d}{dK}}{\sigma }_s(F_s,T)=\sqrt{{\displaystyle \frac{2\pi }{T}}}\left(-D_c(F_s,T)+{\displaystyle \frac{1}{2}}\right)$$

(29)

where $D_c(K,T)$ is the digital call option with payoff $Pa{y}_{D_c}\left(s_T\right)=1_{s_T>K}$.

Proof. 

The option price can be written in terms of the Bachelier spread implied volatility (${\sigma }_s(K,T)$) as

$$\begin{array}{cc}\hfill C(K,T)& =C_B(K,T;{\sigma }_s(K,T),F_s)=-(K-F_s)N(-d)+{\sigma }_s(K,T)\sqrt{{\displaystyle \frac{T}{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{d}^2},\hfill \\ \hfill d& ={\displaystyle \frac{K-F_s}{{\sigma }_s(K,T)\sqrt{T}}}.\hfill \end{array}$$

(30)

Taking the derivative with respect to the strike and setting $K=F_s$, we get

$${\displaystyle \frac{d}{dK}}C(K,T)=-{\displaystyle \frac{1}{2}}+\sqrt{{\displaystyle \frac{T}{2\pi }}}{\partial }_K{\sigma }_s(F_s,T).$$

(31)

The left-hand side is expressed in terms of the digital call option as ${\displaystyle \frac{d}{dK}}C(K,T)=-D_c(K,T)$, which reproduced the stated result (29). □

Table 5. Test results for the ATM spread Bachelier volatility and skew, compared with the short-maturity asymptotics (in the last two columns). The model parameters are as in Table 4, and maturity T = $0.1$. The MC simulation used $N_{MC}=100$ k samples and a discretization with $n=200$ time steps.

${\mathit{\rho }}_{12}$	${\mathit{\sigma }}_{\mathit{s},\mathbf{num}}$	${\mathit{s}}_{\mathit{s},\mathbf{num}}$	${\mathit{\sigma }}_{\mathit{s}}$	${\mathit{s}}_{\mathit{s}}$
−0.8	$9.916\pm 0.045$	$-0.115\pm 0.013$	9.962	−0.118
−0.5	$9.110\pm 0.041$	$-0.104\pm 0.013$	9.097	−0.112
0.0	$7.444\pm 0.034$	$-0.085\pm 0.013$	7.433	−0.101
0.5	$5.287\pm 0.024$	$-0.083\pm 0.013$	5.268	−0.093
0.8	$3.389\pm 0.015$	$-0.098\pm 0.013$	3.354	−0.102

shows the ATM (${\sigma }_{s,num}$) and skew ($s_{s,num}$) of the Bachelier spread implied volatility obtained by MC simulation. These are compared with the analytical results for the ATM level and skew (${\sigma }_s$) and skew ($s_s$) given by Proposition 1, see Equation (27), for several values of ${\rho }_{12}$. The theoretical result reproduces (within errors) the results of the MC simulation.

5. Summary and Conclusions

In this paper, we studied the shape of the Bachelier-implied volatility of a spread option on two assets following correlated local volatility models in the near-ATM region. In this region, the spread-implied volatility can be expanded in moneyness with coefficients given by the ATM level, skew, and convexity. We show that these parameters are determined by the same parameters for the single-asset-implied volatility, and the correlation among assets. We present analytical formulae for the ATM spread skew in terms of single-asset smile parameters for both cases when the single-asset smile is quoted in Black–Scholes (log-normal) and Bachelier (normal) forms. A similar result holds for the ATM spread convexity.

The analytical results follow from the short-maturity asymptotics of multi-asset options obtained by Avellaneda et al. (2002) and become exact in the short-maturity or volatility limit. The results have a local property in the sense that near-ATM spread options depend only on near-ATM single-asset-implied volatilities and the correlation among the two assets. This is in contrast with alternative methods, such as the copula-based methods, where the entire shape of the single-asset smile is required. The availability of analytical results also allows a qualitative understanding of the spread option sensitivities with respect to these parameters.

Numerical testing on spread options on correlated log-normally distributed assets shows that the analytical result reproduces correctly the ATM slope of the Bachelier-implied volatility. The analytical spread skew formula can be used to construct a linear approximation for the exact Bachelier volatility as in (20), which should be useful for pricing spread options with strikes close to the ATM point. Numerical testing shows that the linear approximation is most accurate for highly correlated assets. This is relevant for practical applications, for example, for pricing calendar spreads on futures contracts, which are highly correlated.