Abstract
The simulation of wind power, electricity load, and natural gas prices will allow commodity traders to see the future movement of prices in a more probabilistic manner. The ability to observe possible paths for wind power, electricity load, and natural gas prices enables traders to obtain valuable insights for placing their trades on electricity prices. Since the above processes involve a seasonality factor, the seasonality component was modeled using a truncated Fourier series, and the random component was modeled using stochastic differential equations (SDE). It is evident from the literature that all the above processes are mean-reverting processes; thus, three mean-reverting Ornstein–Uhlenbeck (OU) processes were considered the model for wind power, the electricity load, and natural gas prices. Industry experts believe there is a correlation between wind power, the electricity load, and natural gas prices. For example, when wind power is higher and the electricity load is lower, natural gas prices are relatively low. The novelty of this study is the incorporation of the correlation structure between processes into the mean-reverting OU process using a copula function. Thus, the study utilized a vine copula and integrated it into the simulation. The study was conducted for the Texas energy market and used daily time scales for the simulations, and it was able to conclude that the proposed novel mean-reverting OU process outperforms the classical mean-reverting process in the case of wind power and the electricity load.
1. Introduction
Around the world, after the wave of liberalization of energy markets in the 1990s, organized electricity markets such as those in Texas (USA), California (USA), the Nordic countries (Europe), and Alberta (Canada) emerged. Thus, electricity is sold on the electricity wholesale market hourly, and market forces such as demand and supply decide the price of electricity. Hence, commodity traders can buy and sell electricity and generate a profit (or incur a loss) when trading in wholesale markets. This is not limited to electricity; natural gas and crude oil markets have also been liberalized since the 1990s. When organizations trade electricity, natural gas (commodities) etc., on these markets, traders place their trades based on their experience of the movement of energy prices and current market affairs. In such an environment, simulating the electricity load, wind power generation, and natural gas prices into the future enables traders to look into the future in a probabilistic manner. Thus, this encourages traders to make their decisions in a more informed manner. Hence, the simulation of the above process is important for commodity traders. When simulating the above processes, it is also important to look into the correlation of the above processes. Stakeholders in energy markets believe each process influences other processes in the market. Thus, the objective of this study was to develop simulations for the electricity load, wind power generation, and natural gas prices for an energy market using stochastic differential equations (SDEs) and incorporate correlation into the simulations. To achieve this objective, the researchers introduced a novel stochastic copula model in which the correlation structure is incorporated into the OU model. The study is a collaboration between the University of Calgary, the Mitacs Accelerate Program, and Cascade Trading Ltd. Cascade Trading Ltd. provided the data and necessary assistance for this study. Based on the interest of the above organization, the Texas Energy market was chosen for this study.
Electricity is considered a commodity among research scholars and commodity traders. The classical model for commodities was introduced by Schwartz (1997), in whose work commodity prices were modeled using an exponential mean-reverting process. Lucia and Schwartz (2002) modeled the electricity price process of the Nordic energy market using an extension to the Schwartz (1997) model. The extension was conducted using a one-factor mean-reverting model and a two-factor mean-reverting model. Incorporating jumps into the Schwartz (1997) model, Cartea and Figueroa (2006) used a mean-reverting jump-diffusion model to create a model of electricity prices in the England and Wales energy market. Coulon et al. (2013) used a Brownian-driven mean-reverting OU process to model the electricity load of the Texas energy market. Benth et al. (2008) proposed a Lévy-driven electricity price model for Nordic markets, and Benth et al. (2018) modelled the electricity spot price using a normal inverse Gaussian process. Following Benth et al. (2018), Warunasinghe and Swishchuk (2024) modelled electricity spot prices using a mean-reverting Ornstein–Uhlenbeck (OU) process, which is driven by the variance gamma Lévy process and the normal inverse Gaussian Lévy process for the Alberta, Canada, energy market.
Extensive literature is available on wind power and wind speed modelling. A few popular approaches among the research scholars are to characterize the wind speed or wind power using a probability density function (PDF) of the Weibull distribution, using autoregressive moving average (ARIMA) time-series models, the implementation of artificial neural networks in combination with ARIMA models, and the use of stochastic differential equations (SDEs) and mean-reverting models. According to Jaramillo and Borja (2004), Zárate-Miñano et al. (2013), when modelling wind speed using a PDF of the Weibull distribution, it is not effective for shorter time scales like hourly or 10-minute time intervals. The reason is that Weibull PDF is a static distribution. Hill et al. (2012) and Karki et al. (2006) used the ARIMA model to create a model of hourly wind-speed data in the United Kingdom and Canada, respectively. Rodríguez et al. (2021) implemented the autoregressive fractionally integrated moving average (ARFIMA) on Colombian data. Researchers such as Li et al. (2018) and Wang et al. (2017) introduced novel hybrid neural networks with ARIMA models to forecast wind speed in China. For short time intervals, researchers have used SDE and mean-reverting models. The researchers Loukatou et al. (2018), Benth et al. (2018), and Arenas-López and Badaoui (2020) used the Brownian motion-driven OU process to model the stochastic component of wind speed and wind power. There has also been an increase in the popularity among research scholars using volatility models such as generalized autoregressive conditional heteroskedasticity (GARCH) models to model wind power forecasting. Researchers such as Chen et al. (2019) used asymmetric GARCH models such as Glosten–Jagannathan–Runkle GARCH (GJR-GARCH), Asymmetric Power Autoregressive Conditional Heteroskedasticity (APARCH), and Exponential Generalized Autoregressive Conditional Heteroskedasticity (EGARCH) to model and forecast the wind-power generation of eastern China. Shen and Ritter (2016) used five different types of GARCH models and compared them with the Markov regime-switching GARCH model to forecast the volatility of wind-power production for the German energy market. They identified that the Markov regime-switching GARCH model outperformed classical GARCH models.
Most research scholars used the Schwartz (1997) SDE to model natural gas prices. Clewlow (2000) and Pilipović (1998) incorporated a jump term into the above SDE to capture the spikes of the natural gas price process. Diverting from this path, Benth and Šaltytė Benth (2004) modeled a deseasonalized log of the natural gas price process using an NIG-driven mean-reverting OU process. In the last decade, there has been the development of statistical models and machine learning used to model and forecast natural gas prices. The research scholars Nguyen and Nabney (2010) and Saghi and Rezaee (2021) used a wavelet transformation with different statistical models, artificial neural networks, and the GARCH model to forecast natural gas prices, and they observed that linear models outperformed non-linear models. Čeperić et al. (2017) highlighted that prior variable selection is important for artificial neural networks and support vector machines. They also identified that, if not, a classical time-series model outperforms the above models.
A copula is a powerful tool to capture the dependencies between random variables. Recently, copulas have been utilized to capture dependencies in time-series models in both univariate and multivariate cases. Thus, it can be used to model more complex dependent structures. Tankov and Cont (2003) highlighted the importance of the copula when modeling multivariate models. Tankov and Cont (2003) calibrated two exp-Lévy models driven by the variance gamma process, compared the results when the dependent structure is a Lévy copula versus when the dependent structure is modeled via correlated Brownian motions, and identified that the two dependent structures are widely different. The researchers Hu (2006) and Jondeau and Rockinger (2006) implement copulas to capture the dependence patterns across financial markets around the world. Aloui et al. (2014) used copula-GARCH to capture the dependence structure between crude oil and natural gas for portfolio risk management, while Berrisch et al. (2023) used copula-GARCH to capture the dependence structure between European carbon and energy prices. For a survey on the use of copulas in finance, refer to Genest et al. (2009) for more details.
This paper contributes to the literature by modeling the electricity load, wind power generation, and natural gas prices for the Texas energy market and implementing a copula–OU model to incorporate the dependent structure between the three processes into the simulation based on the OU process. The following is the structure of the paper: Section 2 discusses the data handling and preliminary analysis of the study. Section 3 discusses the modeling of the electricity load, wind power, and natural gas prices, and their model-fitting performance is discussed in Section 4. The calibration of the copula and the integration of the copula into the simulations (copula–OU model) are discussed in Section 5, and following that, Section 6 concludes the results of the study and provides future work expanding upon the study.
2. Data Description
The study was carried out on the ERCOT (Electric Reliability Council of Texas) energy market based on the daily electricity load, wind power generation, and natural gas prices. The hourly values of wind power and the electricity load were converted into daily values by taking the average, while natural gas prices were only available on a daily time scale. The data were collected from 1 January 2019 to 31 May 2024. The electricity load, measured in megawatts (MW), and wind power generation, measured in megawatts (MW), were obtained from the ERCOT energy market, and natural gas prices, measured in USD per million British thermal units (USD per MMBtu), were obtained from the Henry Hub natural gas market. Figure 1 and Figure 2 plot the daily average electricity load and daily average wind power generation, while Figure 3 plots the daily natural gas prices, which allows us to observe the stylized features of the time series.
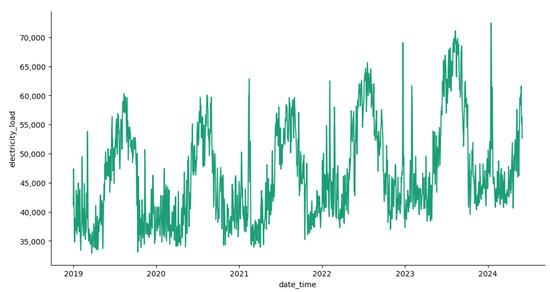
Figure 1.
Average daily electricity historical demand between 1 January 2019 and 31 May 2024.
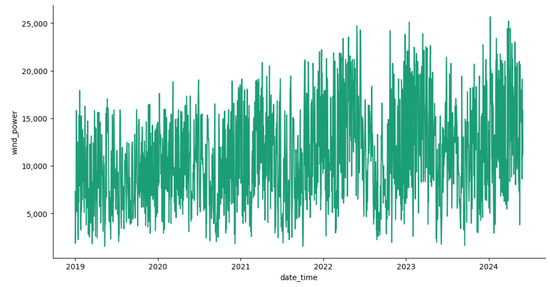
Figure 2.
Average wind power historical generation data between 1 January 2019 and 31 May 2024.
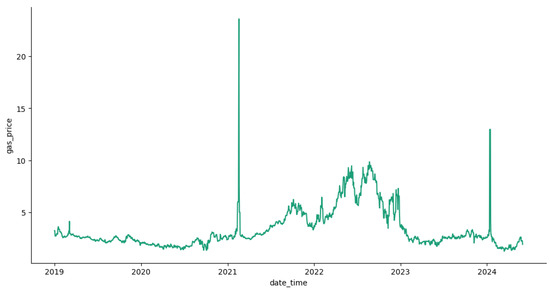
Figure 3.
Daily natural gas historical prices between 1 January 2019 and 31 May 2024.
When the wind power generation for ERCOT in Figure 2 is observed, it can be noticed that there is a slight linear positive trend. This can be due to the following reasons: the first is an increase in wind power production at existing power plants, the second is the addition of new wind farms to the ERCOT electricity grid, and the third is both reasons. Thus, a transformation is required to discount the impact of new power plants in the wind power series. Hence, researchers considered the wind power generation percentage over the actual wind power production; Shen and Ritter (2016) utilized a similar transformation of data. The wind power generation percentage elaborates on the efficiency of all available wind farms in ERCOT. The total capacity of the wind power plant in the ERCOT market is obtained from www.ercot.com. The time series plot of wind power generation percentage is displayed in Figure 4, and it can be observed that the positive linear trend observed in Figure 2 has changed to a negative linear trend. The wind power generation percentage (WPG%) is calculated using the following equation:
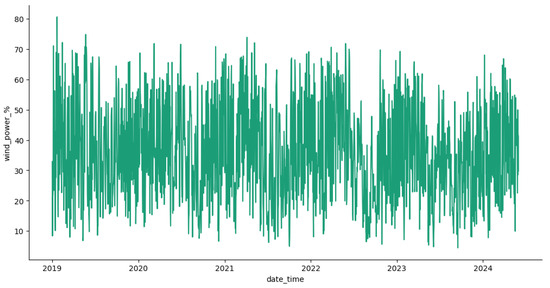
Figure 4.
Average wind power historical generation percentage data between 1 January 2019 and 31 May 2024.
When observing the time series plot for natural gas prices, it can be noticed that there are two large spikes in the series around February 2021 and in January 2024. The reason for these two spikes is as follows: in February 2021, storm Uri occurred, which caused a historic winter in the state of Texas. The storm Uri event occurred during 11–20 February 2021, and many counties in the state of Texas experienced wind chills below zero. Uri was the coldest winter storm for the State of Texas since December 1989. Due to this storm, heating demands in Texas increased rapidly, causing natural gas prices to reach new heights. In January 2024, another freeze event occurred in the State of Texas due to a winter storm, thus increasing demand for heating, which drove the price of natural gas above normal price ranges. Due to these two rare events, we observed outliers in the natural gas price data. These outliers needed to be handled before the calibration process, and the observed outliers were smoothed out using the six-month moving average. Figure 5 displays the smoothed natural gas price process. A comparison of the model parameters of natural gas prices between pre-outlier removal and post-outlier removal is displayed in Table A1 in Appendix A.
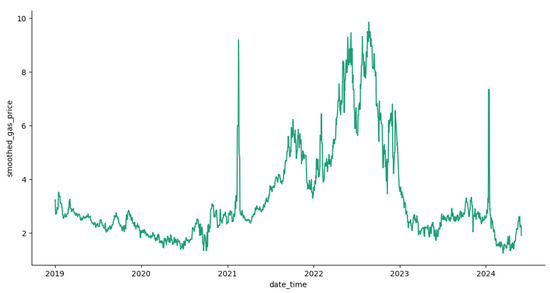
Figure 5.
Daily smoothed natural gas historical prices between 1 January 2019 and 31 May 2024.
After the above modifications were made to the data, the study was conducted for the electricity load, smoothed natural gas price, and percentage of wind power generation in this study. The parameter estimation of the model and model training were performed on the data from 1 January 2019 to 31 December 2023, and the trained model was tested, while performance was measured against the data from 1 January 2024 to 31 May 2024. From here onward, we refer to the electricity load process as the demand process, the smoothed natural gas price process as the gas price process, and the wind power generation percentage process as the wind power process.
3. Deterministic and Stochastic Models Description
This section presents the setup of individual models to accommodate the seasonal, trend, and stochastic properties of the demand, wind power, and gas price processes. The modeling approach for the above-mentioned processes is as follows:
- Decompose seasonal, trend, and stochastic components from the process.
- Model seasonal and trend (deterministic) components with truncated Fourier series (TFS).
- Model the stochastic component with a suitable stochastic model.
In this section, however, the modeling of the dependence structure between processes will not be discussed, and this will be discussed in Section 5.
3.1. Seasonal and Trend Model
By following the framework of Lucia and Schwartz (2002), the process was modeled as follows:
where represents either demand, wind power, or the natural gas price, represents the deterministic or seasonal and trend components of the process, and represents the stochastic component of the process. The deterministic component is modeled using a TFS of the style below:
where , , for , and are constant parameters, and n is the order of TFS. represents the linear trend in the deterministic component, and the and components represent the seasonality of the process. The order n of TFS is determined via the elbow point (beyond the particular n, it has no significant improvement) of the plot between the residual sum of squares (RSS) of the model for different levels of order (n). The reason for selecting the above model for the deterministic component is the periodic pattern. This can be seen in Figure 6, Figure 7 and Figure 8 in the following section, and it is well documented in the literature, for example, in studies conducted by Benth et al. (2008) and Meyer-Brandis and Tankov (2009). The decomposition of seasonal, trend, and stochastic components of the three processes is displayed in the figure below.
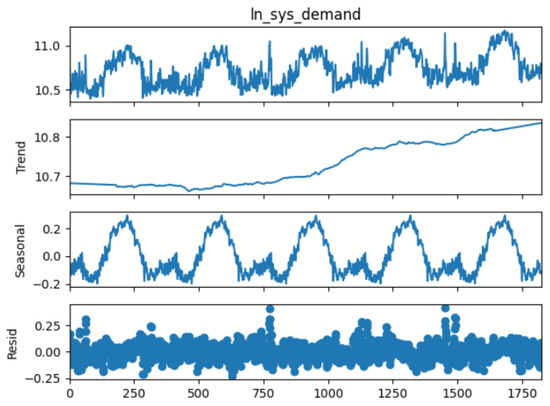
Figure 6.
Time series decomposition of natural logarithmic demand process.
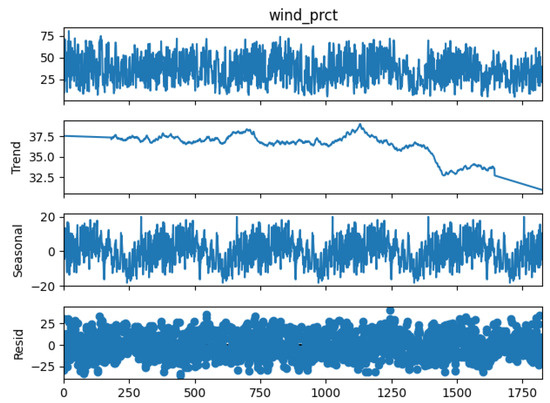
Figure 7.
Time series decomposition of wind power process.
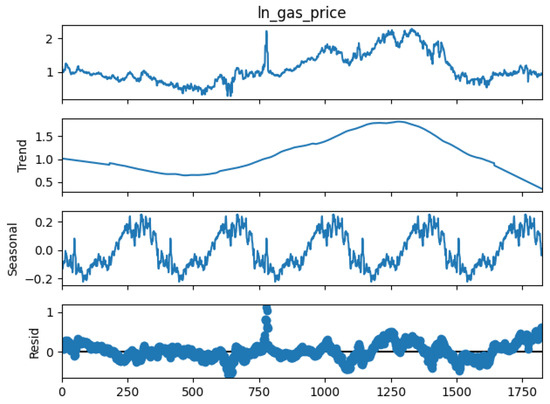
Figure 8.
Time series decomposition of natural logarithmic gas price process.
For the demand and wind power process, a linear trend and a periodic seasonal pattern are observable. Thus, the two components are added together and modeled by the TFS in Equation (3). Observing Figure 9 and Figure 10 reveals that the elbow point for the demand process is , while for the wind power process, it is not evident. In the wind power process, the RSS is high for the TFS for all orders, and it is decreasing rapidly with the increase in order. It can be expected to decrease the RSS further if the order is increased beyond . However, this is computationally expensive; thus, the optimal order for the TFS is considered to be . Even though the elbow point is for the demand process, during modeling, an order of was considered to obtain better performance. Hence, orders and are considered for the TFS of the demand and wind power process, respectively.
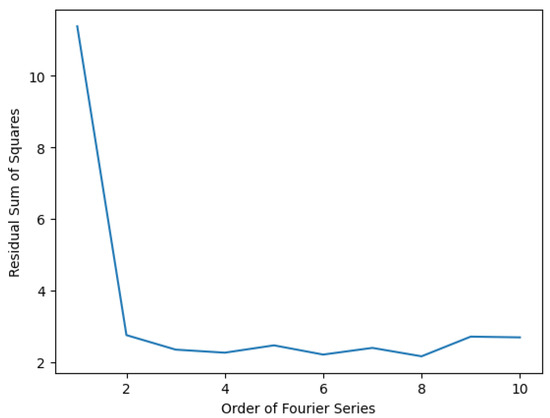
Figure 9.
Order vs. RSS for demand process.
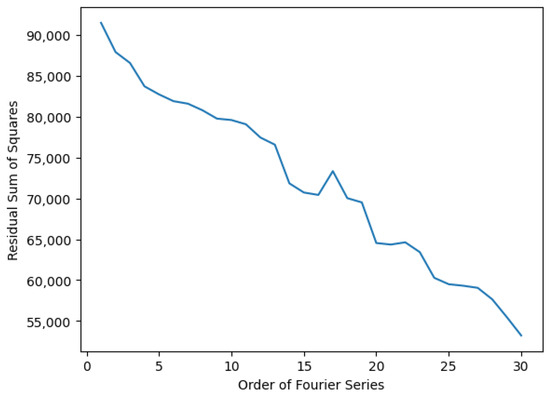
Figure 10.
Order vs. RSS for wind power process.
Contrary to demand and the wind power process, the trend in the gas price process is non-linear and displays a periodic pattern almost similar to a sine curve. Hence, seasonal and trend components are modeled separately in the gas price process. The seasonal component is modeled using Equation (3), while for the trend component, the TFS was modeled with the style below:
The elbow point for both seasonal and trend TFS models is not evident when observing Figure 11 and Figure 12. When considering the seasonal TFS model, the lowest RSS is observable at order , while for the trend TFS model, the lowest is observed at and . Thus, for the seasonal and trend models of the gas price process, the order of the TFS was considered and , respectively. A sensitivity analysis of how changes in the order of TFS affect the natural gas price simulation is presented in Appendix A Table A2 and Table A3.
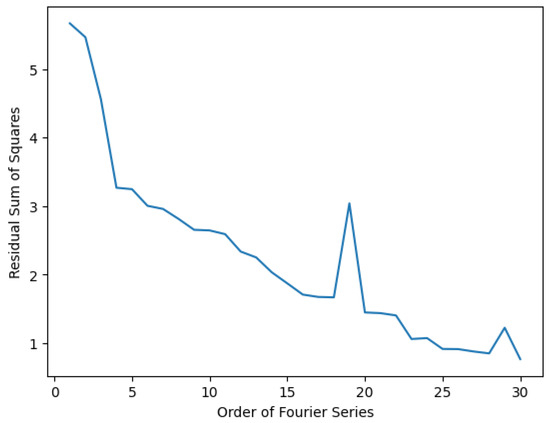
Figure 11.
Order vs. RSS for seasonal component of natural gas price process.
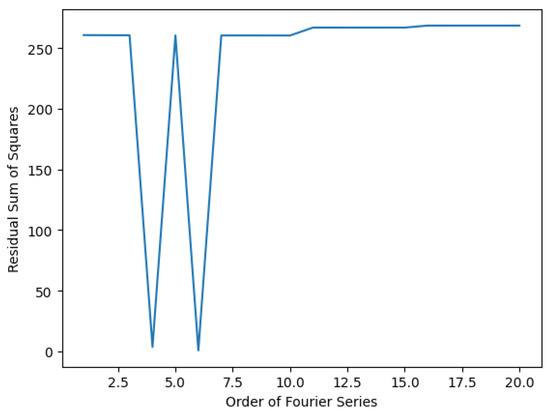
Figure 12.
Order vs. RSS for trend component of natural gas price process.
Let us discuss the trend component of the gas price process more. Even though it can be observed that, for the period of the study, the trend exhibits a sine pattern, it is not the case when comparing data from January 1997 to May 2024. Figure 13 displays the decomposition of seasonal, trend, and stochastic components of gas prices for the above period.
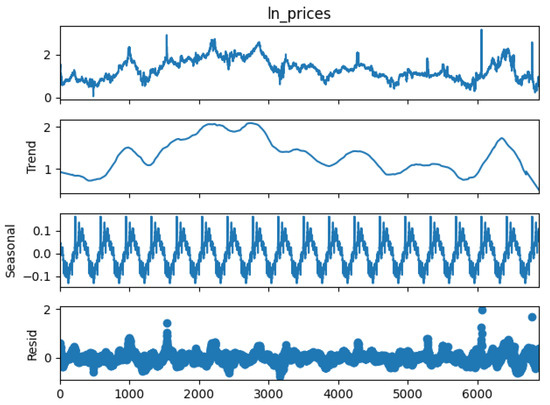
Figure 13.
Time series decomposition of gas prices from 7 January 1997 to 31 May 2024.
When Figure 13 is observed, it can be seen that the trend components do not exhibit the sine pattern displayed in the period of January 2019 to May 2024 and do not show a consistent pattern. The reason behind this might be that, unlike demand and wind power, weather is not the only factor influencing gas prices. Thus, using TFS to model the trend component for gas prices is not ideal. A possible solution is to use a regression-type model in modeling gas prices. However, for the seasonal component, this is not the case, as it can be observed that a consistent pattern is visible throughout the period; thus, modeling using TFS is ideal. Figure 14 reveals that the trend component is the major component in the value of the gas price process, following the stochastic component and the seasonal component. Thus, the trend model has a high impact on the overall simulation.
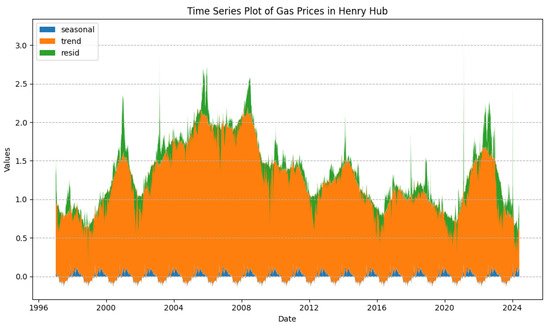
Figure 14.
Time series of gas prices from 7 January 1997 to 31 May 2024.
Figure 15 and Figure 16 display the TFS with for the training period and the out-of-sample period. Even though, for the training period, TFS has been able to capture the pattern, since the pattern is not consistent, as in Figure 13, for the out-of-sample period, TFS performs poorly. This highlights the need to apply a regression-based model for the deterministic component of the gas price process. However, this is considered as a future work of the current study, and thus, for modeling purposes, the current study continued to implement the TFS for the deterministic component of gas prices.
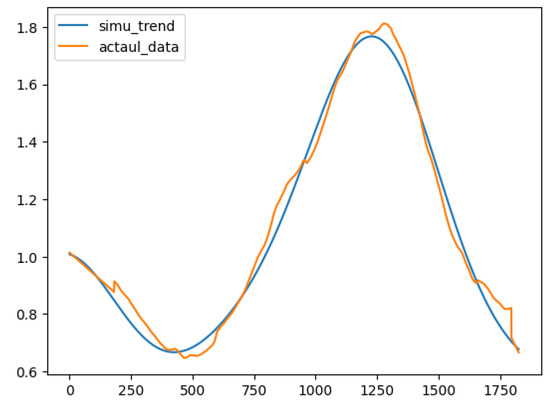
Figure 15.
Training period.
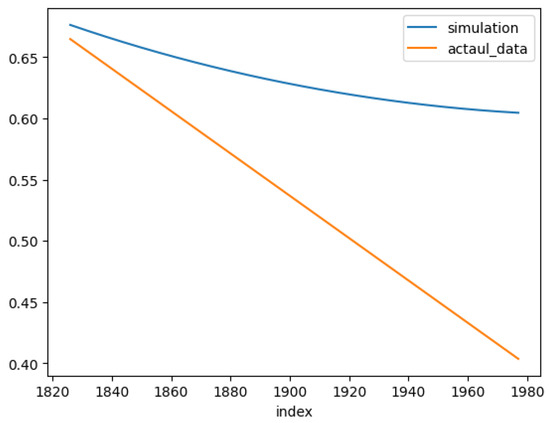
Figure 16.
Out of sample.
3.2. Stochastic Model
Next, the mean-reversion property or stationary assumption needs to be validated for the stochastic component or the de-seasonalized component of the three processes. To validate the stationary assumption, two statistical tests are deployed, namely the augmented Dickey–Fuller (ADF) test and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test. The hypothesis of the ADF test is as below:
Hypothesis 1.
The process is non-stationary.
Hypothesis 2.
The process is stationary.
Meanwhile, the hypothesis test for the KPSS test is as follows:
Hypothesis 1.
The process is trend-stationary.
Hypothesis 2.
The process is non-stationary.
Table 1 displays the results of the two statistical tests for the three processes. The results support the conclusion that the stochastic components of all three processes are stationary.

Table 1.
Stationary test for demand, wind power, and gas prices.
Since all three processes are mean-reverting processes, several types of Ornstein–Uhlenbeck (OU) processes can be modeled for the stochastic component of the processes. A generalized OU process and a jump-diffusion (JD) model are expressed in the equation below:
where is the mean-reverting speed of the process, represents the long-run level of the process or the deterministic level of the process, represents the volatility of the process, represents the Brownian motion, where it is also a Lévy process, and represents the jump size that follows a normal distribution with the mean and the variance , and is a Poisson process with the jump intensity . When the historical data for the demand process and the wind power process in Figure 1 and Figure 4 are observed, it can be noticed that the process moves around the seasonal and trend components. This can also be observed in Figure 6 and Figure 7. Thus, a modification to the OU process is implemented, following Benth and Saltyte Benth (2007). The modified Ornstein–Uhlenbeck (M-OU) process is expressed in the equation below:
Benth and Saltyte Benth (2007) used the above to model temperature data, which has similar style characteristics to demand and wind power processes. For the above M-OU process, when the jump component is added similarly to Equation (7), it can be expressed as follows:
where this model can be expressed as a modified jump–diffusion (M-JD) model. When the JD model or the M-JD model was calibrated, jumps in the data were identified by the following recursive filtering procedure mentioned in Benth et al. (2008). A summary of the recursive procedure is as follows: First, identify jumps higher than the mean level plus three times the standard deviation. Then, remove those data jumps, and recalculate the mean and standard deviation. Again, identify the jumps for the new mean and new standard deviation, and remove those jumps from the data. The process is repeated until no jumps are found in the data. The summation of all jumps is the total number of jumps in the data, and the final standard deviation will be the diffusion rate () for the JD or M-JD model. Further, divide the jumps into positive jumps and negative jumps, and calculate the jump probabilities separately. Thus, our jump component will be a summation of negative jumps and positive jumps. For more details, please refer to Benth et al. (2008).
The stochastic component for demand and wind power processes is modeled using multiple models: an M-OU process, as expressed in Equation (5), an M-JD process, as in Equation (8), and a Lévy-driven M-OU process where the diffusion component () is replaced with a Lévy process (). The Lévy process considered for the demand process is a normal inverse Gaussian (NIG) process, while for the wind power process, it is NIG and exponential Weibull processes. Apart from that, four different Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models are considered when modeling wind power processes and compared against the mean-reverting models. GARCH models are commonly used in the literature as volatility models. The GARCH model is formulated as follows:
where C is a constant, k is the order of an autoregressive term, is the autoregressive coefficient, and is the error term:
where is an independent and identically distributed random variable with a mean of 0, a variance of 1, and volatility. The volatility is defined as follows:
where is a constant, is an ARCH term, and is a GARCH term. The different GARCH models calibrated in this study are as follows:
- A GARCH model with a normal distribution.
- A GARCH model with Student’s T distribution.
- A GARCH model with a skewed Student’s distribution.
- A GJR-GARCH model:where if , and if .
- TARCH model:where if , if , and volatility is .
When it comes to modeling the gas price process, the considered models were as follows: an OU process, a JD process, and an OU process driven by an NIG Lévy process. The rationale for not considering the modified mean-reverting models was that, unlike demand and wind power processes, the gas price process does not revolve around the seasonal mean of the processes. For all models mentioned above, the mean-reversion coefficient is considered to be deterministic.
3.3. Volatility
During the study, the volatility () was considered to be time-dependent. The time-dependent volatility can be calibrated following two approaches: first, using hourly data to calculate daily volatility, and second, using daily data to calculate monthly volatility. Both approaches were tested against the demand process, and it was concluded that the second approach was ideal; thus, for the remaining processes, volatility was modeled monthly for the mean-reversion OU process. The details of this are available in the next section. Figure 17, Figure 18 and Figure 19 display the monthly volatility for the three processes, and Figure 20, Figure 21 and Figure 22 display the volatility by month and year.
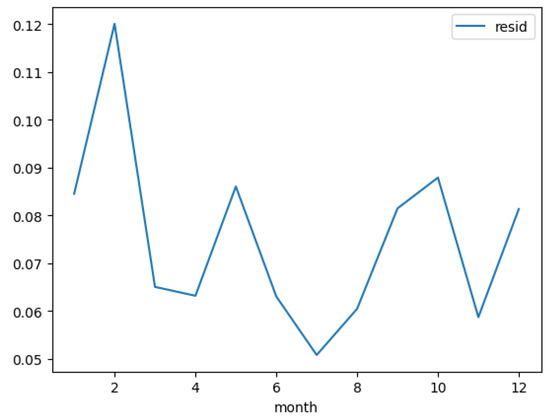
Figure 17.
Monthly volatility curve for demand process.
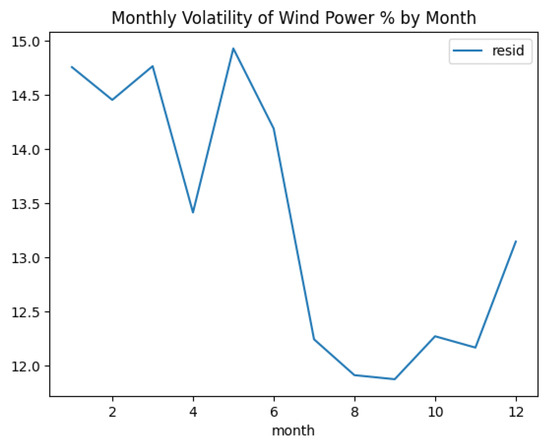
Figure 18.
Monthly volatility curve for wind power process.
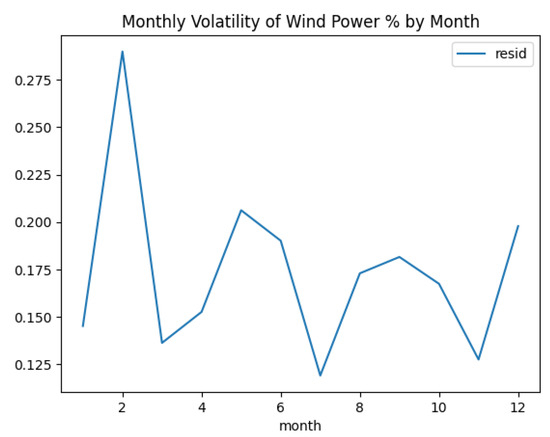
Figure 19.
Monthly volatility curve for natural gas price process.
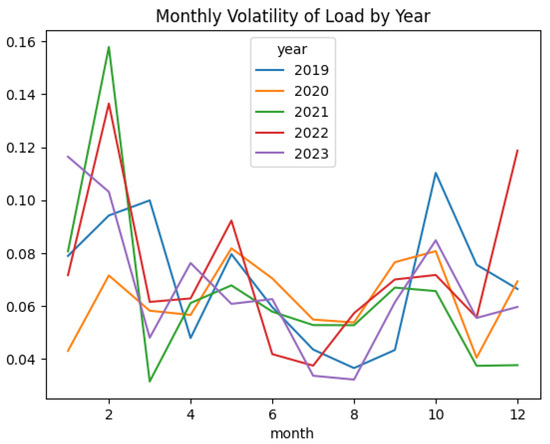
Figure 20.
Volatility by month and year for demand process.
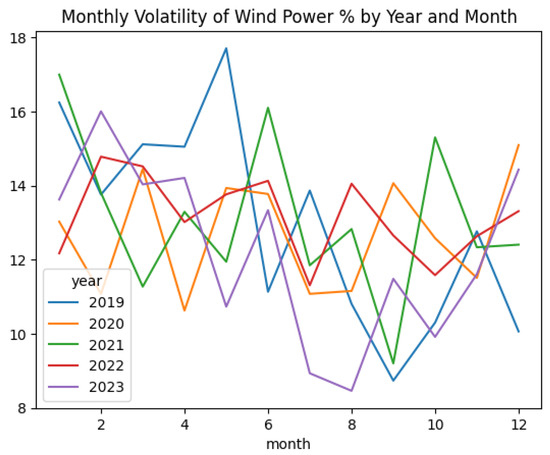
Figure 21.
Volatility by month and year for wind power process.
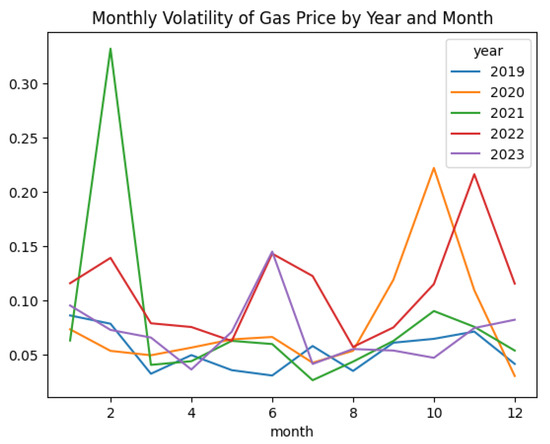
Figure 22.
Volatility by month and year for natural gas price process.
4. Performance of Stochastic Models
This section discusses and evaluates different models from the previous section based on the performance of the models for out-of-sample simulations. The out-of-sample simulation is conducted on the daily average demand process, wind power, and daily gas price process, and it considers the period of 1 January 2024 to 31 May 2024 as out of sample.1 For each model, simulations are plotted against the actual data, and the performance is measured using the mean absolute error (MAE) and the mean absolute percentage error (MAPE). For each model, 1000 out-of-sample simulations are performed, and the MAE and MAPE are computed for each. The average MAE and MAPE for each model are then calculated. The model with the lowest average MAE and MAPE error is considered the best model to simulate the three processes independently. A similar procedure was followed throughout the study when comparing the performance of model simulations using MAE and MAPE. In the case of the gas price process, since TFS is not ideal to model the seasonal and trend component, the models from the previous section are tested against the gas price process as well, with a consideration of only the stochastic component of the process.
The demand process is modeled using Equation (7), and two volatility modeling approaches are compared, i.e., modeling daily volatility versus modeling monthly volatility. Figure 23 displays the simulation from Equation (7) with daily volatility, and Figure 24 displays the same with monthly volatility. It can be observed that the simulated data revolves around the seasonal and trend components due to the modification applied to the OU process. However, the simulated data involves a significant level of noise in the data compared to the actual data, while the simulation with monthly volatility involves similar noise levels to the actual data. The simulations in Figure 24 using monthly volatility exhibit similar patterns to those of the actual data in the figure. When the average MAE and MAPE of 1000 simulations are compared between two simulations in Table 2, it can be seen that the model with monthly volatility performs better compared to the model with daily volatility. When MAE is compared, this difference is approximately 600 MW. Thus, using monthly volatility as is more advantageous for the simulations compared to using daily volatility. Thus, for all processes, monthly volatility was used as the volatility for the OU processes. When the MAE and MAPE of the M-JD model, the M-OU process driven by NIG, and the M-OU model with monthly volatility were evaluated, the M-JD model exhibited better fitting performance for the demand process compared to the other models. Figure 25 displays the out-of-sample simulation for the M-JD model and the demand process, along with the actual data.
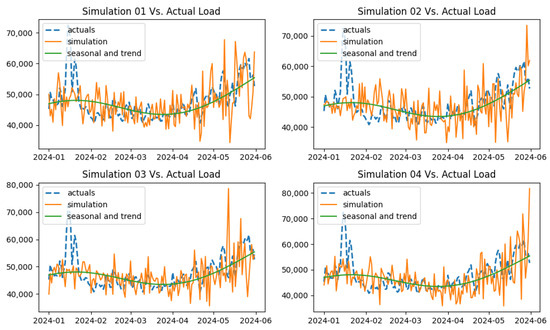
Figure 23.
Out-of-sample simulation (M-OU daily vol.) vs. actual demand.
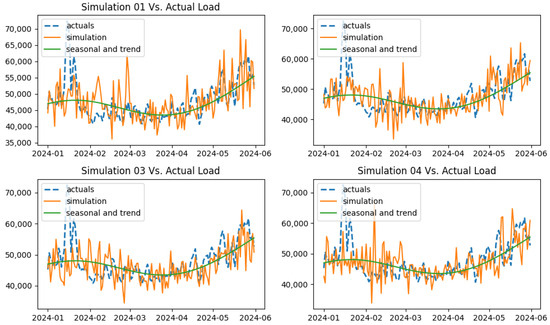
Figure 24.
Out-of-sample simulation (M-OU monthly vol.) vs. actual demand.

Table 2.
Out-of-sample simulation performance for models.
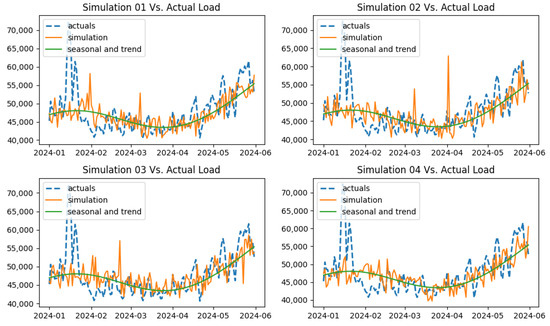
Figure 25.
Out-of-sample simulation (M-JD) vs. actual data for demand process.
When the MAE and MAPE of GARCH models and the OU processes for the wind power process are compared, it is seen that both types of models achieve similar model-fitting performance. However, the GARCH models show slightly better model-fitting performance over the OU processes. Out of all GARCH models, the GARCH models driven by normal distribution and Student’s T distribution show better performance, while in the mean-reverting models, the M-JD process displays better model-fitting performance compared to the others. Figure 26 displays the out-of-sample simulation for the GARCH (normal) and GARCH (Student’s T) models, and Figure 27 displays the same for the M-JD model.
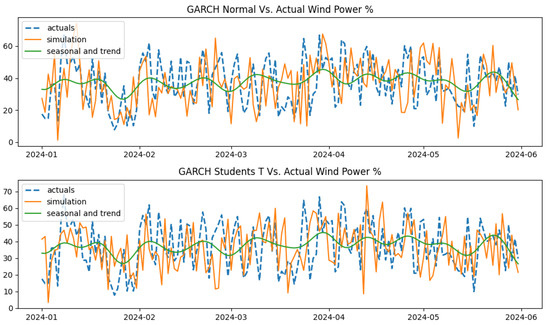
Figure 26.
Out-of-sample simulation (GARCH (normal) and GARCH (Student’s T)) vs. actual data for wind power process.
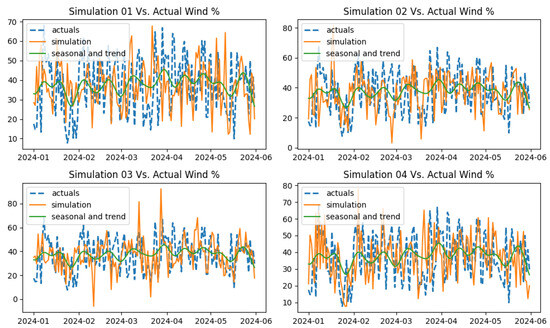
Figure 27.
Out-of-sample simulation (M-JD) vs. actual data for wind power process.
In the gas price process, the OU process driven by the NIG process achieves significantly better model-fitting performance compared to the OU process with Brownian motion. The OU (NIG) achieves only a USD 0.61 average deviation between the true and simulated gas prices, while M-OU achieves about a USD 1.30 average deviation. The JD model achieves superior performance compared to both OU and OU (NIG). When only the stochastic component for the gas price process is considered, again, the JD model achieves superior performance compared with the OU process and the OU process driven by the NIG process. Figure 28 and Figure 29 display the out-of-sample simulation obtained from the JD model for the gas price process.
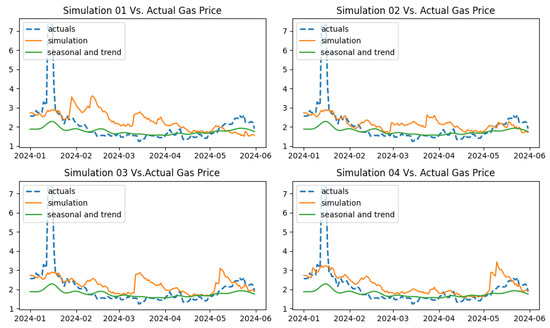
Figure 28.
Out-of-sample simulation (JD model) vs. actual data for natural gas price.
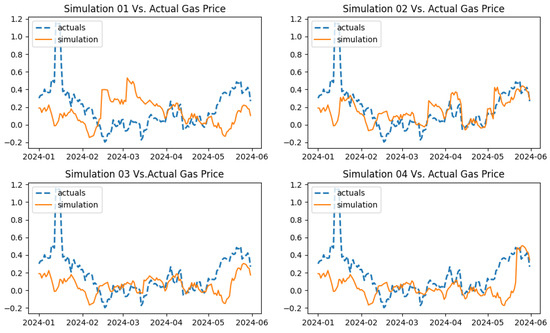
Figure 29.
Out-of-sample simulation (JD model) vs. actual data for natural gas price (stochastic component only).
5. Copula-OU Models and Vine Copula
5.1. Definition of Copula
In general terms, the copula is a function that connects or ”couples” the joint distribution functions of random variables to each random variable’s marginal distribution function (Nelsen (1996)). This relationship is based on Sklar’s theorem. Sklar’s theorem (Sklar (1959)) states the following:
Theorem 1.
Let H be the joint distribution function of marginal distribution functions F and G. Then, there exists a function C, such that, for all x,y in the real line below,
where C is known as the copula function.
To extend this concept from two dimensions to d dimensions (), researchers in the literature have developed the concept of pair copula. To construct a d-dimension copula , we have to develop bivariate copulas. From these bivariate copulas, the bivariate copulas model dependence in the copula C, and the remaining bivariate copulas measure the indirect dependence between other marginals conditioned on previous marginals. Thus, with the increase in d, there are many possible structures for constructing the d-dimension copula. This type of copula is known as a vine copula, and a few common structures of vine copula are R-vine copula, C-vine copula, and D-vine copula. Figure 30 displays the structure of the C-vine copula for .
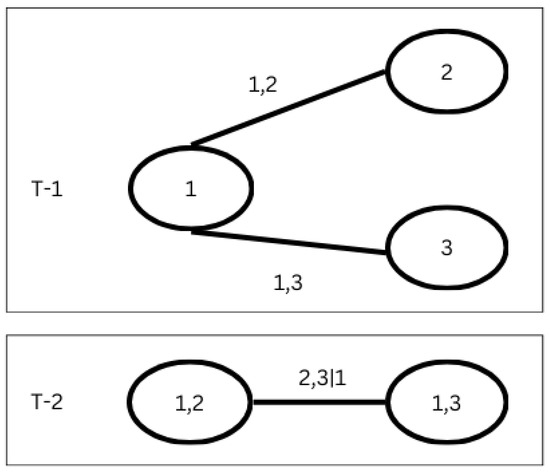
Figure 30.
C-vine copula structure for .
For the above example, bivariate copulas have to be developed in order to construct a vine copula. displays the first tree, and displays the second tree. In the first tree, two bivariate copulas are developed between variables and . To capture the dependence between variable , in the second tree, another bivariate copula is developed between the condition on variable 2. This study implements a three-dimensional vine copula to capture the dependence structure between demand, wind power, and gas prices.
5.2. Correlation Structure
Stakeholders in energy markets believe the processes of demand, wind power, and gas prices are correlated. An example would be that gas prices will be higher during periods of higher demand and lower wind power. Thus, it is vital to observe the correlation and incorporate the said correlation into the simulation, and based on the above example, a C-vine copula structure seems reasonable. The figures below display the correlation between the three processes monthly.
When Figure 31, Figure 32 and Figure 33 are observed, a clear pattern in the correlation by month between wind power and demand is evident. While other plots do not exhibit a clear pattern, it can be noticed that the correlation between variables changes by month. Thus, it is not possible to ignore the dependent structure when modeling and simulating these three processes. Accordingly, to incorporate this dependent structure into this simulation, three-dimensional vine copulas were incorporated.
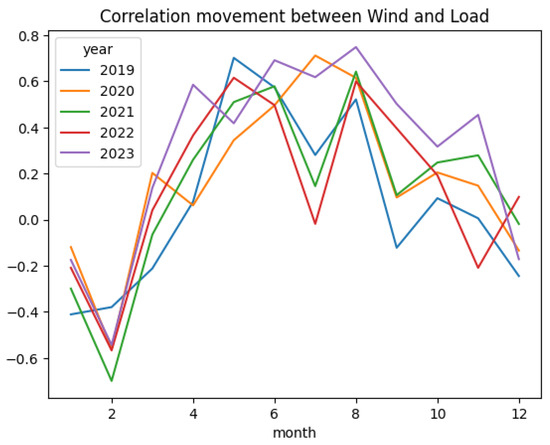
Figure 31.
Wind power and demand.
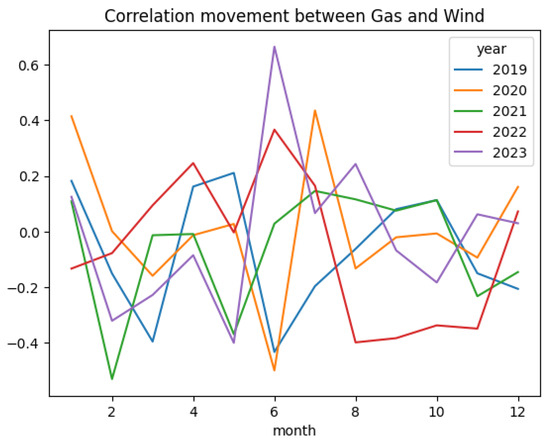
Figure 32.
Natural gas price and wind power.
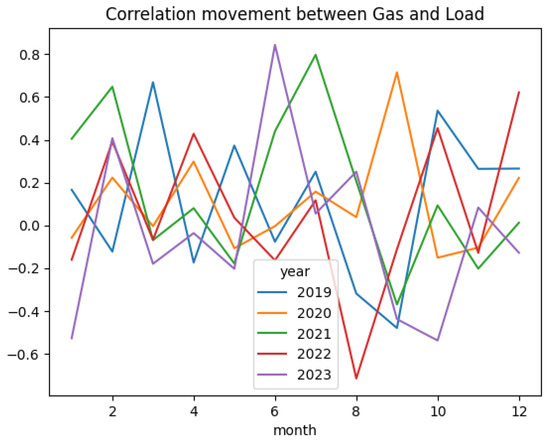
Figure 33.
Natural gas price and demand.
5.3. Calibration of Copula-OU Model
Since correlation does change monthly for the three processes, as in the above figures, instead of using a single vine copula for the simulation, twelve vine copulas were calibrated,2 which represented each month. This enables the capture of the monthly behavior of processes. When calibrating each bivariate copula (a total of three bivariate copulas per one vine copula) for each vine copula, the most optimal copula family from the elliptical and Archimedean copula families was selected by testing each copula family against the data and selecting the best-fitting copula using the Akaike information criterion (AIC). Table A4 in Appendix A provides the list of copulas tested against the data, and Table A5 in Appendix A provides a summary of the selected copula structures, along with the degree of rotation of the copula, the parameter values for the copula function, the Kendal tau measurement, and its AIC shown in the Appendix A. While a C-vine copula structure seems reasonable for the study, the calibration process was not restricted to a C-vine copula; rather, it allowed for identifying the best fit structure based on the data. For this, pyvinecopulib deploys the algorithm proposed by Dissmann et al. (2012) to identify the best fit R-vine structure using the minimum spanning tree concept (the C-vine structure is a special case of the R-vine structure). The details concerning the results of the vine copula structure can be found in Appendix A, Table A5. The copulas are calibrated for the residuals of the AR(1) model of the stochastic component of each process. Figure 34 and Figure 35 represent the copulas for the months of January and February for the training period.
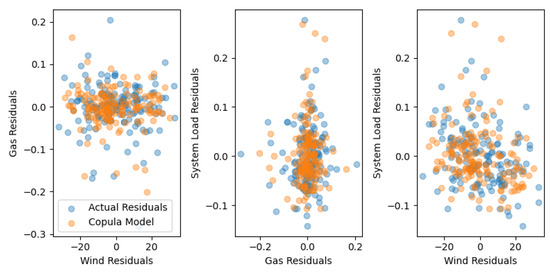
Figure 34.
Copulas for January training period.
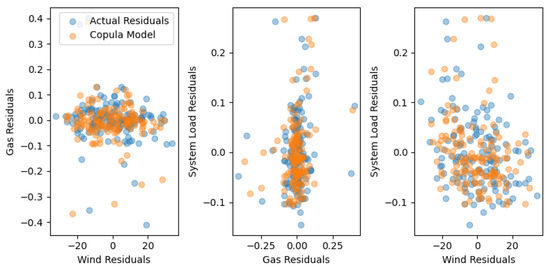
Figure 35.
Copulas for February training period.
Once the copula is calibrated, instead of the diffusion component of the OU process, it was replaced with the calibrated copula. In this methodology, the following OU processes were chosen for simulations: for the demand and wind power processes, the M-OU process, and for the gas price process, the OU process. In all three OU processes, the diffusion component was replaced with the calibrated copula. The equations for the three processes are as follows:
- Demand process.
- Wind power process.
- Gas price process.where is the developed copula, , where are the demand, the power, and gas, respectively. represents the copula calibrated for the three process, which outputs the noise of the demand process, which is influenced by the dependent structure between the three processes. Similarly, and output the noise of wind power and gas prices process, which is influenced by the dependent structure between the three processes.
5.4. Simulation and Performance of Copula-OU
In this subsection, the simulation of copula-OU models and their out-of-sample model-fitting performance are evaluated and compared with the individual models chosen in the previous section. Figure 36 displays the simulation of the demand process for the out-of-sample period. The simulation displays a similar characteristic as the earlier demand simulation based on monthly volatility. However, the noise of the simulated data has been further reduced. Next, when the simulation of the wind power process via the copula-OU model is observed in Figure 37, it is evident that the simulations are well in line with the actual data, apart from a few amplified jumps. Figure 38 displays the 1000 simulations for the gas prices process from the copula-OU model. The simulations consist of jumps at the end of the period, which are not in line with the actual data. The deviation between the simulation and the actual data is due to the error caused when modeling a trend component using a TFS. Thus, the study simulated the gas price process while considering only the stochastic component using the copula-OU model. From Figure 39, it can be observed that simulations for the stochastic component are in line with the actual data, except for the jump observed in January 2024 due to a rare event that occurred in Texas.
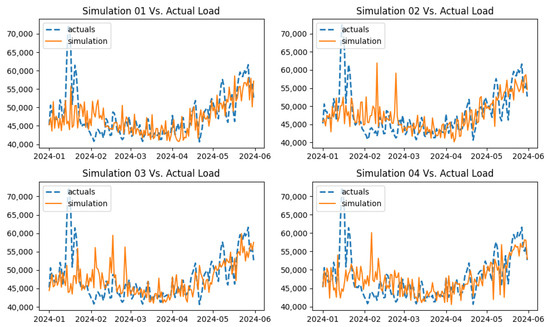
Figure 36.
Simulation of demand based on copula-OU.
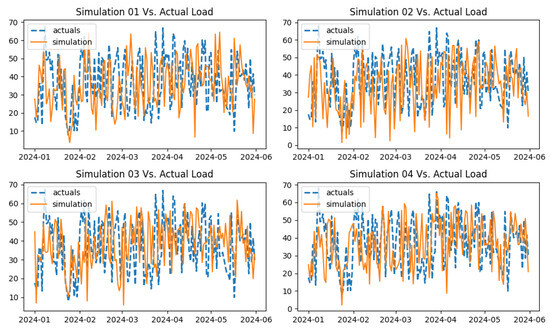
Figure 37.
Simulation of w.p.g.p based on copula-OU.
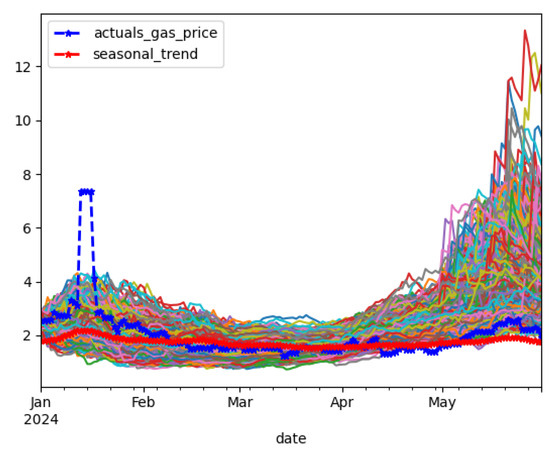
Figure 38.
Simulation of natural gas price process based on copula-OU.
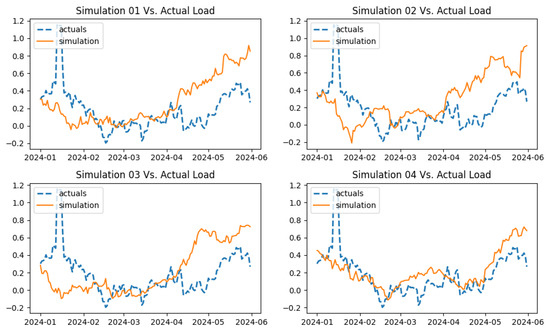
Figure 39.
Simulation of natural gas price process (stochastic component only) based on copula-OU.
Table 3 displays the MAE and MAPE for the demand, wind power, and gas price simulations. When the demand simulation performance is observed, the MAE and MAPE can be seen to have improved compared to the previous demand simulations. Similarly, when the MAE and MAPE of wind simulations are observed, it is clear that the copula-OU model has been able to improve the accuracy of the simulation compared to the model in the previous section. Thus, the results indicate that the copula has improved the simulation of both demand and wind power generation. However, the MAE and MAPE of the gas price process from copula-OU are lower compared to those of the OU process simulation from the previous section, and they are higher compared to those of the JD model simulations for gas prices. But when the MAE and MAPE of the simulation on the stochastic component of the gas price process are compared, it is clear that the copula-OU model has improved the performance of the gas price process simulation when compared with the OU and NIG-driven OU models, and it achieves similar performance to the JD model. Thus, it can be concluded that the copula-OU model does achieve similar performance to the JD model, but an advantage of having the copula-OU model is that the simulation is influenced by the dependent structure between the demand and wind power processes.

Table 3.
Out-of-sample simulation performance for copula-OU model.
6. Conclusions and Future Works
We can arrive at the following conclusion based on the results obtained so far in the study. First, it can be concluded that the mean-reversion models can capture the movement of demand, wind power, and natural gas prices processes in the Texas energy market. Secondly, we can model the seasonality and trend components of the demand and wind power processes through the truncated Fourier series for the same energy market. However, the same success from the truncated Fourier series did not hold for the gas price process. To incorporate the correlation structure between the above processes, the vine copula is a suitable mechanism. As we saw in the above sections, the vine copula successfully captures the correlation between the three processes. We can incorporate the vine copula into the SDE by replacing the diffusion component of the OU process with the calibrated vine copula. This provides successful simulations for demand and wind power and the stochastic component of the natural gas price process. We believe a limitation of the copula-OU models is that, when rare events occur that are driven beyond the correlation-dependent structure between variables (e.g., the 2021 storm Uri and the 2024 freeze event), the copula-OU model will be unable to match the magnitude of the event in the simulation. This may be the reason why the JD model for the natural gas process and the M-JD model in the demand process achieve a slightly better MAE and MAPE compared to those of the copula-OU model. However, the advantage of the copula-OU model lies in the ability to provide correlated simulations, which are more realistic compared to stand-alone simulations. In future work based on this study, as discussed in Section 3.1, a parametric and semi-parametric regression-based model that incorporates macroeconomic and weather variables would be able to capture the deterministic (trend) component more robustly. Hence, firstly, a study should be conducted on identifying the factors that influence the gas price process and modeling the deterministic component using a regression-based model. Secondly, it is also worth exploring other methodologies, such as STL and wavelet-based approaches, to decompose and model deterministic components. In our study, the order of the truncated Fourier series for wind was 30, which may lead to overfitting and a higher computation cost. We leave this work to future iterations of the study. The study should extend and develop SDEs to perform simulations at an hourly time scale in order to better reflect the energy market. Apart from that, the simulations should be regional; thus, future studies should focus on developing the SDEs regionally for demand and wind power. Finally, the simulations should incorporate not only the correlation between processes but also the regional correlation as well. By regional correlation, we imply the correlation between the demand of the east and north regions or the correlation between the wind power of the north and south regions of the Texas energy market, etc. The Figure 40, Figure 41 and Figure 42 display the predefined regions in the Texas energy market by ERCOT. Finally, the study should explore the possibility of incorporating Lévy copulas into the simulation; this adjustment will improve simulations that are conducted at the regional level.
Figure 40.
Electricity demand zones.
Figure 41.
Geographic regions.
Figure 42.
Weather regions.
Author Contributions
Conceptualization, S.W. and A.S.; methodology, S.W.; software, S.W.; validation, S.W. and A.S.; formal analysis, S.W.; investigation, S.W.; resources, A.S.; data curation, S.W.; writing—original draft preparation, S.W.; writing—review and editing, S.W.; visualization, S.W.; supervision, A.S.; project administration, S.W. and A.S.; funding acquisition, S.W. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received external funding from the Mitacs Accelerate Award (to S.W.) with the partnership of Cascade Trading Ltd. and NSERC.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
https://www.eia.gov/ (accessed on 13 May 2024).
Acknowledgments
The authors would like to thank Wes Devauld and the team at Cascade Trading Ltd. for all the support and guidance they provided during the study and express their gratitude to the team at Fin-ML and IVADO for all the guidance and support provided in acquiring the Mitacs Accelerate Award. The authors are also thankful for NSERC and its continuing support and for all the current and former staff at the Department of Mathematics and Statistics of the University of Calgary for their constant support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADF | Augmented Dickey–Fuller |
| ARIMA | Autoregressive moving average |
| APARCH | Asymmetric Power Autoregressive Conditional Heteroskedasticity |
| ERCOT | Electric Reliability Council of Texas |
| EGARCH | Exponential Generalized Autoregressive Conditional Heteroskedasticity |
| GARCH | Generalized autoregressive conditional heteroskedasticity |
| GRJ-GARCH | Glosten–Jagannathan–Runkle GARCH |
| JD | Jump-Diffusion |
| KPSS | Kwiatkowski–Phillips–Schmidt–Shin |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MW | Megawatts |
| NIG | Normal inverse Gaussian |
| OU | Ornstein–Uhlenbeck |
| Probability density function | |
| RSS | Residual sum of squares |
| SDE | Stochastic differential equation |
| TFS | Truncated Fourier series |
Appendix A

Table A1.
Comparison of parameter values between pre- and post-outlier removal of natural gas prices.
Table A1.
Comparison of parameter values between pre- and post-outlier removal of natural gas prices.
| Parameters | Pre-Outlier Removal | Post-Outlier Removal | Absolute Deviations |
|---|---|---|---|
| Mean Reversion | 0.0478 | 0.0334 | 0.0144 |
| Volatility—Jan | 0.1593 | 0.1452 | 0.0141 |
| Volatility—Feb | 0.3490 | 0.2898 | 0.0592 |
| Volatility—Mar | 0.1424 | 0.1363 | 0.0061 |
| Volatility—Apr | 0.1556 | 0.1526 | 0.003 |
| Volatility—May | 0.2087 | 0.2062 | 0.0025 |
| Volatility—Jun | 0.1915 | 0.1901 | 0.0014 |
| Volatility—Jul | 0.1167 | 0.1191 | 0.0024 |
| Volatility—Aug | 0.1704 | 0.1729 | 0.0025 |
| Volatility—Sep | 0.1813 | 0.1816 | 0.0003 |
| Volatility—Oct | 0.1677 | 0.1674 | 0.0003 |
| Volatility—Nov | 0.1277 | 0.1275 | 0.0002 |
| Volatility—Dec | 0.2197 | 0.1978 | 0.0219 |
Table A1 displays the effects of the outlier removal of the natural gas price process on the mean reversion rate and monthly volatility. The parameter values are higher in the original natural gas prices compared with the post-outlier-removed gas prices, except for volatilities in the months of July, and November. When the volatilities are compared, the highest deviation is observed in the months of February, December, and January, respectively, while the least deviation is observed in November, October, and September, respectively. The results from Table A1 indicate that the outlier removal process is an important step in the modeling process.

Table A2.
Sensitivity analysis of the gas price simulation on the order of the TFS of the seasonal component.
Table A2.
Sensitivity analysis of the gas price simulation on the order of the TFS of the seasonal component.
| Order (n) | KPI | OU | JD | OU (NIG) | Copula-OU |
|---|---|---|---|---|---|
| 5 | MAE | 1.40 | 0.52 | 0.61 | 0.73 |
| MAPE | 0.7446 | 0.2424 | 0.2820 | 0.3332 | |
| 10 | MAE | 1.40 | 0.58 | 0.60 | 0.73 |
| MAPE | 0.7424 | 0.2778 | 0.2765 | 0.3338 | |
| 15 | MAE | 1.41 | 0.58 | 0.60 | 0.73 |
| MAPE | 0.7544 | 0.2715 | 0.2778 | 0.3356 | |
| 20 | MAE | 1.34 | 0.55 | 0.59 | 0.74 |
| MAPE | 0.7071 | 0.2683 | 0.2740 | 0.3363 | |
| 25 | MAE | 1.38 | 0.60 | 0.59 | 0.73 |
| MAPE | 0.7320 | 0.2845 | 0.2761 | 0.3367 | |
| 30 | MAE | 1.30 | 0.54 | 0.61 | 0.73 |
| MAPE | 0.6845 | 0.2622 | 0.2820 | 0.3371 |

Table A3.
Sensitivity analysis of the gas price simulation on the order of the TFS of the trend component.
Table A3.
Sensitivity analysis of the gas price simulation on the order of the TFS of the trend component.
| Order (n) | KPI | OU | JD | OU (NIG) | Copula-OU |
|---|---|---|---|---|---|
| 2 | MAE | 2.19 | 1.06 | 1.22 | 1.65 |
| MAPE | 1.2192 | 0.5743 | 0.6706 | 0.8710 | |
| 4 | MAE | 1.38 | 0.60 | 0.59 | 0.73 |
| MAPE | 0.7320 | 0.2845 | 0.2761 | 0.3371 | |
| 6 | MAE | 1.34 | 0.54 | 0.59 | 0.65 |
| MAPE | 0.7110 | 0.2616 | 0.2718 | 0.2939 | |
| 8 | MAE | 2.29 | 1.36 | 1.23 | 1.67 |
| MAPE | 1.2803 | 0.7487 | 0.6732 | 0.8824 | |
| 10 | MAE | 2.23 | 1.51 | 1.25 | 1.67 |
| MAPE | 1.2417 | 0.8544 | 0.68321 | 0.8804 |
Table A2 displays the movement of the MAE and MAPE of the natural gas price simulation when the order of the TFS of the seasonal component changes, while the order of the TFS of the trend component is kept at . Similarly, Table A3 displays the movement of the MAE and MAPE of the natural gas price simulation when the TFS of the trend component changes, while the order of the TFS of the seasonal component is kept at . In Table A2, it can be noticed that, for the OU model, the MAE and MAPE drop when the order increases from 5 to 30, while in the JD model, the MAE and MAPE increase when the order increases and drop again when the order goes from 25 to 30. In OU (NIG), the MAE and MAPE decrease when the order increases but come back to their initial levels when the order , while in the copula-OU model, the MAE held constant up to the second decimal place, but the MAPE increased with the order. Overall, there is not much variation in the MAE and MAPE when the order changes in the TFS of the seasonal component. The reason for this is visible in Figure 14, where it can be observed how little the seasonal component contributes to the overall natural gas price value. This is not the same when Table A3 is observed; here, there is significant movement in the MAE and MAPE when the order changes in TFS. The lowest MAE and MAPE are observed at order and across all models. The reason is that these points have the lowest RSS values in Figure 12, while the other points have higher RSS values. Again, the significant movement in MAE and MAPE can be explained in Figure 14, where it can be observed that the trend component makes the largest contribution to the natural gas prices.

Table A4.
Copula families tested against the data.
Table A4.
Copula families tested against the data.
| Family | Copula Name |
|---|---|
| - | Independence (Indep.) |
| Elliptical | Gaussian |
| Student t | |
| Archimedean | Clayton |
| Gumbel | |
| Frank | |
| Joe | |
| Clayton–Gumbel (BB1) | |
| Joe–Gumbel (BB6) | |
| Joe–Clayton (BB7) | |
| Joe–Frank (BB8) | |
| Extreme Value | Tawn |
| Nonparametric | Transformation Lernel |

Table A5.
Calibrated bivariate copula description of monthly vine copulas.
Table A5.
Calibrated bivariate copula description of monthly vine copulas.
| Month | Variable 1 | Variable 2 | Condi. On | Copula Type | Rotation | Parameter | Tau | AIC |
|---|---|---|---|---|---|---|---|---|
| January | Wind | Demand | - | Frank | 0 | −1.95 | −0.21 | −12.60 |
| Gas | Demand | - | Inde. | - | - | - | 0 | |
| Wind | Gas | Demand | Inde. | - | - | - | 0 | |
| February | Gas | Wind | - | Clayton | 270 | 0.26 | −0.11 | −3.70 |
| Wind | Demand | - | Gaussian | 0 | −0.28 | −0.18 | −8.40 | |
| Gas | Demand | Wind | Joe | 0 | 1.19 | 0.10 | −4.31 | |
| March | Gas | Wind | - | Gumbel | 90 | 1.21 | −0.18 | −11.27 |
| Wind | Demand | - | Inde. | - | - | - | 0 | |
| Gas | Demand | Wind | Inde. | - | - | - | 0 | |
| April | Wind | Demand | - | Gaussian | 0 | 0.34 | 0.22 | −14.28 |
| Gas | Demand | - | Inde. | - | - | - | 0 | |
| Wind | Gas | Demand | Inde. | - | - | - | 0 | |
| May | Wind | Demand | - | Clayton | 0 | 0.99 | 0.33 | −53.77 |
| Gas | Demand | - | Inde. | - | - | - | 0 | |
| Wind | Gas | Demand | Inde. | - | - | - | 0 | |
| June | Gas | Wind | - | Joe | 90 | 1.21 | −0.11 | −4.28 |
| Wind | Demand | - | BB7 | 0 | 1.27,0.87 | 0.36 | −55.13 | |
| Gas | Demand | Wind | Gumbel | 180 | 1.13 | 0.12 | −3.57 | |
| July | Gas | Wind | - | Independence | - | - | - | 0 |
| Wind | Demand | - | Gaussian | 0 | 0.35 | 0.23 | −16.19 | |
| Gas | Demand | Wind | Inde. | - | - | - | 0 | |
| August | Gas | Wind | - | Gumbel | 90 | 1.07 | −0.06 | −0.21 |
| Wind | Demand | - | BB7 | 0 | 1.33, 0.54 | 0.31 | −37.47 | |
| Demand | Gas | Wind | Inde. | - | - | - | 0 | |
| September | Wind | Demand | - | Gaussian | 0 | 0.48 | 0.32 | −34.23 |
| Gas | Demand | - | Student | 0 | 0.07, 2.83 | 0.04 | −7.41 | |
| Wind | Gas | Demand | Inde. | - | - | - | 0 | |
| October | Gas | Wind | - | Frank | 0 | −0.69 | −0.08 | 0 |
| Wind | Demand | - | Frank | 0 | 2.29 | 0.24 | −18.80 | |
| Gas | Demand | Gas | Joe | 180 | 1.19 | 0.10 | −4.83 | |
| November | Gas | Wind | - | Frank | 0 | −0.70 | −0.08 | −0.03 |
| Wind | Demand | - | Clayton | 180 | 0.26 | 0.12 | −3.60 | |
| Gas | Demand | Wind | Student | 0 | 0.07, 4.36 | 0.04 | −1.23 | |
| December | Wind | Gas | - | Inde. | - | - | - | 0 |
| Gas | Demand | - | Joe | 180 | 1.10 | 0.05 | −1.31 | |
| Wind | Demand | Gas | Inde. | - | - | - | 0 |
The decision to employ a monthly copula calibration paid off, as Table A5 shows. It can be seen that, for each month, the bivariate copula structure and vine copula structure are not the same for the twelve months. While it was suggested that the C-vine copula structure is reasonable for the study, the C-vine structure only appears in January, April, May, and September. In these cases, the central node of the C-vine structure is the demand variable, indicating that the demand variable is strongly dependent on wind power and natural gas prices. However, in these months, the individual copulas have different copula families. The same is true in the months of February, March, June, July, August, and November, where they have the same vine structure but different copula families for individual copulas.
Notes
| 1 | The modeling and simulation were carried out using the Google Vertex AI tool with 125.8 GB of RAM and disk space of 94.3 GB. |
| 2 | The calibration was performed using the Python package “pyvinecopulib”, version 0.7.3. |
References
- Aloui, Riadh, Mohamed Ben Aissa, Shawkat Hammoudeh, and Duc Khuong Nguyen. 2014. Dependence and extreme dependence of crude oil and natural gas prices with applications to risk management. Energy Economics 42: 332–42. [Google Scholar] [CrossRef]
- Arenas-López, Jonatan Pablo, and Mohamed Badaoui. 2020. Stochastic modelling of wind speeds based on turbulence intensity. Renewable Energy 155: 10–22. [Google Scholar] [CrossRef]
- Benth, Fred Espen, and Jurate Saltyte Benth. 2007. The volatility of temperature and pricing of weather derivatives. Quantitative Finance 7: 553–61. [Google Scholar] [CrossRef]
- Benth, Fred Espen, and Jūratė Šaltytė Benth. 2004. The Normal Inverse Gaussian Distribution and Spot Price Modelling in Energy Markets. International Journal of Theoretical and Applied Finance 7: 177–92. [Google Scholar] [CrossRef]
- Benth, Fred Espen, Juratė Šaltytė Benth, and Steen Koekebakker. 2008. Stochastic Modelling of Electricity and Related Markets. Advanced Series on Statistical Science & Applied Probability; Singapore: World Scientific, vol. 11. [Google Scholar] [CrossRef]
- Benth, Fred Espen, Luca Di Persio, and Silvia Lavagnini. 2018. Stochastic Modeling of Wind Derivatives in Energy Markets. Risks 6: 56. [Google Scholar] [CrossRef]
- Berrisch, Jonathan, Sven Pappert, Florian Ziel, and Antonia Arsova. 2023. Modeling volatility and dependence of european carbon and energy prices. Finance Research Letters 52: 103503. [Google Scholar] [CrossRef]
- Cartea, Álvaro, and Marcelo G. Figueroa. 2006. Pricing in electricity markets: A mean reverting jump diffusion model with seasonality. Applied Mathematical Finance 12: 313–35. [Google Scholar] [CrossRef]
- Chen, Hao, Jianzhong Zhang, Yubo Tao, and Fenglei Tan. 2019. Asymmetric garch type models for asymmetric volatility characteristics analysis and wind power forecasting. Protection and Control of Modern Power Systems 4: 29. [Google Scholar] [CrossRef]
- Clewlow, Les. 2000. Energy Derivatives: Pricing and Risk Management. London: Lacima Publications. [Google Scholar]
- Coulon, Michael, Warren B. Powell, and Ronnie Sircar. 2013. A model for hedging load and price risk in the Texas electricity market. Energy Economics 40: 976–88. [Google Scholar] [CrossRef]
- Čeperić, Ervin, Saša Žiković, and Vladimir Čeperić. 2017. Short-term forecasting of natural gas prices using machine learning and feature selection algorithms. Energy 140: 893–900. [Google Scholar] [CrossRef]
- Dissmann, Jeffrey, Eike Christian Brechmann, Claudia Czado, and Dorota Kurowicka. 2012. Selecting and estimating regular vine copulae and application to financial returns. arXiv arXiv:1202.2002. [Google Scholar] [CrossRef]
- Genest, Christian, Michel Gendron, and Michaël Bourdeau-Brien. 2009. The advent of copulas in finance. The European Journal of Finance 15: 609–18. [Google Scholar] [CrossRef]
- Hill, David C., David McMillan, Keith R. W. Bell, and David Infield. 2012. Application of Auto-Regressive Models to U.K. Wind Speed Data for Power System Impact Studies. IEEE Transactions on Sustainable Energy 3: 134–41. [Google Scholar] [CrossRef]
- Hu, Ling. 2006. Dependence patterns across financial markets: A mixed copula approach. Applied Financial Economics 16: 717–29. [Google Scholar] [CrossRef]
- Jaramillo, Oscar A., and Marco Antonio Borja. 2004. Wind speed analysis in la ventosa, mexico: A bimodal probability distribution case. Renewable Energy 29: 1613–30. [Google Scholar] [CrossRef]
- Jondeau, Eric, and Michael Rockinger. 2006. The copula-GARCH model of conditional dependencies: An international stock market application. Journal of International Money and Finance 25: 827–53. [Google Scholar] [CrossRef]
- Karki, R., P. Hu, and R. Billinton. 2006. A Simplified Wind Power Generation Model for Reliability Evaluation. IEEE Transactions on Energy Conversion 21: 533–40. [Google Scholar] [CrossRef]
- Li, Hongmin, Jianzhou Wang, Haiyan Lu, and Zhenhai Guo. 2018. Research and application of a combined model based on variable weight for short term wind speed forecasting. Renewable Energy 116: 669–84. [Google Scholar] [CrossRef]
- Loukatou, Angeliki, Sydney Howell, Paul Johnson, and Peter Duck. 2018. Stochastic wind speed modelling for estimation of expected wind power output. Applied Energy 228: 1328–40. [Google Scholar] [CrossRef]
- Lucia, Julio, and Eduardo Schwartz. 2002. Electricity Prices and Power Derivatives: Evidence from the Nordic Power Exchange. Review of Derivatives Research 5: 5–50. [Google Scholar] [CrossRef]
- Meyer-Brandis, Thilo, and Peter Tankov. 2009. Multi-Factor Jump-Diffusion Models of Electricity Prices. International Journal of Theoretical and Applied Finance 11: 503–28. [Google Scholar] [CrossRef]
- Nelsen, Roger B. 1996. An Introduction to Copulas. New York: Springer Science & Business Media. [Google Scholar]
- Nguyen, Hang T., and Ian T. Nabney. 2010. Short-term electricity demand and gas price forecasts using wavelet transforms and adaptive models. Energy 35: 3674–85. [Google Scholar] [CrossRef]
- Pilipović, Dragana. 1998. Energy Risk: Valuing and Managing Energy Derivatives. New York: McGraw-Hill. [Google Scholar]
- Rodríguez, Yeny E., Miguel A. Pérez-Uribe, and Javier Contreras. 2021. Wind Put Barrier Options Pricing Based on the Nordix Index. Energies 14: 1177. [Google Scholar] [CrossRef]
- Saghi, Faramarz, and Mustafa Jahangoshai Rezaee. 2021. An ensemble approach based on transformation functions for natural gas price forecasting considering optimal time delays. PeerJ Computer Science 7: e409. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, Eduardo. 1997. The Stochastic Behavior of Commodity Prices: Implications for Valuation and Hedging. The Journal of Finance 52: 923–73. [Google Scholar] [CrossRef]
- Shen, Zhiwei, and Matthias Ritter. 2016. Forecasting volatility of wind power production. Applied Energy 176: 295–308. [Google Scholar] [CrossRef]
- Sklar, Abe. 1959. Fonctions de répartition à n dimensions et leurs marges [distribution functions with n dimensions and their margins]. Publications de l’Institut de Statistique de L’Université de Paris 8: 229–231. [Google Scholar]
- Tankov, Peter, and Rama Cont. 2003. Financial Modelling with Jump Processes, 1st ed. New York: Chapman and Hall/CRC. [Google Scholar] [CrossRef]
- Wang, Jianzhou, Pei Du, Tong Niu, and Wendong Yang. 2017. A novel hybrid system based on a new proposed algorithm—Multi-Objective Whale Optimization Algorithm for wind speed forecasting. Applied Energy 208: 344–60. [Google Scholar] [CrossRef]
- Warunasinghe, Sudeesha, and Anatoliy Swishchuk. 2024. Stochastic modeling of wind derivatives with application to the alberta energy market. Risks 12: 18. [Google Scholar] [CrossRef]
- Zárate-Miñano, Rafael, Marian Anghel, and Federico Milano. 2013. Continuous wind speed models based on stochastic differential equations. Applied Energy 104: 42–49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).