1. Introduction
The application of machine learning techniques to financial problems presents opportunities to enhance methodologies through domain-specific considerations. A fundamental principle in conventional machine learning practice involves feature decorrelation to eliminate presumed redundancy and improve model performance (
James et al. 2013). However, financial data exhibit correlations that frequently encode essential economic relationships developed through market mechanisms, arbitrage activities, and risk management practices, suggesting potential benefits for specialized approaches rather than treating them as statistical noise requiring elimination.
These findings contribute to the growing evidence that financial machine learning benefits from domain-specific approaches. Building upon
Zeng and Rao (
2025)’s insights on domain knowledge integration and
Maddulety (
2019)’s identification of feature engineering research gaps, our results provide systematic evidence that preserving economic correlations enhances model performance across diverse architectures. The consistency of improvements across neural networks, gradient boosting, and hybrid ensembles suggests fundamental characteristics of financial data that distinguish it from generic statistical applications, supporting the development of specialized methodological frameworks for computational finance.
This study investigates the hypothesis that preserving natural financial correlations can outperform conventional decorrelation approaches in machine learning applications. We employ autocallable structured notes as an empirical laboratory due to their complex mathematical structure, combining multiple financial relationships within a single instrument. These products exhibit pricing functions with mixed regularity properties including smooth regions amenable to neural network approximation and barrier-dependent discontinuities suitable for tree-based methods.
Autocallable notes provide an ideal testing ground because they incorporate several fundamental financial relationships simultaneously. The interaction between spot price movements, volatility dynamics, barrier proximity effects, and time decay creates natural correlations that reflect essential pricing mechanics. The embedded down-and-in up-and-out put option generates additional complexity through path-dependent terms that affect higher-order sensitivities in economically meaningful patterns.
Our analysis extends beyond a simple performance comparison to investigate the mathematical foundations underlying the observed differences. Through component-wise decomposition and automatic differentiation techniques, we examine how feature engineering choices affect model ability to capture complex sensitivity patterns including vanna and volga behaviors near barrier levels. The systematic investigation reveals fundamental tensions between statistical optimization objectives and domain knowledge preservation requirements in financial applications. The systematic investigation reveals that conventional statistical optimization—specifically correlation elimination through orthogonalization—directly conflicts with the preservation of economically meaningful relationships in financial data. While orthogonal features achieve statistical decorrelation and reduce variance inflation factors, they obscure natural dependencies between spot prices, volatility, barrier levels, and time decay that are essential for accurate autocallable pricing. This creates a trade-off where statistical optimization criteria may degrade rather than improve machine learning performance in financial applications.
The remainder of this paper is organized as follows.
Section 2 reviews the literature on computational finance and machine learning applications in derivatives pricing.
Section 3 details our autocallable note pricing framework and feature engineering approaches.
Section 4 presents empirical results comparing basic and orthogonal features across multiple architectures.
Section 5 discusses implications for financial machine learning and risk management.
Section 6 concludes this study with directions for future research.
2. Literature Review
The intersection of machine learning and financial derivatives pricing has evolved rapidly, with recent contributions demonstrating both promising applications and methodological challenges.
Ruf and Wang (
2020) establish neural network approaches for American option pricing, while
Beck et al. (
2021) develop deep learning solutions for high-dimensional partial differential equations relevant to derivatives’ valuation. However, these contributions primarily focus on computational efficiency rather than examining whether conventional machine learning practices suit financial domain characteristics.
Feature engineering literature in machine learning commonly prescribes correlation elimination through orthogonalization techniques. The underlying assumption treats correlation as a redundancy that impedes learning algorithms by creating multicollinearity problems. Principal component analysis, variance inflation factor reduction, and other decorrelation methods are standard practice across machine learning applications (
Jolliffe and Cadima 2016).
Recent financial machine learning literature has begun questioning whether generic statistical techniques appropriately address domain-specific requirements.
Gu et al. (
2020) demonstrate that asset pricing applications benefit from careful consideration of economic theory in feature construction.
L. Chen et al. (
2023) show that incorporating financial constraints improves neural network performance in portfolio optimization contexts. These findings suggest that financial applications may require domain-aware approaches rather than generic statistical optimization.
The literature on structured products provides limited guidance on appropriate machine learning methodologies, despite the significant academic attention these instruments have received since their introduction. Autocallable notes, first formally analyzed in the academic literature by
Wilmott et al. (
1995), represent a class of structured products that combine traditional bond features with embedded barrier options to create early redemption mechanisms. The mathematical foundations for these products emerged from the barrier option literature of the 1990s (
Merton 1973;
Rich 1994), which established the theoretical framework for path-dependent derivatives’ pricing.
The academic treatment of autocallable structures gained momentum in the early 2000s, with
Nelken (
2000) providing a comprehensive analysis of structured product mechanics and
Wystup (
2006) extending the framework to foreign exchange applications.
Guillaume (
2015) develop analytical approaches for autocallable valuation but do not address machine learning applications. A more recent study by
Deng et al. (
2012) establishes pricing frameworks for autocallable notes without investigating computational learning techniques, while
Paletta and Tunaru (
2022) examine Bayesian approaches but focus on calibration rather than machine learning feature engineering.
The evolution of autocallable products reflects broader trends in structured finance, as documented by
Telpner (
2009), where traditional risk–return profiles are modified through embedded option strategies. The complexity of these instruments, particularly their path-dependent characteristics and multiple embedded optionalities, creates unique challenges for computational approaches that distinguish them from simpler derivative structures (
Lipton 2001).
Recent advances in computational derivatives’ pricing have demonstrated both the potential and challenges of applying machine learning to structured products.
Davis et al. (
2021) establish that tree-based techniques can achieve significant computational improvements in derivatives’ pricing while maintaining accuracy, demonstrating orders-of-magnitude speed improvements for exotic derivatives.
Zhang et al. (
2024) develop unified pricing frameworks for autocallable products using Markov chain approximation, revealing the mathematical complexity inherent in barrier-dependent structures.
Cui et al. (
2024) propose machine learning approaches for multi-asset autocallable pricing that achieve 250× computational acceleration over Monte Carlo methods while improving hedging performance through distributional reinforcement learning.
The financial machine learning literature has increasingly recognized that domain-specific approaches may outperform generic statistical methods.
Zeng and Rao (
2025) demonstrate that incorporating domain knowledge through explainable feature construction significantly improves financial prediction accuracy compared to conventional preprocessing approaches.
Maddulety (
2019) identify feature engineering as a critical research gap in banking risk management applications, noting that while machine learning techniques show promise, limited research addresses whether standard preprocessing methods suit financial data characteristics. Our investigation contributes to this research direction.
3. Pricing Formula and Feature Engineering
3.1. Autocallable Note Structure and Pricing Framework
We analyze autocallable notes with the following specification: 100 notional amount, quarterly observation dates over one-year maturity, 5% annual coupon rate paid quarterly when autocall conditions are not triggered, 80% knock-in barrier, 100% autocall barrier, and 90% put strike for the embedded barrier option. This configuration represents typical market structures and provides sufficient complexity for investigating machine learning approaches.
The total price decomposes into four interacting components:
where each component has the following analytical representation:
Here, C represents the quarterly coupon rate, N the notional amount, the first passage time to the autocall barrier U, and the survival probability.
The survival probabilities follow from the reflection principle for geometric Brownian motion:
where
denotes the standard normal cumulative distribution function. These analytical expressions enable exact computation of autocall probabilities and coupon survival rates without Monte Carlo approximation.
The coupon component represents quarterly payments’ conditional on non-autocall events. The autocall component captures the early redemption value when the underlying breaches the upper barrier. The notional component reflects final principal repayment probability. The down-and-in up-and-out put option provides capital protection when the knock-in barrier is breached but becomes worthless if the autocall barrier is subsequently triggered.
We employ exact analytical pricing methods rather than Monte Carlo simulation to ensure that observed performance differences reflect feature engineering choices rather than numerical approximation artifacts. This approach eliminates the confounding effects of Monte Carlo convergence errors, path discretization bias, and random sampling variation that could obscure the relationship between feature construction and model performance. The analytical framework enables generation of precisely labeled training data across the entire parameter space, providing clean experimental conditions essential for isolating feature engineering effects. The DIUO put valuation uses reflection method techniques with Fourier series expansion for computational efficiency (
Carr and Linetsky 2006).
For the DIUO put option with barriers
L (knock-in) and
U (autocall), strike
K, and maturity
T, the analytical value is
where
represents the standard down-and-in put value and
captures the barrier interaction effects through the reflection principle:
with coefficients
determined by the boundary conditions at both barriers. This approach enables the generation of exact pricing labels across the parameter space while maintaining computational tractability for large-scale machine learning applications.
3.2. Parameter Space and Data Generation
Our dataset employs Latin Hypercube Sampling across a seven-dimensional parameter space including spot price, autocall barrier, knock-in barrier, volatility, time to maturity, risk-free rate, and coupon rate. The sampling protocol ensures systematic coverage while respecting no-arbitrage constraints inherent in autocallable structures.
Parameter ranges reflect economically realistic conditions: spot prices from 70% to 130% of notional components, volatilities from 10% to 50% annually, time to maturity from 0.25 to 1.0 years, risk-free rates from 0% to 5% annually, and coupon rates from 2% to 8% annually. Barrier levels maintain economically meaningful relationships with autocall barriers above spot prices and knock-in barriers below initial levels.
The constraint enforcement mechanism ensures financial validity through a proportional adjustment rather than rejection sampling. This approach preserves the statistical properties of Latin Hypercube Sampling while maintaining systematic parameter space coverage. The resulting dataset contains 3000 valid parameter combinations with corresponding exact pricing labels computed through analytical methods.
3.3. Feature Engineering Framework
We compare two distinct feature engineering approaches to investigate the impact of correlation preservation versus elimination on model performance.
Basic features employ raw financial parameters directly: spot price, autocall barrier, knock-in barrier, volatility, time to maturity, risk-free rate, and coupon rate. This representation preserves natural economic relationships while maintaining direct interpretability essential for financial applications. The correlations present in these features reflect fundamental financial principles including volatility–option value relationships, barrier proximity effects, and time decay patterns.
Orthogonal features follow conventional machine learning practice for multicollinearity reduction through mathematical transformations designed to minimize correlation while preserving information content. The transformations include
where
U and
L represent the autocall and knock-in barriers, respectively, and
K represents the put strike. These features achieve statistical decorrelation but obscure direct economic relationships.
The comparison framework enables systematic investigation of whether correlation elimination improves or degrades model performance in financial contexts. The orthogonal transformation achieves substantial variance inflation factor reduction while the basic features maintain high correlations, reflecting natural financial relationships.
3.4. Machine Learning Architecture
Our model selection directly addresses the mathematical heterogeneity inherent in autocallable pricing functions, which exhibit both smooth analytical regions and barrier-induced discontinuities within the same valuation surface. Neural networks excel in smooth regions where the pricing function belongs to Sobolev spaces with continuous derivatives, while gradient boosting algorithms naturally handle threshold effects and jump discontinuities through tree-based splitting mechanisms. Hybrid ensemble approaches enable systematic investigation of whether feature engineering effects persist across fundamentally different approximation paradigms, strengthening the generalizability of our findings.
The neural network architecture employs multi-layer perceptrons with hidden dimensions [256, 128, 64], batch normalization for numerical stability, and dropout regularization. Training uses AdamW optimization with early stopping based on validation loss to prevent overfitting. The architecture balances approximation capability with computational efficiency suitable for real-time applications.
CatBoost gradient boosting provides tree-based approximation, which is particularly effective for bounded variation functions characteristic of barrier options. The algorithm handles threshold effects naturally through splitting mechanisms while maintaining computational efficiency. Configuration parameters include a tree depth of 6, learning rate of 0.1, and early stopping based on validation performance.
The hybrid ensemble combines neural network global approximation with gradient boosting residual modeling. The approach recognizes that different algorithms excel in different regions of the pricing surface by training neural networks on overall structure and gradient boosting on remaining patterns. This decomposition aligns algorithmic strengths with mathematical properties of the underlying pricing function.
Functional Space Decomposition and Algorithm Selection
The mathematical foundation for our hybrid approach leverages function space decomposition theory and the complementary approximation strengths of different machine learning architectures. Autocallable pricing functions exhibit mixed regularity: smooth behavior in regions away from barriers (suitable for neural network approximation) and jump discontinuities near barrier levels (optimal for tree-based methods).
Following approximation theory (
Adams and Fournier 2003), neural networks achieve optimal convergence rates
for smooth functions in Sobolev spaces
, where
represents the degree of smoothness and
d the input dimension. CatBoost excels for functions of bounded variation
through tree splitting mechanisms that naturally approximate piecewise constant functions (
DeVore 1998).
Our hybrid approach exploits functional decomposition:
where the neural network captures smooth components and CatBoost models’ residual discontinuities. This architectural choice ensures that each algorithm operates within its optimal functional space, explaining the systematic performance patterns observed across feature engineering approaches and providing a theoretical justification for our empirical methodology.
3.5. Greeks’ Computation and Analysis
Higher-order sensitivity analysis employs automatic differentiation through PyTorch functional transformations. The framework enables vectorized computation of first- and second-order derivatives across the parameter space:
Component-wise differentiation isolates the contribution of individual pricing elements to overall sensitivity patterns:
where
represents any parameter (spot price, volatility, time, etc.). The automatic differentiation approach ensures numerical accuracy while maintaining computational efficiency for systematic Greeks’ analysis. The component decomposition reveals how autocall mechanisms, coupon payments, and barrier options contribute differently to sensitivity patterns, providing insights into the mathematical sources of pricing complexity.
4. Results
4.1. Model Performance Comparison
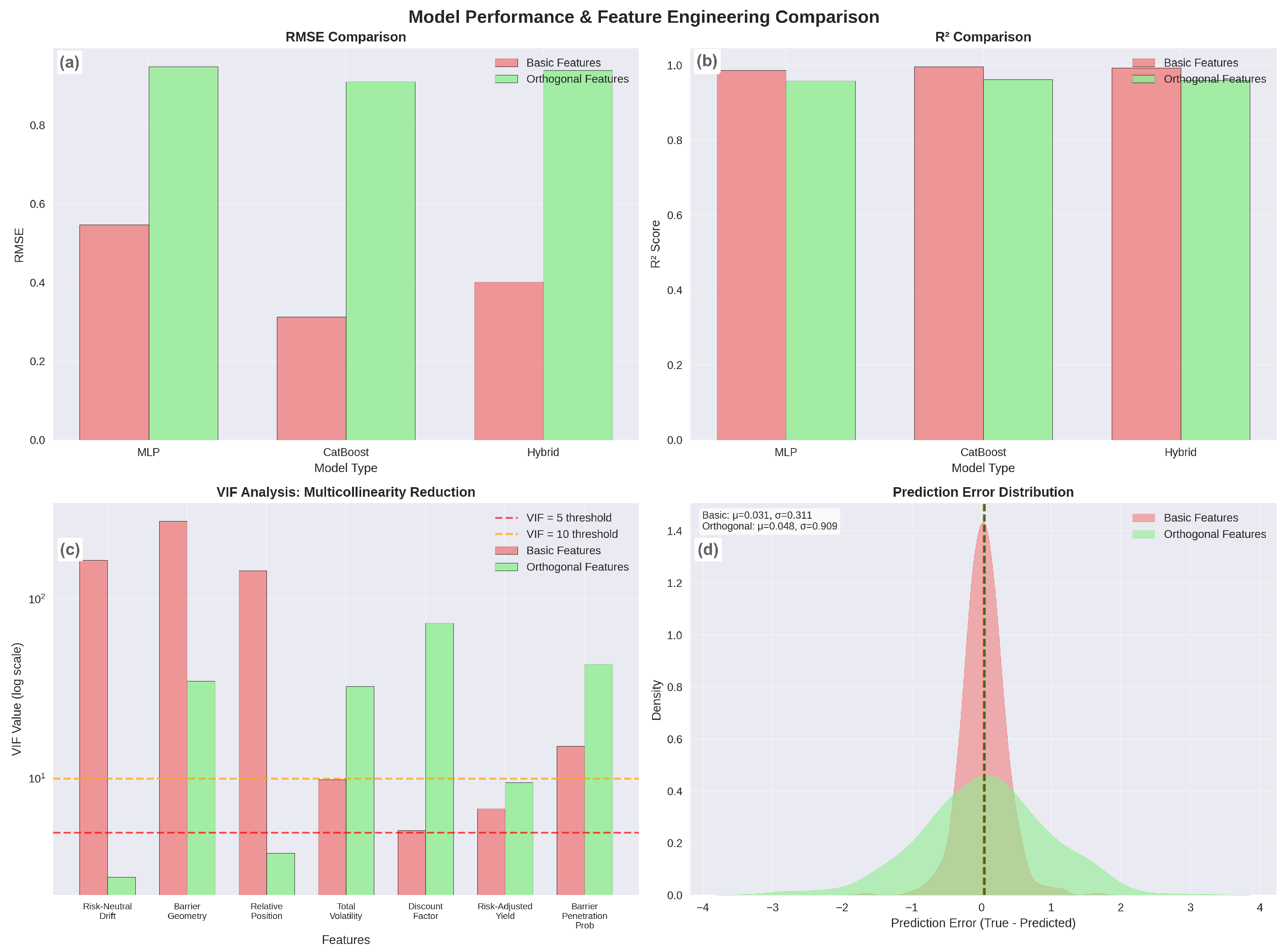
Table 1 presents comprehensive performance metrics comparing basic and orthogonal feature approaches across all model architectures.
The results demonstrate systematic and substantial performance degradation when conventional machine learning feature engineering is applied to financial data. CatBoost experiences the most severe degradation with a 191% RMSE increase, suggesting that tree-based splitting mechanisms perform optimally when operating on economically meaningful variables rather than mathematical combinations. Neural networks show significant degradation of 73%, while hybrid ensembles demonstrate intermediate patterns with 134% performance deterioration.
The differential performance patterns align with functional analysis theory, where CatBoost’s superior baseline performance reflects its natural alignment with the bounded variation characteristics of barrier-induced pricing discontinuities (
DeVore 1998). Neural networks, while exhibiting larger degradation percentages, maintain reasonable absolute performance due to their effectiveness in Sobolev spaces characterizing smooth pricing regions (
Cybenko 1989).
Notably, the hybrid ensemble achieves intermediate performance (RMSE: 0.4012) between the individual components (CatBoost: 0.3122, MLP: 0.5465), rather than outperforming both. This suggests that for autocallable pricing within our parameter ranges, the function exhibits stronger bounded variation characteristics than smooth Sobolev properties. The sequential ensemble design, where MLP captures global structures before CatBoost models’ residuals, may inadvertently reduce CatBoost’s effectiveness by providing preprocessed rather than raw financial features. This observation indicates that the mixed regularity hypothesis, while theoretically sound, may not reflect the empirical dominance of discontinuous components in autocallable pricing, pointing toward the need for weighted or adaptive ensemble strategies that can dynamically favor the more suitable algorithm based on local function properties.
The consistency of degradation across diverse architectures indicates that the phenomenon reflects fundamental characteristics of financial data rather than algorithm-specific effects. The superior performance of basic features suggests that natural financial correlations encode essential information for accurate pricing rather than representing statistical redundancy requiring elimination.
Table 2 shows comprehensive comparison across all model architectures and feature engineering approaches. The table includes RMSE, MAE,
scores, training times, and evaluation times, demonstrating systematic superiority of basic features while confirming computational efficiency across all approaches.
Concurrently,
Figure 1 reveals the feature engineering paradox in financial machine learning.
4.2. Component-Wise Analysis
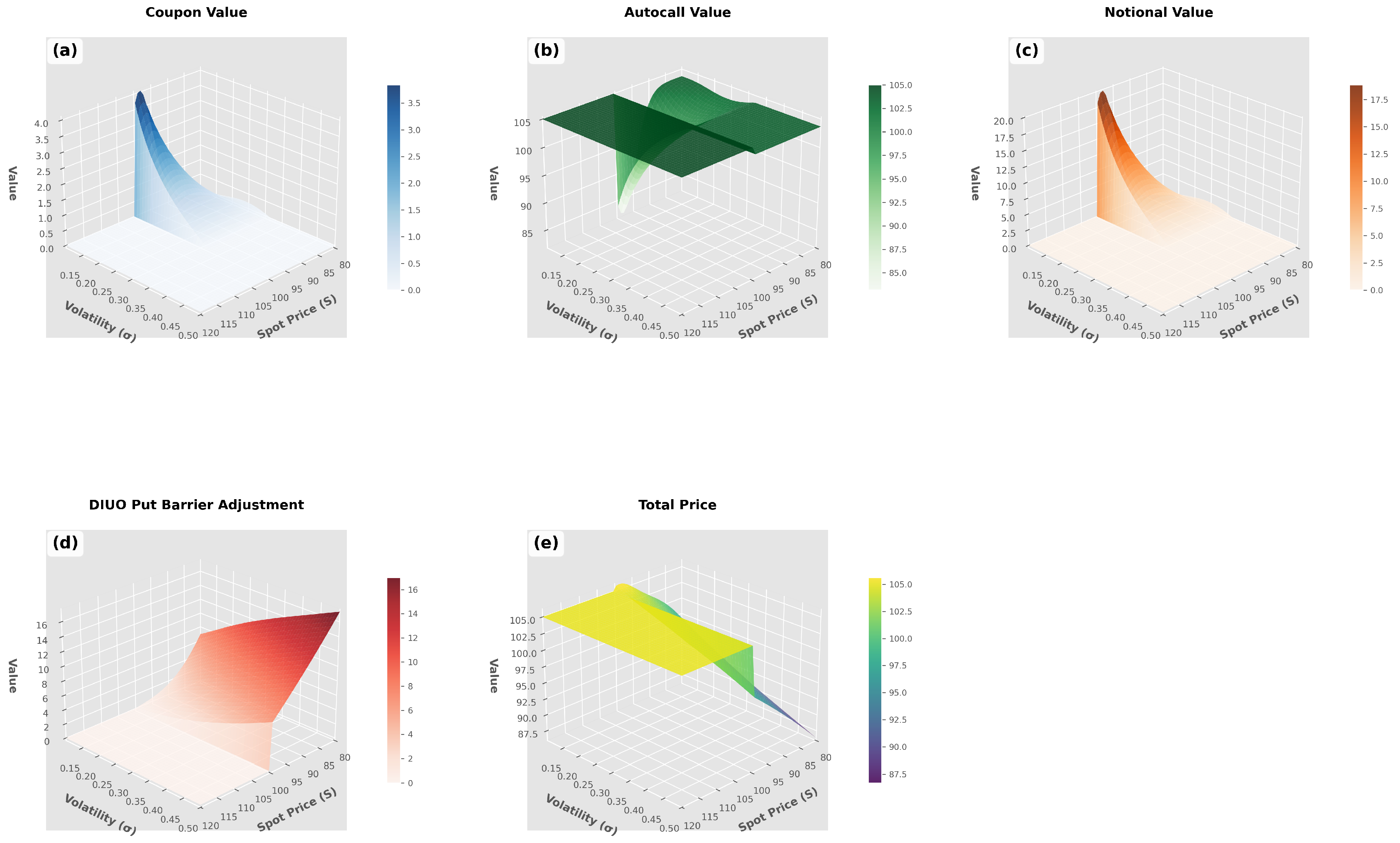
The pricing function decomposition in
Figure 2 reveals how individual components contribute to overall mathematical complexity and machine learning challenges. The coupon component exhibits relatively smooth behavior suitable for neural network approximation, except near barrier transitions, where discrete autocall probabilities create discontinuities. The autocall component demonstrates binary characteristics, generating sharp transitions that favor tree-based methods.
The notional component follows exponential decay patterns modified by survival probability interactions, creating smooth global structure with localized barrier effects. The DIUO put option contributes the most mathematical sophistication through reflection method series expansion, generating oscillatory patterns with multiple local extrema despite its modest contribution to the total option value.
The component analysis demonstrates that autocallable pricing complexity emerges from interactions between structurally different mathematical elements rather than individual component sophistication. This mixed regularity justifies the hybrid ensemble approach while explaining why feature engineering choices significantly affect model performance.
The price surface demonstrates several key characteristics that justify our hybrid machine learning approach. Smooth regions away from barriers exhibit continuous derivatives suitable for neural network approximation, while sharp transitions near barrier levels create discontinuities that favor tree-based methods. The interaction between volatility and barrier proximity creates complex curvature patterns that require sophisticated modeling techniques.
4.3. Greeks’ Analysis and Sensitivity Patterns
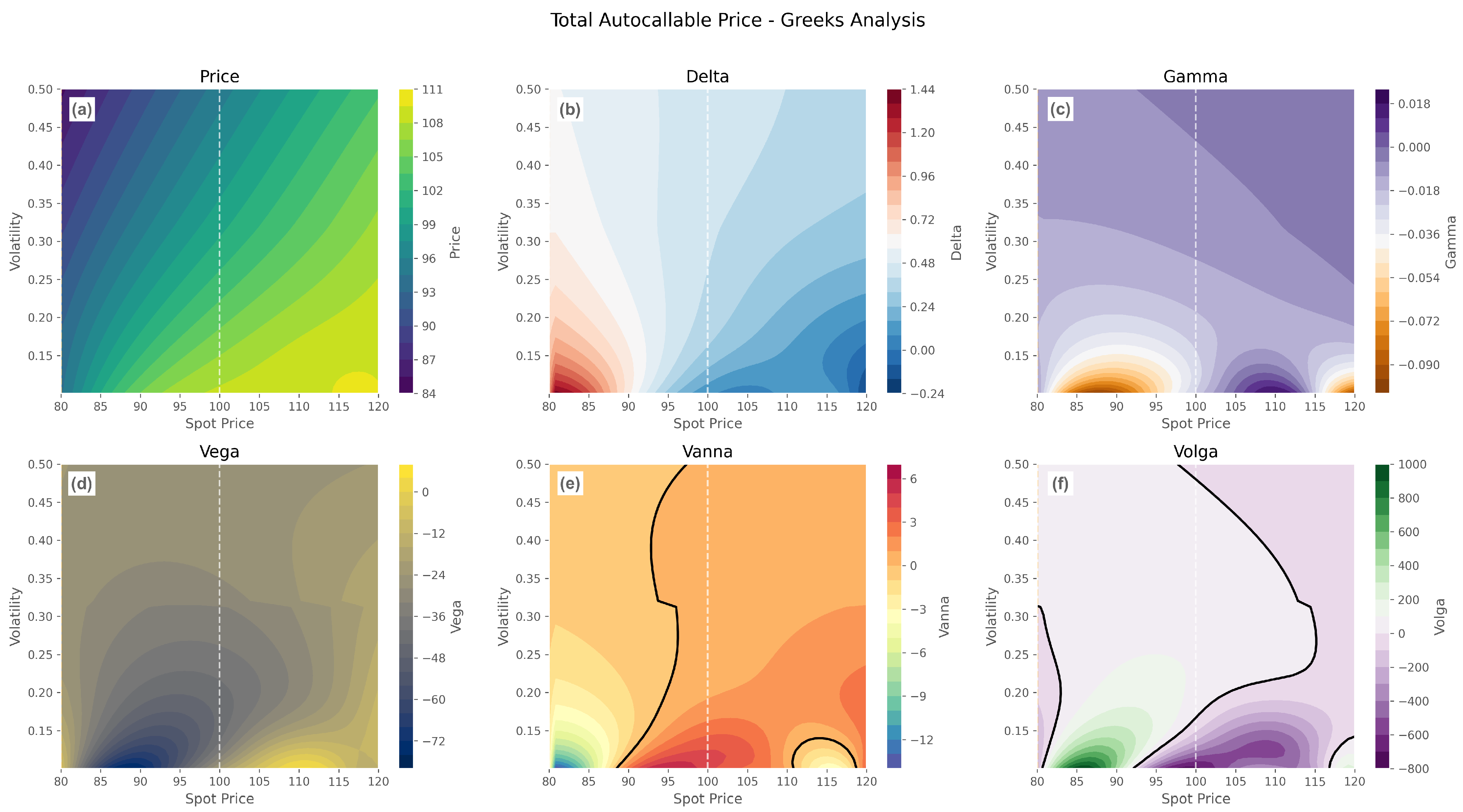
Automatic differentiation analysis in
Figure 3 reveals complex higher-order sensitivity patterns that extend beyond traditional option theory predictions. Delta surfaces exhibit expected increasing relationships with spot price but demonstrate sharp transitions near barriers where discrete autocall probabilities create step-function behavior. Gamma patterns show extreme concentration near autocall barriers with spikes exceeding traditional option levels.
Vanna and volga surfaces demonstrate systematic sign reversals across economically relevant parameter ranges. Vanna exhibits multiple sign changes, particularly near barrier transitions where spot–volatility interactions create complex cross-derivative patterns. Volga shows similar reversals concentrated near barrier levels where volatility changes affect both barrier reach probabilities and relative importance of different barrier effects.
The component-wise Greeks’ decomposition isolates how the DIUO put option creates disproportionate effects on higher-order derivatives. While contributing approximately 15–20% of the total option value, the DIUO put accounts for 60% of vanna complexity and 40% of volga sign reversal patterns. This disproportionate impact demonstrates the component’s critical role in determining sensitivity patterns and associated hedging challenges, providing empirical support for the theoretical barrier option analysis of
Carr and Linetsky (
2006) and extending it to structured product contexts.
The Greeks’ analysis reveals several critical insights for practical risk management that complement recent advances in computational derivatives’ pricing (
Ruf and Wang 2020). The vanna sign reversals occur in multiple economically relevant zones, creating hedging challenges that traditional delta/gamma approaches cannot adequately address, consistent with the findings of
Bossens et al. (
2010) on volatility surface construction. The concentration of gamma near autocall barriers creates rebalancing requirements that may prove costly in practice, while volga patterns demonstrate how volatility risk management becomes increasingly complex near barrier levels where second-order volatility effects exhibit non-monotonic behavior.
6. Conclusions
This investigation establishes that domain-specific machine learning approaches can enhance performance in financial applications where correlations encode fundamental economic relationships. Our systematic analysis using autocallable structured notes reveals performance improvements of 43–191% when natural financial correlations are preserved through domain-aware feature engineering techniques. These findings provide an empirical foundation for advancing financial machine learning through specialized methodologies.
The results establish that correlation can represent essential economic information rather than statistical redundancy requiring elimination in financial contexts, contributing to the literature on domain-specific machine learning approaches (
Gu et al. 2020;
López de Prado 2020). Natural relationships between spot prices, volatility, barrier levels, and time decay encode essential pricing mechanics that can be leveraged for improved model performance. This principle provides a foundation for developing financial machine learning systems that integrate domain knowledge with statistical optimization.
The systematic nature of observed performance improvements across diverse algorithms provides evidence for potential applicability of the domain knowledge preservation principle to other financial instruments. This foundation enables the development of mathematical and machine learning techniques that can enhance both our theoretical understanding and practical applications in computational finance, as demonstrated by the recent advances in related areas (
R. Chen et al. 2018;
Li et al. 2020;
Peters et al. 2017).