A Profitability and Risk Decomposition Analysis of the Open Economy Insurance Sector

Abstract

The objective of this paper is to analyse profitability and risk through the return on equity (ROE) measure of the open economy insurance sector in a non-stable economic period with an economic shock chain, during the years 2018–2022, characterised by an overheating economy, the Covid pandemic, the war in Ukraine, and a high-inflation wave. The ROE pyramid decomposition structure is proposed, along with the detailed CARAMEL version. A static and risk (dynamic) decomposition deviation analysis is used. The yearly non-stable drivers of insurance sector profitability deviation were confirmed. Despite this, the most influential were the earnings ratio deviations in either increasing or decreasing ROE alternatives. Solvency positively influenced the ROE deviation. It turned out that earnings and asset quality enormously increase the risk of the insurance sector. Conversely, risk is decreased mainly by liquidity and management. Simultaneously, significant, influential factors were identified. The results can serve as a background for carrying out operations, strategic analysis, and decision-making.

1. Introduction

The insurance sector is an essential segment of the financial market and institutions. Policymakers are using the sector to decrease and eliminate technical insurance risk. The rational development of the insurance sector is a crucial assumption for satisfactory economic development. The sector’s stability is a crucial problem and is managed by the regulatory rules of the regulatory authority and by inner risk-eliminating measures.

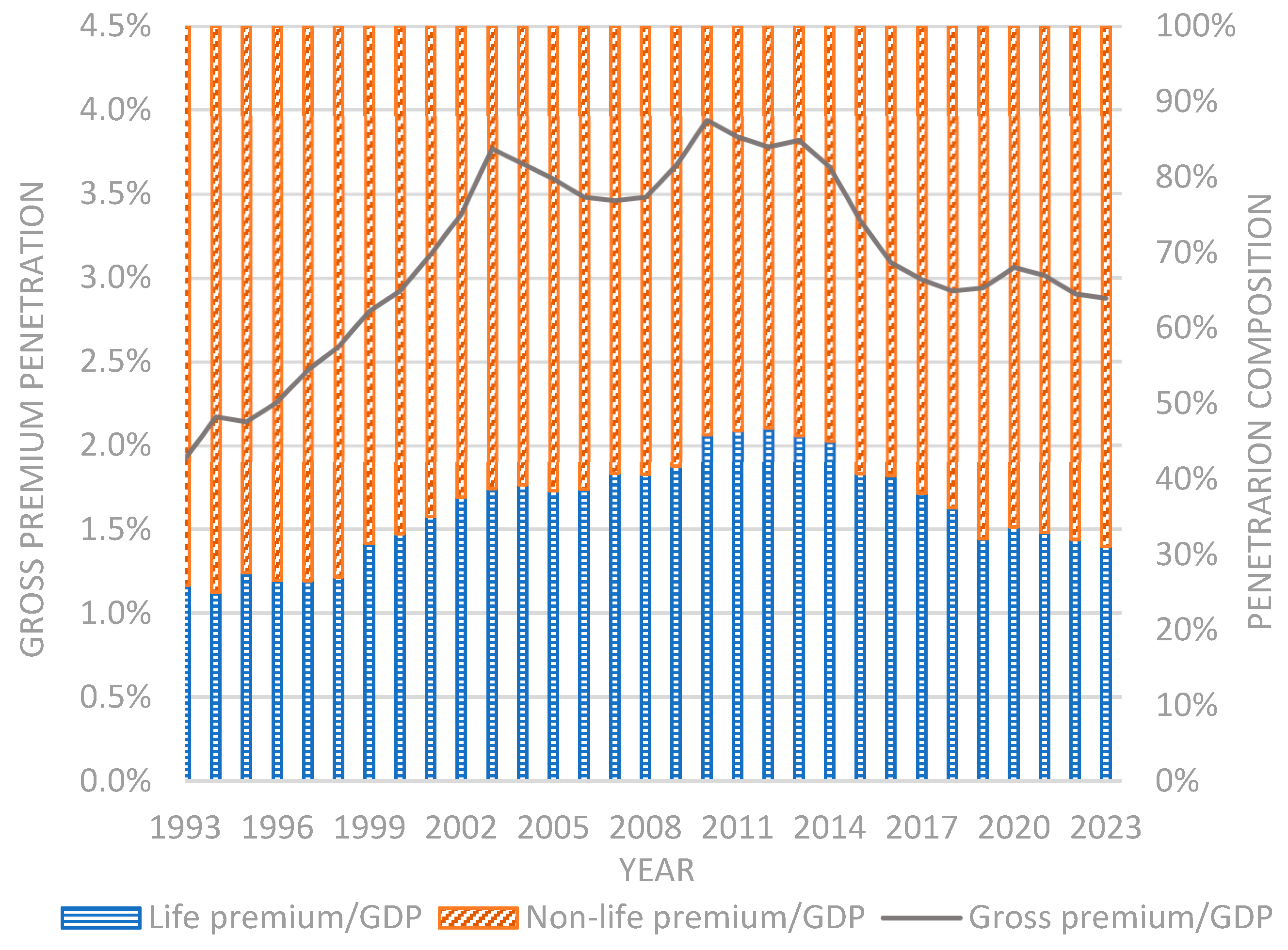
The Czech economy is specifically due to its considerable openness, and the insurance sector is growing, relatively stable, and adaptable to economic cycles and unexpected economic shocks. According to (OECD.Stat 2022; Czech Insurance Association 2023; Czech Statistical Office 2023), the gross penetration (Gross premium/GDP) was 2.9%, the life penetration (life premium/GDP) was 2.1%, and the non-life penetration (non-life premium/GDP) was 0.8% in the year 2023; see the development of ratio and structure in Figure 1. The penetration ratio is relatively low in comparison with Europe’s 6.4%; however, comparability with other countries is not easy because of different tax, social, and health systems. Nine out of 10 Czech inhabitants have some insurance contract. Most often, 61 per cent of Czech inhabitants have household insurance and 47 per cent have life insurance.

The financial performance of the sector is one of the primary objectives for shareholders and a company’s management. A company’s commonly accepted crucial advanced and practically used profitability indicator is Return on Equity (ROE), calculated with accounting data and reflecting the shareholder’s point of view. Many authors have dealt with the financial performance and profitability of the insurance sector (Barua et al. 2018; Doumpos et al. 2012; Eling and Jia 2019; Eling et al. 2022; Green and Segal 2004; Jarraya et al. 2023; Killins 2020; Kwon and Wolfrom 2017; Lorson and Wagner 2014; Torbati and Sayadi 2018; Shiu 2009), insurance companies (Benali and Rochdi 2017; Kirkbeşoğlu et al. 2015; Kaya 2015; Sharma et al. 2021; Siopi and Poufinas 2023), and rating evaluation (Adams et al. 2003; Das et al. 2003; Pottier 1997; Van Gestel et al. 2007).

The analysis of profitability and risk of the ROE ratio is based on finding value drivers, including their significance and impact. The decomposition method can provide profitability analysis using a pyramid analysis, allowing for a deep investigation of the problem. The static profitability deviation analysis explores one-period deviation and finds influential factors (drivers) due to significance. The profitability risk analysis is based on a dynamic analysis stemming from the time-series data of several periods. The variance analysis of the ROE modelling the risk can serve to decompose the risk and find substantial, strategic, and more stable influential factors.

This paper’s goal is to perform a profitability static decomposition analysis and risk (dynamic) decomposition analysis of the ROE measure decomposed by the pyramid approach of the Czech insurance sector from the years 2018 to 2022 by a CARAMEL categorisation. The period is characterised by several non-standard and shock economy development phases. The first stage in 2018 and 2019 is the overheating economy; in the second stage, in 2020 and 2021, there was the Covid pandemic shock; the Ukraine war, an energy crisis, and a high inflation wave governed the economy in 2022.

This paper is structured as follows: (1) a research methodology description of the ROE pyramid decomposition, static and risk (dynamic) deviation methods, and furthermore input data are introduced; (2) the empirical results for a static profitability analysis are computed and analysed; and (3) risk (dynamic) profitability analyses are computed, interpreted, and discussed.

2. Methodology Description and Input Data

This section includes methodologies proposed and applied as follows: the proposal of the pyramid decomposition of the financial performance indicator ROE based on CARAMEL categorisation of the insurance sector. Furthermore, a procedure for an additive relationship is presented, and the functional method for the calculation of influence deviations of multiplicative relationship is introduced. Risk (dynamic) analysis based on a time-series of indices and variance analysis is described.

2.1. The Pyramid Decomposition Proposal of ROE

The pyramid decomposition is a means used for highly developed analysis, and many authors have applied this method (see e.g., Albers 1998; Borodin et al. 2021; Dluhošová 2004; Jencova et al. 2018; Jeppson et al. 2021; Jin 2017; Kryzanowski and Mohsni 2015; Szymańska 2017; Dluhosova et al. 2022; Zmeškal et al. 2023).

The intention of the insurance sector ROE decomposition proposal is to incorporate particular aspects of the insurance sector’s effective and adaptable development. The basic blocks and chosen financial ratios of interest are based on a CARAMEL financial ratios composition (capital adequacy, asset quality, reinsurance and actuarial issues, management, earnings, liquidity) coined by Das et al. (2003) and applied, e.g., by Surya and Sudha (2020).

The pyramid decomposition proposal of ROE is presented in Figure 2 and starts as follows:

$ROE={\displaystyle \frac{EAT}{E}}={\displaystyle \frac{EBT}{E}}-{\displaystyle \frac{CT}{E}}$, substituting for ${\displaystyle \frac{EBT}{E}}={\displaystyle \frac{EBTp}{E}}+{\displaystyle \frac{EBTi}{E}}$,

$ROE={\displaystyle \frac{EAT}{E}}={\displaystyle \frac{EBTp}{E}}+{\displaystyle \frac{EBTi}{E}}-{\displaystyle \frac{CT}{E}}$ and after other substitutions ${\displaystyle \frac{EBTp}{E}}={\displaystyle \frac{EBTp}{NP}}\cdot {\displaystyle \frac{NP}{GP}}\cdot {\displaystyle \frac{GP}{E}}$ and ${\displaystyle \frac{EBTi}{E}}={\displaystyle \frac{EBTi}{Fi}}\cdot {\displaystyle \frac{Fi}{E}}$ then

$ROE={\displaystyle \frac{EAT}{E}}={\displaystyle \frac{EBTp}{NP}}\cdot {\displaystyle \frac{NP}{GP}}\cdot {\displaystyle \frac{GP}{E}}+{\displaystyle \frac{EBTi}{Fi}}\cdot {\displaystyle \frac{Fi}{E}}-{\displaystyle \frac{CT}{E}}$, finally we get the proposed decomposition equation,

$$ROE=-{\displaystyle \frac{CT}{E}}+{\displaystyle \frac{NP}{GP}}\cdot {\displaystyle \frac{GP}{E}}\cdot \left(1-{\displaystyle \frac{NCL}{NP}}-{\displaystyle \frac{OE}{NP}}\right)+{\displaystyle \frac{EBTi}{FI}}\cdot {\displaystyle \frac{FI}{TP}}\cdot {\displaystyle \frac{TP}{LA}}\cdot {\displaystyle \frac{LA}{A}}\cdot {\displaystyle \frac{A}{E}}$$

(1)

Whereas $ROE$ is a return on equity, $EAT$ is earnings after tax, $EBT$ is earnings before tax, $E$ is equity, $CT$ is corporate tax, $NP$ is a net premium, $GP$ is a gross premium, $NCL$ is net claims, $OE$ is operating expenditure, $EBTp$ is earnings before tax from the premium, $EBTi$ is earnings before tax from investments, $FI$ are financial investments, $TP$ is technical provisions (reserves), $LA$ is liquid assets, and $A$ is assets.

Due to the CARAMEL composition, financial ratios are categorised as follows: Capital adequacy (${\displaystyle \frac{GP}{E}}$ solvency ratio), Asset quality (${\displaystyle \frac{A}{E}}$ financial leverage, ${\displaystyle \frac{FI}{TP}}$), Reinsurance and Actuarial issues (${\displaystyle \frac{NP}{GP}}$ retention ratio), Management (${\displaystyle \frac{OE}{NP}}$), Earnings (${\displaystyle \frac{CT}{E}}$, ${\displaystyle \frac{NCL}{NP}}$, ${\displaystyle \frac{EBTi}{FI}}$), and Liquidity (${\displaystyle \frac{TP}{LA}}$, ${\displaystyle \frac{LA}{A}}$ liquidity ratio).

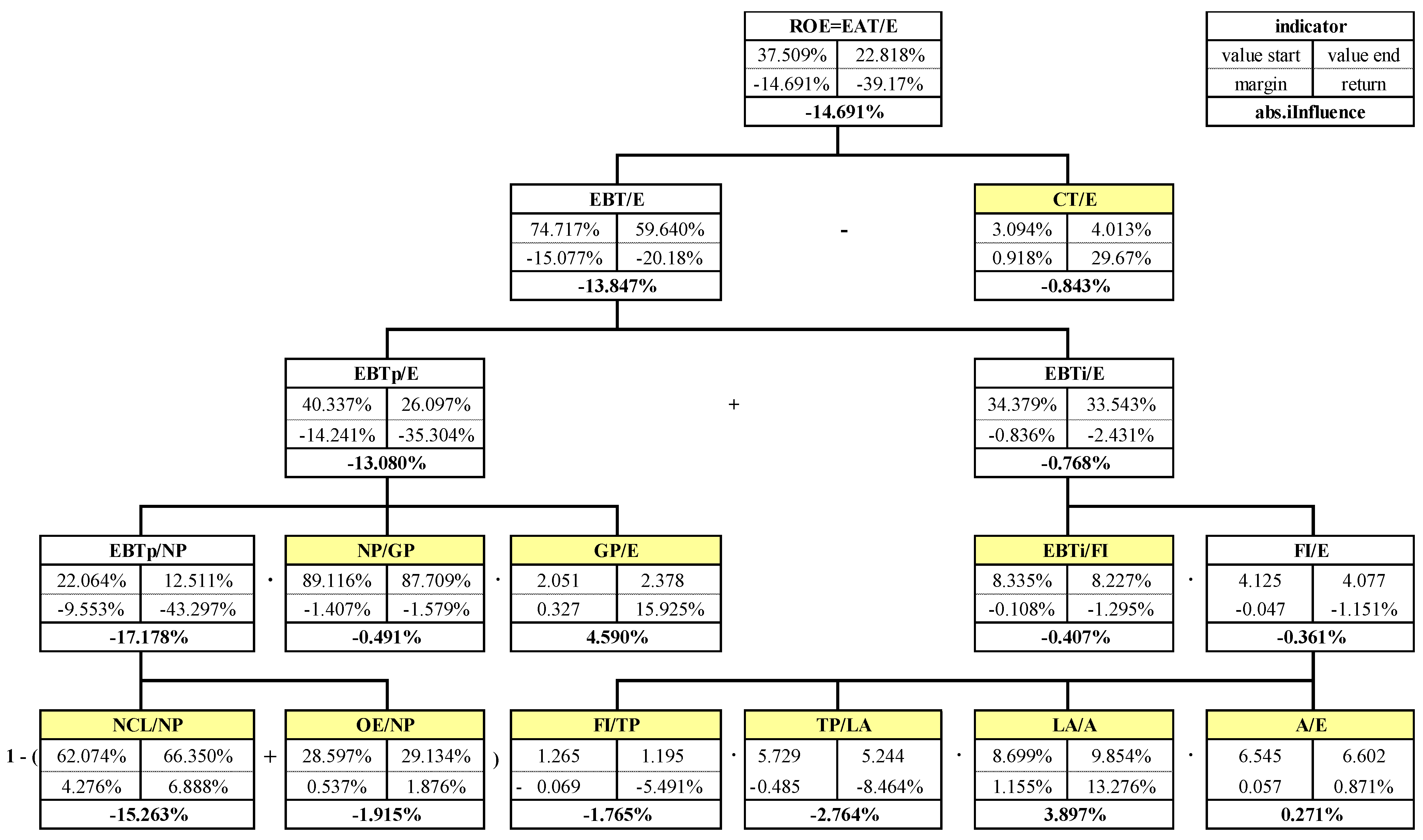
Figure 2. Proposed pyramid decomposition of insurance sector ROE, the deviation for the years 2022/2021.

Figure 2. Proposed pyramid decomposition of insurance sector ROE, the deviation for the years 2022/2021.

2.2. Static Decomposition Deviation Analysis

In the static deviation analysis, a non-linear or linear decomposition function is supposed to be known. A deviation of the (top) analysed measure as the summation of the particular indicator influences is the following: $\Delta y_x={\displaystyle \sum _i\Delta x_{a_i}}$, here $x$ is the analysed measure, $\Delta y_x$ is the deviation of the analysed measure $x$, $a_i$ is a certain explanation indicator, and $\Delta x_{a_i}$ is the influence of the specific indicator $a_i$ on the analysed measure $x$. Influences should be specifically determined for summation and multiplication operations.

For the summation operation $x={\displaystyle \sum _i^n{a}_i}$, then $\Delta x_{a_i}=\Delta a_i/\left({\displaystyle \sum _i\Delta a_i}\right)\cdot \Delta y_x$, here $\Delta a_i=a_{i,1}-a_{i,0}$, and $a_{i,0}$, $a_{i,1}$ are indicator values in the beginning period (index 0) and the subsequent period (index 1).

In the case of the multiplication operation, $x=\underset{i=1}{\overset{4}{{\displaystyle \mathsf{\Pi }}}}{a}_i,$ the procedure is performed by a deviation analysis, which is to be made by applying various methods with pros and cons. The basic techniques used are the following: the method of gradual changes, the method of division with residue, the logarithmic method, the integral method, and the functional method. The advanced logarithmic method is suitable for deviation analysis but is limited to positive changes in the indices (e.g., Ang 1994, 2004, 2005; Ang and Lee 1994; Park 1992). The advanced functional method overcomes the logarithmic method’s restriction and is suitable for both positive and negative indicator changes.

The formulas for four, three, and two indices are derived using the functional method in Appendix A. The formulas for the four explaining indices are the following:

$$\Delta x_{a_1}={\displaystyle \frac{1}{R_x}}\cdot R_{a_1}\cdot \left(\begin{array}{l}\left(1+\left({\displaystyle \frac{1}{2}}\cdot R_{a_2}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_3}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_4}\right)\right)+\\ \left(\left({\displaystyle \frac{1}{3}}\cdot R_{a_2}\cdot R_{a_3}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_2}\cdot R_{a_4}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_3}\cdot R_{a_4}\right)\right)+\\ \left({\displaystyle \frac{1}{4}}\cdot R_{a_2}\cdot R_{a_3}\cdot R_{a_4}\right)\end{array}\right)\cdot \Delta y_x,$$

$$\Delta x_{a_2}={\displaystyle \frac{1}{R_x}}\cdot R_{a_2}\cdot \left(\begin{array}{l}\left(1+\left({\displaystyle \frac{1}{2}}\cdot R_{a_1}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_3}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_4}\right)\right)+\\ \left(\left({\displaystyle \frac{1}{3}}\cdot R_{a_1}\cdot R_{a_3}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_1}\cdot R_{a_4}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_3}\cdot R_{a_4}\right)\right)+\\ \left({\displaystyle \frac{1}{4}}\cdot R_{a_1}\cdot R_{a_3}\cdot R_{a_4}\right)\end{array}\right)\cdot \Delta y,$$

$$\Delta x_{a_3}={\displaystyle \frac{1}{R_x}}\cdot R_{a_3}\cdot \left(\begin{array}{l}\left(1+\left({\displaystyle \frac{1}{2}}\cdot R_{a_1}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_2}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_4}\right)\right)+\\ \left(\left({\displaystyle \frac{1}{3}}\cdot R_{a_1}\cdot R_{a_2}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_1}\cdot R_{a_4}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_2}\cdot R_{a_4}\right)\right)+\\ \left({\displaystyle \frac{1}{4}}\cdot R_{a_1}\cdot R_{a_2}\cdot R_{a_4}\right)\end{array}\right)\cdot \Delta y_x,$$

$$\Delta x_{a_4}={\displaystyle \frac{1}{R_x}}\cdot R_{a_4}\cdot \left(\begin{array}{l}\left(1+\left({\displaystyle \frac{1}{2}}\cdot R_{a_1}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_2}\right)+\left({\displaystyle \frac{1}{2}}\cdot R_{a_3}\right)\right)+\\ \left(\left({\displaystyle \frac{1}{3}}\cdot R_{a_1}\cdot R_{a_2}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_1}\cdot R_{a_3}\right)+\left({\displaystyle \frac{1}{3}}\cdot R_{a_2}\cdot R_{a_3}\right)\right)+\\ \left({\displaystyle \frac{1}{4}}\cdot R_{a_1}\cdot R_{a_2}\cdot R_{a_3}\right)\end{array}\right)\cdot \Delta y_x,$$

where $R_{a_i}={\displaystyle \frac{\Delta a_i}{a_{i,0}}}$ and $R_x={\displaystyle \frac{\Delta x}{x_0}}$. Analogical formulas for three and two influence factors are to be derived.

2.3. Risk (Dynamic) Decomposition Analysis

A variance analysis can be used for risk (dynamic) analysis of deviations. The decomposed function on the pyramid decomposition is computed as a linear function’s variance (e.g., Gaffney et al. 2007; Dluhosova et al. 2022).

A variance is calculated from a linear function $\Delta x={\displaystyle \sum _i{\alpha }_i}\cdot \Delta a_i$. In the case of the original function of indices being non-linear, the linear part of Taylor’s expansion can be used for linearisation, and therefore, ${\alpha }_i={\displaystyle \frac{\partial x(\cdot )}{\partial a_i}}$. Hence, we substitute $z_i={\alpha }_i\cdot \Delta a_i$ so $\Delta x={\displaystyle \sum _i{z}_i}$. Assuming a knowledge of the time series of financial indices, $\Delta \overrightarrow{x}=\left[\Delta x_1;\Delta x_2;\dots \Delta x_N\right]$, ${\overrightarrow{z}}_i=\left[z_{i1};z_{i2};\dots z_{iN}\right]$, the covariance matrix $cov\left({\overrightarrow{z}}_i;{\overrightarrow{z}}_j\right)\in C$ and the correlation matrix $cor\left({\overrightarrow{z}}_i;{\overrightarrow{z}}_j\right)\in R$ can be computed. Afterwards, the variance formula is the following $var(\Delta \overrightarrow{x})={\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^{N}cov\left({\overrightarrow{z}}_i;{\overrightarrow{z}}_j\right)}}={\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N{\sigma }_i\cdot corr\left({\overrightarrow{z}}_i;{\overrightarrow{z}}_j\right)}}\cdot {\sigma }_j$. Conclusively, the influence of the financial indices on the whole variance is expressed as follows,

$$s\left({\overrightarrow{z}}_i\right)={\displaystyle \sum _{j=1}^{N}cov\left({\overrightarrow{z}}_i;{\overrightarrow{z}}_j\right)},$$

(2)

and a standardised influence is provided by

$$w\left({\overrightarrow{z}}_i\right)={\displaystyle \frac{s\left({\overrightarrow{z}}_i\right)}{var(\Delta \overrightarrow{x})}}.$$

(3)

2.4. Input Data

Table 1. Input data of Czech insurance sector indices.

Year	2018	2019	2020	2021	2022
EAT/E	37.51%	19.77%	18.68%	37.51%	22.82%
EBT/E	74.72%	43.96%	39.13%	74.72%	59.64%
CT/E	3.09%	5.62%	4.34%	3.09%	4.01%
EBTp/E	40.34%	24.45%	22.06%	40.34%	26.10%
EBTi/E	34.38%	19.52%	17.06%	34.38%	33.54%
EBTp/NP	22.06%	14.67%	13.27%	22.06%	12.51%
NP/GP	89.12%	91.73%	90.93%	89.12%	87.71%
GP/E	2.05	1.82	1.83	2.05	2.38
EBTi/FI	8.33%	4.99%	4.32%	8.33%	8.23%
FI/E	4.12	3.91	3.95	4.12	4.08
NCL/NP	62.07%	61.67%	61.04%	62.07%	66.35%
OE/NP	28.60%	28.53%	27.36%	28.60%	29.13%
FI/TP	1.26	1.30	1.30	1.26	1.20
TP/LA	5.73	7.23	7.69	5.73	5.24
LA/A	8.70%	7.07%	6.63%	8.70%	9.85%
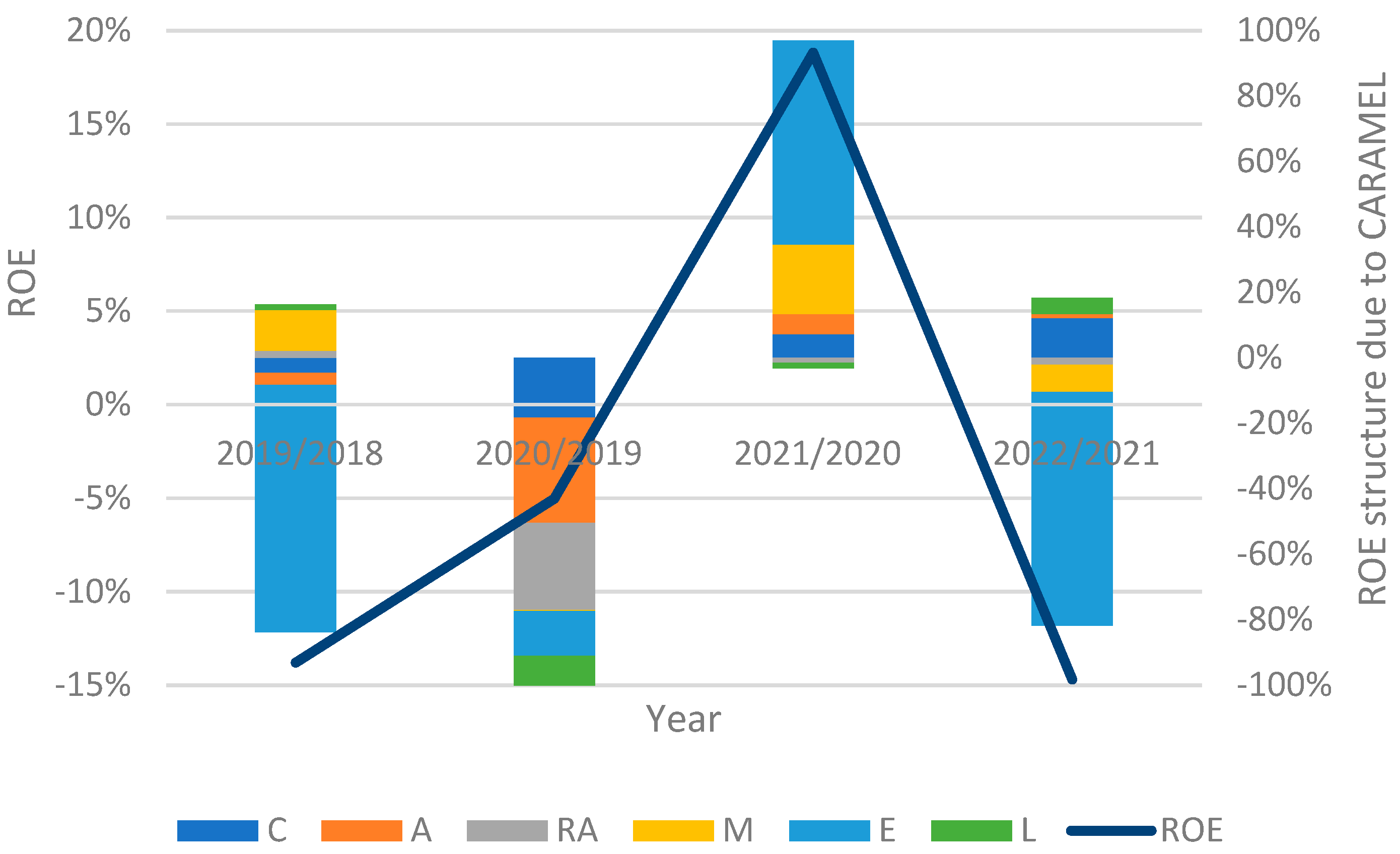
A/E	6.55	5.89	5.96	6.55	6.60

and Figure 3 show the input data of the Czech insurance sector indices, which reflect the proposed pyramid decomposition in Figure 2 of the ROE top measure. Data are on a yearly basis for the period 2018 to 2022. Data sources (Czech Insurance Association 2023) are used to calculate indicator values.

3. The Empirical Results of Decomposition Analyses

The static and risk (dynamic) analyses in the empirical part stem from the methodology introduced in Section 3. It reflects the paper’s goals.

3.1. Static Deviation Analysis

The static analysis is performed due to (Section 2.1), and the functional analysis methodology described in Section 3 is applied because of a generalised conception.

Table 2. The detailed static influence analysis of ROE.

Year	2019/2018		2020/2019		2021/2020		2022/2021
Indicator	Influence	Ranking	Influence	Ranking	Influence	Ranking	Influence	Ranking
ROE	−13.80%		−5.03%		18.83%		−14.69%
CT/E	−0.85%	6	3.34%	2	0.63%	7	−0.84%	6
NP/GP	0.45%	3	−1.34%	7	−0.32%	8	−0.49%	5
GP/E	−1.33%	7	−0.44%	5	1.82%	5	4.59%	1
NCL/NP	−8.70%	10	0.89%	3	3.56%	4	−15.26%	10
OE/NP	2.55%	2	−0.02%	4	4.28%	2	−1.92%	8
EBTi/FI	−5.89%	9	−4.91%	9	8.29%	1	−0.41%	4
FI/TP	0.37%	4	−0.49%	6	−0.36%	9	−1.77%	7
TP/LA	4.61%	1	−8.69%	10	−3.90%	10	−2.76%	9
LA/A	−4.29%	8	8.24%	1	3.59%	3	3.90%	2
A/E	−0.73%	5	−1.61%	8	1.24%	6	0.27%	3

demonstrates the detailed results, and

Table 3. Static deviation analysis of groups due to CARAMEL categorisation.

Year	2019/2018		2020/2019		2021/2020		2022/2021
Group	Influence	Ranking	Influence	Ranking	Influence	Ranking	Influence	Raking
C	−0.952%	5	−0.921%	4	1.455%	3	2.824%	1
A	−0.733%	4	−1.614%	6	1.237%	4	0.271%	3
RA	0.453%	2	−1.342%	5	−0.318%	6	−0.491%	4
M	2.546%	1	−0.018%	1	4.280%	2	−1.915%	5
E	−15.437%	6	−0.681%	3	12.486%	1	−16.513%	6
L	0.325%	3	−0.451%	2	−0.312%	5	1.133%	2

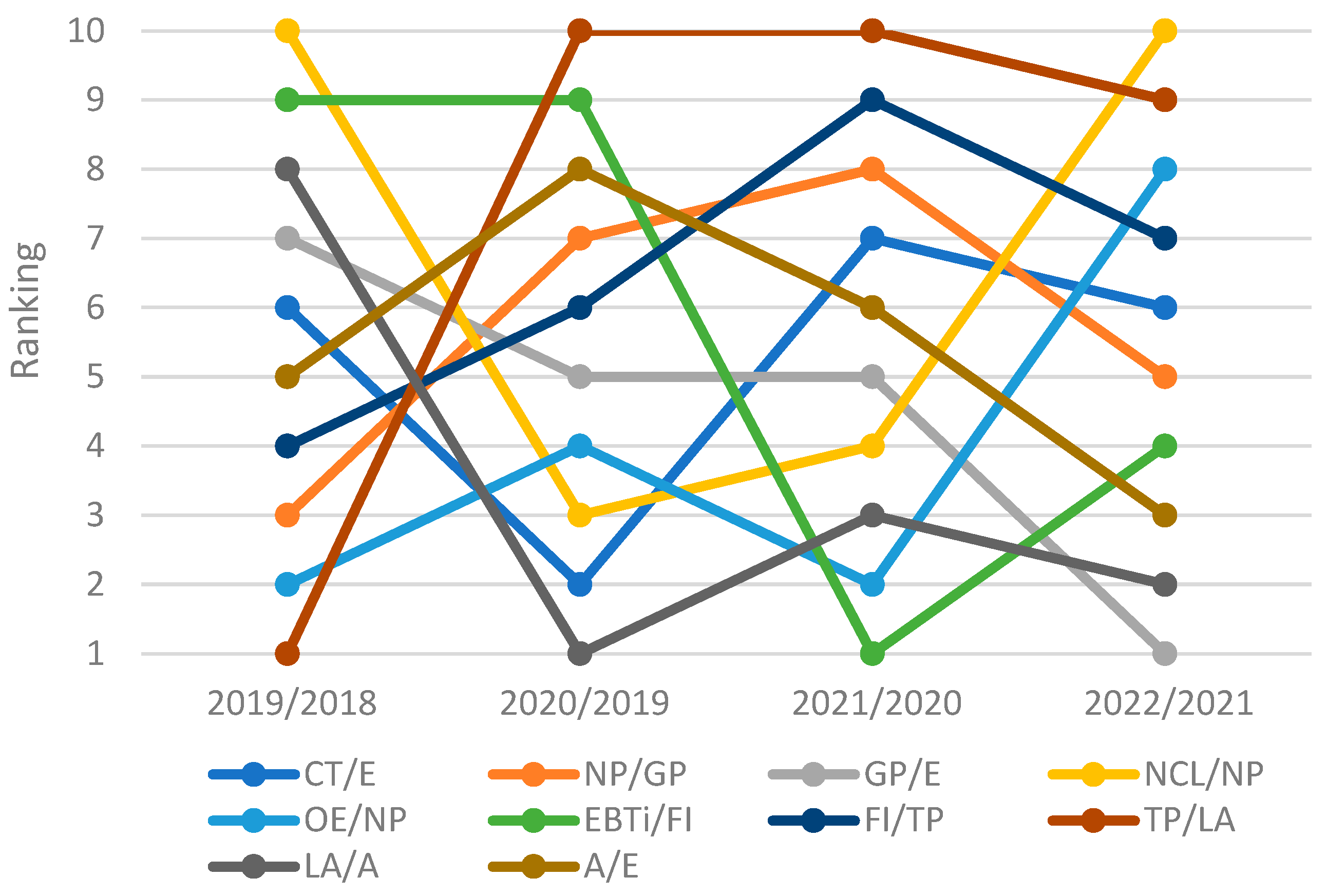
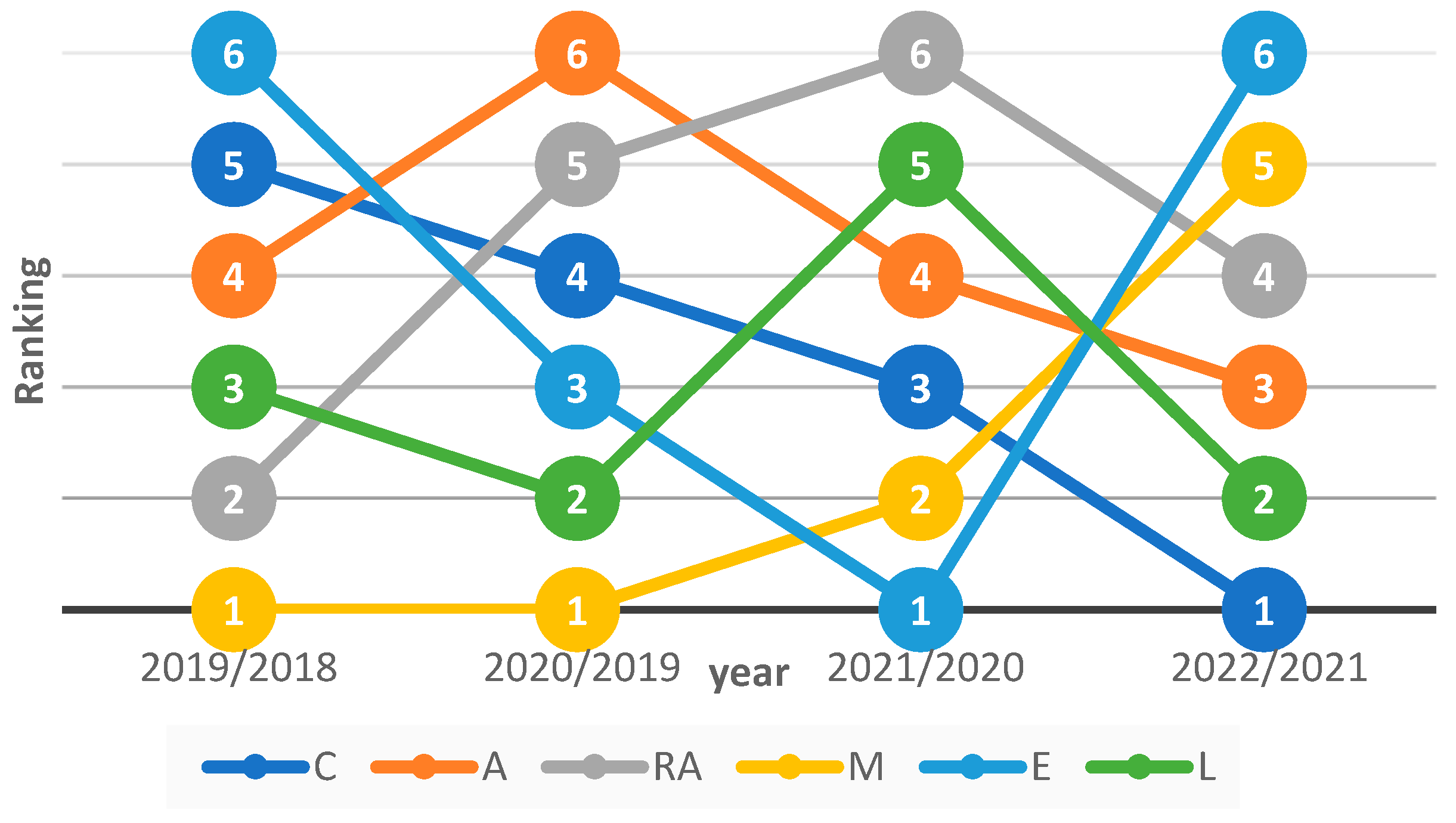
the CARAMEL decomposition results. Figure 4 presents a detailed structure of the indices’ influence, and Figure 5 presents the ranking of the detailed indices’ influence. Figure 6 illustrates the influence structure, and Figure 7 the ranking of the CARAMEL categorisation. Figure 2 presents the computation for the comparison years 2022/2021.

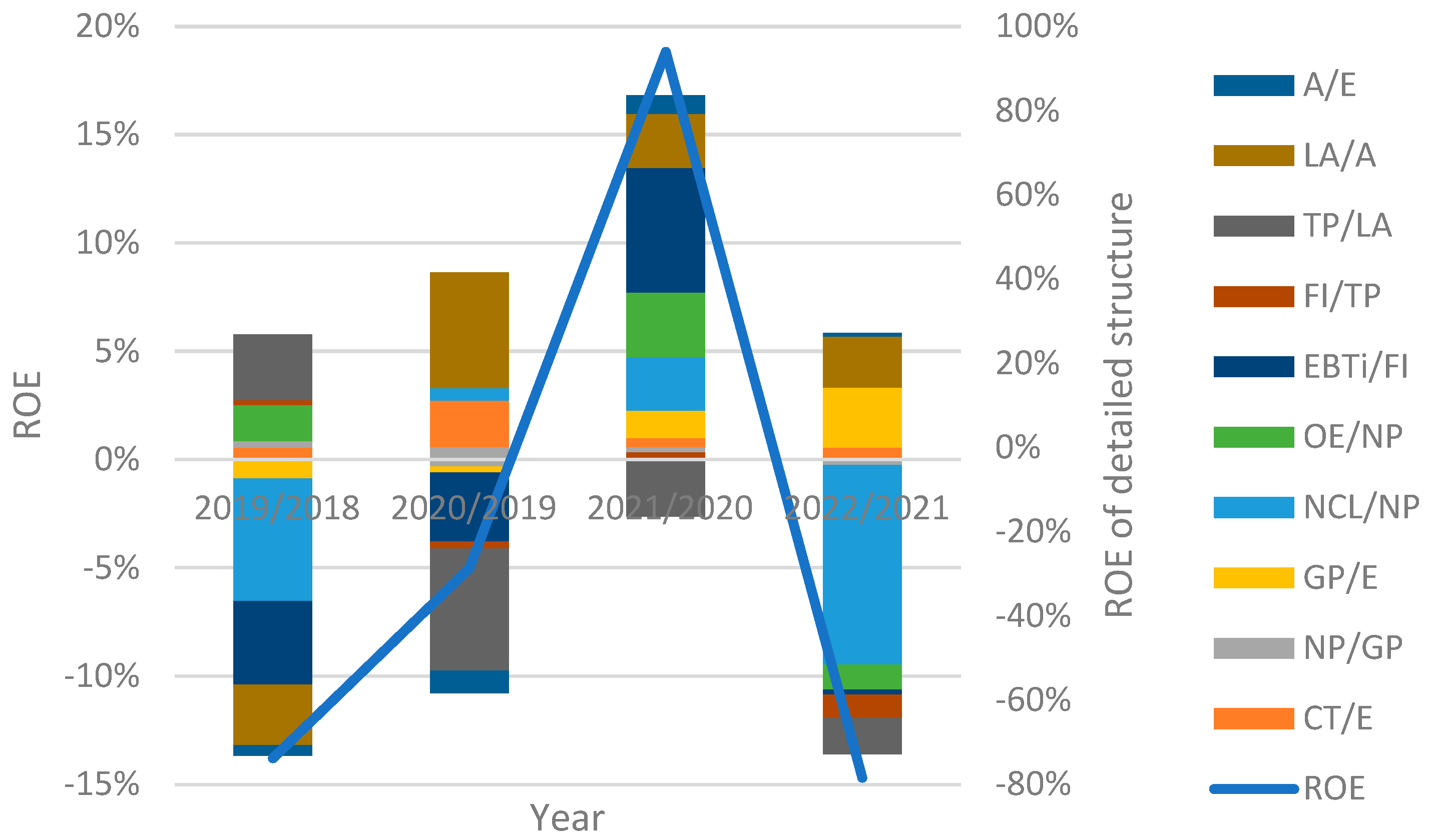
Looking at the detailed decomposition for the years 2022/2021, the most positive impact on the ROE is the solvency ratio (4.59%); the second is the liquidity ratio (3.90%), followed by the financial leverage (0.27%). However, because the ROE is decreased (−14.69%), it is most significantly caused by the ${\displaystyle \frac{NCL}{NP}}$ ratio (−15.26%), followed by a group of indices ${\displaystyle \frac{TP}{LA}}$ (−2.76%), ${\displaystyle \frac{OE}{NP}}$ (−1.92%), and ${\displaystyle \frac{FI}{TP}}$ (−1.77%). The last non-significant group consists of ${\displaystyle \frac{CT}{E}}$ (−0.84%), ${\displaystyle \frac{NP}{GP}}$ (−0.49%), and ${\displaystyle \frac{EBTi}{FI}}$ (−0.41%).

The results of the Caramel decomposition show the positive influence of capital adequacy (2.824%), liquidity (1.133%), and asset quality (0.271%). The earnings group mainly shows a decrease (−16.513%). The more minor impact consists of the management (−1.915%) and the reinsurance (−0.491%).

There are characteristic trends in the Caramel group: management is improving; capital adequacy is worsening; reinsurance and asset quality are of a concave trend; liquidity is relatively stable; earnings show a convex shape.

The correlation matrix for the influence of the yearly Caramel categorisation in

Table 4. The correlation matrix of the yearly Caramel decomposition.

	2019/2018	2020/2019	2021/2020	2022/2021
2019/2018	1	0.0112	−0.8825	0.9214
2020/2019	0.0112	1	0.3102	−0.1895
2021/2020	−0.8825	0.3102	1	−0.9512
2022/2021	0.9214	−0.1895	−0.9512	1

suggests a high positive correlation of 2019/2018 with 2022/2021 (0.9214) and high negative relations of 2019/2018 with 2021/2020 (−0.8825) and 2021/2020 with 2022/2021 (−0.9512). It shows a relative similarity of development in some years.

Apparently, ranking and deviation volumes are unstable and change entirely yearly for both decomposition levels. It is apparent that the earning indices substantially determine the ROE deviation in either increasing or decreasing alternatives. Solvency (capital adequacy) has a positive influence on ROE deviation. The primary reason for indices ranking volatility can be seen in the economic period with an unstable development and unexpected shocks caused by an overheating economy, the Covid pandemic shock, the Ukraine war, the energy crisis, and the high inflation wave. The suitability of the functional method was verified.

3.2. Risk (Dynamic) Analysis

The risk (dynamic) analysis serves to find long-term and risky drivers influencing profitability measured by variance composition. The risk (dynamic) analysis was carried out for the ROE measure due to the method described in Section 3 with the application of (Section 2.2). Input data for every year from 2018 to 2022, introduced in Table 1, are used. The alpha parameters are calculated in the following way:

$$\begin{gathered} {\alpha }_1={\displaystyle \frac{\partial ROE}{\partial \left(CT/E\right)}}=-1, {\alpha }_2={\displaystyle \frac{\partial ROE}{\partial \left(NP/GP\right)}}={\displaystyle \frac{GP}{E}}\cdot \left(1-{\displaystyle \frac{NCL}{NP}}-{\displaystyle \frac{OE}{NP}}\right), {\alpha }_3={\displaystyle \frac{\partial ROE}{\partial \left(GP/E\right)}}={\displaystyle \frac{NP}{GP}}\cdot \left(1-{\displaystyle \frac{NCL}{NP}}-{\displaystyle \frac{OE}{NP}}\right), \\ {\alpha }_4={\displaystyle \frac{\partial ROE}{\partial \left(NCL/NP\right)}}=-{\displaystyle \frac{NP}{GP}}\cdot {\displaystyle \frac{GP}{E}},{\alpha }_5={\displaystyle \frac{\partial ROE}{\partial \left(OE/NP\right)}}=-{\displaystyle \frac{NP}{GP}}\cdot {\displaystyle \frac{GP}{E}}, {\alpha }_6={\displaystyle \frac{\partial ROE}{\partial \left(EB{T}_i/FI\right)}}={\displaystyle \frac{FI}{TP}}\cdot {\displaystyle \frac{TP}{LA}}\cdot {\displaystyle \frac{LA}{A}}\cdot {\displaystyle \frac{A}{E}}, \\ {\alpha }_7={\displaystyle \frac{\partial ROE}{\partial \left(FI/TP\right)}}={\displaystyle \frac{EBTi}{FI}}\cdot {\displaystyle \frac{TP}{LA}}\cdot {\displaystyle \frac{LA}{A}}\cdot {\displaystyle \frac{A}{E}}, {\alpha }_8={\displaystyle \frac{\partial ROE}{\partial \left(TP/LA\right)}}={\displaystyle \frac{EBTi}{FI}}\cdot {\displaystyle \frac{FI}{TP}}\cdot {\displaystyle \frac{LA}{A}}\cdot {\displaystyle \frac{A}{E}}, \\ {\alpha }_9={\displaystyle \frac{\partial ROE}{\partial \left(LA/A\right)}}={\displaystyle \frac{EBTi}{FI}}\cdot {\displaystyle \frac{FI}{TP}}\cdot {\displaystyle \frac{TP}{LA}}\cdot {\displaystyle \frac{A}{E}} \mathrm{and} {\alpha }_{10}={\displaystyle \frac{\partial ROE}{\partial \left(A/E\right)}}={\displaystyle \frac{EBTi}{FI}}\cdot {\displaystyle \frac{FI}{TP}}\cdot {\displaystyle \frac{TP}{LA}}\cdot {\displaystyle \frac{LA}{A}}. \end{gathered}$$

Table 5. The correlation matrix and the standard deviation of insurance ratios.

	CT/E	NP/GP	GP/E	NCL/NP	OE/NP	EBTi/FI	FI/TP	TP/LA	LA/A	A/E	σ
CT/E	1.000	0.790	0.790	0.888	−0.985	0.879	0.883	0.883	−0.677	0.879	1.6175%
NP/GP	0.790	1.000	1.000	0.552	−0.883	0.600	0.574	0.574	−0.973	0.600	0.3015%
GP/E	0.790	1.000	1.000	0.552	−0.883	0.600	0.574	0.574	−0.973	0.600	0.3015%
NCL/NP	0.888	0.552	0.552	1.000	−0.843	0.994	0.998	0.998	0.147	0.994	0.0177%
OE/NP	−0.985	−0.883	−0.883	−0.843	1.000	−0.851	−0.846	−0.846	0.860	−0.851	0.0149%
EBTi/FI	0.879	0.600	0.600	0.994	−0.851	1.000	0.999	0.999	0.187	1.000	0.0014%
FI/TP	0.883	0.574	0.574	0.998	−0.846	0.999	1.000	1.000	0.174	0.999	0.0040%
TP/LA	0.883	0.574	0.574	0.998	−0.846	0.999	1.000	1.000	0.174	0.999	0.0040%
LA/A	0.879	0.600	0.600	0.994	−0.851	1.000	0.999	0.999	1.000	1.000	0.0014%
A/E	0.879	0.600	0.600	0.994	−0.851	1.000	0.999	0.999	1.000	1.000	0.0014%

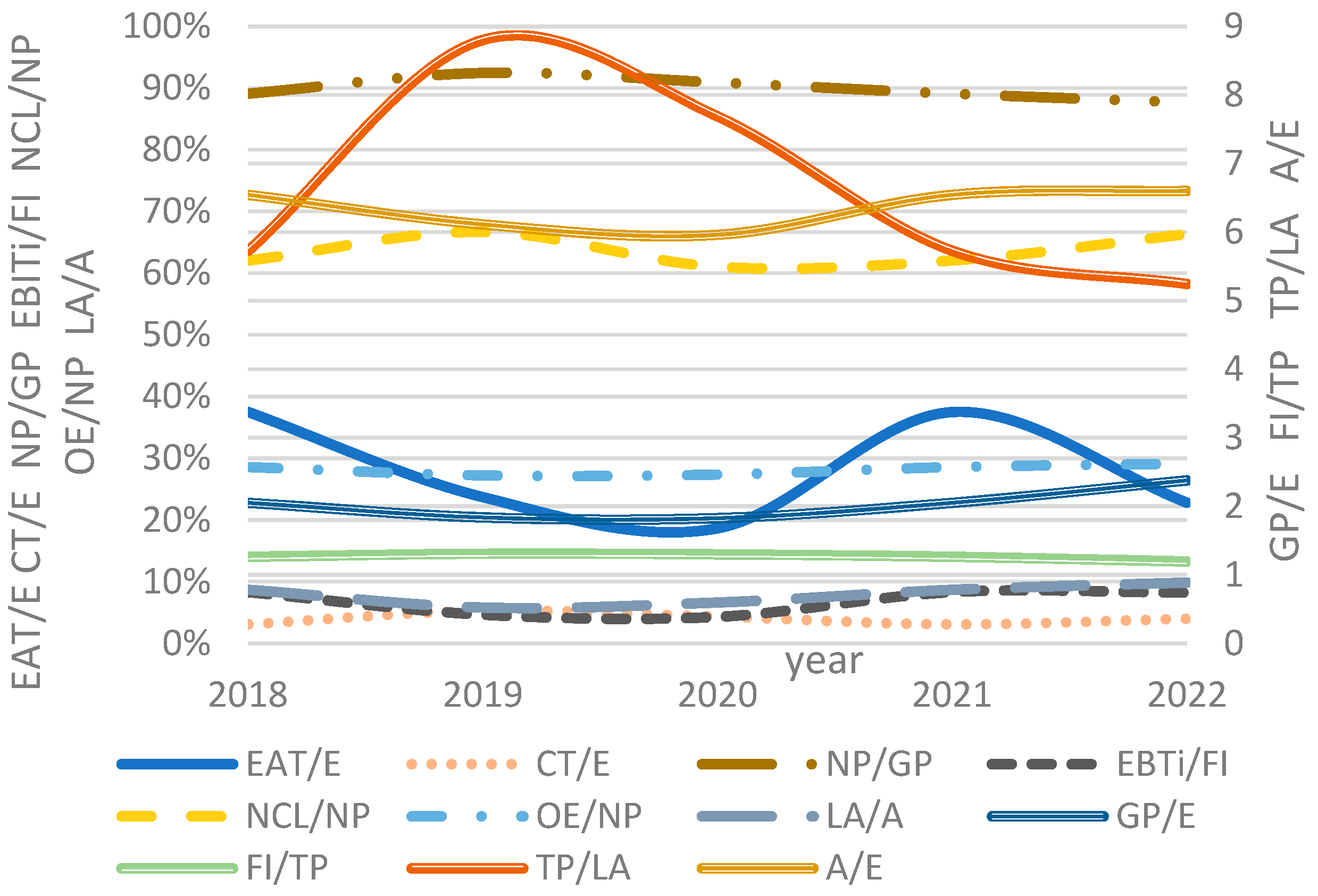
shows the correlation matrix and the standard deviation of ratios. Furthermore, detailed decomposition in

Table 6. Risk (dynamic) decomposition analysis results.

Indicator	$\mathbf{Variance} \mathit{S}\left(\overrightarrow{{\mathit{Z}}_{\mathit{i}}}\right)$	$\mathbf{Influence} \mathit{w}\left(\overrightarrow{{\mathit{Z}}_{\mathit{i}}}\right)$	Ranking
CT/E	0.0025535	9.96%	4
NP/GP	−0.0005988	−2.34%	8
GP/E	0.0017552	6.85%	6
NCL/NP	0.0087843	34.27%	3
OE/NP	−0.0025139	−9.81%	9
EBTi/FI	0.0182202	71.07%	1
FI/TP	−0.0005716	−2.23%	7
TP/LA	−0.0137288	−53.55%	10
LA/A	0.0095839	37.39%	2
A/E	0.0021513	8.39%	5
summary	0.025635	100.000%

and the CARAMEL categorisation in

Table 7. Risk (dynamic) CARAMEL decomposition analysis results.

Group		Influence	Ranking
C	Capital adequacy	4.617%	3
A	Assets quality	8.392%	2
RA	Reinsurance and actuarial issues	−2.336%	4
M	Management	−9.806%	5
E	Earnings	115.302%	1
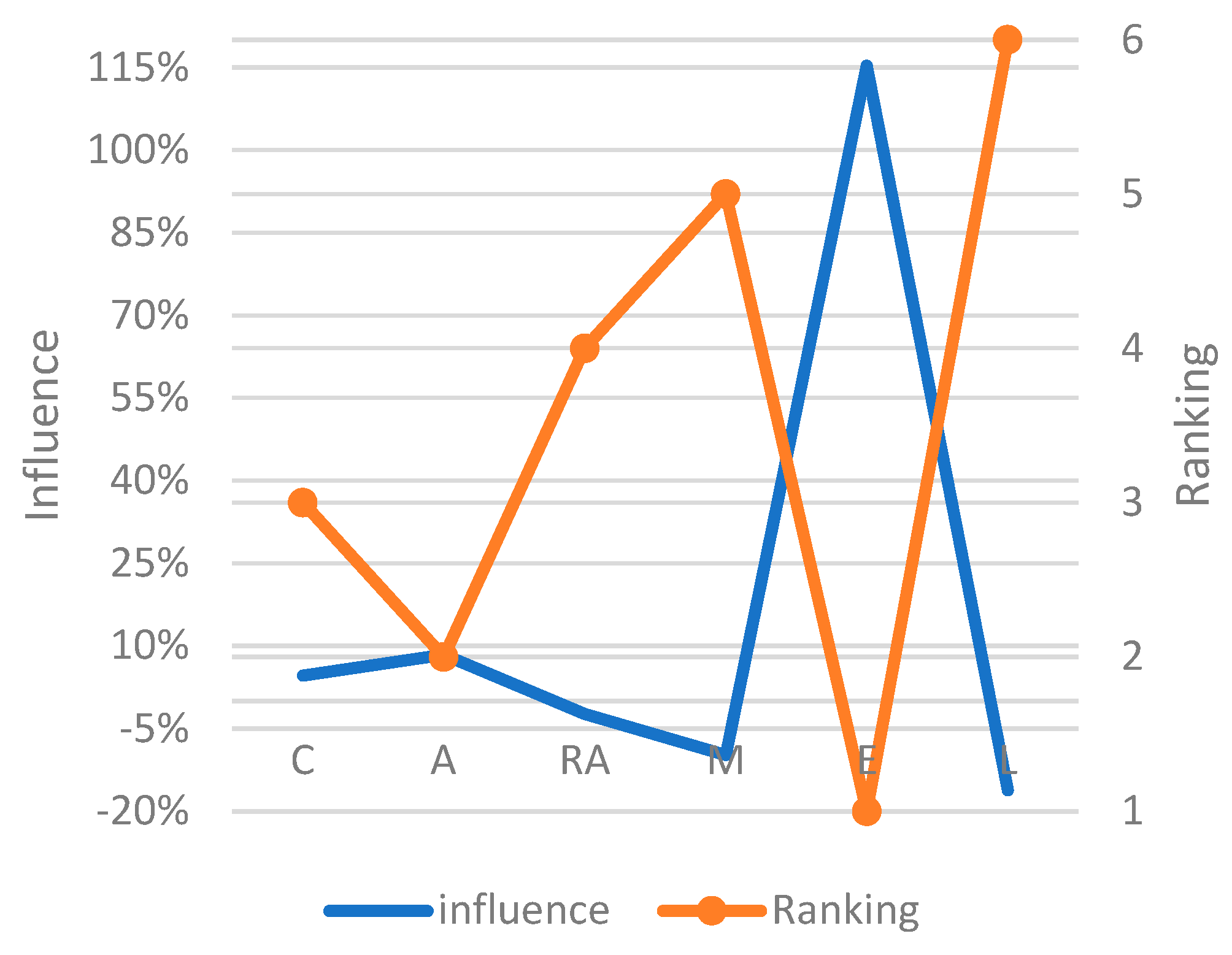
L	Liquidity	−16.169%	6

present ratio influences and variances. A graphical presentation of the profitability risk (dynamic) CARAMEL composition for variance and ranking is illustrated in Figure 8.

The risk (dynamic) analysis serves to find long-term and risky drivers influencing profitability measured by variance composition. Looking at the detailed decomposition, for the given period, the risk is mostly increased by ${\displaystyle \frac{EBTi}{FI}}$ (71.07%), the liquidity ratio 37.39%, ${\displaystyle \frac{NCL}{NP}}$ (34.27%), ${\displaystyle \frac{CT}{E}}$ (9.96%), financial leverage (8.39%), and solvency (6.85%). Decreasing factories are firstly ${\displaystyle \frac{TP}{LA}}$ (−53.55%), ${\displaystyle \frac{OE}{NP}}$ (−9.81%), ${\displaystyle \frac{NP}{GP}}$ (−2.34%), ${\displaystyle \frac{FI}{TP}}$ (−2.23%),

Risk, according to the Caramel categorisation, is increased enormously by the earnings (115.302%), asset quality (8.392%), and capital adequacy (4.617%). Risk is decreased mainly by liquidity (−16.169%), management (−9.806%), and reinsurance (−2.336%).

The results turned out that the substantial drivers increasing risk are earnings and asset quality; on the other hand, risk is reduced by liquidity and management indicators.

The profitability risk (dynamic) analysis of the insurance sector shows the ranking of the influential indices, particularly in a case study of an unstable period with economic shocks. The advantage of this approach is that the findings are valid for a stated period and can be considered to be stable results.

The risk (dynamic) analysis results can be considered valuable information for the long-term strategy of the financial sector. The obtained information can be used to support tactical and strategic analysis and managerial decisions as well.

4. Conclusions

The paper’s goal was to perform a static and risk (dynamic) profitability analysis of the open economy Czech insurance sector in an unstable period with economic shocks.

The pyramid decomposition system of financial ratios was proposed and verified to reflect the CARAMEL categorisation of the insurance financial ratios system.

Static analysis using the functional method was applied and verified. It turned out that the advantage of the functional method consists of common application possibilities, including positive and negative ratio indices in the analysis. The yearly non-stable drivers of insurance sector profitability deviation were confirmed. In spite of this, the most influential were the earnings ratio deviations in either increasing or decreasing ROE alternatives. Solvency (capital adequacy) positively influenced the ROE deviation. So, static pyramid decomposition analysis can be a valuable and effective profitability analysis tool for finding more influential drivers yearly.

The weakness of the static approach lies in the non-stability of the results. Every inter-year comparison is usually different according to economic development and conditions. Applying the risk (dynamic) decomposition method based on the variance analysis can overcome the drawbacks of the static method. From the time-series data, long-term profitability fluctuation drivers can be deduced. It turned out, according to the CARAMEL categorisation, that earnings and asset quality enormously increase the risk of the insurance sector. Conversely, risk is decreased mainly by liquidity and management.

The insurance sector was analysed using real data in a non-stable period of an economic shock chain. Simultaneously, the static and risk (dynamic) methods were verified, and significant influential factors were identified. The limitation of the study lies in that a deep and separate analysis of the economic shocks (overheating economy, Covid, Ukraine war) has not been conducted. The results can serve as a background for an operating (static) and strategic (dynamic) analysis and for making decisions.