Model Misspecification and Data-Driven Model Ranking Approach for Insurance Loss and Claims Data

Abstract

Statistical models are crucial in analyzing insurance loss and claims data, offering insights into various risk elements. The prevailing statistical notion that “all models are wrong, but some are useful” can wield significant influence, particularly when multiple competing statistical models are considered. This becomes particularly pertinent when all models portray similar characteristics within specific subsets of the support of the random variable under scrutiny. Since the actual model is unknown in practical scenarios, the challenge of model selection becomes daunting, complicating the study of associated characteristics of the actual data generation process. To address these challenges, the concept of model averaging is embraced. Often, averaging over multiple models helps alleviate the risk of model misspecification, as different models may capture distinct aspects of the data or modeling assumptions. This enhances the robustness of the estimation process, yielding a more accurate and reasonable estimate compared to relying solely on a single model. This paper introduces two novel data-based model selection methods—one using the likelihood function and the other using the density power divergence measure. The study focuses on estimating the Value-at-Risk (VaR) for non-life insurance claim size data, providing comprehensive insights into potential losses for insurers. The performance of the proposed procedures is evaluated through Monte Carlo simulations under both uncontaminated conditions and in the presence of data contamination. Additionally, the applicability of the methods is illustrated using two real non-life insurance datasets, with the VaR values estimated at different confidence levels.

1. Introduction

In the field of risk and insurance, probability theory and statistical models play important roles in various aspects, such as determining insurance pricing, assessing financial risks, and understanding claim size, claim count, and aggregate-loss distributions (Bahnemann 1996). Due to the stochastic nature of insurance data, the underlying data generation mechanism is always unknown, and choosing a suitable probability model to fit insurance data is a challenging problem. The statistical literature has considered different approaches to handling model uncertainty in such cases. For instance, one may use a statistical model with a larger number of parameters to increase flexibility and then test the significance of the added parameters. Another approach is to impose prior probability distributions on the model parameters in a Bayesian paradigm. While these methods offer benefits and advantages, they also come with their own set of drawbacks. For instance, increasing the number of model parameters amplifies model complexity and presents challenges in parameter estimation. Additionally, the roles of these added parameters in determining the distribution’s location, scale, and shape may become ambiguous. Furthermore, misspecification of the underlying probability model in fitting insurance data may lead to a substantial loss of efficiency in statistical analysis, inaccurate conclusions, and improper decisions. Therefore, it is crucial to identify the best-fit model from a pool of candidate models and understand the consequences of model misspecification in analyzing insurance risk data. This understanding significantly overcomes the negative impact of model misspecification and leads to feasible estimates of the characteristics under study. An interesting insight into the disparity arising from incorrect model identification followed by misspecified inferences can be found in Gustafson (2001).

The consequences of model misspecification have been explored across different domains in the statistical literature. Dumonceaux and Antle (1973) was the first to discuss the effects of model misspecification, in the form of a statistical hypothesis test problem, for analyzing the lifetimes of ball bearings using two competing probability models. Several studies have been dedicated to model discrimination and misspecification themes between two competing models. An interesting application analyzing electromigration failure in the interconnects of integrated circuits was presented by Basavalingappa et al. (2017). Besides such experiments being conducted in accelerated settings, followed by transforming the observed failures to represent lifetimes in regular conditions, the occurrence of failures in ICs is also sporadic. Another study in the context of a rare event, i.e., modeling high magnitude earthquakes in the Himalayan regions and the subsequent effects of model misspecification, can be found in Pasari (2018). The problem of model misspecification has also been explored for censored-sample cases (Block and Leemis 2008; Dey and Kundu 2012). Some other intriguing directions of model misspecification include the analysis of strength distribution for brittle materials by Basu et al. (2009) and one-shot device test data by Ling and Balakrishnan (2017). A comprehensive investigation into the impact of misspecification of statistical models in insurance and risk management, particularly concerning censored, truncated, and outlier-laden insurance loss and claims data, is of practical interest. Following the insights of scholars such as White (1982), Chow (1984), and Fomby and Hill (2003), we examine the misspecification of statistical models and investigate the behavior of point estimators for key risk measures.

Before conducting statistical inference (such as estimation, prediction, hypothesis testing, etc.) on insurance data, it is often assumed that the data originate from a specific parametric probability model on which the analysis is based. A vast array of probability distributions is available in the literature for fitting insurance data. For instance, distributions such as gamma, log-gamma, lognormal, and Weibull are commonly employed to model insurance claim size, while Poisson, negative binomial, and Delaporte distributions are often used to model insurance claim counts (Brazauskas and Kleefeld 2011; Hewitt and Lefkowitz 1979; Rolski et al. 1999; Zelinková 2015). However, in practical applications, when employing a statistical distribution for data analysis, the underlying probability distributions of various risk elements and the stochastic mechanisms that generate loss and claims data are often unknown. Additionally, the probability model may be misspecified, and the insurance datasets may be contaminated or contain outliers.

Broadly, an insurance company encounters two types of fund claim variables. One is the extent of the payout, in monetary terms, commonly referred to as the claim severity (size) variable, and the other is the variable representing the number of claims (also known as claim frequency) arising in a given period (Loss Data Analytics Core Team 2020). In this study, our interest lies in exploring the risks associated with the amount paid for the claim, commonly referred to as the claim size. An important characteristic of a claim severity model is its ability to represent the worst potential loss due to adverse events such as natural disasters, accidents, or other unforeseen circumstances that an insurer might experience over a specified duration at a certain confidence level $\delta \in (0,1)$, commonly referred to as Value-at-Risk (VaR) (Jorion 2006, chap. 5; Christoffersen 2012). Thus, VaR helps assess the potential financial impact of extreme but plausible events over a specific time horizon. By quantifying the maximum expected loss within a certain confidence level (e.g., $95\%$ or $99\%$), insurers can better understand their exposure to risk and make informed decisions regarding capital reserves, reinsurance arrangements, and pricing strategies. Let X be the random variable representing the loss size. For a pre-specified value $\delta \in (0,1)$ (e.g., $\delta =0.95$), a general definition of VaR with confidence level $100\delta \%$ is $Pr(X>VaR)\le 1-\delta$. Thus, for a confidence level of $100\delta \%$, the VaR can be interpreted as the threshold loss such that the probability of incurring a loss greater than this amount is at most $1-\delta$. If the loss variable X has CDF $F_{\mathit{\theta }}(·)$ with parameter vector $\mathit{\theta }$, then its quantile function is denoted by $Q_{\mathit{\theta }}\left(\delta \right)=F_{\mathit{\theta }}^{-1}\left(\delta \right)$ (Tse 2023). Therefore, the VaR with confidence level $100\delta \%$ corresponds to the $100\delta \%$ quantile of the loss distribution, i.e., $VaR=Q_{\mathit{\theta }}\left(\delta \right)$, for a given time horizon.

In the context of the importance of selecting a suitable distribution for analyzing insurance data, Yu (2020) considered six parametric distributions for modeling and analyzing operational loss data related to external fraud types in retail banking branches of major commercial banks in China from 2009 to 2015. They observed that different distributional assumptions yielded significantly different VaR estimates, leading to inconsistent conclusions. As emphasized by Wang et al. (2020), selecting an appropriate claim severity distribution is crucial, especially in the presence of extreme values. Hogg and Klugman (1984) investigated claim severities in non-life insurance, such as those resulting from hurricane damage or automobile accidents, and noted their tendency to exhibit a heavy-tailed skewed nature. Various heavy-tailed as well as regular models, including gamma, lognormal, log-gamma, Weibull, Pareto, and log-logistic, have been employed in modeling non-life insurance data (see, for example, Kleiber and Kotz 2003; Klugman et al. 2012, and the references cited therein). Additionally, when claim sizes are large, settlements are often delayed due to case-by-case handling, necessitating consideration of the role of inflation, which can contaminate claim sizes (Hogg and Klugman 1984; Kaas et al. 2008). Hence, a robust estimation procedure is required to analyze claim severities.

In this paper, we aim to examine the effects of model misspecification on modeling insurance data. Since the underlying data-generating mechanism of insurance data is often unknown, and such data frequently contain influential observations and/or outliers, we propose two robust weighted estimation criteria based on likelihood and divergence measures. We then compare the performance of the proposed methods through Monte Carlo simulation. Our goal is to advance the understanding of model fitting and analysis for insurance and risk data, as well as the related inferential methods, and help practicing actuaries and academic actuaries better understand the effects and consequences of model misspecification when model uncertainty is present. With an emphasis on practical implementation and pedagogical clarity, this paper provides accessible and robust tools for practitioners and educators in actuarial science and risk analysis.

The rest of this paper is organized as follows. Section 2 provides an overview of the probability models used in this study, along with a brief review of their applications for non-life insurance claim size data. In Section 3, we discuss the estimation of model parameters and VaR using the likelihood method and density power divergence (DPD) method. Section 4 introduces the rationale of the proposed data-driven model ranking and selection approach based on likelihood and DPD measures, followed by a Monte Carlo simulation study in Section 5 that details the performance of the proposed procedures, considering both the presence and absence of data contamination. Section 6 presents two real data analyses to illustrate the proposed model ranking and selection method developed in this work. Finally, in Section 8, we provide concluding remarks and directions for future work.

2. Probability Models for Claim Severity

In this section, we consider six commonly used probability models in insurance and finance, namely the Fisk, Fréchet, Lomax, lognormal, paralogistic, and Weibull distributions, to model the severity of claims for non-life insurance data. For notation convenience, we denote these six models as ${\mathcal{M}}_j;j=1,\dots ,6$ in the remaining length of the article, where ${\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3,{\mathcal{M}}_4,{\mathcal{M}}_5$ and ${\mathcal{M}}_6$ represents the Fisk, Fréchet, Lomax, lognormal, paralogistic, and Weibull distributions, respectively. The corresponding probability density functions (PDFs), cumulative distribution functions (CDFs), and VaR values of model ${\mathcal{M}}_j$ with parameter vectors ${\mathit{\theta }}_j$ are denoted as $f_{{\mathit{\theta }}_j}(·)$, $F_{{\mathit{\theta }}_j}(·)$ and $Q_{{\mathit{\theta }}_j}\left(\delta \right)$, $\delta \in (0,1)$ ($j=1,\dots ,6$), respectively. Although we primarily considered six probability distributions in this paper, the methodologies developed can be applied to any candidate models with different probability distributions. Moreover, the methodologies can be extended to candidate statistical models with different numbers of parameters by suitably penalizing models with more parameters based on the practitioner’s preference and the parsimony principle. Additionally, the methodologies discussed here can be extended directly to truncated probability distributions, which are often more appropriate for claims subject to deductibles or policy limits.

2.1. Fisk Distribution

The Fisk distribution was originally proposed by Fisk (1961) as a limiting form of the Champernowne distribution Champernowne (1952) in connection with modeling income. A random variable X following a Fisk distribution (denoted as $FS({\beta }_1,{\lambda }_1)$) has PDF, CDF, and VaR $Q_{{\mathit{\theta }}_1}\left(\delta \right)$

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_1}\left(x\right)& =& \left\{\begin{array}{cc}{\displaystyle \frac{{\beta }_1{\lambda }_1^{{\beta }_1}{x}^{{\beta }_1-1}}{{(x^{{\beta }_1}+{\lambda }_1^{{\beta }_1})}^2}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill F_{{\mathit{\theta }}_1}\left(x\right)& =& \left\{\begin{array}{cc}{\displaystyle \frac{x^{{\beta }_1}}{x^{{\beta }_1}+{\lambda }_1^{{\beta }_1}}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill Q_{{\mathit{\theta }}_1}\left(\delta \right)& =& \left\{\begin{array}{cc}{\lambda }_1{\left({\displaystyle \frac{\delta }{1-\delta }}\right)}^{1/{\beta }_1},\hfill & \mathrm{for} 0<\delta <1;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(3)

respectively, where ${\mathit{\theta }}_1=({\beta }_1,{\lambda }_1)$ is the parameter vector with ${\beta }_1>0$ as the shape parameter and ${\lambda }_1>0$ representing the median of the distribution.

The Fisk distribution is also known as the log-logistic distribution because it can be obtained by using the logarithmic transformation of the logistic distribution. The Fisk distribution offers insight into the distribution of income sizes, derived from the reasoning of income generation processes Singh and Maddala (1976). In the context of income inequality, the Fisk distribution provides a mathematical representation of the unequal distribution of income. For more details on income distribution and income inequality, the readers may refer to Kakwani (1980) and Kakwani and Son (2022). Buch-larsen et al. (2005) discussed the suitability of the Fisk distribution to model non-life insurance data since it is capable of accommodating small as well as large claim sizes, owing to its heavy-tailed nature, which is otherwise a challenge for regular models.

2.2. Fréchet Distribution

The Fréchet distribution, named after mathematician Maurice René Fréchet, is a probability distribution derived as the limiting distribution of extreme values. It is also known as the inverse Weibull distribution, which has various applications in economics, hydrology, and meteorology to model extreme events or phenomena. It is often employed to describe the distribution of extreme values in a dataset, such as maximum wind speeds, flood levels, or income levels (Kotz and Nadarajah 2000).

A random variable X follows a Fréchet distribution (denoted as $FR({\beta }_2,{\lambda }_2)$) with PDF, CDF, and VaR $Q_{{\mathit{\theta }}_2}\left(\delta \right)$:

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_2}\left(x\right)& =& \left\{\begin{array}{cc}{\beta }_2{\lambda }_2^{{\beta }_2}{x}^{-({\beta }_2+1)}{e}^{-{\left(x/{\lambda }_2\right)}^{-{\beta }_2}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill F_{{\mathit{\theta }}_2}\left(x\right)& =& \left\{\begin{array}{cc}{e}^{-{\left(x/{\lambda }_2\right)}^{-{\beta }_2}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill Q_{{\mathit{\theta }}_2}\left(\delta \right)& =& \left\{\begin{array}{cc}{\lambda }_2{(-ln\delta )}^{-1/{\beta }_2},\hfill & \mathrm{for} 0<\delta <1;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(6)

where ${\mathit{\theta }}_2=({\beta }_2,{\lambda }_2)$ is a parameter vector, ${\lambda }_2>0$ is the scale parameter and ${\beta }_2>0$ is the shape parameter.

2.3. Lomax Distribution

The Lomax distribution was introduced by K. S. Lomax (1954), which is commonly employed in modeling income distributions, insurance claim sizes, and other phenomena where observations are bounded from below and exhibit heavy-tailed behavior. This distribution offers valuable insights into extreme events and tail behavior, making it a valuable tool in various analytical and modeling contexts. A random variable X has a Lomax distribution (denoted as $LM({\beta }_3,{\lambda }_3)$) with PDF, CDF, and VaR $Q_{{\mathit{\theta }}_3}\left(\delta \right)$:

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_3}\left(x\right)& =& \left\{\begin{array}{cc}{\beta }_3{\lambda }_3^{{\beta }_3}{(x+{\lambda }_3)}^{-({\beta }_3+1)},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill F_{{\mathit{\theta }}_3}\left(x\right)& =& \left\{\begin{array}{cc}1-{\left({\displaystyle \frac{{\lambda }_3}{x+{\lambda }_3}}\right)}^{{\beta }_3},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill Q_{{\mathit{\theta }}_3}\left(\delta \right)& =& \left\{\begin{array}{cc}{\lambda }_3\left({(1-\delta )}^{-1/{\beta }_3}-1\right),\hfill & \mathrm{for} 0<\delta <1;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(9)

respectively, where ${\mathit{\theta }}_3=({\beta }_3,{\lambda }_3)$ is a parameter vector, ${\lambda }_3>0$ is the scale parameter and ${\beta }_3>0$ is the shape parameter.

2.4. Lognormal Distribution

The lognormal distribution is often used to model phenomena where the logarithm of the variable of interest is normally distributed, such as the distribution of stock prices, income levels, or the size of biological populations. Mathematically, if a random variable $Z=lnX$ is normally distributed, then the distribution of X is said to be lognormal. It is particularly useful when dealing with variables that are inherently positive and skewed, as the lognormal distribution naturally accommodates these characteristics. The lognormal distribution is also known as the Galton distribution. For more details on lognormal distribution, one may refer to Chapter 14 of Johnson et al. (1994), the book by Crow and Shimizu (1988), and the references therein.

The PDF, CDF, and VaR $Q_{{\mathit{\theta }}_4}\left(\delta \right)$ of a lognormal variate X (denoted as $LN({\beta }_4,{\lambda }_4)$) are

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_4}\left(x\right)& =& \left\{\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{2\pi }{\beta }_{4}x}}exp\left[-{\displaystyle \frac{{(lnx-{\lambda }_4)}^2}{2{\beta }_4^2}}\right],\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill F_{{\mathit{\theta }}_4}\left(x\right)& =& \left\{\begin{array}{cc}\Phi \left({\displaystyle \frac{lnx-{\lambda }_4}{{\beta }_4}}\right),\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill Q_{{\mathit{\theta }}_4}\left(\delta \right)& =& \left\{\begin{array}{cc}exp\left({\lambda }_4+{\beta }_4{\Phi }^{-1}\left(\delta \right)\right),\hfill & \mathrm{for} 0<\delta <1;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(12)

respectively, where ${\mathit{\theta }}_4=({\beta }_4,{\lambda }_4)$ is a parameter vector with $exp\left({\lambda }_4\right)$ as the scale parameter, ${\beta }_4>0$ as the shape parameter, $\Phi (·)$ and ${\Phi }^{-1}(·)$ representing the CDF and inverse CDF (quantile function) of the standard normal distribution.

2.5. Paralogistic Distribution

The paralogistic distribution is a statistical distribution used primarily in econometrics, finance, and risk management, which is characterized by its flexibility in modeling skewed or heavy-tailed data. As demonstrated by Kleiber and Kotz (2003), the paralogistic distribution can be applied to economic modeling of wealth and income. The paralogistic distribution allows for asymmetry and heavier tails, which provides flexibility in capturing the tail behavior of the data.

A random variable X has a paralogistic distribution (denoted as $PL({\beta }_5,{\lambda }_5)$) with PDF, CDF, and VaR $Q_{{\mathit{\theta }}_5}\left(\delta \right)$:

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_5}\left(x\right)& =& \left\{\begin{array}{cc}{\displaystyle \frac{{\beta }_5^2{(x/{\lambda }_5)}^{{\beta }_5}}{x{\left(1+{(x/{\lambda }_5)}^{{\beta }_5}\right)}^{{\beta }_5+1}}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill F_{{\mathit{\theta }}_5}\left(x\right)& =& \left\{\begin{array}{cc}1-{\left(1+{(x/{\lambda }_5)}^{{\beta }_5}\right)}^{-{\beta }_5},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill Q_{{\mathit{\theta }}_5}\left(\delta \right)& =& \left\{\begin{array}{cc}{\lambda }_5{\left({(1-\delta )}^{-1/{\beta }_5}-1\right)}^{1/{\beta }_5},\hfill & \mathrm{for} 0<\delta <1;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(15)

respectively, where ${\mathit{\theta }}_5=({\beta }_5,{\lambda }_5)$ is a parameter vector, ${\lambda }_5>0$ is the scale parameter and ${\beta }_5>0$ is the shape parameter.

2.6. Weibull Distribution

Weibull distribution has been used for analyzing data from different domains like life-testing experiments, inter-arrival times of earthquakes, wind speed data across different seasons and years, lead time demand in inventory control, water pollution levels, size of non-life insurance claims (Abubakar and Sabri 2023; Bowden et al. 1983; Das and Nath 2022; Adeleke and Ibiwoye 2011; Kreer et al. 2015; Luko 1999; Smith 2003; Tadikamalla 1978; Wais 2017). The theory of extreme values shows that the Weibull distribution can be used to model the minimum of many independent positive random variables from a specific class of statistical distributions. For well-documented, detailed references on the theory and applications of the Weibull distribution, one may refer to Chapter 21 of Johnson et al. (1994) and the book by Rinne (2008).

A random variable X is said to follow a Weibull distribution (denoted as $WE({\beta }_6,{\lambda }_6)$) with PDF, CDF, and VaR $Q_{{\mathit{\theta }}_6}\left(\delta \right)$:

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_6}\left(x\right)& =& \left\{\begin{array}{cc}{\displaystyle \frac{{\beta }_6}{{\lambda }_6}}{\left({\displaystyle \frac{x}{{\lambda }_6}}\right)}^{{\beta }_6-1}exp\left[-{\left(x/{\lambda }_6\right)}^{{\beta }_6}\right],\hfill & \mathrm{for}x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill F_{{\mathit{\theta }}_6}\left(x\right)& =& \left\{\begin{array}{cc}1-exp\left[-{\left(x/{\lambda }_6\right)}^{{\beta }_6}\right],\hfill & \mathrm{for}x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill Q_{{\mathit{\theta }}_6}\left(\delta \right)& =& \left\{\begin{array}{cc}{\lambda }_6{(-ln(1-\delta ))}^{1/{\beta }_6},\hfill & \mathrm{for}0<\delta <1;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(18)

respectively, where ${\mathit{\theta }}_6=({\beta }_6,{\lambda }_6)$ is a parameter vector, ${\lambda }_6>0$ is the scale parameter and ${\beta }_6>0$ is the shape parameter.

3. Motivation and Estimation of Model Parameters

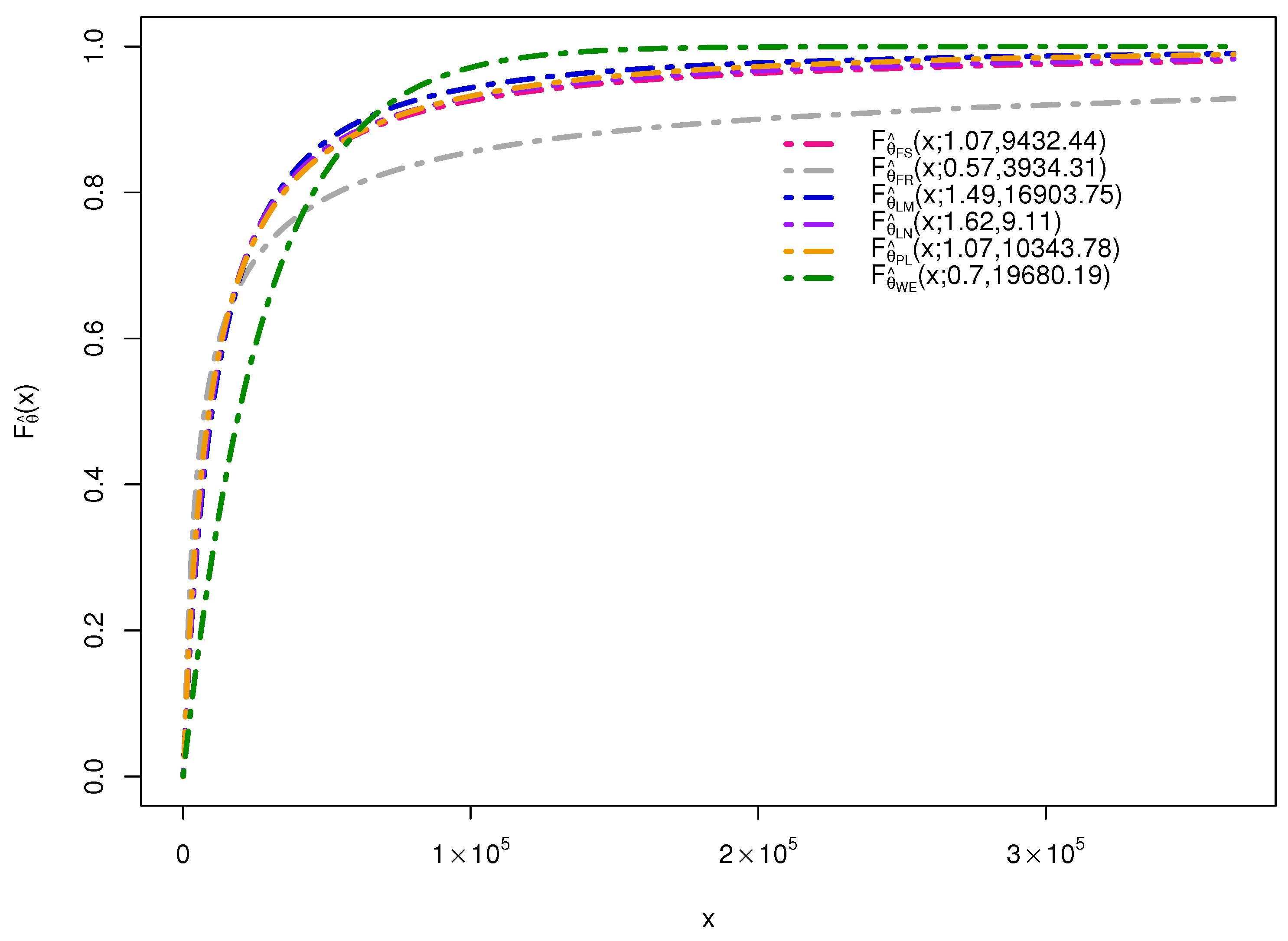
Given the pivotal role of statistical distributions in modeling insurance and claims data, this study aims to investigate the implications and consequences of model misspecification and offer practical and transparent solutions to mitigate its adverse effects. In this section, we use the real dataset dataCar from the insuranceData package (Wolny-Dominiak and Trzesiok 2014) in R (R Core Team 2025) to motivate the study by examining the behavior of the estimated PDFs and CDFs for all candidate models described in Section 2, as illustrated in Figure 1. The dataset contains information on vehicle insurance policies issued between 2004 and 2005, with variables such as vehicle value (in $10,000), the number of claims filed, and the amount of claims. The variable of interest is the claim amount. Specifically, we use the numeric variable clmcst0 for cases in which a claim was filed (based on the clm variable, where 0 indicates no claim, and 1 indicates at least one claim). From Figure 1, the fitted PDFs and CDFs appear broadly similar. However, the maximum likelihood estimates (MLEs) of the parameters, presented in

Table 1. Point estimates and associated MLEs of VaR values (expressed in multiples of ${10}^3$), denoted as ${\widehat{Q}}_{{\mathit{\theta }}_j}(·)$, of the considered models for $\delta =0.95$ and 0.99 for dataCar ^#.

Distribution	Shape	Scale	${\widehat{\mathit{Q}}}_{{\mathit{\theta }}_{\mathit{j}}}\left(0.95\right)$	${\widehat{\mathit{Q}}}_{{\mathit{\theta }}_{\mathit{j}}}\left(0.99\right)$
$FS$	1.43	834.95	6.51	20.60
$FR$	1.05	518.75	8.71	40.97
$LN$	1.19	6.81	7.33	18.74
$LM$	2.04	2202.85	6.42	14.43
$PL$	1.27	1117.04	6.54	18.66
$WE$	0.79	1690.57	6.83	11.81

^# available in the insuranceData package in R.

, differ substantially among different models. Because tail behavior affects the value of VaR with confidence level $100\delta \%$, especially when $\delta$ is close to 1, and is sensitive to model choice, we also report parameter estimates from the minimum density power divergence (MDPD) estimator, a more robust alternative, which will be introduced in subsequent sections and used later in our selection and ranking procedures (

Table 2. VaR estimates (in ${10}^3$) of all the models for $\delta =0.95$ and 0.99, along with weighted VaR estimates, in addition to the associated model ranks based on likelihood and divergence method when $k^{*}=2,3$, respectively, for the dataCar dataset.

Method	$\mathit{\alpha }$	${\widehat{\mathit{Q}}}_{\mathit{j}}\left(\mathit{\delta }\right)$ or ${\tilde{\mathit{Q}}}_{\mathit{j}}\left(\mathit{\delta }\right)$						${\widehat{\mathit{Q}}}^{*}\left(\mathit{\delta }\right)$ or ${\tilde{\mathit{Q}}}^{*}\left(\mathit{\delta }\right)$
		$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$	${\mathit{k}}^{*}=2$	${\mathit{k}}^{*}=3$
$\delta =0.95$
Ranks ‡		3	1	5	2	4	6
Likelihood		6.51	8.71	7.33	6.42	6.54	6.83	7.56	7.21
Divergence	0.05	6.31	8.89	7.31	6.14	6.33	6.36	7.52	7.12
	0.10	6.04	8.94	7.29	5.86	6.07	5.87	7.40	6.95
	0.20	5.44	8.72	6.99	5.24	5.46	4.88	6.99	6.48
$\delta =0.99$
Likelihood		20.60	40.97	18.74	14.43	18.66	11.81	27.66	25.29
Divergence	0.05	19.78	42.41	18.63	13.68	17.84	10.77	28.07	25.31
	0.10	18.71	42.93	18.54	12.89	16.84	9.73	27.96	24.89
	0.20	16.32	41.74	17.11	11.24	14.51	7.79	26.61	23.21

^‡ The model ranks are the same for the likelihood and all the values of $\alpha$ used for the divergence-based method for both the values of $\delta$ considered.

).

In such cases, fitting candidate models to a real dataset and comparing the fits with the empirical density or distribution may suggest that all the models are suitable for explaining the random phenomenon of interest. However, these models can differ substantially, especially in their tail behavior. Given the heavy-tailed nature of non-life insurance claims, parameter estimation or model discrimination based solely on likelihood-based criteria can be restrictive due to their lack of robustness. Tail-related statistics, such as VaR, are particularly sensitive to the choice of the underlying model, which may lead to misleading conclusions and decisions. To illustrate this point, we report the true VaR values at the 95% and 99% levels for these candidate distributions in Table 1, where it is evident that the VaR estimates differ considerably across models. In such situations, it is intuitively appealing to estimate model parameters using robust procedures, such as the minimum DPD estimation method.

Furthermore, since the VaR values of all the considered models differ significantly (see Table 1), in such a situation, estimating the VaR based on the given data using a single model will likely yield an estimator with a much higher risk of incorrect conclusions, intuitively, it may be argued that for such cases, adopting a model averaging method for estimating the parameters of interest would substantially reduce the risks associated with model uncertainty and misspecification (Steel 2020).

In the following, we first discuss the estimation procedures used to estimate the parameters of the considered models. Subsequently, we provide a mathematical framework for the proposed model averaging techniques used to obtain VaR estimates. For the estimation of the unknown parameter vector of a considered model, under the assumption that the data has originated from $f_{{\mathit{\theta }}_j}(·),j=1,\dots ,6$, we adopt the method of maximum likelihood and the method of minimized density power divergence, respectively. Since the true population is unknown, assuming any of the above six models to be true is considerable for the type of random variable being studied here, irrespective of the true underlying model.

3.1. Likelihood-Based Estimation

Let $\mathit{x}=(x_1,x_2,\dots ,x_n)$ be an independent and identically distributed (i.i.d.) sample of size n from $f_{{\mathit{\theta }}_j}(·)$, $j=1,\dots ,6$. Then, the likelihood function (LF) for the parameter vector ${\mathit{\theta }}_j$ based on the observed sample x is

$$\begin{array}{c}\hfill L\left({\mathit{\theta }}_j\right|\mathit{x})=\prod _{i=1}^n{f}_{{\mathit{\theta }}_j}\left(x_i\right);j=1,2,\dots ,6.\end{array}$$

(19)

The maximum likelihood estimate (MLE) of the parameter vector ${\mathit{\theta }}_j$, denoted as ${\widehat{\mathit{\theta }}}_j$, is obtained by maximizing $L\left({\mathit{\theta }}_j\right|\mathit{x})$ or, equivalently, the log-likelihood $lnL\left({\mathit{\theta }}_j\right|\mathit{x})$ with respect to ${\mathit{\theta }}_j$, i.e.,

$$\begin{array}{c}\hfill {\widehat{\mathit{\theta }}}_j=arg\underset{{\mathit{\theta }}_j}{max}L\left({\mathit{\theta }}_j\right|\mathit{x})\equiv arg\underset{{\mathit{\theta }}_j}{max}lnL\left({\mathit{\theta }}_j\right|\mathit{x}).\end{array}$$

(20)

Owing to the invariance property of MLEs, we can obtain the MLE of a function $g\left({\mathit{\theta }}_j\right)$ by substituting ${\widehat{\mathit{\theta }}}_j$ into $g\left({\mathit{\theta }}_j\right)$, i.e., $g\left({\widehat{\mathit{\theta }}}_j\right)$ is the MLE of $g\left({\mathit{\theta }}_j\right)$. Hence, the MLE of VaR for a specific confidence level $\delta$ of the j-th model can be obtained as ${\widehat{Q}}_{{\widehat{\mathit{\theta }}}_j}\left(\delta \right)$. For notational convenience, we denote the MLE of VaR with confidence level $\delta$ under distribution $f_{{\mathit{\theta }}_j}(·)$ as ${\widehat{Q}}_j\left(\delta \right)={\widehat{Q}}_{{\widehat{\mathit{\theta }}}_j}\left(\delta \right)$.

3.2. Divergence-Based Estimation

The minimum density power divergence estimation method was proposed by Basu et al. (1998) as a contemporary to the existing estimation methods based on density-based divergence measures. The density power divergence (DPD) measures the difference between a data-driven PDF $g(·)\in \mathcal{G}$ and an assumed parametric model $f_{\mathit{\theta }}(·)\in \mathcal{G}$ with parameter vector $\mathit{\theta }$, $\mathcal{G}$ being the set of distributions having densities conforming to a dominating measure. Mathematically, it is defined as

$$\begin{array}{ccc}\hfill d_{\alpha }(g,f_{\mathit{\theta }})& =& \int \left\{f_{\mathit{\theta }}^{(1+\alpha )}\left(z\right)-\left(1+{\displaystyle \frac{1}{\alpha }}\right)g\left(z\right)f_{\mathit{\theta }}^{\alpha }\left(z\right)+{\displaystyle \frac{1}{\alpha }}{g}^{(1+\alpha )}\left(z\right)\right\}dz,\alpha >0,\hfill \end{array}$$

(21)

where $d_{\alpha }(g,f_{\mathit{\theta }})>0$ for all PDFs on the Lebesgue measure and is 0 almost everywhere if and only if $f_{\mathit{\theta }}\equiv g$. The MDPD estimator of the parameter vector $\mathit{\theta }$, denoted as $\tilde{\mathit{\theta }}$, is obtained by minimizing the DPD measure in Equation (21) with respect to $\mathit{\theta }$, i.e., $\tilde{\mathit{\theta }}=arg\underset{\mathit{\theta }}{min}{d}_{\alpha }(g,f_{\mathit{\theta }})$.

For general families of distribution, the MDPD estimating equation has the form

$$\begin{array}{c}\hfill U_n\left(t\right)=\int u_t\left(z\right)f_t^{1+\alpha }\left(z\right)dz-n^{-1}\sum _{i=1}^n{u}_t\left(X_i\right)f_t^{\alpha }\left(X_i\right)=0,\end{array}$$

where $u_t\left(z\right)=\partial ln{f}_t\left(z\right)/\partial t$ is the score function. For $\alpha >0$, $U_n\left(t\right)$ induces a down-weighting mechanism, in which observations that are outliers under the assumed model receive smaller weights. As $\alpha \to 0$, minimizing Equation (21) reduces to the MLE, yielding fully efficient estimators in which all observations (outliers included) are effectively weighted equally. At $\alpha =1$, minimizing Equation (21) corresponds to the minimum $L_2$ distance criterion. Thus, $\alpha$ acts as a tuning parameter that controls the trade-off between robustness and efficiency of the resulting estimators.

Thus, based on a random sample x of size n from $f_{{\mathit{\theta }}_j}$, the MDPD estimate ${\tilde{\mathit{\theta }}}_j$ can be obtained by minimizing the empirical form of Equation (21) given below:

$$\begin{array}{cc}\hfill H_{\alpha }\left({\mathit{\theta }}_j\right|\mathit{x})& =\int f_{{\mathit{\theta }}_j}^{1+\alpha }\left(x\right)dx-\left(1+{\displaystyle \frac{1}{\alpha }}\right)n^{-1}\sum _{i=1}^n{f}_{{\mathit{\theta }}_j}^{\alpha }\left(x_i\right);j=1,2,\dots ,6\hfill \end{array}$$

(22)

or by solving

$$\begin{array}{c}\hfill \int u_{{\mathit{\theta }}_j}\left(x\right)f_{{\mathit{\theta }}_j}^{1+\alpha }\left(x\right)dx-n^{-1}\sum _{i=1}^n{u}_{{\mathit{\theta }}_j}\left(x_i\right)f_{{\mathit{\theta }}_j}^{\alpha }\left(x_i\right)=0;j=1,2,\dots ,6,\end{array}$$

(23)

where $u_{{\mathit{\theta }}_j}\left(x\right)=\partial ln{f}_{{\mathit{\theta }}_j}\left(x\right)/\partial {\mathit{\theta }}_j$ is the score function corresponding to the density $f_{{\mathit{\theta }}_j}$, instead of minimizing Equation (21), since the term $\int g^{1+\alpha }\left(z\right)dz$ in Equation (21) is independent of $\mathit{\theta }$ and the term $\int g\left(z\right)f_{\mathit{\theta }}^{\alpha }\left(z\right)dz$ can be replaced by $\int f_{\mathit{\theta }}^{\alpha }\left(z\right)dG\left(z\right)$, where $dG\left(z\right)$ serves an empirical estimate of $g\left(z\right)$, owing to its linear involvement. Note that, as a limiting case, when $\alpha \to 0$, the DPD reduces to the Kullback-Leibler divergence and yields an estimator equivalent to the MLE. On the other hand, the MDPD estimator is equivalent to the minimum mean square error estimator for $\alpha =1$. Pertaining to the behavior of the DPD measure for $\alpha$ in $(0,1)$, a reasonable choice of $\alpha$ lies between 0 and 1 since the efficiency of the estimators gradually decreases with the increase in $\alpha$ (Ghosh et al. 2017; Jones et al. 2001).

One of the interesting properties of the MDPD estimation method is that the MDPD estimators also adhere to the invariance principle, akin to the MLEs. This property allows us to study the behavior of VaR or any other characteristic of a probability model based on MDPD estimates without delving into any complicated mathematical framework. Thus, the MDPD estimator of VaR for a given model $f_{{\mathit{\theta }}_j}$ can be obtained as ${\tilde{Q}}_{{\tilde{\mathit{\theta }}}_j}\left(\delta \right)$, corresponding to the chosen confidence level $\delta$. Once again, for notational convenience, we denote the MDPD estimate of VaR with confidence level $\delta$ as ${\tilde{Q}}_j\left(\delta \right)={\tilde{Q}}_{{\tilde{\mathit{\theta }}}_j}\left(\delta \right)$.

4. Estimating Value-at-Risk via Model Averaging

Based on earlier discussions, it is essential to identify the best-fitting model to minimize the degree of uncertainty and inconclusiveness in estimating the quantity of interest. However, owing to the closeness of these models in highly dense regions and highly dissimilar tail behaviors, the effect of misspecification on the VaR in the case of claim size data requires special attention. Two significant kinds of model misspecifications can be considered: (i) a wrongly specified model (e.g., the underlying model is lognormal, but a Weibull model is assumed) and (ii) a contaminated-observation model (e.g., the underlying model is Weibull, but some contaminated observations/outliers follow a different distribution or the same class of distributions with different parameters). For empirical investigation, following White (1982) and Chow (1984), we examine the consequences of model misspecification in terms of the relative bias and relative variability when the MLE and MDPD are used to estimate the VaR through a Monte Carlo simulation study.

This section describes the proposed model selection and ranking approaches based on the maximum likelihood method and the minimum density power divergence method. We consider the practical situation that a specific model ${\mathcal{M}}_j$ with probability density $f_{{\mathit{\theta }}_j}$ ($j=1,2,\dots ,6$) is considered as the assumed model for modeling a given dataset. Based on this assumption, the MLEs and MDPD estimates of the model parameters, as well as the VaR, can be obtained, along with the associated maximized value of the LF and minimized value of the DPD measure, for the given dataset.

4.1. Model Selection Approach

We consider a model selection approach to select the best-fitting model for a particular dataset. Here, we consider two different approaches for model selection based on the maximized value of the LF and the minimized value of the DPD function for a given dataset x.

For the approach based on the maximized LF, the probability distribution with the maximized value of the likelihood has an intuitive appeal and can be reasonably claimed to be the best among all the considered models. Thus, for a given dataset, we can order all the k candidate models based on the magnitude of the maximized value of the LF if these models have the same number of parameters. Specifically, we denote ${\mathcal{M}}_{\left[1\right]}>{\mathcal{M}}_{\left[2\right]}>\dots >{\mathcal{M}}_{\left[k\right]}$, where the subscript $[·]$ indicates the ordered position of a model, and the notation “>” means “is preferable to”. The same idea can be implemented using the DPD measure. For a given dataset x, the model yielding the minimum value of the DPD statistic $H_{\alpha }\left({\tilde{\mathit{\theta }}}_j\right|\mathit{x})$ in Equation (21) can be considered as the closest one to the true model $g(·)$ among all the candidate models. Hence, based on the minimized value of the DPD statistic, one can order the models such that ${\mathcal{M}}_{\left[1\right]}^{*}>{\mathcal{M}}_{\left[2\right]}^{*}>\dots >{\mathcal{M}}_{\left[k\right]}^{*}$, where ${\mathcal{M}}_{\left[1\right]}^{*}$ is the model with the smallest value of the DPD statistic, ${\mathcal{M}}_{\left[2\right]}^{*}$ is the model with the second smallest value of the DPD statistic, and so on. In other words, ${\mathcal{M}}_{\left[1\right]}={\mathcal{M}}_j$ means model ${\mathcal{M}}_j$ is the most preferable model based on the likelihood function approach, and ${\mathcal{M}}_{\left[1\right]}^{*}={\mathcal{M}}_j$ means model ${\mathcal{M}}_j$ is the most preferable model based on the DPD measure approach. For the model selection approach, after selecting the most probable model, we can estimate the VaR with the selected models based on likelihood function and DPD measure, i.e., models ${\mathcal{M}}_{\left[1\right]}$ and ${\mathcal{M}}_{\left[1\right]}^{*}$, respectively.

4.2. Model Ranking Approach

To reduce the risk of misspecification and improve the accuracy of estimating the quantity of interest, model averaging methods have been widely adopted and found useful across various domains (see, for example, Chatfield 1995; Dormann et al. 2018; Okoli et al. 2018; Wintle et al. 2003). One argument for using the VaR estimates from multiple models for a given dataset is to mitigate the potential risks associated with relying on a single selected model, especially since the true model is unknown in practice. Model averaging essentially protects against a potentially suboptimal or misspecified model. Moreover, estimates from an individual model may exhibit high variance, whereas combining estimates from multiple models can effectively reduce this variance, leading to a more stable and accurate overall estimate. An ensemble estimate is typically less susceptible to the limitations of any single model and leverages the collective strengths of multiple models. Kass and Raftery (1995) and Raftery (1995) discussed the implementation of model averaging in the Bayesian paradigm through the use of posterior odds and/or the Bayes factor. However, the Bayesian model averaging methods can be sensitive to the choice of priors. An interesting yet simple method for model averaging in the frequentist framework was explored by Buckland et al. (1997) in which scaled weights $w_j$ are assigned to each of the candidate models ${\mathcal{M}}_j$ ($j=1,\dots ,k$) and the weighted average is the final estimate of the quantity of interest.

Following Buckland et al. (1997), we compute the weighted estimate of the quantity of interest. For instance, if the quantity of interest is VaR, instead of estimating the VaR based on the model with the maximized value of the LF or the model with the minimum value of the DPD statistic (i.e., the model selection approach in Section 4.1), we consider the best $k^{*}(<k)$ models to obtain an estimate of VaR. Suppose the MLEs and MDPD estimates of VaR at $\delta$ level based on models ${\mathcal{M}}_{[\ell ]}$ and ${\mathcal{M}}_{[\ell ]}^{*}$ are ${\widehat{Q}}_{[\ell ]}\left(\delta \right)$ and ${\tilde{Q}}_{[\ell ]}\left(\delta \right)$, respectively, then using the model ranking approach, the weighted VaR estimates based on maximum likelihood and DPD, denoted as ${\widehat{Q}}^{*}\left(\delta \right)$ and ${\tilde{Q}}^{*}\left(\delta \right)$, can be obtained as follows:

$$\begin{array}{ccc}\hfill {\widehat{Q}}^{*}\left(\delta \right)& =& \sum _{\ell =1}^{k^{*}}{w}_{\ell }·{\widehat{Q}}_{[\ell ]}\left(\delta \right)\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill \mathrm{and} {\tilde{Q}}^{*}\left(\delta \right)& =& \sum _{\ell =1}^{k^{*}}{w}_{\ell }^{*}·{\tilde{Q}}_{[\ell ]}\left(\delta \right)\hfill \end{array}$$

(25)

respectively, with weights $w_{\ell }$ and $w_{\ell }^{*}$, $\ell =1,2,\dots k^{*}$, such that ${\sum }_{l=1}^{k^{*}}{w}_{\ell }={\sum }_{l=1}^{k^{*}}{w}_{\ell }^{*}=1.$ The associated weights $w_{\ell }$ ($w_{\ell }^{*}$) are considered proportional to the maximized (minimized) value of LF (DPD), i.e., $w_1>\dots >w_{k^{*}}$ ( $w_1^{*}>\dots >w_{k^{*}}^{*}$). Specifically, for the likelihood approach, suppose $L{F}_{[\ell ]}$ is the value of maximum likelihood based on model ${\mathcal{M}}_{[\ell ]}$ and hence, $L{F}_{\left[1\right]}>L{F}_{\left[2\right]}>L{F}_{\left[3\right]}>\dots >L{F}_{\left[k\right]}$, then, for the top $k^{*}$ models, the weights in terms of the maximized value of the LF can be expressed as

$$\begin{array}{c}\hfill w_{\ell }={\displaystyle \frac{L{F}_{[\ell ]}}{{\displaystyle \sum _{{\ell }^{\prime }=1}^{k^{*}}}L{F}_{\left[{\ell }^{\prime }\right]}}},\end{array}$$

for $\ell =1,2,\dots ,k^{*}$, such that $w_1>w_2>\dots >w_{k*}$, and ${\sum }_{{\ell }^{\prime }=1}^{k^{*}}{w}_{{\ell }^{\prime }}=1$. Similarly, for the divergence approach, suppose $DP{D}_{[\ell ]}$ is the value of density power divergence based on model ${\mathcal{M}}_{[\ell ]}^{*}$, hence, $DP{D}_{\left[1\right]}<DP{D}_{\left[2\right]}<\dots <DP{D}_{\left[k\right]}$, and since the values of $H_{\alpha }\left(\tilde{\mathit{\theta }}\right|\mathit{x})$ for all considered models are less than 0, for the top $k^{*}$ models, the weights in terms of the minimized values of the DPD can be expressed as

$$\begin{array}{c}\hfill w_{\ell }^{*}={\displaystyle \frac{|DP{D}_{[\ell ]}|}{{\displaystyle \sum _{{\ell }^{\prime }=1}^{k^{*}}}\left|DP{D}_{\left[{\ell }^{\prime }\right]}\right|}},\end{array}$$

for $\ell =1,2,\dots ,k^{*}$, such that $w_1^{*}>w_2^{*}>\dots >w_{k*}^{*}$, and ${\sum }_{{\ell }^{\prime }=1}^{k*}{w}_{{\ell }^{\prime }}^{*}=1$.

Note that the model selection approach discussed in Section 4.1 can be formulated as a special case of the model ranking approach by setting $w_1=1$ and $w_2=\dots =w_{k*}=0$ (or $w_1^{*}=1$ and $w_2^{*}=\dots =w_{k*}^{*}=0$). Furthermore, employing a specific model ${\mathcal{M}}_j$ without model selection can be viewed as a special case within the framework of the proposed model ranking approach, achieved by assigning $w_j=1$ and $w_{\ell }=0$ for $\ell \ne j$. Consequently, the efficacy of the proposed model ranking approach aligns with that of the non-model selection approach when suitable values for $k^{*}$ and the weights are chosen. See Li et al. (2020); Mehrabani and Ullah (2020); Miljkovic (2025); Miljkovic and Grün (2021) and related work for further discussion of weighted estimates from multiple models.

5. Monte Carlo Simulation Study

In this section, a Monte Carlo simulation study is used to evaluate the performance of the proposed methodologies in the presence and absence of contamination. To compare the performance of different approaches and estimators, we consider the simulated biases and root mean square errors (RMSEs) of the MLE and MDPD estimates of VaR with confidence level $\delta$ under statistical distribution $f_{{\mathit{\theta }}_j}$ based on $N=1000$ simulations, which can be computed as

$$\begin{array}{ccc}\hfill Bias\left({\widehat{Q}}_j\left(\delta \right)\right)& =& {\displaystyle \frac{1}{N}}\sum _{s=1}^N{\widehat{Q}}_j^{\left(s\right)}\left(\delta \right)-Q_j\left(\delta \right),\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill RMSE\left({\widehat{Q}}_j\left(\delta \right)\right)& =& {\left\{{\displaystyle \frac{1}{N}}\sum _{s=1}^N{\left[{\widehat{Q}}_j^{\left(s\right)}\left(\delta \right)-Q_j\left(\delta \right)\right]}^2\right\}}^{1/2},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill Bias\left({\tilde{Q}}_j\left(\delta \right)\right)& =& {\displaystyle \frac{1}{N}}\sum _{s=1}^N{\tilde{Q}}_j^{\left(s\right)}\left(\delta \right)-Q_j\left(\delta \right),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill RMSE\left({\tilde{Q}}_j\left(\delta \right)\right)& =& {\left\{{\displaystyle \frac{1}{N}}\sum _{s=1}^N{\left[{\tilde{Q}}_j^{\left(s\right)}\left(\delta \right)-Q_j\left(\delta \right)\right]}^2\right\}}^{1/2},\hfill \end{array}$$

(29)

where ${\widehat{Q}}_j^{\left(s\right)}\left(\delta \right)$ and ${\tilde{Q}}_j^{\left(s\right)}\left(\delta \right)$ are the MLE and MDPD estimate of VaR of $f_{{\mathit{\theta }}_j}$ with confidence level $\delta$ in the s-th simulation, and $Q_j\left(\delta \right)$ is the true value of VaR of $f_{{\mathit{\theta }}_j}$ with confidence level $\delta$.

To facilitate the comparison of the various estimation methods and the proposed model selection/ranking strategies for addressing model uncertainty, we compute the relative bias and relative RMSE of two estimators, say ${\widehat{Q}}_{\left(1\right)}$ and ${\widehat{Q}}_{\left(2\right)}$, defined as

$$\begin{array}{ccc}\hfill RBias({\widehat{Q}}_{\left(1\right)},{\widehat{Q}}_{\left(2\right)})& =& {\displaystyle \frac{Bias\left({\widehat{Q}}_{\left(1\right)}\right)}{Bias\left({\widehat{Q}}_{\left(2\right)}\right)}}\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill \mathrm{and} RRMSE({\widehat{Q}}_{\left(1\right)},{\widehat{Q}}_{\left(2\right)})& =& {\displaystyle \frac{RMSE\left({\widehat{Q}}_{\left(1\right)}\right)}{RMSE\left({\widehat{Q}}_{\left(2\right)}\right)}},\hfill \end{array}$$

(31)

respectively. The absolute value of the relative bias in Equation (30) and the value of relative RMSE in Equation (31) less than 1 indicate that estimator ${\widehat{Q}}_{\left(2\right)}$ is a better estimator compared to ${\widehat{Q}}_{\left(1\right)}$. The sign of the relative bias in Equation (30) indicates if the directions of the biases of the two estimators ${\widehat{Q}}_{\left(1\right)}$ and ${\widehat{Q}}_{\left(2\right)}$ are the same (positive RBias) or they are opposite to each other. The simulation results are obtained based on a simulation size $N=1000$ and reported in the Appendices.

First, considering the assumed model and the true model agree (i.e., without model misspecification), we compare the performance of the likelihood-based and divergence-based parameter estimation procedures presented in Section 3. The average MLEs and MDPD estimates of $Q_j\left(0.99\right)$ for the six probability models in Section 2 ($j=1,2,\dots ,6)$, the biases and RMSEs of the MLEs, and the relative biases and relative RMSEs of the MDPD estimates relative to the MLEs (i.e., $RBias({\tilde{Q}}_j\left(\delta \right),{\widehat{Q}}_j\left(\delta \right))$ and $RRMSE({\tilde{Q}}_j\left(\delta \right),{\widehat{Q}}_j\left(\delta \right))$) are presented in

Table A1. Simulated average estimate of VaR with associated bias and RMSEs (relative bias and relative RMSEs of divergence estimators) for $\delta =0.99$, when the true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$, denoted as $FS$, $FR$, $LM$, $LN$, $PL$ and $WE$ respectively.

n	Estimator	$\mathit{\alpha }$		Model
				$\mathit{j}=1$	$\mathit{j}=2$	$\mathit{j}=3$	$\mathit{j}=4$	$\mathit{j}=5$	$\mathit{j}=6$
			Statistics (a)	$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
			${\mathit{Q}}_{\mathit{j}}\left(\mathit{\delta }\right)$	2.076	4.146	1.885	0.770	1.900	1.168
50	Likelihood		${\mathrm{AV}}_{\mathit{L}}$	2.228	4.596	2.014	0.779	2.077	1.167
			${\mathrm{BS}}_{\mathit{L}}^{\mathit{T}}$	0.152	0.450	0.128	0.009	0.177	−0.002
			${\mathrm{MS}}_{\mathit{L}}^{\mathit{T}}$	1.044	3.286	1.382	0.268	1.209	0.275
	Divergence	0.05	${\mathrm{AV}}_{\mathit{D}}$	2.238	4.613	2.080	0.784	2.099	1.175
			${\mathrm{BS}}_D$	1.067	1.037	1.518	1.617	1.124	−3.974
			${\mathrm{MS}}_D$	1.015	1.002	1.077	1.029	1.024	1.028
		0.10	${\mathrm{AV}}_D$	2.250	4.653	2.165	0.790	2.124	1.181
			${\mathrm{BS}}_D$	1.146	1.126	2.177	2.209	1.264	−8.247
			${\mathrm{MS}}_D$	1.053	1.030	1.271	1.075	1.076	1.076
		0.20	${\mathrm{AV}}_D$	2.276	4.755	2.493	0.800	2.181	1.194
			${\mathrm{BS}}_D$	1.318	1.352	4.733	3.324	1.588	−16.199
			${\mathrm{MS}}_D$	1.165	1.126	2.324	1.199	1.259	1.268
100	Likelihood		${\mathrm{AV}}_L$	2.136	4.325	1.904	0.787	2.002	1.165
			${\mathrm{BS}}_L^T$	0.060	0.179	0.019	0.018	0.102	−0.003
			${\mathrm{MS}}_L^T$	0.656	1.816	0.841	0.177	0.715	0.199
	Divergence	0.05	${\mathrm{AV}}_D$	2.145	4.331	1.944	0.789	2.014	1.168
			${\mathrm{BS}}_D$	1.145	1.034	3.150	1.083	1.118	0.135
			${\mathrm{MS}}_D$	1.030	1.012	1.057	1.010	1.028	1.009
		0.10	${\mathrm{AV}}_D$	2.154	4.344	1.989	0.790	2.027	1.170
			${\mathrm{BS}}_D$	1.294	1.102	5.549	1.154	1.243	−0.601
			${\mathrm{MS}}_D$	1.073	1.041	1.159	1.037	1.079	1.032
		0.20	${\mathrm{AV}}_D$	2.171	4.372	2.121	0.791	2.055	1.174
			${\mathrm{BS}}_D$	1.573	1.259	12.578	1.241	1.513	−1.889
			${\mathrm{MS}}_D$	1.171	1.122	1.572	1.124	1.217	1.121

^(a) expressed as a multiplier of ${10}^4$.

. From Table A1, it is evident that when the assumed model is indeed the true model and without any contaminated observations, the performance of the MLE is better than that of the MDPD estimator in terms of MSE, while the MDPD estimator provides smaller biases compared to the MLE in some situations.

In the following subsection, we present the results of the Monte Carlo simulation study to investigate the performance of the estimation procedures and the proposed model selection and ranking approaches under model misspecification with and without contamination. In Section 5.1, we compare the performance of the proposed model selection and model ranking procedures based on likelihood and divergence methods where contamination is not present. Additionally, since estimators based on DPD measures are known to be robust, we consider a contamination model in Section 5.2 and compare the performances of the proposed procedures to determine whether methods based on DPD are relatively better than those based on LF.

5.1. Performance of the Proposed Methods in the Absence of Contamination

To assess the performance of the proposed methods in the absence of contamination, the data is assumed to be governed by one of the six candidate distributions discussed in Section 2. Specifically, we generate random samples of size n from $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$, and $WE(0.79,1690.57)$ for $N=1000$ simulations.

Before evaluating the performance of the proposed model selection and model ranking approaches, we study the performance of the MLE and MDPD estimation methods for VaR under model misspecification with the non-model-selection approach (i.e., estimate the VaR under the assumed model ${\mathcal{M}}_j$). For each dataset simulated from a true model (say, model ${\mathcal{M}}_h$), the parameter vector and the corresponding VaR values are estimated under the assumed model using MLE and MDPD estimation methods. In

Table A2. Simulated average estimate of VaR (expressed as a multiplier of ${10}^4$), relative bias and relative RMSE with $\delta =0.99$ when the non-model selection approach is adopted for true models $FS(1.43,834.95)$ and $FR(1.05,518.75)$. Values in bold indicate the results obtained under the true model.

True Model  $\mathbf{\left(}\mathit{h}\mathbf{\right)}$	$\mathit{n}$	Method	$\mathit{\alpha }$		Assumed Model
					$\mathit{j}=\mathbf{1}$	$\mathit{j}=\mathbf{2}$	$\mathit{j}=\mathbf{3}$	$\mathit{j}=\mathbf{4}$	$\mathit{j}=\mathbf{5}$	$\mathit{j}=\mathbf{6}$
					$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$FS(1.43,834.95)$	50	Likelihood based		${\mathrm{AV}}_L$	2.228	36.727	1.717	1.667	1.830	1.240
				${\mathrm{BS}}_L$	1.000	228.288	−2.365	-2.691	−1.622	−5.509
				${\mathrm{MS}}_L$	1.000	223.204	1.259	0.833	0.972	1.163
		Divergence based	0.05	${\mathrm{AV}}_D$	2.238	41.121	1.621	1.620	1.784	1.027
				${\mathrm{BS}}_D$	1.067	257.236	−2.999	−3.007	−1.921	−6.908
				${\mathrm{MS}}_D$	1.015	149.300	1.149	0.807	0.943	1.105
			0.10	${\mathrm{AV}}_D$	2.250	46.241	1.520	1.589	1.747	0.857
				${\mathrm{BS}}_D$	1.146	290.970	−3.662	−3.209	−2.169	−8.030
				${\mathrm{MS}}_D$	1.053	158.270	1.088	0.819	0.950	1.208
			0.20	${\mathrm{AV}}_D$	2.276	71.710	1.328	1.565	1.695	0.676
				${\mathrm{BS}}_D$	1.318	458.761	−4.926	−3.368	−2.513	−9.222
				${\mathrm{MS}}_D$	1.165	418.429	1.069	0.884	1.027	1.357
	100	Likelihood based		${\mathrm{AV}}_L$	2.136	31.208	1.609	1.620	1.728	1.242
				${\mathrm{BS}}_L$	1.000	482.290	−7.734	−7.548	−5.767	−13.814
				${\mathrm{MS}}_L$	1.000	115.236	1.276	1.011	1.049	1.544
		Divergence based	0.05	${\mathrm{AV}}_D$	2.145	30.075	1.506	1.569	1.682	0.991
				${\mathrm{BS}}_D$	1.145	463.527	−9.440	−8.399	−6.524	−17.961
				${\mathrm{MS}}_D$	1.030	97.245	1.277	1.040	1.071	1.712
			0.10	${\mathrm{AV}}_D$	2.154	30.388	1.403	1.534	1.643	0.832
				${\mathrm{BS}}_D$	1.294	468.718	−11.146	−8.971	−7.172	−20.586
				${\mathrm{MS}}_D$	1.073	74.042	1.332	1.080	1.111	1.921
			0.20	${\mathrm{AV}}_D$	2.171	35.501	1.212	1.498	1.582	0.662
				${\mathrm{BS}}_D$	1.573	553.361	−14.309	−9.560	−8.172	−23.407
				${\mathrm{MS}}_D$	1.171	94.815	1.518	1.151	1.205	2.166
$FR(1.05,518.75)$	50	Likelihood based		${\mathrm{AV}}_L$	1.852	4.596	2.866	1.695	1.883	2.248
				${\mathrm{BS}}_L$	−5.095	1.000	−2.843	−5.443	−5.025	−4.216
				${\mathrm{MS}}_L$	0.771	1.000	1.063	0.828	0.804	1.380
		Divergence based	0.05	${\mathrm{AV}}_D$	1.620	4.613	2.439	1.362	1.572	1.335
				${\mathrm{BS}}_D$	−5.609	1.037	−3.790	−6.184	−5.717	−6.242
				${\mathrm{MS}}_D$	0.810	1.002	0.909	0.875	0.838	0.897
			0.10	${\mathrm{AV}}_D$	1.447	4.653	2.077	1.151	1.338	0.924
				${\mathrm{BS}}_D$	−5.994	1.126	−4.596	−6.652	−6.235	−7.155
				${\mathrm{MS}}_D$	0.849	1.030	0.844	0.926	0.884	0.992
			0.20	${\mathrm{AV}}_D$	1.213	4.755	1.518	0.903	1.026	0.578
				${\mathrm{BS}}_D$	−6.514	1.352	−5.836	−7.202	−6.927	−7.924
				${\mathrm{MS}}_D$	0.909	1.126	0.867	0.994	0.962	1.088
	100	Likelihood based		${\mathrm{AV}}_L$	1.772	4.325	2.589	1.604	1.773	2.082
				${\mathrm{BS}}_L$	−13.255	1.000	−8.695	−14.190	−13.247	−11.523
				${\mathrm{MS}}_L$	1.357	1.000	1.183	1.447	1.374	1.741
		Divergence based	0.05	${\mathrm{AV}}_D$	1.562	4.331	2.238	1.313	1.500	1.263
				${\mathrm{BS}}_D$	−14.427	1.034	−10.651	−15.817	−14.774	−16.098
				${\mathrm{MS}}_D$	1.454	1.012	1.237	1.579	1.494	1.614
			0.10	${\mathrm{AV}}_D$	1.399	4.344	1.928	1.117	1.286	0.890
				${\mathrm{BS}}_D$	−15.340	1.102	−12.386	−16.909	−15.967	−18.180
				${\mathrm{MS}}_D$	1.535	1.041	1.335	1.679	1.597	1.801
			0.20	${\mathrm{AV}}_D$	1.171	4.372	1.430	0.880	0.991	0.568
				${\mathrm{BS}}_D$	−16.608	1.259	−15.165	−18.234	−17.617	−19.975
				${\mathrm{MS}}_D$	1.651	1.122	1.541	1.803	1.748	1.972

,

Table A3. Simulated average VaR estiamtes (expressed as a multiplier of ${10}^4$), relative bias and relative RMSE with $\delta =0.99$ when non-model selection approach is adopted for true models $LM(2.04,2202.85)$ and $LN(1.19,6.81)$. Values in bold indicate the results obtained under the true model.

True Model  $\mathbf{\left(}\mathit{h}\mathbf{\right)}$	$\mathit{n}$	Method	$\mathit{\alpha }$		Assumed Model
					$\mathit{j}=\mathbf{1}$	$\mathit{j}=\mathbf{2}$	$\mathit{j}=\mathbf{3}$	$\mathit{j}=\mathbf{4}$	$\mathit{j}=\mathbf{5}$	$\mathit{j}=\mathbf{6}$
					$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$LM(2.04,2202.85)$	50	Likelihood based		${\mathrm{AV}}_L$	4.016	687.827	2.014	2.681	3.158	1.327
				${\mathrm{BS}}_L$	16.594	5.34$\times {10}^3$	1.000	6.201	9.913	–4.349
				${\mathrm{MS}}_L$	2.087	5.20$\times {10}^3$	1.000	1.084	1.587	0.694
		Divergence based	0.05	${\mathrm{AV}}_D$	4.393	2.36$\times {10}^3$	2.080	2.858	3.477	1.206
				${\mathrm{BS}}_D$	19.534	1.84$\times {10}^4$	1.518	7.575	12.396	−5.291
				${\mathrm{MS}}_D$	2.486	3.03$\times {10}^4$	1.077	1.285	1.992	0.585
			0.10	${\mathrm{AV}}_D$	4.781	799.436	2.165	3.063	3.845	1.101
				${\mathrm{BS}}_D$	22.553	6.21$\times {10}^3$	2.177	9.176	15.268	−6.109
				${\mathrm{MS}}_D$	2.934	3.20$\times {10}^3$	1.271	1.567	2.543	0.623
			0.20	${\mathrm{AV}}_D$	5.573	4.34$\times {10}^3$	2.493	3.607	4.769	0.962
				${\mathrm{BS}}_D$	28.725	3.38$\times {10}^4$	4.733	13.411	22.462	−7.192
				${\mathrm{MS}}_D$	4.009	3.27$\times {10}^4$	2.324	2.621	4.336	0.701
	100	Likelihood based		${\mathrm{AV}}_L$	3.963	227.069	1.904	2.629	3.066	1.306
				${\mathrm{BS}}_L$	110.731	1.20$\times {10}^4$	1.000	39.665	62.930	−30.905
				${\mathrm{MS}}_L$	2.948	1.32$\times {10}^3$	1.000	1.343	1.979	0.852
		Divergence based	0.05	${\mathrm{AV}}_D$	4.323	269.232	1.944	2.787	3.349	1.189
				${\mathrm{BS}}_D$	129.950	1.43$\times {10}^4$	3.150	48.080	78.030	-37.124
				${\mathrm{MS}}_D$	3.467	1.08$\times {10}^3$	1.057	1.573	2.417	0.905
			0.10	${\mathrm{AV}}_D$	4.680	341.819	1.989	2.964	3.655	1.091
				${\mathrm{BS}}_D$	148.990	1.81$\times {10}^4$	5.549	57.516	94.355	−42.327
				${\mathrm{MS}}_D$	4.009	1.53$\times {10}^3$	1.159	1.857	2.937	0.991
			0.20	${\mathrm{AV}}_D$	5.359	755.957	2.121	3.369	4.321	0.956
				${\mathrm{BS}}_D$	185.177	4.02$\times {10}^4$	12.578	79.093	129.827	−49.531
				${\mathrm{MS}}_D$	5.120	6.52$\times {10}^3$	1.572	2.598	4.239	1.133
$LN(1.19,6.81)$	50	Likelihood based		${\mathrm{AV}}_L$	1.138	6.933	0.705	0.779	0.889	0.519
				${\mathrm{BS}}_L$	40.417	676.477	−7.122	1.000	13.163	−27.521
				${\mathrm{MS}}_L$	2.166	34.744	1.315	1.000	1.472	1.154
		Divergence gence	0.05	${\mathrm{AV}}_D$	1.170	8.847	0.703	0.784	0.901	0.485
				${\mathrm{BS}}_D$	43.985	886.568	−7.346	1.617	14.414	−31.273
				${\mathrm{MS}}_D$	2.331	49.121	1.329	1.029	1.544	1.208
			0.10	${\mathrm{AV}}_D$	1.196	10.905	0.695	0.790	0.907	0.448
				${\mathrm{BS}}_D$	46.764	1.11$\times {10}^3$	−8.226	2.209	15.133	−35.335
				${\mathrm{MS}}_D$	2.480	67.405	1.346	1.075	1.616	1.302
			0.20	${\mathrm{AV}}_D$	1.228	15.344	0.670	0.800	0.909	0.386
				${\mathrm{BS}}_D$	50.304	1.60$\times {10}^3$	−10.913	3.324	15.278	−42.048
				${\mathrm{MS}}_D$	2.726	121.488	1.383	1.199	1.755	1.491
	100	Likelihood based		${\mathrm{AV}}_L$	1.137	6.732	0.720	0.787	0.891	0.538
				${\mathrm{BS}}_L$	20.945	340.029	−2.821	1.000	6.946	−13.194
				${\mathrm{MS}}_L$	2.631	40.628	1.352	1.000	1.529	1.502
		Divergence based	0.05	${\mathrm{AV}}_D$	1.164	8.029	0.711	0.789	0.897	0.497
				${\mathrm{BS}}_D$	22.471	414.027	−3.356	1.083	7.283	−15.548
				${\mathrm{MS}}_D$	2.808	49.078	1.332	1.010	1.577	1.650
			0.10	${\mathrm{AV}}_D$	1.183	9.265	0.697	0.790	0.898	0.456
				${\mathrm{BS}}_D$	23.592	484.521	−4.158	1.154	7.337	−17.875
				${\mathrm{MS}}_D$	2.955	57.909	1.325	1.037	1.618	1.838
			0.20	${\mathrm{AV}}_D$	1.204	11.749	0.659	0.791	0.889	0.390
				${\mathrm{BS}}_D$	24.805	626.190	−6.330	1.241	6.800	−21.625
				${\mathrm{MS}}_D$	3.163	77.375	1.351	1.124	1.683	2.175

and

Table A4. Simulated average VaR estimates (expressed as a multiplier of ${10}^4$), relative bias and relative RMSE with $\delta =0.99$ when non-model selection approach is adopted for true models $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$. Values in bold indicate the results obtained under the true model.

True Model  $\mathbf{\left(}\mathit{h}\mathbf{\right)}$	$\mathit{n}$	Method	$\mathit{\alpha }$		Assumed Model
					$\mathit{j}=\mathbf{1}$	$\mathit{j}=\mathbf{2}$	$\mathit{j}=\mathbf{3}$	$\mathit{j}=\mathbf{4}$	$\mathit{j}=\mathbf{5}$	$\mathit{j}=\mathbf{6}$
					$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$PL(1.27,1117.04)$	50	Likelihood based		${\mathrm{AV}}_L$	2.603	84.381	1.721	1.875	2.077	1.219
				${\mathrm{BS}}_L$	3.977	466.850	−1.016	−0.143	1.000	−3.857
				${\mathrm{MS}}_L$	1.201	470.828	1.110	0.727	1.000	0.910
		Divergence based	0.05	${\mathrm{AV}}_D$	2.685	87.852	1.674	1.880	2.099	1.047
				${\mathrm{BS}}_D$	4.443	486.497	−1.280	−0.114	1.124	−4.829
				${\mathrm{MS}}_D$	1.285	295.427	1.088	0.721	1.024	0.798
			0.10	${\mathrm{AV}}_D$	2.764	111.779	1.623	1.898	2.124	0.914
				${\mathrm{BS}}_D$	4.885	621.925	−1.568	−0.016	1.264	−5.586
				${\mathrm{MS}}_D$	1.385	543.075	1.102	0.752	1.076	0.860
			0.20	${\mathrm{AV}}_D$	2.905	146.298	1.521	1.957	2.181	0.749
				${\mathrm{BS}}_D$	5.685	817.306	−2.147	0.319	1.588	−6.516
				${\mathrm{MS}}_D$	1.611	572.347	1.202	0.891	1.259	0.972
	100	Likelihood based		${\mathrm{AV}}_L$	2.547	57.314	1.645	1.854	2.002	1.219
				${\mathrm{BS}}_L$	6.348	543.883	−2.504	−0.455	1.000	−6.687
				${\mathrm{MS}}_L$	1.444	322.779	1.065	0.793	1.000	1.158
		Divergence based	0.05	${\mathrm{AV}}_D$	2.623	54.594	1.579	1.853	2.014	1.044
				${\mathrm{BS}}_D$	7.089	517.186	−3.153	−0.470	1.118	−8.407
				${\mathrm{MS}}_D$	1.567	131.347	1.029	0.791	1.028	1.269
			0.10	${\mathrm{AV}}_D$	2.692	57.748	1.507	1.860	2.027	0.908
				${\mathrm{BS}}_D$	7.774	548.144	−3.861	−0.399	1.243	−9.741
				${\mathrm{MS}}_D$	1.696	131.301	1.027	0.817	1.079	1.422
			0.20	${\mathrm{AV}}_D$	2.813	69.931	1.361	1.894	2.055	0.743
				${\mathrm{BS}}_D$	8.955	667.718	−5.290	−0.066	1.513	−11.362
				${\mathrm{MS}}_D$	1.944	172.143	1.100	0.918	1.217	1.634
$WE(0.79,1690.57)$	50	Likelihood based		${\mathrm{AV}}_L$	5.835	1.08$\times {10}^4$	1.488	3.732	4.269	1.167
				${\mathrm{BS}}_L$	−2.95$\times {10}^3$	−6.81$\times {10}^6$	−202.110	−1.62$\times {10}^3$	−1.96$\times {10}^3$	1.000
				${\mathrm{MS}}_L$	20.235	7.02$\times {10}^5$	2.721	12.039	14.748	1.000
		Divergence gence	0.05	${\mathrm{AV}}_D$	7.056	2.24$\times {10}^5$	1.697	4.427	5.473	1.175
				${\mathrm{BS}}_D$	−3.72$\times {10}^3$	−1.41$\times {10}^8$	−334.238	−2.06$\times {10}^3$	−2.72$\times {10}^3$	−3.974
				${\mathrm{MS}}_D$	26.742	2.44$\times {10}^7$	4.323	16.692	22.635	1.028
			0.10	${\mathrm{AV}}_D$	8.534	1.47$\times {10}^7$	2.070	5.408	7.306	1.181
				${\mathrm{BS}}_D$	−4.66$\times {10}^3$	−9.33$\times {10}^9$	−570.471	−2.68$\times {10}^3$	−3.88$\times {10}^3$	−8.247
				${\mathrm{MS}}_D$	36.210	1.70$\times {10}^9$	9.252	28.572	40.200	1.076
			0.20	${\mathrm{AV}}_D$	13.312	2.51$\times {10}^{11}$	7.310	18.255	50.427	1.194
				${\mathrm{BS}}_D$	−7.68$\times {10}^3$	−1.59$\times {10}^{14}$	−3.88$\times {10}^3$	−1.08$\times {10}^4$	−3.12$\times {10}^4$	−16.199
				${\mathrm{MS}}_D$	143.473	2.89$\times {10}^{13}$	182.046	960.227	4.16$\times {10}^3$	1.268
	100	Likelihood based		${\mathrm{AV}}_L$	5.561	1.97$\times {10}^3$	1.414	3.613	3.942	1.165
				${\mathrm{BS}}_L$	−1.41$\times {10}^3$	−6.31$\times {10}^5$	−78.692	−784.091	−889.330	1.000
				${\mathrm{MS}}_L$	23.902	4.97$\times {10}^4$	2.476	13.696	15.796	1.000
		Divergence based	0.05	${\mathrm{AV}}_D$	6.586	2.54$\times {10}^3$	1.540	4.129	4.826	1.168
				${\mathrm{BS}}_D$	−1.74$\times {10}^3$	−8.15$\times {10}^5$	−119.045	−949.515	−1.17$\times {10}^3$	0.135
				${\mathrm{MS}}_D$	29.921	1.12$\times {10}^5$	3.390	16.782	21.422	1.009
			0.10	${\mathrm{AV}}_D$	7.740	3.55$\times {10}^3$	1.715	4.745	5.958	1.170
				${\mathrm{BS}}_D$	−2.11$\times {10}^3$	−1.14$\times {10}^6$	−175.210	−1.15$\times {10}^3$	−1.54$\times {10}^3$	−0.601
				${\mathrm{MS}}_D$	36.956	1.57$\times {10}^5$	4.954	20.747	29.188	1.032
			0.20	${\mathrm{AV}}_D$	10.388	9.62$\times {10}^3$	2.402	6.405	9.232	1.174
				${\mathrm{BS}}_D$	−2.96$\times {10}^3$	−3.08$\times {10}^6$	−395.750	−1.68$\times {10}^3$	−2.59$\times {10}^3$	−1.889
				${\mathrm{MS}}_D$	54.636	3.82$\times {10}^5$	15.422	33.644	56.212	1.121

, we present the average VaR estimates with confidence level $0.99$, the relative biases relative to the bias of the MLEs, when the assumed model is the true model (i.e., $RBias({\widehat{Q}}_j\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ and $RBias({\tilde{Q}}_j\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$) and the relative RMSEs relative to the RMSE of the MLEs when the assumed model is the true model (i.e., $RRMSE({\widehat{Q}}_j\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ and $RRMSE({\tilde{Q}}_j\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$) respectively. Therefore, when the assumed model is the true model (values highlighted in boldface), the value of $RBias({\widehat{Q}}_j\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ and $RRMSE({\widehat{Q}}_j\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ is 1 under the likelihood method. Table A2, Table A3 and Table A4 illustrate that when the model is misspecified, biases in estimation arise, regardless of the method used for estimating the VaR. Furthermore, although some RMSEs may be smaller in certain instances compared to those observed under correct model specifications, overall, RMSEs tend to be higher when the model is misspecified. Particularly noteworthy is the substantial increase in biases and RMSEs when the model is misspecified as a Fréchet distribution. These findings underscore the imperative of developing effective strategies to mitigate the impact of model misspecification.

Here, we also evaluate the performance of VaR estimates based on the proposed model selection and model ranking approach presented in Section 4. For each simulated dataset, we perform the model selection approach by using the likelihood-based and the divergence-based approaches; then, based on the selected model (i.e., the most probable model), we compute the estimate of VaR by using the MLE or MDPD estimation methods, as ${\widehat{Q}}^{†}\left(\delta \right)$ and ${\tilde{Q}}^{†}\left(\delta \right)$, respectively. To evaluate the performance of the estimates ${\widehat{Q}}^{†}\left(\delta \right)$ and ${\tilde{Q}}^{†}\left(\delta \right)$ using the model selection approach, we compute the relative biases and relative RMSEs relative to the biases and RMSEs of the MLEs under the correctly specified model ${\mathcal{M}}_h$, i.e., $RBias({\widehat{Q}}^{†}\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ and $RRMSE({\widehat{Q}}^{†}\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ for the model selection approach using MLE, and $RBias({\tilde{Q}}^{†}\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ and $RRMSE({\tilde{Q}}^{†}\left(\delta \right),{\widehat{Q}}_h\left(\delta \right))$ for the DPD measure approach).

In

Table A5. VaR estimates (expressed as a multiplier of ${10}^4$), relative biases and relative RMSEs for $k^{*}=1,\delta =0.99$, when true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$. Values in bold indicate the smallest $M{S}_S$ among all the estimators.

n		Likelihood Based	Divergence Based			Likelihood Based	Divergence Based
			$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$		$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$
		True model: $FS(1.43,834.95)$				True model: $LN(1.19,6.81)$
		True $Q_1\left(0.99\right)=2.076$				True $Q_4\left(0.99\right)=0.770$
50	${\mathrm{AV}}_s$	1.130	1.146	1.187	1.255	0.481	0.542	0.597	0.722
	${\mathrm{BS}}_s$	−6.235	−6.127	−5.854	−5.409	−31.646	−24.982	−18.901	−5.191
	${\mathrm{MS}}_s$	2.324	2.477	2.734	3.331	3.043	3.755	4.476	5.846
100	${\mathrm{AV}}_s$	0.949	0.962	0.945	0.929	0.437	0.469	0.506	0.632
	${\mathrm{BS}}_s$	−18.654	−18.437	−18.725	−18.995	−18.949	−17.164	−15.006	−7.862
	${\mathrm{MS}}_s$	2.587	2.678	2.701	2.794	3.675	4.113	4.790	7.318
		True model: $FR(1.05,518.75)$				True model: $PL(1.27,1117.04)$
		True $Q_2\left(0.99\right)=4.146$				True $Q_5\left(0.99\right)=1.900$
50	${\mathrm{AV}}_s$	2.097	2.085	2.091	2.056	1.011	1.096	1.118	1.264
	${\mathrm{BS}}_s$	−4.550	−4.577	−4.564	−4.641	−5.033	−4.553	−4.428	−3.605
	${\mathrm{MS}}_s$	1.143	1.137	1.147	1.165	1.509	2.095	2.309	3.120
100	${\mathrm{AV}}_s$	2.101	2.103	2.107	2.106	0.963	0.968	0.964	0.969
	${\mathrm{BS}}_s$	−11.420	−11.405	−11.387	−11.388	−9.202	−9.155	−9.189	−9.147
	${\mathrm{MS}}_s$	1.774	1.775	1.781	1.806	2.134	2.153	2.155	2.212
		True model: $LM(2.04,2202.85)$				True model: $WE(0.79,1690.57)$
		True $Q_3\left(0.99\right)=1.885$				True $Q_6\left(0.99\right)=1.168$
50	${\mathrm{AV}}_s$	0.985	1.067	1.137	1.381	0.646	0.674	0.715	0.852
	${\mathrm{BS}}_s$	−7.015	−6.372	−5.826	−3.930	330.374	312.732	286.627	200.286
	${\mathrm{MS}}_s$	1.199	1.404	1.684	2.498	3.238	3.321	3.467	4.616
100	${\mathrm{AV}}_s$	0.972	1.007	1.043	1.148	0.606	0.619	0.637	0.690
	${\mathrm{BS}}_s$	−48.666	−46.801	−44.888	−39.318	180.380	176.138	170.449	153.560
	${\mathrm{MS}}_s$	1.749	1.810	1.865	2.223	4.238	4.278	4.352	4.729

, the average values of the estimates of VaR, based on the model selection approach, along with the associated relative biases and the relative RMSEs of all the proposed estimators, relative to the corresponding bias and RMSEs of the MLEs obtained under the assumption of the correctly specified model. Moreover, we present the simulation proportion of the best-fitting model in

Table A6. Proportion of models included for the VaR estimates reported in Table A5 for sample sizes 50 and 100 when the true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$. Values in bold indicate the results obtained under the true model.

True Model	n	Method	$\mathit{\alpha }$	Assumed Model
				$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$FS(1.43,834.95)$	50	Likelihood		0.281	0.102	0.073	0.320	0.180	0.044
		Divergence	0.05	0.284	0.100	0.072	0.308	0.199	0.037
			0.10	0.287	0.103	0.072	0.294	0.210	0.034
			0.20	0.273	0.103	0.064	0.304	0.222	0.034
	100	Likelihood		0.408	0.028	0.054	0.271	0.234	0.005
		Divergence	0.05	0.405	0.032	0.043	0.264	0.252	0.004
			0.10	0.394	0.029	0.043	0.262	0.268	0.004
			0.20	0.358	0.029	0.04	0.295	0.272	0.006
$FR(1.05,518.75)$	50	Likelihood		0.031	0.887	0.000	0.082	0.000	0.000
		Divergence	0.05	0.035	0.892	0.000	0.073	0.000	0.000
			0.10	0.040	0.895	0.000	0.065	0.000	0.000
			0.20	0.050	0.882	0.000	0.067	0.001	0.000
	100	Likelihood		0.012	0.961	0.000	0.027	0.000	0.000
		Divergence	0.05	0.015	0.964	0.000	0.021	0.000	0.000
			0.10	0.017	0.966	0.000	0.017	0.000	0.000
			0.20	0.017	0.961	0.000	0.022	0.000	0.000
$LM(2.04,2202.85)$	50	Likelihood		0.063	0.007	0.341	0.257	0.091	0.241
		Divergence	0.05	0.070	0.014	0.337	0.260	0.099	0.220
			0.10	0.076	0.016	0.307	0.264	0.115	0.222
			0.20	0.088	0.031	0.270	0.264	0.124	0.223
	100	Likelihood		0.042	0.000	0.514	0.145	0.139	0.160
		Divergence	0.05	0.048	0.001	0.511	0.144	0.146	0.150
			0.10	0.056	0.002	0.497	0.155	0.146	0.144
			0.20	0.074	0.004	0.436	0.177	0.152	0.157
$LN(1.19,6.81)$	50	Likelihood		0.089	0.096	0.062	0.601	0.094	0.058
		Divergence	0.05	0.097	0.115	0.053	0.586	0.104	0.045
			0.10	0.101	0.126	0.046	0.577	0.115	0.035
			0.20	0.112	0.156	0.031	0.547	0.125	0.029
	100	Likelihood		0.106	0.031	0.026	0.730	0.094	0.013
		Divergence	0.05	0.119	0.044	0.017	0.710	0.100	0.010
			0.10	0.131	0.056	0.016	0.693	0.097	0.007
			0.20	0.145	0.088	0.009	0.655	0.099	0.004
$PL(1.27,1117.04)$	50	Likelihood		0.184	0.051	0.158	0.324	0.210	0.073
		Divergence	0.05	0.194	0.058	0.154	0.310	0.220	0.064
			0.10	0.195	0.060	0.151	0.310	0.225	0.059
			0.20	0.197	0.070	0.144	0.303	0.221	0.065
	100	Likelihood		0.238	0.011	0.177	0.243	0.320	0.011
		Divergence	0.05	0.231	0.011	0.166	0.244	0.340	0.008
			0.10	0.218	0.010	0.155	0.253	0.355	0.009
			0.20	0.216	0.011	0.154	0.256	0.350	0.013
$WE(0.79,1690.57)$	50	Likelihood		0.000	0.000	0.123	0.063	0.018	0.796
		Divergence	0.05	0.003	0.000	0.132	0.073	0.019	0.773
			0.10	0.006	0.000	0.137	0.093	0.022	0.742
			0.20	0.014	0.002	0.149	0.132	0.024	0.679
	100	Likelihood		0.001	0.000	0.140	0.005	0.000	0.854
		Divergence	0.05	0.001	0.000	0.148	0.011	0.001	0.839
			0.10	0.001	0.000	0.153	0.015	0.004	0.827
			0.20	0.002	0.000	0.156	0.032	0.005	0.805

(in terms of maximized likelihood or minimized divergence) among all competing models. The boldfaced proportions in Table A6 represent the proportions of the true model from which the data is generated, being selected as the best model in terms of maximized likelihood or minimized DPD in $N=1000$ simulations. The other proportions for different assumed models against a given true model indicate the proportions of the assumed model being chosen as the best model in the $N=1000$ simulations, which is the model then used to compute the final VaR estimates with Equation (24).

For the model ranking approach, we consider $k^{*}=2$ and 3, i.e., use the top two and top three most probable models to compute the weighted average estimate of VaR. In

Table A7. VaR estimates (expressed as a multiplier of ${10}^4$), relative biases and relative RMSEs for $k^{*}=2,\delta =0.99$, when true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$. Values in bold indicate the smallest $M{S}_{k^{*}}$ among all the estimators.

n		Likelihood Based	Divergence Based			Likelihood Based	Divergence Based
			$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$		$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$
		True model: $FS(1.43,834.95)$				True model: $LN(1.19,6.81)$
		True $Q_1\left(0.99\right)=2.076$				True $Q_4\left(0.99\right)=0.770$
50	${\mathrm{AV}}_{k^{*}}$	1.077	1.124	1.170	1.292	0.499	0.563	0.642	0.816
	${\mathrm{BS}}_{k^{*}}$	−6.584	−6.269	−5.970	−5.162	−29.730	−22.714	−13.959	5.104
	${\mathrm{MS}}_{k^{*}}$	1.306	1.355	1.429	1.676	1.640	1.804	2.189	3.209
100	${\mathrm{AV}}_{k^{*}}$	0.956	0.948	0.959	0.968	0.483	0.537	0.586	0.719
	${\mathrm{BS}}_{k^{*}}$	−18.547	−18.680	−18.491	−18.349	−16.350	−13.259	−10.452	−2.882
	${\mathrm{MS}}_{k^{*}}$	1.843	1.853	1.857	1.893	2.044	2.253	2.495	3.568
		True model: $FR(1.05,518.75)$				True model: $PL(1.27,1117.04)$
		True $Q_2\left(0.99\right)=4.146$				True $Q_5\left(0.99\right)=1.900$
50	${\mathrm{AV}}_{k^{*}}$	1.541	1.474	1.420	1.358	1.054	1.117	1.176	1.409
	${\mathrm{BS}}_{k^{*}}$	−5.785	−5.935	−6.054	−6.192	−4.790	−4.436	−4.099	−2.783
	${\mathrm{MS}}_{k^{*}}$	0.892	0.888	0.881	0.901	1.024	1.079	1.190	2.002
100	${\mathrm{AV}}_{k^{*}}$	1.485	1.436	1.390	1.311	0.992	1.021	1.055	1.133
	${\mathrm{BS}}_{k^{*}}$	−14.859	−15.131	−15.389	−15.831	−8.916	−8.636	−8.297	−7.532
	${\mathrm{MS}}_{k^{*}}$	1.503	1.526	1.549	1.592	1.395	1.396	1.399	1.576
		True model: $LM(2.04,2202.85)$				True model: $WE(0.79,1690.57)$
		True $Q_3\left(0.99\right)=1.885$				True $Q_6\left(0.99\right)=1.168$
50	${\mathrm{AV}}_{k^{*}}$	1.120	1.225	1.396	1.876	0.761	0.908	1.196	2.774
	${\mathrm{BS}}_{k^{*}}$	−5.958	−5.141	−3.812	−0.074	257.901	164.620	−17.435	−1015.696
	${\mathrm{MS}}_{k^{*}}$	0.812	0.865	1.141	2.350	2.510	3.508	6.069	38.488
100	${\mathrm{AV}}_{k^{*}}$	1.081	1.151	1.226	1.406	0.659	0.725	0.837	1.393
	${\mathrm{BS}}_{k^{*}}$	−42.852	−39.123	−35.150	−25.559	163.240	142.046	106.259	−71.952
	${\mathrm{MS}}_{k^{*}}$	1.132	1.117	1.118	1.590	2.705	2.945	3.720	9.341

and

Table A8. VaR estimates (expressed as a multiplier of ${10}^4$), relative biases and relative RMSEs for $k^{*}=3,\delta =0.99$, when true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$. Values in bold indicate the smallest $M{S}_{k^{*}}$ among all the estimators.

n		Likelihood Based	Divergence Based			Likelihood Based	Divergence Based
			$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$		$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$
		True model: $FS(1.43,834.95)$				True model: $LN(1.19,6.81)$
		True $Q_1\left(0.99\right)=2.076$				True $Q_4\left(0.99\right)=0.770$
50	${\mathrm{AV}}_{k^{*}}$	0.713	0.730	0.753	0.801	0.332	0.367	0.410	0.498
	${\mathrm{BS}}_{k^{*}}$	−8.976	−8.868	−8.717	−8.399	−48.002	−44.178	−39.463	−29.769
	${\mathrm{MS}}_{k^{*}}$	1.402	1.398	1.401	1.439	1.789	1.742	1.748	1.893
100	${\mathrm{AV}}_{k^{*}}$	0.633	0.626	0.624	0.643	0.330	0.357	0.393	0.461
	${\mathrm{BS}}_{k^{*}}$	−23.890	−23.996	−24.034	−23.722	−25.090	−23.505	−21.499	−17.606
	${\mathrm{MS}}_{k^{*}}$	2.240	2.248	2.253	2.280	2.601	2.526	2.462	2.548
		True model: $FR(1.05,518.75)$				True model: $PL(1.27,1117.04)$
		True $Q_2\left(0.99\right)=4.146$				True $Q_5\left(0.99\right)=1.900$
50	${\mathrm{AV}}_{k^{*}}$	0.906	0.838	0.797	0.747	0.718	0.752	0.788	0.901
	${\mathrm{BS}}_{k^{*}}$	−7.195	−7.347	−7.438	−7.548	−6.693	−6.498	−6.297	−5.659
	${\mathrm{MS}}_{k^{*}}$	1.012	1.023	1.033	1.046	1.074	1.075	1.077	1.286
100	${\mathrm{AV}}_{k^{*}}$	0.853	0.802	0.761	0.712	0.677	0.688	0.702	0.743
	${\mathrm{BS}}_{k^{*}}$	−18.388	−18.671	−18.898	−19.172	−12.012	−11.896	−11.765	−11.364
	${\mathrm{MS}}_{k^{*}}$	1.823	1.849	1.870	1.897	1.749	1.740	1.728	1.730
		True model: $LM(2.04,2202.85)$				True model: $WE(0.79,1690.57)$
		True $Q_3\left(0.99\right)=1.885$				True $Q_6\left(0.99\right)=1.168$
50	${\mathrm{AV}}_{k^{*}}$	0.849	0.927	1.045	1.367	0.777	0.975	1.283	6.694
	${\mathrm{BS}}_{k^{*}}$	−8.074	−7.466	−6.544	−4.039	247.431	121.999	−72.393	−3494.306
	${\mathrm{MS}}_{k^{*}}$	0.844	0.829	0.871	1.297	2.163	3.124	5.933	468.866
100	${\mathrm{AV}}_{k^{*}}$	0.824	0.891	0.956	1.111	0.718	0.842	1.017	1.587
	${\mathrm{BS}}_{k^{*}}$	−56.578	−52.988	−49.546	−41.279	144.572	104.563	48.518	−134.183
	${\mathrm{MS}}_{k^{*}}$	1.325	1.264	1.219	1.255	2.545	2.450	2.947	7.726

, we present the average estimates, the relative biases, and relative RMSEs relative to the MLEs under the true model for ${\widehat{Q}}^{*}\left(\delta \right)$ and ${\tilde{Q}}^{*}\left(\delta \right)$ with $k^{*}=2$ and 3, respectively. To evaluate the performance of the proposed model ranking approach in identifying the true model, in

Table A9. Proportion of inclusion of true model as per order of preference for the VaR estimates reported in Table A7 for sample sizes 50 and 100 when the true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$.

n	Estimator	$\mathit{\alpha }$	Order of Preference			Order of Preference
			0 $\mathit{\tau }$	1	2	0 $\mathit{\tau }$	1	2
			True model: $FS(1.43,834.95)$			True model: $LN(1.19,6.81)$
50	Likelihood		0.391	0.281	0.328	0.240	0.601	0.159
	Divergence	0.05	0.362	0.284	0.354	0.236	0.586	0.178
		0.10	0.357	0.287	0.356	0.236	0.577	0.187
		0.20	0.360	0.273	0.367	0.243	0.547	0.210
100	Likelihood		0.231	0.408	0.361	0.152	0.730	0.118
	Divergence	0.05	0.208	0.405	0.387	0.161	0.710	0.129
		0.10	0.185	0.394	0.421	0.168	0.693	0.139
		0.20	0.193	0.358	0.449	0.175	0.655	0.170
			True model: $FR(1.05,518.75)$			True model: $PL(1.27,1117.04)$
50	Likelihood		0.065	0.887	0.048	0.446	0.210	0.344
		0.05	0.062	0.892	0.046	0.434	0.220	0.346
	Divergence	0.10	0.058	0.895	0.047	0.437	0.225	0.338
	Likelihood	0.20	0.063	0.882	0.055	0.470	0.221	0.309
			0.013	0.961	0.026	0.236	0.320	0.444
100	Divergence	0.05	0.013	0.964	0.023	0.239	0.340	0.421
		0.10	0.013	0.966	0.021	0.251	0.355	0.394
		0.20	0.021	0.961	0.018	0.289	0.350	0.361
			True model: $LM(2.04,2202.85)$			True model: $WE(0.79,1690.57)$
50	Likelihood		0.322	0.341	0.337	0.101	0.796	0.103
	Divergence	0.05	0.351	0.337	0.312	0.122	0.773	0.105
		0.10	0.388	0.307	0.305	0.147	0.742	0.111
		0.20	0.451	0.270	0.279	0.206	0.679	0.115
100	Likelihood		0.210	0.514	0.276	0.034	0.854	0.112
	Divergence	0.05	0.237	0.511	0.252	0.043	0.839	0.118
		0.10	0.270	0.497	0.233	0.060	0.827	0.113
		0.20	0.339	0.436	0.225	0.080	0.805	0.115

^$\tau$ non-inclusion of the VaR estimate of the true model.

and

Table A10. Proportion of inclusion of true model as per order of preference for the VaR estimates reported in Table A8 for sample sizes 50 and 100 when the true models are $FS(1.43,834.95)$, $FR(1.05,518.75)$, $LM(2.04,2202.85)$, $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$.

n	Estimator	$\mathit{\alpha }$	Order of Preference				Order of Preference
			0 $\mathit{\tau }$	1	2	3	0 $\mathit{\tau }$	1	2	3
			True model: $FS(1.43,834.95)$				True model: $LN(1.19,6.81)$
50	Likelihood		0.172	0.281	0.328	0.219	0.096	0.601	0.159	0.144
	Divergence	0.05	0.131	0.284	0.354	0.231	0.088	0.586	0.178	0.148
		0.10	0.108	0.287	0.356	0.249	0.089	0.577	0.187	0.147
		0.20	0.094	0.273	0.367	0.266	0.090	0.547	0.210	0.153
100	Likelihood		0.064	0.408	0.361	0.167	0.035	0.730	0.118	0.117
	Divergence	0.05	0.046	0.405	0.387	0.162	0.036	0.710	0.129	0.125
		0.10	0.040	0.394	0.421	0.145	0.030	0.693	0.139	0.138
		0.20	0.036	0.358	0.449	0.157	0.028	0.655	0.170	0.147
			True model: $FR(1.05,518.75)$				True model: $PL(1.27,1117.04)$
50	Likelihood		0.042	0.887	0.048	0.023	0.125	0.210	0.344	0.321
	Divergence	0.05	0.038	0.892	0.046	0.024	0.122	0.220	0.346	0.312
		0.10	0.033	0.895	0.047	0.025	0.129	0.225	0.338	0.308
		0.20	0.033	0.882	0.055	0.030	0.148	0.221	0.309	0.322
	Likelihood		0.008	0.961	0.026	0.005	0.034	0.320	0.444	0.202
100	Divergence	0.05	0.006	0.964	0.023	0.007	0.034	0.340	0.421	0.205
		0.10	0.005	0.966	0.021	0.008	0.035	0.355	0.394	0.216
		0.20	0.007	0.961	0.018	0.014	0.046	0.350	0.361	0.243
			True model: $LM(2.04,2202.85)$				True model: $WE(0.79,1690.57)$
50	Likelihood		0.204	0.341	0.337	0.118	0.070	0.796	0.103	0.031
	Divergence	0.05	0.234	0.337	0.312	0.117	0.090	0.773	0.105	0.032
		0.10	0.268	0.307	0.305	0.120	0.119	0.742	0.111	0.028
		0.20	0.329	0.270	0.279	0.122	0.174	0.679	0.115	0.032
100	Likelihood		0.102	0.514	0.276	0.108	0.022	0.854	0.112	0.012
	Divergence	0.05	0.126	0.511	0.252	0.111	0.030	0.839	0.118	0.013
		0.10	0.152	0.497	0.233	0.118	0.039	0.827	0.113	0.021
		0.20	0.210	0.436	0.225	0.129	0.067	0.805	0.115	0.013

^$\tau$ non-inclusion of the VaR estimate of the true model.

, we present the proportion of times the true model is ranked within the top $k^{*}$ (denoted by order of preference $=1,2$ for $k^{*}=2$; and order of preference $=1,2,3$ for $k^{*}=3$) and the proportion of times the true model is not ranked as top $k^{*}$ (denoted by order of preference = 0). In other words, the order of preference 0 indicates the case when the true model is not used for computing the weighted average VaR estimate.

The results in Table A7, Table A8, Table A9 and Table A10 indicate that, as expected, estimation procedures without knowledge of the true model generally perform worse than MLEs under the true model. Among the model selection ($k^{*}=1$) and model ranking approaches ($k^{*}=2$ and $k^{*}=3$), the relative MSEs are smaller for $k^{*}=2$ compared to $k^{*}=1$ or $k^{*}=3$ for most models considered, except that of the Weibull distribution. The value of $k^{*}$ is subjective and is determined by the degree of confidence in the performance of the estimator under study. Specifically, when the level of uncertainty in the quantity to be estimated is high, larger values of $k^{*}$ are more appropriate, and vice versa.

Although these estimators do not perform as well as those using the true model, model averaging offers better credibility since an incorrect model would be highly inconsistent. Additionally, Table A9 and Table A10 show that the proposed model selection and ranking techniques may not have high discriminating power for all models. For example, models like Fisk, Lomax, and paralogistic have proportions of the true model used for VaR calculation via the model ranking method of less than 0.5, likely due to the similarity of the candidate distributions, as discussed in Section 3.

5.2. Performance of the Proposed Methods in the Presence of Contamination

In non-life insurance claims, it is common to encounter some exceptionally high-magnitude observations. Although these occurrences are infrequent, yet, they can significantly distort model fitting and model selection if the criteria used are not robust. Literature suggests that the density power divergence method is a robust estimation criterion (see, for example, Basu et al. 1998, 2013; Jones et al. 2001, and the articles cited therein). When analyzing and fitting probability models to contaminated datasets, two key questions often arise. The first is how to identify and estimate the effect of contamination or outliers, especially if they are of significant importance. The second is how to design an estimator that is minimally affected by outliers, allowing the true characteristics of the data, free from contamination, to be accurately studied. In practical applications, contamination models can be treated as a convex mixture of two distributions (Brownie et al. 1983; Punzo and Tortora 2021).

In this subsection, we evaluate the performance of the model selection and model ranking approaches under contamination models. We generate contaminated data under a fixed contamination model, where a fixed proportion $ϵ$ of the sample is obtained from the contamination model, and the remaining observations in the sample come from the original model of interest. Here, the observed random sample from the original model $f_{\mathit{\theta }}$ is denoted as ${\underset{\sim }{\mathit{x}}}^{\left(o\right)}$, and the observed random sample from the contamination model $f_{{\mathit{\theta }}^{\left(c\right)}}$ is respectively denoted as ${\underset{\sim }{\mathit{x}}}^{\left(c\right)}$. The following algorithm is used to generate a contaminated sample of size n for a given $ϵ$:

• Generate ${\underset{\sim }{\mathit{x}}}^{\left(c\right)}$ $=(x_1,x_2,\dots ,x_{[n·ϵ]}$) from $f_{{\mathit{\theta }}^{\left(c\right)}}$, where $[n·ϵ]$ is integer value of $(n·ϵ)$;
• Generate ${\underset{\sim }{\mathit{x}}}^{\left(o\right)}$ $=(x_{[n·ϵ]+1},x_{[n·ϵ]+2},\dots ,x_{n-[n·ϵ]}$) from $f_{\mathit{\theta }}$;
• Return the sample $\underset{\sim }{\mathit{x}}=({\underset{\sim }{\mathit{x}}}^{\left(o\right)},{\underset{\sim }{\mathit{x}}}^{\left(c\right)})$.

For the probability distributions $f_{\mathit{\theta }}$ and $f_{{\mathit{\theta }}^{\left(c\right)}}$, we consider the six probability distributions described in Section 2, where $f_{{\mathit{\theta }}^{\left(c\right)}}$ has the same probability law as $f_{\mathit{\theta }}$, but with different values of scale parameters. The values of parameters of the contamination models were chosen to yield significantly high values of claim sizes, which would mostly appear as outliers for the original model (Wellmann and Gather 1999).

The performances of the proposed methods are evaluated in terms of their relative biases and relative RMSEs in connection with the biases and RMSEs of the MLEs of VaR values obtained based on the correctly specified model in the presence of contamination. An intuitive justification for comparing the proposed methods to the MLEs in the presence of contamination is that divergence-based measures are known to be robust. Therefore, it is reasonable to believe that one or more deviant observations should not significantly affect the divergence-based estimator’s general behavior for the characteristic of interest, which is the estimate of VaR of the original model.

As discussed in the contamination-free case in Section 5.1, before evaluating the performance of the proposed model selection and model ranking approaches, we examine the performance of the MLE and MDPD estimation methods for VaR under model misspecification and contamination without employing model selection.

Table A18. True VaR and the simulated average VaR estimates with associated biases and RMSEs (relative biases and relative RMSEs of divergence estimators) for $\delta =0.99$, in the presence of $ϵ=0.1$ contamination, for true models $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$, contaminated by $LN(1.19,18.54)$, $PL(1.27,89363.2)$ and $WE(0.79,84528.5)$ respectively.

n	Estimator	$\mathit{\alpha }$	Statistics (a)	True Model
				${\mathit{f}}_{\mathit{\theta }}$: $\mathit{LN}(1.19,6.81)$	$\mathit{PL}(1.27,1117.04)$	$\mathit{WE}(0.79,1690.57)$
				${\mathit{f}}_{{\mathit{\theta }}^{\left(\mathit{c}\right)}}$: $\mathit{LN}(1.19,18.54)$	$\mathit{PL}(1.27,89363.2)$	$\mathit{WE}(0.79,84528.5)$
			${\mathit{Q}}_{{\mathit{\theta }}_{\mathit{j}}}\left(\mathit{\delta }\right)$	0.770	1.900	1.168
50			${\mathrm{AV}}_L$	1.53 $\times {10}^3$	481.674	8.504
	Likelihood		${\mathrm{BS}}_L^T$	1526.004	481.659	7.335
			${\mathrm{MS}}_L^T$	1673.085	531.072	8.340
	Divergence	0.05	${\mathrm{AV}}_D$	45.113	15.815	6.378
			${\mathrm{BS}}_D$	0.029	0.033	0.710
			${\mathrm{MS}}_D$	0.028	0.034	0.702
		0.10	${\mathrm{AV}}_D$	1.027	1.968	4.317
			${\mathrm{BS}}_D$	1.69 $\times {10}^4$	0.004	0.429
			${\mathrm{MS}}_D$	3.18 $\times {10}^4$	0.005	0.430
		0.20	${\mathrm{AV}}_D$	0.976	1.063	1.907
			${\mathrm{BS}}_D$	1.35 $\times {10}^4$	0.002	0.101
			${\mathrm{MS}}_D$	2.50 $\times {10}^4$	0.002	0.147
100			${\mathrm{AV}}_L$	8.345	13.409	8.345
	Likelihood		${\mathrm{BS}}_L^T$	1490.96	11.508	7.177
			${\mathrm{MS}}_L^T$	1560.373	12.553	7.682
	Divergence	0.05	${\mathrm{AV}}_D$	6.204	9.732	6.204
			${\mathrm{BS}}_D$	0.702	0.681	0.702
			${\mathrm{MS}}_D$	0.697	0.692	0.697
		0.10	${\mathrm{AV}}_D$	4.167	7.189	4.167
			${\mathrm{BS}}_D$	0.418	0.460	0.418
			${\mathrm{MS}}_D$	0.418	0.487	0.418
		0.20	${\mathrm{AV}}_D$	1.843	4.555	1.843
			${\mathrm{BS}}_D$	0.094	0.231	0.094
			${\mathrm{MS}}_D$	0.115	0.284	0.115

^(a) expressed as a multiplier of ${10}^4$.

presents the average VaR estimates along with their associated biases and RMSEs for the MLEs, and the relative biases and relative RMSEs for the MDPD estimates for some selected models. The table highlights the significant deviations of the VaR estimates from those obtained from the correctly specified model. Additionally, the biases and RMSEs of the MLEs for VaR are notably higher in the presence of contamination compared to the scenario without contamination.

We then evaluate the performance of the MLE and MDPD estimation methods for VaR under model misspecification with data contamination. Specifically, for the case with 10% contamination (i.e., $ϵ=0.1$),

Table A19. Simulated average VaR estimates (expressed as a multiplier of ${10}^4$) for $\delta =0.99$, relative bias and relative RMSE when a non-model selection approach is adopted for the true model $LN(1.19,6.81)$ with $ϵ=0.1$ contamination from $LN(1.19,18.54)$. Values in bold indicate the results obtained under the true model.

True Model	n	Method	$\mathit{\alpha }$		Assumed Model
					$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$X^{\left(\mathit{c}\right)}\sim LN(1.19,18.54)$	50	Likelihood based		${\mathrm{AV}}_L$	109.971	363.687	4.25 $\times {10}^3$	$1.53\times {10}^3$	481.674	7.29 $\times {10}^3$
				${\mathrm{BS}}_L$	0.072	0.238	2.787	1.000	0.315	4.779
				${\mathrm{MS}}_L$	0.071	0.263	2.875	1.000	0.317	4.958
		Divergence based	0.05	${\mathrm{AV}}_D$	5.804	52.335	188.278	45.113	15.815	1.09 $\times {10}^3$
				${\mathrm{BS}}_D$	0.003	0.034	0.123	0.029	0.010	0.712
				${\mathrm{MS}}_D$	0.004	0.045	0.130	0.028	0.011	0.692
			0.10	${\mathrm{AV}}_D$	1.882	24.361	10.285	1.027	1.968	0.460
				${\mathrm{BS}}_D$	0.001	0.015	0.006	$\mathbf{1.69}\times {\mathbf{10}}^{\mathbf{4}}$	0.001	−2.03$\times {10}^4$
				${\mathrm{MS}}_D$	0.001	0.024	0.008	$\mathbf{3.18}\times {\mathbf{10}}^{\mathbf{4}}$	0.001	2.06 $\times {10}^4$
			0.20	${\mathrm{AV}}_D$	1.399	21.003	0.886	0.976	1.063	0.401
				${\mathrm{BS}}_D$	4.12 $\times {10}^4$	0.013	7.63 $\times {10}^5$	$\mathbf{1.35}\times {\mathbf{10}}^{\mathbf{4}}$	1.93 $\times {10}^4$	−2.41 $\times {10}^4$
				${\mathrm{BS}}_D$	5.71 $\times {10}^4$	0.023	4.99 $\times {10}^4$	$\mathbf{2.50}\times {\mathbf{10}}^{\mathbf{4}}$	4.16 $\times {10}^4$	2.33 $\times {10}^4$
$X^{\left(0\right)}\sim LN(1.9,6.81)$	100	Likelihood based		${\mathrm{AV}}_L$	108.003	344.371	4.08 $\times {10}^3$	$\mathbf{1.49}\times {\mathbf{10}}^{\mathbf{3}}$	467.613	7.08 $\times {10}^3$
				${\mathrm{BS}}_L$	0.072	0.230	2.735	1.000	0.313	4.748
				${\mathrm{MS}}_L$	0.071	0.242	2.764	1.000	0.313	4.842
		Divergence based	0.05	${\mathrm{AV}}_D$	5.594	46.778	178.362	44.869	15.068	1.07 $\times {10}^3$
				${\mathrm{BS}}_D$	0.003	0.031	0.119	0.030	0.010	0.719
				${\mathrm{MS}}_D$	0.003	0.037	0.122	0.029	0.010	0.710
			0.10	${\mathrm{AV}}_D$	1.803	20.469	9.157	0.942	1.816	0.460
				${\mathrm{BS}}_D$	0.001	0.013	0.006	$\mathbf{1.15}\times {\mathbf{10}}^{\mathbf{4}}$	0.001	−2.08 $\times {10}^4$
				${\mathrm{MS}}_D$	0.001	0.017	0.006	$\mathbf{2.07}\times {\mathbf{10}}^{\mathbf{4}}$	0.001	2.09 $\times {10}^4$
			0.20	${\mathrm{AV}}_D$	1.346	16.691	0.772	0.913	1.003	0.400
				${\mathrm{BS}}_D$	3.87 $\times {10}^4$	0.011	1.34 $\times {10}^6$	$\mathbf{9.61}\times {\mathbf{10}}^{\mathbf{5}}$	1.57 $\times {10}^4$	−2.48 $\times {10}^4$
				${\mathrm{MS}}_D$	4.80 $\times {10}^4$	0.016	2.50 $\times {10}^4$	$\mathbf{1.77}\times {\mathbf{10}}^{\mathbf{4}}$	2.92 $\times {10}^4$	2.43 $\times {10}^4$

,

Table A20. Simulated average VaR estimates for $\delta =0.99$ (expressed as a multiplier of ${10}^4$), relative bias and relative RMSE when the non-model selection approach is adopted for the true model $PL(1.27,1117.04)$ with $ϵ=0.1$ contamination from $PL(1.27,89363.2)$. Values in bold indicate the results obtained under the true model.

True Model	n	Method	$\mathit{\alpha }$		Assumed Model
					$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$X^{\left(o\right)}\sim PL(1.27,1117.04);$    $X^{\left(c\right)}\sim PL(1.27,89363.2)$	50	Likelihood based		${\mathrm{AV}}_L$	109.971	363.687	4.25 $\times {10}^3$	1.53 $\times {10}^3$	481.674	7.29 $\times {10}^3$
				${\mathrm{BS}}_L$	0.228	0.755	8.831	3.170	1.000	15.141
				${\mathrm{MS}}_L$	0.223	0.830	9.058	3.152	1.000	15.620
		Divergence based	0.05	${\mathrm{AV}}_D$	5.804	52.335	188.278	45.113	15.815	1.09 $\times {10}^3$
				${\mathrm{BS}}_D$	0.012	0.109	0.391	0.094	0.033	2.256
				${\mathrm{MS}}_D$	0.012	0.144	0.410	0.089	0.034	2.181
			0.10	${\mathrm{AV}}_D$	1.882	24.361	10.285	1.027	1.968	0.460
				${\mathrm{BS}}_D$	0.004	0.051	0.021	0.002	0.004	0.001
				${\mathrm{MS}}_D$	0.004	0.075	0.026	0.002	0.005	0.001
			0.20	${\mathrm{AV}}_D$	1.399	21.003	0.886	0.976	1.063	0.401
				${\mathrm{BS}}_D$	0.003	0.044	0.002	0.002	0.002	0.001
				${\mathrm{MS}}_D$	0.003	0.074	0.002	0.002	0.002	0.001
	100	Likelihood based		${\mathrm{AV}}_L$	10.483	1013.921	26.310	10.283	13.409	11.893
				${\mathrm{BS}}_L$	0.746	87.937	2.121	0.728	1.000	0.868
				${\mathrm{MS}}_L$	0.736	2116.957	2.170	0.721	1.000	1.381
		Divergence based	0.05	${\mathrm{AV}}_D$	8.003	168.714	20.783	7.536	9.732	7.351
				${\mathrm{BS}}_D$	0.530	14.495	1.641	0.490	0.681	0.474
				${\mathrm{MS}}_D$	0.534	26.828	1.681	0.483	0.692	0.472
			0.10	${\mathrm{AV}}_D$	6.406	173.302	15.590	5.641	7.189	4.092
				${\mathrm{BS}}_D$	0.391	14.894	1.190	0.325	0.460	0.190
				${\mathrm{MS}}_D$	0.408	28.656	1.243	0.331	0.487	0.198
			0.20	${\mathrm{AV}}_D$	4.829	188.798	8.307	3.700	4.555	1.070
				${\mathrm{BS}}_D$	0.254	16.240	0.557	0.156	0.231	−0.072
				${\mathrm{MS}}_D$	0.288	41.126	0.649	0.190	0.284	0.074

and

Table A21. Simulated average estimate of VaR for $\delta =0.99$ (expressed as a multiplier of ${10}^4$), relative bias and relative RMSE when non-model selection approach is adopted for true model $WE(0.79,1690.57)$ with $ϵ=0.1$ contamination from $WE(0.79,84528.5)$. Values in bold indicate the results obtained under the true model.

True Model	n	Method	$\mathit{\alpha }$		Assumed Model
					$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$
$X^{\left(o\right)}\sim WE(0.79,1690.57)$;    $X^{\left(c\right)}\sim WE(0.79,84528.5)$	50	Likelihood based		${\mathrm{AV}}_L$	17.677	1.25 $\times {10}^5$	23.804	13.476	20.715	8.504
				${\mathrm{BS}}_L$	2.251	1.70 $\times {10}^4$	3.086	1.678	2.665	1.000
				${\mathrm{MS}}_L$	2.311	4.45 $\times {10}^5$	3.599	1.789	2.939	1.000
		Divergence based	0.05	${\mathrm{AV}}_D$	17.644	2.29 $\times {10}^4$	23.628	13.174	21.365	6.378
				${\mathrm{BS}}_D$	2.246	3.13 $\times {10}^3$	3.062	1.637	2.753	0.710
				${\mathrm{MS}}_D$	2.429	2.42 $\times {10}^4$	4.025	2.080	3.400	0.702
			0.10	${\mathrm{AV}}_D$	18.283	1.46 $\times {10}^5$	24.429	14.238	23.759	4.317
				${\mathrm{BS}}_D$	2.333	1.98 $\times {10}^4$	3.171	1.782	3.080	0.429
				${\mathrm{MS}}_D$	2.837	2.64 $\times {10}^5$	5.279	4.899	5.161	0.430
			0.20	${\mathrm{AV}}_D$	30.019	5.19 $\times {10}^{15}$	56.731	407.538	2.43 $\times {10}^3$	1.907
				${\mathrm{BS}}_D$	3.933	7.07 $\times {10}^{14}$	7.575	55.398	330.565	0.101
				${\mathrm{MS}}_D$	35.030	1.97 $\times {10}^{16}$	48.841	1.48 $\times {10}^3$	9.06 $\times {10}^3$	0.147
	100	Likelihood based		${\mathrm{AV}}_L$	16.531	4.81 $\times {10}^4$	21.058	12.792	18.592	8.345
				${\mathrm{BS}}_L$	2.141	6.70 $\times {10}^3$	2.771	1.620	2.428	1.000
				${\mathrm{MS}}_L$	2.144	1.57 $\times {10}^5$	2.971	1.626	2.504	1.000
		Divergence based	0.05	${\mathrm{AV}}_D$	16.194	4.86 $\times {10}^3$	19.856	12.083	18.256	6.204
				${\mathrm{BS}}_D$	2.094	677.407	2.604	1.521	2.381	0.702
				${\mathrm{MS}}_D$	2.136	2.93 $\times {10}^3$	2.870	1.555	2.533	0.697
			0.10	${\mathrm{AV}}_D$	16.267	8.81 $\times {10}^3$	18.594	11.776	18.501	4.167
				${\mathrm{BS}}_D$	2.104	1.23 $\times {10}^3$	2.428	1.478	2.415	0.418
				${\mathrm{MS}}_D$	2.207	5.44 $\times {10}^3$	2.835	1.567	2.720	0.418
			0.20	${\mathrm{AV}}_D$	17.708	6.54 $\times {10}^4$	18.254	12.589	21.715	1.843
				${\mathrm{BS}}_D$	2.305	9.11 $\times {10}^3$	2.381	1.591	2.863	0.094
				${\mathrm{MS}}_D$	2.631	7.40 $\times {10}^4$	3.738	1.938	4.027	0.115

present the average VaR estimates along with their associated relative biases and relative RMSEs. These metrics are compared to the bias and MSE of the MLEs under the correctly specified model. The results in these tables indicate that the MDPD estimator for VaR outperforms the MLE in terms of reduced relative risks, particularly for values of the tuning parameter that are away from 0. Additionally, the findings highlight that using a non-model selection approach can lead to misleading VaR estimates when the model is misspecified.

Table A22. VaR estimates (expressed as a multiplier of ${10}^4$), relative biases and relative RMSEs for $k^{*}=1,\delta =0.99$, when true models are $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$; contaminated with $ϵ=0.1$ from $LN(1.19,18.54)$, $PL(1.27,89363.2)$ and $WE(0.79,84528.5)$ respectively. Values in bold indicate the smallest $M{S}_S$ among all the estimators.

True Model	n		Likelihood Based	Divergence Based
				$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$
$LN$	50	${\mathrm{AV}}_s$	1.91 $\times {10}^3$	26.404	7.359	1.775
		${\mathrm{BS}}_s$	1.249	0.017	0.004	0.001
		${\mathrm{MS}}_s$	1.977	0.032	0.009	0.003
	100	${\mathrm{AV}}_s$	1.92 $\times {10}^3$	23.821	7.191	1.415
		${\mathrm{BS}}_s$	1.289	0.015	0.004	4.33 $\times {10}^4$
		${\mathrm{MS}}_s$	1.919	0.027	0.008	0.002
$PL$	50	${\mathrm{AV}}_s$	1.91 $\times {10}^3$	26.404	7.359	1.775
		${\mathrm{BS}}_s$	3.96	0.055	0.015	0.004
		${\mathrm{MS}}_s$	6.229	0.103	0.030	0.009
	100	${\mathrm{AV}}_s$	18.307	15.576	12.506	8.123
		${\mathrm{BS}}_s$	1.426	1.188	0.922	0.541
		${\mathrm{MS}}_s$	2.357	2.228	2.079	1.745
$WE$	50	${\mathrm{AV}}_s$	11.977	11.996	12.041	11.941
		${\mathrm{BS}}_s$	1.473	1.476	1.482	1.469
		${\mathrm{MS}}_s$	2.570	2.806	3.114	5.429
	100	${\mathrm{AV}}_s$	10.185	9.525	8.938	7.737
		${\mathrm{BS}}_s$	1.256	1.164	1.083	0.915
		${\mathrm{MS}}_s$	1.999	1.888	1.834	1.703

,

Table A23. VaR estimates (expressed as a multiplier of ${10}^4$), relative biases and relative RMSEs for $k^{*}=2,\delta =0.99$, $ϵ=0.1$, when true models are $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$; contaminated with $ϵ=0.1$ from $LN(1.19,18.54)$, $PL(1.27,89363.2)$ and $WE(0.79,84528.5)$ respectively. Values in bold indicate the smallest $M{S}_{k^{*}}$ among all the estimators.

True Model	n		Likelihood Based	Divergence Based
				$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$
$LN$	50	${\mathrm{AV}}_{k^{*}}$	1.15 $\times {10}^3$	59.950	5.073	1.543
		${\mathrm{BS}}_{k^{*}}$	0.755	0.039	0.003	0.001
		${\mathrm{MS}}_{k^{*}}$	0.778	0.042	0.004	0.002
	100	${\mathrm{AV}}_{k^{*}}$	1.10 $\times {10}^3$	56.131	4.692	1.287
		${\mathrm{BS}}_{k^{*}}$	0.740	0.037	0.003	0.000
		${\mathrm{MS}}_{k^{*}}$	0.747	0.038	0.003	0.001
$PL$	50	${\mathrm{AV}}_{k^{*}}$	1.15 $\times {10}^3$	59.950	5.073	1.543
		${\mathrm{BS}}_{k^{*}}$	2.392	0.124	0.011	0.003
		${\mathrm{MS}}_{k^{*}}$	2.451	0.132	0.015	0.006
	100	${\mathrm{AV}}_{k^{*}}$	15.089	12.249	9.136	5.813
		${\mathrm{BS}}_{k^{*}}$	1.146	0.899	0.629	0.340
		${\mathrm{MS}}_{k^{*}}$	1.312	1.150	0.929	0.686
$WE$	50	${\mathrm{AV}}_{k^{*}}$	11.439	11.600	12.220	18.288
		${\mathrm{BS}}_{k^{*}}$	1.400	1.422	1.507	2.334
		${\mathrm{MS}}_{k^{*}}$	1.621	1.780	2.209	11.184
	100	${\mathrm{AV}}_{k^{*}}$	9.718	9.297	9.037	9.442
		${\mathrm{BS}}_{k^{*}}$	1.191	1.133	1.097	1.153
		${\mathrm{MS}}_{k^{*}}$	1.250	1.203	1.230	1.852

and

Table A24. VaR estimates (expressed as a multiplier of ${10}^4$), relative biases and relative RMSEs for $k^{*}=3,\delta =0.99$, when true models are $LN(1.19,6.81)$, $PL(1.27,1117.04)$ and $WE(0.79,1690.57)$; contaminated with $ϵ=0.1$ from $LN(1.19,18.54)$, $PL(1.27,89363.2)$ and $WE(0.79,84528.5)$ respectively. Values in bold indicate the smallest $M{S}_{k^{*}}$ among all the estimators.

True Model	n		Likelihood Based	Divergence Based
				$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.10$	$\mathit{\alpha }=0.20$
$LN$	50	${\mathrm{AV}}_{k^{*}}$	561.130	28.389	2.830	0.879
		${\mathrm{BS}}_{k^{*}}$	0.367	0.018	0.001	7.18 $\times {10}^5$
		${\mathrm{MS}}_{k^{*}}$	0.378	0.020	0.002	$7.18\times {10}^4$
	100	${\mathrm{AV}}_{k^{*}}$	538.197	26.619	2.629	0.758
		${\mathrm{BS}}_{k^{*}}$	0.360	0.017	0.001	−7.91 $\times {10}^6$
		${\mathrm{MS}}_{k^{*}}$	0.364	0.018	0.002	$\mathbf{4.74}\times {\mathbf{10}}^{\mathbf{4}}$
$PL$	50	${\mathrm{AV}}_{k^{*}}$	561.130	28.389	2.830	0.879
		${\mathrm{BS}}_{k^{*}}$	1.165	0.059	0.006	0.002
		${\mathrm{MS}}_{k^{*}}$	1.191	0.063	0.008	0.003
	100	${\mathrm{AV}}_{k^{*}}$	8.372	6.881	5.517	3.653
		${\mathrm{BS}}_{k^{*}}$	0.562	0.433	0.314	0.152
		${\mathrm{MS}}_{k^{*}}$	0.649	0.545	0.445	0.336
$WE$	50	${\mathrm{AV}}_{k^{*}}$	7.262	7.370	7.567	272.877
		${\mathrm{BS}}_s$	0.831	0.845	0.872	37.041
		${\mathrm{MS}}_{k^{*}}$	0.991	1.098	1.267	994.725
	100	${\mathrm{AV}}_{k^{*}}$	6.234	6.025	5.885	6.195
		${\mathrm{BS}}_s$	0.706	0.677	0.657	0.700
		${\mathrm{MS}}_{k^{*}}$	0.756	0.746	0.765	1.042

present the average VaR estimates using the model selection approach (i.e., model ranking approach with ($k^{*}=1$) and the model ranking approach with ($k^{*}=2$) and ($k^{*}=3$), along with their corresponding relative biases and relative RMSEs, compared to the MLE under the correctly specified model with 10% data contamination. Additionally, the simulation proportions of the true model being included in the final VaR estimate calculation based on the model selection approach and the model ranking approach with ($k^{*}=2$) and ($k^{*}=3$) are shown in Table A19, Table A20 and Table A21. These simulation results demonstrate that the proposed model selection and ranking approaches, particularly those based on the minimized DPD, provide more accurate VaR estimates compared to using a prespecified model when contamination is present in the dataset. Interestingly, there are cases (e.g., when the true model is lognormal or Weibull) where the true model is rarely used in the final VaR estimates. Overall, the model averaging technique based on minimized DPD offers a more accurate procedure for estimating VaR, with significantly better reliability in the presence of contamination, even though the true model may seldom be correctly identified.

To keep this paper concise, we present only some representative simulation results here; additional simulation results are provided in Appendices Appendix B and Appendix D.

6. Practical Data Analyses

In this section, we demonstrate the application of the proposed model selection and ranking approaches for estimating VaR using real claim size data from non-life insurance. Section 6.1 applies the methodology to the dataset introduced earlier in Section 3, which was used to motivate the study and illustrate the behavior of the candidate models. Section 6.2 extends the analysis to a different dataset from the insuranceData package in R (R Core Team 2025), thereby providing an additional example to assess the robustness and practical applicability of the proposed procedures across distinct non-life insurance contexts.

6.1. Vehicle Insurance Data

For the dataCar dataset discussed in Section 3, we estimate the VaR under the six candidate models and apply the model selection and model averaging approaches presented in the previous sections. The VaR estimates based on the model selection (for this dataset, the Fréchet distribution is the selected model) and based on the model ranking approach (with $k^{*}=2$ and 3) for both maximum likelihood and minimum density power divergence methods are reported in Table 2.

From the results in Table 2, it is both interesting and expected to observe significant variations in the VaR estimates, particularly at the 99% level. Given the unknown ground truth of the underlying probability model for vehicle insurance claim amounts, these results suggest that selecting different models can lead to substantially different conclusions. Conversely, the model ranking and averaging approaches moderate these differences, providing a more balanced estimate of VaR. We will further illustrate this point in the following numerical example.

6.2. Partial Casco Motorcycles Insurance Data

The dataset called dataOhlsson comprises partial casco insurance for motorcycles insured and claimed from the Swedish insurance company from 1994 to 1998. We are interested in the non-zero claim amounts in Swedish Krona (SEK) of those partial casco motorcycle insurance claims described in the variable skadkost. The fitted CDFs of the six candidate models for this dataset are plotted in Figure 2, and the corresponding VaR estimates based on the six candidate models are presented in

Table 3. VaR estimates (in ${10}^4$) of all the models for $\delta =0.95,0.99$ along with weighted VaR estimates based on likelihood and divergence method when $k^{*}=2$ and 3, respectively, for the dataOhlsson dataset.

Method	$\mathit{\delta }$	$\mathit{\alpha }$	${\widehat{\mathit{Q}}}_{\mathit{j}}\left(\mathit{\delta }\right)$ or ${\tilde{\mathit{Q}}}_{\mathit{j}}\left(\mathit{\delta }\right)$						${\widehat{\mathit{Q}}}^{*}\left(\mathit{\delta }\right)$ or ${\tilde{\mathit{Q}}}^{*}\left(\mathit{\delta }\right)$
			$\mathit{FS}$	$\mathit{FR}$	$\mathit{LM}$	$\mathit{LN}$	$\mathit{PL}$	$\mathit{WE}$	${\mathit{k}}^{*}=2$	${\mathit{k}}^{*}=3$
Likelihood	0.95		14.81	69.57	10.99	12.83	13.66	9.46	11.15	11.10
	0.99		69.33	1190.63	35.77	38.59	59.02	17.52	28.05	30.62
		Ranks →	5	6	3	1	4	2
Divergence	0.95	0.05	15.76	82.58	12.11	13.53	14.72	9.30	12.82	13.45
		0.10	16.49	95.45	12.59	14.19	15.68	9.12	13.39	14.15
		0.20	17.19	121.24	14.49	15.30	17.16	8.66	14.90	15.65
	0.99	0.05	76.09	1469.99	43.81	41.36	66.67	17.09	42.59	50.61
		0.10	81.45	1774.31	46.87	43.96	73.85	16.65	45.41	54.89
		0.20	86.98	2452.49	61.32	48.42	84.97	15.55	54.86	64.89
		Ranks † →	4	6	2	1	3	5

^† The model ranks are the same for all the values of $\alpha$ used for the divergence-based method.

. In Table 3, we highlight the VaR estimates based on the model selection (here, the lognormal distribution is the selected model) and present the VaR estimates using the model ranking approach (with $k^{*}=2$ and 3) for both maximum likelihood and minimum density power divergence methods.

Once again, we observe significant variations in the VaR estimates, particularly at the 99% level. These variations highlight the risks associated with relying on a single assumed model for VaR estimation, especially when the model is misspecified. For instance, if one considers the distribution of non-zero claim amounts for partial casco motorcycle insurance claims follows a Fréchet distribution, the maximum likelihood method indicates a 99% probability that future claim amounts will not exceed 1.19 billion. In stark contrast, if a Weibull distribution is assumed, the same method suggests a 99% probability that future claim amounts will not exceed 17.52 million, which is approximately 68 times smaller than the Fréchet estimate. This discrepancy highlights the importance of model selection in estimating VaR.

Although these numerical examples cannot prove the superiority of the proposed model selection and ranking approaches due to the unknown ground truth, they demonstrate that these approaches help mitigate the risk of drawing highly inaccurate conclusions resulting from model misspecification.

7. Extension to Candidate Models with Unequal Number of Parameters

In the preceding sections, the candidate probability models (see Section 2) are all two-parameter models, implying equal model complexity. This choice is common in comparative studies, as models with the same number of parameters allow for a fair comparison.

However, in some situations, researchers may consider probability models with different numbers of parameters. In such cases, model complexity must be explicitly accounted for when comparing model fits. In this section, we address the question of whether the model selection and ranking procedure based on either the LF or the DPD measure remains valid and practical when the candidate set contains models with unequal numbers of parameters. Although our earlier development assumed that all candidate models have the same number of unknown parameters, this section demonstrates how the proposed method can be extended to accommodate models with differing parameter counts.

When the likelihood-based estimation method described in Section 3.1 is used for parameter estimation, information-based criteria—such as the Akaike information criterion (AIC), the Bayesian information criterion (BIC), and the deviance information criterion (DIC)—are widely adopted for model selection (see, for example, Burnham and Anderson 2002; Castilla et al. 2020; Karagrigoriou and Mattheou 2009). These criteria incorporate a penalty for the number of model parameters, thereby addressing differences in model complexity. For example, the AIC is given by

$$\begin{array}{c}\hfill AIC=2\kappa -2ln\left(L\left(\widehat{\mathit{\theta }}\right|\mathit{x})\right],\end{array}$$

where $\kappa$ is the number of parameters in the model, $L\left(\widehat{\mathit{\theta }}\right|\mathit{x})$ is the value of maximized likelihood function defined in Equation (19) evaluated at the MLE $\widehat{\mathit{\theta }}$ defined in Equation (20). The AIC balances goodness-of-fit with parsimony by penalizing excessive parameters, favoring models that remain simple yet adequately explain the data. A smaller AIC value reflects a more desirable trade-off between fit and complexity.

When the divergence-based estimation method described in Section 3.2 is employed, the robust divergence-based Bayesian criterion (DBBC) proposed by Kurata and Hamada (2020), denoted $RC{C}_{\alpha }$ can serve as a model selection and ranking tool. It is defined as

$$\begin{array}{c}\hfill RC{C}_{\alpha }=2n{H}_{\alpha }(\mathit{x};\tilde{\mathit{\theta }})+\kappa ln\left(n\right),\forall \alpha \ge 0,\end{array}$$

where $\kappa$ denotes the number of parameters in the model and $H_{\alpha }(\mathit{x};\tilde{\mathit{\theta }})$ is the minimized value of the DPD measure given in Equation (22), evaluated at $\mathit{\theta }=\tilde{\mathit{\theta }}$. Like the AIC, $RC{C}_{\alpha }$ penalizes models with more parameters, and a lower value indicates a better compromise between model fit and complexity.

For illustration, consider a set of four candidate models, where two are generalized versions of the other two and naturally include them as special cases. Specifically, we use the exponentiated Weibull distribution, denoted as $EW({\beta }_7,\nu ,{\lambda }_7)$, (Mudholkar and Srivastava 1993), and the exponentiated Fréchet distribution, denoted as $EF({\beta }_8,\eta ,{\lambda }_8)$, (Nadarajah and Kotz 2003), analyze the vehicle insurance dataset discussed in Section 3 and Section 6.1. The PDFs of $EW({\beta }_7,\nu ,{\lambda }_7)$ and $EF({\beta }_8,\eta ,{\lambda }_8)$ are given by

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_7}\left(x\right)& =& \left\{\begin{array}{cc}\nu {\beta }_7{\lambda }_7{x}^{{\beta }_7-1}{\left[1-e^{-{\lambda }_7{x}^{{\beta }_7}}\right]}^{\nu -1}{e}^{-{\lambda }_7{x}^{{\beta }_7}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill f_{{\mathit{\theta }}_8}\left(x\right)& =& \left\{\begin{array}{cc}\eta {\beta }_8{\lambda }_8^{{\beta }_8}{\left[1-e^{-{\left({\lambda }_8/x\right)}^{{\beta }_8}}\right]}^{\eta -1}{x}^{-(1+{\beta }_8)}{e}^{-{\left({\lambda }_8/x\right)}^{{\beta }_8}},\hfill & \mathrm{for} x>0;\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(33)

where ${\mathit{\theta }}_7=({\beta }_7,\nu ,{\lambda }_7)$ and ${\mathit{\theta }}_8=({\beta }_8,\eta ,{\lambda }_8)$ are the respective parameter vectors; ${\lambda }_7>0$ and ${\lambda }_8>0$ are the scale parameters, while ${\beta }_7,\nu >0$ and ${\beta }_8,\eta >0$ are the shape parameters.

Table 4. Model ranking for four candidate models with two or three parameters based on AIC and $RC{C}_{\alpha }$ for the vehicle insurance dataset.

Models	AIC	${\mathit{RCC}}_{\mathit{\alpha }}$
		$\mathit{\alpha }=0.05$	$\mathit{\alpha }=0.1$	$\mathit{\alpha }=0.2$
$FR$	77,195.22	−122,251	−40,651.3	−9130.11
$EF$	76,956.88	−122,350	−40,750.3	−9208.57
$WE$	78,987.19	−120,976	−39,756.6	−8699.82
$EW$	77,304.19	−122,147	−40,571.3	25.31705

presents the model ranking results based on the AIC and the $RC{C}_{\alpha }$ criteria for $\alpha =0.05,0.1$ and $0.2$. The four candidate models include two basic two-parameter models (the Fréchet (FR) and Weibull (WE) distributions) and their corresponding three-parameter generalizations, the exponentiated Fréchet (EF) and exponentiated Weibull (EW) distributions.

Across both AIC and $RC{C}_{\alpha }$ measures, the EF and EW models consistently outperform their simpler counterparts ($FR$ and $WE$, respectively) for all $\alpha$ values considered here. This improvement can be attributed to the inclusion of an additional shape parameter in the EF and EW distributions, which increases model flexibility and allows a better adaptation to the tail behavior and overall distributional shape of the data.

Importantly, both AIC and $RC{C}_{\alpha }$ incorporate a penalty term for model complexity, ensuring that a model is not favored solely because it has more parameters. The fact that EF and EW achieve lower (better) values for these penalized criteria indicates that the improvement in goodness of fit more than compensates for the increase in parameter count. In other words, the additional shape parameter provides meaningful explanatory power rather than overfitting noise in the data.

These results suggest that, in this application, allowing greater distributional flexibility via an additional shape parameter can lead to a statistically justifiable improvement in model performance, even when penalizing for increased complexity. For explanatory purposes, the VaR estimates at $\delta =0.95$ for the four candidate models are reported in

Table 5. VaR estimates (in 1000) based on likelihood and divergence method for $\delta =0.95$ for the four considered models.

Method	$\mathit{\alpha }$	${\widehat{\mathit{Q}}}_{\mathit{j}}\left(0.95\right)$ or ${\tilde{\mathit{Q}}}_{\mathit{j}}\left(0.95\right)$				${\widehat{\mathit{Q}}}^{*}\left(0.95\right)$ or ${\tilde{\mathit{Q}}}^{*}\left(0.95\right)$
		$\mathit{FR}$	$\mathit{EF}$	$\mathit{WE}$	$\mathit{EW}$	${\mathit{k}}^{*}=2$	${\mathit{k}}^{*}=3$
Likelihood		8.712	19.445	6.830	7.118	14.065	11.745
Divergence	0.05	8.895	15.142	6.364	6.959	12.020	10.334
	0.1	8.943	18.619	5.866	6.944	13.787	11.511
	Ranks †	2	1	4	3
	0.2	8.729	21.478	4.884	0.001	15.134	11.837
	Ranks	2	1	3	4

^† The model ranks are the same for the likelihood method as well as the divergence-based method for $\alpha =0.05$ and $0.10$.

.

It is worth noting that the methodology proposed here can be applied with model-selection criteria beyond AIC and $RC{C}_{\alpha }$. For example, goodness-of-fit measures, such as the Kolmogorov-Smirnov distance and the Anderson-Darling statistic, can be considered.

8. Concluding Remarks

The findings presented in this article provide significant insights into the implications and mitigation strategies for model misspecification in insurance claims data analysis. By exploring various probability models and adopting both likelihood-based and divergence-based estimation methods, this study highlights the importance of accurate model selection and ranking in minimizing the adverse effects of model uncertainty. The numerical examples and simulation studies demonstrate that the proposed model selection and ranking approaches, particularly those based on the divergence measure, offer robust solutions for estimating risk measures such as VaR.

The practical implications of this research are profound, as these methods effectively address inaccuracies arising from model misspecification. These methods provide practicing and academic actuaries with advanced tools to mitigate risks and achieve more reliable outcomes in their risk assessments, even in the presence of model misspecification. Practically, relying on a single, potentially misspecified model can yield large errors and misleading conclusions for VaR. By aggregating across competing models and using robust estimators when appropriate, our approach yields more stable VaR estimates and decisions that are less sensitive to outliers, which are common in insurance claims data.

This, in turn, enhances the reliability of insurance data analysis, ultimately leading to better decision-making in the insurance industry. Future research could expand on these methods to refine the accuracy and applicability of model selection and ranking approaches in various actuarial contexts.

A few limitations of the proposed methodologies should also be acknowledged. Under model uncertainty, the true data-generating process is unknown, and all candidate parametric models are approximations; likelihood-based and divergence-based estimators target pseudo-true parameters, and the resulting risk measures may still be biased if the candidate models are poorly specified. Although aggregating across multiple probability distributions and employing robust estimators such as the MDPD can substantially reduce sensitivity to misspecification and outliers, the performance of the approach ultimately depends on the researcher’s ability to select a reasonably rich and flexible set of candidate models. If these candidates are uniformly inadequate, the resulting estimates may remain unreliable.