A Novel Federated Transfer Learning Framework for Credit Card Fraud Detection Under Heterogeneous Data Conditions

Abstract

The exponential growth of e-commerce and advancements in financial technology have escalated credit card fraud into a major threat, resulting in billions of dollars in global losses annually. This necessitates the development of sophisticated fraud detection systems capable of real-time anomaly interception to safeguard financial activities. While federated learning frameworks have been employed to address data privacy concerns in financial applications, existing approaches often fail to account for the heterogeneity in data distributions across different institutions, such as banks, which hinders collaborative model training. In response, this paper introduces the FED-SPFD model, an innovative federated learning framework designed to detect credit card fraud amidst multi-party heterogeneous data. The model employs a share–private segmentation approach to distinguish shared from private data attributes, facilitating unified feature representation learning. It aligns disparate shared features through local sufficient statistics, thus preventing privacy breaches without directly sharing sample data. Additionally, the integration of a “private autoencoder + standard Gaussian alignment” mechanism stabilizes the training process by ensuring consistent private feature distributions. The efficacy of the FED-SPFD model is demonstrated using a real-world dataset from Kaggle, showcasing significant improvements in recall rate compared to state-of-the-art methodologies. Comprehensive evaluation through ablation studies further validates the framework’s robust contributions to accurate and privacy-preserving fraud detection. Practically, this work offers policymakers a compliant cross-institutional risk collaboration paradigm and provides financial institutions with a privacy-protective solution to enhance fraud detection without data sharing violations.

1. Introduction

In recent decades, with the rise of e-commerce and the rapid development of financial technology, credit card fraud has become one of the greatest threats faced by businesses (Khanh and To 2024). With various transaction scenarios lacking rigorous verification and oversight, credit card fraud has emerged as one of the most pervasive threats to the global financial ecosystem, with losses exceeding USD 32 billion annually worldwide (Wang et al. 2025), and it is expected that global credit card fraud will reach USD 43 billion by 2026 (https://merchantcostconsulting.com/lower-credit-card-processing-fees/credit-card-fraud-statistics/#key-credit-card-fraud-statistics-2025, accessed on 1 September 2025). Although preventive technologies are the best means to reduce fraud, fraudsters exhibit adaptability, continually innovating their fraudulent techniques. This not only incurs significant economic losses but also disrupts the normal order of financial markets. Consequently, the effective detection of credit card fraud has emerged as a research hotspot in the field of financial risk control, necessitating real-time monitoring and rapid responses to promptly intercept abnormal transactions and mitigate the security risks associated with illegal activities (Alarfaj et al. 2022).

Currently, the daily transactions of credit cards have become a massive flow of data, making manual verification for credit card fraud detection evidently impractical (Dastidar et al. 2024). An increasing number of researchers are employing machine learning or deep learning methods to achieve the detection of fraudulent activities related to credit cards. For example, Forough and Momtazi (2021) proposed a federated model based on deep recurrent neural network data sequence modeling and a novel voting mechanism rooted in artificial neural networks for fraud detection. This model employs LSTM and GRU networks as its base classifiers, learning from the outputs of these base classifiers and making final inferences through a feedforward neural network (FFNN) based on the patterns predicted by the learned base classifiers. Similarly, Zhang et al. (2021) introduced a feature engineering framework based on homogeneity-oriented behavior analysis (HOBA) to generate feature variables for fraud detection models, integrating deep learning techniques into the fraud detection system to enhance performance. Additionally, Fanai and Abbasimehr (2023) proposed a two-stage framework that combines deep autoencoders as a representation learning method with supervised deep learning techniques for detecting fraudulent transactions.

However, within these data-driven fraud detection methods, the issue of data imbalance remains an unavoidable challenge. In the vast dataset of credit card transactions, the number of normal transactions (i.e., legitimate transactions) far exceeds that of fraudulent transactions, with studies indicating that this proportion can be as low as 0.5% (Gupta et al. 2023; Mondal et al. 2021; Xie et al. 2025). This discrepancy implies that classification models primarily train on data from normal transactions. In severely imbalanced supervised learning scenarios, the patterns of the minority class are often overwhelmed by the majority class data, which significantly affects classification performance (Khalid et al. 2024), thereby greatly diminishing the efficacy of fraud detection models. Although several papers and studies have proposed specific improvements to mitigate the data imbalance problem in credit card fraud detection, such as Dornadula and Geetha (2019) employing meta-classification and meta-learning approaches to address highly imbalanced data, Varmedja et al. (2019) utilizing the Synthetic Minority Over-sampling Technique (SMOTE) to generate additional minority class samples near observed instances, and Xie et al. (2021) first employing under-sampling based on data distribution, followed by clustering to create balanced data subsets, which achieved results surpassing those of SMOTE, these approaches merely compensate for the manifestations of data imbalance without addressing the root cause of the problem.

To fundamentally address the issue of a scarcity of fraudulent samples, federated learning presents itself as an appropriate choice. The concept of federated learning (FL) was first proposed by Google in 2016 (McMahan et al. 2017). It is essentially a distributed machine learning framework equipped with privacy protection and secure encryption technologies, aimed at enabling decentralized participants to collaboratively train machine learning models while ensuring that they do not disclose private data to other participants. Within this framework, samples from multiple parties can be simultaneously utilized while considering data privacy, thus enlarging the total number of samples related to fraudulent behavior. This allows the model to learn more generalized and comprehensive characteristics of fraud, thereby inherently addressing the data imbalance problem.

Currently, the application of federated learning in credit card fraud detection is an active research area, with numerous scholars proposing mature and effective models, significantly enhancing performance compared to traditional fraud detection models. For instance, Wang et al. (2023) designed a federated credit fraud detection algorithm for balanced data, using salting and perturbation techniques within the learning module. Reddy et al. (2024) proposed a deep learning technique based on hybrid algorithm optimization: they preprocessed data via quantile normalization, selected features using distance measurements, enhanced features with bootstrapping, and applied SpinalNet for fraud detection. Tang and Liang (2024) integrated federated learning (FL) with graph neural networks (GNNs) to deeply explore associations between transaction data. Another work by Tang and Liu (2024) proposed an algorithm combining a Structured Data Transformer (SDT) and FL: they organized credit card data into sequences, added learnable tokens for classification, and deployed the model across banks in a distributed manner. Aljunaid et al. (2025) developed an Explainable FL (XFL) model, which combines SHAP and LIME to balance privacy, accuracy, and interpretability for financial fraud detection. Most recently, Zheng (2025) constructed an improved adaptive data protection architecture by fusing FL and differential privacy and designed a fraud recognition model based on Generative Adversarial Networks (WGAN) to boost convergence performance.

While the issues of data imbalance and data privacy have been addressed in the application of federated learning, there remain challenges in achieving more accurate detection of credit fraud. In the aforementioned studies, whether employing machine learning, deep learning, or the federated learning framework, the problem of data heterogeneity among multiple institutions has not been considered. The issue of data heterogeneity refers to the significant differences in the distribution, scale, and feature space of the datasets held by various institutions participating in federated learning (such as banks and financial institutions), leading to a mismatch in the model parameters of each participating party that hinders cooperative training. Recently, some research (Feng et al. 2022) has utilized methods for expanding overlapping user features to address the problem of heterogeneous features from different parties. However, in the financial sector, different banks are not permitted to share customer identity information freely; thus, direct augmentation of heterogeneous features at the user level is not feasible. 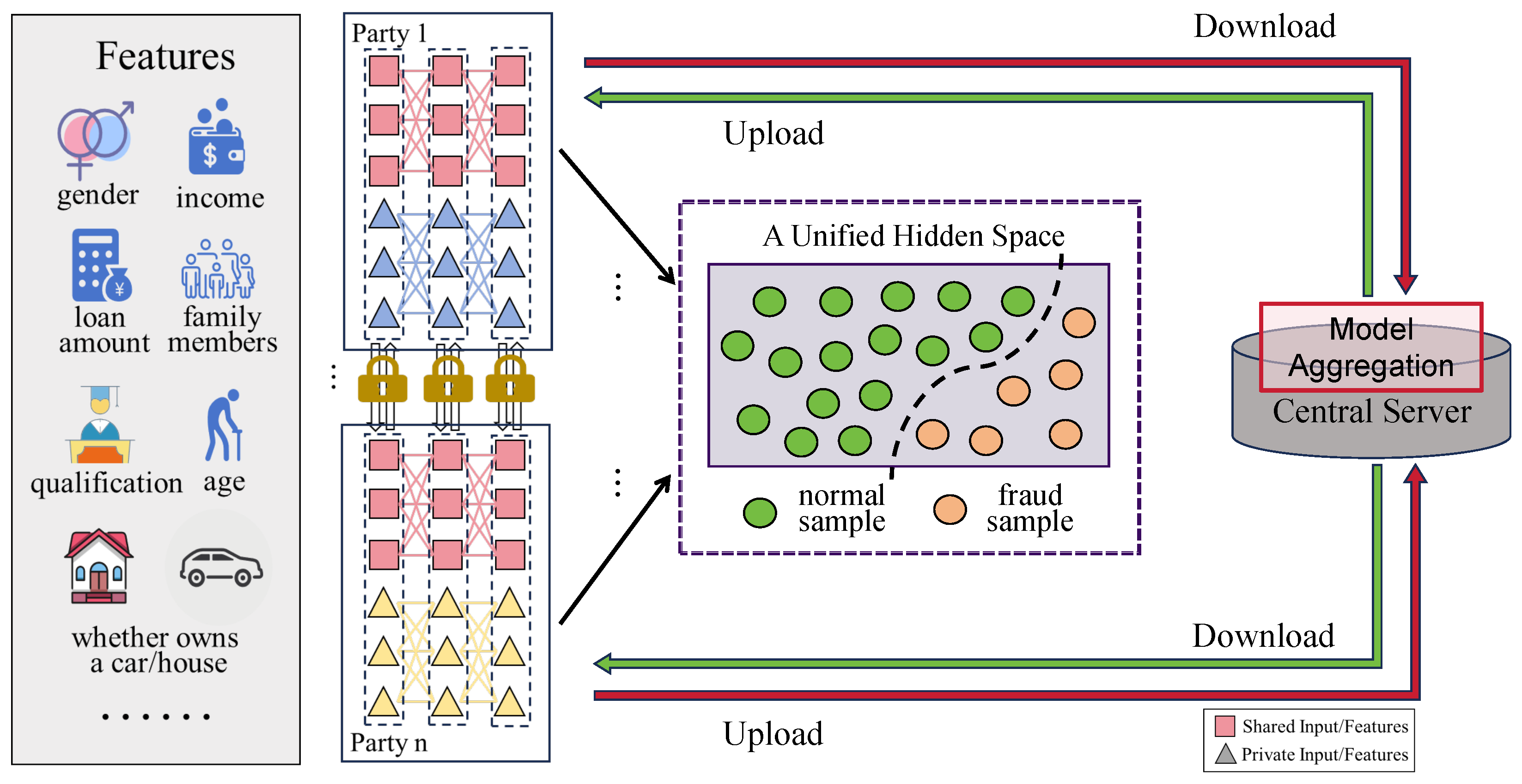Figure 1 intuitively illustrates this scenario: each institution holds both shared fraud-relevant features and private sensitive data, but without a way to align these heterogeneous data sources without sharing samples, individual institutions are stuck with limited fraud detection capabilities—missing emerging threats and incurring avoidable losses. The figure thus underscores why resolving multi-party heterogeneous data collaboration is not just a technical need, but an urgent requirement to mitigate ongoing financial risks.

Based on the aforementioned consideration, we propose the FED-SPFD model. This model employs a share–private (S–P) segmentation approach for different parties, distinguishing between private variables within each party and shared variables among parties. For shared attributes, the FED-SPFD framework adopts a shared-encoding mechanism that enables multiple parties to collaboratively train a unified encoder, mapping the distributionally disparate shared attributes of various parties into a common feature space. Importantly, during the multi-party feature alignment process, in order to prevent privacy leakage, the FED-SPFD framework avoids the direct sharing of sample-level features. Instead, it aligns the shared features across parties through local sufficient statistics, simultaneously addressing the imbalance between normal and fraudulent samples from a statistical perspective. Regarding private variables, FED-SPFD treats them as private additional features unique to each party, with feature extraction and modeling conducted internally, thus not participating in the cross-party federated model aggregation. Furthermore, the “private Autoencoding + standard Gaussian aligning” mechanism constrains the private embedding feature space, ensuring that each party’s private embeddings share the same feature distribution, which stabilizes the joint training across multiple parties. Ultimately, by merging private and shared feature embeddings and conducting multi-party aggregated training of downstream fraud classifiers, the model facilitates each party in augmenting its fraudulent samples while ensuring privacy safety, thereby enhancing the effectiveness and accuracy of fraud detection models.

The contributions of this study can be summarized as follows:

• Novel Share–Private Segmentation for Feature-Heterogeneous Federated Learning: We propose a principled share–private (S–P) segmentation methodology that advances beyond existing methods like FedPer and pFedMe. While FedPer separates shared and personalized components at the model architecture level and pFedMe balances global–local performance through regularization, our approach operates at the data feature level—systematically identifying shared fraud-relevant features and institution-specific private features. This enables effective collaboration when participating institutions have fundamentally different feature spaces, addressing a critical limitation of existing methods that assume feature homogeneity.
• Privacy-Preserving Statistical Alignment Mechanism: FED-SPFD introduces a distinctive alignment approach using local sufficient statistics (mean and covariance) for shared features and Gaussian alignment for private features. This surpasses existing methods by achieving effective feature distribution alignment while maintaining strict privacy constraints, avoiding the computational overhead and privacy risks of full-feature alignment methods like MMD-based approaches.
• Superior Performance with Comprehensive Validation: Our method achieves 73.62% recall (3.5% improvement over pFedMe’s 70.12%) and 80.90% F1-score while requiring fewer training iterations (38 vs. 68). The validation includes ablation studies, t-SNE visualizations demonstrating feature alignment effectiveness, and communication efficiency analysis, providing comprehensive evidence of practical value in fraud detection contexts.

2. Problem Definition

This study focuses on the scenario of multi-party collaborative credit card fraud detection in the financial field, where multiple participating entities (e.g., banks, payment service providers, and financial technology companies) independently hold transaction-related data of their users. These entities share the need to improve fraud detection accuracy—yet face obstacles in collaboration due to inherent data heterogeneity and strict privacy constraints, which form the core problem addressed herein. We assumed that there are a total of ${\mathcal{U}}_a$ parties. For the ith party, its data includes user transaction records and corresponding fraud labels: legitimate transactions are labeled 0 (e.g., a user’s monthly grocery purchase), while fraudulent transactions are labeled 1 (e.g., an unexpected cross-border transaction exceeding the user’s usual spending limit). Mathematically, this data and label set can be defined as follows:

$$({\mathbf{x}}^i,y^i)\sim {\mathcal{U}}^i,{\mathbf{x}}^i\in {\mathbb{R}}^{m_i},y^i\in \mathbb{R},i=1,2,...,{\mathcal{U}}_a$$

(1)

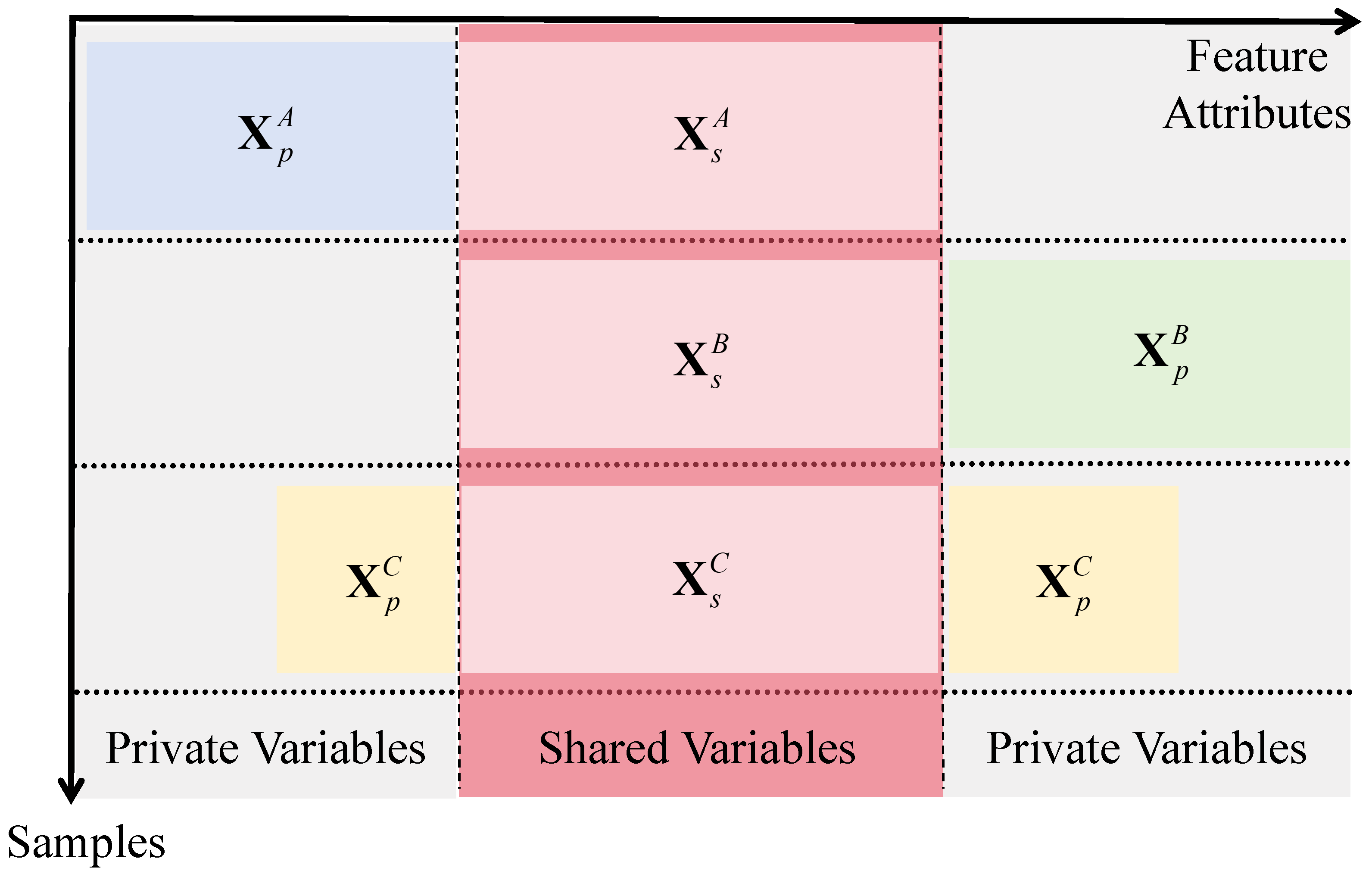
where $m_i$ denotes the number of features in the dataset of party i. In practice, $m_i$ varies across parties due to differences in business focuses and data collection scopes—reflecting one key aspect of data heterogeneity (e.g., some parties may collect more detailed user credit-related features, while others focus on transaction behavior features). And Figure 2 presents the division of shared and private variables via a sample-feature matrix: shared variables are features owned by all parties, while private variables are unique to each party, clarifying the data heterogeneity addressed in this study.

Furthermore, considering the issue of data heterogeneity, the data ${\mathbf{x}}^i$ from the ith party can be further divided into the shared variables ${\mathbf{x}}_s^i$, which are common to all parties, and the private variables ${\mathbf{x}}_p^i$, which are unique to party i. These can be represented as follows:   

$${\mathbf{x}}^i=[{\mathbf{x}}_s^i,{\mathbf{x}}_p^i],{\mathbf{x}}_s^i\in {\mathbb{R}}^{m_s},{\mathbf{x}}_p^i\in {\mathbb{R}}^{m_i-m_s}$$

(2)

Here, $m_s$ denotes the number of shared features (selected based on industry-common fraud detection indicators to ensure cross-party relevance).

In the practical collaborative scenario, this heterogeneity creates critical challenges: without proper handling, the mismatched feature spaces and data distributions across parties lead to inconsistent model parameters during federated training. This undermines the effectiveness of collaborative fraud detection—for instance, parties with fewer features may fail to capture complex fraud patterns, while parties with distinct data distributions may train local models that cannot generalize to other participants.

To resolve this, this study uses a shared encoder $f_{\mathrm{enc},\mathrm{s}}(·)$ for shared variables and a private encoder $f_{\mathrm{enc},\mathrm{p}}^i(·)$ for private variables. The shared encoder is jointly trained by all parties, while $f_{\mathrm{enc},{\mathrm{p}}^i}$ is exclusive to party i. Inputting the relevant variables yields their respective hidden states, mathematically represented as

$${\mathbf{Z}}_s^i=f_{\mathrm{enc},\mathrm{s}}\left({\mathbf{X}}_s^i\right),i\in {\mathcal{U}}_a$$

(3)

$${\mathbf{Z}}_p^i=f_{\mathrm{enc},\mathrm{p}}^i\left({\mathbf{X}}_p^i\right),i\in {\mathcal{U}}_a$$

(4)

Here, ${\mathbf{X}}_s^i$ represents the set of all shared variables ${\mathbf{x}}^i$ for the ith party, where ${\mathbf{X}}_s^i\in {\mathbb{R}}^{n_i\times m}$, and ${\mathbf{X}}_p^i$ denotes the set of all private variables ${\mathbf{x}}_p^i$ for the ith party, where ${\mathbf{X}}_p^i\in {\mathbb{R}}^{n_i\times (m_i-m)}$. ${\mathbf{Z}}_s^i$ represents the hidden embeddings of shared attributes in party i and ${\mathbf{Z}}_p^i$ represents the hidden embeddings of private attributes. Additionally, $n_i$ indicates the total number of samples for the ith party.

After encoding the shared variables, to address data heterogeneity, this framework aligns the shared variable features and private variable features from different parties using two distinct strategies, ${\mathrm{ALG}}_s$ and ${\mathrm{ALG}}_p$. This alignment produces a unified distribution of shared features $p_s\left({\mathbf{z}}_s\right)$ and a distribution of private features $p_p\left({\mathbf{z}}_p\right)$. The mathematical expressions are as follows:

$$\begin{array}{cc}\hfill p_s\left({\mathbf{z}}_s\right|{\mathbf{x}}_p)& ={\mathrm{ALG}}_s\left(\bigcup _{i\in {\mathcal{U}}_a}{\mathbf{Z}}_s^i\right)\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill p_p\left({\mathbf{z}}_p\right|{\mathbf{x}}_p)& ={\mathrm{ALG}}_p\left(\bigcup _{i\in {\mathcal{U}}_a}{\mathbf{Z}}_p^i\right)\hfill \end{array}$$

(6)

Finally, a classification mapping function $f_{\mathrm{cls}}(·)$ is established to relate the joint distribution of shared and private hidden features to the sample labels across all parties. This function combines the aligned shared feature representations and locally encoded private feature representations to predict the fraud probability of each transaction. The corresponding mathematical formula is given by

$${\widehat{y}}^i=f_c^i\left([{\mathbf{z}}_s^i,{\mathbf{z}}_p^i]\right)$$

(7)

where ${\widehat{y}}^i$ represents the model’s estimated probability that the input sample is fraudulent—supporting real-time decision-making (e.g., flagging high-probability fraud cases for interception) in practical financial scenarios.

3. Proposed Method

3.1. Shared Encoding

In terms of the shared attributes ${\mathbf{x}}_s^{i,j},i\in {\mathcal{U}}_a,j=1,\dots ,K^i$ from each party i, where $K^i$ represents the number of samples in party i, a shared encoder $f_{\mathrm{enc},s}$ is jointly optimized to project these attributes into a unified feature space. For clarity, we denote the local shared encoder for each party i as $f_{\mathrm{enc},s}^i$, with all parties employing the same model architecture and hyperparameters. Practically, we select the Multi-layer Feed-forward Neural Network (MFFN) as the encoder backbone due to its concise composition and high interpretability of the non-linear correlations within the input data. The shared embedding of each party is obtained through their encoder by

$${\mathbf{Z}}_s^i=[{\mathbf{z}}_s^{i,j},j=1,\dots ,K^i]=f_{enc,s}^i\left({\mathbf{X}}_s^i\right),$$

(8)

where ${\mathbf{Z}}_s^i$ represents the combination of all hidden embeddings of shared attributes in party i. However, due to the inconsistency in data distribution among the datasets ${\mathbf{X}}_s^i$ from various parties, the unprocessed ${\mathbf{Z}}_{s,t}^i$ cannot be guaranteed to maintain the same distribution characteristics across all parties. This inconsistency complicates the joint training of the downstream fraud classifier. Therefore, this paper adopts a non-sample-level feature alignment method to map the features from multiple parties into a common space.

Firstly, we calculate the sample mean ${\widehat{\mathit{\mu }}}_s^i$ and sample covariance ${\widehat{\mathbf{\Sigma }}}_s^i$ statistics for each party, with the computation being as follows:

$$\begin{array}{cc}\hfill {\widehat{\mathit{\mu }}}_s^i& ={\displaystyle \frac{1}{n_i}}\sum _{j=1}^{K^i}{\mathbf{z}}_s^{i,j},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Sigma }}}_s^i& ={\displaystyle \frac{1}{n_i}}\sum _{j=1}^{K^i}({\mathbf{z}}_s^{i,j}-{\widehat{\mathit{\mu }}}_s^i){({\mathbf{z}}_s^{i,j}-{\widehat{\mathit{\mu }}}_s^i)}^{\top }.\hfill \end{array}$$

(10)

Subsequently, the central server receives the statistics from each party and estimates the global statistics using a weighted average based on the number of samples contributed by each party:

$$\begin{array}{cc}\hfill {\widehat{\mathit{\mu }}}_s^g& ={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{n}_i}}\sum _{i\in {\mathcal{U}}_a}{\widehat{\mathit{\mu }}}_s^i·K^i,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Sigma }}}_s^g& ={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{n}_i}}\sum _{i\in {\mathcal{U}}_a}{\widehat{\mathbf{\Sigma }}}_s^i·K^i.\hfill \end{array}$$

(12)

Thereafter, the central server distributes the global statistics ${\widehat{\mathit{\mu }}}_s^g$ and ${\widehat{\mathbf{\Sigma }}}_s^g$ to each party. Each party then calculates the differences between its own statistics and the global statistics using Kullback–Leibler divergence, which is computed as follows:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{alg}}& ={\displaystyle \frac{1}{2}}(log{\displaystyle \frac{det{\widehat{\mathbf{\Sigma }}}_s^g}{det{\widehat{\mathbf{\Sigma }}}_s^i}}+\mathrm{tr}({({\widehat{\mathbf{\Sigma }}}_s^i)}^{-1}{\widehat{\mathbf{\Sigma }}}_s^g)\hfill \\ \hfill & +{{\left({\widehat{\mathit{\mu }}}_s^i-{\widehat{\mathit{\mu }}}_s^g\right)}^{\top }{\widehat{\mathbf{\Sigma }}}_s^i}^{-1}({\widehat{\mathit{\mu }}}_s^i-{\widehat{\mathit{\mu }}}_s^g)-h_s).\hfill \end{array}$$

(13)

The aforementioned expression achieves its minimum value of 0 if and only if ${\widehat{\mathbf{\Sigma }}}_s^i={\widehat{\mathbf{\Sigma }}}_s^g$ and ${\widehat{\mathit{\mu }}}_s^i={\widehat{\mathit{\mu }}}_s^g$. By optimizing the neural network parameters to minimize this loss, we align the local embeddings ${\mathbf{Z}}_s^i$ with the unified global shared distribution $\mathcal{N}\left(\mathbf{z}\right|{\mathit{\mu }}_s^g,{\mathbf{\Sigma }}_s^g)$.

3.2. Private Autoencoding

To fully leverage the private variables ${\mathbf{x}}_p^i$ from each party, we adopt an encode–decode approach to transform the original data into abstract feature representations. For the ith party, we utilize party-independent private encoders $f_{\mathrm{enc},\mathrm{p}}(·)$ and decoders $f_{\mathrm{dec},\mathrm{p}}(·)$ to characterize ${\mathbf{x}}_p^i$. The mathematical expressions are as follows:

$$\begin{array}{c}\hfill {\mathbf{Z}}_p^i=\left[{\mathbf{z}}_p^{i,j}{|}_{j=1}^{K^i}\right]=f_{\mathrm{enc},\mathrm{p}}^i\left({\mathbf{X}}_p^i\right)\end{array}$$

(14)

$$\begin{array}{c}\hfill {\widehat{\mathbf{X}}}_p^i=f_{\mathrm{dec},\mathrm{p}}^i\left({\mathbf{X}}_p^i\right)\end{array}$$

(15)

Here, ${\mathbf{Z}}_p^i$ represents the private hidden embeddings obtained from the encoder. To measure the reconstruction error, we employ the mean squared error between the original value ${\mathbf{x}}_p^i$ and the reconstructed value ${\widehat{\mathbf{x}}}_p^i$. Additionally, we impose an ${\ell }_2$-norm sparsity constraint on the hidden features to enhance their generalization performance. The loss function can be expressed as follows:

$${\mathcal{L}}_{\mathrm{rec}}^i={\parallel f_{dec,p}^i\left({\mathbf{Z}}_p^i\right)-{\mathbf{X}}_p^i\parallel }_2+\sum _{j=1}^{n_i}{\left({\mathbf{z}}_p^{i,j}\right)}^{\top }{\mathbf{z}}_p^{i,j}$$

(16)

Although private autoencoding transforms the original private variables into hidden state representations, the physical significance of the private variables from different parties is not the same, and they exhibit distinct original data distributions. To enable better integration of these features with the shared characteristics for training within the unified fraud classifier, it is essential to impose consistency in the distribution characteristics of heterogeneous private data at the encoding/embedding level across each party. Consequently, we align the private hidden embeddings to a standard Gaussian distribution, thereby standardizing the private embedding characteristics of all parties to enhance the robustness of the model. This process occurs independently and non-collaboratively within each party.

To achieve this, we first compute the sample mean vector ${\widehat{\mathbf{z}}}_p^i$ and the sample covariance for party i by taking the average as follows:

$$\begin{array}{cc}\hfill {\widehat{\mathit{\mu }}}_p^i& ={\displaystyle \frac{1}{n_i}}\sum _{j=1}^{n_i}{\mathbf{z}}_p^{i,j}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Sigma }}}_p^i& ={\displaystyle \frac{1}{n_i-1}}\sum _{j=1}^{n_i}({\mathbf{z}}_p^{i,j}-{\widehat{\mathit{\mu }}}_p^i){({\mathbf{z}}_p^{i,j}-{\widehat{\mathit{\mu }}}_p^i)}^T\hfill \end{array}$$

(18)

After obtaining the sample mean vector and sample covariance, we can finally calculate the KL divergence, expressed mathematically as (19):

$${\mathcal{L}}_{\mathrm{p}-\mathrm{n}}={\displaystyle \frac{1}{2}}\left(\mathrm{tr}\left(S\right)+{\left({\widehat{\mathit{\mu }}}_p^i\right)}^T{\widehat{\mathit{\mu }}}_p^i-h_p-ln(det\left(S\right))\right)$$

(19)

Here, $h_p$ denotes the dimensionality of the private embedding obtained from encoding. This formula evaluates the divergence between the sample distribution and the standard normal distribution through sample statistical properties; a larger KL divergence indicates a greater discrepancy between the sample and the standard normal distribution. Therefore, our objective is to continuously adjust the parameters to minimize the KL divergence.

3.3. Overall Pipeline

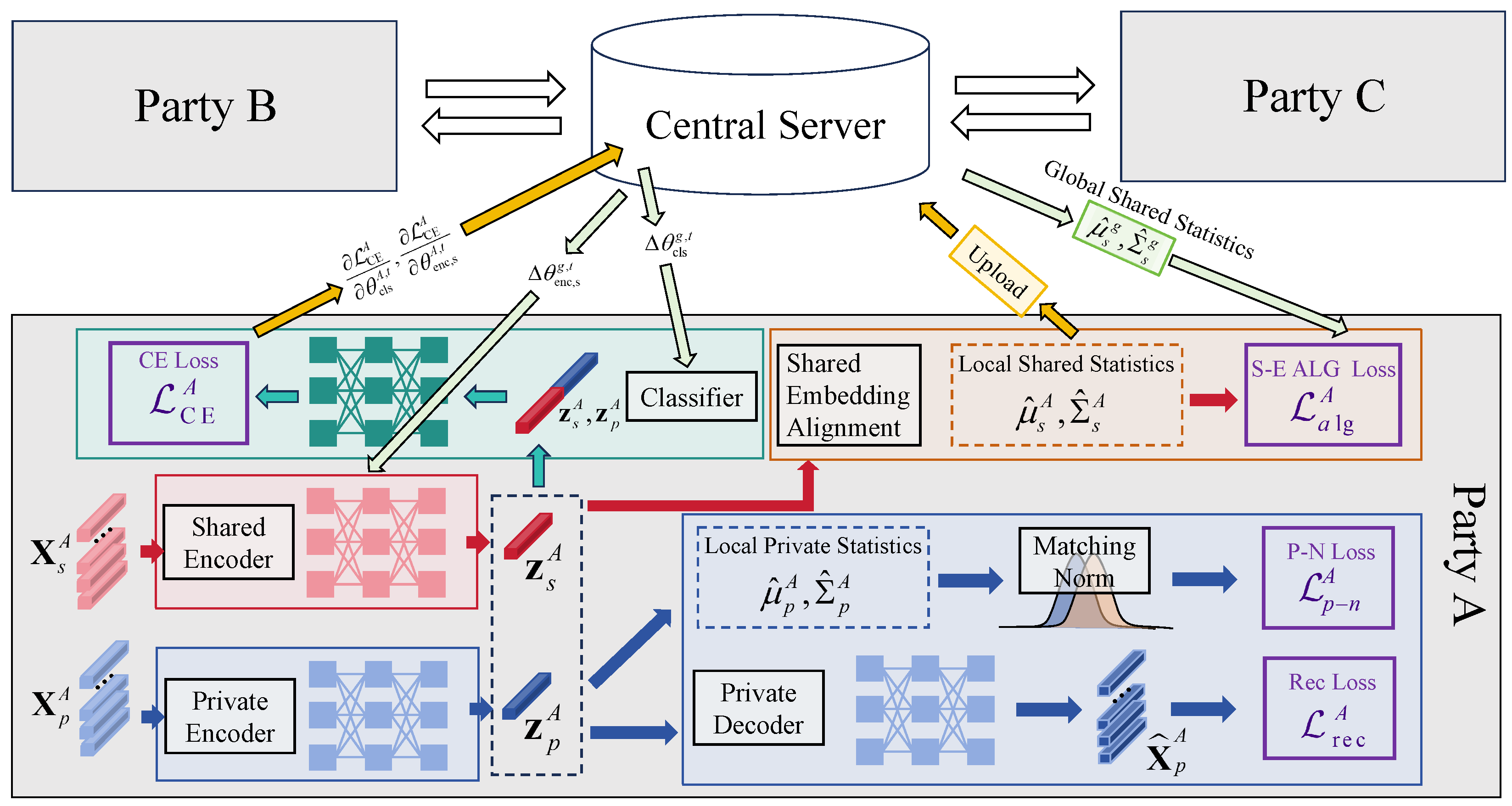
In this section, we present the technical details of the federated optimization procedure for jointly training the fraud detection classifier $f_{cls}(·)$, leveraging the shared and private encoding structures described in Section 3.1 and Section 3.2. Figure 3 outlines the FED-SPFD model’s workflow, including local encoding of shared/private variables, statistic-based alignment, and FedAvg-based parameter aggregation, visualizing how the model achieves privacy-preserving collaborative training.

At the beginning of each global communication round t, each party i independently performs R steps of local stochastic gradient descent (SGD) on its private dataset ${\mathcal{U}}^i$. In each local step $r=1,\dots ,R$, party i samples a mini-batch $({\mathbf{X}}_{s,t,r}^i,{\mathbf{X}}_{p,t,r}^i,{\mathbf{y}}_{t,r}^i)$ and computes the corresponding shared and private embeddings via the local encoders $f_{\mathrm{enc},\mathrm{s}}^i$ and $f_{\mathrm{enc},\mathrm{p}}^i$. The following four local loss components are then calculated:

• Alignment loss ${\mathcal{L}}_{\mathrm{alg}}^i$: Aligns the local shared embedding distribution to the global shared statistics.
• Private-to-normal loss ${\mathcal{L}}_{\mathrm{p}-\mathrm{n}}^i$: Regularizes the private embedding distribution towards a standard normal distribution.
• Reconstruction loss with sparsity ${\mathcal{L}}_{\mathrm{rec}}^i$: Ensures accurate reconstruction of private data and enforces sparsity on the private embeddings.
• Cross-entropy loss ${\mathcal{L}}_{\mathrm{CE}}^i$: Supervises the fraud classification task.

The overall local objective for each party i is defined as a weighted sum of the above four losses:

$${\mathcal{L}}_{\mathrm{local}}^i={\mathcal{L}}_{\mathrm{CE}}^i+{\lambda }_{\mathrm{alg}}{\mathcal{L}}_{\mathrm{alg}}^i+{\lambda }_{\mathrm{p}-\mathrm{n}}{\mathcal{L}}_{\mathrm{p}-\mathrm{n}}^i+{\lambda }_{\mathrm{rec}}{\mathcal{L}}_{\mathrm{rec}}^i$$

(20)

where ${\lambda }_{\mathrm{alg}},{\lambda }_{\mathrm{p}-\mathrm{n}},{\lambda }_{\mathrm{rec}}$ are non-negative hyperparameters controlling the contribution of each loss term.

During each local update step, all model parameters—including the shared encoder, private encoder, private decoder, and classifier—are optimized via gradient descent with respect to the local objective function. The parameters are updated according to the gradients of the local loss, and the explicit update formulas are omitted here for brevity.

After R local update steps, each party i uploads only the updated parameters of the shared encoder and classifier, i.e., ${\theta }_{\mathrm{enc},\mathrm{s}}^{i,t+1}$ and ${\theta }_{\mathrm{cls}}^{i,t+1}$, to the central server. The parameters of the private encoder and decoder remain strictly local and are never shared or aggregated.

The central server aggregates the received shared encoder and classifier parameters from all participating parties using the FedAvg algorithm:

$$\begin{array}{cc}\hfill {\theta }_{\mathrm{enc},\mathrm{s}}^{g,t+1}& ={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{B}_i}}\sum _{i\in {\mathcal{U}}_a}{B}_i·{\theta }_{\mathrm{enc},\mathrm{s}}^{i,t+1}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\theta }_{\mathrm{cls}}^{g,t+1}& ={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{B}_i}}\sum _{i\in {\mathcal{U}}_a}{B}_i·{\theta }_{\mathrm{cls}}^{i,t+1}\hfill \end{array}$$

(22)

where $B_i$ is the number of samples used by party i in the current round and ${\mathcal{U}}_a$ denotes the set of active parties.

The aggregated shared encoder and classifier parameters $({\theta }_{\mathrm{enc},\mathrm{s}}^{g,t+1},{\theta }_{\mathrm{cls}}^{g,t+1})$ are then distributed back to all parties and overwrite the corresponding local parameters, serving as the initialization for the next communication round. The private encoder and decoder parameters are always updated and maintained locally.

This federated optimization framework ensures that only the shared representation and classifier are collaboratively learned across parties, while private feature extraction remains strictly local, thus preserving data privacy and enhancing model generalization under heterogeneous data distributions. To systematically formalize the federated optimization workflow described above, the complete training procedure of the FED-SPFD model—covering warm-start pre-training, local SGD updates, statistic/parameter interaction, and global aggregation—is summarized in Algorithm 1.

It is important to note that, during the initial stage of training, the local shared embeddings may not be stable, which can cause large fluctuations in the global statistics and negatively impact the alignment process. To address this, a “warm start” strategy is adopted: each party first performs local reconstructive representation learning on ${\mathbf{X}}_s^i$ using a decoder symmetric to the shared encoder, before federated training begins, to stabilize the shared embedding space.

Algorithm 1 Federated optimization for heterogeneous fraud detection.

Require:  Datasets ${\mathcal{U}}^i=\left\{({\mathbf{x}}^i,y^i)\right\}$; shared encoder $f_{\mathrm{enc},\mathrm{s}}^i$, private encoder $f_{\mathrm{enc},\mathrm{p}}^i$, private decoder $f_{\mathrm{dec},\mathrm{p}}^i$, classifier $f_{\mathrm{cls}}^i$; communication rounds E; local steps R; loss weights ${\lambda }_{\mathrm{alg}},{\lambda }_{\mathrm{p}-\mathrm{n}},{\lambda }_{\mathrm{rec}}$.   1: Warm Start: Each party i locally pre-trains $f_{\mathrm{enc},\mathrm{s}}^i$ and $f_{\mathrm{dec},\mathrm{s}}^i$ on ${\mathbf{x}}_s^i$ via reconstructive learning to stabilize the shared embedding space.   2: for global round $t=1$ to E do   3:       for each party i in parallel do   4:             for local step $r=1$ to R do   5:                   Sample mini-batch $({\mathbf{X}}_{s,t,r}^i,{\mathbf{X}}_{p,t,r}^i,{\mathbf{y}}_{t,r}^i)$ from ${\mathcal{U}}^i$   6:                   Compute shared and private embedding: ${\widehat{\mathbf{Z}}}_{s,t,r}^i=f_{\mathrm{enc},\mathrm{s}}^i\left({\mathbf{X}}_{s,t,r}^i\right)$, ${\widehat{\mathbf{Z}}}_{p,t,r}^i=f_{\mathrm{enc},\mathrm{p}}^i\left({\mathbf{X}}_{p,t,r}^i\right)$   7:                   Compute reconstructed private data: ${\widehat{\mathbf{X}}}_{p,t,r}^i=f_{\mathrm{dec},\mathrm{p}}^i({\widehat{\mathbf{Z}}}_{p,t,r}^i)$   8:                   Predict label: ${\widehat{\mathbf{y}}}_{t,r}^i=f_{\mathrm{cls}}^i\left({\widehat{\mathbf{Z}}}_{t,r}^i\right)$   9:                   Compute local statistics: mean ${\widehat{\mathit{\mu }}}_{s,t,r}^i$, covariance ${\widehat{\mathbf{\Sigma }}}_{s,t,r}^i$ of ${\widehat{\mathbf{Z}}}_{s,t,r}^i$ 10:                   Compute total loss: ${\mathcal{L}}_{\mathrm{local}}^i={\mathcal{L}}_{\mathrm{CE}}^i+{\lambda }_{\mathrm{alg}}{\mathcal{L}}_{\mathrm{alg}}^i+{\lambda }_{\mathrm{p}-\mathrm{n}}{\mathcal{L}}_{\mathrm{p}-\mathrm{n}}^i+{\lambda }_{\mathrm{rec}}{\mathcal{L}}_{\mathrm{rec}}^i$ 11:                   Update all local model parameters by gradient descent on ${\mathcal{L}}_{\mathrm{local}}^i$ 12:            end for 13:            Upload updated ${\theta }_{\mathrm{enc},\mathrm{s}}^{i,t+1}$, ${\theta }_{\mathrm{cls}}^{i,t+1}$, and local statistics ${\widehat{\mathit{\mu }}}_{s,t}^i$, ${\widehat{\mathbf{\Sigma }}}_{s,t}^i$ to the server 14:     end for 15:     Server aggregates $\left\{{\theta }_{\mathrm{enc},\mathrm{s}}^{i,t+1}\right\}$ and $\left\{{\theta }_{\mathrm{cls}}^{i,t+1}\right\}$ from all parties using FedAvg: 16:            ${\theta }_{\mathrm{enc},\mathrm{s}}^{g,t+1}={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{B}_i}}{\sum }_{i\in {\mathcal{U}}_a}{B}_i·{\theta }_{\mathrm{enc},\mathrm{s}}^{i,t+1}$ 17:            ${\theta }_{\mathrm{cls}}^{g,t+1}={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{B}_i}}{\sum }_{i\in {\mathcal{U}}_a}{B}_i·{\theta }_{\mathrm{cls}}^{i,t+1}$ 18:     Server aggregates local statistics $\{{\widehat{\mathit{\mu }}}_{s,t}^i,{\widehat{\mathbf{\Sigma }}}_{s,t}^i\}$ from all parties to compute global statistics: 19:            ${\widehat{\mathit{\mu }}}_{s,t}^g={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{n}_i}}{\sum }_{i\in {\mathcal{U}}_a}{\widehat{\mathit{\mu }}}_{s,t}^i·n_i$ 20:            ${\widehat{\mathbf{\Sigma }}}_{s,t}^g={\displaystyle \frac{1}{{\sum }_{i\in {\mathcal{U}}_a}{n}_i}}{\sum }_{i\in {\mathcal{U}}_a}{\widehat{\mathbf{\Sigma }}}_{s,t}^i·n_i$ 21:     Server broadcasts $({\theta }_{\mathrm{enc},\mathrm{s}}^{g,t+1},{\theta }_{\mathrm{cls}}^{g,t+1},{\widehat{\mathit{\mu }}}_{s,t}^g,{\widehat{\mathbf{\Sigma }}}_{s,t}^g)$ to all parties 22:     Each party updates local ${\theta }_{\mathrm{enc},\mathrm{s}}^i\leftarrow {\theta }_{\mathrm{enc},\mathrm{s}}^{g,t+1}$, ${\theta }_{\mathrm{cls}}^i\leftarrow {\theta }_{\mathrm{cls}}^{g,t+1}$, and uses global statistics ${\widehat{\mathit{\mu }}}_{s,t}^g,{\widehat{\mathbf{\Sigma }}}_{s,t}^g$ for alignment 23: end for 24: Output: Final shared encoder and classifier parameters, and locally trained private encoder/decoder for each party.

4. Experiments and Results

4.1. Dataset Description

The dataset utilized in this study is sourced from Kaggle, as part of a well-documented social experiment (Mishra 2019) focused on credit card transaction risk assessment. This Kaggle dataset is publicly accessible and has undergone strict desensitization (e.g., removing direct personal identifiers such as full names and official ID numbers) to comply with global privacy regulations, ensuring no violation of user confidentiality. Its feature design closely aligns with real-world credit card transaction data dimensions—covering personal identification background, asset status, credit history, and current loan application information—making it representative of the data financial institutions typically use for fraud detection. Researchers can access the dataset via the official Kaggle link provided in the references, where the platform offers clear access guidelines (e.g., free registration and compliance with Kaggle’s data usage terms) to facilitate reproducibility. Excluding the transaction item IDs and sample labels, the dataset comprises a total of 120 data features related to the transactions, encompassing 307,511 sample records. These sample features include aspects such as personal identification background, asset status, credit history, and information pertinent to the current loan application.

In terms of personal background, there are 15 features, which include attributes such as the borrower’s gender, educational level, nature of employment, and family status. The asset status section includes 52 features that encompass factors like the borrower’s income from employment, ownership and age of vehicles, homeownership status, and housing conditions. The credit history includes five features, which capture the borrower’s past repayment behavior, the number of inquiries made at credit agencies, and the completeness and congruence of their information. Furthermore, the information related to the current loan application contains 48 features, including the loan amount, purposes of the loan, and loan annuity details.

In terms of data variable types, the dataset comprises 69 continuous variables, 33 Boolean variables, and 18 categorical variables. The dataset includes complete sample labels, where borrowers are categorized as experiencing payment difficulties—denoted by the label 1—if they have at least one instance of overdue repayment exceeding a specified number of days during a predetermined period prior to this loan. All other cases are labeled as 0.

4.2. Experiment Settings

4.2.1. Data Preprocessing

First, we exclude data columns of Boolean variables where the ratio of 0 s and 1 s is less than 0.01%. This portion of feature data exhibits severe distributional skewness, resulting in negligible information gain for the model. Next, for the categorical variables in the original dataset, a binary encoding approach is employed to transform the originally non-meaningful category labels into encoded features. Subsequently, for variables with an absolute range exceeding 50, we take the absolute value and apply a logarithmic transformation, while reintroducing the original sign to preserve the sign’s integrity. This process helps to narrow the range of the variable distributions, eliminates heteroscedasticity, and stabilizes the data. For dealing with missing values in the dataset, this study employs the Sentinel Value Imputation method (SVI) (Little and Rubin 2019) for imputation. The rationale for adopting this method is twofold: Firstly, it is a simple and commonly utilized engineering solution, and the primary contribution of this study does not focus on the imputation of missing values. Additionally, as the dataset is derived from social experiments, the mechanisms behind the missing data are often unknown and varied; hence, a hasty application of other imputation methods could lead to inaccurate estimation of missing values. Secondly, the model used in this study is a neural network, which possesses strong capabilities for extracting non-linear features from data. By employing Sentinel Value Imputation, even when utilizing values that are clearly outside the distribution for imputation, we can effectively identify instances of missing data and allow the model to learn from this portion of information effectively.

4.2.2. Dataset Split

In the experiment, we utilized the complete dataset, which was partitioned into three independent datasets corresponding to different parties in order to simulate the federated learning scenario under heterogeneous data conditions and to validate the proposed algorithm. The specific method involved a correlation analysis with the target labels, through which we identified variables with high correlation coefficients. Further filtering yielded 19 groups of frequently used features in financial institutions as shared variables. These variables comprise 10 characteristics related to personal identity background, 4 characteristics related to asset status, and 5 characteristics related to the loan information for this instance, as detailed in

Table 1. List of attributes in dataset.

Personal Identification Background	Asset Status	Loan Information
CODE-GENDER	FLAG-OWN-CAR	NAME-CONTRACT-TYPE
CNT-CHILDREN	FLAG-OWN-REALTY	AMT-CREDIT
NAME-EDUCATION-TYPE	AMT-INCOME-TOTAL	AMT-ANNUITY
NAME-FAMILY-STATUS	NAME-INCOME-TYPE	AMT-GOODS-PRICE
NAME-HOUSING-TYPE		NAME-TYPE-SUITE
REGION-POPULATION-RELATIVE
DAYS-BIRTH
DAYS-EMPLOYED
DAYS-REGISTRATION
DAYS-ID-PUBLISH

. After fixing the shared variables, the remaining feature variables were categorized as private variables, and the samples were randomly divided into three groups, simulating private data from three different parties. The final division resulted in Party 1 containing a total of 19 features and 147,666 sample data; Party 2 containing a total of 47 features and 92,465 sample data; and Party 3 containing a total of 26 features and 67,196 sample data.

Regarding the train–validate–test partitioning, we designated 80% of the data as the training set, 10% as the validation set, and 10% as the test set. Specifically, for Party 1,118,133 samples were allocated to the training set, 14,766 samples to the validation set, and 14,767 samples to the test set; for Party 2,73,972 samples were designated as the training set, 9246 samples as the validation set, and 9247 samples as the test set; and for Party 3,53,757 samples were assigned to the training set, 6719 samples to the validation set, and 6720 samples to the test set.

4.2.3. Experiment Platform

All the experiments are conducted using an AMAX workstation with an Intel(R) Xeon(R) Gold 6226R CPU @ 2.90GHz $\times 64$, RAM 256GB, and RTX3090 $\times 8$.

4.3. Baselines

This paper conducts a comparative analysis of various federated learning frameworks under heterogeneous data conditions, specifically selecting FedAvg (McMahan et al. 2017), FedProx (Li et al. 2020), pFedMe (T. Dinh et al. 2020), FedPer (Arivazhagan et al. 2019), and the proposed FED-SPFD model for fraud detection purposes. For the traditional federated learning frameworks of FedAvg and FedProx, which do not incorporate heterogeneous data handling, all parties utilize a shared attribute as the dataset for both training and testing. In contrast, for the two frameworks capable of personalized learning, pFedMe and FedPer, each party employs its complete dataset for training. All frameworks utilize the same neural network architecture as that employed by the proposed FED-SPFD for the anomaly classification task. Below is a brief introduction to the four methods.

4.3.1. FedAvg

The FedAvg algorithm, introduced by Google in a seminal federated learning paper, was the first widely adopted algorithm in this field. It effectively handles non-IID and unbalanced data by training a global model with local data while preserving privacy, lowering communication costs, and enhancing model accuracy. In FedAvg, a central server initializes the global model and shares it with client devices. Each client trains its local model and sends back the updated parameters. The server aggregates these updates using a weighted average to refine the global model. This cycle continues until convergence or a set stopping criterion is achieved.

4.3.2. FedProx

FedProx was developed to address the challenges of system heterogeneity and statistical heterogeneity in federated learning. By building upon FedAvg, it incorporates a proximal term that permits devices to execute variable workloads while ensuring model convergence. During local updates on the client side, FedProx not only optimizes the loss function of the model with respect to local data but also introduces an additional term during the updating process to penalize updates that significantly deviate from the global model.

4.3.3. pFedMe

pFedMe is an algorithm designed for personalized federated learning, which offers more accurate and customized models for different clients while safeguarding data privacy. In pFedMe, a regularized loss function utilizing the L2 norm is applied to each client, thereby achieving a balance between the performance of personalized models and the global model. This approach allows clients to update their models in diverse directions without straying from the reference point contributed by each client.

4.3.4. FedPer

FedPer is also a personalized federated learning algorithm that achieves personalization by dividing the model into shared and personalized layers. The shared layer is distributed across all clients, and FedPer performs federated aggregation and updates solely on this shared layer. The personalized layer, typically located at the end of the model, is responsible for extracting personalized information from the shared features and is optimized only locally.

4.4. Metric Definition

This study employs precision, recall, and F1-score as evaluation metrics to conduct a comprehensive performance comparison of all fraud detection methods. Given the significant class imbalance inherent in the dataset, where the number of legitimate transactions substantially exceeds that of fraudulent transactions, we implement class balancing techniques prior to metric computation to ensure fair and reliable performance assessment.

The three evaluation metrics are calculated as follows.

Precision measures the proportion of correctly identified fraudulent transactions among all transactions classified as fraudulent:

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

(23)

Recall (also known as sensitivity or true positive rate) quantifies the proportion of actual fraudulent transactions that are correctly identified:

$$\mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}}$$

(24)

F1-score represents the harmonic mean of precision and recall, providing a balanced measure that considers both false positives and false negatives:

$$\mathrm{F}1-\mathrm{score}=2\times {\displaystyle \frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}={\displaystyle \frac{2\times TP}{2\times TP+FP+FN}}$$

(25)

where the confusion matrix components are defined as follows: $TP$ (True Positive) represents fraudulent transactions that are correctly identified as fraudulent; $FP$ (False Positive) denotes legitimate transactions that are erroneously classified as fraudulent; $FN$ (False Negative) corresponds to fraudulent transactions that are misclassified as legitimate; and $TN$ (True Negative) indicates legitimate transactions that are accurately classified as legitimate.

4.5. Training Results

This section focuses on in-depth analysis of the experimental work and results of the FED-SPFD model, exploring its performance advantages, the necessity of core components, practical application trade-offs, and connections to existing research—with the goal of clarifying the model’s technical value and potential application boundaries.

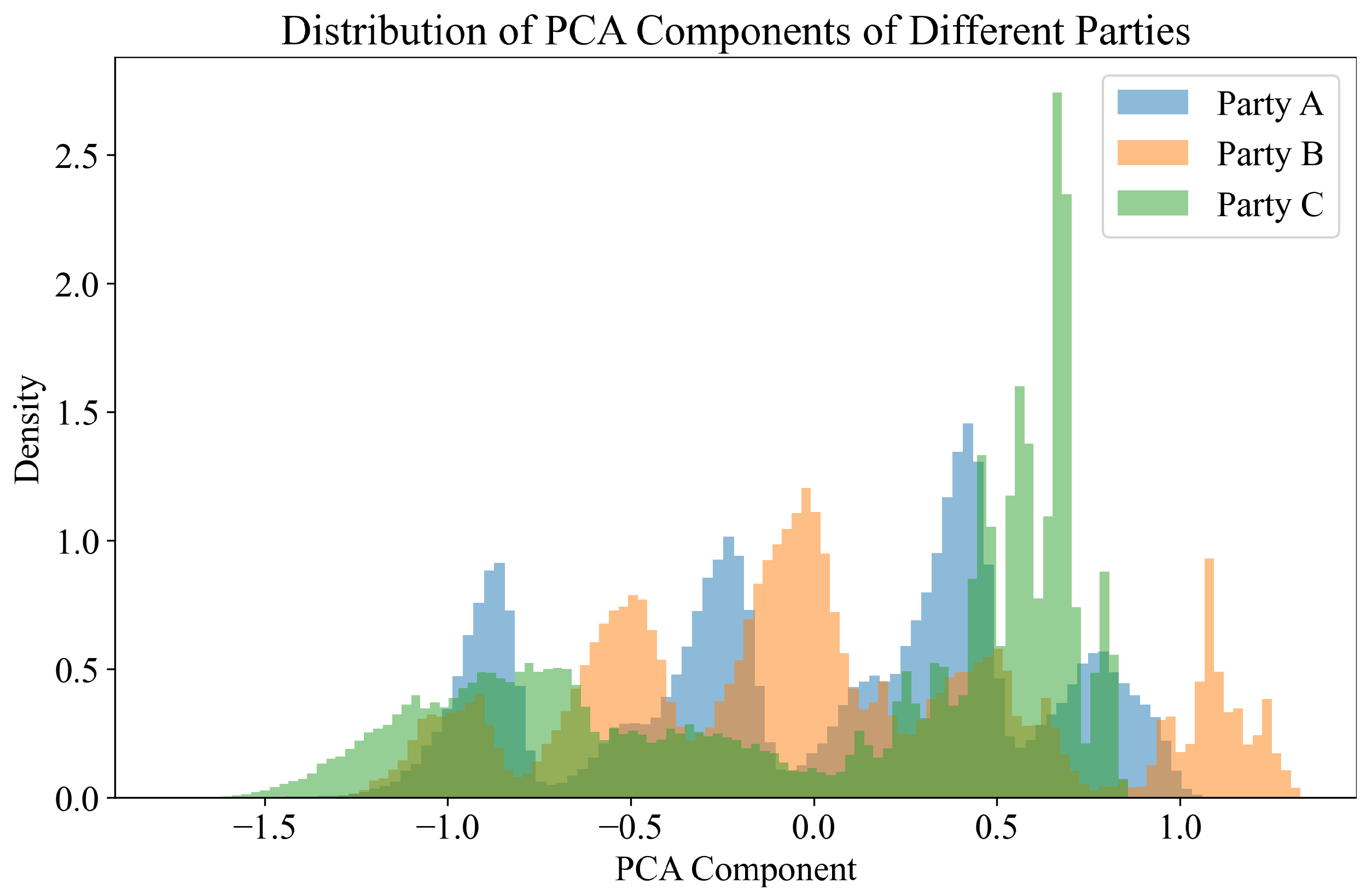
Figure 4 presents the histogram of the data distribution of the shared data among three parties, with the horizontal axis representing the principal component obtained from PCA and the vertical axis indicating the data distribution density. Given that the original shared data is multivariate, it is inadequate to observe the data distribution based solely on a single variable. Therefore, we first applied the PCA dimensionality reduction method to extract the principal features of the multivariate data, followed by a comparison of the distribution differences of those principal features across the three parties. From Figure 4, it is evident that the data distributions of the three parties exhibit distinct characteristics, with Party C displaying a significant peak in data distribution density around the PCA principal component value of approximately 0.7. This inconsistency in distribution can complicate the joint training of fraud classifiers, thereby reinforcing the necessity of aligning the shared embedding features in our proposed methodology.

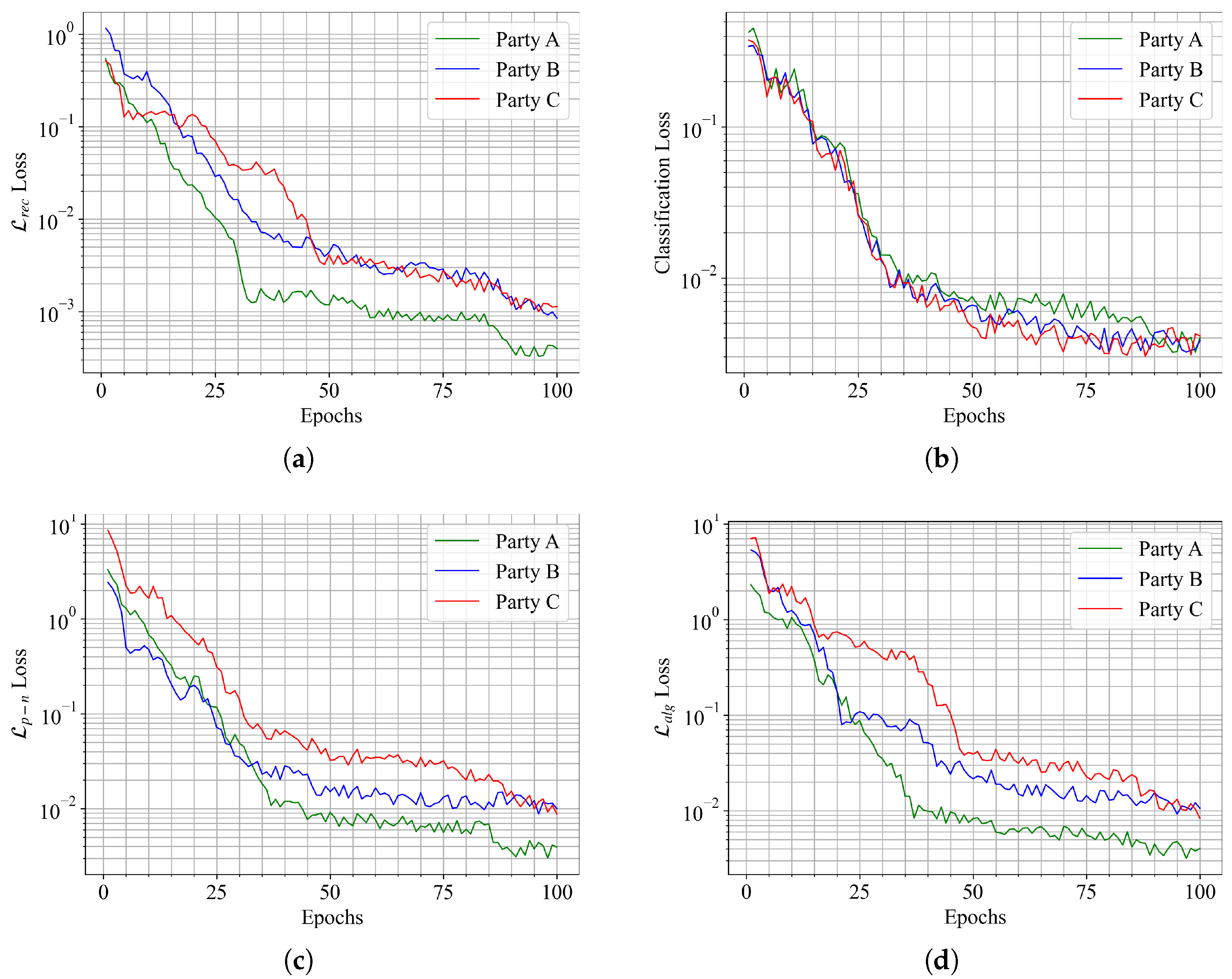
Figure 5 illustrates the private autoencoding reconstruction loss curve graph, the classifier BCE loss curve graph, the private embedding matching loss curve graph, and the shared embedding alignment loss curve graph. The horizontal axis represents the number of training iterations, while the vertical axis displays the loss values during the training process. From the figures, it is evident that as the number of training iterations increases, all loss curves decrease rapidly until convergence, eventually stabilizing. This indicates that the model exhibits a strong capacity for learning throughout the training. Specifically, Figure 5a,b,d converge around the 50th iteration, with convergence magnitudes of approximately ${10}^{-3}$, ${3\times 10}^{-3}$, and ${10}^{-2}$, respectively. In contrast, Figure 5c reaches convergence after around 40 iterations, with a convergence magnitude of ${10}^{-2}$.

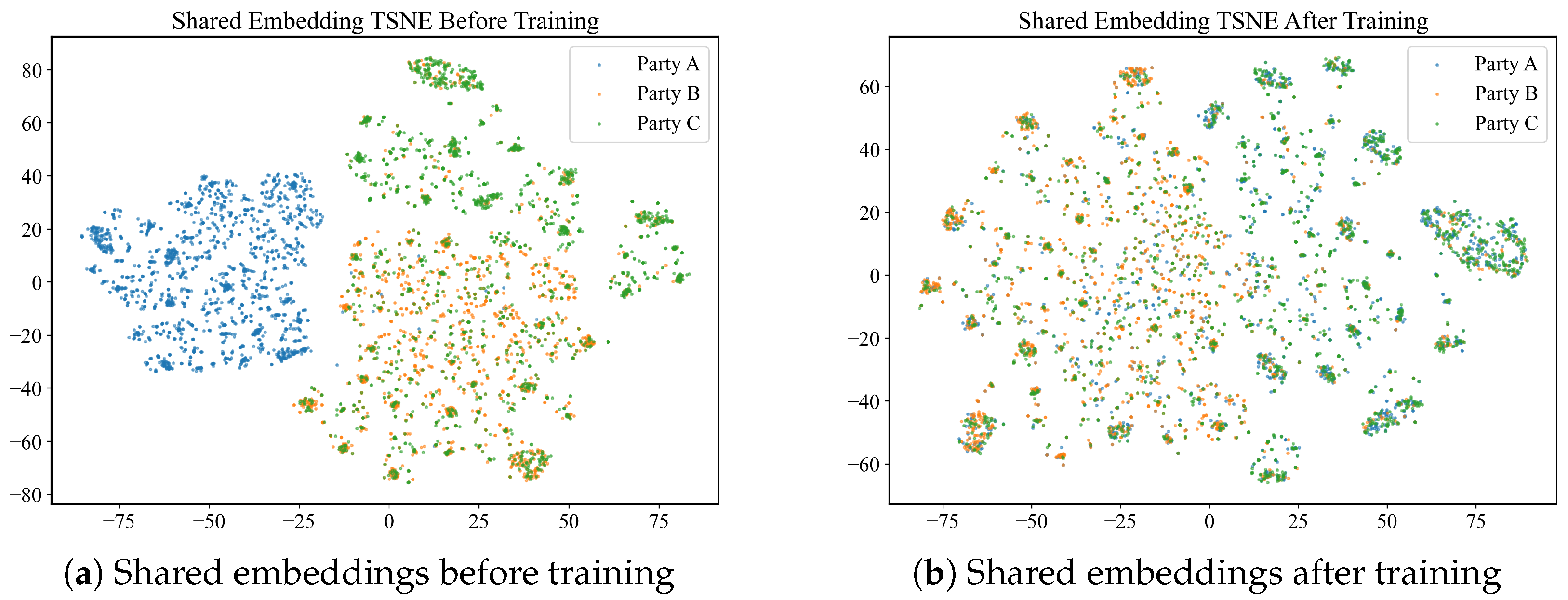
Figure 6 illustrates the comparison of the hidden features of shared variables and private variables through t-SNE visualizations before and after training, with the horizontal and vertical axes representing the first and second compressed dimensions of t-SNE, respectively. Figure 6a,b show the t-SNE scatter plots of the hidden features of shared variables before and after feature alignment. From Figure 6a, it is evident that prior to training, there is considerable overlap between the data points of party B and party C, while party A appears to be more independent of the other two parties. In contrast, as observed in Figure 6b, after the training process is completed, the data points of the three parties are well interleaved and mixed within the ranges of (−75, 75) for the first compressed dimension and (−60, 60) for the second compressed dimension. This indicates that the shared embedding successfully mapped the hidden features of shared variables to a common and unified feature space.

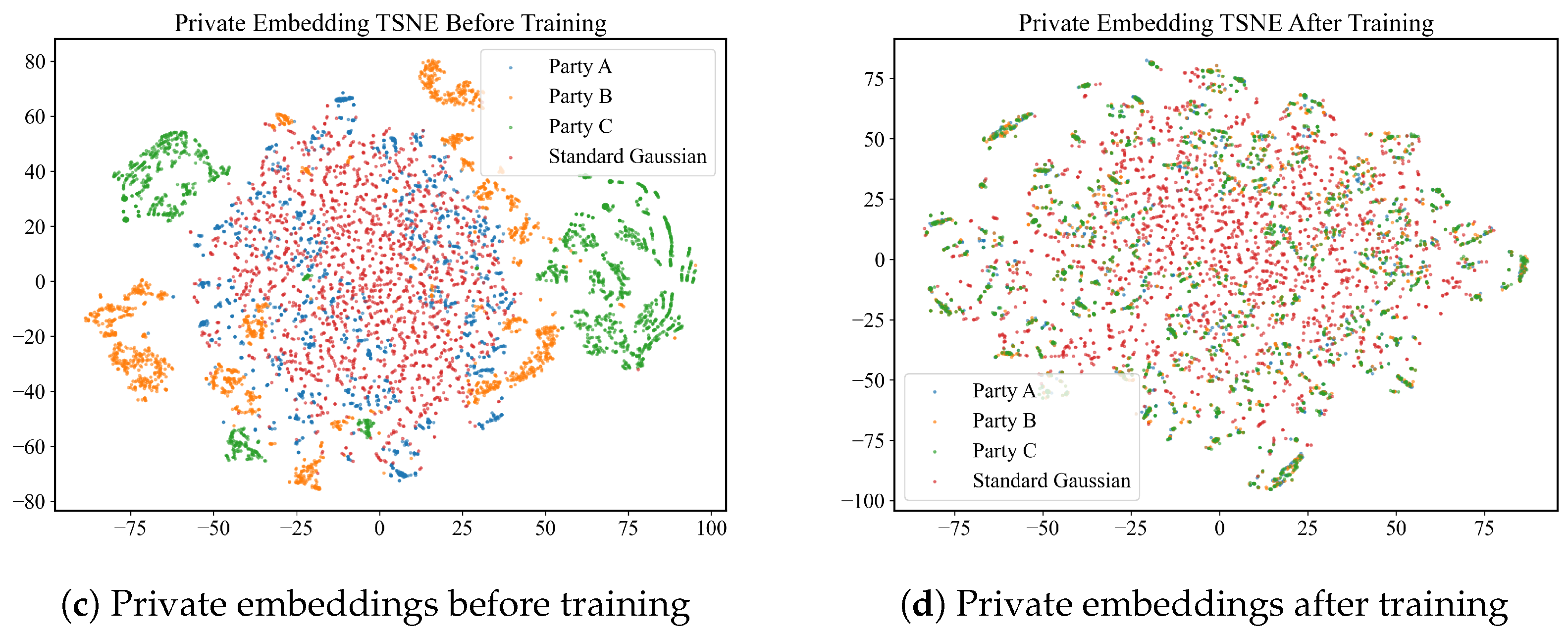
Figure 6c,d depict the t-SNE visualizations of the hidden features of private variables before and after alignment with the standard Gaussian distribution. In Figure 6c, it can be seen that the standard Gaussian distribution is positioned at the center of the t-SNE plot, and before training, party A’s data points largely coincide with the standard Gaussian distribution, whereas the scatter points for party B and party C are predominantly located outside of the standard Gaussian distribution. Following the training, as evidenced by Figure 6d, the data points for all three parties are effectively mixed with the standard Gaussian distribution. This outcome suggests that through the private embedding, the hidden features of private variables have been successfully aligned with the standard Gaussian distribution.

4.6. Comparative Experiments

In the first type of comparative experiment, a horizontal comparison method was employed, utilizing the FedAvg algorithm to conduct experiments on the same dataset. For classification accuracy metrics, we selected recall, precision, accuracy, and F1-score. Meanwhile, given the particularities of the federated learning scenario, network communication costs, the number of model iterations, and the capability for privacy protection are also crucial evaluation indicators. Therefore, in our comparison, we also include the volume of parameters that need to be shared during the optimization process in federated learning, measured in MB per instance; the total amount of data transferred upon completion of training, also measured in MB; the number of iterations required for training to finish; and the type of data interaction (model parameters, model gradients, or model features). The results of the experiments compared with the FED-SPFD model proposed in this paper are presented in

Table 2. Model performance under horizontal comparison.

	Comparison Factors	Classification Accuracy Metrics				Federated Learning Metrics
Algorithm		Recall (%)	Precision (%)	Accuracy (%)	F1-Score	Shared Parameter (MB)	Total Transmission (MB)	Iterations Number
FedAvg		67.45	78.32	92.15	72.48	16.21	680.82	42
FedProx		62.78	85.47	90.23	72.38	16.21	713.24	44
pFedMe		70.12	87.65	93.45	79.91	24.85	1689.8	68
FedPer		66.89	79.54	91.78	72.66	16.43	920.08	56
Our proposed		73.62	89.77	95.34	80.90	18.64	708.32	38

.

The results of the horizontal comparison experiment, as presented in Table 2, demonstrate the superior performance of the proposed FED-SPFD model across multiple evaluation metrics. Here the data highlighted in red represents the best, while the data highlighted in green represents the second best. Notably, the FED-SPFD model achieved the highest recall (73.62%), precision (89.77%), accuracy (95.34%), and F1-score (80.90%) among all the algorithms tested. This indicates a significant improvement in classification accuracy, suggesting that the FED-SPFD model is more effective in identifying fraudulent transactions compared to the other federated learning frameworks. Furthermore, the FED-SPFD model also exhibited competitive performance in terms of federated learning metrics. It required fewer iterations (38) to converge, which is the lowest among the models, indicating a more efficient training process. Although the shared parameter size (18.64 MB) and total transmission (708.32 MB) were slightly higher than some other models, these values are justified by the substantial gains in classification performance. The results underscore the efficacy of the FED-SPFD model in balancing the trade-offs between communication efficiency and model accuracy, making it a robust choice for federated learning applications in credit card fraud detection.

Secondly, a method involving the alteration of the usage of the dataset is employed to conduct the second type of longitudinal comparison experiment. Prior to the start of the experiment, a certain proportion of data is randomly sampled from each party to form a test set, and it is required that all comparison experiment groups are tested against this test set. Four sets of longitudinal comparative experiments were conducted, with the dataset selection method outlined as follows:

• Each party individually utilizes the remaining shared data to train a local model, which is subsequently tested on the testing set.
• Each party employs its entire remaining dataset, encompassing both shared and private data. After training their local models, the parties apply the SVI method to label the missing values, followed by testing on the testing set.
• All parties’ remaining shared data is consolidated into a single comprehensive dataset. A model is trained on this consolidated dataset, which is then evaluated on the testing set.
• The remaining shared data and private data from all parties are merged into a total dataset. For the missing values in the private data, the SVI method is employed for labeling. A model is subsequently trained on this total dataset and tested on the testing set.

The specific results are presented in the table below.

The longitudinal comparison experiment, as detailed in

Table 3. Model performance under vertical comparison.

	Comparison Factor	Recall (%)	Precision (%)	Accuracy (%)	F1-Score
Group
1		55.67	65.32	75.45	60.23
2		60.45	70.12	80.34	65.78
3		62.89	72.45	82.56	67.34
4		65.12	75.67	85.23	70.45
Our proposed		73.62	89.77	95.34	80.90

, highlights the effectiveness of the proposed FED-SPFD model in leveraging both shared and private data for enhanced fraud detection. Here the data highlighted in red represents the best, while the data highlighted in green represents the second best. The results indicate that the FED-SPFD model significantly outperforms all other experimental groups across all evaluation metrics. This superior performance underscores the model’s ability to effectively integrate heterogeneous data sources, thereby enhancing its predictive accuracy. Notably, the fourth group, which combined shared and private data from all parties, achieved the best results among the baseline groups, with a recall of 65.12%, precision of 75.67%, accuracy of 85.23%, and F1-score of 70.45%. However, the FED-SPFD model’s performance surpasses even this group, demonstrating the advantages of its federated learning framework in addressing data heterogeneity and privacy concerns. These findings affirm the robustness and efficacy of the FED-SPFD model in real-world applications where data are distributed across multiple parties with varying data characteristics.

4.7. Ablation Study

To verify the impact of each component of the proposed FED-SPFD model on the classification performance and to eliminate redundant parts, this study conducts ablation experiments by selectively removing certain parts of the model and observing how these removals affect overall performance.

1. w.o.private-decoder In this experiment, the private decoder component is removed to evaluate the representational capability of private autoencoding for private data.

2. w.o.p-n loss In this experiment, the p-n loss component is eliminated, meaning that the alignment of private embeddings with the standard normal distribution is no longer performed.

3. w.o.alg loss In this experiment, the alg loss component is omitted to assess the effects when the shared embedding of different parties is not aligned, thereby examining the influence of the alignment mechanism on the consistency of multi-party embeddings.

4. w.mmd loss For the feature alignment with shared data, the proposed privacy-preserving method based on sufficient statistics is replaced with the full-feature MK-MMD loss. It is important to note that this comparison serves as a “what-if” analysis against a non-private upper bound for alignment performance, as MMD operates on sample-level features and would violate the core privacy premise of federated learning by requiring raw data sharing. This ablation helps evaluate the performance trade-off between privacy preservation and alignment effectiveness.

5. w.o.SMOTE In this experiment, the SMOTE resampling strategy is removed. By omitting this strategy, the impact of class balancing techniques on model performance is assessed.

The ablation study, as illustrated in

Table 4. Ablation experiment.

	Comparison Factor	Recall (%)	Precision (%)	Accuracy (%)	F1-Score
Group
w.o.private-decoder		68.45	74.32	79.12	78.45
w.o.p-n loss		66.78	70.38	77.47	75.23
w.o.alg loss		62.12	68.91	72.65	70.45
w.mmd loss		70.89	75.66	80.54	79.78
w.o.SMOTE		60.12	65.45	70.67	68.23
Our proposed		73.62	89.77	95.34	80.90

, provides a comprehensive analysis of the contributions of individual components within the FED-SPFD model to its overall classification performance. The results reveal that the complete FED-SPFD model, with all components intact, achieves the highest performance indicators, underscoring the synergistic effect of its integrated components. Notably, the removal of the private decoder component results in a noticeable decline in performance, with a recall of 68.45% and an F1-score of 78.45%, indicating the critical role of private autoencoding in capturing nuanced data representations. Similarly, the absence of p-n loss, which aligns private embeddings with a standard normal distribution, leads to a further reduction in performance metrics, highlighting its importance in maintaining consistent feature distributions. The omission of alg loss, responsible for aligning shared embeddings across parties, results in the most significant drop in performance, emphasizing the necessity of this alignment mechanism for effective multi-party collaboration.

The w.mmd loss comparison reveals particularly important insights about the privacy–performance trade-off inherent in federated learning. While replacing our sufficient statistics approach with MMD-based alignment yields performance metrics (70.89% recall and 79.78% F1-score) that approach but do not exceed our proposed method, this comparison must be interpreted as a non-private upper-bound analysis. The MMD approach requires sample-level feature sharing, fundamentally violating the privacy constraints that are central to federated learning applications. Therefore, the fact that our privacy-preserving sufficient statistics method achieves superior performance (73.62% recall and 80.90% F1-score) while maintaining strict privacy guarantees demonstrates a favorable balance between alignment effectiveness and privacy preservation—a critical advantage for real-world deployment in privacy-sensitive financial applications.

Lastly, the exclusion of the SMOTE resampling strategy markedly diminishes the model’s ability to handle class imbalance, as evidenced by the lowest recall and F1-score among the ablated models. These findings collectively affirm the integral role of each component in enhancing the FED-SPFD model’s robustness and accuracy in fraud detection tasks while maintaining essential privacy protections.

5. Discussion

The experimental results demonstrate that the FED-SPFD model achieves significant improvements over existing federated learning approaches in fraud detection tasks. The model attained a recall rate of 73.62%, representing a 3.5% improvement over the best-performing baseline (pFedMe at 70.12%), while simultaneously maintaining high precision (89.77%) and F1-score (80.90%). This performance gain is particularly noteworthy given the challenging nature of fraud detection under heterogeneous data conditions.

The superior performance can be attributed to several key innovations in our approach. First, the share–private (S–P) segmentation methodology enables effective utilization of both common fraud indicators across institutions and institution-specific private features. This dual-encoding strategy allows the model to capture comprehensive fraud patterns while preserving data privacy—a critical advancement over traditional federated learning approaches that typically treat all features uniformly.

Second, the statistical alignment mechanism for shared features addresses a fundamental challenge in heterogeneous federated learning. By aligning local embeddings through sufficient statistics rather than raw data sharing, the model achieves feature distribution consistency without compromising privacy. The t-SNE visualizations clearly demonstrate the effectiveness of this approach, showing how initially disparate feature distributions from different parties converge into a unified embedding space after training.

5.1. Practical Implications

The FED-SPFD model proposed in this study offers substantial practical value for credit card fraud detection in the financial industry, addressing core pain points faced by institutions, customers, and regulators:

• For financial institutions (e.g., banks and payment service providers), the model enables collaborative fraud detection without sharing raw customer data—a critical advantage in contexts where data privacy regulations (e.g., GDPR and China’s Personal Information Protection Law) strictly prohibit arbitrary data sharing. By aligning heterogeneous shared features via local sufficient statistics and stabilizing private feature distributions through Gaussian alignment, the model allows institutions to leverage multi-party data to improve fraud recall (73.62% in our experiments) while retaining control over their exclusive business data (e.g., institution-specific customer credit metrics). This not only reduces economic losses from fraud but also avoids the operational risks of non-compliance with privacy laws.
• For customers, the model enhances the security of credit card transactions by enabling more accurate and real-time anomaly interception—particularly crucial given the adaptability of fraudsters. The privacy-preserving design also ensures that personal sensitive information (e.g., income and family status) remains within the institution that collects it, mitigating the risk of identity theft or data breaches.
• For regulators, the FED-SPFD framework provides a compliant paradigm for cross-institutional risk collaboration. It demonstrates how federated learning can balance “data sharing for risk control” and “privacy protection,” offering a reference for formulating industry standards for financial fraud detection under distributed data conditions.

5.2. Research Limitations

Despite its contributions, this study has several limitations that should be acknowledged:

• The representativeness and timeliness of the dataset are subject to certain limitations. We selected a real dataset from Kaggle, which has a relatively high level of credibility and can provide good evidence for the experimental conclusions. But if real-time transaction flows from different institutions can be used, it can better fully reflect the dynamic characteristics of credit card fraud in the real world and the wider heterogeneity of data from hundreds of small and medium-sized financial institutions.
• Model deployment complexity and efficiency need further optimization. The FED-SPFD model integrates multiple components—shared encoding, private autoencoders, KL divergence alignment, and FedAvg aggregation—which increases the computational burden on local institutions—especially those with limited computing resources (e.g., regional banks). Additionally, the warm-start pre-training and multiple local update steps may extend the model’s training cycle, making it less suitable for scenarios requiring ultra-low-latency fraud detection (e.g., real-time online transactions).
• The simulated data heterogeneity may not fully align with real institutional differences in banking scenarios. While we simulated multi-party heterogeneity by partitioning the Kaggle dataset into three parties with distinct shared/private feature sets (19 shared features + party-specific private features), this approach cannot replicate the full complexity of real-world bank transaction data differences. In practice, financial institutions (e.g., regional community banks vs. large national banks and domestic vs. cross-border payment platforms) exhibit far more nuanced and impactful heterogeneities than what is captured by feature quantity or distribution alone: these include institution-specific regulatory compliance requirements (e.g., varying rules for collecting customer geolocation data), customized risk assessment protocols (e.g., some banks prioritize asset status while others focus on real-time transaction behavior), divergent customer demographics (e.g., a regional bank serving rural users vs. a platform targeting young urban consumers), and unique operational data processing pipelines (e.g., differences in how transaction time stamps or merchant categories are encoded). Our current simulation, which primarily relies on “shared core features + private supplementary features” to mimic heterogeneity, fails to capture these institution-specific contextual differences. This gap means that while the FED-SPFD model performs well in the controlled heterogeneous environment of our experiments, its adaptability to the more complex, context-rich heterogeneities of real banking institutions may require further validation—for instance, the model may need additional adjustments to accommodate institution-specific data encoding rules or regulatory constraints when deployed across diverse financial entities.

5.3. Suggestions for Future Work

• Integration of advanced optimization techniques for federated training: The current model uses stochastic gradient descent (SGD) for local updates and FedAvg for parameter aggregation. Future work can explore more sophisticated optimization methods—such as adaptive optimizers (e.g., AdamW and RMSprop)—to accelerate local convergence or federated aggregation algorithms with communication compression (e.g., FedNova and SCAFFOLD) to reduce parameter transmission volume. This would improve the model’s efficiency for resource-constrained institutions and real-time scenarios.
• Development of explainable AI (XAI)-enhanced federated fraud detection: The FED-SPFD model, like most deep learning-based fraud detectors, lacks interpretability—financial institutions cannot easily explain why a transaction is classified as fraudulent (a key requirement for regulatory audits and customer dispute resolution). Future work can integrate XAI techniques (e.g., SHAP and LIME) into the model: for example, adding an interpretability module to the classifier that outputs feature importance scores while preserving privacy.
• Expanding to diverse data, federation scales, and real institutional contexts: Future experiments should leverage collaborative efforts with multiple financial institutions to access real-world bank transaction data, validating the model’s performance under genuine institutional heterogeneity (e.g., varying regulatory compliance rules, customized risk assessment protocols, and divergent customer demographics across banks). This addresses the gap between current simulated heterogeneity and real institutional differences, ensuring the model adapts to context-rich real banking scenarios. Second, extending the model to handle multi-modal data—combining numerical transaction features with customer behavior sequences (e.g., login frequency) or device fingerprint data—via modality-specific encoders would further enhance fraud detection capability. For large-scale federations, developing dynamic shared feature selection using federated mutual information algorithms could align with varying data collection rules.

6. Conclusions

In conclusion, this study presents the FED-SPFD model, a novel federated learning framework designed to enhance credit card fraud detection under heterogeneous data conditions. Through comprehensive experiments, including horizontal and longitudinal comparisons, as well as ablation studies, the FED-SPFD model demonstrated superior performance in terms of recall, precision, accuracy, and F1-score compared to existing federated learning frameworks. The model’s ability to effectively integrate shared and private data, while addressing data heterogeneity and privacy concerns, underscores its robustness and efficacy in real-world applications. The ablation study further validated the critical contributions of each component within the model, highlighting the importance of private autoencoding, alignment mechanisms, and class balancing techniques in achieving optimal performance. These findings suggest that the FED-SPFD model offers a promising solution for enhancing fraud detection capabilities in distributed and privacy-sensitive environments.