Estimating Policy Impact in a Difference-in-Differences Hazard Model: A Simulation Study
Abstract
1. Introduction
2. The Difference-in-Differences Hazard Model
2.1. The Difference-in-Differences Regression Model
2.2. The Difference-in-Differences Hazard Model
2.3. Estimators of the Policy Impact Parameter
3. Simulation Setup
4. Simulation Results
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPMLE | Nonparametric maximum likelihood estimator |
| DiD | Difference-in-differences |
| Cox_3S | Three-step Cox estimator proposed by Wu and Wen (2022) |
| Cox_TV | Cox proportional hazard estimator extended to time-varying covariates by Therneau and Grambsch (2000) |
| LinProb | Linear probability estimator |
References
- An, Mark, and Zhikun Qi. 2012. Competing Risks Models using Mortgage Duration Data under the Proportional Hazards Assumption. Journal of Real Estate Research 35: 1–26. [Google Scholar] [CrossRef]
- Angrist, Joshua, and Jörn-Steffen Pischke. 2009. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton: Princeton University Press. [Google Scholar]
- Ashin, Taha. 2021. Red Tape, Greenleaf: Creditor Behavior Under Costly Collateral Enforcement. Working Paper. Available online: https://ssrn.com/abstract=3928964 (accessed on 11 September 2025).
- Baker, Michael, and Angelo Melino. 2000. Duration dependence and nonparametric heterogeneity: A Monte Carlo Experiment. Journal of Econometrics 96: 357–93. [Google Scholar] [CrossRef]
- Card, David, and Alan Kreuger. 1994. Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania. American Economic Review 84: 772–93. [Google Scholar]
- Conti, Simon, I-Chun Thomas, Judith Hagedom, Benjamin Chung, Glenn Chertow, Todd Wagner, James Brooks, Sandy Srivivas, and John Leppert. 2013. Utilization of cytoreductive nephrectomy and patient survival in the targeted therapy era. International Journal of Cancer 134: 2245–52. [Google Scholar] [CrossRef] [PubMed]
- Cox, David. 1972. Regression Models and Life Tables. Journal of the Royal Statistical Society, Series B 34: 187–220. [Google Scholar] [CrossRef]
- Deng, Yonghend, John Quigley, and Robert Van Order. 2000. Mortgage Termations, Heterogeneity and the Exercise of Mortgage Options. Econometrica 68: 275–307. [Google Scholar] [CrossRef]
- Feng, Li, and Tim Sass. 2018. The Impact of Incentives to Recruit and Retain Teachers in “Hard-to-Staff” Subjects. Journal of Policy Analysis and Management 37: 112–35. [Google Scholar] [CrossRef]
- Gaure, Simen, Knut Roed, and Tao Zhang. 2007. Time and Causality: A Monte Carlo Assessment of the Timing-of-Events Approach. Journal of Econometrics 141: 1159–95. [Google Scholar] [CrossRef]
- Han, Aaron, and Jerry Hausman. 1990. Flexible Parametric Estimation of Duration and Competing Risk Models. Journal of Applied Econometrics 5: 325–53. [Google Scholar] [CrossRef]
- Heckman, James, and Burton Singer. 1984. A Method for Minimizing the Impact of Distributional Assumptions in Econometric Models for Duration Data. Econometrica 52: 271–320. [Google Scholar] [CrossRef]
- Henningsen, Arne, and Ott Toomet. 2011. maxLik: A package for maximum likelihood estimation in R. Computational Statistics 26: 443–58. [Google Scholar] [CrossRef]
- Hsieh, David. 2025. Estimating Proportional Hazards in Default and Prepayment of Personal Loans with Unobserved Heterogeneity. Working Paper. Available online: https://ssrn.com/abstract=4266207 (accessed on 11 September 2025).
- Mastrobuoni, Giovanni, and Paolo Pinotti. 2015. Legal Status and the Criminal Activity of Immigrants. American Economic Journal: Applied Economics 7: 175–206. [Google Scholar] [CrossRef]
- O’Malley, Terry. 2021. The Impact of Repossession Risk on Mortgage Default. Journal of Finance 76: 623–50. [Google Scholar] [CrossRef]
- Sueyoshi, Glenn. 1992. Semiparametric Proportional Hazards Estimation of Competing Risks Models with Time-Varying Covariates. Journal of Econometrics 51: 25–58. [Google Scholar] [CrossRef]
- Therneau, Terry. 2022. A Package for Survival Analysis in R. R Package Version 3.3-1. Available online: https://CRAN.R-project.org/package=survival (accessed on 11 September 2025).
- Therneau, Terry, and Patricia Grambsch. 2000. Modeling Survival Data: Extending the Cox Model. New York: Springer. ISBN 0-387-98784-3. [Google Scholar]
- Wu, Lawrence, and Fangqi Wen. 2022. Hazard Versus Linear Probability Difference-in-Differences Estimators for Demographic Processes. Demography 59: 1911–28. [Google Scholar] [CrossRef] [PubMed]

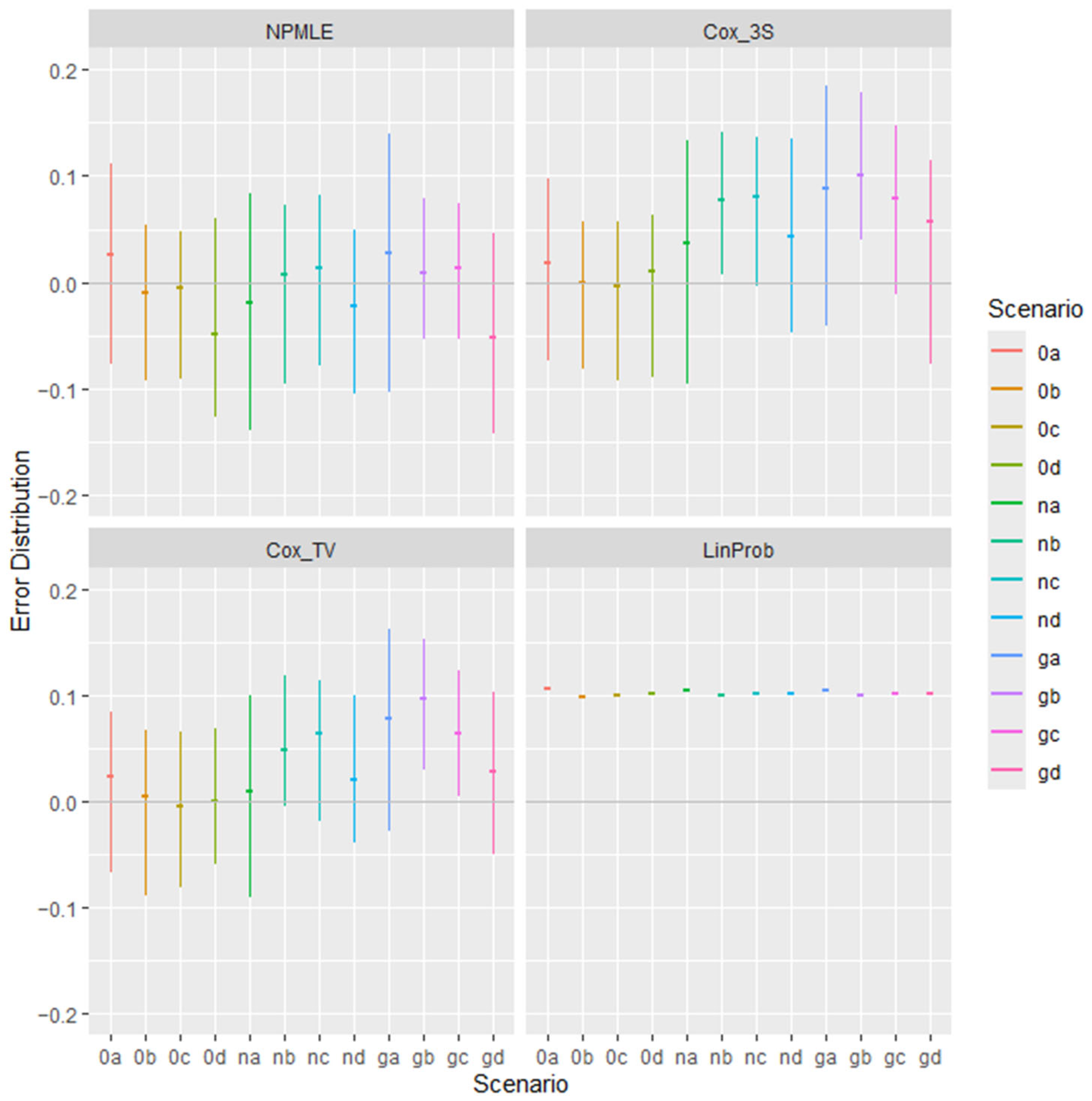
| Panel A. Mean Error of Estimators in 100 Trials | ||||
| Scenario | NPMLE | Cox_3S | Cox_TV | LinProb |
| 0a | 0.00414 | −0.00914 | −0.00862 | 0.10492 |
| 0b | −0.01072 | −0.00587 | −0.00237 | 0.09741 |
| 0c | −0.00592 | −0.00103 | 0.00071 | 0.10014 |
| 0d | −0.03560 | −0.00198 | 0.00183 | 0.10064 |
| na | 0.00283 | 0.03994 | 0.02711 | 0.10424 |
| nb | −0.01157 | 0.07143 | 0.05451 | 0.09928 |
| nc | 0.00585 | 0.06379 | 0.05306 | 0.10091 |
| nd | −0.02241 | 0.04902 | 0.03624 | 0.10134 |
| ga | 0.02163 | 0.06390 | 0.05120 | 0.10454 |
| gb | −0.00340 | 0.09586 | 0.07646 | 0.09950 |
| gc | −0.00574 | 0.06923 | 0.05134 | 0.10089 |
| gd | −0.02193 | 0.05632 | 0.03678 | 0.10132 |
| The mean error is the average estimate minus the true parameter (−0.1) in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the lowest absolute mean error in each row. | ||||
| Panel B. Standard Deviation of Estimators in 100 Trials | ||||
| Scenario | NPMLE | Cox_3S | Cox_TV | LinProb |
| 0a | 0.06954 | 0.05480 | 0.05158 | 0.00063 |
| 0b | 0.04197 | 0.04236 | 0.03891 | 0.00061 |
| 0c | 0.05240 | 0.05354 | 0.04744 | 0.00057 |
| 0d | 0.08727 | 0.05163 | 0.04341 | 0.00072 |
| na | 0.08643 | 0.06542 | 0.06267 | 0.00062 |
| nb | 0.05970 | 0.04780 | 0.04806 | 0.00059 |
| nc | 0.05015 | 0.05217 | 0.04375 | 0.00045 |
| nd | 0.08124 | 0.05798 | 0.04675 | 0.00061 |
| ga | 0.07356 | 0.06755 | 0.06122 | 0.00062 |
| gb | 0.05481 | 0.05081 | 0.04701 | 0.00059 |
| gc | 0.05684 | 0.05138 | 0.05148 | 0.00055 |
| gd | 0.07883 | 0.05210 | 0.03823 | 0.00053 |
| The standard deviation is the sample standard deviation of the estimator in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the smallest standard deviation in each row. | ||||
| Panel C. Root Mean Squared Error of Estimators in 100 Trials | ||||
| Scenario | NPMLE | Cox_3S | Cox_TV | LinProb |
| 0a | 0.06931 | 0.05529 | 0.05204 | 0.10492 |
| 0b | 0.04312 | 0.04255 | 0.03878 | 0.09741 |
| 0c | 0.05247 | 0.05328 | 0.04721 | 0.10014 |
| 0d | 0.09385 | 0.05141 | 0.04323 | 0.10064 |
| na | 0.08604 | 0.07637 | 0.06800 | 0.10424 |
| nb | 0.06052 | 0.08582 | 0.07251 | 0.09928 |
| nc | 0.05024 | 0.08224 | 0.06863 | 0.10091 |
| nd | 0.08388 | 0.07571 | 0.05897 | 0.10134 |
| ga | 0.07632 | 0.09274 | 0.07957 | 0.10454 |
| gb | 0.05465 | 0.10837 | 0.08963 | 0.09950 |
| gc | 0.05684 | 0.08606 | 0.07252 | 0.10089 |
| gd | 0.08145 | 0.07654 | 0.05291 | 0.10132 |
| Root mean square error (RMSE) is the square root of the mean squared estimation error in the 100 trials of each of the twelve scenarios. Green denotes the estimator with the lowest RMSE in each row. | ||||
| Panel A. Mean Error in 100 Trials | ||||
| Scenario | NPMLE | Cox_3S | Cox_TV | LinProb |
| 0a | 0.02510 | 0.01567 | 0.01672 | 0.10520 |
| 0b | −0.01995 | −0.01315 | −0.00993 | 0.09729 |
| 0c | −0.01204 | −0.00897 | −0.00286 | 0.10003 |
| 0d | −0.05055 | −0.00339 | 0.00181 | 0.10062 |
| na | −0.02932 | 0.01975 | 0.00624 | 0.10415 |
| nb | −0.00785 | 0.07007 | 0.05705 | 0.09933 |
| nc | 0.00691 | 0.06818 | 0.05481 | 0.10092 |
| nd | −0.02222 | 0.03725 | 0.02986 | 0.10128 |
| ga | 0.00968 | 0.07392 | 0.06150 | 0.10470 |
| gb | 0.00919 | 0.10213 | 0.08737 | 0.09965 |
| gc | 0.00547 | 0.07514 | 0.06582 | 0.10107 |
| gd | −0.06225 | 0.05472 | 0.02338 | 0.10113 |
| The mean error is the average estimate minus the true parameter (−0.1) in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the lowest ab-solute mean error in each row. | ||||
| Panel B. Standard Deviation of Error in 100 Trials | ||||
| Scenario | NPMLE | Cox_3S | Cox_TV | LinProb |
| 0a | 0.15775 | 0.13639 | 0.12467 | 0.00148 |
| 0b | 0.10634 | 0.09910 | 0.09921 | 0.00152 |
| 0c | 0.12082 | 0.12639 | 0.11766 | 0.00140 |
| 0d | 0.17306 | 0.12399 | 0.09874 | 0.00155 |
| na | 0.17562 | 0.16060 | 0.14456 | 0.00140 |
| nb | 0.12324 | 0.11617 | 0.10972 | 0.00138 |
| nc | 0.11187 | 0.11295 | 0.10568 | 0.00110 |
| nd | 0.15796 | 0.13624 | 0.10838 | 0.00136 |
| ga | 0.17670 | 0.15347 | 0.14843 | 0.00142 |
| gb | 0.10789 | 0.10845 | 0.10097 | 0.00134 |
| gc | 0.11071 | 0.11851 | 0.10296 | 0.00112 |
| gd | 0.17668 | 0.12664 | 0.10759 | 0.00145 |
| The standard deviation is the sample standard deviation of the estimator in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the smallest standard deviation in each row. | ||||
| Panel C. Root Mean Squared Error in 100 Trials | ||||
| Scenario | NPMLE | Cox_3S | Cox_TV | LinProb |
| 0a | 0.15896 | 0.13660 | 0.12517 | 0.10492 |
| 0b | 0.10767 | 0.09948 | 0.09921 | 0.09741 |
| 0c | 0.12081 | 0.12608 | 0.11711 | 0.10014 |
| 0d | 0.17946 | 0.12342 | 0.09827 | 0.10064 |
| na | 0.17719 | 0.16102 | 0.14397 | 0.10424 |
| nb | 0.12287 | 0.13517 | 0.12317 | 0.09928 |
| nc | 0.11153 | 0.13145 | 0.11858 | 0.10091 |
| nd | 0.15873 | 0.14058 | 0.11190 | 0.10134 |
| ga | 0.17608 | 0.16965 | 0.15998 | 0.10454 |
| gb | 0.10774 | 0.14858 | 0.13314 | 0.09950 |
| gc | 0.11029 | 0.13983 | 0.12177 | 0.10089 |
| gd | 0.18649 | 0.13091 | 0.10957 | 0.10132 |
| Root mean square error (RMSE) is the square root of the mean squared estimation error in the 100 trials of each of the twelve scenarios. Green denotes the estimator with the lowest RMSE in each row. | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, D.A. Estimating Policy Impact in a Difference-in-Differences Hazard Model: A Simulation Study. Risks 2025, 13, 200. https://doi.org/10.3390/risks13100200
Hsieh DA. Estimating Policy Impact in a Difference-in-Differences Hazard Model: A Simulation Study. Risks. 2025; 13(10):200. https://doi.org/10.3390/risks13100200
Chicago/Turabian StyleHsieh, David A. 2025. "Estimating Policy Impact in a Difference-in-Differences Hazard Model: A Simulation Study" Risks 13, no. 10: 200. https://doi.org/10.3390/risks13100200
APA StyleHsieh, D. A. (2025). Estimating Policy Impact in a Difference-in-Differences Hazard Model: A Simulation Study. Risks, 13(10), 200. https://doi.org/10.3390/risks13100200




