Using Daily Stock Returns to Estimate the Unconditional and Conditional Variances of Lower-Frequency Stock Returns

Abstract

If intraday price data are unavailable, then using daily returns to construct realized measures of the variances of lower-frequency returns is a natural substitute for using high-frequency returns in this context. Notably, a suitable application of this approach yields realized measures that are unbiased estimators of the unconditional and conditional variances of holding period returns for any investment horizon. I use a long sample of daily S&P 500 index returns to investigate the merits of constructing realized measures in this fashion. First, I conduct a Monte Carlo study using a data generating process that reproduces the key dynamic properties of index returns. The results of the study suggest that using realized measures constructed from daily returns to estimate the conditional and unconditional variances of lower-frequency returns should lead to substantial increases in efficiency. Next, I fit a multiplicative error model to the realized measures for weekly and monthly index returns to obtain out-of-sample forecasts of their conditional variances. Using the forecasts produced by a generalized autoregressive conditional heteroskedasticity model as a benchmark, I find that the forecasts produced by the multiplicative error model always generate lower mean absolute errors. Furthermore, the improvements in forecasting performance are statistically significant in most cases.

1. Introduction

Realized variances are ex-post measures of return variation that are typically constructed by summing the squared values of high-frequency log returns (see, e.g., Andersen and Bollerslev 1998; Andersen et al. 2003; Barndorff-Nielsen et al. 2008). The use of realized variances has revolutionized methods of modeling and forecasting volatility over the past two decades. Indeed, realized variances are now employed in a wide variety of intriguing applications. Some recent examples include forecasting volatility for stocks included the S&P 500 index via machine learning methods (Zhu et al. 2023), forecasting volatility for international real estate investment trusts (Bonato et al. 2022), modeling time-varying conditional skewness in equity markets (Kirby 2024), pricing options on the Chicago Board Options Exchange volatility index (Tong and Huang 2021), developing dynamic tail-risk models to aid in measuring and managing financial risk (Chen et al. 2023), and studying volatility spillovers across cryptocurrency markets (Ben Ameur et al. 2024).

Many of the econometric studies that employ realized variances are conducted using either daily log returns or daily simple returns (see, e.g., Gorgi et al. 2019; Hansen et al. 2012, 2024; Noureldin 2022; Noureldin et al. 2012). Researchers seldom feel the need to differentiate between simple returns and log returns in such studies because doing so is unnecessary from an empirical perspective. If the holding period for a stock or stock index is a single day, then the difference between the variance of a simple return and the variance of the corresponding log return will typically be negligible. However, the differences between the statistical properties of simple returns and those of log returns become more pronounced as the holding period increases. Thus, they are unlikely to be negligible for research that addresses asset pricing, portfolio optimization, and related topics, which is usually conducted using simple returns for weekly, monthly, or quarterly holding periods (see, e.g., Avramov et al. 2006; Kirby and Ostdiek 2012; Yogo 2006).

For instance, the covariance matrix of simple returns plays a central role in Markowitz (1952) portfolio selection. Although it would be straightforward to use realized variances computed from log returns to construct an estimator of the covariance matrix of simple returns, the estimator would typically be biased given that simple returns are nonlinearly related to log returns. Consider the case in which log returns are normally distributed. Because simple returns have a lognormal distribution under these circumstances, the variance of simple returns is typically higher than the variance of log returns in this case. This clearly suggests that it would be useful to develop a procedure for constructing realized variances that are unbiased estimators of the variances of simple returns.

More broadly, it is important to note that the high-frequency data needed to construct daily realized variances may not be available for the full sample period of interest. The first year of the Trade and Quote data provided by the New York Stock Exchange is 1993. In contrast, the coverage of the daily stock file of the Center for Research in Security Prices begins in 1926. The widespread availability of daily historical data makes it well suited for estimating the unconditional and conditional variances of lower-frequency stock returns. I investigate this approach using a new technique for constructing realized measures. Unlike the conventional construction technique pioneered by Andersen and Bollerslev (1998), the new technique delivers realized measures that are unbiased estimators of the unconditional and conditional variances of simple returns in a discrete time setting under relatively mild assumptions that are frequently invoked in the volatility modeling literature.

I begin by conducting a Monte Carlo study of the relative estimation errors that result from using the new and conventional realized measures as estimators of the unconditional and conditional variances of simple returns and log returns for a range of different holding periods. The results of the study demonstrate that my technique for constructing realized measures of the variances of simple returns works as intended. I find no evidence of bias for any holding period and the proposed realized measures deliver improvements in estimation efficiency that are comparable to those produced by conventional realized measures of the variances of log returns.

To develop further insights, I use S&P 500 index data to investigate the performance of pseudo out-of-sample variance forecasts that are constructed using the new realized measures. The empirical analysis employs the generalized autoregressive conditional heteroskedasticity (GARCH) model of Bollerslev (1986) as a benchmark and is conducted in a manner that isolates the incremental gains from using the new realized measures for modeling purposes. First, I fit a GARCH(1,1) model to simple returns for both weekly and monthly holding periods. Next, I replace the squared demeaned simple returns in the recurrence relation for the conditional variance under the GARCH(1,1) model with the corresponding realized measures. Finally, If fit the resultant specification, which is a multiplicative error model (MEM) of the type introduced by Engle (2002), to the same sample of simple returns for weekly and monthly holding periods.

Because the only difference between the recurrence relations for the conditional variances under the GARCH(1,1) and MEM(1,1) specifications is that former employs squared demeaned simple returns and the latter employs realized measures, the performance advantage of the MEM(1,1) specification (if any) is due to the incremental gains from using realized measures. I use the Giacomini and White (2006) test of equal predictive ability to assess whether the differences in performance are statistically significant. As anticipated, I find that the MEM forecasts produce smaller mean errors, smaller mean absolute errors, and smaller root mean square errors than the GARCH forecasts for every forecast horizon under consideration at both the weekly frequency and the monthly frequency. However, the results for the monthly observations are stronger from the standpoint of statistical significance. I find that the smallest t-statistic produced by the test of equal predictive ability is 2.61 in this case. Because I reject the hypothesis that the GARCH forecasts of monthly variances are just as accurate as the MEM forecasts of monthly variances at the 1% significance level, irrespective of the forecast horizon, I conclude that the proposed realized measures of the variances of simple returns deliver meaningful performance gains.

Although these results are illustrative, the proposed realized measures could obviously be exploited in other ways. For example, researchers have developed a variety of specifications that use conventional realized measures to model volatility dynamics, such as the heterogeneous autoregressive volatility (HAR) model of Corsi (2009), the high-frequency-based (HEAVY) model of Shephard and Sheppard (2010), and the realized GARCH model of Hansen et al. (2012). By replacing the realized measures constructed from high-frequency log returns with realized measures constructed from daily simple returns, any of these specifications could be used to model and forecast the conditional variances of simple returns for weekly, monthly, or quarterly holding periods.

It is also clear that the proposed realized measures can be employed to model and forecast the conditional variances of lower-frequency returns for any asset or commodity for which daily price data are readily available (e.g., the Eurodollar exchange rate, crude oil, or Bitcoin). Of course, using this approach for seasonal commodities would require a volatility model that is capable of capturing seasonality, such as a periodic MEM analog of the periodic GARCH model of Bollerslev and Ghysels (1996). But implementing this extension should be relatively straightforward from an econometric perspective.

The rest of the article is organized as follows. Section 2 shows how to construct realized measures that are unbiased estimators of the unconditional and conditional variances of simple returns. Section 3 discusses the results of the Monte Carlo study. Section 4 describes the GARCH(1,1) and MEM(1,1) specifications used to forecast conditional variances for the S&P 500 index and presents the results of the pseudo out-of-sample performance comparisons. Finally, Section 5 offers some concluding remarks.

2. Realized Measures

Suppose that $P\left(t_i\right)$ denotes the price of a stock or stock index at time $t_i$. Further suppose that the price is recorded at a fixed frequency such that there is always one time period between successive elements of the sequence ${\left\{P\left(t_i\right)\right\}}_{i=0}^{KT}$, where $K>1$ and $T>0$ are integers to be specified later. To develop realized measures that are unbiased estimators of the variance of simple returns in a discrete-time setting, I invoke assumptions that eliminate the need to employ the type of fill-in asymptotics that underpin the arguments of Andersen et al. (2003). Henceforth, $\mathcal{F}\left(t_i\right)$ denotes the information set that contains all prices realized prior to time $t_{i+1}$. I presume throughout the discussion that log returns and simple returns are weakly-stationary random variables.

2.1. Realized Measures Computed from Log Returns

Andersen and Bollerslev (1998) pioneered the use of high-frequency log returns to construct realized measures. It is easy to formulate discrete-time analogs of the basic arguments that motivate their methodology. Let $\tilde{r}(t_i,t_{i+k})=logP\left(t_{i+k}\right)-logP\left(t_i\right)$ denote the log return for the k-period interval that begins at time $t_i$ and ends at time $t_{i+k}$, where $0\le k\le K$. I assume for simplicity that $\mathrm{E}\left[\tilde{r}(t_i,t_{i+1})\right]=0$ and use ${\tilde{\sigma }}_K^2:=\mathrm{var}\left(\tilde{r}(t_i,t_{i+K})\right)$ to denote the variance of K-period log returns.

The starting point is to consider a scenario in which the single-period log returns are serially uncorrelated. Because $\tilde{r}(t_i,t_{i+K})$ can be expressed as $\tilde{r}(t_i,t_{i+K})={\sum }_{j=1}^K\tilde{r}(t_{i+j-1},t_{i+j})$, it follows immediately that

$${\tilde{\sigma }}_K={\left(\mathrm{E}\left[\sum _{j=1}^K{\tilde{r}}^2(t_{i+j-1},t_{i+j})\right]\right)}^{MM1/2},$$

(1)

where ${\tilde{r}}^2(t_{i+j-1},t_{i+j})$ denotes the square of $\tilde{r}(t_{i+j-1},t_{i+j})$. Thus, $\tilde{v}(t_i,t_{i+K})={\left({\sum }_{j=1}^K{\tilde{r}}^2(t_{i+j-1},t_{i+j})\right)}^{MM1/2}$ is a realized measure of volatility that satisfies $\mathrm{E}\left[{\tilde{v}}^2(t_i,t_{i+K})\right]={\tilde{\sigma }}_K^2$.

It is also easy to see that $T^{-1}{\sum }_{j=1}^T{\tilde{v}}^2(t_{(j-1)K},t_{jK})$ and $T^{-1}{\sum }_{j=1}^T{\tilde{r}}^2(t_{(j-1)K},t_{jK})$ are unbiased estimators of ${\tilde{\sigma }}_K^2$. But the former is a lot more efficient than the latter in general. More broadly, $\tilde{v}(t_i,t_{i+K})$ satisfies $\mathrm{E}\left[{\tilde{v}}^2(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right)]=\mathrm{var}\left(\tilde{r}(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right))$ under suitable assumptions about the dynamic properties of log returns. To grasp the basic requirements for conditional unbiasedness, let ${\tilde{\sigma }}^2(t_i,t_{i+K}):=\mathrm{var}\left(\tilde{r}(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right))$ and think about a data generating process (DGP) of the form

$$\tilde{r}(t_i,t_{i+1})=\tilde{\sigma }(t_i,t_{i+1})\tilde{z}(t_i,t_{i+1}),i=0,1,\dots ,KT-1,$$

(2)

where $\tilde{\sigma }(t_i,t_{i+1})\in \mathcal{F}\left(t_i\right)$, $\mathrm{E}\left[\tilde{z}(t_i,t_{i+1})\right|\mathcal{F}\left(t_i\right)]=0$, and $\mathrm{E}\left[{\tilde{z}}^2(t_i,t_{i+1})\right|\mathcal{F}\left(t_i\right)]=1$ for all i. For example, the DGP could be a GARCH(1,1) model (see Bollerslev 1986). Because a DGP of this form implies that $\mathrm{E}\left[\tilde{r}(t_i,t_{i+1})\tilde{r}(t_{i+j},t_{i+j+1})\right|\mathcal{F}\left(t_i\right)]=0$ for all $j\ne 0$, it follows that $\tilde{\sigma }(t_i,t_{i+K})={\left({\sum }_{j=1}^K\mathrm{E}\left[{\tilde{r}}^2(t_{i+j-1},t_{i+j})\right|\mathcal{F}\left(t_i\right)]\right)}^{MM1/2}$ by iterated expectations.

2.2. Realized Measures Computed from Simple Returns

In a typical finance application (portfolio optimization, risk management, etc.), the analysis focuses on simple returns rather than log returns. Furthermore, the simple returns of interest are often measured at relatively low frequencies (monthly observations, quarterly observations, etc.). I therefore propose a new strategy for constructing realized measures that are unbiased estimators of the unconditional and conditional variances of simple returns. Henceforth, simple returns are just called returns.

Let $r(t_i,t_{i+k})=P\left(t_{i+k}\right)/P\left(t_i\right)-1$ denote the return for the k-period interval that begins at time $t_i$ and ends at time $t_{i+k}$. By straightforward algebra, this quantity can be expressed as

$$r(t_i,t_{i+k})=\sum _{j=1}^{k}R(t_i,t_{i+j-1})r(t_{i+j-1},t_{i+j}),$$

(3)

where $R(t_i,t_{i+k})=P\left(t_{i+k}\right)/P\left(t_i\right)$ denotes the gross return for the k-period interval under consideration. I assume for simplicity that $\mathrm{E}\left[r(t_i,t_{i+1})\right]=0$ and explain how to relax this assumption later on.

Now let ${\sigma }_K^2:=\mathrm{var}\left(r(t_i,t_{i+K})\right)$, ${\sigma }^2(t_i,t_{i+K}):=\mathrm{var}\left(r(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right))$, and consider a scenario in which single-period returns satisfy

$$\mathrm{cov}(r(t_{i+j-1},t_{i+j}),R(t_i,t_{i+j-1})r(t_{i+k-1},t_{i+k})R(t_i,t_{i+k-1}))=0$$

(4)

for all $j>k\ge 1$. Under these circumstances,

$$v(t_i,t_{i+K})={\left(\sum _{j=1}^K{R}^2(t_i,t_{i+j-1})r^2(t_{i+j-1},t_{i+j})\right)}^{MM1/2}$$

(5)

is a realized measure of ${\sigma }_K$ that satisfies $\mathrm{E}\left[v^2(t_i,t_{i+K})\right]={\sigma }_K^2$. Furthermore, it is apparent that $v(t_i,t_{i+K})$ satisfies $\mathrm{E}\left[v^2(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right)]={\sigma }^2(t_i,t_{i+K})$ under suitable assumptions about the dynamic properties of returns. This is the case, for example, if the DGP takes the form

$$r(t_i,t_{i+1})=\sigma (t_i,t_{i+1})z(t_i,t_{i+1}),i=0,1,\dots ,KT-1,$$

(6)

where $\sigma (t_i,t_{i+1})\in \mathcal{F}\left(t_i\right)$, $\mathrm{E}\left[z(t_i,t_{i+1})\right|\mathcal{F}\left(t_i\right)]=0$, and $\mathrm{E}\left[z^2(t_i,t_{i+1})\right|\mathcal{F}\left(t_i\right)]=1$ for all i. To see why, simply note that

$$\mathrm{E}\left[R(t_i,t_{i+j-1})r(t_{i+j-1},t_{i+j})R(t_i,t_{i+k-1})r(t_{i+k-1},t_{i+k})\right|\mathcal{F}\left(t_i\right)]=0$$

(7)

for all $j\ge 1$, $k\ge 1$, and $j\ne k$ under the DGP in Equation (6).

2.3. Some Useful Extensions

The methodology can easily be modified to address situations in which the maintained assumptions are deemed too restrictive. For instance, if single-period returns display serial correlation, then a realized kernel approach can be used to construct the realized measures. Barndorff-Nielsen et al. (2008) show that this is an effective way of addressing the presence of serial correlation that is due to microstructure effects.

To illustrate, let J denote the lag truncation value employed by the realized kernel estimator of Barndorff-Nielsen et al. (2008). An analogous estimator for simple returns can be obtained by specifying $J<K$ and computing $v(t_i,t_{i+K})$ as

$$v(t_i,t_{i+K})={\left(\sum _{j=-J}^{J}w\left({\displaystyle \frac{j}{J+1}}\right)g_j(P\left(t_i\right),\dots ,P\left(t_{i+K}\right))\right)}^{MM1/2},$$

(8)

where

$$g_j(P\left(t_i\right),\dots ,P\left(t_{i+K}\right))=\sum _{l=\left|j\right|+1}^K{\displaystyle \frac{P\left(t_{i+l-1}\right)}{P\left(t_i\right)}}r(t_{i+l-1},t_{i+l}){\displaystyle \frac{P\left(t_{i+l-\left|j\right|-1}\right)}{P\left(t_i\right)}}r(t_{i+l-\left|j\right|-1},t_{i+l-\left|j\right|})$$

(9)

and

$$w\left(x\right)=\left\{\begin{array}{cc}1-6x^2+6{\left|x\right|}^3\hfill & 0\le \left|x\right|\le 1/2\hfill \\ 2{(1-|x\left|\right)}^3\hfill & 1/2\le \left|x\right|\le 1.\hfill \end{array}\right.$$

(10)

is the weight function for the Parzen kernel.

The assumption that expected returns are equal to zero can also be relaxed. Suppose, for instance, that $\mathrm{E}\left[r(t_i,t_{i+1})\right|\mathcal{F}\left(t_i\right)]=\mu$ for all i. In this case,

$$\mathrm{E}[{(1+\mu )}^{-k}R(t_i,t_{i+k})-1|\mathcal{F}\left(t_i\right)]=0$$

(11)

for all i and $k\ge 0$, so it is a simple matter to show that

$$\mathrm{var}\left(\left.{\displaystyle \frac{R(t_i,t_{i+K})}{{(1+\mu )}^K}}\right|\mathcal{F}\left(t_i\right)\right)=\mathrm{E}\left[\left.\sum _{j=1}^K{\left({\displaystyle \frac{R(t_i,t_{i+j-1})}{{(1+\mu )}^{j-1}}}\right)}^2{\left({\displaystyle \frac{r(t_{i+j-1},t_{i+j})-\mu }{1+\mu }}\right)}^2\right|\mathcal{F}\left(t_i\right)\right]$$

(12)

by mirroring the arguments for the $\mu =0$ case. The realized measure

$$v^{*}(t_i,t_{i+K})={\left(\sum _{j=1}^K{(1+\mu )}^{2(K-j)}{R}^2(t_i,t_{i+j-1}){(r(t_{i+j-1},t_{i+j})-\mu )}^2\right)}^{MM1/2}$$

(13)

therefore satisfies $\mathrm{E}\left[v^{*2}(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right)]=\mathrm{var}\left(r(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right))$.

It is clear that $v^2(t_i,t_{i+K})$ is a biased estimator of ${\sigma }^2(t_i,t_{i+K})$ for cases in which $\mu \ne 0$, just as ${\tilde{v}}^2(t_i,t_{i+K})$ is a biased estimator of ${\tilde{\sigma }}^2(t_i,t_{i+K})$ for cases in which $\mathrm{E}\left[\tilde{r}(t_i,t_{i+1})\right|\mathcal{F}\left(t_i\right)]\ne 0$. But the results also show how to implement a simple bias correction for $v^2(t_i,t_{i+K})$. In particular, a bias-corrected realized measure for returns can be obtained by substituting a consistent estimator of $\mathrm{E}\left[r(t_i,t_{i+1})\right]$ that is available at time $t_i$ for $\mu$ in Equation (13). The effect of this correction will typically be quite small for realized measures that are constructed from daily stock returns because the sample mean of daily returns is typically only a few basis points. This is the reason why studies that fit volatility models to daily stock returns often assume that expected returns are equal to zero (see, e.g., Visser 2011).

3. Monte Carlo Analysis

I use Monte Carlo integration to document the properties of the unbiased variance estimators discussed in Section 2. The DGP for the study is a well-known variant of the GARCH(1,1) model of Bollerslev (1986). In particular, I generate the single-period log returns from the model

$$\begin{array}{cc}\hfill \tilde{r}(t_i,t_{i+1})& =\kappa {\tilde{\sigma }}^2(t_i,t_{i+1})+\tilde{\sigma }(t_i,t_{i+1})\tilde{z}(t_i,t_{i+1}),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\tilde{\sigma }}^2(t_i,t_{i+1})& =\omega +\beta {\tilde{\sigma }}^2(t_{i-1},t_i)+\alpha {(\tilde{z}(t_{i-1},t_i)-\gamma \tilde{\sigma }(t_{i-1},t_i))}^2,\hfill \end{array}$$

(15)

where $\omega \ge 0$, $\beta \ge 0$, $\alpha \ge 0$, $(\beta +\alpha {\gamma }^2)<1$, and $\tilde{z}(t_i,t_{i+1})$ is an $\mathrm{NID}(0,1)$ random variable. This specification is well suited to Monte Carlo work because it allows ${\tilde{\sigma }}_K^2$, ${\sigma }_K^2$, ${\tilde{\sigma }}^2(t_i,t_{i+K})$, and ${\sigma }^2(t_i,t_{i+K})$ to be computed analytically.1

Daily S&P 500 index data for the years 1946 through 2023 (19,835 observations) are used to calibrate the DGP. The data are from two sources: the daily stock file of the Center for Research in Security Prices for 3 July 1962 to 29 December 2023 and a dataset compiled by Schwert (1990) for 2 January 1946 to 2 July 1962.2 First, I use the method of maximum likelihood to fit the model to daily log index returns subject to $\kappa =0$ and $\omega =0$.3 Second, I set the values of $\alpha$, $\beta$, and $\gamma$ in Equations (14) and (15) equal to their maximum likelihood estimates, generate $\{\tilde{r}{(t_i,t_{i+1}\}}_{i=0}^{KT-1}$ with $\kappa =0$ and $\omega =0$, and construct $\{r{(t_i,t_{i+1}\}}_{i=0}^{KT-1}$ by setting $\kappa =-1/2$ and computing $r(t_i,t_{i+1})=exp(\kappa {\tilde{\sigma }}^2(t_i,t_{i+1})+\tilde{r}(t_i,t_{i+1}))-1$ for all i.4 Third, I use the simulated data to calculate ${\tilde{v}}^2(t_i,t_{i+K})$ and $v^2(t_i,t_{i+K})$ for each $i\in \{0,K,2K,\dots ,(T-1\left)K\right\}$. Because there are roughly 252 trading days per year for the S&P 500 index, I consider $K=5$, $K=21$, $K=63$, $K=126$, and $K=252$ to approximate weekly, monthly, quarterly, semiannual, and annual holding periods.

Table 1. Monte Carlo study of the relative estimation errors for unconditional and conditional variances.

Panel A
	${\displaystyle \frac{{\tilde{r}}^2(t_i,t_{i+K})}{{\tilde{\sigma }}_K^2}-1}$			${\displaystyle \frac{r^2(t_i,t_{i+K})}{{\sigma }_K^2}-1}$			${\displaystyle \frac{{\tilde{v}}^2(t_i,t_{i+K})}{{\tilde{\sigma }}_K^2}-1}$			${\displaystyle \frac{v^2(t_i,t_{i+K})}{{\sigma }_K^2}-1}$
K	ME	MAE	RMSE	ME	MAE	RMSE	ME	MAE	RMSE	ME	MAE	RMSE
1	$-0.000$	$1.015$	$1.617$	$-0.000$	$1.015$	$1.618$	$-0.000$	$1.015$	$1.617$	$-0.000$	$1.015$	$1.618$
5	$\phantom{-}0.000$	$1.027$	$1.692$	$\phantom{-}0.000$	$1.025$	$1.666$	$\phantom{-}0.000$	$0.615$	$0.864$	$\phantom{-}0.000$	$0.612$	$0.856$
21	$\phantom{-}0.000$	$1.013$	$1.734$	$\phantom{-}0.000$	$1.005$	$1.635$	$\phantom{-}0.000$	$0.432$	$0.576$	$\phantom{-}0.000$	$0.417$	$0.548$
63	$\phantom{-}0.000$	$0.997$	$1.698$	$\phantom{-}0.000$	$0.984$	$1.532$	$\phantom{-}0.000$	$0.317$	$0.412$	$\phantom{-}0.000$	$0.284$	$0.362$
126	$\phantom{-}0.000$	$0.987$	$1.617$	$\phantom{-}0.000$	$0.972$	$1.446$	$\phantom{-}0.000$	$0.244$	$0.313$	$\phantom{-}0.000$	$0.204$	$0.258$
252	$-0.000$	$0.978$	$1.537$	$-0.000$	$0.966$	$1.407$	$\phantom{-}0.000$	$0.181$	$0.229$	$\phantom{-}0.000$	$0.153$	$0.194$
Panel B
	${\displaystyle \frac{{\tilde{r}}^2(t_i,t_{i+K})}{{\tilde{\sigma }}^2(t_i,t_{i+K})}-1}$			${\displaystyle \frac{r^2(t_i,t_{i+K})}{{\sigma }^2(t_i,t_{i+K})}-1}$			${\displaystyle \frac{{\tilde{v}}^2(t_i,t_{i+K})}{{\tilde{\sigma }}^2(t_i,t_{i+K})}-1}$			${\displaystyle \frac{v^2(t_i,t_{i+K})}{{\sigma }^2(t_i,t_{i+K})}-1}$
K	ME	MAE	RMSE	ME	MAE	RMSE	ME	MAE	RMSE	ME	MAE	RMSE
1	$-0.000$	$0.968$	$1.414$	$-0.000$	$0.968$	$1.415$	$-0.000$	$0.968$	$1.414$	$-0.000$	$0.968$	$1.415$
5	$-0.000$	$0.990$	$1.559$	$-0.000$	$0.988$	$1.533$	$\phantom{-}0.000$	$0.537$	$0.732$	$\phantom{-}0.000$	$0.534$	$0.723$
21	$\phantom{-}0.000$	$0.995$	$1.676$	$\phantom{-}0.000$	$0.988$	$1.579$	$\phantom{-}0.000$	$0.380$	$0.506$	$\phantom{-}0.000$	$0.362$	$0.476$
63	$\phantom{-}0.000$	$0.993$	$1.684$	$\phantom{-}0.000$	$0.980$	$1.519$	$\phantom{-}0.000$	$0.300$	$0.391$	$\phantom{-}0.000$	$0.265$	$0.338$
126	$\phantom{-}0.000$	$0.985$	$1.613$	$\phantom{-}0.000$	$0.971$	$1.441$	$-0.000$	$0.238$	$0.306$	$\phantom{-}0.000$	$0.197$	$0.249$
252	$-0.000$	$0.978$	$1.536$	$-0.000$	$0.965$	$1.406$	$\phantom{-}0.000$	$0.178$	$0.227$	$\phantom{-}0.000$	$0.150$	$0.191$

Note: I use Monte Carlo integration to document the performance of competing estimators of ${\tilde{\sigma }}_K^2:=\mathrm{var}\left(\tilde{r}(t_i,t_{i+K})\right)$, ${\sigma }_K^2:=\mathrm{var}\left(r(t_i,t_{i+K})\right)$, ${\tilde{\sigma }}^2(t_i,t_{i+K}):=\mathrm{var}\left(\tilde{r}(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right))$, and ${\sigma }^2(t_i,t_{i+K}):=\mathrm{var}\left(r(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right))$, where $\tilde{r}(t_i,t_{i+K})$ and $r(t_i,t_{i+K})$ denote the log return and return for the K-period interval that begins at time $t_i$ and ends at time $t_{i+K}$ and $\mathcal{F}\left(t_i\right)=\{\tilde{r}(t_0,t_1),\dots ,\tilde{r}(t_{i-1},t_i)\}$. The columns labeled ME, MAE, and RMSE report the mean, mean absolute, and root mean square values of the relative estimation errors for the indicated estimators. The analysis is carried out using a data generating process (DGP) of the form shown in Equations (14) and (15), where $\omega =0$, $\beta =0.8754$, $\alpha =4.554\times {10}^{-6}$, $\gamma =127.0$, and $\tilde{z}(t_i,t_{i+1})\sim \mathrm{NID}(0,1)$. First, I generate the sequence $\{\tilde{r}{(t_i,t_{i+1}\}}_{i=0}^{KT-1}$ with $\kappa =0$ and $T=10000000$. Next, I construct the sequence $\{r{(t_i,t_{i+1}\}}_{i=0}^{KT-1}$ by setting $\kappa =-1/2$ and computing $r(t_i,t_{i+1})=exp(\kappa {\tilde{\sigma }}^2(t_i,t_{i+1})+\tilde{r}(t_i,t_{i+1}))-1$ for all i. Finally, I calculate ${\tilde{v}}^2(t_i,t_{i+K})={\sum }_{j=1}^K{\tilde{r}}^2(t_{i+j-1},t_{i+j})+2{\sum }_{j=1}^{K-1}\tilde{r}(t_{i+j-1},t_{i+j})\tilde{r}(t_{i+j},t_{i+j+1})$ and $v^2(t_i,t_{i+K})={\sum }_{j=1}^K{R}^2(t_i,t_{i+j-1})r^2(t_{i+j-1},t_{i+j})+2{\sum }_{j=1}^{K-1}R(t_i,t_{i+j-1})r(t_{i+j-1},t_{i+j})R(t_i,t_{i+j})r(t_{i+j},t_{i+j+1})$ along with ${\tilde{\sigma }}^2(t_i,t_{i+K})$ and ${\sigma }^2(t_i,t_{i+K})$ for all $i\in \{0,K,2K,\dots ,(T-1\left)K\right\}$, where $R(t_i,t_{i+j})=1+r(t_i,t_{i+j})$. Simple algebra yields ${\tilde{\sigma }}^2(t_i,t_{i+K})=K{\tilde{\sigma }}_1^2+{(1-\rho )}^{-1}(1-{\rho }^K)({\tilde{\sigma }}^2(t_i,t_{i+1})-{\tilde{\sigma }}_1^2)$ and ${\tilde{\sigma }}_K^2=K{\tilde{\sigma }}_1^2$, where $\rho =\beta +\alpha {\gamma }^2$ and ${\tilde{\sigma }}_1^2={(1-\rho )}^{-1}(\omega +\alpha )$. To obtain analytic expressions for ${\sigma }^2(t_i,t_{i+K})=\mathrm{E}\left[R^2(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right)]-1$ and ${\sigma }_K^2=\mathrm{E}\left[R^2(t_i,t_{i+K})\right]-1$, I rely on results from the option pricing literature (see Heston and Nandi 2000, for details). Specifically, it is well known that $\mathrm{E}\left[R^{\tau }(t_i,t_{i+K})\right|\mathcal{F}\left(t_i\right)]=exp(a_K\left(\tau \right)+b_K\left(\tau \right){\tilde{\sigma }}^2(t_i,t_{i+1}))$ under the DGP for the study, where $a_K\left(\tau \right)$ and $b_K\left(\tau \right)$ are given by the recurrence relations $a_K\left(\tau \right)=a_{K-1}\left(\tau \right)+\omega b_{K-1}\left(\tau \right)-{\displaystyle \frac{1}{2}}log(1-2\alpha b_{K-1}\left(\tau \right))$ and $b_K\left(\tau \right)=\tau (\kappa +\gamma )-{\displaystyle \frac{1}{2}}{\gamma }^2+\beta b_{K-1}\left(\tau \right)+{\displaystyle \frac{(1/2){(\tau -\gamma )}^2}{1-2\alpha b_{K-1}\left(\tau \right)}}$ with $a_0\left(\tau \right)=b_0\left(\tau \right)=0$. Setting $\tau =2$ produces an expression for ${\sigma }^2(t_i,t_{i+K})+1$, which in turn yields ${\sigma }_K^2+1=exp\left(a_K\left(2\right)\right)\mathrm{E}[exp\left(b_K\left(2\right){\tilde{\sigma }}^2(t_i,t_{i+1})\right)]$ by the law of iterated expectations. Because $\mathrm{E}[exp\left(\xi {(z+\nu )}^2\right)]={(1-2\xi )}^{-MM1/2}exp\left({\nu }^2\xi {(1-2\xi )}^{-1}\right)$ given that $z\sim \mathrm{N}(0,1)$, the law of iterated expectations also implies that $\mathrm{E}[exp\left(b_K\left(2\right){\tilde{\sigma }}^2(t_i,t_{i+1})\right)]=exp({\sum }_{j=1}^{\infty }\omega c_{j-1}-(1/2)log(1-2\alpha c_{j-1}))$, where $c_j$ satisfies the recurrence relation $c_j=\beta c_{j-1}+\alpha c_{j-1}{(1-2\alpha c_{j-1})}^{-1}{\gamma }^2$ with $c_0=b_K\left(2\right)$.

summarizes the results for 10 million simulated observations (i.e., T = 1,000,000). Panel A examines the properties of the relative estimation errors for unconditional variances. The initial six columns report the mean, mean absolute, and root mean square values of ${\tilde{r}}^2(t_i,t_{i+K})/{\tilde{\sigma }}_K^2-1$ and $r^2(t_i,t_{i+K})/{\sigma }_K^2-1$ for the six values of K under consideration (denoted by ME, MAE, and RMSE). For $K=1$, the results for log returns are nearly identical to those for returns. But differences emerge as K increases.

As anticipated, the mean errors are quite small (zero to three decimal places) because ${\tilde{r}}^2(t_i,t_{i+K})$ and $r^2(t_i,t_{i+K})$ are unbiased estimators of ${\tilde{\sigma }}_K^2$ and ${\sigma }_K^2$. The largest RMSEs correspond to $K=21$ for log returns and $K=5$ for returns. An increase in the RMSE is always indicative of an increase in kurtosis, which can be expressed as 1 plus the mean square error. The smallest MAEs and RMSEs correspond to $K=252$.

Now consider the results in the final six columns of panel A, which contain the mean, mean absolute, and root mean square values of ${\tilde{v}}^2(t_i,t_{i+K})/{\tilde{\sigma }}_K^2-1$ and $v^2(t_i,t_{i+K})/{\sigma }_K^2-1$ for the six values of K under consideration.5 The realized measures show no indications of bias and are clearly much more efficient estimators of ${\tilde{\sigma }}_K^2$ and ${\sigma }_K^2$ for $K>1$ than ${\tilde{r}}^2(t_i,t_{i+K})$ and $r^2(t_i,t_{i+K})$. Notice, for example, that replacing $r^2(t_i,t_{i+K})$ with $v^2(t_i,t_{i+K})$ reduces the RMSE from $1.666$ to $0.856$ with $K=5$. This is a reduction of $48.6\%$. Furthermore, the improvements in efficiency become more pronounced as K increases. The RMSE drops from $1.407$ to $0.194$ for the $K=252$ case, which is a reduction of 86.2%.

Panel B examines the properties of the relative estimation errors for the conditional variances using the same layout as panel A. Once again, the mean errors are zero to three decimal places in all cases and there are large gains in efficiency from employing the realized measures. The reduction in the RMSEs relative to those reported in panel A is an indicator of the benefits exploiting conditioning information. The RMSEs drop by 0.203 (12.6%) in all cases for $K=1$. As K increases, the drop always becomes smaller in raw numerical terms. But the percentage drop in the RMSE does not display a monotonic relation with K. For example, the RMSE for $v^2(t_i,t_{i+K})$ drops by $0.133(15.5\%)$ for $K=5$.

Overall, the Monte Carlo evidence indicates that the proposed technique for constructing realized measures that are unbiased estimators of the variances of holding-period returns works as intended. It achieves improvements in efficiency that are comparable to those achieved by the conventional technique for constructing realized measures of the variances of multiperiod log returns. I now turn to an empirical application that focuses on forecasting the conditional variances of weekly and monthly S&P 500 index returns.

4. Out-of-Sample Results for the S&P 500 Index

To lay the groundwork for the discussion, assume that the objective is to forecast the variance of a financial variable $y(t+s)$ using a realization of the sequence $\left\{y\right(1),\dots ,y(t\left)\right\}$ for some $s\ge 1$. Because the GARCH(1,1) model of Bollerslev (1986) is known to perform well in a variety of settings, it is often used to construct such forecasts. If the DGP is a GARCH(1,1) specification, then $y(t+s)$ can be expressed as

$$\begin{array}{cc}\hfill y(t+s)& =\mu +h^{MM1/2}(t+1,s)z(t+s),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill h(t+1,s)& =(1-{\varphi }^{s-1})\eta +{\varphi }^{s-1}h(t+1,1),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill h(t+1,1)& =\eta +\varphi (h(t,1)-\eta )+\delta (e^2\left(t\right)-h(t,1)),\hfill \end{array}$$

(18)

where $\mathrm{E}\left[z\right(t+s\left)\right|y\left(1\right),\dots ,y\left(t\right)]=0$, $\mathrm{E}\left[z^2(t+s)\right|y\left(1\right),\dots ,y\left(t\right)]=1$, and $e^2\left(t\right)={(y\left(t\right)-\mu )}^2$. Thus, $h(t+1,s)$ is a conditionally-unbiased s-step-ahead forecast of $e^2(t+s)$.

Now consider an alternative s-step-ahead forecast of $e^2(t+s)$ that is constructed from a realization of the sequence $\left\{x\right(1),\dots ,x(t\left)\right\}$, where $x\left(t\right)$ is a conditionally-unbiased realized measure of the variance of $y\left(t\right)$ with dynamics that are described by an MEM specification of the type introduced by Engle (2002). If the DGP is an MEM(1,1) specification, then $x(t+s)$ can be expressed as

$$\begin{array}{cc}\hfill x(t+s)& =m(t+1,s)u(t+s),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill m(t+1,s)& =(1-{\phi }^{s-1})\varsigma +{\phi }^{s-1}m(t+1,1),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill m(t+1,1)& =\varsigma +\phi \left(m\right(t,1)-\varsigma )+\lambda \left(x\right(t)-m(t,1\left)\right),\hfill \end{array}$$

(21)

where $u(t+s)$ is strictly non-negative and satisfies $\mathrm{E}\left[u\right(t+s\left)\right|x\left(1\right),\dots ,x\left(t\right)]=1$. Because $m(t+1,s)$ is a conditionally unbiased s-step-ahead forecast of $x(t+s)$, it clearly has the potential to outperform $h(t+1,s)$ as a forecast of $e^2(t+s)$.

I focus on the case in which $y(t+s)$ is a weekly or monthly return on the S&P 500 index and the realized measure of its variance is constructed from daily returns. Presumably, variance forecasts based on realized measures should generally be more accurate than those based on weekly or monthly returns. I therefore use the pseudo out-of-sample forecasts produced by the GARCH(1,1) specification to benchmark the performance of the pseudo out-of-sample forecasts produced by the MEM(1,1) specification. As in Giacomini and White (2006), I conduct the analysis using limited-memory estimators of the parameters.

Because the GARCH(1,1) model implies that $e^2(t+1)=h(t+1,1)z^2(t+1)$, it is essentially a MEM(1,1) specification for $e^2(t+1)$. Furthermore, the recurrence relation for $h(t+1,1)$ in Equation (18) can be transformed into the recurrence relation for $m(t+1,1)$ in Equation (21) by replacing $e^2\left(t\right)$ with $x\left(t\right)$ and relabeling the parameters. It is apparent, therefore, that the research design ensures that performance advantage of the MEM(1,1) specification (if any) is due to the incremental gains from using realized measures as long as the approach used to fit the GARCH and MEM specifications puts them on an equal footing. This poses no issues because fitting the GARCH specification under the assumption that $z(t+1)\sim \mathrm{NID}(0,1)$ produces the same results as treating $e^2(t+1)=h(t+1,1)z^2(t+1)$ as an MEM specification and fitting it by assuming that $z^2(t+1)$ is a serially independent exponential random variable with a unit mean (see Engle 2002, for further elaboration).

To illustrate, suppose $W+s-1>0$ is the number of observations in a rolling window of weekly or monthly returns. For each choice of s and value of $N\in \{1,\dots ,T-W-s+1\}$, I construct an estimate of $h(t+1,s)$ for $t=N+W-1$ using the estimate of $\mathit{\theta }:=(\mu ,\eta ,\varphi ,\delta )$ obtained by minimizing

$${\mathcal{Q}}_h(\mathit{\theta };s,N)=\sum _{t=N}^{N+W-1}{\displaystyle \frac{1}{2}}log\left(h(t,s)\right)+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{e^2(t+s-1)}{h(t,s)}}\right)$$

(22)

subject to $h(N,1)=\eta$, $\mu =\widehat{\mu }$, and $\eta =\widehat{\eta }$, where $\widehat{\mu }=W^{-1}{\sum }_{t=N}^{N+W-1}y\left(t\right)$ and $\widehat{\eta }=W^{-1}{\sum }_{t=N}^{N+W-1}{(y\left(t\right)-\widehat{\mu })}^2$. Similarly, for each choice of s and value of N, I construct an estimate of $m(t+1,s)$ for $t=N+W-1$ using the estimate of $\mathit{\vartheta }:=(\varsigma ,\phi ,\lambda )$ obtained by minimizing

$${\mathcal{Q}}_m(\mathit{\vartheta };s,N)=\sum _{t=N}^{N+W-1}log\left(m(t,s)\right)+{\displaystyle \frac{x(t+s-1)}{m(t,s)}}$$

(23)

subject to $m(N,1)=\varsigma$ and $\varsigma =\widehat{\varsigma }$, where $\widehat{\varsigma }=W^{-1}{\sum }_{t=N}^{N+W-1}x\left(t\right)$. The resultant estimated values of $\mu$, $h(t+1,s)$, and $m(t+1,s)$ are denoted by $\widehat{\mu }(t+1,s)$, $\widehat{h}(t+1,s)$, and $\widehat{m}(t+1,s)$.

Several features of this procedure are worthy of further comment. First, apart from an additive constant, $-{\mathcal{Q}}_h(\mathit{\theta };s,N)$ and $-{\mathcal{Q}}_m(\mathit{\vartheta };s,N)$ are the log quasi-likelihood functions that result from treating $z\left(t\right)$ as $N(0,1)$ and $u\left(t\right)$ as an exponential random variable with a rate parameter of one. Thus, the estimators of $\mathit{\theta }$ and $\mathit{\vartheta }$ are consistent under the usual regularity conditions for quasi-maximum likelihood estimation. Second, I use the sample mean of $y\left(t\right)$, sample variance of $y\left(t\right)$, and sample mean of $x\left(t\right)$ that are computed from the initial W observations of the rolling window as estimators of $\mu$, $\eta$, and $\varsigma$. This targeting approach simplifies optimization. Third, the procedure produces horizon-tuned forecasts because the estimates of $\varphi$, $\delta$, $\phi$, and $\lambda$ are specific to the value of s under consideration.6

To formally compare the accuracy of $\widehat{h}(t+1,s)$ and $\widehat{m}(t+1,s)$ as s-step-ahead forecasts of ${\widehat{e}}^2(t+s)={(y(t+s)-\widehat{\mu }(t+1,s))}^2$, I use the unconditional version of the Giacomini and White (2006) test of equal predictive ability. The test is based on the criterion

$$\Delta L(t+s)=\left|{\displaystyle \frac{{\widehat{e}}^2(t+s)}{\widehat{h}(t+1,s)}}-1\right|-\left|{\displaystyle \frac{{\widehat{e}}^2(t+s)}{\widehat{m}(t+1,s)}}-1\right|,t=W,W+1,\dots ,T-s,$$

(24)

which is the difference between the absolute error losses produced by $\widehat{h}(t+1,s)$ and $\widehat{m}(t+1,s)$.7 The null hypothesis for the test is $H_0:\mathrm{E}[\Delta L(t+s)]=0$. Hence, inference is conducted using the t-statistic for

$$\Delta \overline{L}\left(s\right)={\displaystyle \frac{1}{T-W-s+1}}\sum _{t=W}^{T-s}\Delta L(t+s).$$

(25)

If $\Delta \overline{L}\left(s\right)$ is positive and statistically significant, then the test indicates that the s-step-ahead MEM forecasts outperform the s-step-ahead GARCH(1,1) forecasts under MAE loss.8

The weekly and monthly index returns along with their realized variances are computed from daily index data for the years 1946 through 2023. As is typical in the finance literature, I use the actual number of trading days in a given week or given month rather than a fixed value of K for the computations. Because the daily index returns display some evidence of negative first-order serial correlation, I account for the impact of this feature by computing the realized measures as

$$\begin{array}{c}{v}^2(t_i,t_{i+D})=\sum _{j=1}^D{R}^2(t_i,t_{i+j-1})r^2(t_{i+j-1},t_{i+j})+\hfill \\ \hfill 2\sum _{j=1}^{D-1}R(t_i,t_{i+j-1})r(t_{i+j-1},t_{i+j})R(t_i,t_{i+j})r(t_{i+j},t_{i+j+1})\end{array}$$

(26)

rather than as shown in Section 2.9 Here D denotes the number of trading days for the week or month in question. I specify $W=2034$ for the weekly data and $W=468$ for the monthly data (50% of the number of available observations in each case). To aid in interpreting the findings, I also conduct tests of equal predictive ability using weekly and monthly observations of log returns and their realized variances.

4.1. Properties of the Rolling-Window Parameter Estimates

Table 2. Selected properties of rolling-window parameter estimates for GARCH and MEM specifications.

Panel A: Weekly log returns
	GARCH with s-step-ahead conditional variances						MEM with s-step-ahead conditional variances
	$\varphi$			$\delta$			$\phi$			$\lambda$
s	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max
1	$0.943$	$0.963$	$0.977$	$0.098$	$0.129$	$0.198$	$0.959$	$0.966$	$0.975$	$0.143$	$0.173$	$0.200$
3	$0.937$	$0.968$	$0.992$	$0.051$	$0.116$	$0.194$	$0.936$	$0.964$	$0.975$	$0.160$	$0.210$	$0.307$
6	$0.949$	$0.976$	$0.994$	$0.027$	$0.093$	$0.208$	$0.930$	$0.961$	$0.976$	$0.140$	$0.205$	$0.313$
12	$0.968$	$0.983$	$0.994$	$0.019$	$0.054$	$0.091$	$0.971$	$0.984$	$0.992$	$0.027$	$0.046$	$0.064$
Panel B: Weekly returns
1	$0.946$	$0.964$	$0.977$	$0.097$	$0.126$	$0.193$	$0.961$	$0.967$	$0.976$	$0.143$	$0.170$	$0.194$
3	$0.941$	$0.968$	$0.991$	$0.056$	$0.116$	$0.191$	$0.938$	$0.965$	$0.976$	$0.159$	$0.208$	$0.304$
6	$0.952$	$0.976$	$0.994$	$0.029$	$0.093$	$0.195$	$0.933$	$0.962$	$0.977$	$0.140$	$0.199$	$0.307$
12	$0.968$	$0.983$	$0.994$	$0.020$	$0.054$	$0.091$	$0.972$	$0.984$	$0.992$	$0.028$	$0.048$	$0.069$
Panel C: Monthly log returns
1	$0.874$	$0.940$	$0.975$	$0.056$	$0.087$	$0.132$	$0.821$	$0.867$	$0.922$	$0.472$	$0.552$	$0.667$
3	$0.867$	$0.942$	$0.971$	$0.091$	$0.129$	$0.173$	$0.872$	$0.936$	$0.963$	$0.151$	$0.196$	$0.251$
6	$0.861$	$0.934$	$0.964$	$0.084$	$0.141$	$0.175$	$0.882$	$0.929$	$0.960$	$0.212$	$0.449$	$0.812$
12	$0.749$	$0.898$	$0.939$	$0.204$	$0.347$	$0.760$	$0.874$	$0.921$	$0.955$	$0.242$	$0.351$	$0.423$
Panel D: Monthly returns
1	$0.880$	$0.942$	$0.975$	$0.060$	$0.091$	$0.136$	$0.845$	$0.889$	$0.937$	$0.404$	$0.493$	$0.613$
3	$0.861$	$0.941$	$0.971$	$0.102$	$0.137$	$0.180$	$0.875$	$0.937$	$0.963$	$0.154$	$0.211$	$0.276$
6	$0.853$	$0.931$	$0.963$	$0.094$	$0.145$	$0.185$	$0.888$	$0.934$	$0.963$	$0.214$	$0.356$	$0.569$
12	$0.749$	$0.890$	$0.938$	$0.178$	$0.321$	$0.762$	$0.885$	$0.923$	$0.954$	$0.245$	$0.342$	$0.416$

Note: The table reports selected properties of limited-memory parameter estimates that are computed using s-step-ahead forecasts of the conditional variances of weekly and monthly S&P 500 index returns. The forecasts of the conditional variances are generated by GARCH(1,1) and MEM(1,1) specifications of the form shown in Equations (16) through (18) and Equations (19) through (21). I conduct the analysis using a quasi-maximum likelihood (QML) approach that employs a rolling window of $W+s-1$ observations to estimate the parameters. In particular, I construct the estimated values of $h(t+1,s)$ and $m(t+1,s)$ for $t=N+W-1$ using a window of observations that begins in period N and ends in period $N+W+s-1$, where $N\in \{1,\dots ,T-W-s+1\}$. To compute the log quasi-likelihood functions, I treat $z\left(t\right)$ as an $\mathrm{NID}(0,1)$ random variable and $u\left(t\right)$ as a serially-independent exponential random variable with a rate parameter of one. Note that this methodology produces horizon-tuned forecasts of the conditional variances because the estimates of $\varphi$, $\delta$, $\phi$, and $\lambda$ are specific to the value of s under consideration. I specify $W=2034$ for the weekly data and $W=468$ for the monthly data, which is 50% of the number of available observations in each case. The sample period is January 1946 to December 2023.

examines the properties of the sequence of parameter estimates produced by the rolling-window optimizations for each specification. Panels A and B present the results for weekly log returns and weekly returns. Not surprisingly, the average estimates of $\varphi$ and $\phi$ for $s=1$ point to strong persistence in the conditional variances for both log returns and returns. The results also indicate that the estimates of $\varphi$ and $\phi$ are quite stable over time. In panel A, for example, the estimate of $\varphi$ for $s=1$ ranges from 0.943 to 0.977 and the estimate of $\phi$ for $s=1$ ranges from 0.959 to 0.975.

The results for $\delta$ and $\lambda$ in panel A display some interesting patterns. First, the average estimate of $\delta$ is somewhat smaller than the average estimate of $\lambda$ for $s=1$, $s=3$, and $s=6$. This finding suggests the conditional variance process of weekly log returns displays a weaker response to shocks under the GARCH specification than under the MEM specification. Second, the average estimate of $\delta$ declines monotonically with s, whereas the average estimate of $\lambda$ does not. But there is a sharp drop in the average estimate of $\lambda$ for $s=12$. Although the underlying mechanism that leads to this finding is not immediately apparent, the findings for weekly returns mirror those for weekly log returns in all respects.

Panels C and D present the results for monthly log returns and monthly returns. As anticipated, the average estimates of $\varphi$ and $\phi$ are somewhat lower than the corresponding values in panels A and B, which is consistent with returns following a stationary stochastic process. But the results still point to a substantial degree of persistence in the conditional variances. There is also more variation in the estimates of $\varphi$ and $\phi$ over time for the monthly observations, which is an expected consequence of the sharp reduction in the number of observations in the rolling window used for estimation purposes.

Perhaps the most intriguing aspect of the results in panels C and D is that the average estimate of $\delta$ is considerably smaller than the average estimate of $\lambda$ for $s=1$, $s=6$, and $s=12$. This pattern suggests that the GARCH specification produces a smoother sequence of conditional variance forecasts than the MEM specification, which could indicate that the latter specification has an advantage in tracking the conditional variances. Notice that the average estimate of $\lambda$ for $s=3$ is relatively low by comparison. Because $s=3$ for monthly observations is roughly equivalent to $s=12$ for weekly observations, the relation between the average estimate of $\lambda$ and the forecast horizon is similar at both frequencies.

4.2. Conditional Volatility Forecasts

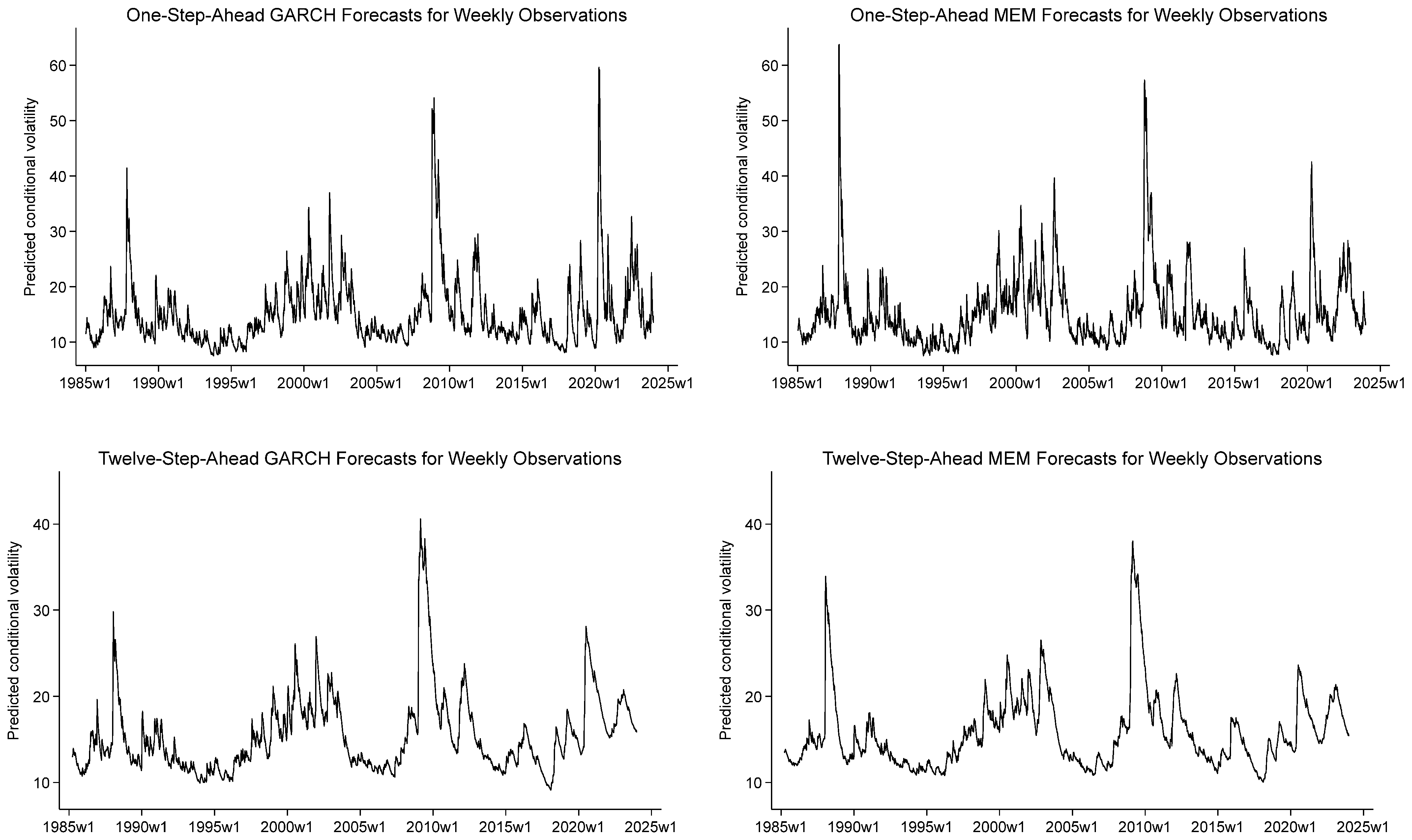
To develop further insights, I plot the conditional volatility forecasts for weekly returns and monthly returns. Figure 1 shows side-by-side plots of the GARCH and MEM forecasts for weekly returns. The upper panels are for $s=1$ and lower panels are for $s=12$. Although the side-by-side comparisons highlight the broad similarities in the forecasts for both forecast horizons, it is easy to spot a few differences. For instance, the spike in the one-step-ahead forecast of conditional volatility that follows the 1987 stock market crash is larger for the MEM specification than for the GARCH specification. But it is clear from the plots that the GARCH and MEM forecasts are highly correlated as a general rule.

Of course, this finding does not necessarily imply that the differences in the predictive ability of GARCH and MEM forecasts is negligible. If the MEM forecasts are more efficient than the GARCH forecasts, then they should have a performance advantage in formal statistical tests provided that the sample size is sufficiently large. Furthermore, the results of the Monte Carlo analysis indicate that gains from employing realized measures are inversely related to the investment horizon used for the analysis.

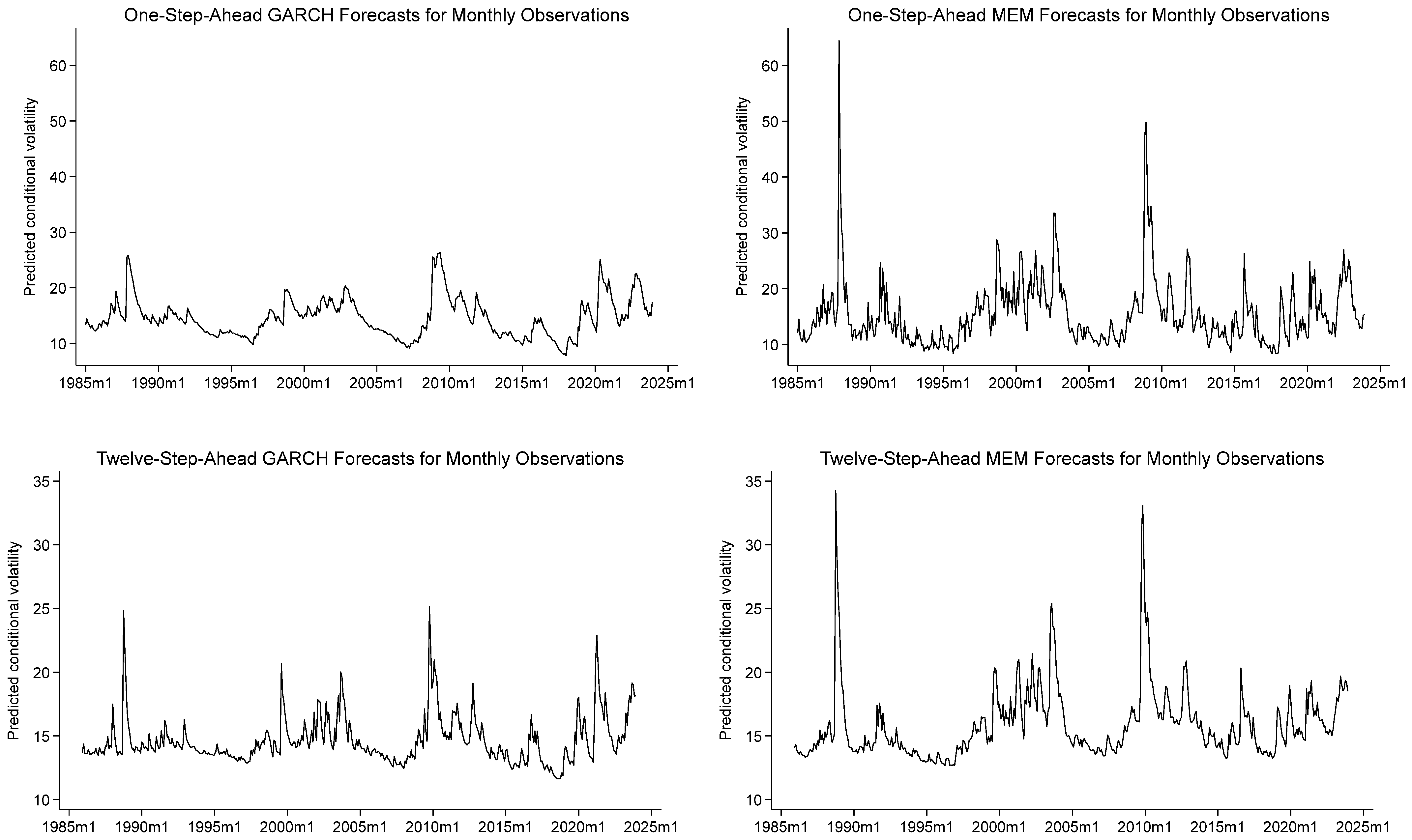
Consider the side-by-side plots of the GARCH and MEM forecasts for monthly returns, which are shown in Figure 2. The visual differences in the plots are certainly more pronounced in this case. Not only are the one-step-ahead GARCH forecasts relatively smooth, they are also confined to a much narrower range than one-step-ahead MEM forecasts. These features are broadly consistent with a scenario in which the realized measures are more efficient estimators of the conditional variances than the squared demeaned returns.

4.3. Hypothesis Tests

The tests of equal predictive ability provide formal evidence in this regard. The results of the tests are presented in

Table 3. Tests of equal predictive ability using realized measures constructed from daily observations.

Panel A: Weekly log returns
	GARCH forecasts (s-step-ahead)				MEM forecasts (s-step-ahead)				$H_0:\mathrm{E}[\Delta L(t+s)]=0$
s	ME	MAE	RMSE	MSE	ME	MAE	RMSE	MSE	$\Delta \overline{L}\left(s\right)$	t-stat	pval
1	$0.067$	$1.083$	$2.172$	$4.716$	$0.039$	$1.061$	$2.127$	$4.522$	$0.022$	$1.41$	$0.157$
3	$0.167$	$1.198$	$3.604$	$12.992$	$0.096$	$1.124$	$2.440$	$5.953$	$0.075$	$1.52$	$0.129$
6	$0.211$	$1.262$	$3.802$	$14.459$	$0.170$	$1.216$	$3.481$	$12.118$	$0.046$	$1.75$	$0.079$
12	$0.205$	$1.269$	$3.671$	$13.476$	$0.153$	$1.235$	$3.615$	$13.068$	$0.034$	$2.30$	$0.021$
Panel B: Weekly returns
1	$0.062$	$1.077$	$2.063$	$4.258$	$0.033$	$1.054$	$2.010$	$4.042$	$0.023$	$1.58$	$0.115$
3	$0.150$	$1.179$	$3.178$	$10.100$	$0.088$	$1.115$	$2.293$	$5.258$	$0.064$	$1.55$	$0.120$
6	$0.197$	$1.244$	$3.462$	$11.987$	$0.151$	$1.195$	$3.150$	$9.921$	$0.049$	$1.93$	$0.054$
12	$0.193$	$1.255$	$3.401$	$11.567$	$0.144$	$1.223$	$3.345$	$11.191$	$0.032$	$2.31$	$0.021$
Panel C: Monthly log returns
1	$0.080$	$1.104$	$2.535$	$6.425$	$-0.059$	$0.971$	$1.900$	$3.612$	$0.133$	$2.83$	$0.005$
3	$0.153$	$1.174$	$2.655$	$7.049$	$-0.057$	$1.040$	$2.284$	$5.217$	$0.134$	$4.10$	$0.000$
6	$0.160$	$1.187$	$2.586$	$6.689$	$-0.010$	$1.068$	$2.130$	$4.536$	$0.119$	$2.36$	$0.018$
12	$0.157$	$1.195$	$2.705$	$7.316$	$-0.026$	$1.077$	$2.301$	$5.293$	$0.118$	$2.89$	$0.004$
Panel D: Monthly returns
1	$0.064$	$1.080$	$2.177$	$4.740$	$-0.068$	$0.956$	$1.727$	$2.982$	$0.124$	$3.28$	$0.001$
3	$0.137$	$1.150$	$2.336$	$5.458$	$-0.052$	$1.029$	$2.028$	$4.114$	$0.121$	$4.04$	$0.000$
6	$0.136$	$1.158$	$2.272$	$5.163$	$-0.026$	$1.043$	$1.873$	$3.510$	$0.115$	$2.61$	$0.009$
12	$0.129$	$1.164$	$2.343$	$5.490$	$-0.022$	$1.066$	$2.043$	$4.173$	$0.098$	$3.02$	$0.003$

Note: The table reports the results of tests of equal predictive ability for the S&P 500 index. The tests are conducted using the s-step-ahead variance forecasts produced by GARCH(1,1) and MEM(1,1) models for weekly and monthly observations (see Equations (16) through (18) and Equations (19) through (21) for details). I use a quasi-maximum likelihood approach that employs a rolling window of $W+s-1$ observations to estimate the parameters, which produces horizon-tuned forecasts because the estimates of $\varphi$, $\delta$, $\phi$, and $\lambda$ are specific to the value of s under consideration. In particular, I construct the estimated values of $h(t+1,s)$ and $m(t+1,s)$ for $t=N+W-1$ using a window of observations that begins in period N and ends in period $N+W+s-1$, where $N\in \{1,\dots ,T-W-s+1\}$. The estimated values of $h(t+1,s)$ and $m(t+1,s)$ are denoted by $\widehat{h}(t+1,s)$ and $\widehat{m}(t+1,s)$. I base the tests on the criterion $\Delta L(t+s)=|{\displaystyle \frac{{\widehat{e}}^2(t+s)}{\widehat{h}(t+1,s)}}-1|-|{\displaystyle \frac{{\widehat{e}}^2(t+s)}{\widehat{m}(t+1,s)}}-1|,t=W,W+1,\dots ,T-s$, where ${\widehat{e}}^2(t+s)={(y(t+s)-\widehat{\mu }(t+1,s))}^2$ and $\widehat{\mu }(t+1,s)$ is the sample mean of $\left\{r\right(t-W+1),\dots ,r(t\left)\right\}$. The null hypothesis is $H_0:\mathrm{E}[\Delta L(t+s)]=0$. Hence, inference is conducted using the t-statistic for $\Delta \overline{L}\left(s\right)={\displaystyle \frac{1}{T-W-s+1}}{\sum }_{t=W}^{T-s}\Delta L(t+s)$. If $\Delta \overline{L}\left(s\right)$ is positive and statistically significant, then the test indicates that the s-step-ahead MEM forecasts outperform the s-step-ahead GARCH(1,1) forecasts under the specified loss function. The initial eight columns report the mean, mean absolute, root mean square, and mean square values of ${\widehat{e}}^2(t+s)/\widehat{h}(t+1,s)-1$ and ${\widehat{e}}^2(t+s)/\widehat{m}(t+1,s)-1$ for the four choices of s: 1, 3, 6, and 12. I specify $W=2034$ for the weekly data and $W=468$ for the monthly data, which is 50% of the number of available observations in each case. The sample period is January 1946 to December 2023.

. The initial eight columns of the table report the mean, mean absolute, root mean square, mean square values of ${\widehat{e}}^2(t+s)/\widehat{h}(t+1,s)-1$ and ${\widehat{e}}^2(t+s)/\widehat{m}(t+1,s)-1$ for the four choices of s: 1, 3, 6, and 12. The final three columns report $\Delta \overline{L}\left(s\right)$, its t-statistic, and the associated p-value.

The results in panel A are for weekly log returns. Notably, the MEM forecasts produce smaller MEs, MAEs, and RMSEs than the GARCH forecasts at every forecast horizon. The largest difference in the RMSE corresponds to $s=3$: 3.604 versus 2.440. But the test of equal predictive ability produces a p-value of 0.129 in this case. Broadly speaking, however, the test favors the MEM forecasts. Note that it produces a t-statistic of 1.75 ($p=0.079$) for $s=6$ and 2.30 ($p=0.021$) for $s=12$.

The results in panel B are for weekly returns. Once again, the MEM forecasts produce smaller MEs, MAEs, and RMSEs than the GARCH forecasts at every forecast horizon. The other findings are also similar to those for weekly log returns. The test of equal predictive ability favors the MEM forecasts, yielding a t-statistic of 1.93 ($p=0.054$) for $s=6$ and 2.31 ($p=0.021$) for $s=12$.

The results in panels C and D are for monthly log returns and monthly returns. The overall pattern of the MAEs and RMSEs mirrors that in panels A and B. However, the evidence regarding the superiority of the MEM forecasts is considerably stronger at the monthly frequency. The smallest t-statistics in panels C and D are 2.36 and 2.61, which have p-values of 0.018 and 0.009. Hence, the null hypothesis of equal predictive ability is rejected at the 1% level for every forecast horizon for monthly returns. This finding highlights the extent to which the new realized measures for lower-frequency returns deliver meaningful performance gains.

4.4. Broader Implications of the Analysis

The implications of the results for the MEM(1,1) specification extend beyond the specification itself because they suggest that replacing squared demeaned returns with the proposed realized measures can be adopted as a general strategy for improving the performance of volatility models for lower-frequency returns. Indeed, if the objective is to model the conditional variances of lower-frequency returns, then the proposed realized measures could be in place of conventional realized measures in any existing specification that uses conventional realized measures. Some prominent examples of such specifications include the heterogeneous HAR model of Corsi (2009), the HEAVY model of Shephard and Sheppard (2010), and the realized GARCH model of Hansen et al. (2012).

As for potential applications of the methodology, it can be implemented for any asset or commodity for which daily price data are readily available. This includes international equity indexes, exchange rates, commodities, and cryptocurrencies. It should therefore prove useful in many types of research, especially if the focus is on volatility modeling, asset pricing, or risk management over medium- to long-term horizons. Depending on the application, it might be necessary to address additional features of the DGP. One that immediately comes to mind is deterministic patterns in the volatility of seasonal commodity returns. In this case, the methodology could be implemented using a volatility model that is capable of capturing seasonality, such as a periodic MEM analog of the periodic GARCH model of Bollerslev and Ghysels (1996).

4.5. Caveats

The discussion in Section 2.3 addresses two of the key assumptions that underpin the methodology and outlines techniques for relaxing these assumptions should they fail to hold in the setting of interest. But it is worthwhile to mention a few other caveats about implementing the methodology using a given specification of the DGP. Although the basic MEM(1,1) specification is useful for illustrating the incremental improvements in forecasting performance that result from using the proposed realized measures in place of squared demeaned returns, it should clearly be subject to specification tests before being adopted in a particular application. A potential concern is that, like the benchmark GARCH(1,1) specification, the basic MEM(1,1) specification is incapable of capturing leverage effects. This concern could easily be addressed by replacing Equation (21) with

$$m(t+1,1)=\varsigma +\phi (m(t,1)-\varsigma )+({\lambda }_{1}I(y\left(t\right)\le 0)+{\lambda }_{2}I(y\left(t\right)>0))(x\left(t\right)-m(t,1)),$$

(27)

where $I(·)$ is the indicator function. This would yield an asymmetric MEM(1,1) analog of the threshold GARCH(1,1) specification of Glosten et al. (1993).

It is also important to consider the potential impact of phenomena, such as structural breaks, that would invalidate the assumption that simple returns are weakly stationary. Note, however, that this caveat is applicable to any volatility model that assumes weak stationarity. If an MEM(1,1) model is misspecified due the presence of a structural break or breaks, then the same is true of a GARCH(1,1) model.

5. Conclusions

The availability of high-frequency data on stock prices has transformed the volatility modeling literature over the past two decades. But there are still good arguments for using daily returns to estimate the volatility of longer-horizon returns, especially for sample periods that begin prior to 1993. Because the statistical properties of log returns differ from those of returns and the differences increase with the investment horizon, I show how to construct realized measures that are unbiased estimators of the unconditional and conditional variances of returns in a discrete-time setting, provided that the DGP satisfies relatively mild assumptions that are often invoked in the volatility-modeling literature. The empirical evidence indicates that using the proposed realized measures to compute out-of-sample forecasts of the variances of weekly and monthly returns on the S&P 500 index leads to significant improvements in forecast accuracy. Hence, the measures should be useful in research that addresses asset pricing, portfolio optimization, and related topics, which is typically conducted using returns for weekly, monthly, or quarterly holding periods.

For example, suppose an investor wants to estimate the conditional value at risk for a long position in an equity index over a one-month holding period. This could be accomplished in two simple steps. First, use the realized measures constructed from daily index returns to fit an MEM specification to the monthly index returns. Second, use the resultant sequence of estimated conditional volatilities to standardize the sequence of monthly index returns, find the quantile of the standardized index returns that corresponds to the desired confidence level for the value-at-risk criterion, and compute the conditional value at risk using the estimated conditional volatility for the month that follows the final month in the sample period.

The methodology could also be exploited in macro-finance applications. Suppose, for instance, that a researcher is interested in assessing the influence of macroeconomic variables, such as industrial production, on the volatility of monthly stock market returns. One approach for doing so would be to fit an autoregressive model to the logarithm of the gross monthly growth rate of industrial production, use the resultant parameter estimates to compute the estimated multiplicative shocks to the growth rate, and augment the conditional variance recursion of an MEM specification for monthly stock market returns with lagged values of the estimated growth-rate shocks. This approach would allow a long sample period to be used for the analysis because a century’s worth of monthly data on U.S. industrial production and daily data on U.S. market returns are currently available.