A Novel Hybrid Deep Learning Method for Accurate Exchange Rate Prediction

Abstract

The global foreign exchange (FX) market represents a critical and sizeable component of our financial system. It is a market where firms and investors engage in both speculative trading and hedging. Over the years, there has been a growing interest in FX modeling and prediction. Recently, machine learning (ML) and deep learning (DL) techniques have shown promising results in enhancing predictive accuracy. Motivated by the growing size of the FX market, as well as advancements in ML, we propose a novel forecasting framework, the MVO-BiGRU model, which integrates variational mode decomposition (VMD), data augmentation, Optuna-optimized hyperparameters, and bidirectional GRU algorithms for monthly FX rate forecasting. The data augmentation in the Prevention module significantly increases the variety of data combinations, effectively reducing overfitting issues, while the Optuna optimization ensures optimal model configuration for enhanced performance. Our study’s contributions include the development of the MVO-BiGRU model, as well as the insights gained from its application in FX markets. Our findings demonstrate that the MVO-BiGRU model can successfully avoid overfitting and achieve the highest accuracy in out-of-sample forecasting, while outperforming benchmark models across multiple assessment criteria. These findings offer valuable insights for implementing ML and DL models on low-frequency time series data, where artificial data augmentation can be challenging.

1. Introduction

Foreign exchange (FX) rates among currencies are some of the most important indicators that are closely watched by firms, traders, and investors in our global financial system. The FX market is not only the world’s largest but also a highly lucrative market (Baillie and McMahon 2000). Accurate FX rate forecasting is thus of critical importance to traders, investors, and financial institutions, as it helps them to make informed decisions and manage risks effectively. However, various factors make it a challenging and complicated task. Besides the complexity of financial markets and their nonlinear dynamics, these include government monetary policies, political stability, and uncertain events. The uncertainty in the FX market can be hindered by economic activity, particularly cross-border trade. For these reasons and challenges, FX market prediction has drawn significant attention from researchers in the past few decades.

Various approaches have been explored to model currency FX rates. The fundamental analysis relies on economic theory to identify the variables that influence exchange rates in the long term, such as trade imbalances, and the economic conditions for firms in their respective countries. The technical analysis focuses on identifying patterns in past price data to predict future movements, often without considering the economic fundamentals. Econometrics and time series approaches, like autoregressive integrated moving averages (ARIMAs) and generalized autoregressive conditional heteroscedastic (GARCH) models, analyze historical data to understand FX rate movements. However, it is important to understand that stochastic factors like interest rates, inflation rates, and political risk can impact exchange rates significantly and non-linearly.

Conventional economic theories may not fully explain the behaviors of exchange rates, prompting the need for alternative approaches in modeling (Rossi 2013). The recent progress in machine learning (ML) and deep learning (DL) techniques is proving to be promising in enhancing prediction accuracy (Hassani and Silva 2015). ML models, leveraging artificial neural networks (ANNs) and support vector machines, have gained popularity for their ability to analyze large datasets and forecast FX rates based on intricate patterns (Rodrigues et al. 2020). DL models can use several neurons and hidden layers to analyze sequential data and make more accurate predictions than support vector regressions (SVRs) (Liu 2019). Bao et al. (2017) integrated wavelet transformations, stacked autoencoders (SAEs), and a long short-term memory (LSTM) model for predicting stock prices. Sezer et al. (2020) provided a comprehensive literature review of studies on DL for FX market prediction. Li and Bastos (2020) focused on the technical analysis of DL models applied to stock market prediction. Kelany et al. (2020) evaluated DL and other prediction approaches for the risk factor of equities. Dautel et al. (2020) compared LSTM networks, gated recurrent units (GRUs), and feedforward networks in terms of their directional forecasting accuracy and their empirical findings indicated the suitability of deep networks in FX rate forecasting in general and also demonstrated the difficulty of implementing and tuning corresponding architectures. Ayitey Junior et al. (2023) provided an exhaustive review of the literature and a meta-analysis focusing on the application of ML in the prediction of foreign exchange markets and concluded that ANNs and LSTM models are the commonly used ML and DL algorithms for FX market prediction.

In recent years, the application of hybrid models, which combine ML and DL techniques, in FX market prediction has increased significantly. Lee and Wong (2007) proposed a hybrid multivariate model incorporating various macroeconomic and microstructure variables from the FX market. Shen and Liang (2016) predicted FX rates using a hybrid DL technique that combines SAEs and SVRs. Das et al. (2018) suggested a hybrid forecasting model for predicting FX rates, integrating empirical mode decomposition (EMD) with a rapidly reduced kernel extreme learning machine. An intelligent event-sentiment-based daily FX rate forecasting system was suggested by Yasir et al. (2019) and their results indicated the superiority of their approach over conventional statistical methods in predicting FX rates.

A hybrid model that combines complete ensemble empirical mode decomposition (CEEMDAN) with multilayer LSTM (MLSTM) networks was proposed by Lin et al. (2020) and their results showed that the proposed hybrid model can learn complex correlations from the exchange rate data compared with traditional time series models. Yasar and Kilimci (2020) used DL techniques and a time series analysis to examine the exchange rates between the United States Dollar (USD) and the Turkish Lira. The hybrid ML and prediction model of Adewale et al. (2021) showed a superior performance compared with the ARMA and deep belief network techniques. The forecasting accuracy of the GRU-LSTM neural network was found to be superior to the simple moving average, LSTM, and GRU models by Islam and Hossain (2021). Yilmaz and Arabaci (2021) exploited ten distinct models, including the econometrics, time series, DL, and hybrid models, and two forecasting methods, to predict the monthly exchange rate returns of the Australian and Canadian Dollars and the British Pound against the USD. An ensemble DL method that combines Bagging Ridge (BR) regression with a bidirectional LSTM (Bi-LSTM) model was proposed by Abedin et al. (2021) and the results demonstrated that the ensemble approach achieved lower prediction errors than the other models in predicting exchange rates. Sarangi et al. (2022) studied the short-term currency exchange rates of the Indian Rupee (INR) against the USD using ML approaches. Kausar et al. (2023) proposed a hybrid model by integrating two decomposition methods (VMD-CEEMDAN) with DL models for currency exchange rate forecasting.

While recent research has made significant strides in FX rate prediction through hybrid ML and DL models, challenges persist, particularly when dealing with low-frequency data. Such data often suffer from a limited sample size and information, hindering the model’s performance. Moreover, though existing research has explored the use of decomposition techniques, hyperparameter optimization, and RNNs in FX forecasting, there remains a gap in effectively combining these techniques to address the challenges posed by low-frequency data.

This study augments monthly exchange rates using the VMD decomposition method to avoid generating artificial data and to enhance prediction accuracy. The primary framework outlines the specific operational procedures below. First, we decomposed the currency exchange rates into $K$ distinct subseries with varying fluctuation frequencies using the VMD. Then, we implemented two BiGRU modules with identical structures using the idea suggested by Baek and Kim (2018). More specifically, the Prevention module is designed to handle various combinations of random $n_K$ VMFs, while the Prediction module processes all VMFs. Though the combination operation greatly broadens the range of the input data, using these dynamic combinations as direct predictive factors may result in suboptimal forecasting accuracy. The Prevention module aids the model to learn, prevents overfitting, and enhances generalization, whereas the Prediction module allows the model to capture a wide range of information for prediction purposes. The processing mechanism in the Prevention module pulls out general feature patterns from combinations of VMFs. This makes the model more accurate at predicting and stops overfitting in the Prediction module when there are not enough training samples. However, our model maintains a high degree of prediction accuracy even as the ratio of the train–test dataset declines, further demonstrating its exceptional robustness in prediction performance. The proposed model then combines the outcomes of these two modules into a new input feature and feeds them into a fully connected NN to predict currency exchange rates.

Models with manually set hyperparameters may not achieve the same level of performance as those optimized using tools like Optuna, potentially resulting in suboptimal predictions. The number $n_K$ and hyperparameters (window length, number of layers, number of neurons, learning rate, dropout probability) of BiGRU were optimized using Optuna and the proposed model is called MVO-BiGRU (where M, V, and O stand for Modified VMD and Optuna, respectively) to differentiate it from earlier studies that directly forecast the target variable using only decomposed subseries. Using Optuna optimization to determine the optimal number of VMFs for data augmentation offers advantages in terms of flexibility, data-driven decision-making, generalization, performance, and dynamic adaptation. This approach can lead to an optimized model configuration that maximizes forecasting accuracy and efficiency.

We perform a series of empirical experiments to determine if the MVO-BiGRU model can effectively mitigate overfitting and offer outstanding prediction capabilities. Five assessment criteria—the coefficient of determination ($R^2)$, mean absolute error (MAE), mean squared error (MSE), mean absolute percentage error (MAPE), and directional accuracy (DA)—are chosen for the comparison of the forecasts of the MVO-BiGRU and benchmark models. Furthermore, the model confidence set (MCS) and Pesaran–Timmermann (PT) tests are used to statistically check the significance of the evaluation measures of the models. The results of the study demonstrate that the suggested model outperforms the competing benchmark models regarding accuracy and reliability across all the scenarios. We summarize the primary contributions and findings below.

We model and forecast two distinct currency exchange rates using the proposed model. The study findings on exchange rates show that the suggested model can successfully avoid overfitting and achieve the highest accuracy in out-of-sample forecasting. Further, the use of data augmentation in the Prevention module significantly increases the variety of data combinations, which can successfully reduce overfitting issues. This could offer insights on implementing ML and DL models in low-frequency time series data, where artificial data augmentation is difficult. Thirdly, empirical investigations of multiple exchange rate datasets validate the effectiveness and stability of the suggested model. The statistical tests further confirmed the correctness of the comparative results.

2. Methodological Framework

All the experiments and simulations in this study were carried out using Python 3.7 as the programming language, with PyCharm and Anaconda3 as the development tools, and Keras based on TensorFlow in order to construct the network model structure.

2.1. Variational Mode Decomposition

Dragomiretskiy and Zosso (2014) developed a multiresolution technique called VMD, an entirely self-adaptive and non-recursive signal decomposition technique based on Wiener filtering and Hilbert transform. The method overcomes EMD’s shortcomings, namely mode mixing and noise sensitivity, and is extensively used in prediction research (Li et al. 2019).

The original input signal $f\left(t\right)$ is decomposed into quasi-orthogonal band-limited discrete subsignals $u_k$ and most of each mode is tightly centered around the center frequency $w_k$. The total bandwidth of each mode must be minimized, but the combined bandwidth of all modes should match the original signal (Zhang et al. 2017). The optimization procedure is as follows:

• The Hilbert transform of each mode $u_k$ is calculated and then transformed into a respective uni-sided frequency spectrum;
• To estimate the center frequency of each mode $u_k$, the mode is multiplied by the exponential tuned signal. This will modulate the mode spectra to the relevant baseband;
• The bandwidth of each mode $u_k$ is obtained by conducting the $H^1$ Gaussian smoothness on the demodulated signal.

The calculation process of automatically iteration variational framework is shown as follows:

$$\begin{gathered} \underset{\left\{u_k\right\},\left\{w_k\right\}}{\min }\left\{{\sum }_k{‖{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\otimes u_k\left(t\right)\right]e^{-j{w}_{k}t}‖}_2^2\right\} \\ s.t.{\sum }_k{u}_k=f\left(t\right) \end{gathered}$$

(1)

where $\left\{u_k\right\}=\{u_1,\dots ,u_k\}$ are the modes and $\left\{w_k\right\}=\{w_1,\dots ,w_k\}$ are their corresponding center frequencies, and ${\sum }_k=\sum _{k=1}^K,K$ denotes the number of subsequences to be decomposed, $f\left(t\right)$ denotes the original input signal, $u_k$ denotes the $k$th subsequence of $f\left(t\right),\delta \left(t\right)$ denotes the Dirac distribution, and $\otimes$ represents the convolution operator.

Next, a quadratic penalty function $\alpha$ and a Lagrangian multiplier $\lambda$ are introduced to obtain the optimal solution of the constrained optimization problem in Equation (1). The augmented Lagrangian multiplier function $L$ is obtained as follows:

$$\begin{array}{cc}L\left(\left\{u_k\right\},\left\{w_k\right\},\lambda \right)\hfill & \\ & \hfill =\alpha \left\{{\sum }_k{‖{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\otimes u_k\left(t\right)\right]e^{-j{w}_{k}t}‖}_2^2\right\}+{‖f\left(t\right)-{\sum }_k{u}_k\left(t\right)‖}_2^2+〈\lambda \left(t\right),f\left(t\right)-{\sum }_k{u}_k\left(t\right)〉\end{array}$$

The Lagrange functions are subsequently converted from the time domain to the frequency domain, and the associated extreme values are computed. The mode components $u_k$ and $w_k$ are expressed as follows:

$${\widehat{u}}_k^{n+1}\left(w\right)={\displaystyle \frac{\widehat{f}\left(w\right)-{\sum }_{i\ne k}{\widehat{u}}_i\left(w\right)+\frac{\widehat{\lambda }\left(w\right)}{2}}{1+2\alpha {\left(w-w_k\right)}^2}}$$

$$w_k^{n+1}={\displaystyle \frac{{\int }_0^{\mathrm{\infty }}w{\left|{\widehat{u}}_k\left(w\right)\right|}^{2}dw}{{\int }_0^{\mathrm{\infty }}{\left|{\widehat{u}}_k\left(w\right)\right|}^{2}dw}}$$

Finally, the optimal solution is achieved by employing the alternative direction method of multipliers (Hestenes 1969), and the original input signal is decomposed into $K$ subsignal modes.

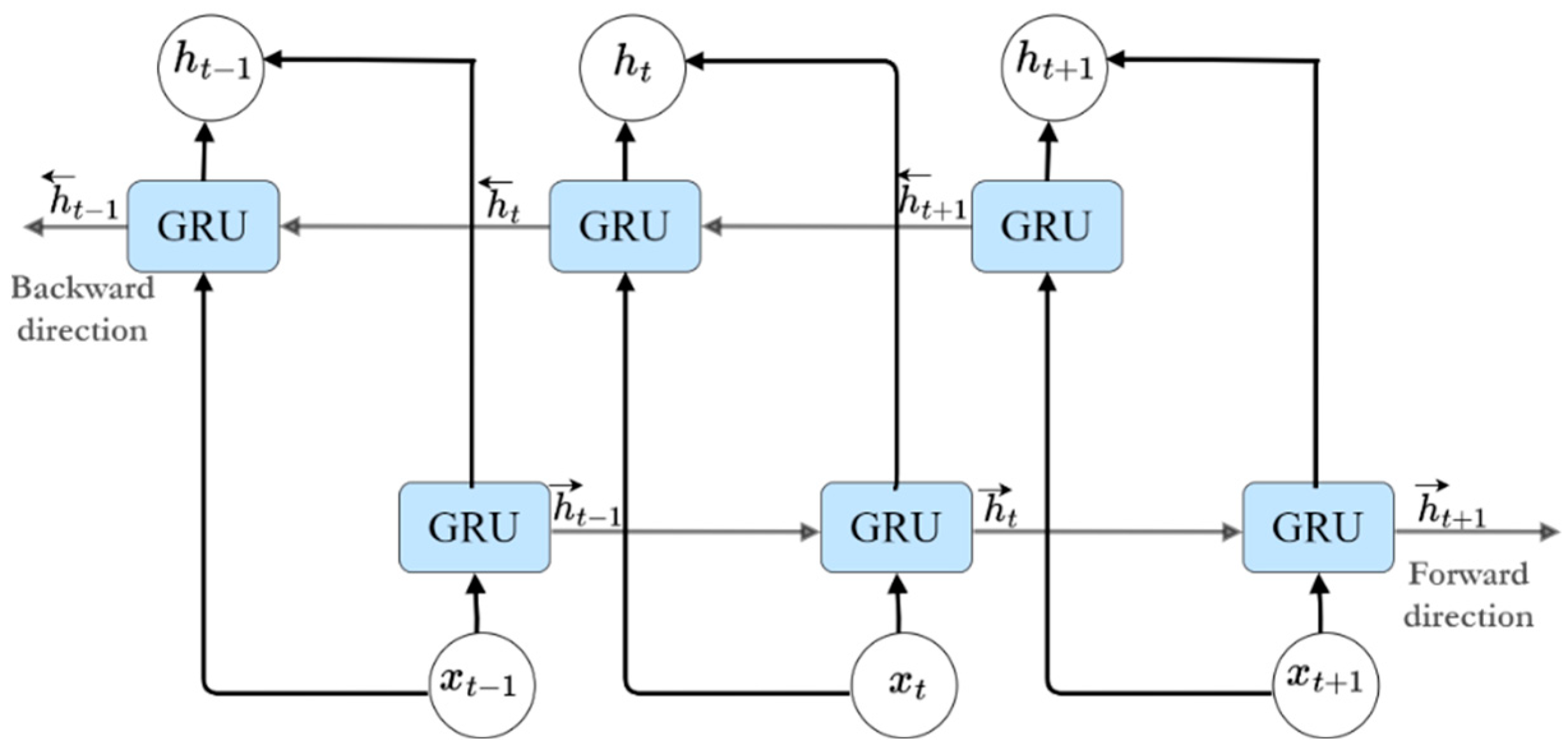
2.2. Bidirectional Gated Recurrent Unit Model

Recurrent neural networks (RNNs) are specially designed for sequential data processing as they are capable of remembering each piece of information over time. The gated recurrent unit (GRU), a variant of RNN, introduced by Chung et al. (2014), has the “memory” function of processing time series data, similar to RNN. The GRU deals with the vanishing gradient problem that may occur during RNN training. The LSTM network, a type of RNN, performs similarly to GRU, although GRU has a simpler structure, leading to a reduced computational load and enhanced training efficiency (Liu et al. 2020).

The GRU cell consists of two gates: an update gate ($z_t$) and a reset gate ($r_t$), as illustrated in Figure 1 (Mou et al. 2017). The amount of new information entering the current state from the input data is regulated by the update gate $z_t$; a higher $z_t$ value allows more additional information to be accessed from the input data. The degree to which the status information from the previous time step is disregarded is determined using the reset gate ($r_t$); a lower $r_t$ value results in more prior status information being disregarded. At time $t$, $x_t$ and $h_t$ represent the input and the hidden state, respectively. The symbol ⊗ represents the element-wise multiplication. The ${\tilde{h}}_t$, also known as the candidate vector, is a modulation operation that determines the extent to which fresh input information is incorporated into the cell state. The sigmoid function is denoted by σ, while the tanh function is represented by tanh. The update gate ($z_t$) and the reset gate ($r_t$) are computed using Equations (2)–(6), with $W_r,W_z$, and $W_{{\tilde{h}}_t}$ representing the weight matrices.

The symbol $\mathrm{\ast }$ represents the element-wise multiplication, and [ ] signifies that the two vectors are linked together.

$$r_t=\sigma \left(W_r\cdot \left[h_{t-1},x_t\right]\right)$$

(2)

$$z_t=\sigma \left(W_z\cdot \left[h_{t-1},x_t\right]\right)$$

(3)

$${\tilde{h}}_t=\tanh \left(W_{{\tilde{h}}_t}\cdot \left[r_t\ast h_{t-1},x_t\right]\right)$$

(4)

$$h_t=\left(1-z_t\right)\ast h_{t-1}+z_t\ast {\tilde{h}}_t$$

(5)

$$y_t=\sigma (W_o\cdot h_t)$$

(6)

The conventional GRU architecture propagates unidirectionally throughout the sequence processing, capturing only the past historical information up to the present time step, disregarding the future information. The BiGRU can collect both front and back information properties as its structure consists of a forward GRU and a backward GRU (Chen et al. 2019). It links two hidden layers with opposite transmission directions to a shared output layer, allowing it to receive information from both the past and future states. This bidirectional structure of BiGRU enhances the accuracy of its predictions. The BiGRU technique entails partitioning the conventional GRU neurons into forward states (representing the positive time direction) and backward states (representing the negative time direction) (Figure 2).

The accuracy of ML models substantially depends on the selection of hyperparameters (Andonie 2019). Optuna (Yang and Shami 2020) is a newly developed tool for optimizing ML models by selecting the best hyperparameters. One of the primary advantages of using Optuna is its define-by-run API. Another advantage of using Optuna is the implementation of a highly effective pruning and sampling framework, along with the simplicity of the setup process. A deep learning framework inspires the design of an API using a define-by-run methodology. Users can dynamically determine the search space for hyperparameter optimization. Efficient searching and efficient performance estimation are two highly successful sampling and pruning policies that necessitate a cost-effective optimization process. Independent sampling is one of the most widely used sampling methods. The tree-structured Parzen estimator (TPE) embodies this approach. Optuna specifically enables the use of personalized sampling methods.

The pruning mechanism went through two phases. At the beginning, we consistently monitored the intermediate objective values. Furthermore, the trial ends when the predetermined condition is no longer satisfied. The final design element of Optuna is related to its simplicity of setup, which enables it to be quickly set up for everything from simple experiments to complex distributed computations, thanks to its adaptable architecture (Chintakindi et al. 2022; Sipper 2022).

2.3. Data

This study examines the forecasting capability of the proposed model using currency exchange rate data on the Saudi Riyal against the Euro (EUR/SAR) and the Chinese Yuan against the Euro (EUR/CNY). We collected the monthly exchange rate prices of both currencies from January 2000 to December 2023, totaling 288 observations. Figure 3 displays the time series plots for both datasets.

We divided the datasets into train–test (90%–10%) datasets, as shown in Figure 3. We trained the models on the training dataset (January 2000 to February 2019, 227 observations) and evaluated their predictive ability on the testing dataset (March 2019 to December 2023, 58 observations).

Table 1. Descriptive statistics of the exchange rates.

	EUR/SAR Exchange Rate	EUR/CNY Exchange Rate
Mean	4.480	8.465
Std. Dev.	0.597	1.167
Minimum	3.173	6.652
Maximum	5.916	11.222
Skewness	−0.058	0.642
Kurtosis	2.624	2.155
Jarque–Bera	1.859	28.348 ***

*** represents significance at the 1% level.

presents the descriptive statistics of both exchange rates. The skewness is slightly negative for the EUR/SAR exchange rate, whereas for EUR/CNY it is positive, indicating a right-tailed distribution for the exchange rate. On the other hand, the kurtosis values show that both the currency exchange rates exhibit excess kurtosis. However, the Jarqeu–Bera test for normality is rejected for the EUR/CNY exchange rate.

2.4. Data Augmentation

This research utilized a decomposition procedure and data augmentation strategy to enhance the predictive accuracy of the DL models. The initial exchange rate data were decomposed into $K$ variational mode functions (VMFs) using the VMD algorithm through the vmdpy module in Python (Carvalho et al. 2020). The penalty factor, number of modes, convergence criteria tolerance, and noise tolerance were set to 2000, 9, 1 × 10⁻⁶, and 1 × 10⁻⁷, respectively.

Figure 4 depicts the EUR/SAR exchange rate and its corresponding decomposed modes using VMD. We will use the EUR/SAR exchange rate as an example for brevity. The decomposed subseries appear in a sequence from low to high frequency. The component $VM{F}_0$ has a substantial correlation with the peak information and long-term pattern of the original sequence, whereas the remaining elements appear to capture medium-term or short-term fluctuations in currency exchange rates.

To expand the number of data combinations, we apply a data augmentation method on the VMFs, taking into account the limited amount of training data (Baek and Kim 2018). In the first stage, we select the $n_K$ ($1<n_K<K$) randomly chosen VMFs as the input features, resulting in a $\left(\begin{array}{c}K\\ n_K\end{array}\right)$-fold increase in the number of data combinations. This increase is sufficient to compensate for the lack of training data. Every ten epochs, the neural network module receives a randomly chosen combination of VMFs for the next 500 iterations. Given that the network is not yet learning from a specific combination, this results in the network extracting predictive general feature patterns from a holistic perspective throughout the training process. Each of the $\left(\begin{array}{c}K\\ n_K\end{array}\right)$ possibilities are trained by the model for 4–5 rounds to minimize the influence of random selection on the model’s predictions. This improves the overall reproducibility and robustness of the model. Furthermore, as these VMFs are derived from the original currency exchange data, it can be concluded that in each historical period, the unique information within each sequence holds an equal influence on the price prediction. The degree of influence does not vary throughout historical periods due to the dynamic proportions of the VMF components.

2.5. The Proposed Model

In this study, we propose a novel hybrid forecasting model for currency exchange rates that combines data decomposition with DL models. The proposed model has a Prevention module and a Prediction module (Baek and Kim 2018). A random combination of VMFs every ten epochs as an input feature is provided to the Prevention module, whereas all the VMFs obtained from the decomposing exchange rates are given as input features to the Prediction module. The Optuna algorithm is employed to select the number of random input features for the Prevention module. Subsequently, we implement L2 regularization during the training process and incorporate a dropout layer into the BiGRU. We again utilize the Optuna algorithm to determine the optimal hyperparameters for the BiGRU model. Specifically, the Optuna algorithm determines the optimal values of window length, number of neurons, number of layers, dropout probability, and learning rate for the BiGRU model. The MVO-BiGRU model is trained using the Adam optimizer. The results obtained from the Prevention and Prediction modules are then combined and input into a fully connected NN to forecast the currency exchange rates. Figure 5 displays the proposed model framework.

2.6. Evaluation Measures

A conventional approach for assessing the superiority of the forecasts of the suggested model is to choose one based on the lowest number of forecasting errors. However, selecting a particular loss function to serve as the evaluation metric for the forecast comparison is challenging. Following the recommendation of Hansen and Lunde (2005), we utilize a wide range of loss functions to assess the forecasting performance of the models. This research uses the MSE as the loss function to train the model. Four evaluation measurements—$R^2$, MSE, MAE, and MAPE—are used to evaluate the goodness of fit of the models. The formulae for which are as follows:

$$R^2=1-{\displaystyle \frac{\sum _{t=1}^N{e}_t^2}{{\sum }_{t=1}^N{\left(a_t-\overline{a}\right)}^2}};\hspace{1em}\hspace{1em}MAE={\displaystyle \frac{1}{N}}\sum _{t=1}^N\left|e_t\right|$$

$$MSE={\displaystyle \frac{1}{N}}\sum _{t=1}^N{e}_t^2;\hspace{1em}\hspace{1em}\hspace{1em}MAPE={\displaystyle \frac{1}{N}}\sum _{t=1}^N\left|{\displaystyle \frac{e_t}{p_t}}\right|$$

where $e_t=(a_t-p_t)$ is the forecast error, $a_t$ and $p_t$ represent the actual and predicted values, respectively, and $N$ is the number of samples to be predicted. The definition shows that $R^2$ can range from 0 to 1, with a higher value indicating a better forecasting performance of the model. $R^2$, also called a risk-adjusted return ratio in finance, helps investors to assess existing and potential investments. Additionally, the MAE and MSE quantify the difference between the actual and predicted values; therefore, choosing the model with the lowest MSE and MAE values can lead to more precise forecasting outcomes. The MSE squares the errors before averaging them, giving greater weight to the larger error. The MSE is well suited for FX prediction, where a large error is very undesirable. On the other hand, the MAE is not too sensitive to outliers compared with the MSE, but it is a useful evaluation metric for the time series data. Similarly, we also applied the MAPE as a nonlinear loss metric with a value range of [0, +∞). The smaller the MAPE value, the better the model’s forecasting performance.

Moreover, we employ directional accuracy (DA) as an alternative measure to further assess the model’s market-trend predictive ability (Yu et al. 2008). A large value of DA indicates the model’s better market trend predictive ability. Therefore, investors may prioritize the DA while evaluating the financial market, as a higher DA has the potential to yield greater profits for speculative investors.

$$DA={\displaystyle \frac{1}{N}}\sum _{t=1}^N{Z}_t$$

where $Z_t=\left\{\begin{array}{l}1,\left(a_t-a_{t-1}\right)\left(p_t-p_{t-1}\right)\ge 0\\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$.

2.7. Benchmark Models and Parameter Values

To evaluate the accuracy of the proposed MVO-BiGRU model and test the reliability of the forecasting results, we select a group of regularly used ML models as benchmark models. These include the Ridge regression, Multilayer Perceptron, and LightGBM models, which are implemented as benchmark ML models. Additionally, we design several DL models to further investigate the proposed model’s superiority. These include: (i) simple DL models with three-month lagged currency exchange rates as input features, denoted as (RNN); (ii) models based on the Prediction module, where three lagged currency exchange rates and all the VMFs are used as input features, denoted as (V-RNN); and (iii) models based on the Prevention and Prediction modules, denoted as (MV-RNN). Hence, we use the ANN, V-ANN, MV-ANN, RNN, V-RNN, MV-RNN, BiLSTM, V-BiLSTM, BiGRU, and V-BiGRU models and compare their forecasting performance with the proposed MVO-BiLSTM and MVO-BiGRU models.

We run the Optuna algorithm on 50 trials to determine the optimal set of hyperparameter values. The following range of values for the different hyperparameters is set for Optuna to search: window_length [1:6], no. of neurons [32:256], no. of layers [1:3], learning rate [1 × 10⁻⁵:1 × 10⁻¹], and dropout probability [0.1:0.4], $n_K$ [2:(K − 1)].

3. Results and Discussion

Figure 6 displays the fitted values of the benchmark ML models (top panel) and the fitted values of the benchmark DL models (bottom panel) against the full sample’s real EUR/SAR exchange rates. The dashed line divides the display into two halves. The in-sample results are displayed on the left side, while the out-of-sample forecasting results are shown on the right side. To provide a clearer and more intuitive comparison of the models’ forecasting performance, we focus closely on the testing results, as shown in the rectangular box. From Figure 6, we can see that several of the ML and DL models provide reasonable results for the training dataset; however, their forecasting performance deteriorates in the testing dataset.

To closely compare the forecasting performances,

Table 2. The results of evaluation measures for the training and testing datasets (EUR/SAR).

Models	Training					Testing
	MSE	MAE	MAPE	${\mathit{R}}^{\mathbf{2}}$	DA (%)	MSE	MAE	MAPE	${\mathit{R}}^{\mathbf{2}}$	DA (%)
Ridge	0.0179	0.0993	0.0218	0.9551	51.77	0.0072	0.0704	0.0170	0.8377	45.61
MLP	0.0436	0.1634	0.0366	0.8907	56.63	0.0295	0.1533	0.0371	0.3319	43.86
LightGBM	0.0089	0.0633	0.0139	0.9777	79.65	0.0112	0.0860	0.0210	0.7464	57.90
ANN	0.0174	0.0981	0.0214	0.9565	53.98	0.0074	0.0720	0.0173	0.8333	45.61
V-ANN	0.0037	0.0476	0.0105	0.9907	81.86	0.0025	0.0396	0.0097	0.9442	82.46
MV-ANN	0.0194	0.1078	0.0233	0.9514	54.87	0.0075	0.0663	0.0159	0.8312	63.16
RNN	0.0179	0.1009	0.0224	0.9552	57.52	0.0115	0.0861	0.0209	0.7401	49.12
V-RNN	0.0036	0.0481	0.0108	0.9909	81.86	0.0018	0.0341	0.0082	0.9597	89.47
MV-RNN	0.0345	0.1429	0.0318	0.9136	61.50	0.0484	0.1866	0.0458	0.8368	57.37
BiLSTM	0.0176	0.0987	0.0216	0.9559	54.42	0.0075	0.0727	0.0175	0.8302	45.61
V-BiLSTM	0.0036	0.0481	0.0108	0.9909	82.31	0.0020	0.0350	0.0085	0.9554	85.97
MVO-BiLSTM	0.0025	0.0399	0.0088	0.9938	82.32	0.0011	0.0262	0.0063	0.9744	89.49
BiGRU	0.0175	0.0986	0.0216	0.9561	53.54	0.0077	0.0737	0.0178	0.8264	45.61
V-BiGRU	0.0041	0.0516	0.0118	0.9897	81.86	0.0029	0.0446	0.0109	0.9336	82.46
MVO-BiGRU	0.0015	0.0303	0.0066	0.9963	89.38	0.0007	0.0208	0.0050	0.9846	94.77

The bold values in each column represent the optimal model based on the indicator, while the underlined values represent the second-best model.

shows the results of the evaluation measures of all the models for the EUR/SAR exchange rate. The ML models failed to provide satisfactory forecasting results. The in-sample performance of LightGBM was reasonable, with an $R^2$ value of 0.9777 and a DA of 79.85%; however, its out-of-sample forecasts declined significantly, with an $R^2$ value of 0.7464 and a DA of 57.90%. Similarly, when we consider the results of the DL models where only the exchange rates are used as input features, the ANN and BiLSTM out-of-sample performance is relatively better than that of RNN and BiGRU, with $R^2$ values of 0.8333 and 0.8302, respectively, but their DA is found to be below 50%. Their in-sample performance is found to be slightly inferior to the Ridge regression model, which has a higher $R^2$ value of 0.8377.

The results in Table 2 also show that decomposing the exchange rates into VMFs and using them as input features in the DL models has improved both the in-sample and out-of-sample performance of the models. For example, the in-sample $R^2$ of ANN increases from 0.9565 to 0.9907 for the V-ANN model, from 0.952 to 0.9909 for the RNN model, and from 0.9561 to 0.9897 for the BiGRU model. Moreover, the use of VMFs as inputs significantly increases the DA for all the models. However, when the fitting performance yielded unsatisfactory results, it was believed that the DA values lacked practical guiding relevance since the fitting performance served as the foundation for assessing the accuracy of these models. The DA values of the ANN models increased from 53.98% to 81.86% and from 57.52% to 81.86%, respectively. Similarly, including VMFs as input features also improved the out-of-sample forecasting results of the DL models. We found that the hybrid models with VMD improved the values of all the evaluation measures. For example, the MAPE of the V-RNN (V-BiGRU) model decreased from 0.0209 (0.0178) to 0.0082 (0.109), showing an improvement in the forecasts. In addition, significant improvements in the DA were also observed. These results suggest that combining the decomposition with the DL models enhances the predictive accuracy of the models.

Finally, we investigate the impact of using the Prevention module in the DL models, as well as decomposition and parameter optimization using Optuna. All the DL models significantly improve their forecasting performance on the testing dataset compared with the simple and decomposed models. We find the MVO-BiGRU model to be the best forecasting model, achieving the highest $R^2$ (0.9846) and DA (94.77%) values. The MSE, MAE, and MAPE values of the proposed model are also found to be the lowest for both the training and testing datasets. Compared with the out-of-sample results of the V-BiGRU model, the MVO-BiGRU model has reduced forecasting errors: 54.13% for MAPE and 75.86% for MSE; and the $R^2$ improved from 0.9336 to 0.9846, all of which indicate the importance of data augmentation and hyperparameter optimization in forecasting models. The MVO-BiLSTM model also provides excellent results and was found to be second best to the MVO-BiGRU model. These results indicate that data augmentation plays an important role in improving the predictive ability of DL models. The forecasting results of the MV-ANN and MV-RNN models do not show improvement compared with the V-ANN and V-RNN models. One of the reasons could be due to the default choices made for the hyperparameter values. This confirms the importance of using optimal hyperparameter values in complex DL models. Overall, the results show that the proposed methodology does improve the forecasting ability and capability of predicting the market trend of DL models in low-frequency complex time series. The best hyperparameter values chosen by the Optuna algorithms for the EUR/SAR exchange rate are: window_length = 3, no. of neurons = 40, no. of layers = 1, learning rate = 0.0045, and dropout probability = 0.1350 and $n_K$ = 7.

Figure 7 shows the forecasting results of the best-performing MVO-BiGRU model. It can be seen (left panel) that the proposed model provides accurate fits for the training and testing datasets. The figure (right panel) also illustrates the scatter point comparison between the actual values on the horizontal axis and the predicted values on the vertical axis. Almost all the points are closer to the dashed line, suggesting excellent forecasted values for the model. Besides, the MAE, MSE, and $R^2$ values of 0.001, 0.028, and 0.996, respectively, for the entire sample further suggest that the proposed model is providing an accurate fit for the currency exchange rate. The model effectively captures significant fluctuations in the exchange rates, as demonstrated in both the training and testing datasets with a high DA (90.5%) value. This indicates the model’s exceptional forecasting capability.

Subsequently, we replicate the tests using an alternative currency exchange rate dataset (EUR/CNY) to validate the reliability of the aforementioned findings.

Table 3. The results of evaluation measures for training and testing datasets (EUR/CNY).

Models	Training					Testing
	MSE	MAE	MAPE	${\mathit{R}}^{\mathbf{2}}$	DA (%)	MSE	MAE	MAPE	${\mathit{R}}^{\mathbf{2}}$	DA (%)
Ridge	0.0610	0.1830	0.0211	0.9578	53.09	0.0153	0.0988	0.0130	0.8524	54.39
MLP	0.1060	0.2465	0.0286	0.9267	54.42	0.0345	0.1570	0.0209	0.6683	56.14
LightGBM	0.0200	0.1015	0.0117	0.9862	80.09	0.0301	0.1372	0.0179	0.7105	50.88
ANN	0.0583	0.1791	0.0207	0.9597	54.87	0.0157	0.0995	0.0131	0.8486	50.88
V-ANN	0.0134	0.0946	0.0109	0.9907	80.53	0.0111	0.0832	0.0108	0.8930	75.43
MV-ANN	0.0693	0.1971	0.0229	0.952	63.72	0.0190	0.1101	0.0146	0.8177	56.14
RNN	0.0605	0.1881	0.0218	0.9582	53.54	0.0230	0.1192	0.0155	0.7790	52.63
V-RNN	0.0129	0.0925	0.0107	0.9911	80.53	0.0626	0.1860	0.0254	0.3979	70.18
MV-RNN	0.1163	0.2571	0.0296	0.9196	55.75	0.0325	0.1467	0.0193	0.6871	56.14
BiLSTM	0.0562	0.177	0.0204	0.9611	56.64	0.0163	0.1038	0.0136	0.8435	45.61
V-BiLSTM	0.0129	0.0924	0.0106	0.9911	80.53	0.0109	0.0810	0.0106	0.8955	75.44
MVO-BiLSTM	0.0049	0.0528	0.0061	0.9966	88.05	0.0063	0.0587	0.0076	0.9392	78.95
BiGRU	0.0560	0.1773	0.0205	0.9613	53.98	0.0166	0.1056	0.0139	0.8405	45.61
V-BiGRU	0.0128	0.0918	0.0106	0.9911	80.97	0.0147	0.0959	0.0124	0.8586	70.18
MVO-BiGRU	0.0010	0.0249	0.0029	0.9993	91.15	0.0039	0.051	0.0067	0.9624	85.96

The bold values in each column represent the optimal model based on the indicator, while the underlined values represent the second-best model.

shows the results of both the training and testing datasets for all the models. Here, we will concentrate on the out-of-sample forecasting results, given their significance and the understanding that a model that produces accurate in-sample forecasts cannot ensure accurate out-of-sample forecasts (Wang et al. 2019). A similar phenomenon can be observed from the numerical results of all the evaluation measures: the proposed MVO-BiGRU model shows the lowest MAE, MSE, and MAPE values and the highest $R^2$ and DA values, followed by the MVO-BiLSTM model. More specifically, the $R^2$ (DA) values are 0.9624 (85.96%) for the MVO-BiGRU model and 0.9392 (78.95%) for the MVO-BiLSTM model. Other competing models, such as MV-ANN and MV-RNN, have a significantly lower forecasting performance than the proposed models. The DL models with decomposition offer accurate exchange rate forecasts, suggesting that VMF sequences effectively capture latent temporal information, enabling the DL models to produce superior forecasts. In general, the empirical findings confirm the excellent predictive performance of the proposed MVO-BiGRU model, and its ability to make accurate predictions remains robust in various datasets. The best hyperparameter values chosen by the Optuna algorithms for the EUR/CNY exchange rate are: window_length = 3, no. of neurons = 32, no. of layers = 1, learning rate = 0.0176, dropout probability = 0.3583, and $n_K$ = 4.

Figure 8 depicts the forecasting results of the MVO-BiGRU model for the EUR/CNY exchange rate data. Again, the proposed model provides the most accurate fit for the training and testing datasets. The scatter point comparison between the actual and forecasted values further suggests that the forecasts are accurate. The MAE, MSE, and $R^2$ values of 0.001, 0.002, and 0.999, respectively, of the proposed model for the entire sample are indications of the superior fit to the data. Besides, the DA value of 90.1% shows that the proposed model successfully captures significant fluctuations in exchange rates. These findings further confirm the exceptional predictive capability of the proposed model.

Subsequently, we employ the model confidence set (MCS) test (Hansen et al. 2011) to reveal any substantial deviations in the loss functions across the models. In general, we can infer that Model A has superior forecasting accuracy compared with Model B under those specific conditions if the value of a given loss function for Model A in empirical research is lower than that of Model B. However, it is evident that this assessment is not robust enough to apply to other comparable datasets or alternative evaluation criteria. It is crucial to acknowledge that even a small number of data points that deviate greatly from the rest can have a substantial impact on the calculated loss values. This, in turn, can lead to an erroneous evaluation of the model’s predictive performance (Hansen and Lunde 2005).

The MCS test is designed to control the overall error rate. It uses evaluation measures to determine a group of values that exhibit no significant statistical variation. We use the p-values of this test to identify the models in the confidence set. A larger p-value (p > 0.1) is an indication that the model is in the MCS. In contrast, a smaller p-value indicates a higher likelihood of rejecting the null hypothesis that the model is the best fit. The values of MAE, MSE, and MAPE of the testing dataset of all the models are used to conduct the MCS test.

Table 4. The results of the MCS test for the out-of-sample forecasts.

Models	EUR/SAR			EUR/CNY
	MSE	MAE	MAPE	MSE	MAE	MAPE
Ridge	0.000	0.000	0.000	0.000	0.000	0.000
MLP	0.000	0.000	0.000	0.000	0.000	0.000
LightGBM	0.002	0.000	0.000	0.000	0.000	0.000
ANN	0.000	0.000	0.000	0.000	0.000	0.000
V-ANN	0.006	0.000	0.000	0.003	0.000	0.000
MV-ANN	0.000	0.000	0.000	0.000	0.000	0.000
RNN	0.000	0.000	0.000	0.000	0.000	0.000
V-RNN	0.000	0.000	0.000	0.075	0.046	0.050
MV-RNN	0.005	0.000	0.000	0.001	0.000	0.000
BiLSTM	0.000	0.000	0.000	0.000	0.000	0.000
V-BiLSTM	0.002	0.000	0.000	0.003	0.000	0.000
MVO-BiLSTM	0.046	0.036	0.043	0.327	0.517	0.546
BiGRU	0.000	0.000	0.000	0.000	0.000	0.000
V-BiGRU	0.002	0.000	0.000	0.003	0.000	0.000
MVO-BiGRU	1.000	1.000	1.000	1.000	1.000	1.000

The table presents the p-values of the MCS test. A small value (p-value < 0.1) indicates rejection of the model from the set that includes the best model. The bold numbers in each column are the optimal metric values achieved using the loss function.

shows the results of the MCS test of all the models and for both datasets. Figure 9 illustrates the same results in an intuitive way. The table displays numerical values representing p-values. A higher p-value indicates better performance of the model. It can be seen from the results that all the p-values are equal to one (under the three loss functions) for the MVO-BiGRU model for both the currency exchange rates. The MVO-BiLSTM model is included in the MCS for the EUR/CNY data, indicating that its forecasting performance is not significantly different from the MVO-BiGRU model. In addition, the MCS excludes all the other models due to their extremely low p-values, indicating a significantly lower forecasting performance compared with the proposed models. The results suggest that implementing the Prevention Module greatly improves the model’s capacity to extract hidden temporal information from combinations of VMFs. The model can then efficiently capture this information, leading to improved forecasting accuracy. Furthermore, Optuna has also played an important role in selecting the best hyperparameters for DL models.

Based on the findings of this study, we infer that though the commonly used ML and DL models have good in-sample fitting capabilities, they often fail to produce accurate out-of-sample forecasts, have a restricted role in predicting unfamiliar patterns in the data, and have limited practical significance in real-world forecasting problems. Nevertheless, the suggested approach can successfully avoid the overfitting problem by making use of data augmentation.

Finally, we employed the Pesaran–Timmermann (PT) test, created by Pesaran and Timmermann (1992), to establish the statistical significance of the correlation between the predicted values and observed values. The purpose of this test is to evaluate the importance of accurately predicting the direction of a forecast. The null hypothesis of this test posits that the likelihood of a model accurately predicting changes in the real exchange rate should not exceed that of randomly flipping a coin with a probability of 0.5. We can infer that a model is more precise in predicting directions than the no-change forecast if its success ratio of directional forecasting exceeds 0.5. The test’s purpose is to assess the effectiveness of a forecasting model in accurately predicting changes in direction. Specifically, it measures the degree to which the predicted values align with the actual values in terms of both upward and downward trends. Specifically, it measures the degree to which the predicted values align with the actual values in terms of both upward and downward trends.

Table 5. The results of the PT test for out-of-sample forecasts.

Models	EUR/SAR		EUR/CNY
	DA (%)	p-Value	DA (%)	p-Value
Ridge	45.61	0.316	54.39	0.869
MLP	43.86	0.316	56.14	0.963
LightGBM	57.90	0.513	50.88	0.977
ANN	45.61	0.479	50.88	0.796
V-ANN	82.46 ***	0.000	75.43 ***	0.000
MV-ANN	63.16	0.233	56.14	0.963
RNN	49.12	0.423	52.63	0.844
V-RNN	89.47 ***	0.000	70.18 ***	0.000
MV-RNN	57.37	0.034	56.14	0.156
BiLSTM	45.61	0.316	45.61	0.703
V-BiLSTM	85.97 ***	0.000	75.44 ***	0.000
MVO-BiLSTM	89.49 ***	0.000	78.95 ***	0.000
BiGRU	45.61	0.409	45.61	0.703
V-BiGRU	82.46 ***	0.000	70.18 ***	0.000
MVO-BiGRU	94.77 ***	0.000	85.96 ***	0.000

The bold values indicate the statistical significance of the directional accuracy (DA) as measured by the PT test. *** implies rejecting the null hypothesis at a 1% significance level.

displays the results of the PT test applied to the out-of-sample forecasts of all the models for both datasets. The MVO-BiGRU model has the highest DA for EUR/SAR (94.77%) and EUR/CNY (85.96%). The proposed model has successfully rejected the null hypothesis of the PT test at a significance level of 1%, demonstrating the accuracy of the suggested framework in predicting the direction. The MVO-BiLSTM model, which is also developed on the proposed framework, also shows excellent forecasting results on the testing dataset. Furthermore, all the DL models with VMD decomposition (V-ANN, V-RNN, and V-BiLSTM) have rejected the PT test at a 1% significance level among all the other models. The performance of these models in predicting the direction is better than that of the individual DL models, suggesting that the VMFs may have extra predictive information about the direction that can be utilized to identify general patterns in features, resulting in improved DL modeling and forecasting.

4. Conclusions

This study suggests a novel forecasting framework called the MVO-BiGRU model, which combines variational mode decomposition (VMD), data augmentation, Optuna-optimized hyperparameters, and bidirectional GRU algorithms to enhance the robustness of the DL models and address the issue of overfitting. The Prevention module’s data augmentation greatly expands the range of possible data combinations, which effectively minimizes overfitting problems. Meanwhile, Optuna optimization ensures that the best possible model configuration is used for improved performance. We conducted a series of tests using various ML and DL models as benchmark models to confirm the better forecasting performance of the suggested approach. Furthermore, we empirically analyzed all the trials using two currency exchange rate datasets to verify the robustness of the models. We then utilized five evaluation measures, as well as the MCS and PT tests, to assess the performance of all the models.

The empirical results of the study indicate that the MVO-BiGRU model achieves the highest in-sample and out-of-sample forecasting performance for both datasets. Compared with the benchmark models, the proposed model excels at extracting nonlinear features from the data and effectively addresses the issue of overfitting due to insufficient data. We find that the proposed model has the lowest evaluation measures and the MCS test confirms its superior predictive ability. Additionally, by looking at the outcomes of the DA and PT tests, we can conclude that the decomposed VMFs hold extra predictive data that help the model better predict the direction of the time series.

We thoroughly examined the VMO-BiGRU model’s effectiveness in predicting monthly exchange rates by combining the VMD approach with the optimized DL models. Our findings confirmed that the suggested model is superior and resilient. Furthermore, the implementation of the Prevention Module technique is compelling because it effectively captures the overall temporal feature pattern, enhancing the forecasting performance and generalization capacity of the model. These findings suggest that forecasters and investors might use this method to identify predictive indicators that can help to predict changes in FX markets, leading to enhanced risk management.

The findings of the study can be used to assess the potential impact of exchange rate fluctuations on the economy and adjust macroeconomic policies accordingly. The model can provide insights on the potential effects of trade policies on the exchange rate and the economy. Accurate FX forecasts can contribute to maintaining financial stability by identifying potential risks and vulnerabilities. The model’s ability to offer more accurate forecasts enables it to guide trading decisions, which has the potential to generate higher returns. The MVO-BiGRU model has the potential to significantly enhance decision-making across various economic sectors by improving the accuracy of FX rate forecasts. For example, consumers can optimize their purchasing methods, exporters can hedge against currency changes, and investors can allocate their portfolios intelligently. Furthermore, governments can create efficient monetary and fiscal regulations that affect trade balances, inflation, and economic growth by using precise forecasts. This can lead to increased efficiency, reduced risk, and ultimately, improved economic performance.

While the proposed MVO-BiGRU model shows promising results, it is important to address its limitations. The FX market is highly volatile and influenced by numerous factors, including economic indicators, geopolitical events, and investor sentiment. Capturing all these variables and their interactions is challenging. Additionally, the performance of the MVO-BiGRU model is highly sensitive to hyperparameter tuning. Finding the optimal hyperparameter configuration can be time-consuming and computationally expensive.

By leveraging the strengths of this research, we can explore several promising avenues for future research. Expanding the feature set to include alternative factors, such as social media and news sentiments, and economic and technical indicators, could potentially enhance the forecasting accuracy of the model. Furthermore, ensemble methods that combine multiple models may improve prediction accuracy. Finally, exploring the use of the MVO-BiGRU model in risk management applications, such as value-at-risk (VaR) estimation, would be interesting future research.