Fair and Sustainable Pension System: Market Equilibrium Using Implied Options

Abstract

This study contributes to the discussion about a fair and balanced pension system with a collectively funded pension scheme or social security and a defined contribution pillar. With an invigorated risk approach using financial option positions, it considers the variance of socioeconomic interests of different society-earning cohorts. By that, it enables the assumption of un-uniformity in interests about the fair and sustainable pension design. Specifically, we claim that the alternative cost of hedging the ideal position to the counterparty position studies the implied risks and returns that participants are willing to absorb and hence may lead to a fair compromise when there are different interests. The novelty of the introduced method is mainly based on the variety of participants’ risks and not on the utility function. Accordingly, we spare the discussion about the right shape of the utility function and the proper calibrations.

1. Introduction

The problem of optimal consumption and saving over the life cycle has become a canonical issue of debate in the literature of risk since Merton, who was the first to mathematically solve it in a continuous-time setting. His seminal work has been extended in many dimensions. Many of these life-cycle papers assume standard preferences: they assume that the individual exhibits either constant relative risk aversion (CRRA) utility or Epstein–Zin utility (for example, Gollier 2008). Still, the classical pension economy literature has usually been limited to the debate of relatively simple individual motivations. An extensive body of the literature in behavioral economics, insurance, and finance, however, documents experimental and empirical departures from the key assumptions underlying these preference models in a wide variety of risky choice situations as well as from the consumption and portfolio implications they generate. This has triggered researchers to develop a variety of alternative theories of decision-making under risk such as Sugden and Bilsen et al. and the well-known Prospect theory originally proposed by Kahneman and Tversky.

The current study emphasizes the relevance of political subgroups in society as a key player in modern funded pension design, in addition to the public and the government, who are represented as traditional actors in the literature. By that, we support extending the literature regarding the individual’s motivation for long-term saving and consumption. More specifically, this paper offers a new approach to analyzing the fair and balanced pension system with funded and unfunded pillars, where there are socioeconomic pressures in implementing each of these pension designs. By that, we emphasize the interest of the society as a whole, as opposed to the narrow individual participant perspective. This perspective enables the classic economic funding condition of Aaron (1966) to be enriched through the dimension of risk. Using simple financial option positions, the suggested theory implies a tradeoff between insurance and return in pension accounts but is not disconnected from social welfare. In addition, this perspective of financial standing equilibrium allows for differentiation in society, as a substitute for expensive risk-sharing mechanisms.

At the macroeconomic level, the role of private pensions in the provision of retirement income has grown significantly in the past two decades, reflecting efforts by many countries to relieve pressure on unsustainable pay-as-you-go (PAYG) benefits (Altiparmakov 2018). Some scholars argue that the unstable pension landscape is due to a lack of risk-sharing mechanisms (Fultz and Hirose 2019; Ebbinghaus 2015; Grech 2015). Others emphasize a lack of political equilibrium among different interest groups (Wolf et al. 2021; García-Miralles and Leganza 2024).

In the literature strands of optimal pension design, we witness more room for intergenerational risk-sharing, specifically support in some weight to the unfunded pillar. Here, we add the importance of the income redistribution mechanism or expressing low-income cohorts’ interests. Gollier (2008) studied the role of shareholder-sponsored financial intermediaries in facilitating intemporal risk smoothing. He finds welfare improvement if participants accumulate a sufficiently large financial buffer as a means for intertemporal smoothing. However, without mandatory contribution, he finds that the system breaks down and goes back to the market solution. Dong and Zheng (2020) and De Menil et al. (2006) further analyzed the optimal pillar size of the unfunded PAYG pillar and the funded pillar, utilizing an overlapping generation (OLG) model with two periods and maximizing the utility function. Wolf and Caridad y Ocerin (2021) derive the optimal portfolio mix with an OLG model when people care about their consumption relative to a reference group. According to these papers, risk considerations might change the relative attractiveness of funded and unfunded systems. In other words, more funding will result in an efficiency loss when individuals cannot insure themselves against wage shocks or severe market risk. Other papers quantify the welfare gains from intergenerational risk-sharing using a technical variation of OLG models and calibrate them to a specific economy (Jensen et al. 2019; Cui et al. 2011). Based on the American market, Maestas et al. (2023) discuss the tradeoff between less volatile PAYG funds and financial market returns. Their simulation results suggest that some mix between these two pillars is preferable. They suggest that risk-sharing mechanisms are critical to incentivize the labor force and take care of aging markets. Alonso-García and Devolder (2016) studied the cohort’s optimal mix between funded and unfunded pension schemes and whether there are diversification benefits for the specific context of a notional-defined contribution scheme with a constant contribution rate. This mixed pension scheme takes into account the aging of society and the yields of both the market and the GDP per capita. Bouhakkou et al. (2019) derived the optimal sizes of pension pillars while considering a mean-variance approach for a sample of eight OECD countries. They find that, in most cases, a mix of funded and unfunded systems is desirable, with a larger magnitude of the PAYG system as they have captured attitudes towards asymmetry and tail risks that are typical to equity markets. Wolf and Caridad y Ocerin (2021) and Hanna and Devolder (2023) are one of the few who consider multiple earning cohorts in their optimization and not only one single representative agent. Recently, Hanna and Devolder (2023) derived the optimal mix of pension schemes under the assumption of maximizing utility function in line with the Prospect theory. They find different balances between the cash balance scheme and the defined contribution (DC) scheme from the worker and the employee perspectives.

The political economy also contributes to the debate on the optimal pension design. Wolf et al. (2021) assert that in an attempt to reduce the probability of pension reversal, the government has an incentive to increase pension accumulations to the low tail of the accumulation distribution. Particularly when in an unequal economy, the pension design does not represent enough of the low-earning interests. They tried to solve this problem by approaching this situation as an economic “Externalities”, for example, by balancing the economy with a minimum pension guarantee or other intra-generational compensation in return for keeping the DC pension scheme, as middle and high earners wish (Alonso-García and Devolder 2016; Grande and Visco 2010).

In this study, we innovate by suggesting a replacement for the use of the traditional utility function in finding the optimal mix of pension schemes. The fallbacks of the utility function in the pension literature come to be realized in the context of the Prospect theory when the preferences of participants are not consistent and the fund cannot track the cohort expectations (Van Bilsen and Laeven 2020). Hence, this study suggests attributing this to risk and not preferences in the form of financial standing. In other words, it replicates the earning cohorts’ expectation to return in the form of a theoretical option position to the alternative pension design. Using a financial position of exchange options to describe pension designs is not new in the literature. Implementing pension guarantees, such as in Uruguay or Chile, is attributed to a long position in a Put option on bealf of the individual. Romaniuk (2009) also describes pension pillars via different option positions. Chen et al. (2014) describe the exit policy from pension. Wolf et al. (2021) calculate the minimum pension guarantees in pension arrangements around the world.

Our key contributions are the following: We offer a social pension design equilibrium, considering not the median nor the average participant but different participants, disconnected from their preferences but with recognition of their different incomes. We achieve that by recognizing the inherent financial position of both the Call and Put options. Here, we enable another kind of stable and fair equilibrium without naturally maximizing the agent utility function. Besides its social effect, equilibrium enriches the literature in the debate on the right utility function, its shape, and its ingredients when attributing to pension and biology–economy.

We find that ceteris paribus, only a few high-income deciles prefer the individual account while most of the agents in a representative Western society prefer an intergenerational risk-sharing mechanism, or at least a mixed pension scheme. This includes a lower risk to contributions but with a higher commitment to the next generations. We are also capable of studying the effect of wage dispersion and market performance on the pension scheme design. In a high-income dispersion, there is a higher chance of more weight to the unfunded pillar. Hence, those who prefer an independent stable individual account pension design must first invest in lowering inequality in the economy.

The remainder of this paper is structured as follows: Section 2 presents the model, while Section 3 presents the benchmark parameter setting. Section 4 explores the equilibrium and details the simulations and calculations. In Section 5, we present our main insights from the model and the sustainability equilibrium it offers. In Appendix A, we conclude the main text of this paper. The technical details are found in Appendix A.

2. Theoretical Model

The model introduced above argues that the question of pension reform sustainability is linked to the economic gain/loss of participants and not necessarily to the rate of return and the population coefficient growth, similar to what used to be addressed in the traditional economy (Aaron 1966). The model asserts that the Aaron–Samuelson rule is valid in an economy with identical consumers or, at least, almost homogenous savers. In reality, the question of pension reform depends on statistical/political considerations. The hidden assumption in the base of the model is the warning that if a significant mass of participants will be negatively affected by the transition, the probability of reversal is higher (Ebbinghaus 2015). According to this model, the central planner has to improve the financial benefit status of enough participants to maintain the pension scheme. We achieve this by considering the financial position of different earning cohorts in the pension market.

We relate the pension system as an option market with different players. Different pension schemes are described using the financial positions of exchange options with nonlinear risks. The pension market includes three major players: retirees, the working generation, and the government. However, we differentiate earning cohorts to concern unequal interests among the participants and social welfare.

Excluding utility optimization, we claim that the market equilibrium of mixed pillars derives from the population cohorts’ interests (see also Jensen et al. 2019). Analyzing option positions enables us to quantify the cohort position or “interest” relative to the other cohort interest or in other words to the alternative, measure it, and compare between interests. This vector of relative interests is quantified, in this model, as the willingness to pay for hedging the financial position between the group’s interest and the opposing group’s interest. It resembles the theoretical transformation of resources from one group to the other.

The innovation in this model is by independence in utility preferences and risk aversion. Additionally, the quantification is not relative to a base scenario but to the counterparty position. The proportion of these net transfers, or the financial theoretical position, implies the proportions of a fair mix of the systems.

2.1. Economy, Overlapping Generation, and Preferences

Our model economy is populated by overlapping generations of participants who may live up to the maximum possible lifespan of $J$ periods. We employ a simple OLG model to characterize optimal pension pillar sizes. In each period, a new generation of unity mass is borne. The model includes three major life period cycle frameworks as in Chen et al. (2014).

We assume that an arbitrage-free financial market exists. We follow Merton by assuming a continuous time Markov structure and all variables follow the Ito process. The instantaneous return of a risky asset, $S_t$ can then be written as

$${\displaystyle \frac{d{S}_j}{S_j}}={\mu }_j\left(X\left(t\right),t\right)dt+{\sigma }_j\left(X\left(t\right),t\right)d{Z}_t$$

(1)

where ${\sigma }_j$ is the volatility of a risky asset.

The participant works during the working period, $T_w$. During that period, the wage level for the participant $i$ from generation $t$ is defined as $w_{i,t}$. During the working period, the individual contributes a pre-determined share of $\tau$ from their wage to future pension benefits. The rest of their income is consumed. At retirement (t ≥ T_R), the participant is paid pension benefits by two different systems—funded individual accounts (p^f) and DB PAYG by the government (p^U). Wage and pension enable consumption along the life cycle.

$$C_{i,t}=\left(1-\tau \right)w_{i,t} t<T_R C_{i,t}=P_{i,t}^f+P_{i,t}^U for t\ge T_R$$

(2)

$T_R$ is the participant’s retirement age, and $t=1$ is the time of enrolment in the pension fund. This model avoids actuarial factors related to the probabilities of survival.

2.2. The Government

The government acts as a central planner, which coordinates and balances the multiple interests of the market’s players, which include, among others, the retirees and the working generations. By corresponding financial streams among the agents, the government is exposed to the financial market and credit risks. The only reason for that exposure is the commitment of the worker to have a predetermined pension level. Naturally, if the income streaming is not efficient, the government has to manage expenses by levying taxes on participants. Hence, the government tries to find political stabilization in the pension market, avoiding reversals in the future.

2.3. Unfunded DB PAYG Pension System

During the working period, the participants contribute a fraction of ${\tau }_u$ from their wages to the unfunded/social security pension scheme. During retirement, the unfunded pillar pays according to a pre-determined accrued rule independently from market (asset) performance. This scheme benefit is a function of the adjacent generation’s personal working period and age (Romaniuk 2009). At the macroeconomic level, the liabilities of the PAYG pension scheme for the generation $j$ are the total benefits of the unfunded pillar to the retirees from generation $j+1$; thus, the unfunded pension benefit for the individual $i$ in generation $j$ is:

$$P_{i,j}^U={\displaystyle \sum }_{i=j}^N{\displaystyle \sum }_{t=T_R}^T{\tau }_U{\overline{w}}_{i,t}{\theta }_t{\left(1+g\right)}^{t-1}{\left(1+n\right)}^{t-1}$$

(3)

Here, $N$ is the number of individuals in the generation $j$ and $n$ is the rate of change in the generation side as we consider the aging of societies, which has a direct influence on the unfunded benefit level. We refer to $g$ as the average expected growth rate of the GDP per capita, and ${\overline{w}}_{i,t}$ is the average equivalent gross earnings at the beginning of each year.

Clearly, at the participant level, the benefit is a function of their security average accrued rate, ${\theta }_t$ or the Notional Defined Contribution (NDC) rule, which produces at the aggregate level the market’s replacement rate. This is consistent with the logic that those who contribute more will benefit more from that scheme.

2.4. Individual Accounts

In addition to ${\tau }_U$, the participant contributes to their pension individual account a fraction of ${\tau }_f$ from their monthly wage, where ${\tau }_U+{\tau }_f=\tau$. The pension benefit from this pillar is linked to the market yield and wage path levels along the participant’s career. The funded benefit to the participant $i$ in generation $j$ admits the following:

$$P_{i,j}^f={\displaystyle \sum }_{T=t}^{T_R-1}{\tau }_f{\overline{w}}_{i,t}{\displaystyle \prod }_{T=t}^{T_R-1}(1+r_s)$$

(4)

Here, $r_s$ is the stochastic average rate of return earned by the DC plan on the participant accumulation portfolio. The funded share of benefits is a function of contribution from wages like the unfunded benefits but is also a function of the market yield, along with the participant’s career life.

2.5. The Economic Position Model

We relate to the mixed pension scheme as acquiring a financial position in exchange options and bonds. The limited funded pillar is represented by a long position in a Call option, where the underlying asset is the participant’s own funded accumulation, and the strike price is the expected pension benefits of the alternative pension scheme—the unfunded pillar. More precisely, one may describe the participant’s position on the funded scheme as

$$C_t\left({\overline{w}}_{i,t}\right)=\max \left\{0,\left({\tau }_f{S}_{T_R}^f-L_{t+1}^U\right)\right\}$$

(5)

where ${\tau }_f{S}_{T_R}^f$ is the pension accumulation in retirement, where the participant saves a fraction of ${\tau }_f$ from their wage to old age by the funded pillar. The $L_t^U$, on the other hand, represents the liabilities of the pension fund if the participant was insured in the unfunded pillar. If positive, the cash flow of the Call option is the difference between the two different pension schemes for the same participant. $L_t^U$ depends also on the overall economic state such as fertility and the GDP growth rate. For the high earners, the Call option is cheaper than for the low earners for two reasons: in the long term, $r>g$, and the strike price is a function of the average wage.

With the same rationale, economically, the individual admits an alternative European Put option, which will be exercised if their accumulation in old age will be less than the unfunded liabilities barrier:

$$P_t\left({\overline{w}}_{i,t}\right)=\max \left\{0,\left(L_{t+1}^U-{\tau }_f{S}_{T_R}^f\right)\right\}$$

(6)

Naturally, for high-income individuals, the Call option is more significant as it being exercised is likely to happen in old age and vice versa.

The use of the strike price of the Call option as the unfunded pillar benefit is here to measure the preference for the pension design. In other research that aims to find the absolute financial position of the participant, the strike price can be different, as it depends on a variety of parameters. Some countries may mark the poverty line as a floor that ensures a proper standard of living in old age (Grande and Visco 2010).

The parameters in (5) and (6) are directly observable. The value of the Put option or the Call option can be evaluated without any additional assumptions about the preferences using the Black–Scholes option pricing theorem. If we assume that the instantaneous real rate of return of the accumulation follows the Markov process as detailed in Equation (1), we can value the Put option as follows:

$$P_t\left({\overline{w}}_{i,t}\right)=L_{t+1}^U{e}^{-qt}\mathrm{\Phi }\left(-d_2\right)-S_{T_R}^f\mathrm{\Phi }\left(-d_1\right)$$

(7)

Here, using the Black–Scholes formula,

$$d_1=(\ln \left({\displaystyle \frac{S_0}{L_{t+1}}}\right)+\left(r+0.5{\sigma }^2\right)T_R)/\sigma \sqrt{T_R}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{d}_2=d_1-\sigma \sqrt{T_R}.$$

$\mathrm{\Phi }$ is the distribution function of a N(0,1) random variable. $r$ is the periodical risk-free rate.

The options include financial risks and future benefits. The total economic position of the $i$ individual on time $t$ includes a long Call and long Put. The Call option value is calculated on the unfunded pillar, whereas the Put option is on the funded pillar, respectively.

According to the Black–Scholes model, the delta of a European option written on a non-dividend stock is

$${\Delta }_c=\mathrm{\Phi }\left(d_1\right)\ast underlying asset {\Delta }_p=\mathrm{\Phi }\left(d_1\right)\ast underlying asset$$

(8)

In terms of our study,

$${\Delta }_c=\mathrm{\Phi }\left(d_1\right)\ast funded benefit {\Delta }_p=\left(\mathrm{\Phi }\left(d_1\right)-1\right)\ast funded benefit$$

(9)

Option delta represents the relative price movement that an option will experience given a one-point move in the underlying asset. The delta therefore results in a sort of proxy for the underlying pension accumulation, that is, the number itself tells you the proportion of equivalent shares position in a long/short. Hence, hedging the option financial position exposure, the participant should buy $\Delta$ shares of the underlying asset.

In this study, the delta option is being used to compare the position of each interest group. Since we describe the interest group position using the option position to the opposite pension strategy, a higher delta suggests higher relative ‘utility’ concerning the other group of interest’s favorite position. We relate these group interests from society as equal in magnitude (earning deciles) but not equal in financial resources, and hence, we normalize these “costs” of hedging in relation to the group average contributions.

We assert that the equilibrium between two different interests must be in correlation to the extent that each population group is willing to pay to hedge their position. Accordingly, the deltas values along the earning deciles $d$ in (10) signify the alternative relative cost or the willingness to stay in position. The portion of the two position sums hence represents the relatively fair portion of the pension scheme designs. This can be described as

$${\displaystyle \frac{\frac{1}{D}{\sum }_{d=1}^D{\Delta }_{c,d}}{\frac{1}{D}{\sum }_{d=1}^{10}{\Delta }_{p,d}}}={\displaystyle \frac{{\tau }_f}{{\tau }_u}} where {\tau }_u+{\tau }_f=\tau$$

(10)

In (10), notice we do not calculate the absolute term of the theoretical hedging cost for each decile, but we keep it on the parameter form of delta. The reason is that in the absolute form, there is a deflection in favor of high-earning cohorts, who are seeking the compromise point. Politically, The compromise point is important to keep the funded scheme relevant in inequality market.

While analyzing this problem using the utility function, the analog for the equilibrium point is where the contribution rates cause equivalent utility shortfall among different interest groups (Wolf and Caridad y Ocerin 2021). Both methods consider some kind of wage difference and multiple earning cohorts.

3. Simulation and Calibration

We calibrate the market’s parameters and wage levels according to a small, open, and average OECD country. We begin with a standard set of baseline parameter values (all expressed in real terms), as presented in

Table 1. Calibration.

Assets
Net annual funded pillar return	4%
Annual expected GDP per capita - g	1.6%
Annual expected S.D. of funded pillar	20%
Annual GDP S.D	2%
Macro-Economic Parameters
Risk aversion coeff. (Base Scenario)	5
Individual annual discount factor	2%
Pension parameters
Contribution rate	28%
Insurances in funded pension funds from contribution	25%
Funded Benefit tax rate	20%
Demographics
Total population annual growth rate	0.3%
Dependency ratio annual change	0.4%
Working/retired period ratio	2:1

. The aggregate wage income and the PAYG asset return are approximately set by the GDP per capita growth rate. Here, ${\overline{g}}_t=1.6\%$ and ${\sigma }_g=2\%$; these values also correspond to the average OECD countries (OECD 2019).

Calibrating the second pillar, we assume the average OECD portfolio allocation, which includes 70% risky assets—specifically, 40% debt and 30% equities. Accordingly, we set the net annual rate of return in a private capitalized pension fund to be 4% after reducing administrative costs.

Another factor that could influence the results is the correlation between average funded pension return and GDP growth rate. Hanna and Devolder (2023) cite several papers that have studied the correlation between domestic stock market returns and GDP growth, but their analysis yielded rather mixed and inconclusive results. We model the joint distribution of the outcomes between the returns of the two pillars (see Appendix A for a detailed calculation).

In (3), we assume an increase of 0.4% per annum, which summed to nearly 9% of the total aging influence on the unfunded scheme per period. Hence, we calibrate $n$ to stand on 0.91.

We calculate the Call and the Put options values for a wide variety of random stochastic return variables—$r_t$ and $g_t$. The stochastic variable, $g_t,$ also influences the wage level and hence the consumption and pension benefits levels along the OLG life cycle. Based on the stochastic variables, we run 5000 simulations calculating the option values and the respective data values. These series of simulations are produced for each of the 10 earning deciles. The average values on the simulations are set in (9) in order to derive the net position of each earning decile. We repeat this series of computations for some robustness checks, including higher market volatility and lower time to maturity. The compromise point in the market is detailed in the next section.

4. Results and Discussion

Figure 1 plots the options’ values per earning decile based on the calibration detailed above. For low earners, the Put option is dominant and vice versa. The unsymmetric values of the two option types among the two edges of the earning deciles signify the income inequality of the economy. As income dispersion is higher, the graph of the option value should be more concave due to the quadratic influence of wages on pension accumulation.

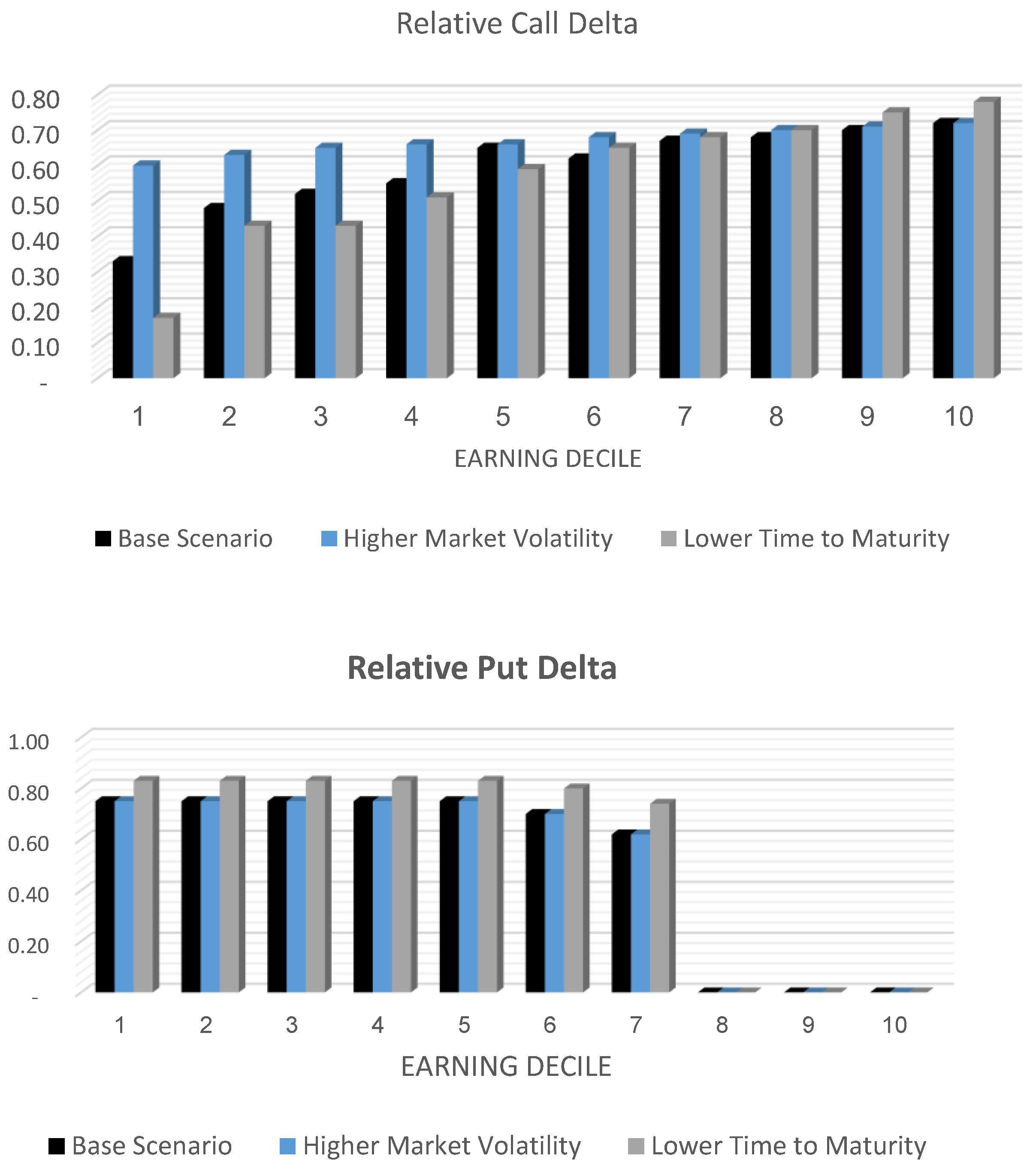
Figure 2 plots the relative deltas of the base scenario and sensitive analysis. Over the base scenario, the weighted arithmetic mean of the delta Call option holders is 0.59 compared to 0.51 for the delta Put option holders. Hence, the relation between the funded pillar to the unfunded pillar is ${\displaystyle \frac{0.59}{0.51}}$. While assuming both measures summed to the total contribution rate of 33%, we obtain that the normalized funded rate is 0.18 from the total wage, and the normalized unfunded rate is 0.15. By designing a fair pension market, these contribution rates are the equilibrium balance point between the two population interests.

In a robustness check, in the color blue in both figures, when increasing the market sigma from 20% to 35% per year, naturally the Call option’s value increases following the Black–Scholes option pricing model and consequently its relative delta. This increase is mainly shown among the lower-earning deciles as the Call option value converged to its maximum value in deciles 9 and 10. Naturally, the Put option, which is not connected to the market but to the GDP per capita, is not affected. We conclude that in a riskier market, there is a higher tendency to a funded pension scheme. This phenomenon was validated by Naczyk and Domonkos (2016).

In line with the Black–Scholes pricing model, the Call option’s value decreases when the exercise date approaches. Therefore, it is determined there is a negative correlation between the average dependency ratio in society to preferences for individual accounts. In economies with high inequality levels, where the Put option value increases, that tendency is strengthened.

The scenario of narrowing the time to maturity is marked in a gray color in the graphs in Figure 1 and Figure 2. This robustness check increases the odds for options exercise if it is in the money and vice versa, reducing the odds of the option to be exercised if the option is out of the money area. Witnessing the Call option, its value is reduced, as expected, subtracting an option’s intrinsic value. What is interesting in this time-decay scenario is the higher values of the Put option and its deltas, especially for low-earning deciles. This implies the significant financial position in the Put option for this society group, or, in other words, ‘deep-in-the-money’. The Put option deltas are more expensive than the base scenario, implying the higher cost to hedge that financial position and a strong preference for the unfunded scheme over the funded one.

Analyzing what may influence the compromise equilibrium point, the market yield has significant importance. Intuitively, a higher rate of return, $r$, increases the underlying asset’s value of the Call option. There is a higher chance of exceeding the strike price of the unfunded pension benchmark. Consequently, the balance point of the pension design will tend to a higher portion of the funded scheme at the expense of the unfunded one.

When income dispersion is low, the wages are distributed close to the average market value. In such an economic state, with a low redistribution amount transferred from high earners to low earners, the funded scheme can be increased. With high-income inequality, statistically, there is a higher probability of individuals’ Put options being exercised at retirement. As a consequence, the balance point in earning values will be lower. Hence, by influencing long-term pension design, high earners have an interest in narrowing income inequality in the market.

5. Conclusions

In the era of aging societies, it is not advisable to lean on the younger cohort to finance the older ones. Economically, it would be efficient for every generation to compensate according to its poverty rate and income dispersion. Yet, for low-earning cohorts whose old-age benefits are below the average, the replacement rate is negatively affected by the pension transition to a funded one. The lower their average pensions accumulate below the former average replacement rate and/or the more the number of participants below the average replacement, the more the sustainability of the funded pension reform is at stake (Ebbinghaus 2015; Fultz and Hirose 2019).

As there are different reasons for the pension evolution in each country, global experience confirms a growing demand for redistribution mechanisms in the late design of pension reforms around the globe. Indeed, some scholars assert that first, the government must take care of modern economic Western sickness, which is income inequality and poverty, especially in old age (Barr and Diamond 2009).

By preserving funded pension schemes with an alternative to the redistribution mechanism, the suggested model comes to solve the balance between funded and unfunded schemes, based on the agents’ positions in the market. This equilibrium also advises the magnitude of the intergenerational risk-sharing, such as social security or minimum pension guarantee.

We count several strengths of this model:

• Attribution of risk in participants’ decisions by the exchange option’s financial position.
• Finding equilibrium pension design, when the utility function is not observable or the risk aversion parameters are not known.
• Enabling diversified interests and not only analyzing representative agents. Here, the different earning cohorts’ risks and time to maturity replace the risk aversion component in the utility function. The model gives weight to different agents in the field, especially when income inequality is high.

This equilibrium method using option financial position can be utilized to solve other problems in the public economy, such as tax rates and the prioritization of social services. It is worth further investigating that process in the future.