Navigating Inflation Challenges: AI-Based Portfolio Management Insights

Abstract

After 2010, the consumer price index fell to a low level in the EU. In the euro area, it remained low between 2010 and 2020. The European Central Bank has even had to take action against the emergence of deflation. The situation changed significantly in 2021. Inflation jumped to levels not seen for 40 years in the EU. Our study aims to use artificial intelligence to forecast inflation. We also use artificial intelligence to forecast stock index changes. Based on the forecasts, we propose portfolio reallocation decisions to protect against inflation. The forecasting literature does not address the importance of structural breaks in the time series, which, among other things, can affect both the pattern recognition and prediction capabilities of various machine learning models. The novelty of our study is that we used the Zivot–Andrews unit root test to determine the breakpoints and partitioned the time series into training and testing datasets along these points. We then examined which database partition gives the most accurate prediction. This information can be used to re-balance the portfolio. Two different AI-based prediction algorithms were used (GRU and LSTM), and a hybrid model (LSTM–GRU) was also included to investigate the predictability of inflation. Our results suggest that the average error of the inflation forecast is a quarter of that of the stock market index forecast. Inflation developments have a fundamental impact on equity and government bond returns. If we obtain a reliable estimate of the inflation forecast, we have time to rebalance the portfolio until the inflation shock is incorporated into government bond returns. Our results not only support investment decisions at the national economy level but are also useful in the process of rebalancing international portfolios.

1. Introduction

After 2010, the consumer price index fell to a low level in the EU. In the euro area, it remained low between 2010 and 2020. It only slightly exceeded 3% (3.29%) in 2011 (Macrotrends 2024). The European Central Bank has even had to take action against the emergence of deflation. The situation changed significantly in 2021, as the COVID-19 epidemic passed and the economies of individual countries opened up in turn. Households wanted to spend the savings they had accumulated during the epidemic. The need to meet this demand quickly appeared on the market. Governments’ stimulus measures also generated demand. Moreover, supply chains had not yet been restored, so rapidly growing demand caused price increases in producer markets and in consumer goods markets. The outbreak of the Russia–Ukraine war in early 2022 led to a surge in energy and commodity prices. This rise in energy prices and commodity prices fed through to consumer prices. Consumer prices rose at a rate not seen in forty years (Bouri et al. 2023).

Inflation can devalue the savings of savers if they are not invested properly. Looking at the data, although the European Union is a single economic area, inflation rates (Harmonized Index of Consumer Prices (HICP)) vary between Member States. There are also differences in the euro area countries sharing a single currency. In our study, we examine how portfolio re-allocation can be an effective hedge against inflation. We assume an investor who holds a portfolio of stocks and government bonds and actively manages the portfolio. In portfolio management, they invest in equity indices of each EU Member State. An artificial intelligence-based process is used to optimize the investment. This is used to forecast inflation trends in each country to identify investment opportunities with the highest expected real returns, broadening the active portfolio management toolbox.

1.1. Inflation Forecast

Several researchers have previously worked on predicting inflation using artificial intelligence. The new methods are intended to achieve better results than the statistical forecasting models used previously. Theoharidis et al. (2023) proposed a deep learning model. In their hybrid model, they wanted to combine Variational Autoencoders and Convolutional LSTM Network (VAE-ConvLSTM) models for prediction. In their study, they used monthly US data for inflation from January 1978 to December 2019. The output results of their model were compared with several commonly used models such as Ridge regression, LASSO regression, Random Forests, Bayesian methods, and multilayer perceptron. In presenting their results, they found that deep learning models provide more accurate predictions than traditional statistical methods. Aras and Lisboa (2022) investigated the applicability of machine learning methods for forecasting inflation in Turkey. Turkish inflation was high during the period they analysed and showed a high volatility. The authors’ intention was, therefore, to find a more efficient method than the factor models that have generally been used in the past. As a result of their investigations, they advocated the use of machine learning methods for forecasting. Choudhary and Haider (2011) emphasized the predictive ability of machine learning methods using Brazilian inflation data. In their study, they tested traditional statistical methods and modern machine learning methods using extensive datasets. Summarising their results, they found that the forecasting accuracy of machine learning methods generally outperforms the forecasting ability of traditional econometric methods. This is mainly due to the treatment of nonlinear relationships. Masini et al. (2023) provided an overview of methods used to analyse and forecast financial time series. In their study they evaluated both linear and nonlinear methods. They compared the performance of traditional regression methods, machine learning methods, and also evaluated hybrid methods. They found that nonlinear machine learning methods can be very useful for analysing large datasets.

The literature suggests that the use of artificial intelligence is preferable to traditional statistical methods in economic forecasting and can be used to handle large numbers of input variables and to model nonlinear relationships.

1.2. Protection against Inflation through Portfolio Re-Allocation

The literature provides a rich source of studies on the future evolution of various financial instruments and macroeconomic data. Most of the research focuses on the forecasting of financial markets (Liu et al. 2021; Ayala et al. 2021; Bhandari et al. 2022; Hanauer and Kalsbach 2023; Vancsura and Bareith 2023; Md et al. 2023; Vancsura et al. 2023). Among the publications dealing with macro data, the topic of inflation is quite popular (Ülke et al. 2018; Medeiros et al. 2021; Joseph et al. 2021; Aras and Lisboa 2022; Araujo and Gaglianone 2023). It is a restricted group of studies where researchers analyse inflation data and stock markets combined. Constantinos et al. (2012) examined the hypothesized relationship between inflation and stock returns for Greece. They argue that previous empirical research did not take into account asymmetric dynamic effects. Their research suggests that monetary policy reacts to inflation and that monetary policy actions affect stock prices; however, monetary intervention has different effects on inflation and stock prices. Economic agents use shares as a hedge against inflation. Their purchases raise the price of shares. When inflation falls, portfolio adjustments lead to sales. This causes stock prices to fall. Their empirical results show that there is a positive relationship between inflation and stock prices. Nevertheless, monetary intervention has less effect on the change in stock prices than on the change of the inflation rate. Nwude (2013) analysed how the share prices of the chemical and paint industries listed on the Nigerian Stock Exchange have evolved between 2000 and 2011. The objective of the study was to determine whether the shares provided a hedge against inflation during the given period. The author conducted a regression analysis between real stock prices and inflation. This was used to filter out stocks that provided a real hedge against inflation and a positive real return. As a result of the analysis, the author concluded that equities did not provide a significant hedge against inflation. Chaves and Silva (2019) examined the relationship between stock returns and expected inflation in the Brazilian stock market. The study covered the period 2003–2016. They found a negative correlation between stock returns and inflation. This suggests that it makes sense to actively manage investments. They recommend that if expected inflation rises, it is worth selling equities and investing in fixed-income, short-term assets. When the magnitude of inflation expectations falls, the portfolio should be held back in equities. Marjohan et al. (2023) investigated the factors affecting stock returns in the Indonesian banking sector. Their quantitative analysis showed that investment risk did not significantly affect the returns of the stocks studied. In contrast, market liquidity had a significant impact on the assessed stock returns. They also found that the magnitude of inflation influences the relationship between the above factors and stock returns. Higher inflation may strengthen the relationship between investment risk and stock returns. The same amplifying effect was found between liquidity and returns when inflation increases. The aim of the study by Eldomiaty et al. (2020) was to assess the relationship between inflation rates, interest rates, and stock prices of non-financial companies included in the DJIA30 and NASDAQ100 indices. The period under study was from 1999 to 2016. For the analysis, the authors used standard statistical tools, such as Johansen’s co-integration test, linearity and normality tests, and co-integration regression calculation. According to their results, both the change in inflation rate and the change in real interest rates have a significant effect on the evolution of stock prices. A negative relationship between the change in inflation rate and the evolution of stock prices was found according to the authors’ results. The starting point of the study by Neville et al. (2021) was that there has been no significant inflation in developed countries over the past three decades. In their study, they examined the exchange rate developments of different asset classes in the UK, the US, and Japan over a period of about 100 years. Their analyses showed that active strategies could also provide a hedge against rising inflation in equity investments. Stock prices fell in the face of soaring inflation, but profitable strategies could be developed with active portfolio management. Active portfolio management proved more effective than passive investment strategies. Karimi et al. (2015) evaluated the relationship between stock returns and inflation rates using a study of 546 companies on the Tehran Stock Exchange. They studied the period between 2007 and 2013. At a 95% confidence level, they showed that there was a significant positive relationship between stock returns and the inflation rate of the companies included in the study. They pointed out in their conclusions that quantifying the relationship using a price index rather than the consumer price index yields different results. Bouri et al. (2023) evaluated the relationship between expected inflation and stock returns in the US stock market using time series from January 2003 to December 2022. Their method of analysis was multiple correlation calculation. The time series data covered the period of the 2008 global financial crisis, the COVID-19 pandemic and the beginning of the Russian–Ukrainian war. Their results were heterogeneous, which may be due to the intervention of monetary policy in the deflationary period following the global financial crisis. In the period of rising inflation following the COVID-19 pandemic, the correlations took increasingly positive values. Yeoh (2023) investigated the relationship between the diversified portfolio represented by the Malaysian Stock Exchange index and the inflation rate over a 20 year time series, using data from 2002 to 2021. The research method used was correlation and regression calculation. The calculations showed a weak positive correlation between the factors. However, it showed that the average annual increase in the value of the portfolio represented by the stock market index exceeded the increase in the consumer price index. They concluded that investing in a stock portfolio could provide a hedge against inflation. Giofré (2012) analysed whether, after the establishment of the monetary union, portfolio convergence in the member countries of the monetary union was faster relative to each other than relative to non-euro area member countries. The study covered the period 1997–2004. The faster convergence could have been based on convergence of inflation rates as a result of the common monetary policy and exposure to the common currency. In addition, investment barriers have also disappeared. The result of the study was that the convergence of investment portfolios in the Member States belonging to the monetary union was faster. This was despite the fact that the convergence of inflation rate fluctuations was not significant. The convergence in portfolio composition cannot, therefore, be seen as a similarity in hedging strategies against inflation. Ni et al. (2023) tested a neural network method for portfolio optimization. The optimal dynamic allocation was studied for a high inflation period. The objective was to outperform a benchmark portfolio. The optimal asset allocation was achieved using a novel neural network model. The performance of their model was measured using historical data from a high inflation environment. Their results showed that their neural network method has a 90% probability of outperforming the benchmark portfolio constructed using the alternative method used in the test.

Our study aims to use artificial intelligence to forecast inflation. We also use artificial intelligence to forecast stock index changes. Based on the forecasts, we propose portfolio re-allocation decisions to protect against inflation.

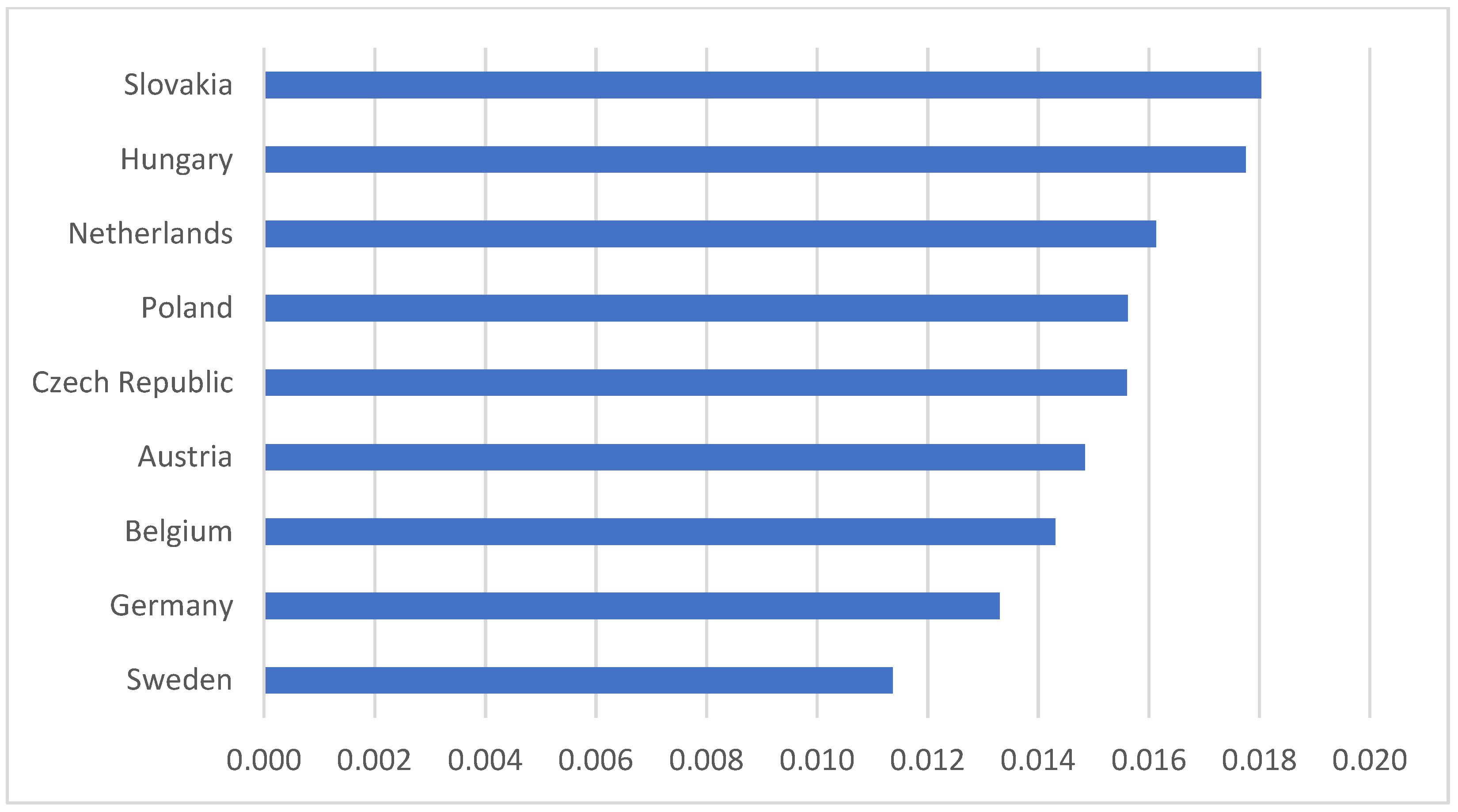
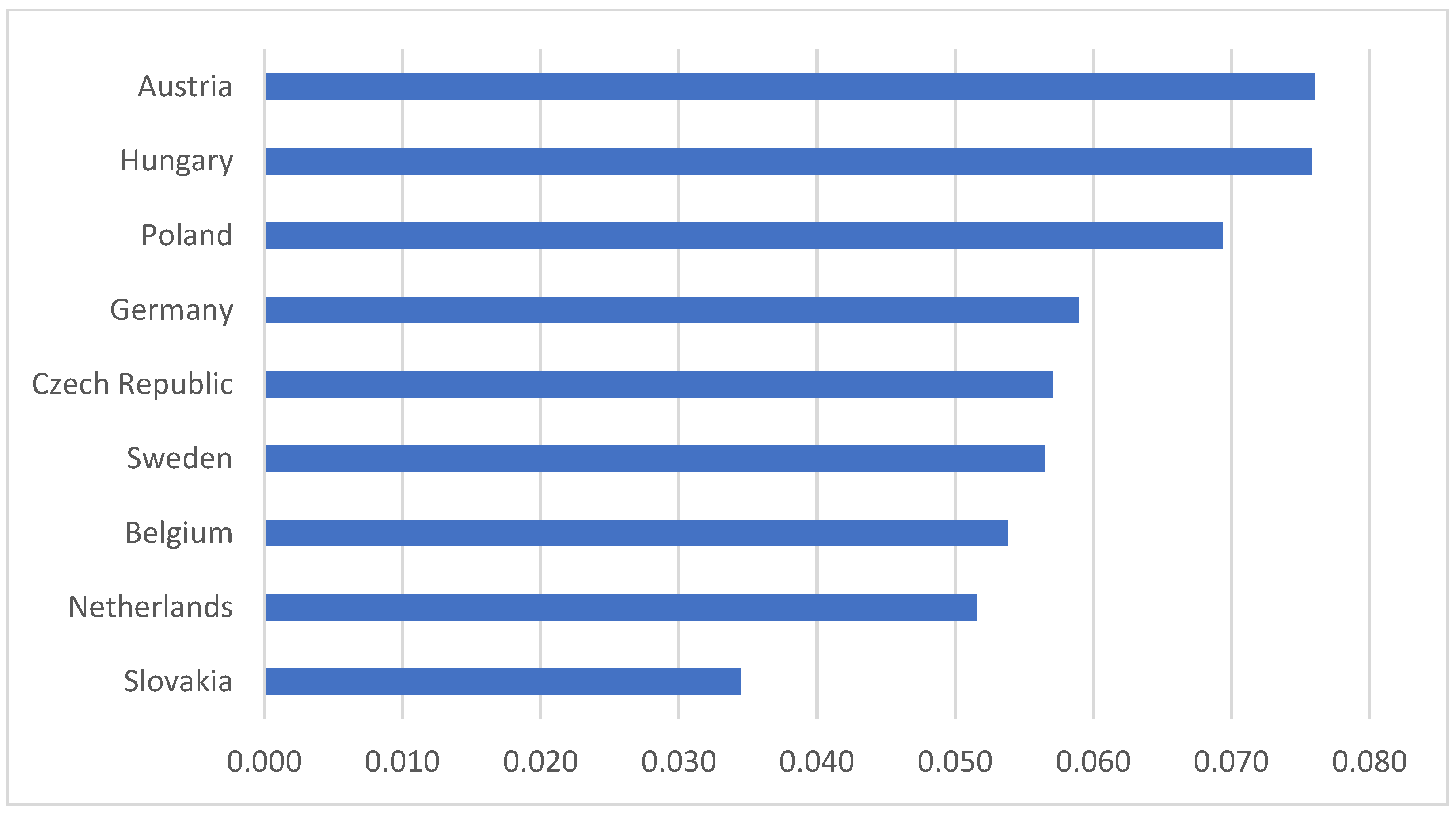
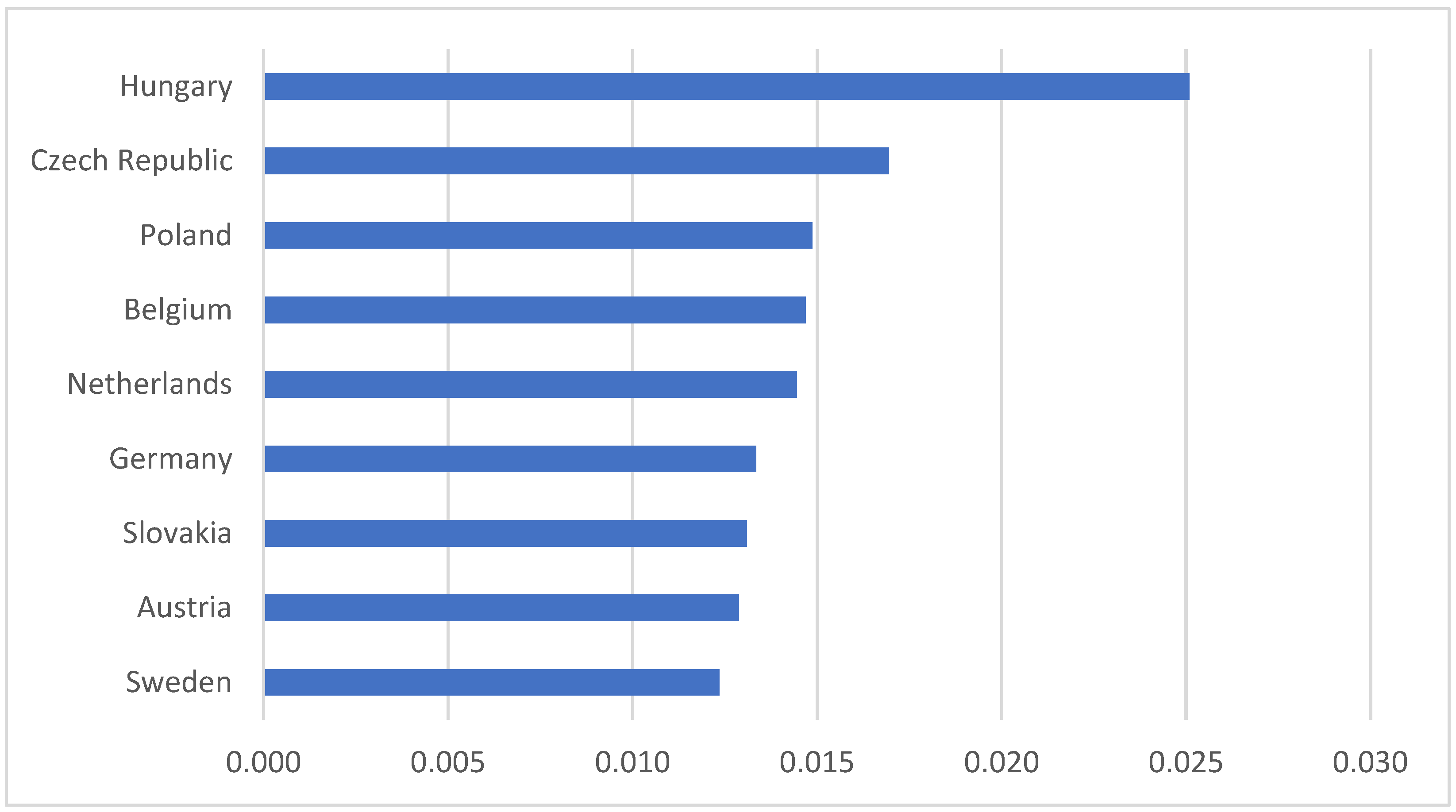
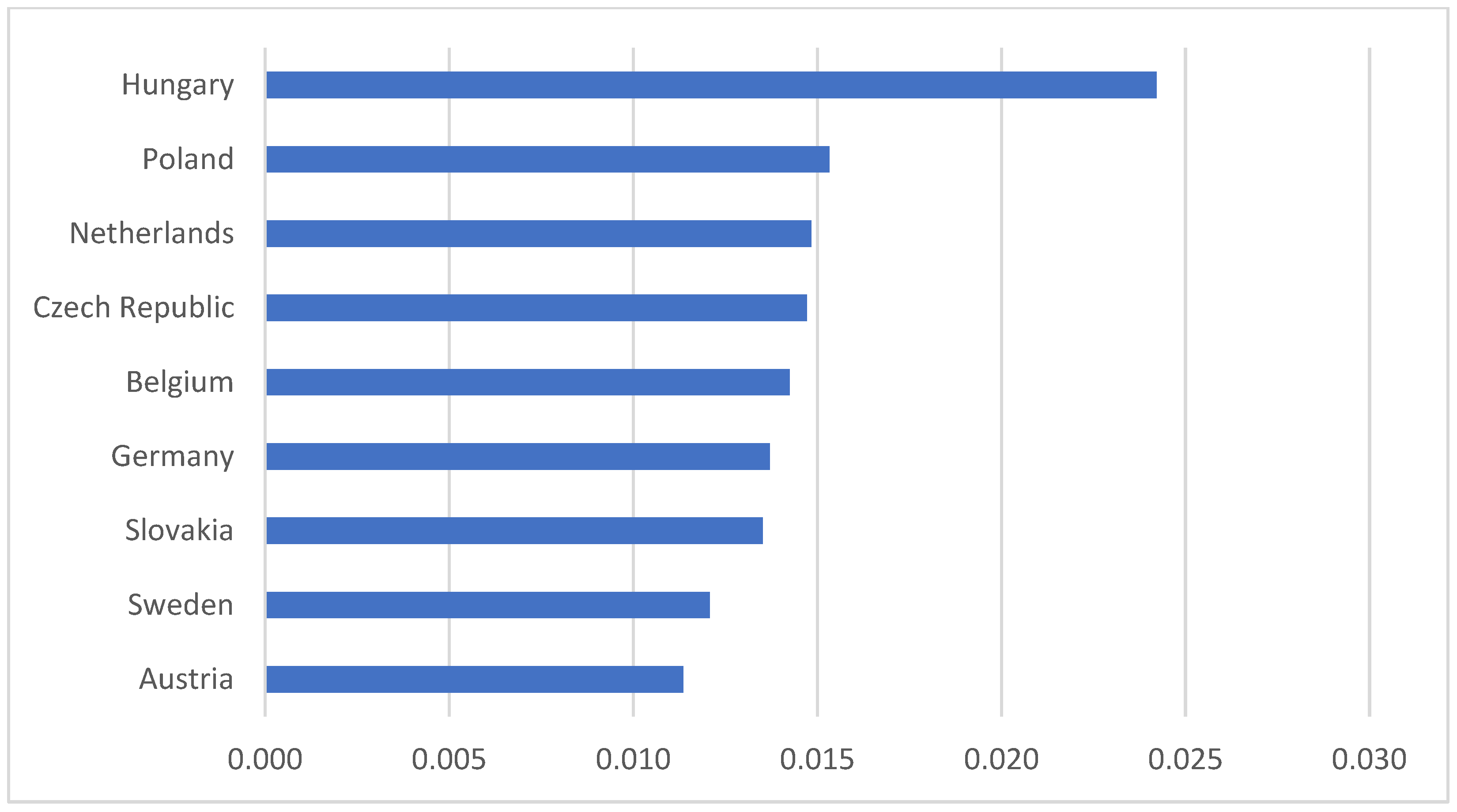
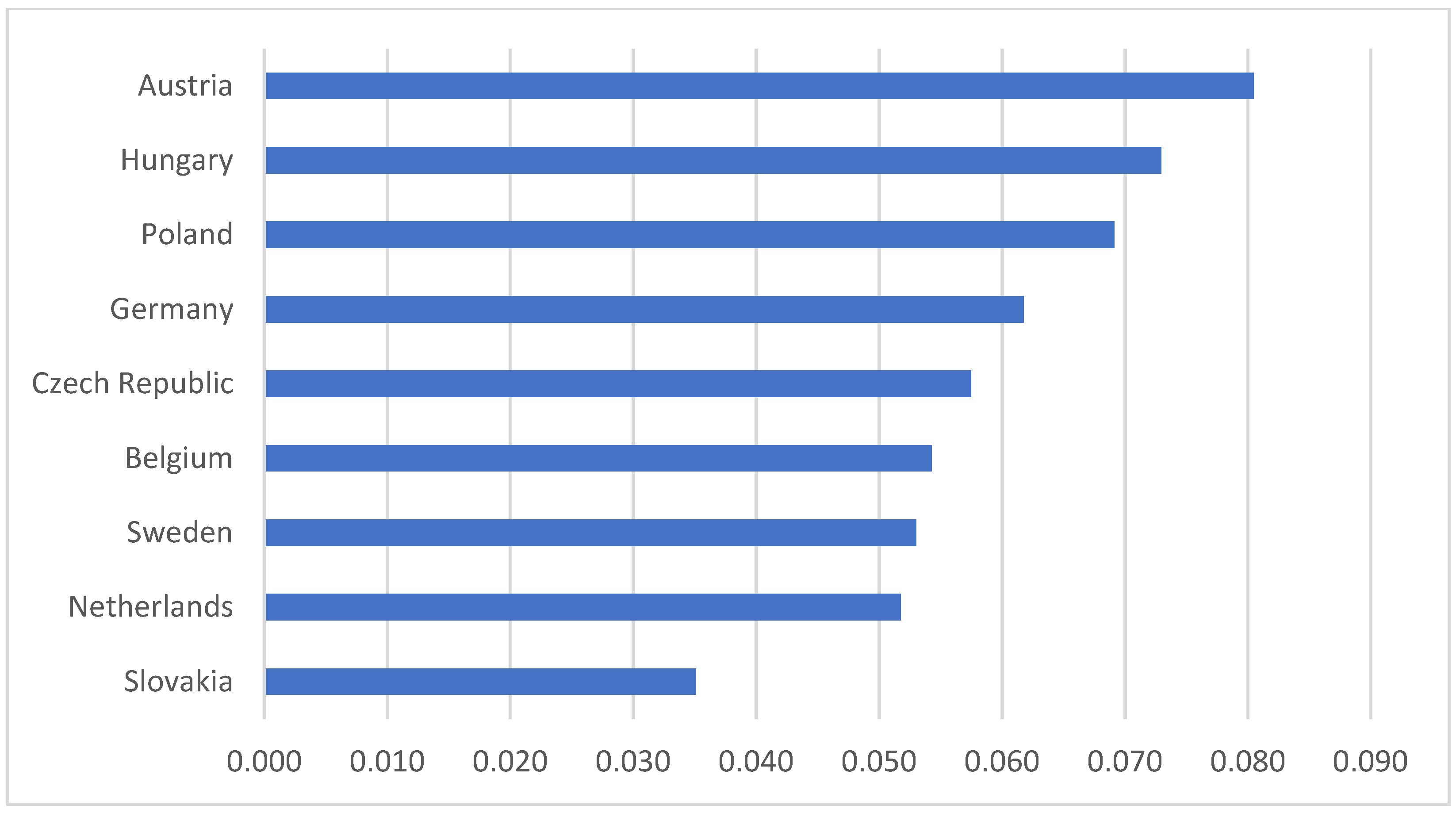
The forecasting literature does not address the importance of structural breaks in the time series, which, among other things, can affect both the pattern recognition and prediction capabilities of various machine learning models. The novelty of our study is that we used the Zivot–Andrews unit root test to determine the breakpoints and partitioned the time series into training and testing datasets along these points. We then examined which database partition gives the most accurate prediction.

2. Results

Forecasts have always played an important role in investment decisions. In most cases, a forecast can be an estimate based on intuition or some kind of technical or fundamental analysis. With the development of information technology and AI, the availability of technical forecasts has improved a lot. There are many free solutions available on the internet, but of course they require programming and/or mathematical skills. The automation of technical forecasts is relatively simple, no human decision is required and results are obtained in a flash according to predefined criteria.

Speed is only one aspect, however, and equally, or more importantly, is the accuracy and reliability of these algorithms. In the absence of accuracy, portfolio rebalancing carries a significant risk, as the main motivation for their use is to maximise the returns while reducing the risk. Based on the literature, there is no single recipe, and not one predictive algorithm can be said to be better or worse than another. Different economic time series have different characteristics and, therefore, it is unlikely that a single algorithm can be applied in all cases. In our study, we investigate which forecasting model performs better in different European countries, whether similarities can be observed, or whether stock market and inflation data behave completely differently. A further research question is whether these forecasts are sufficiently accurate to make portfolio restructuring decisions (risk-free share).

The results are presented separately for each of the forecasting algorithms, including inflation and the stock market index forecasts for the country in question. In total, nine countries were included in the study: Austria, Belgium, Czech Republic, Germany, Hungary, the Netherlands, Poland, Slovakia, and Sweden. For the train–test database splitting, we first divided the database into two parts along the structural breaks defined by the Zivot–Andrews unit root test, followed by the 80% - 20% split ratio most commonly used in the literature and finally the 90% - 10% split.

A total of two predictive models (GRU, LSTM) and a hybrid model (LSTM–GRU) were used in the study. The advantages and disadvantages of each predictive model are discussed in the methodology chapter. Also in the methodology chapter are the indicators used to evaluate the predictions (RMSE, MAPE, and MAE).

2.1. GRUs

The results of the GRU (Gated Recurrent Unit) forecasts are shown in

Table 1. GRU forecast MAPE values. (Source: own editing).

	Inflation			Stock Indices
	80%-20%	85%-15%	90%-10%	80%-20%	85%-15%	90%-10%
Austria	0.013	0.010	0.021	0.077	0.079	0.072
Belgium	0.013	0.010	0.019	0.052	0.055	0.054
Czech Republic	0.011	0.016	0.019	0.052	0.062	0.057
Germany	0.015	0.012	0.012	0.068	0.059	0.050
Hungary	0.017	0.014	0.022	0.070	0.071	0.086
Netherlands	0.015	0.013	0.021	0.047	0.048	0.060
Poland	0.014	0.019	0.014	0.064	0.071	0.073
Slovakia	0.011	0.022	0.021	0.033	0.035	0.035
Sweden	0.009	0.012	0.014	0.052	0.060	0.057

, with the forecast errors for inflation in the top half of the table and the forecast accuracy of the stock market index for the country in the second half. The table follows the same pattern for the next two forecasting techniques. For all values in the table, the lower one is the better value. Due to its scale independence, the MAPE can also be used for comparisons between countries.

In the case of inflation, a ratio of 85% - 15% for most of the different indicators gives the best results. Based on the GRU-based forecast, the forecast of inflation shows a significantly higher accuracy. When the best model is selected for each country, the average MAPE for inflation is 1.17%, compared to a forecast error of 5.53% for the stock market index. One reason for this is that expert forecasts of macroeconomic indicators are also typically more accurate than exchange rate forecasts.

Examining the average MAPE values of the three database distributions using country-specific criteria, we see that the GRU model is the most accurate for Swedish inflation and the least accurate for Slovak inflation (Figure 1). At the same time, the stock market indices were analysed, with the Slovak index (SAX) performing the best and the Austrian index (ATX) performing the worst (Figure 2).

2.2. LSTM

For LSTM, the 90% - 10% database split for inflation does not give the best result for any country, with 80% - 20% and 85% - 15% giving the best result with almost equal frequency. For the stock market index, the picture is clearer, with the 80% - 20% ratio dominating, while for the MAPE it is the only one that gives the best result. In terms of estimation accuracy, the MAPE indicator can still be relied on, with an error of 1.32% for inflation and 5.66% for the stock market index, using the best models. This shows no significant difference compared to the GRU, as the difference is not significant (

Table 2. LSTM forecast MAPE values. (Source: own editing).

	Inflation			Stock Indices
	80%-20%	85%-15%	90%-10%	80%-20%	85%-15%	90%-10%
Austria	0.011	0.014	0.014	0.072	0.081	0.072
Belgium	0.014	0.012	0.018	0.055	0.056	0.055
Czech Republic	0.013	0.015	0.024	0.051	0.059	0.054
Germany	0.012	0.015	0.013	0.056	0.068	0.063
Hungary	0.023	0.023	0.030	0.066	0.071	0.076
Netherlands	0.014	0.014	0.016	0.048	0.069	0.062
Poland	0.015	0.014	0.016	0.067	0.071	0.082
Slovakia	0.008	0.017	0.014	0.039	0.035	0.034
Sweden	0.012	0.012	0.013	0.055	0.067	0.050

).

Examining the average MAPE values of the database distributions using country-specific criteria, we see that the LSTM model is the most accurate for Swedish inflation and the least accurate for Hungarian inflation (Figure 3). When examining stock market indices, similar to the GRU, the best results were observed for the Slovak (SAX) index and the worst were observed for the Austrian (ATX) index (Figure 4).

2.3. LSTM–GRU

Hybrid models are designed to give a more accurate estimate than predictive algorithms alone. For inflation, the situation is similar to that of the LSTM with the ratios 80% - 20% and 85% - 15% giving the lowest error in most cases. For the stock market indices, the 80% - 20% learner-testing database gives the best results. For inflation, the average MAPE is 1.22%; for the stock market index the same value is 5.39%. The hybrid model does not give the lowest error among the inflation forecasts, but the LSTM–GRU is 0.05 percentage points weaker than the best value (GRUs), with no significant difference. For the stock market index, the hybrid model gave the best result, but there is no significant difference from the second place (

Table 3. LSTM–GRU forecast MAPE values. (Source: own editing).

	Inflation			Stock indices
	80%-20%	85%-15%	90%-10%	80%-20%	85%-15%	90%-10%
Austria	0.013	0.011	0.010	0.083	0.078	0.079
Belgium	0.013	0.011	0.018	0.052	0.064	0.045
Czech Republic	0.011	0.016	0.017	0.052	0.057	0.062
Germany	0.015	0.013	0.014	0.053	0.066	0.066
Hungary	0.023	0.022	0.027	0.062	0.080	0.076
Netherlands	0.012	0.013	0.019	0.048	0.052	0.054
Poland	0.011	0.020	0.015	0.062	0.071	0.072
Slovakia	0.013	0.010	0.017	0.033	0.034	0.037
Sweden	0.010	0.016	0.011	0.056	0.048	0.054

).

In the case of the hybrid model (LSTM–GRU), examining the average MAPE values of the database split using country-specific criteria, we see that the most accurate inflation estimate is for Austria, while the least accurate is for Hungary (Figure 5). As before, when looking at the stock market indices, the best results were found for the Slovak (SAX) index and the worst for the Austrian (ATX) index (Figure 6).

The average MAPE values are presented in

Table 4. Average MAPE values. (Source: own editing).

Model	Inflation	Stock Indices
GRU	1.17%	5.53%
LSTM	1.32%	5.66%
LSTM–GRU	1.22%	5.39%

, which shows that the GRU model is the best model for forecasting inflation data, while the hybrid LSTM–GRU model is the best model for forecasting stock prices.

3. Materials and Methods

3.1. Gated Recurrent Units (GRUs)

Recurrent neural networks (RNNs) of the kind called GRUs are exceptionally accurate at predicting time series. While GRUs and the other type of neural network model (LSTM) are similar, GRUs use less processing power, which can greatly increase learning efficiency.

They have the same input and output structures as a basic RNN. The update gate $z_t$ and the reset gate $r_t$ are the only two gates that make up the internal structure of the GRU. The update gate $z_t$ascertains the value of the previous memory saved for the current time, while the restoration gate rt defines how the new input data is to be combined with the previous memory value. Unlike the LSTM technique, the $z_t$ update gate can forget and choose memory contents, improving computational efficiency and lowering runtime requirements. The GRU is determined using the following equations (Xiao et al. 2022):

$$z_t=\sigma \left(W_z{h}_{t-1}+U_z{x}_t\right)$$

(1)

$$r_t=\sigma \left(W_r{h}_{t-1}+U_r{x}_t\right)$$

(2)

$${\tilde{h}}_t=\tanh \left(W_0\left(h_{t-1}\odot r\right)+U_0{x}_t\right)$$

(3)

$$h_t=z_t\odot {\tilde{h}}_t+\left(1-z_t\right)\odot h_{t-1}$$

(4)

In this case, $h_{t-1}$ represents the hidden state of the neuron at the previous time and σ(·) is a logistic sigmoid function, meaning $\sigma \left(x\right)=1/1+e^{-x}.$ The weight matrices of the update gate are $W_z$ and $U_z$. The weight matrices of the reset gate are $W_r$ and $U_r$. The weight matrices of the intermediate output are denoted by $W_0$ and $U_0$. The input value at time t is denoted by $x_t$, whereas the information vectors $\widetilde{h_t}$ and $h_t$ represent the hidden layer output and temporary unit state, respectively, at time t (Xiao et al. 2022). The hyperparameters of the GRU model are specified in

Table 5. Hyperparameters of GRU model. (Source: own editing based on Nabipour et al. (2020)).

Model	Parameters	Value
GRU	Hidden Layers	2
	Hidden layer neuron count	150
	Batch size	32
	Epochs	100
	Activation	tanh
	Learning rate	0.001
	Optimizer	Adam

.

3.2. Long–Short Term Memory (LSTM)

Recurrent neural networks (RNNs), like LSTM, are frequently used in sequential data analysis. While short-term memory is associated with internal cell states, long-term memory is correlated with learning weights. LSTM was created to solve the issue of disappearing gradients in RNNs; the main distinction is that an LSTM block is used in place of the RNN’s intermediate layer. The primary benefit of LSTM is its capacity for long-term affiliations learning, a skill that RNNs were not previously able to provide. The initial time interval data must be preserved in order to update the weight values of the network and forecast the data associated with the following time point. An RNN is not able to learn long-term time series, but it can learn a finite number of short-term associations. It is possible for LSTM to manage the problem effectively. Memory blocks, or recurrent subnets, make up the LSTM model. Three multiple units (input, output, and forget) that regulate the continuous write, read, and cell operation are present in each block along with one or more autoregressive memory cells (Ortu et al. 2022). The following formulas constitute the LSTM model (Dai et al. 2022):

$$I_t=\sigma (X_t{W}_{xi}+H_{t-1}{W}_{hi}+b_i)$$

(5)

$$F_t=\sigma (X_t{W}_{xf}+H_{t-1}{W}_{hf}+b_f)$$

(6)

$${\tilde{C}}_t=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(X_t{W}_{xc}+H_{t-1}{W}_{hc}+b_c)$$

(7)

$$C_t=F_t\odot C_{t-1}+I_t\odot {\tilde{C}}_t$$

(8)

$$O_t=\sigma (X_t{W}_{xo}+H_{t-1}{W}_{ho}+b_o)$$

(9)

$W_{xc}$ and $W_{hc}$ are the gated unit’s weight matrix and $b_c$ is the offset term of the gated unit. $C_t$ is the new cell state at this moment and $C_{t-1}$ is the cell state at the preceding time. $W_{xo}$ and $W_{ho}$ are the weight matrices of the output gate and $b_o$ is the offset term of the output gate (Dai et al. 2022).

Where $X_t$ is the small batch input of a given time unit t, $H_{t-1}$ is the hidden state of the data from the previous period, $W_{xi}$ and $W_{hi}$ are the weight matrices of the input gate, and $b_i$ is the offset term of the input gate. σ represents the sigmoid function in this equation. The weight matrices of the forgetting gate are $W_{xf}$ and $W_{hf}$, and its offset term is $b_f$. The candidate memory cells are $\widetilde{C_t}$. The weight matrices of the gated unit are $W_{xc}$ and $W_{hc}$, and its offset term is $b_c$. The current cell state, $C_t$, is different from the previous cell state, $C_{t-1}$, at this moment. The output gate’s weight matrices are $W_{xo}$ and $W_{ho}$, and its offset term is $b_o$ (Dai et al. 2022). Hyperparameters of the LSTM model are specified in

Table 6. Hyperparameters of LSTM model. (Source: own editing based on Nabipour et al. (2020)).

Model	Parameters	Value
LSTM	Hidden Layers	2
	Hidden layer neuron count	150
	Batch size	32
	Epochs	100
	Activation	tanh
	Learning rate	0.001
	Optimizer	Adam

.

3.3. LSTM–GRU Hybrid

Both the GRU and the LSTM can selectively remember important information and forget irrelevant information. The LSTM uses its own three-gated devices to control the flow of data and information across the network, solving the problem of long-term dependency. However, due to the excessive number of parameters set by the LSTM network, each cell has four fully interconnected layers. In practice, if a large time interval is involved and the LSTM network is deep, overfitting is likely to occur. This generates high computational capacity requirements. Compared to LSTM, GRUs replace the input gate, forget gate, and output gate of LSTM with a $z_t$ update gate and an $r_t$ reset gate. GRUs are a simplification of LSTM with fewer parameters, which reduces the risk of overfitting. However, for large datasets, it does not perform as well as LSTM. A hybrid LSTM–GRU model based on LSTM and GRU retains the advantages of both models, reduces overfitting, and, thus, allows highly accurate forecasts to be achieved (Zhao et al. 2023). In this model, the first hidden layer is LSTM. Each LSTM neuron collects the data and a weighted value is then generated. Then, data are passed from the LSTM to the GRU layer, which is the second hidden layer. A weighted value is, again, generated along the path from the LSTM layer to the GRU layer. Similarly, data are then passed to the third hidden layer (dense layer). A weighted value is generated from the GRU to the dense layer as well. The dense layer is a normal neural network layer that is used to produce output. From the dense layer, the data are then passed to the output neuron (Islam and Hossain 2021).

3.4. Performance Evaluation

The Mean Absolute Percentage Error (MAPE) was employed in our study to assess the predictive models. For a given set of forecasts, this indicator computes the average magnitude of the error I and displays the deviations as a percentage.

$$MAPE=\frac{1}{n}\sum _{i=1}^n\left|\frac{{y_i-\widehat{y}}_i}{y_i}\right|$$

Forecasts have a greater accuracy and dependability when the indicator has a lower value. The MAPE is a scale-independent indicator, as it is not affected by the nominal magnitude of prices. Therefore, it is an excellent tool for comparing different models and instruments, as well as different time periods.

3.5. Zivot–Andrews Unit Root Test

To obtain a more accurate understanding of the time series, a Zivot–Andrews unit root test (

Table A1. Results of the Zivot–Andrews unit test (Source: own editing).

Country	Date of Structural Break	Inflation (%) January 1996 = 100%
Austria	December 2018	148.7
Belgium	December 2018	152.4
Czech Republic	December 2018	179.1
Germany	November 2018	137.6
Hungary	November 2018	336.9
Netherlands	November 2018	150.2
Poland	November 2018	223.2
Slovakia	November 2018	236.4
Sweden	December 2018	139.6

) was also applied to account for structural breaks in the time series (Zivot and Andrews 2002). For this test, the information of interest was the structural breakage test, i.e., whether we could identify a point in time where the “behaviour” of the time series suddenly changes and a break occurs. This is a common phenomenon for macroeconomic variables (Glynn et al. 2007) and we could make our estimates in further analysis with this in mind and could control for this.

To forecast the inflation time series with AI, we do not need stationary time series, as this information is not used in the Zivot–Andrews unit root test. The purpose of running the test is to find the break point at which the time series will break into a new trend. We incorporated this information into the prediction model by separating the learning and testing databases at this point. In this way, we selected an objective point in time to choose the learning–testing period, rather than making a decision based on habit (80% - 20%). At the same time, we were hopeful that the prediction accuracy would improve with it.

In our analysis, we used, monthly, the Harmonised Index of Consumer Prices (HICP) and stock market index data for Austria, Belgium, the Czech Republic, Germany, Hungary, the Netherlands, Poland, Slovakia, and Sweden for the period January 1996 (base period) to January 2023. Inflation data were collected from Eurostat, while the stock index information was collected from the stock exchange data platforms of the individual countries. Descriptive statistics for inflation data are shown in

Table A2. Descriptive statistics, inflation (Source: own editing).

Country	N	Average	Median	StD	Min	Max
Austria	325	126.22	123.7	19.09	99.40	177.00
Belgium	325	129.25	128.4	20.21	99.20	183.50
Czech Republic	325	154.03	155.9	28.76	96.90	248.40
Germany	325	121.78	121.2	15.15	99.20	163.10
Hungary	325	258.62	271.5	85.01	92.30	493.80
Netherlands	325	132.51	132.4	19.61	98.70	190.20
Poland	325	190.24	196.4	41.80	93.00	302.00
Slovakia	325	196.22	207.6	48.31	98.00	307.70
Sweden	325	122.94	124.4	14.97	99.00	165.50

and for stock indices in

Table A3. Descriptive statistics, stock market indices (Source: own editing).

Index	N	Average	Median	StD	Min	Max
Austria_ATX	325	2371.14	2396.9	980.77	1028.70	4885.38
Belgium_BEL20	325	3060.06	3096.91	726.32	1635.22	4697.86
Czech_PX	325	935.83	973.1	360.78	331.90	1908.30
Germany_DAX	325	7693.88	6772.26	3561.29	2423.87	15,884.86
Hungary_BUX	325	20,826.46	19,023.96	12,736.30	2068.06	54,197.71
Netherlands_AEX	325	456.11	449.83	131.96	216.98	810.91
Poland_WIG	325	38,366.72	42,405.83	17,819.53	10,413.10	73,586.32
Slovakia_SAX	325	258.74	241.25	110.82	73.66	475.23
Sweden_OMX_Stockholm30	325	1142.94	1072.45	469.47	343.82	2419.73

. Correlation matrices are presented in

Table A4. Correlation with inflation data (Source: own editing).

	Austria	Belgium	Czech Republic	Germany	Hungary	The Netherlands	Poland	Slovakia	Sweden
Austria	1
Belgium	0.9976	1
Czech Republic	0.9831	0.9861	1
Germany	0.9978	0.9983	0.9876	1
Hungary	0.9807	0.9864	0.9903	0.9860	1
Netherlands	0.9866	0.9904	0.9902	0.9908	0.9923	1
Poland	0.9634	0.9710	0.9886	0.9700	0.9936	0.9852	1
Slovakia	0.9481	0.9584	0.9670	0.9571	0.9869	0.9782	0.9857	1
Sweden	0.9934	0.9962	0.9897	0.9957	0.9908	0.9924	0.9771	0.9658	1

(inflation) and

Table A5. Correlation of stock market index data (Source: own editing).

	Austria_ATX	Belgium_BEL20	Czech_PX	Germany_DAX	Hungary_BUX	Netherlands_AEX	Poland_WIG	Slovakia_SAX	Sweden_OMX_Stockholm30
Austria_ATX	1
Belgium_BEL20	0.7477	1
Czech_PX	0.9591	0.6098	1
Germany_DAX	0.5408	0.7198	0.4283	1
Hungary_BUX	0.7404	0.7008	0.6506	0.8981	1
Netherlands_AEX	0.2990	0.7568	0.1577	0.6972	0.5576	1
Poland_WIG	0.8255	0.6957	0.7751	0.8481	0.8968	0.3806	1
Slovakia_SAX	0.8570	0.5695	0.8434	0.4527	0.7037	0.1522	0.6821	1
Sweden_OMX_Stockholm30	0.5548	0.7220	0.4724	0.9781	0.8860	0.7328	0.8365	0.4467	1

(stock indices). For both inflation and the stock market index, univariate models were applied, using a 36 month time frame for estimation.

4. Conclusions

In our study we investigated the usefulness of artificial intelligence in portfolio management. We assumed that the portfolio consists of a well-diversified set of stocks and government securities. The well-diversified stock portfolio is represented by the stock market indices of each country. We sought to capture government bond returns indirectly through inflation. In a high-inflation environment, equity prices fall while government bond yields typically rise. By forecasting inflation as accurately as possible, we can rebalance the portfolio in time to maximise returns.

In total, two different AI-based prediction algorithms were used (GRU and LSTM), and a hybrid model (LSTM–GRU) was also included in the study. In addition to the predictability of inflation, we also examined the forecast accuracy of stock market indices from a risk management perspective. The avoidance of stock price declines may be an important objective. We used three splits for the split of the train–test database: 80% - 20%, 85% - 15%, and 90% - 10%. The split 85% - 15% was selected based on the time series break established by the Zivot–Andrews unit tests. Furthermore, we investigated what happens in the case where the break falls in the learner or in the tester database part.

Our results show that when inflation is more predictable, the mean error of forecasting (MAPE) is smaller. This is due to the significantly lower volatility of inflation, which makes it easier to forecast. For the train–test-database split, the 80% - 20% split gave the most accurate forecast in most cases, while for inflation, 85% - 15% gave the better result for some countries. Therefore, we can say that the excellent pattern recognition ability of neural models is not significantly affected by structural breaks in the time series.

Contrary to the literature, the hybrid model (LSTM–GRU) did not perform better than its non-hybrid counterparts. In fact, there was no significant difference in prediction accuracy between the three models. Table 4 summarises the average MAPE values based on the AI models. As can be seen, there is no significant difference between the individual MAPE values; these differences are most likely due to chance.

When looking at the inflation and stock market index forecasts as a whole, taking country-specific aspects into account, we can conclude that Slovakia’s data were the most accurate and Hungary’s data the least accurate. This is supported by all the methodologies used, which is not so surprising in the light of the fact that all the algorithms belong to the group of recurrent neural networks.

Our results show that the average error of the inflation forecast is a quarter of the forecast of the stock market index. Inflation developments have a fundamental impact on stock and government bond returns. If we obtain a reliable estimate of the inflation forecast, we can expect to have time to rebalance the portfolio until the inflation shock is incorporated into government bond returns. Our results not only support investment decisions at the national economy level but are also useful in the process of rebalancing international portfolios.

The limitations of the study include the use of univariate estimation on both inflation and stock index data. Also, we have not explored the potential of various AI-based portfolio management tools such as BlackRock Aladdin, Wealthfront, Betterment, SigFid, Qplum, Alpaca, etc. Future research could be based on the inclusion of additional machine learning models, the use of multivariate estimators, and the expansion of the range of investment products.