A Compound Up-and-In Call like Option for Wind Projects Pricing
Abstract
1. Introduction
2. Methodology
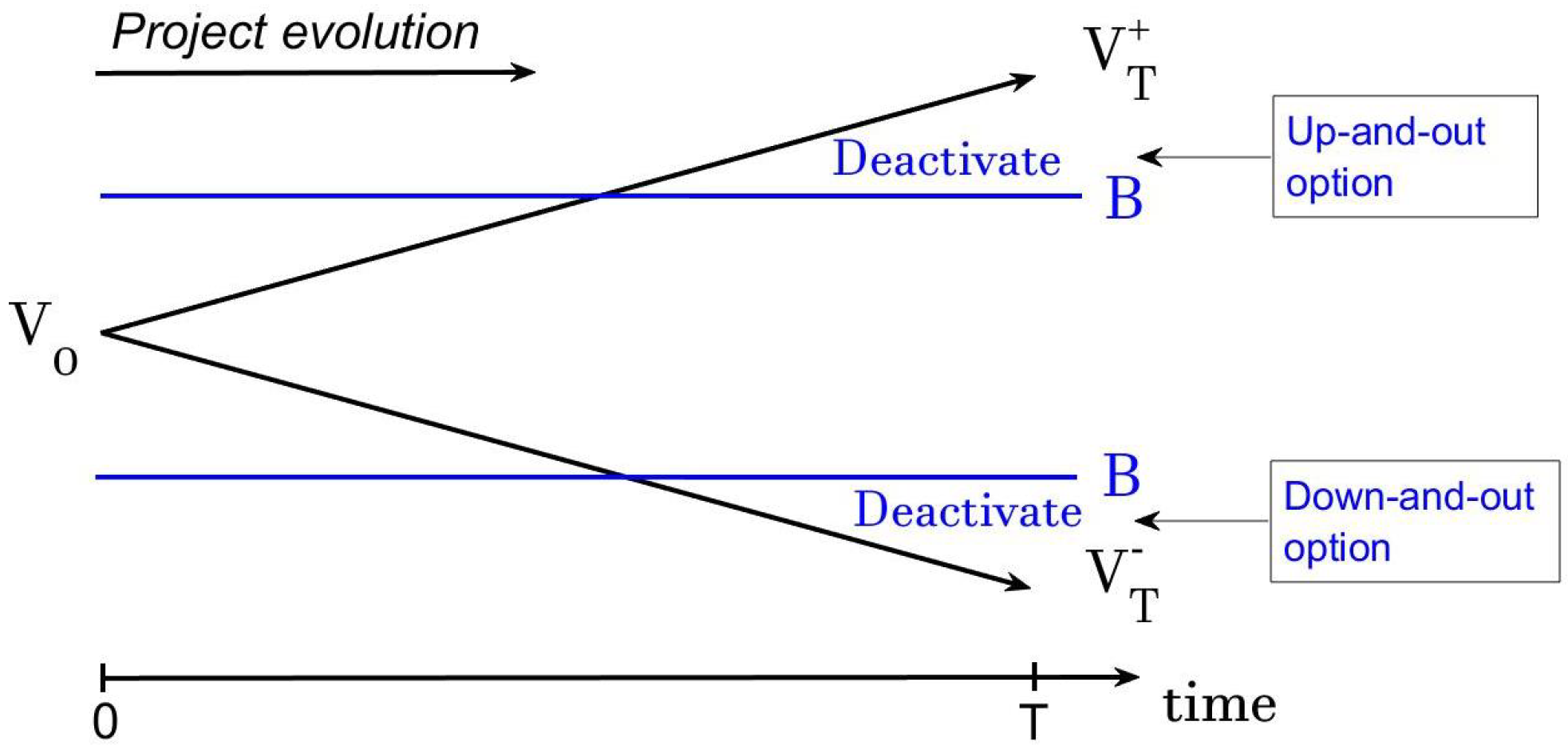
2.1. Up-and-In Option
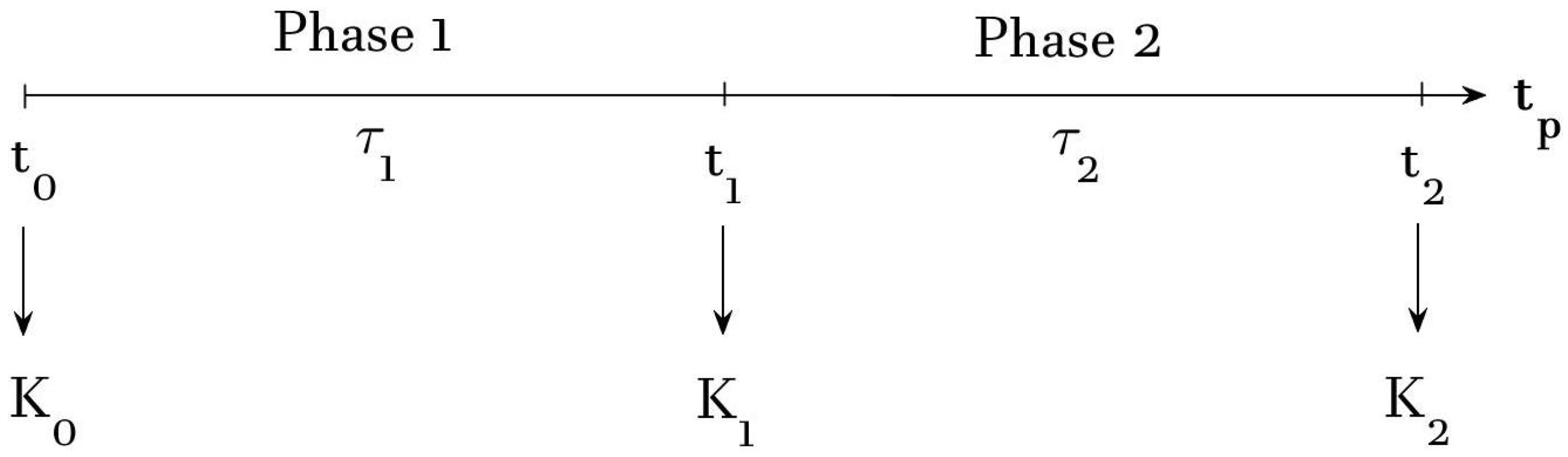
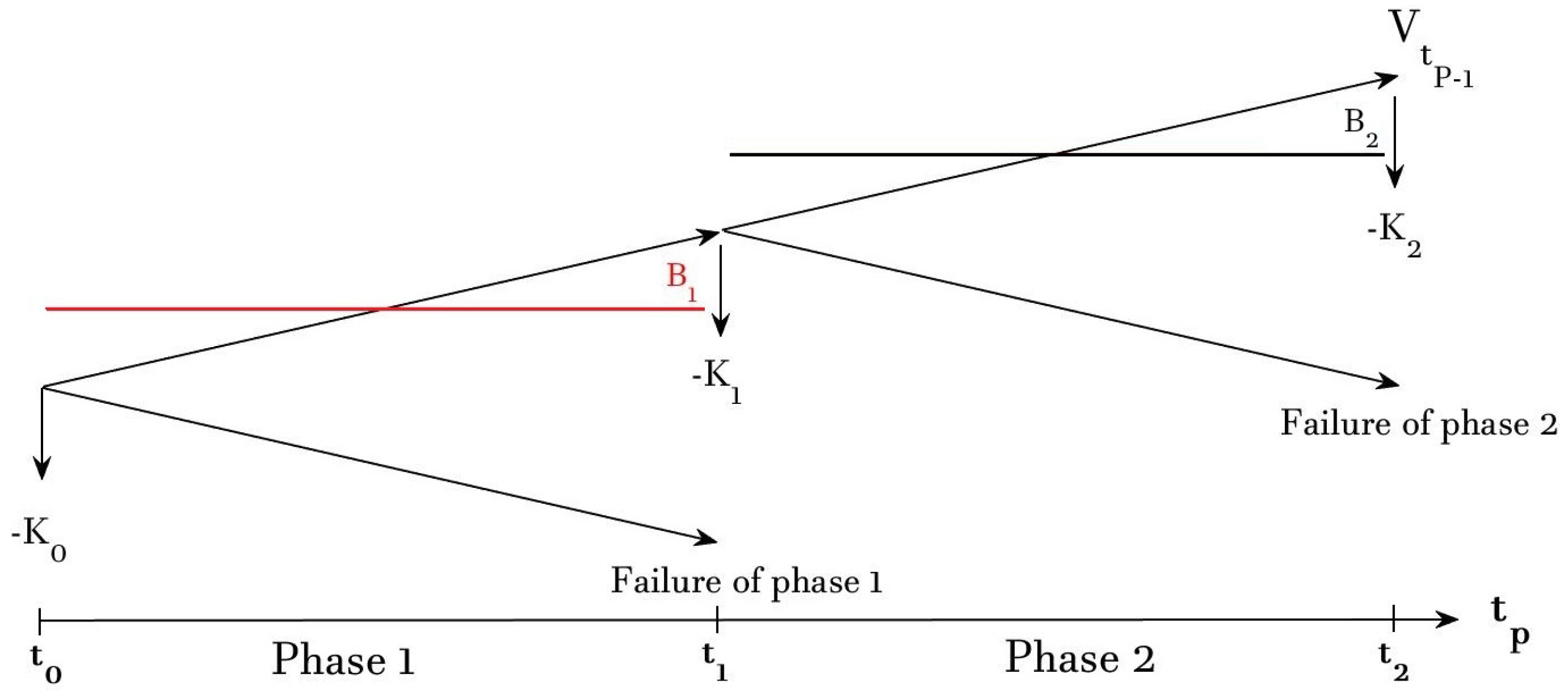
2.2. Compound Up-and-in-Like Option for Wind Projects Valuation
2.3. Valuation of Vega
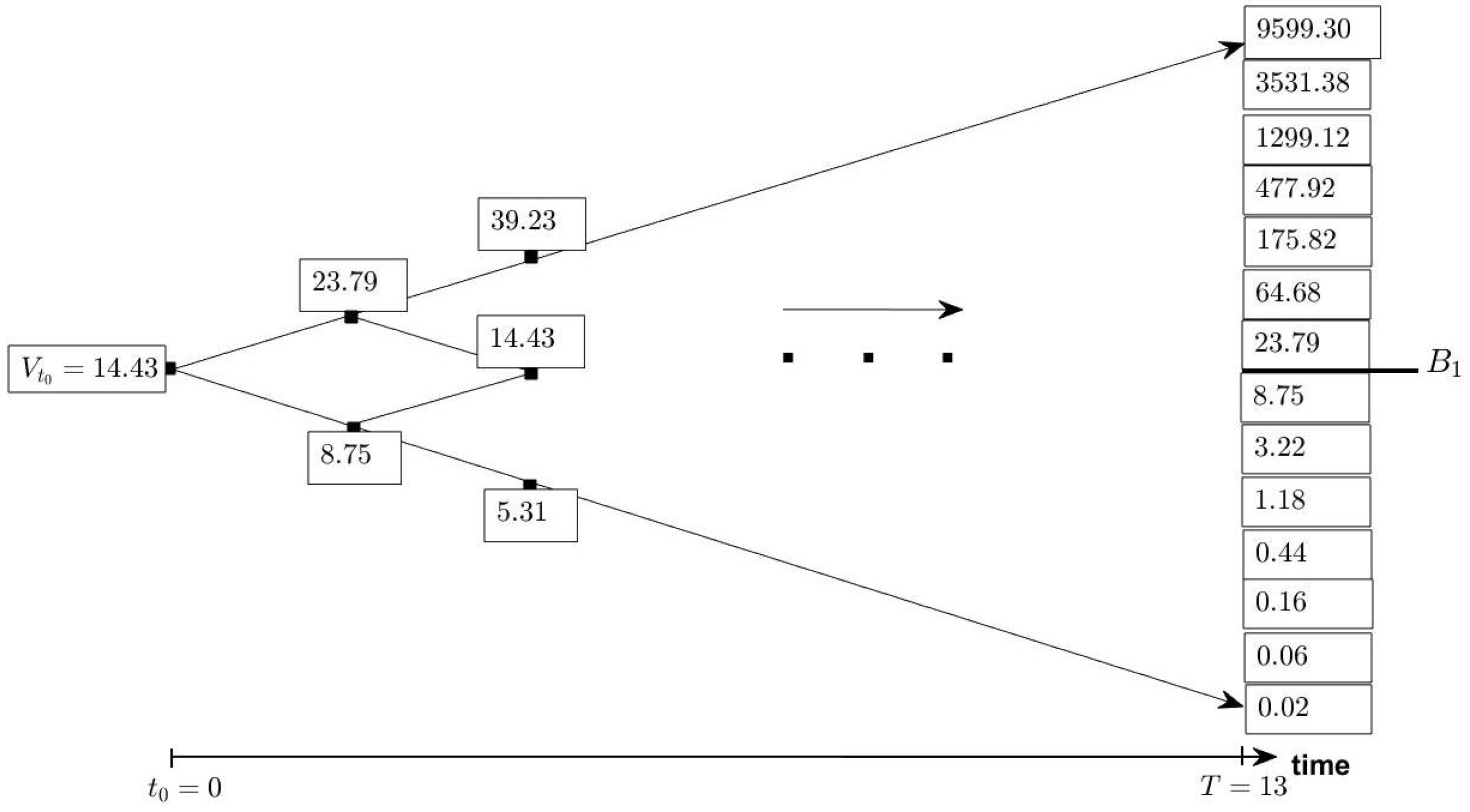
3. Case Study
Discussion of Results: Findings and Implications
4. Conclusions and Limitations
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
| 1 | In this work, we assume that the project value can change over the time. This means that we consider changing revenues that are affected by various variables, such as unpredictable market demand or other reasons. |
| 2 | Notice that the risk-neutral approach is often required to be applied by the Solvency II Directive to valuate the best estimate of many financial products. This approach implies that all assets considered in the financial projection have a risk-free return independently from their credit characteristics and are consequently discounted with risk-free rates. Other valuations, differently from the risk-neutral world, may lead to arbitrage opportunities. Moreover, in some contexts, such as the insurance liabilities, it is proved that other approaches (e.g., the real world deflator) lead to similar results both at inception and for subsequent measurement. For more details, a reader can refer to Ouelega (2013), Jouini et al. (2005). |
| 3 | The power generation has been chosen considering likely wind speed circumstances. |
| 4 | The proportions of costs has been chosen considering the study of Bufalo et al. (2022). |
| 5 | A FiT is a measure to encourage the projects in renewable energy sources. This policy is often realized by providing producers with an above-market price for the renewable energy produced. It is just an assumption. It is not excluded that there could be other mechanisms according to the various governments of the world. |
| 6 | The amount of FiT has been chosen considering the study of Loncar et al. (2017). |
| 7 | The discount rate equal to 8% has been extrapolated by the study of Loncar et al. (2017). |
| 8 | The value of has been extrapolated by the study of Bufalo et al. (2022). |
| 9 | The value of satisfies the up-option condition (Gaudenzi and Lepellere 2006). |
| 10 | The value has been extrapolated by the study of Loncar et al. (2017) |
| 11 | The value of satisfies the up-option condition . |
| 12 | This result is obtained by considering our assumptions and and it is not extended to all wind farm projects. Results could drastically change by varying data or by changing the assumptions. |
References
- Attalienti, Antonio, and Michele Bufalo. 2020. Option pricing formulas under a change of numèraire. Opuscula Mathematica 40: 451–73. [Google Scholar] [CrossRef]
- Attalienti, Antonio, and Michele Bufalo. 2022. Expected vs. real transaction costs in European option pricing. Discrete and Continuous Dynamical Systems—Series S 15: 3517–39. [Google Scholar] [CrossRef]
- Biancardi, Marta Elena, Antonio Di Bari, and Giovanni Villani. 2021. R&D investment decision on smart cities: Energy sustainability and opportunity. Chaos, Solitons and Fractals 153: 111554. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bufalo, Michele, Antonio Di Bari, and Giovanni Villani. 2022. Multi-stage real option evaluation with double barrier under stochastic volatility and interest rate. Annals of Finance 18: 247–66. [Google Scholar] [CrossRef]
- Cassimon, Danny, Peter Jan Engelen, L. Thomassen, and Martine Van Wouwe. 2004. The valuation of a NDA using a 6-fold compound option. Research Policy 33: 41–51. [Google Scholar] [CrossRef]
- Cox, John C., Sthephen A. Ross, and Mark Rubinstein. 1979. Option pricing: A simplified approach. Journal of Financial Economics 7: 229–63. [Google Scholar] [CrossRef]
- Di Bari, Antonio. 2021. A barrier real option approach to evaluate public-private partnership projects and prevent moral hazard. SN Business & Economics 1: 43. [Google Scholar]
- Engelen, Peter Jan, Clemens Kool, and Ye Li. 2016. A barrier options approach to modeling project failure: The case of hydrogen fuel infrastructure. Resources and Energy Economics 43: 33–56. [Google Scholar] [CrossRef]
- Gaudenzi, Marcellino, and Maria Antonietta Lepellere. 2006. Pricing and hedging american barrier options by a modified binomial method. International Journal of Theoretical and Applied Finance 9: 533–53. [Google Scholar] [CrossRef]
- Geske, Robert. 1979. The valuation of compound options. Journal of Financial Economics 7: 63–81. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2003. Monte Carlo Methods in Financial Engineering. New York: Springer. [Google Scholar]
- Hauschild, Bastian, and Daniel Reimsbach. 2015. Modeling sequential R&D investment: A binomial compound option approach. Business Research 8: 39–59. [Google Scholar]
- Hull, John C. 2013. Fundamentals of Futures and Option Markets, 8th ed. Englewood Cliffs: Prentice Hall. [Google Scholar]
- Jouini, Elyès, Clotilde Napp, and Walter Schachermayer. 2005. Arbitrage and state price deflators in a general intertemporal framework. Journal of Mathematical Economics 41: 722–34. [Google Scholar] [CrossRef]
- Kellogg, David, and John M. Charnes. 2000. Real-options valuation for a biotechnology company. Financial Analysts Journal 56: 76–84. [Google Scholar] [CrossRef]
- Lee, Shun Chung. 2011. Using real option analysis for highly uncertain technology investments: The case of wind energy technology. Renewable and Sustainable Energy Reviews 15: 4443–50. [Google Scholar] [CrossRef]
- Liu, Yu-hong, I-Ming Jiang, and Li-chun Chen. 2018. Valuation of n-fold compound barrier options with stochastic interest rates. Asia Pacific Management Review 23: 169–85. [Google Scholar] [CrossRef]
- Loncar, Dragan, Ivan Milovanovic, Biljana Rakic, and Tamara Radjenovic. 2017. Compound real options valuation of renewable energy projects: The case of a wind farm in Serbia. Renewable and Sustainable Energy Reviews 75: 354–67. [Google Scholar] [CrossRef]
- Martinez-Cesena, Eduardo Alejandro, and Joseph Mutale. 2012. Wind power projects planning considering real options for the wind resource assessment. IEEE Transactions on Sustainable Energy 3: 158–66. [Google Scholar] [CrossRef]
- Muroi, Yoshifumi, and Shintaro Suda. 2017. Computation of Greeks using binomial tree. Journal of Mathematical Finance 7: 597–623. [Google Scholar] [CrossRef]
- Ouelega, Bell Fanon. 2013. State-Price Deflators and Risk-Neutral Valuation of Life Insurance Liabilities. Technical Report. Association of African Young Economists. [Google Scholar]
- Panayi, Sylvia, and Lenos Trigeorgis. 1998. Multi-stage real options: The cases of information technology infrastructure and international bank expansion. The Quartely Review of Economics and Finance 38: 675–92. [Google Scholar] [CrossRef]
- Rambaud, Salvador Cruz, and Ana María Sánchez Pérez. 2016. Valuation of Barrier Options with the Binomial Pricing Model. Ratio Mathematica 31: 25–35. [Google Scholar]
- Reimer, Matthias, and Klaus Sandmann. 1995. A Discrete Time Approach for European and American Barrier Options. Working Paper. Bonn: Department of Statistics, Rheinische-Friedrich-Wilhelms-Universität Bonn. [Google Scholar]
- Rodríguez, Yeny E., Miguel A. Pérez-Uribe, and Javier Contreras. 2021. Wind put barrier options pricing based on the nordix Index. Energies 14: 1177. [Google Scholar] [CrossRef]
- Ross, Stephen A. 1995. Uses, Abuses and Alternatives to the Net-Present-Value Rule. Financial Management 24: 96–102. [Google Scholar] [CrossRef]
- Soltes, Vincent, and Martina Rusnakova. 2013. Hedging against a price drop using the inverse vertical ratio put spread strategy formed by barrier options. Engineering Economics 24: 18–27. [Google Scholar] [CrossRef]
- Trigeorgis, Lenos. 1993. Real Options and Interactions with Financial Flexibility. Financial Management 22: 202–24. [Google Scholar] [CrossRef]
- van Zee, Roger D., and Stefan Spinler. 2014. Real option valuation of public sector R&D investments with down-and-out barrier option. Technovation 34: 477–84. [Google Scholar]
- Venetsanos, Kostantinos, Penelope Angelopoulou, and Theocharis Tsoutsos. 2002. Renewable energy sources project appraisal under uncertainty—The case of wind energy exploitation within a changing energy market environment. Energy Policy 30: 293–307. [Google Scholar] [CrossRef]


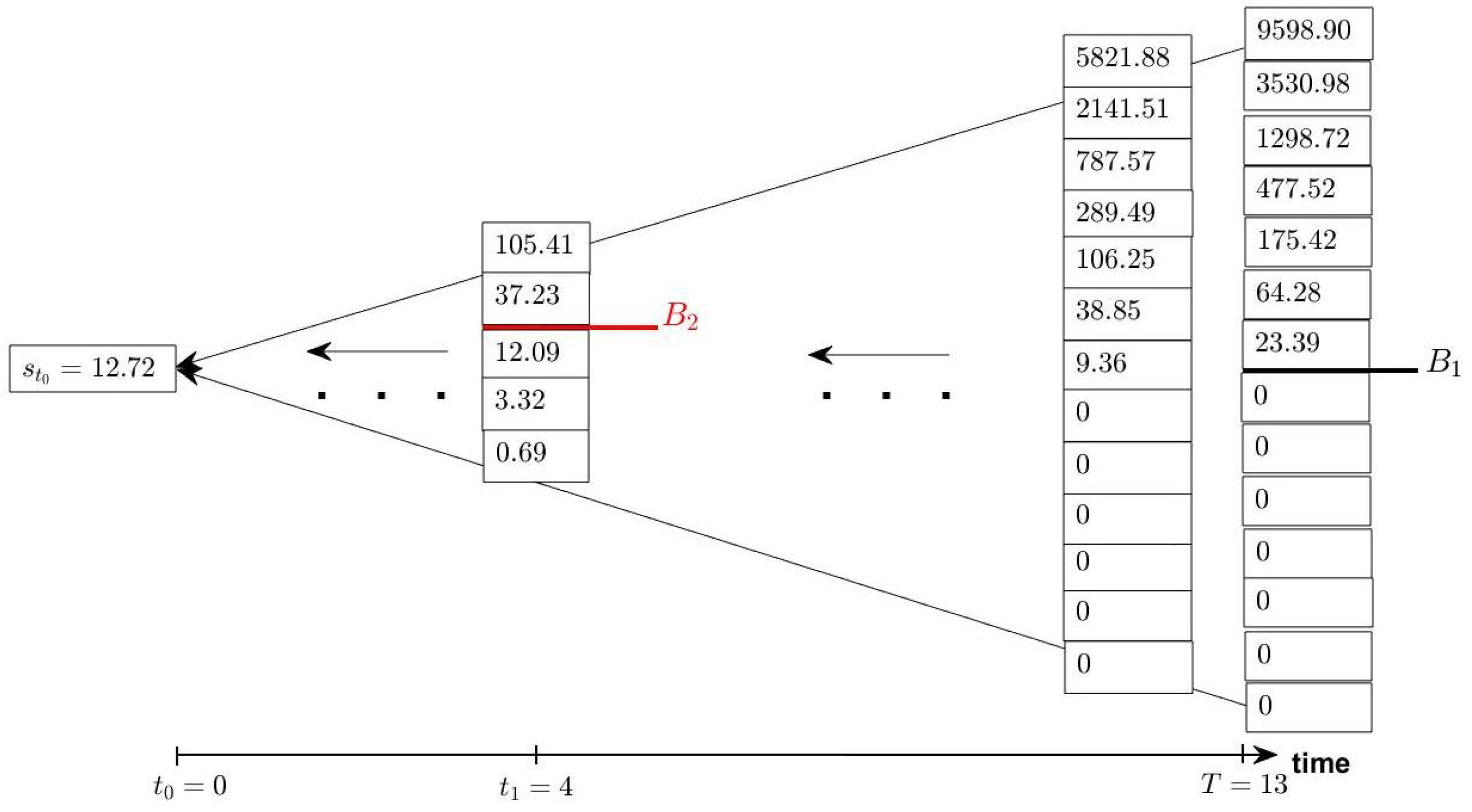
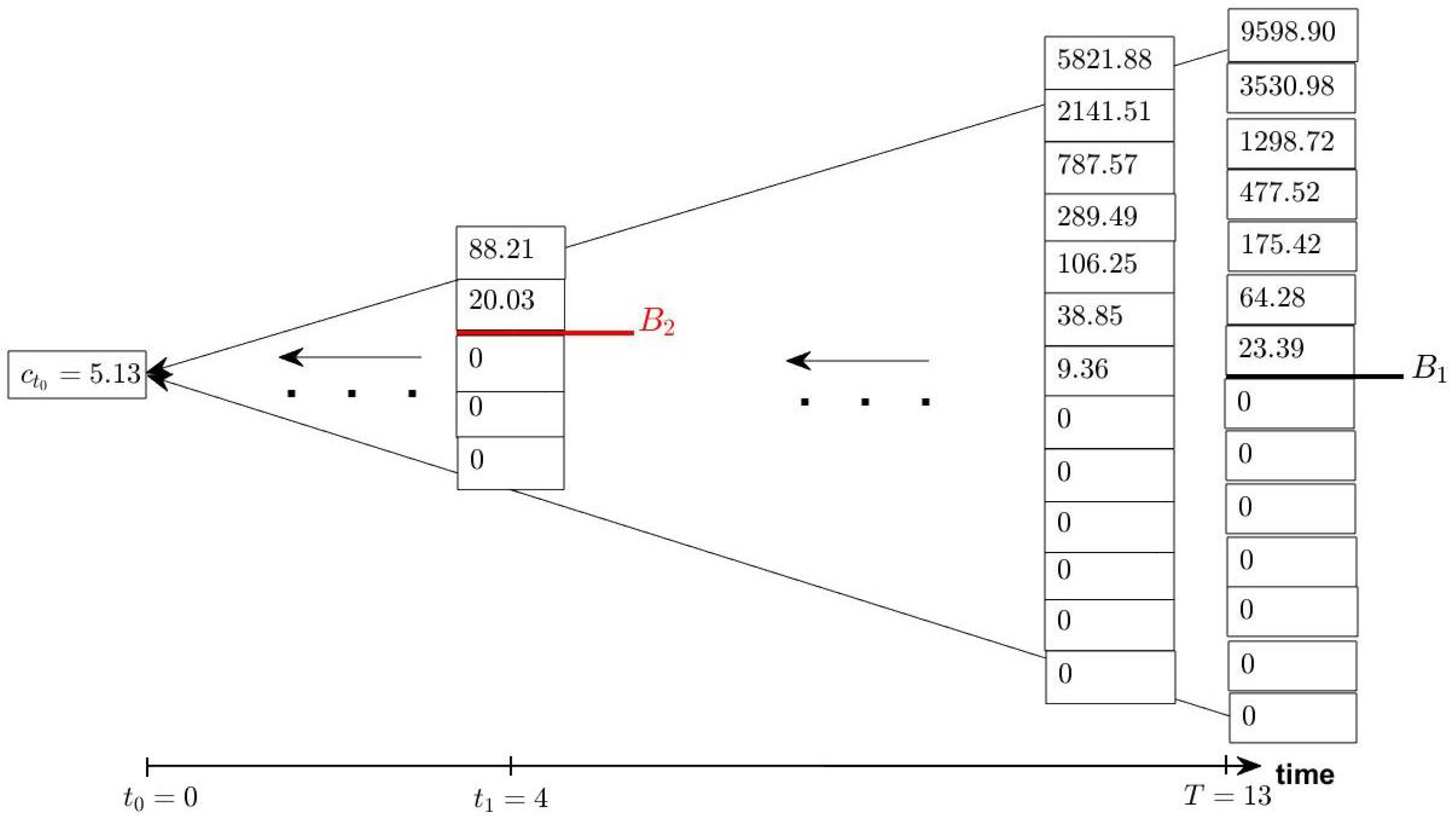
| Years | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Revenues | 3.14 | 3.14 | 3.14 | 3.14 | 3.14 | 3.14 | 3.14 | 3.14 | 3.14 | |||||
| Costs | −2.4 | −17.2 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bufalo, M.; Di Bari, A.; Villani, G. A Compound Up-and-In Call like Option for Wind Projects Pricing. Risks 2023, 11, 90. https://doi.org/10.3390/risks11050090
Bufalo M, Di Bari A, Villani G. A Compound Up-and-In Call like Option for Wind Projects Pricing. Risks. 2023; 11(5):90. https://doi.org/10.3390/risks11050090
Chicago/Turabian StyleBufalo, Michele, Antonio Di Bari, and Giovanni Villani. 2023. "A Compound Up-and-In Call like Option for Wind Projects Pricing" Risks 11, no. 5: 90. https://doi.org/10.3390/risks11050090
APA StyleBufalo, M., Di Bari, A., & Villani, G. (2023). A Compound Up-and-In Call like Option for Wind Projects Pricing. Risks, 11(5), 90. https://doi.org/10.3390/risks11050090






