Underwriting Cycles in Property-Casualty Insurance: The Impact of Catastrophic Events
Abstract
1. Introduction
2. Previous Research
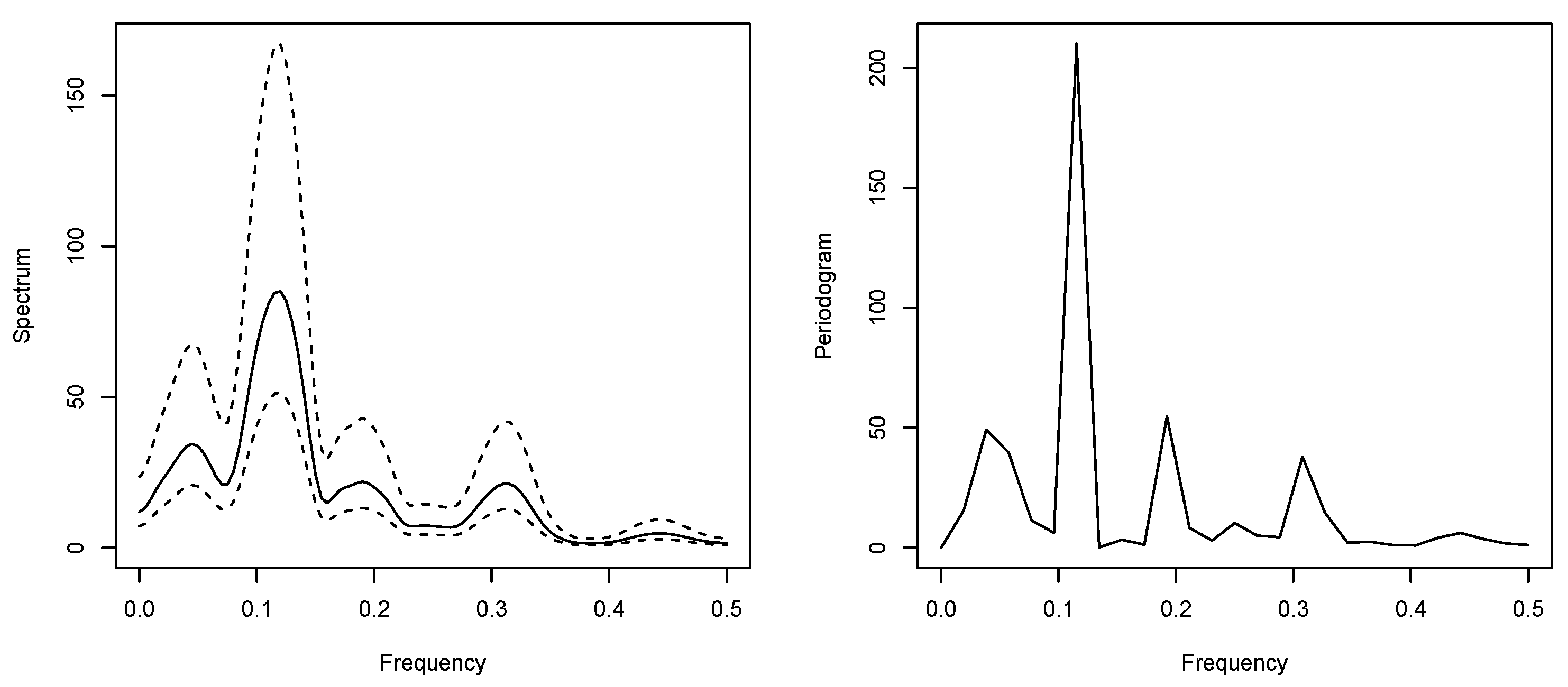
3. Are Underwriting Cycles Real?
- 1.
- Calculate the value of the test statistic .
- 2.
- Determine the critical value at significance level :or, alternatively, the p-value
- 3.
- Reject at significance level if
4. An Intervention Model for Quarterly Underwriting Data
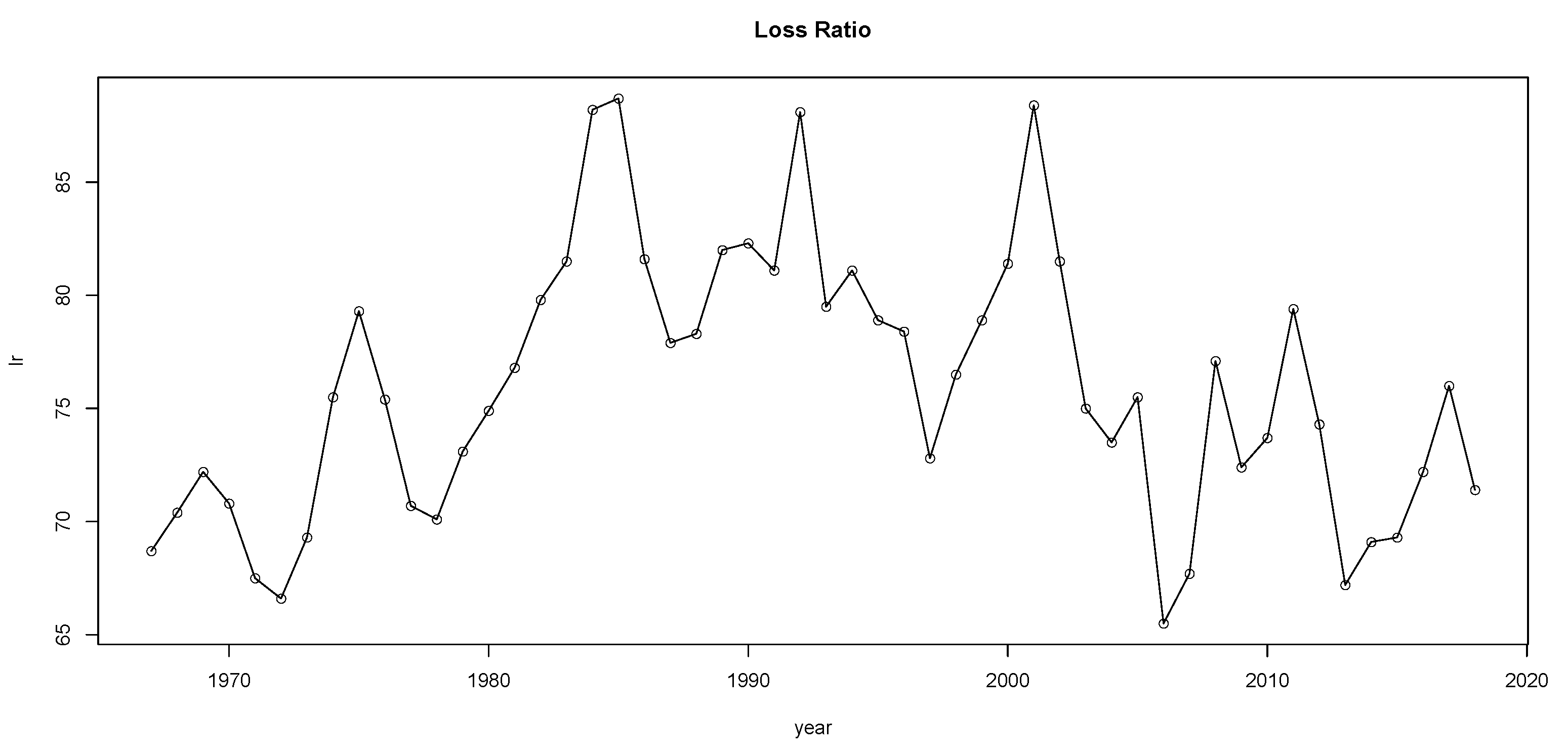
5. The Data
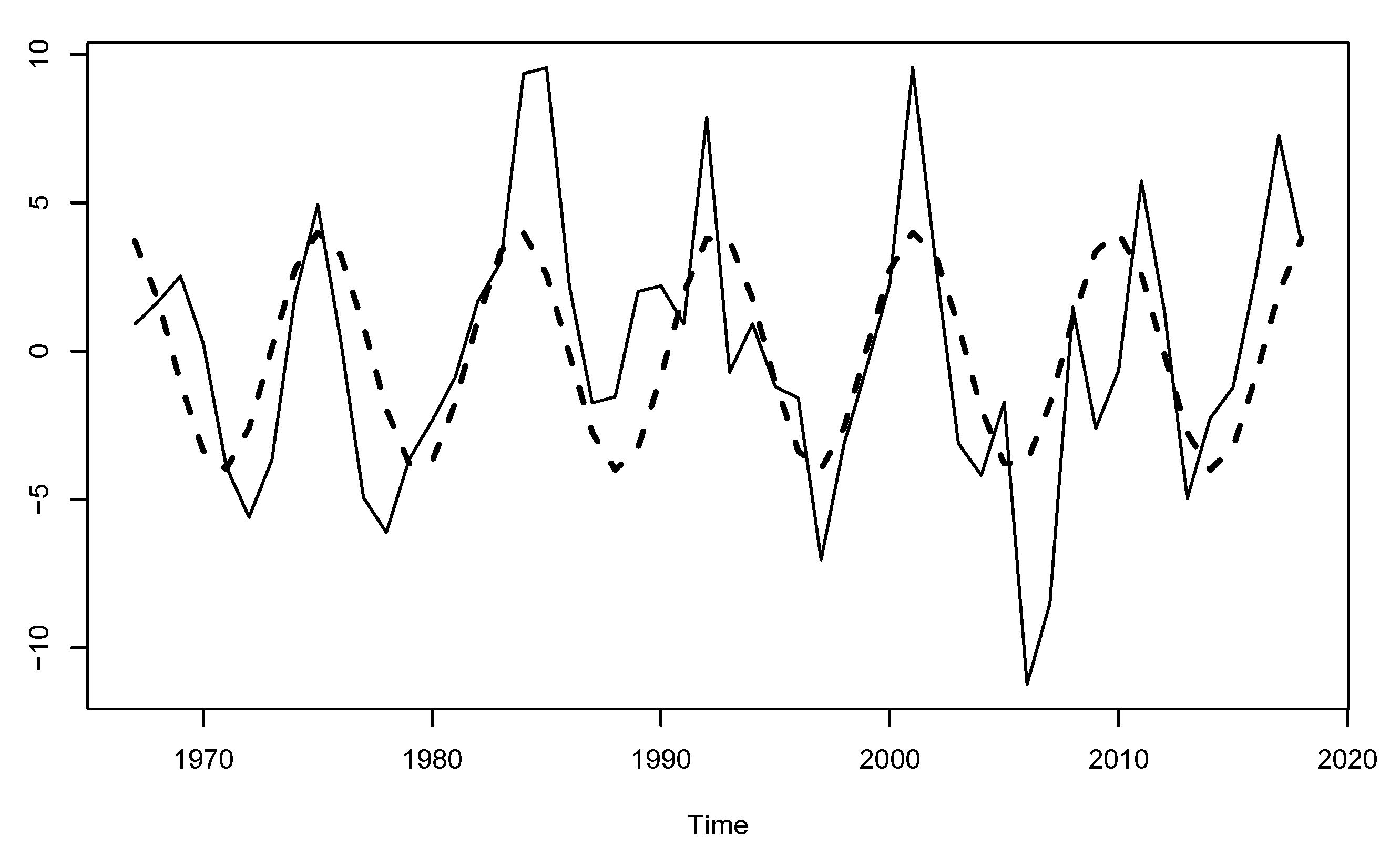
6. An Ex-Post Analysis of Intervention Effects
7. Forecasting Results
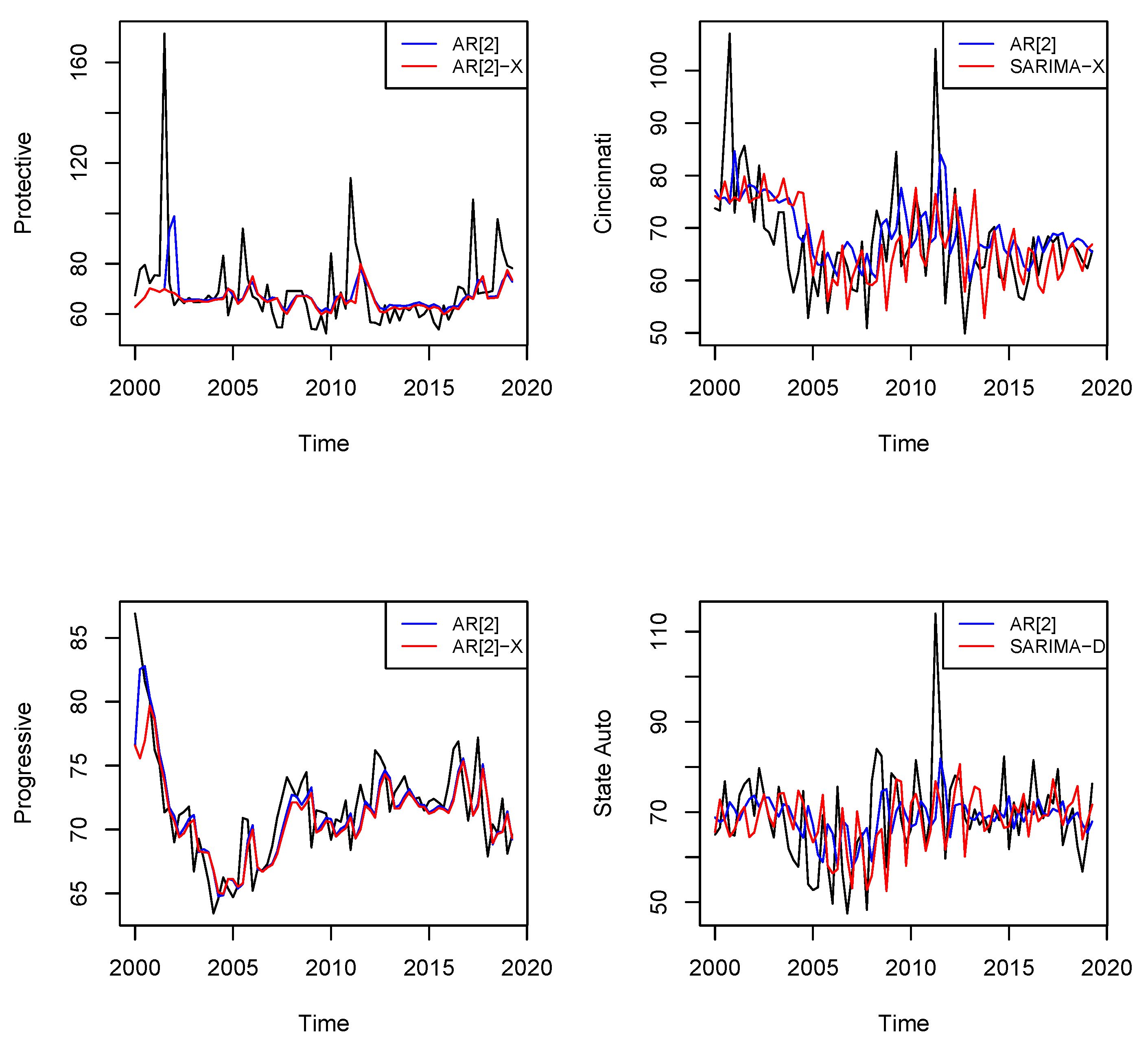
7.1. The Employed Models
- -
- The AR[2] model,
- -
- The ARIMA[2,1,0] model,
- -
- At least two SARIMA specifications,
- -
- The AR[2]-D model,
- -
- The ARIMA[2,1,0]-D model,
- -
- The corresponding SARIMA-D specifications, e.g., SARIMA[0,0,0]x[1,1,1]-D for Cincinnati.
7.2. The Forecasting Design
7.3. Forecast Evaluation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Regression Diagnostics
| Variable | Parameter Est. | Std. Error | t-Test | p-Value | ||
|---|---|---|---|---|---|---|
| 3.795 | 0.667 | 5.690 | 6.6 × 10 ** | |||
| 1.323 | 0.667 | 1.984 | 0.0528 * | |||
| Multiple : 0.421 | Adjusted : 0.398 | |||||
| p-value F-test: 1.18 × 10 | ||||||
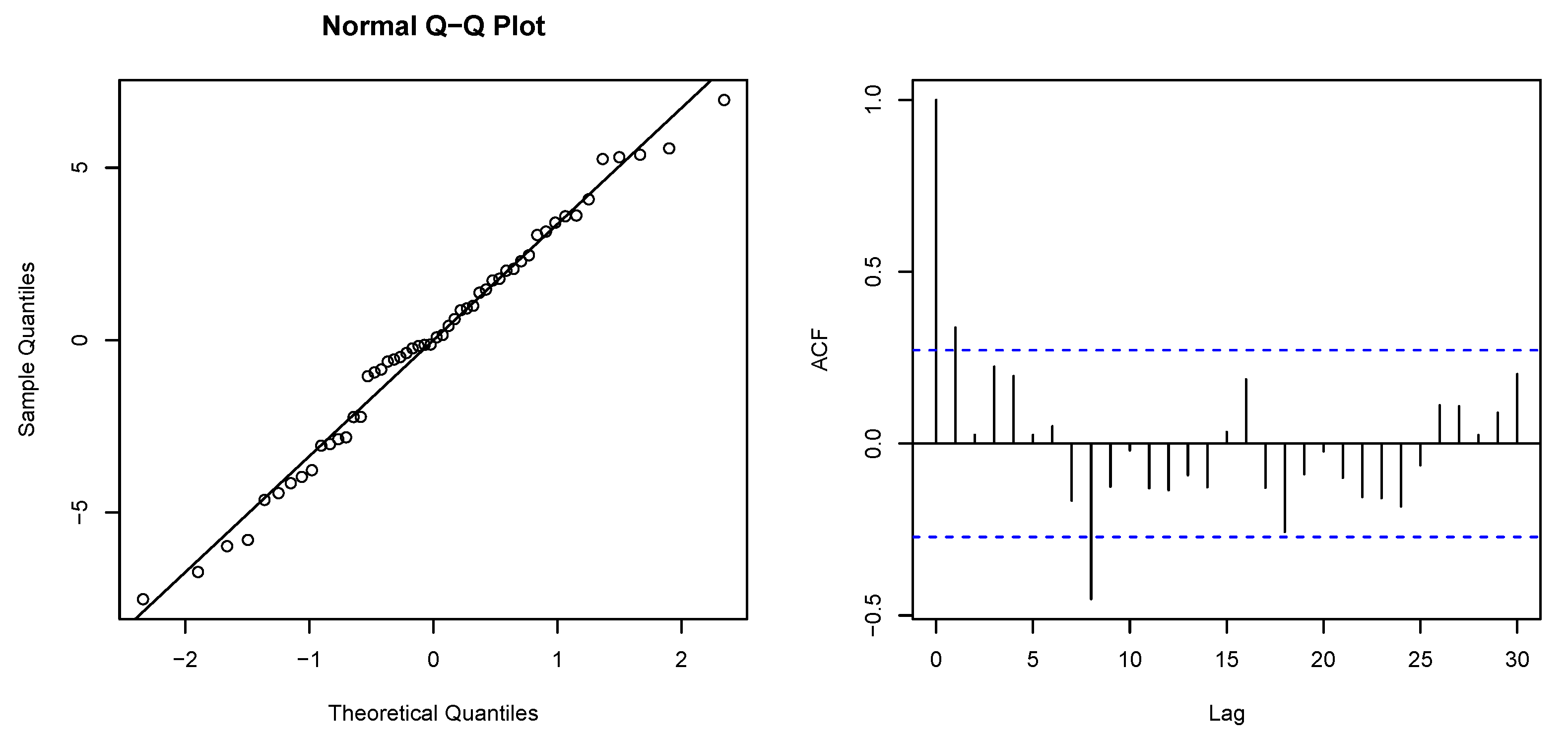
Appendix B. ACF and PACF Plots
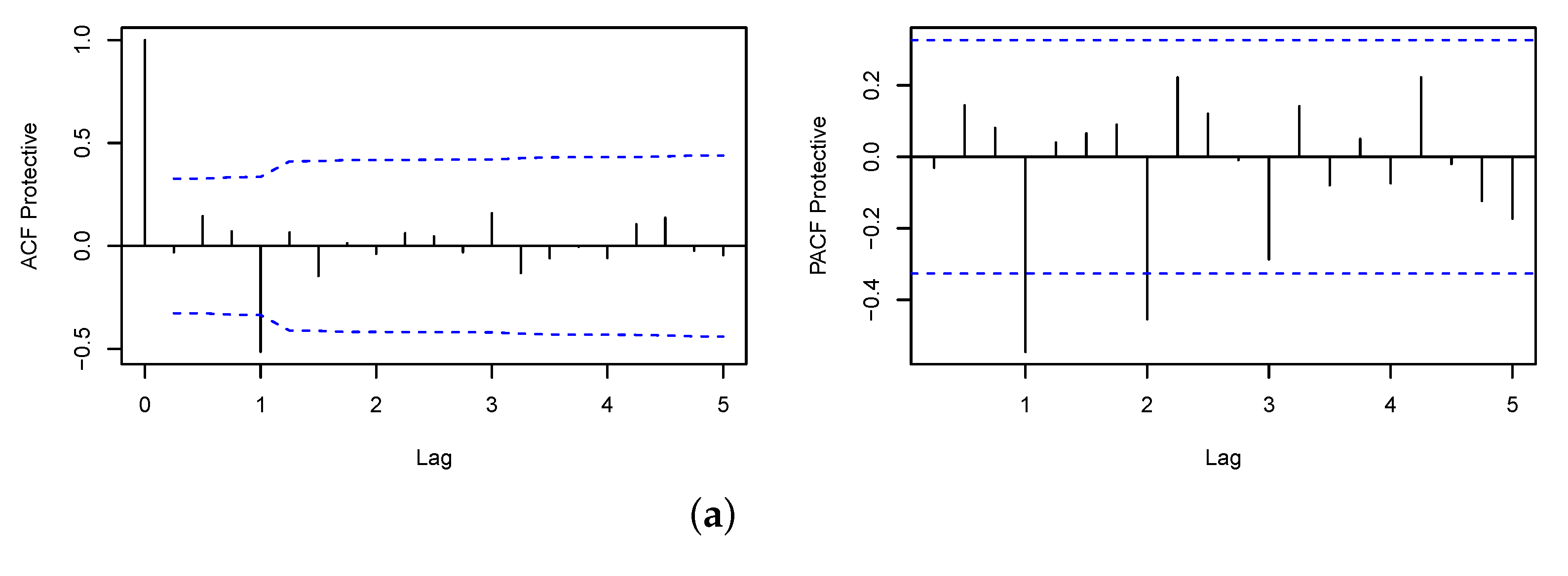
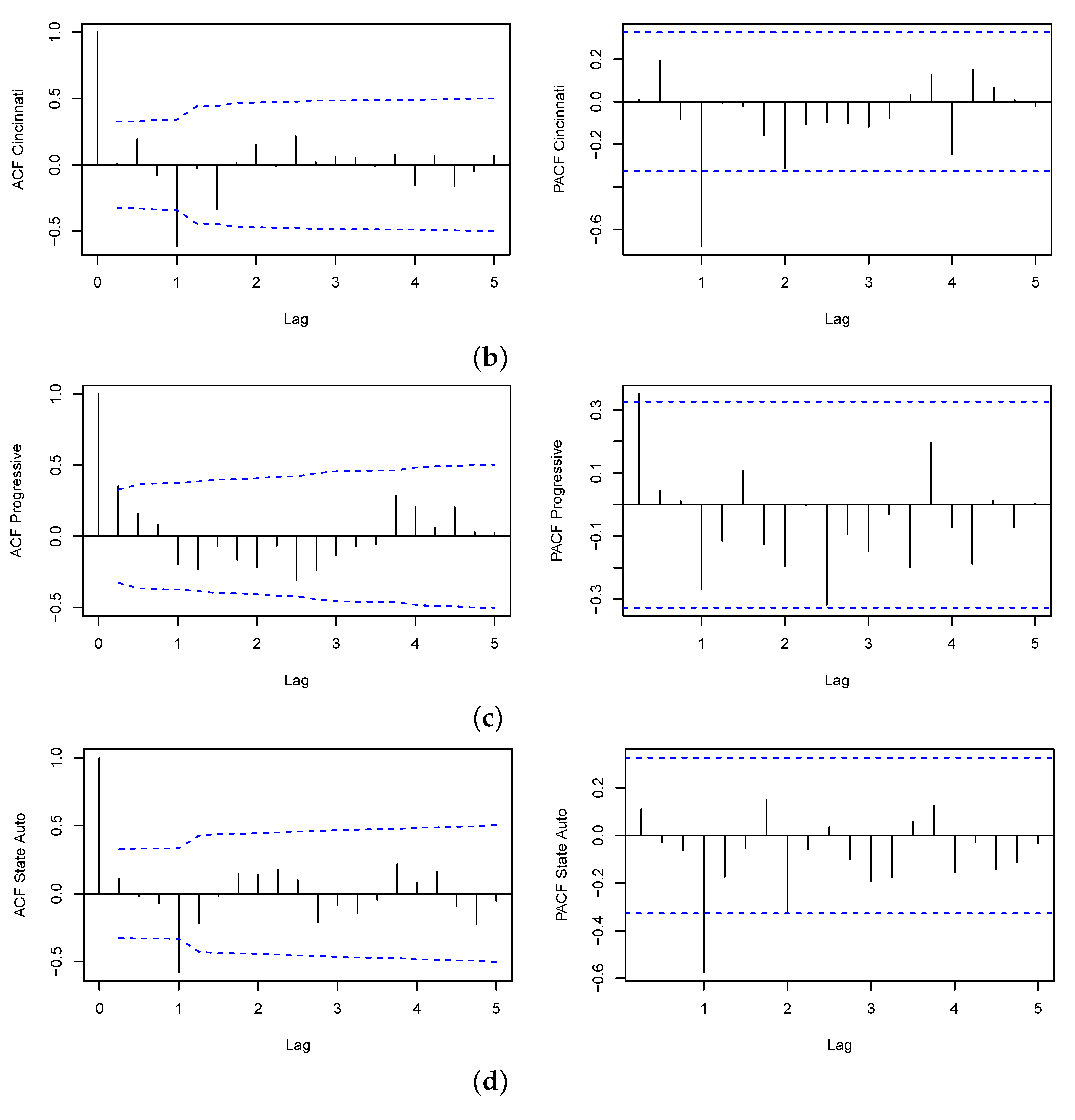
| 1 | |
| 2 | |
| 3 | Note that the benchmark autoregressive model can also generate cycles. |
| 4 | Note that unit roots are not compatible with the loss ratio dynamics of insurance companies per se. |
| 5 | Cycle analysis results based on the estimation of autoregressive models have proven of poor statistical significance due to the particularly short time series available in the insurance industry (Boyer and Owadally 2015; Boyer et al. 2012; Owadally et al. 2019b; Venezian and Leng 2006). On account of this we abstain from any evaluation of cycles based on these models in this paper. Instead, we set the focus on short- and mid-term forecasts and on the evaluation of intervention effects using quarterly underwriting data. |
| 6 | |
| 7 | Note that in a perfect insurance market, insurers can adjust their capital to bring down insolvency risk. |
| 8 | Mourdoukoutas et al. (2022) propose a multi-stage insurance game with observable actions, implying open-loop and closed-loop equilibrium premium profiles that might be cyclical in nature. However, cycles may not always occur, as demonstrated by Wang and Murdock (2019). The impact of a loss shock on an insurer’s cash flows might spread out and amplify over time due to the interaction between its underwriting capability and ability to raise external capital, generating a non-cyclical pattern of changes in underwriting coverage and access to external capital. |
| 9 | The annual loss ratio is defined as insurance claims paid plus adjustment expenses divided by total earned premiums for a given year. |
| 10 | See also Brockwell and Davis (1991) for a brief overview. |
| 11 | As a matter of fact, the authors report higher power for their test procedure compared to Fisher’s test even in the case of Gaussian data. The robust test of Ahdesmäki et al. (2005) was implemented with package ‘ptest’ by Lai and McLeod (2016) using R (R Core Team 2020). Lai and McLeod (2016) calculate p-values with the response surface regression method (MacKinnon 2002) which is more accurate and computationally more efficient than the time-consuming simulation method. |
| 12 | The term autoregressive in ARIMA refers to a linear regression model that uses its own lags as predictors. |
| 13 | Note that the intervention model can be easily extended to capture any loss reporting delay. |
| 14 | Given the particular regulatory framework of the insurance industry, permanent effects on loss ratios are not reasonable, e.g., one cannot assume that catastrophes would induce a permanent shift in the mean level. Following these considerations we only use pulse dummy variables to model catastrophes. |
| 15 | The plots of the relevant autocorrelation functions (ACF) and partial autocorrelation functions (PACF) can be found in Appendix B. |
| 16 | Bloomberg provides quarterly data on 63 companies in the property and casualty business traded and domiciled in the US. We selected only those companies with fairly large series, starting in the first quarter 1990 at the latest, i.e., with at least 118 observations. We checked our data against annual company data from SNL and selected only the series consistent for both data sources in order to avoid potentially false information. |
| 17 | Throughout, models were fitted to the series of logarithmic loss ratio values to stabilize variance. We employed package TSA by Chan and Ripley (2020) using R (R Core Team 2020). |
| 18 | The parameter for the dummy variable flagging the time point 2011/Q1 of the second event is not statistically significant, and so we removed it from the model. |
| 19 | Note that the estimation of a polynomial trend might have severe consequences on inference results, e.g., the significance level (probability of error) might no longer be satisfied. See Chan et al. (1977), Nelson and Kang (1981), as well as Nelson and Kang (1984). |
| 20 | |
| 21 | We fit our models to the logarithmic loss ratios and convert forecasts back into forecasts of absolute loss ratio for the purpose of evaluation. |
| 22 | |
| 23 | We have also experimented with a higher number of bootstrap replications, as well as with the circular block bootstrap leading to irrelevant results changes. |
References
- Adam, Klaus, and Sebastian Merkel. 2019. Stock Price Cycles and Business Cycles. Available online: https://ssrn.com/abstract=3329820 (accessed on 10 December 2022).
- Ahdesmäki, Miika, Harri Lähdesmäki, Ron Pearson, Heikki Huttunen, and Olli Yli-Harja. 2005. Robust detection of periodic time series measured from biological systems. BMC Bioinformatics 6: 1–18. [Google Scholar] [CrossRef] [PubMed]
- Artis, Michael J., Mathias Hoffmann, Dilip M. Nachane, and Juan Toro. 2004. The Detection of Hidden Periodicities: A Comparison of Alternative Methods. Working Paper EUI ECO, 2004/10. Fiesole: European University Institute. [Google Scholar]
- Bartlett, Maurice S. 1957. Discussion on symposium on spectral approach to time series. Journal of the Royal Statistical Society: Series B 19: 1–63. [Google Scholar]
- Bølviken, Erik. 1983. New tests of significance in periodogram analysis. Scandinavian Journal of Statistics 1: 1–9. [Google Scholar]
- Boonen, Tim J., Athanasios A. Pantelous, and Renchao Wu. 2018. Non-cooperative dynamic games for general insurance markets. Insurance: Mathematics and Economics 78: 123–35. [Google Scholar] [CrossRef]
- Box, George E. P., and George C. Tiao. 1975. Intervention analysis with applications to economic and environmental problems. Journal of the American Statistical Association 70: 70–79. [Google Scholar] [CrossRef]
- Box, George E. P., and Gwilym M. Jenkins. 1970. Time Series Analysis, Forecasting and Control. San Francisco: Holden-Day. [Google Scholar]
- Boyer, M. Martin, and Iqbal Owadally. 2015. Underwriting apophenia and cryptids: Are cycles statistical figments of our imagination? Geneva Papers on Risk and Insurance—Issues and Practice 40: 232–55. [Google Scholar] [CrossRef]
- Boyer, M. Martin, Eric Jacquier, and Simon Van Norden. 2012. Are underwriting cycles real and forecastable? Journal of Risk and Insurance 79: 995–1015. [Google Scholar] [CrossRef]
- Brockwell, Peter J., and Richard. A. Davis. 1991. Time Series: Theory and Methods, 2nd ed. New York: Springer. [Google Scholar]
- Browne, Mark J., Lan Ju, and Zhiyong Tu. 2014. Broker monitoring of premium adequacy: The role of contingent commissions. Applied Economics 46: 2375–86. [Google Scholar] [CrossRef]
- Cagle, Julie A. B., and Scott E. Harrington. 1996. Insurance supply with capacity constraints and endogenous insolvency risk. Insurance Mathematics and Economics 2: 148. [Google Scholar] [CrossRef]
- Canova, Fabio. 1996. Three tests for the existence of cycles in time series. Ricerche Economiche 50: 135–62. [Google Scholar] [CrossRef]
- Chan, K. Hung, Jack C. Hayya, and J. Keith Ord. 1977. A note on trend removal methods—The case of polynomial versus variate differencing. Econometrica 45: 737–44. [Google Scholar] [CrossRef]
- Chan, Kung-Sik, and Brian Ripley. 2020. TSA: Time Series Analysis. R Package Version 1.3. Available online: https://cran.r-project.org/web/packages/TSA/index.html (accessed on 9 October 2020).
- Chatfield, Chris. 1993. Calculating interval forecasts. Journal of Business & Economic Statistics 11: 121–35. [Google Scholar]
- Chiu, Shean-Tsong. 1989. Detecting periodic components in a white gaussian time series. Journal of the Royal Statistical Society: Series B (Methodological) 51: 249–59. [Google Scholar] [CrossRef]
- Cryer, Jonathan D., and Kung-Sik Chan. 2010. Time Series Analysis. With Applications in R, 2nd ed.New York: Springer. [Google Scholar]
- Cummins, J. David, and David W. Sommer. 1996. Capital and risk in property-liability insurance markets. Journal of Banking & Finance 20: 1069–92. [Google Scholar]
- Cummins, J. David, and J. Francois Outreville. 1987. An international analysis of underwriting cycles in property-liability insurance. Journal of Risk and Insurance 54: 246–62. [Google Scholar] [CrossRef]
- Doherty, Neil A., and Han Bin Kang. 1988. Interest rates and insurance price cycles. Journal of Banking & Finance 12: 199–214. [Google Scholar]
- Doherty, Neil A., and James R. Garven. 1995. Insurance cycles: Interest rates and the capacity constraint model. Journal of Business 68: 383–404. [Google Scholar] [CrossRef]
- Doherty, Neil A., and Lisa Posey. 1997. Availability crises in insurance markets: Optimal contracts with asymmetric information and capacity constraints. Journal of Risk and Uncertainty 15: 55–80. [Google Scholar] [CrossRef]
- Fisher, Ronald A. 1929. Tests of significance in harmonic analysis. Proceedings of the Royal Society of London. Series A 125: 54–59. [Google Scholar]
- Fung, Hung-Gay, Gene C. Lai, Gary A. Patterson, and Robert C. Witt. 1998. Underwriting cycles in property and liability insurance: An empirical analysis of industry and by-line data. Journal of Risk and Insurance 65: 539–61. [Google Scholar] [CrossRef]
- Grace, Martin F., and Julie L. Hotchkiss. 1995. External impacts on the property-liability insurance cycle. Journal of Risk and Insurance 62: 738–54. [Google Scholar] [CrossRef]
- Gron, Anne. 1994a. Capacity constraints and cycles in property-casualty insurance markets. The RAND Journal of Economics 25: 110–27. [Google Scholar] [CrossRef]
- Gron, Anne. 1994b. Evidence of capacity constraints in insurance markets. The Journal of Law and Economics 37: 349–77. [Google Scholar] [CrossRef]
- Guo, Feng, Hung-Gay Fung, and Ying Sophie Huang. 2009. The dynamic impact of macro shocks on insurance premiums. Journal of Financial Services Research 35: 225–44. [Google Scholar] [CrossRef]
- Hannan, Eduard J. 1961. Testing for a jump in the spectral function. Journal of the Royal Statistical Society: Series B (Methodological) 23: 394–404. [Google Scholar]
- Hansen, Peter, Asger Lunde, and James Nason. 2011. The model confidence set. Econometrica 79: 453–97. [Google Scholar] [CrossRef]
- Harrington, Scott E., and Greg Niehaus. 2000. Volatility and underwriting cycles. In Handbook of Insurance. Berlin: Springer, pp. 657–86. [Google Scholar] [CrossRef]
- Harrington, Scott E., and Patricia M. Danzon. 1994. Price cutting in liability insurance markets. Journal of Business 67: 511–38. [Google Scholar]
- Harrington, Scott E., Greg Niehaus, and Tong Yu. 2013. Insurance price volatility and underwriting cycles. In Handbook of Insurance. Berlin: Springer, pp. 647–67. [Google Scholar] [CrossRef]
- Hohensinn, Roland, Simon Häberling, and Alain Geiger. 2020. Dynamic displacements from high-rate gnss: Error modeling and vibration detection. Measurement 157: 107655. [Google Scholar] [CrossRef]
- Jawadi, Fredj, Catherine Bruneau, and Nadia Sghaier. 2009. Nonlinear cointegration relationships between non-life insurance premiums and financial markets. Journal of Risk and Insurance 76: 753–83. [Google Scholar] [CrossRef]
- Jiang, Shi-jie, and Chien-Chung Nieh. 2012. Dynamics of underwriting profits: Evidence from the u.s. insurance market. International Review of Economics & Finance 21: 1–15. [Google Scholar]
- Kay, Steven M., and Stanley Lawrence Marple. 1981. Spectrum analysis—A modern perspective. Proceedings of the IEEE 69: 1380–419. [Google Scholar] [CrossRef]
- Lai, Yuanhao, and A. Ian McLeod. 2016. ptest: Periodicity Tests in Short Time Series. R Package Version 1.0-8. Available online: https://cran.r-project.org/web/packages/ptest/index.html (accessed on 12 August 2021).
- Lamm-Tennant, Joan, and Mary A. Weiss. 1997. International insurance cycles: Rational expectations/institutional intervention. Journal of Risk and Insurance 64: 415–39. [Google Scholar] [CrossRef]
- Lazar, Dorina, and Michel M. Denuit. 2012. Multivariate analysis of premium dynamics in p&l insurance. Journal of Risk and Insurance 79: 431–48. [Google Scholar]
- Lei, Yu, and Mark J. Browne. 2017. Underwriting strategy and the underwriting cycle in medical malpractice insurance. The Geneva Papers on Risk and Insurance-Issues and Practice 42: 152–75. [Google Scholar] [CrossRef]
- MacKinnon, James G. 2002. Computing numerical distribution functions in econometrics. In High Performance Computing Systems and Applications. Berlin: Springer, pp. 455–71. [Google Scholar]
- Malinovskii, Vsevolod K. 2010. Competition-originated cycles and insurance strategies. ASTIN Bulletin: The Journal of the IAA 40: 797–843. [Google Scholar]
- Marx, Brian. 2013. Hard Market vs. Soft Market: The Insurance Industry’s Cycle and Why We Are Currently in a Hard Market. PSA Financial. Available online: https://www.psafinancial.com/2013/01/hard-market-vs-soft-market-the-insurance-industrys-cycle-and-why-were-currently-in-a-hard-market/ (accessed on 15 December 2022).
- MathWorks. 2018. MATLAB R2018a. Available online: http://www.mathworks.com/ (accessed on 9 April 2020).
- McSweeney, Laura A. 2006. Comparison of periodogram tests. Journal of Statistical Computation and Simulation 76: 357–69. [Google Scholar] [CrossRef]
- Meier, Ursina B. 2006. Multi-national underwriting cycles in property-liability insurance: Part I—Some theory and empirical results. The Journal of Risk Finance 7: 64–82. [Google Scholar] [CrossRef]
- Meier, Ursina B., and J. François Outreville. 2006. Business cycles in insurance and reinsurance: The case of france, germany and switzerland. The Journal of Risk Finance 7: 160–76. [Google Scholar] [CrossRef]
- Mourdoukoutas, Fotios, Athanasios A. Pantelous, and Greg Taylor. 2022. Competitive Insurance Pricing Strategies for Multiple Lines of Business: A Game Theoretic Approach. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4049437 (accessed on 10 December 2022).
- Nelson, Charles R., and Heejoon Kang. 1981. Spurious periodicity in inappropiately detrended time series. Econometrica 49: 741–51. [Google Scholar] [CrossRef]
- Nelson, Charles R., and Heejoon Kang. 1984. Pitfalls in the use of time as an explanatory variable in regression. Journal of Business & Economic Statistics 2: 73–82. [Google Scholar]
- Niehaus, Greg, and Andy Terry. 1993. Evidence on the time series properties of insurance premiums and causes of the underwriting cycle: New support for the capital market imperfection hypothesis. Journal of Risk and Insurance 60: 466–79. [Google Scholar] [CrossRef]
- Owadally, Iqbal, Feng Zhou, and Douglas Wright. 2018. The insurance industry as a complex social system: Competition, cycles, and crises. Journal of Artificial Societies and Social Simulation 21: 2. [Google Scholar] [CrossRef]
- Owadally, Iqbal, Feng Zhou, Rasaq Otunba, Jessica Lin, and Douglas Wright. 2019a. An agent-based system with temporal data mining for monitoring financial stability on insurance markets. Expert Systems with Applications 123: 270–82. [Google Scholar] [CrossRef]
- Owadally, Iqbal, Feng Zhou, Rasaq Otunba, Jessica Lin, and Douglas Wright. 2019b. Time series data mining with an application to the measurement of underwriting cycles. North American Actuarial Journal 23: 469–84. [Google Scholar] [CrossRef]
- Pisarenko, Vladilen F. 1973. The retrieval of harmonics from a covariance function. Geophysical Journal International 33: 347–66. [Google Scholar] [CrossRef]
- Politis, Dimitris N., and Joseph P. Romano. 1994. The stationary bootstrap. Journal of the American Statistical Association 89: 1303–13. [Google Scholar] [CrossRef]
- R Core Team. 2020. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 9 April 2020).
- Sheppard, Kevin. 2009. MFE Toolbox, Version 4.0. Available online: https://www.kevinsheppard.com/code/matlab/mfe-toolbox/ (accessed on 9 April 2020).
- Siegel, Andrew F. 1980. Testing for periodicity in a time series. Journal of the American Statistical Association 75: 345–48. [Google Scholar] [CrossRef]
- Telesca, Luciano, Alessandro Giocoli, Vincenzo Lapenna, and Tony Alfredo Stabile. 2015. Robust identification of periodic behavior in the time dynamics of short seismic series: The case of seismicity induced by pertusillo lake, southern italy. Stochastic Environmental Research and Risk Assessment 29: 1437–46. [Google Scholar] [CrossRef]
- Venezian, Emilio C. 1985. Ratemaking methods and profit cycles in property and liability insurance. Journal of Risk and Insurance 52: 477–500. [Google Scholar] [CrossRef]
- Venezian, Emilio C. 2006. The use of spectral analysis in insurance cycle research. The Journal of Risk Finance 7: 177–88. [Google Scholar] [CrossRef]
- Venezian, Emilio C., and Chao-Chun Leng. 2006. Application of spectral and arima analysis to combined-ratio patterns. The Journal of Risk Finance 7: 189–214. [Google Scholar] [CrossRef]
- Wang, Ning, and Maryna Murdock. 2019. A dynamic model of an insurer: Loss shocks, capacity constraints and underwriting cycles. The Journal of Risk Finance 20: 82–93. [Google Scholar] [CrossRef]
- Wang, Shaun S., John A. Major, Charles H. Pan, and Jessica W. K. Leong. 2011. Us property-casualty: Underwriting cycle modeling and risk benchmarks. Variance 5: 91–114. [Google Scholar]
- Whittle, Peter. 1952. Tests of fit in time series. Biometrika 39: 309–18. [Google Scholar] [CrossRef]
- Winter, Ralph A. 1988. The liability crisis and the dynamics of competitive insurance markets. Yale Journal on Regulation 5: 455. [Google Scholar]
- Winter, Ralph A. 1994. The dynamics of competitive insurance markets. Journal of Financial Intermediation 3: 379–415. [Google Scholar] [CrossRef]
- Yilmaz, A. K. D. İ., Serdar Varlik, and Hakan Berument. 2018. Cycle duration in production with periodicity—Evidence from Turkey. International Econometric Review 10: 24–32. [Google Scholar]
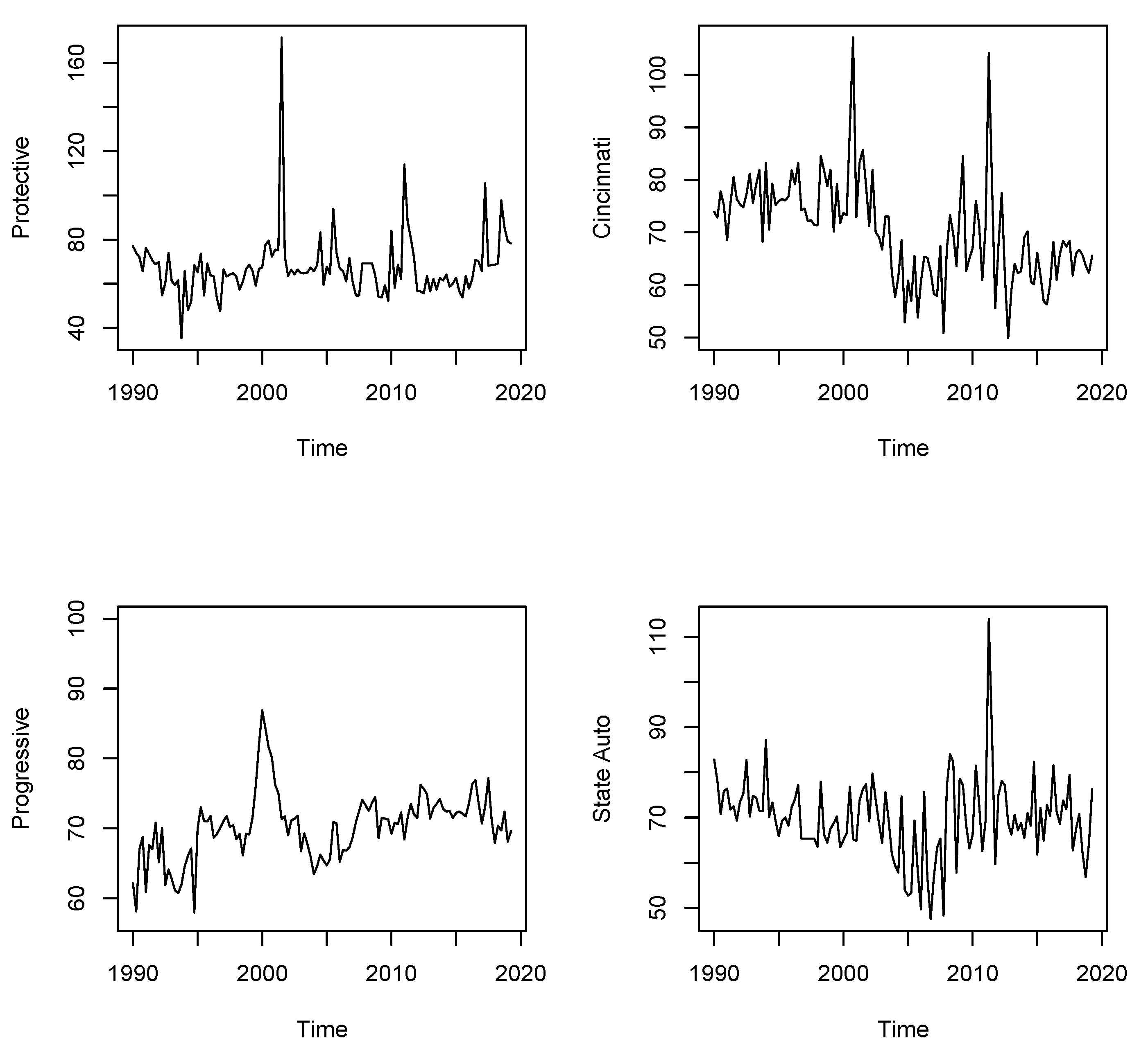

| Quarterly Loss Ratios on US Property and Casualty Companies | ||||
|---|---|---|---|---|
| Company | No. Obs. | No Obs. | Cat 1 | Cat 2 |
| Pre-Interv. | ||||
| Protective | 118 | 46 | 2001/Q3 | 2011/Q1 |
| Cincinnati | 118 | 43 | 2000/Q4 | 2011/Q2 |
| Progressive | 118 | 40 | 2000/Q1 | |
| State Auto | 118 | 85 | 2011/Q2 | |
| SARIMA Parameters | |||||
|---|---|---|---|---|---|
| Intercept | |||||
| PROT. | ** | ** | ** | ||
| (0.0248) | (0.0889) | (0.0902) | |||
| CINC. | ** | ||||
| (0.1050) | |||||
| PROGR. | ** | ** | * | ||
| (0.0178) | (0.0911) | (0.0934) | |||
| Intervention Parameters | |||||
| PROT. | ** | ** | ** | ||
| (0.1223) | (0.1239) | (0.1325) | |||
| CINC. | * | * | ** | ||
| (0.1005) | (0.0725) | (0.0751) | |||
| PROGR. | ** | ** | |||
| (0.0423) | (0.1559) | ||||
| Root Mean Squared Errors of Forecasts of Underwriting Ratios | ||||
|---|---|---|---|---|
| Model | h = 1 Quarter | h = 2 Quarters | h = 4 Quarters | h = 8 Quarters |
| PROTECTIVE | ||||
| AR[2] | 16.44 | 17.03 | 17.15 | 12.02 |
| AR[2]-D | 15.98 | 16.44 | 16.94 | 12.09 |
| ARIMA[2,1,0] | 17.65 | 18.41 | 19.00 | 16.90 |
| ARIMA[2,1,0]-D | 16.07 | 16.70 | 16.69 | 14.35 |
| SARIMA[0,0,0]x[2,1,0] | 18.65 | 18.86 | 18.95 | 15.40 |
| SARIMA[0,0,0]x[2,1,0]-D | 17.43 | 17.58 | 17.61 | 13.92 |
| SARIMA[0,0,0]x[0,1,1] | 18.19 | 18.41 | 18.46 | 13.71 |
| SARIMA[0,0,0]x[0,1,1]-D | 17.45 | 17.56 | 17.54 | 12.57 |
| AR[2]-X | 15.94 | 16.45 | 16.97 | 12.14 |
| CINCINNATI | ||||
| AR[2] | 9.67 | 10.44 | 10.22 | 10.90 |
| AR[2]-D | 9.50 | 9.90 | 9.69 | 10.36 |
| ARIMA[2,1,0] | 9.27 | 9.97 | 9.88 | 10.58 |
| ARIMA[2,1,0]-D | 9.02 | 9.45 | 9.08 | 9.17 |
| SARIMA[0,0,0]x[0,1,1] | 9.15 | 9.33 | 9.59 | 10.41 |
| SARIMA[0,0,0]x[0,1,1]-D | 8.57 | 8.66 | 8.93 | 9.39 |
| SARIMA[0,0,0]x[1,1,1] | 9.31 | 9.82 | 10.11 | 11.00 |
| SARIMA[0,0,0]x[1,1,1]-D | 8.76 | 8.85 | 9.18 | 9.30 |
| SARIMA[0,0,0]x[0,1,1]-X | 8.50 | 8.55 | 8.82 | 9.30 |
| PROGRESSIVE | ||||
| AR[2] | 2.51 | 2.84 | 2.97 | 3.45 |
| AR[2]-D | 2.70 | 2.98 | 3.02 | 3.39 |
| ARIMA[2,1,0] | 2.58 | 3.10 | 3.71 | 4.92 |
| ARIMA[2,1,0]-D | 2.64 | 3.04 | 3.53 | 4.63 |
| SARIMA[1,0,0]x[0,1,0] | 3.04 | 3.61 | 3.86 | 5.22 |
| SARIMA[1,0,0]x[0,1,0]-D | 3.19 | 3.47 | 3.58 | 4.70 |
| SARIMA[0,0,1]x[0,1,0] | 3.37 | 3.97 | 3.68 | 5.02 |
| SARIMA[0,0,1]x[0,1,0]-D | 3.51 | 3.78 | 3.50 | 4.57 |
| AR[2]-X | 2.75 | 3.06 | 3.10 | 3.52 |
| STATE AUTO | ||||
| AR[2] | 10.20 | 10.33 | 10.10 | 10.75 |
| AR[2]-D | 10.37 | 10.28 | 10.12 | 10.76 |
| ARIMA[2,1,0] | 10.53 | 10.62 | 10.26 | 11.90 |
| ARIMA[2,1,0]-D | 10.67 | 10.23 | 10.15 | 11.51 |
| SARIMA[0,0,0]x[1,1,0] | 10.03 | 10.09 | 10.15 | 12.38 |
| SARIMA[0,0,0]x[1,1,0]-D | 9.38 | 9.42 | 9.48 | 11.56 |
| SARIMA[0,0,0]x[0,1,1] | 9.70 | 9.73 | 9.84 | 11.65 |
| SARIMA[0,0,0]x[0,1,1]-D | 9.26 | 9.27 | 9.37 | 11.05 |
| SARIMA[0,0,0]x[1,1,1] | 9.22 | 9.28 | 9.42 | 10.95 |
| SARIMA[0,0,0]x[1,1,1]-D | 9.00 | 9.05 | 9.17 | 10.70 |
| Mean Absolute Errors of Forecasts of Underwriting Ratios | ||||
|---|---|---|---|---|
| Model | h = 1 Quarter | h = 2 Quarters | h = 4 Quarters | h = 8 Quarters |
| PROTECTIVE | ||||
| AR[2] | 8.65 | 9.21 | 9.66 | 8.10 |
| AR[2]-D | 8.18 | 8.69 | 9.18 | 7.94 |
| ARIMA[2,1,0] | 10.15 | 10.94 | 12.04 | 11.95 |
| ARIMA[2,1,0]-D | 8.93 | 9.77 | 10.29 | 10.19 |
| SARIMA[0,0,0]x[2,1,0] | 11.64 | 11.87 | 11.73 | 10.78 |
| SARIMA[0,0,0]x[2,1,0]-D | 10.32 | 10.48 | 10.33 | 9.81 |
| SARIMA[0,0,0]x[0,1,1] | 10.45 | 10.73 | 10.45 | 9.04 |
| SARIMA[0,0,0]x[0,1,1]-D | 9.83 | 9.93 | 9.70 | 8.34 |
| AR[2]-X | 8.04 | 8.68 | 9.15 | 7.92 |
| CINCINNATI | ||||
| AR[2] | 6.91 | 7.79 | 7.89 | 8.98 |
| AR[2]-D | 6.85 | 7.38 | 7.41 | 8.25 |
| ARIMA[2,1,0] | 6.63 | 7.27 | 7.12 | 8.02 |
| ARIMA[2,1,0]-D | 6.67 | 7.01 | 6.61 | 7.12 |
| SARIMA[0,0,0]x[0,1,1] | 6.83 | 7.05 | 7.26 | 8.05 |
| SARIMA[0,0,0]x[0,1,1]-D | 6.41 | 6.53 | 6.75 | 7.35 |
| SARIMA[0,0,0]x[1,1,1] | 7.16 | 7.56 | 7.82 | 8.56 |
| SARIMA[0,0,0]x[1,1,1]-D | 6.65 | 6.77 | 7.06 | 7.34 |
| SARIMA[0,0,0]x[0,1,1]-X | 6.28 | 6.38 | 6.57 | 7.23 |
| PROGRESSIVE | ||||
| AR[2] | 1.84 | 2.18 | 2.39 | 2.91 |
| AR[2]-D | 1.94 | 2.28 | 2.41 | 2.85 |
| ARIMA[2,1,0] | 1.91 | 2.45 | 2.75 | 3.83 |
| ARIMA[2,1,0]-D | 1.95 | 2.41 | 2.65 | 3.73 |
| SARIMA[1,0,0]x[0,1,0] | 2.24 | 2.69 | 2.85 | 3.94 |
| SARIMA[1,0,0]x[0,1,0]-D | 2.29 | 2.67 | 2.70 | 3.74 |
| SARIMA[0,0,1]x[0,1,0] | 2.44 | 2.91 | 2.74 | 3.85 |
| SARIMA[0,0,1]x[0,1,0]-D | 2.43 | 2.78 | 2.65 | 3.64 |
| AR[2]-X | 2.03 | 2.36 | 2.53 | 2.94 |
| STATE AUTO | ||||
| AR[2] | 7.64 | 7.62 | 7.50 | 7.89 |
| AR[2]-D | 7.78 | 7.58 | 7.51 | 7.91 |
| ARIMA[2,1,0] | 8.08 | 8.14 | 7.78 | 9.34 |
| ARIMA[2,1,0]-D | 8.09 | 7.74 | 7.56 | 8.92 |
| SARIMA[0,0,0]x[1,1,0] | 7.74 | 7.84 | 7.84 | 9.78 |
| SARIMA[0,0,0]x1,1,0]-D | 7.31 | 7.39 | 7.36 | 9.30 |
| SARIMA[0,0,0]x[0,1,1] | 7.49 | 7.58 | 7.65 | 9.14 |
| SARIMA[0,0,0]x[0,1,1]-D | 7.08 | 7.13 | 7.19 | 8.69 |
| SARIMA[0,0,0]x[1,1,1] | 6.82 | 6.92 | 7.04 | 8.31 |
| SARIMA[0,0,0]x[1,1,1]-D | 6.64 | 6.72 | 6.80 | 8.04 |
| MCS p-Values Based on the MSE as a Loss Function | ||||
|---|---|---|---|---|
| Model | h = 1 Quarter | h = 2 Quarters | h = 4 Quarters | h = 8 Quarters |
| PROTECTIVE | ||||
| AR[2] | 0.78 | 0.79 | 0.60 | 1.00 |
| AR[2]-D | 0.78 | 1.00 | 0.80 | 0.58 |
| ARIMA[2,1,0] | 0.20 | 0.01 | 0.015 | 0.00 |
| ARIMA[2,1,0]-D | 0.78 | 0.83 | 1.00 | 0.04 |
| SARIMA[0,0,0]x[2,1,0] | 0.20 | 0.26 | 0.015 | 0.05 |
| SARIMA[0,0,0]x[2,1,0]-D | 0.20 | 0.26 | 0.20 | 0.05 |
| SARIMA[0,0,0]x[0,1,1] | 0.01 | 0.01 | 0.02 | 0.00 |
| SARIMA[0,0,0]x[0,1,1]-D | 0.02 | 0.01 | 0.02 | 0.00 |
| AR[2]-X | 1.00 | 0.83 | 0.60 | 0.58 |
| CINCINNATI | ||||
| AR[2] | 0.06 | 0.03 | 0.00 | 0.00 |
| AR[2]-D | 0.07 | 0.03 | 0.08 | 0.25 |
| ARIMA[2,1,0] | 0.11 | 0.09 | 0.08 | 0.25 |
| ARIMA[2,1,0]-D | 0.11 | 0.09 | 0.34 | 1.00 |
| SARIMA[0,0,0]x[0,1,1] | 0.11 | 0.09 | 0.08 | 0.16 |
| SARIMA[0,0,0]x[0,1,1]-D | 0.30 | 0.12 | 0.34 | 0.83 |
| SARIMA[0,0,0]x[1,1,1] | 0.07 | 0.03 | 0.00 | 0.00 |
| SARIMA[0,0,0]x[1,1,1]-D | 0.11 | 0.09 | 0.08 | 1.00 |
| SARIMA[0,0,0]x[0,1,1]-X | 1.00. | 1.00 | 1.00 | 0.96 |
| PROGRESSIVE | ||||
| AR[2] | 1.00 | 1.00 | 1.00 | 0.70 |
| AR[2]-D | 0.40 | 0.52 | 0.41 | 1.00 |
| ARIMA[2,1,0] | 0.40 | 0.52 | 0.41 | 0.54 |
| ARIMA[2,1,0]-D | 0.40 | 0.52 | 0.41 | 0.54 |
| SARIMA[0,0,1]x[0,1,0] | 0.33 | 0.27 | 0.41 | 0.54 |
| SARIMA[0,0,1]x[0,1,0]-D | 0.33 | 0.23 | 0.41 | 0.54 |
| SARIMA[1,0,0]x[0,1,0] | 0.33 | 0.52 | 0.11 | 0.37 |
| SARIMA[1,0,0]x[0,1,0]-D | 0.33 | 0.52 | 0.11 | 0.29 |
| AR[2]-X | 0.33 | 0.52 | 0.41 | 0.70 |
| STATE AUTO | ||||
| AR[2] | 0.16 | 0.20 | 0.34 | 0.92 |
| AR[2]-D | 0.16 | 0.22 | 0.34 | 0.78 |
| ARIMA[2,1,0] | 0.09 | 0.20 | 0.27 | 0.01 |
| ARIMA[2,1,0]-D | 0.16 | 0.20 | 0.34 | 0.16 |
| SARIMA[0,0,0]x[0,1,1] | 0.16 | 0.22 | 0.34 | 0.33 |
| SARIMA[0,0,0]x[0,1,1]-D | 0.19 | 0.27 | 0.45 | 0.55 |
| SARIMA[0,0,0]x[1,1,0] | 0.16 | 0.20 | 0.27 | 0.06 |
| SARIMA[0,0,0]x[1,1,0]-D | 0.19 | 0.22 | 0.45 | 0.10 |
| SARIMA[0,0,0]x[1,1,1] | 0.52 | 0.27 | 0.45 | 0.66 |
| SARIMA[0,0,0]x[1,1,1]-D | 1.00 | 1.00 | 1.00 | 1.00 |
| MCS p-Values Based on the MAE as a Loss Function | ||||
|---|---|---|---|---|
| Model | h = 1 Quarter | h = 2 Quarters | h = 4 Quarters | h = 8 Quarters |
| PROTECTIVE | ||||
| AR[2] | 0.49 | 0.61 | 0.21 | 0.41 |
| AR[2]-D | 0.49 | 0.88 | 0.67 | 0.85 |
| ARIMA[2,1,0] | 0.01 | 0.03 | 0.00 | 0.00 |
| ARIMA[2,1,0]-D | 0.06 | 0.04 | 0.05 | 0.00 |
| SARIMA[0,0,0]x[2,1,0] | 0.01 | 0.03 | 0.05 | 0.12 |
| SARIMA[0,0,0]x[2,1,0]-D | 0.01 | 0.03 | 0.05 | 0.12 |
| SARIMA[0,0,0]x[0,1,1] | 0.00 | 0.00 | 0.00 | 0.00 |
| SARIMA[0,0,0]x[0,1,1]-D | 0.00 | 0.00 | 0.00 | 0.00 |
| AR[2]-X | 1.00 | 1.00 | 1.00 | 1.00 |
| CINCINNATI | ||||
| AR[2] | 0.00 | 0.00 | 0.00 | 0.00 |
| AR[2]-D | 0.00 | 0.00 | 0.00 | 0.20 |
| ARIMA[2,1,0] | 0.28 | 0.00 | 0.14 | 0.20 |
| ARIMA[2,1,0]-D | 0.28 | 0.00 | 0.97 | 1.00 |
| SARIMA[0,0,0]x[0,1,1] | 0.00 | 0.00 | 0.00 | 0.03 |
| SARIMA[0,0,0]x[0,1,1]-D | 0.28 | 0.06 | 0.14 | 0.76 |
| SARIMA[0,0,0]x[1,1,1] | 0.00 | 0.00 | 0.00 | 0.00 |
| SARIMA[0,0,0]x[1,1,1]-D | 0.00 | 0.00 | 0.00 | 0.76 |
| SARIMA[0,0,0]x[0,1,1]-X | 1.00 | 1.00 | 1.00 | 0.82 |
| PROGRESSIVE | ||||
| AR[2] | 1.00 | 1.00 | 1.00 | 0.67 |
| AR[2]-D | 0.37 | 0.42 | 0.55 | 1.00 |
| ARIMA[2,1,0] | 0.54 | 0.42 | 0.55 | 0.63 |
| ARIMA[2,1,0]-D | 0.53 | 0.42 | 0.55 | 0.63 |
| SARIMA[0,0,1]x[0,1,0] | 0.09 | 0.39 | 0.55 | 0.63 |
| SARIMA[0,0,1]x[0,1,0]-D | 0.09 | 0.39 | 0.55 | 0.63 |
| SARIMA[1,0,0]x[0,1,0] | 0.09 | 0.42 | 0.07 | 0.47 |
| SARIMA[1,0,0]x[0,1,0]-D | 0.09 | 0.42 | 0.49 | 0.47 |
| AR[2]-X | 0.09 | 0.42 | 0.55 | 0.67 |
| STATE AUTO | ||||
| AR[2] | 0.04 | 0.06 | 0.34 | 1.00 |
| AR[2]-D | 0.04 | 0.06 | 0.34 | 0.67 |
| ARIMA[2,1,0] | 0.00 | 0.05 | 0.24 | 0.00 |
| ARIMA[2,1,0]-D | 0.01 | 0.06 | 0.34 | 0.06 |
| SARIMA[0,0,0]x[0,1,1] | 0.04 | 0.06 | 0.34 | 0.10 |
| SARIMA[0,0,0]x[0,1,1]-D | 0.10 | 0.16 | 0.34 | 0.10 |
| SARIMA[0,0,0]x[1,1,0] | 0.03 | 0.05 | 0.19 | 0.00 |
| SARIMA[0,0,0]x[1,1,0]-D | 0.04 | 0.06 | 0.34 | 0.00 |
| SARIMA[0,0,0]x[1,1,1] | 0.48 | 0.44 | 0.34 | 0.55 |
| SARIMA[0,0,0]x[1,1,1]-D | 1.00 | 1.00 | 1.00 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmann, A.; Sattarhoff, C. Underwriting Cycles in Property-Casualty Insurance: The Impact of Catastrophic Events. Risks 2023, 11, 75. https://doi.org/10.3390/risks11040075
Hofmann A, Sattarhoff C. Underwriting Cycles in Property-Casualty Insurance: The Impact of Catastrophic Events. Risks. 2023; 11(4):75. https://doi.org/10.3390/risks11040075
Chicago/Turabian StyleHofmann, Annette, and Cristina Sattarhoff. 2023. "Underwriting Cycles in Property-Casualty Insurance: The Impact of Catastrophic Events" Risks 11, no. 4: 75. https://doi.org/10.3390/risks11040075
APA StyleHofmann, A., & Sattarhoff, C. (2023). Underwriting Cycles in Property-Casualty Insurance: The Impact of Catastrophic Events. Risks, 11(4), 75. https://doi.org/10.3390/risks11040075





