Estimating the Value-at-Risk by Temporal VAE
Abstract
1. Introduction
- The signal identification analysis of the model applied to financial time series where we in particular show that the TempVAE possesses the auto-pruning property;
- A test procedure to demonstrate that the TempVAE identifies the correct number of latent factors to adequately model the data;
- The demonstration that our newly developed TempVAE approach for the VaR estimation performs excellently and beats the benchmark models; and
- The detailed documentation of the hyperparameter choice in the appendix (the ablation study).
2. Comparison to Related Work
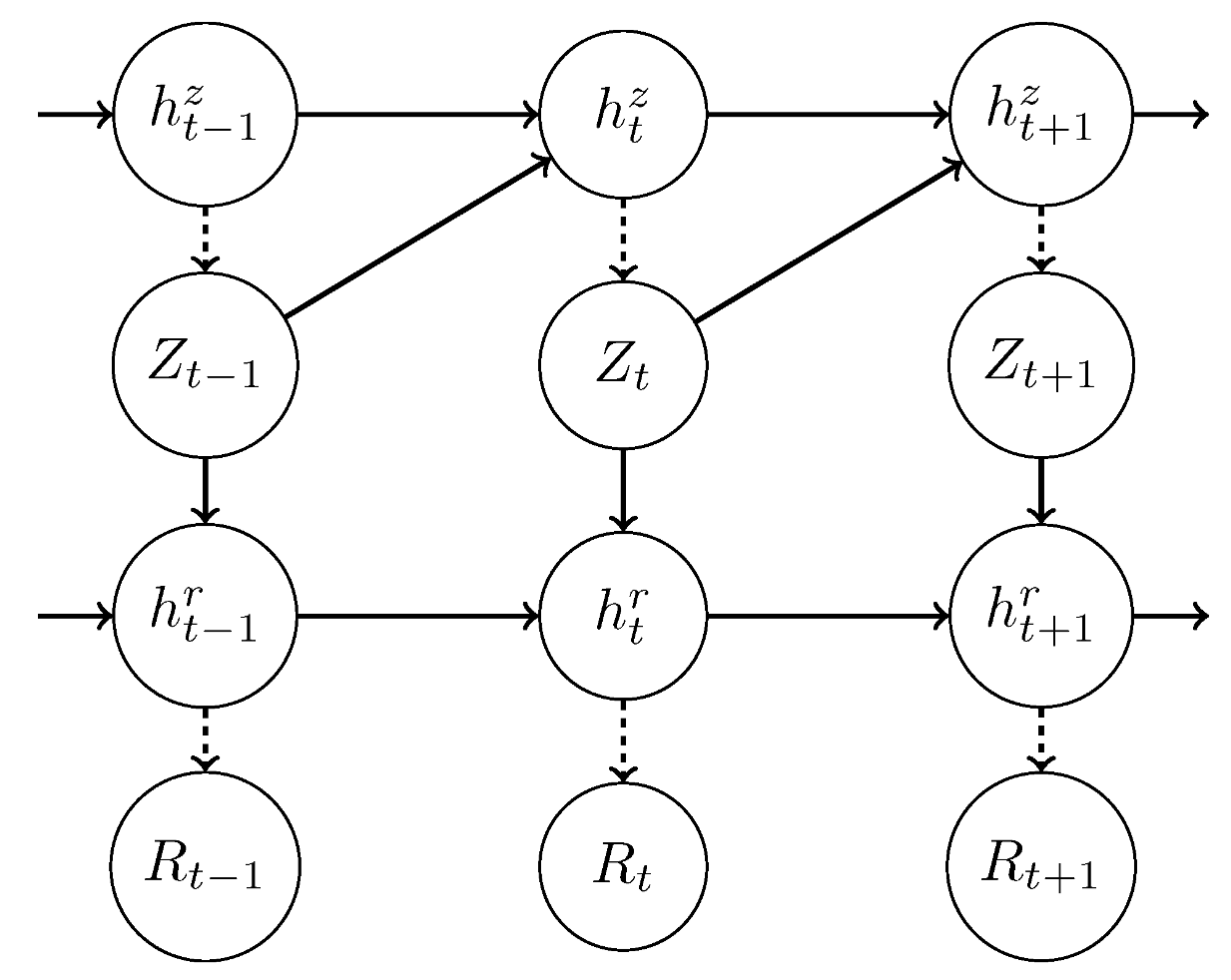
3. The Temporal Variational Autoencoder
The Auto-Pruning Property of VAEs and the Posterior Collapse
4. Implementation, Experiments and VaR-Estimation
4.1. Description of the Used Data Sets
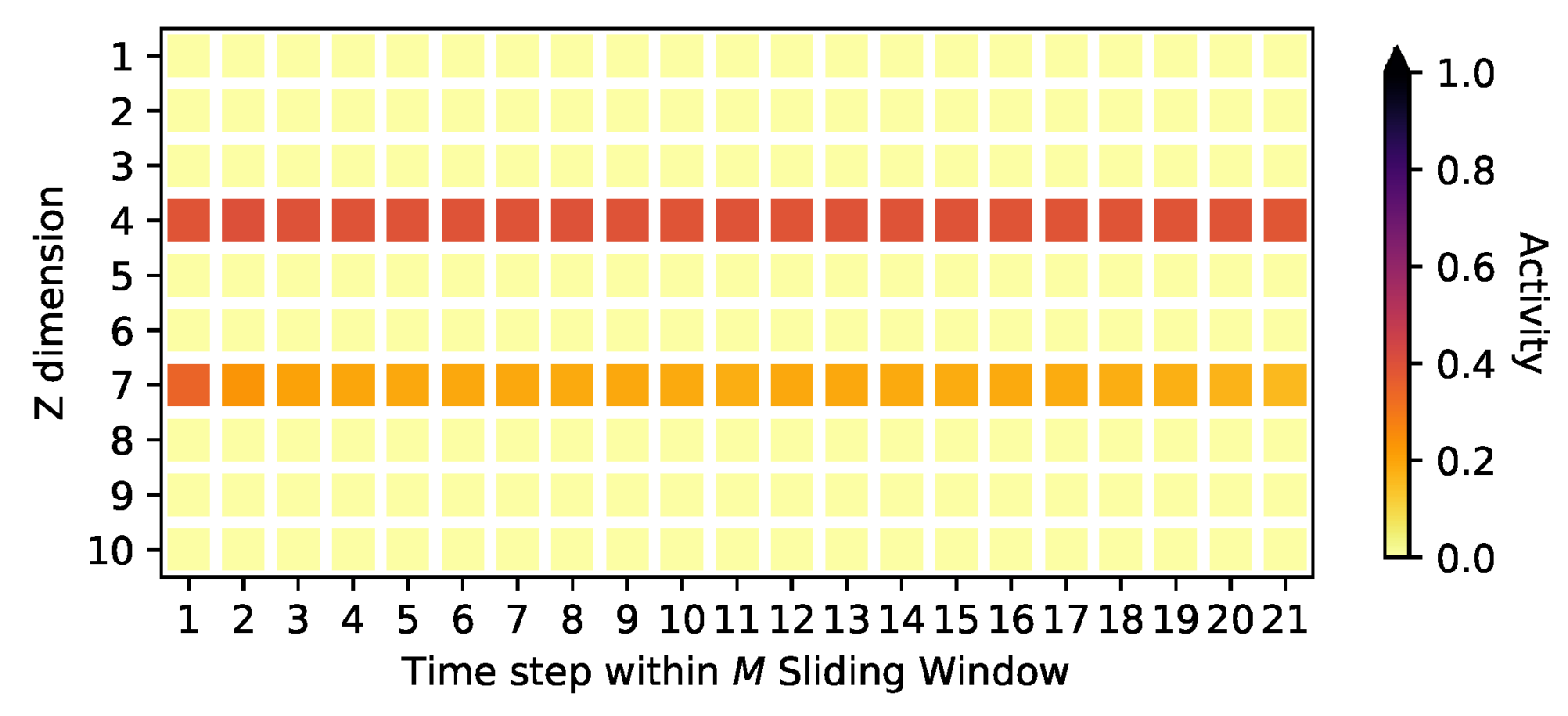
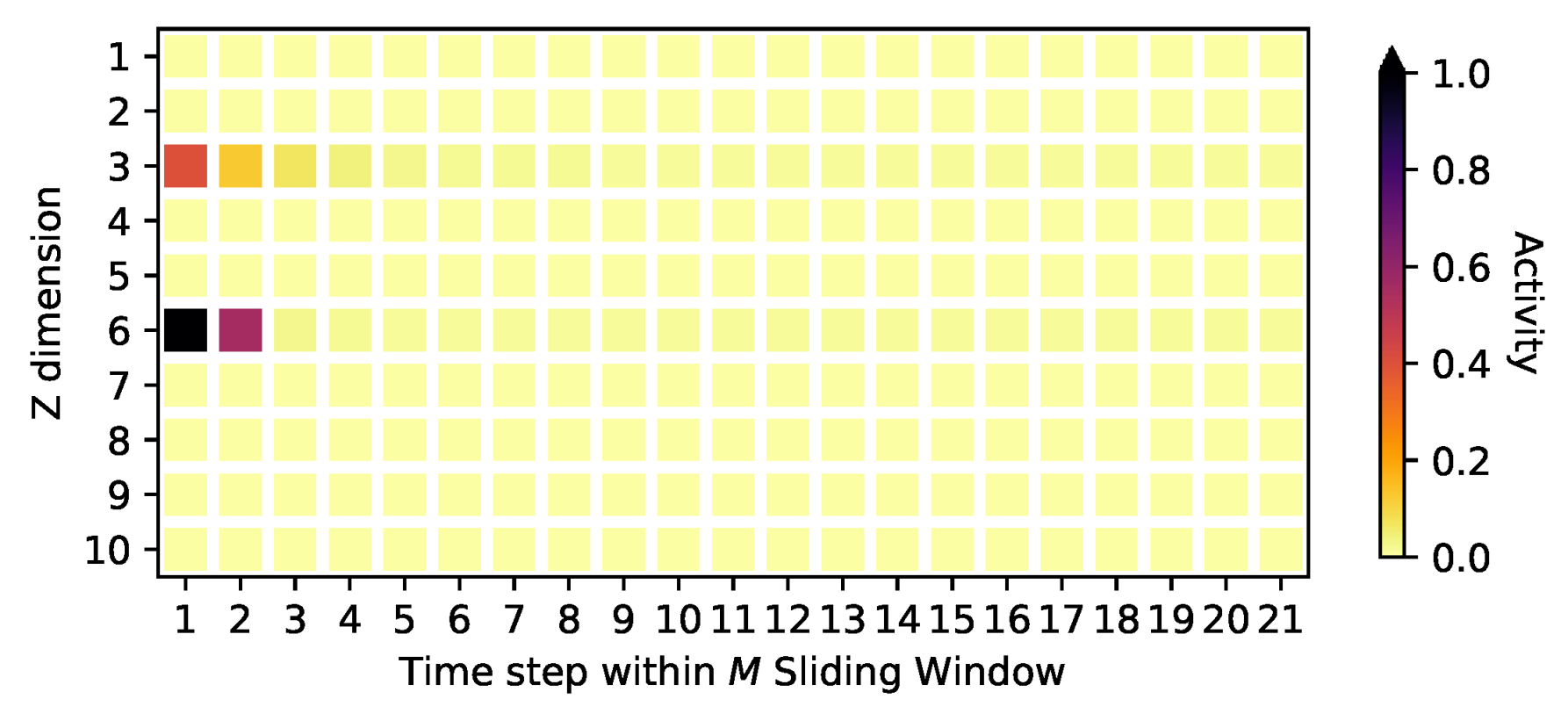
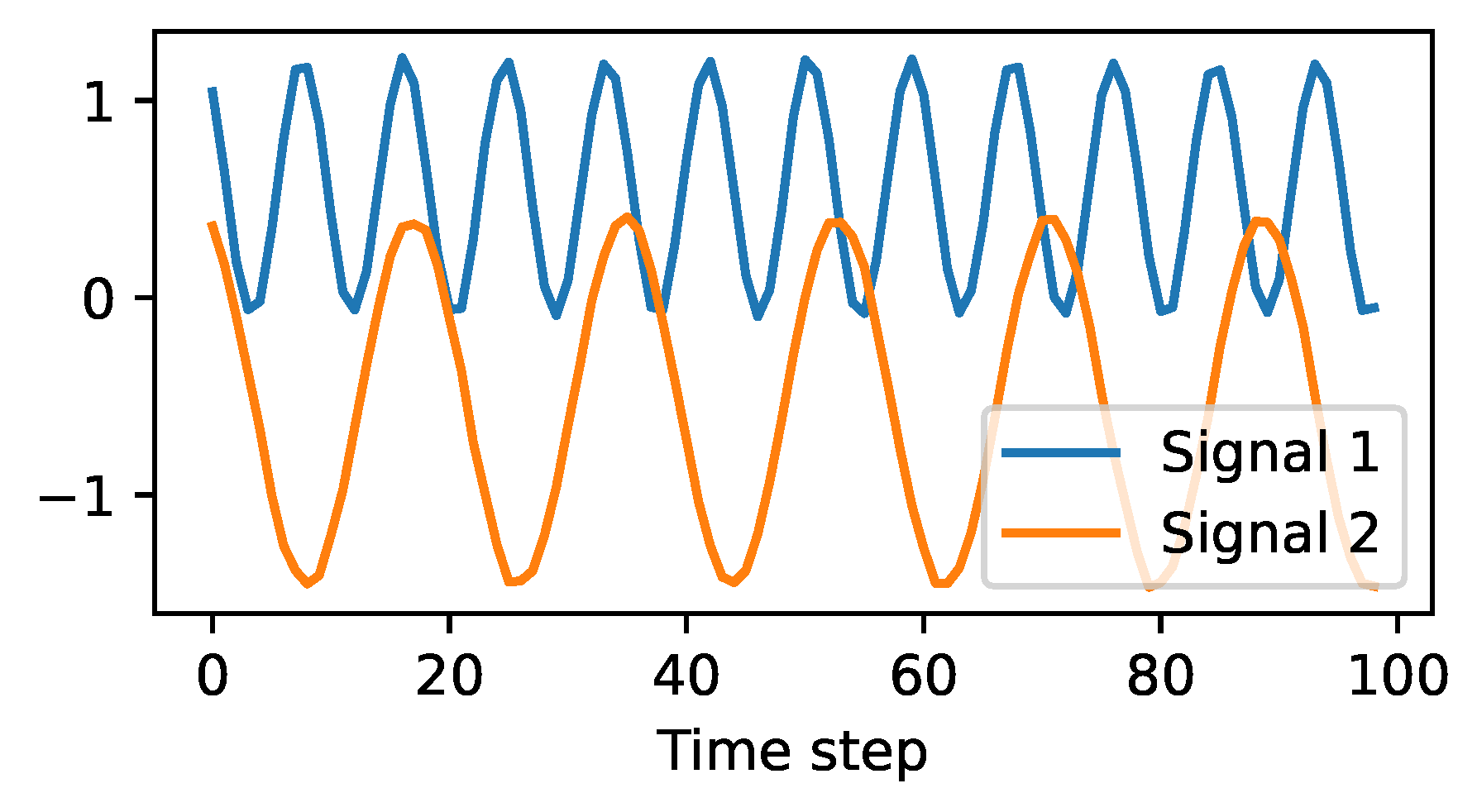
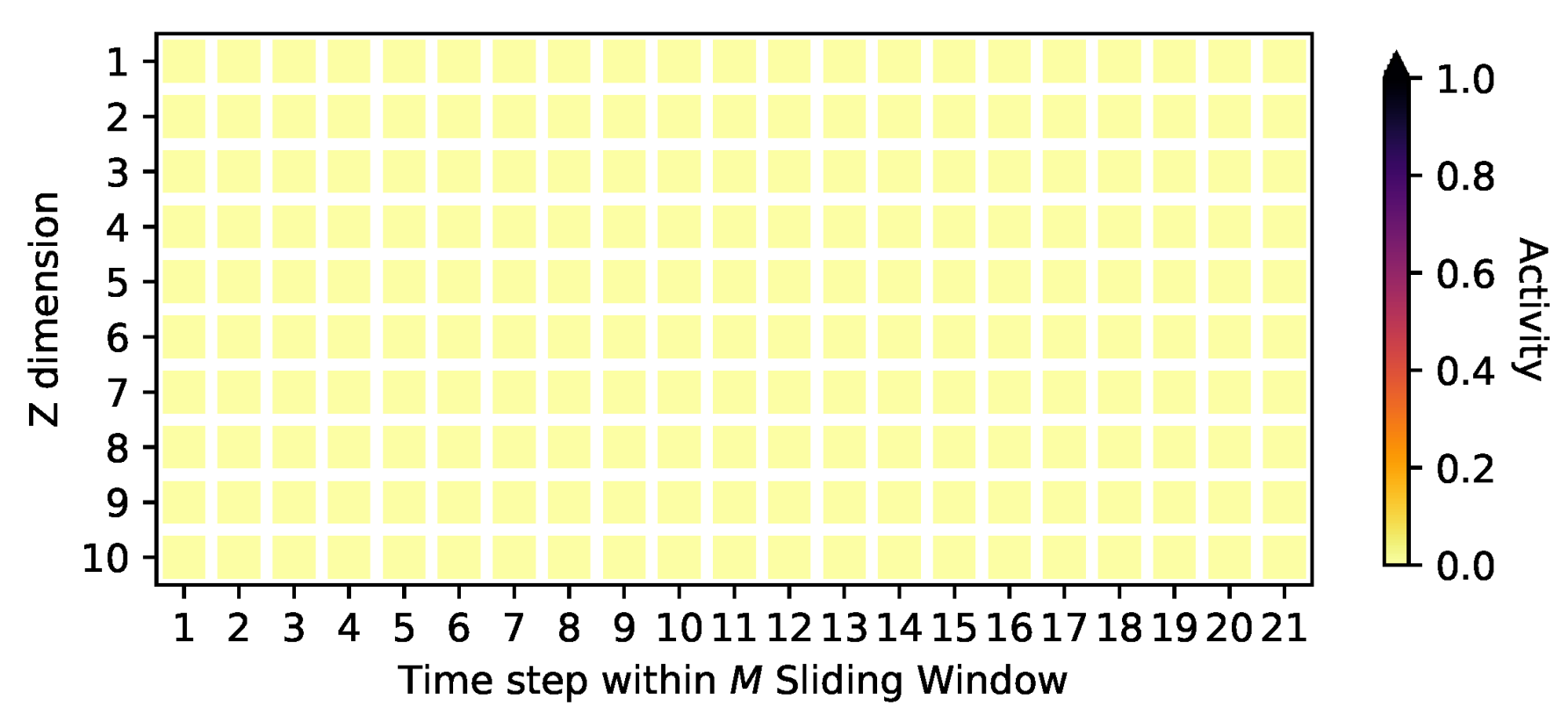
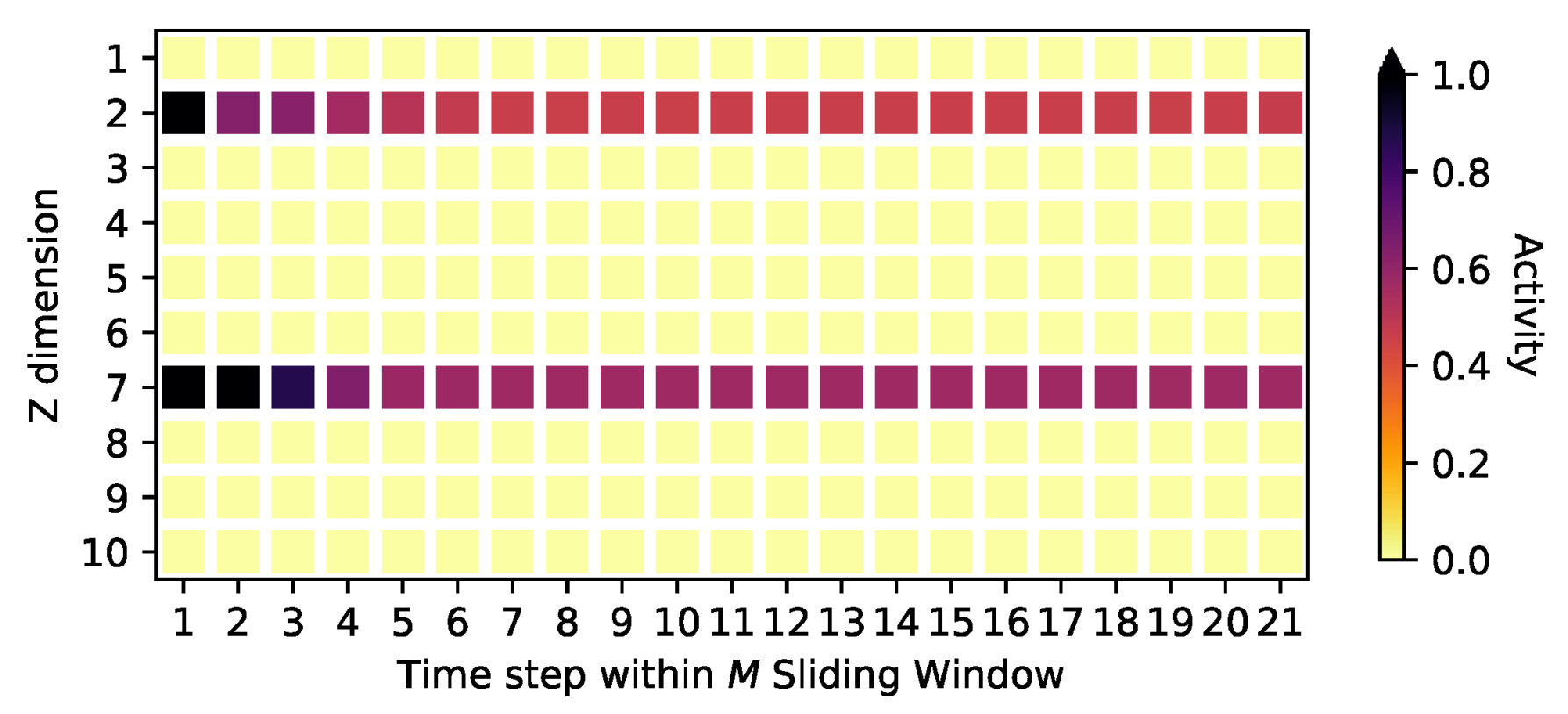
4.2. Signal Identification
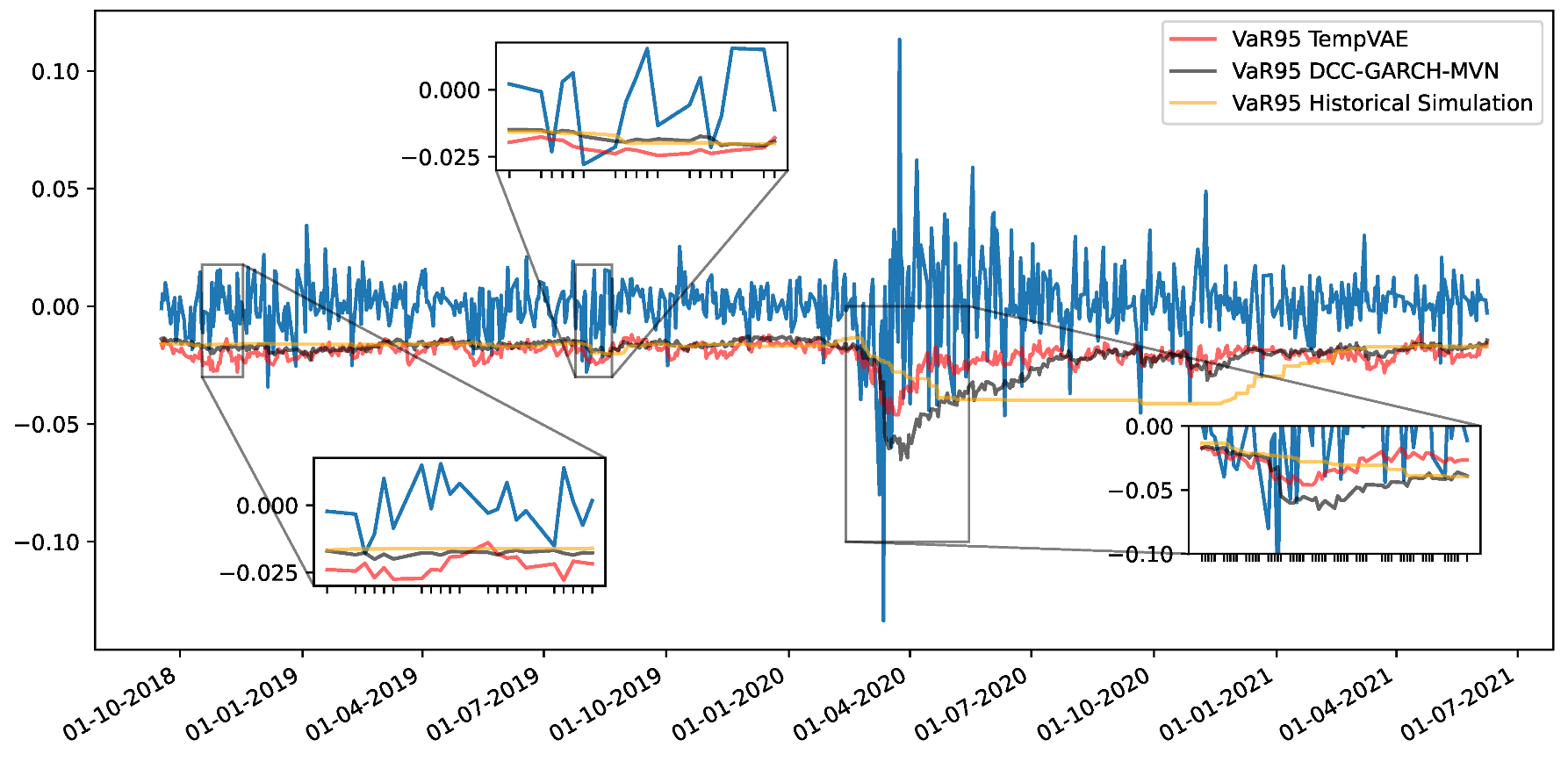
4.3. Fit to Financial Data and Application to Risk Management
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. β-Annealing, Model Implementation and Data Preprocessing
Appendix A.1. β-Annealing
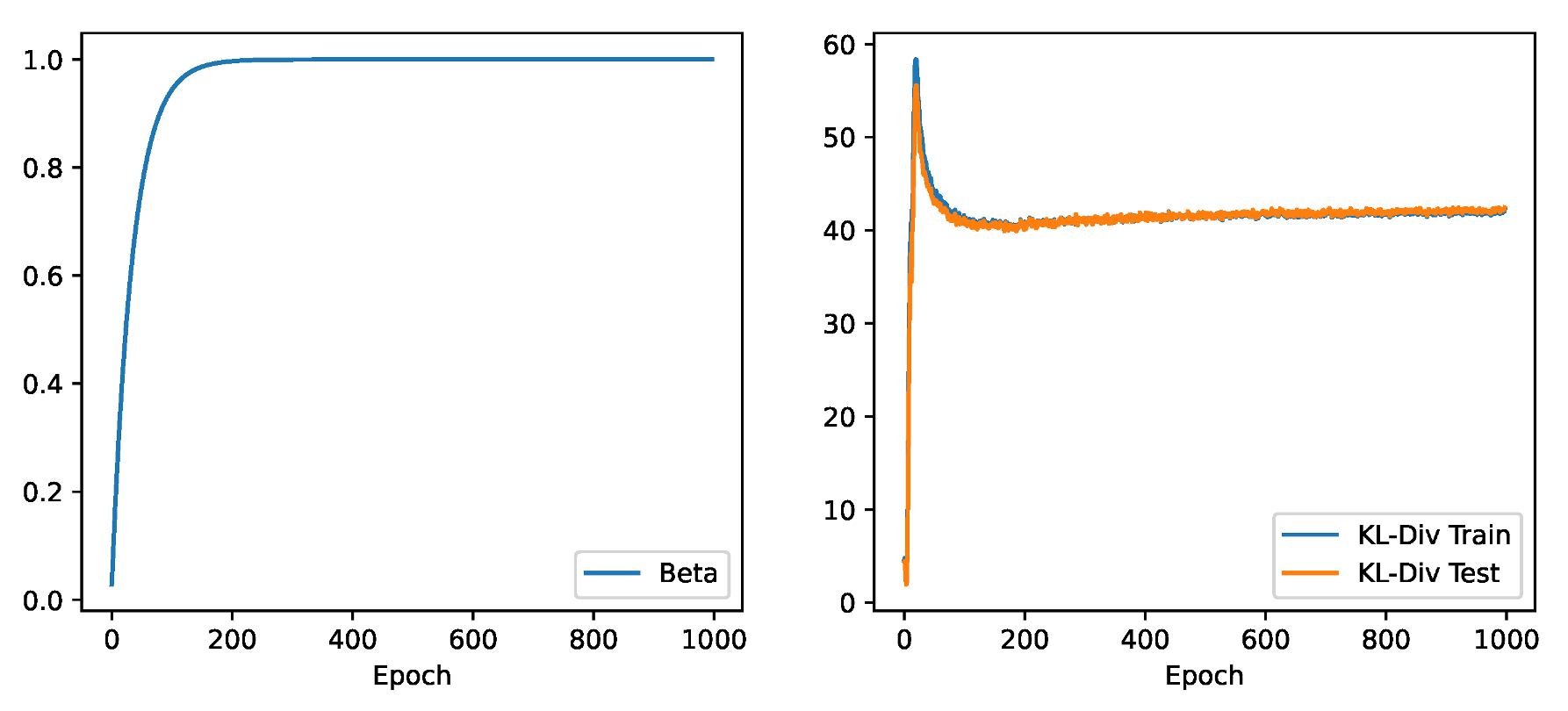
Appendix A.2. Model Implementation
Appendix A.3. Data Preprocessing
- For the DAX data, 5061 observations were split at into 3340 training observations and 1721 test observations.
- For the S&P500 data, 4872 observations were split at into 3215 training observations and 1657 test observations.
- For the noise data, 5050 observations were split at into 3333 training observations and 1717 test observations.
- For each of the oscillating PCA datasets, 9979 observations were split at into 6586 training observations and 3393 test observations.
Appendix B. Ablation Studies
Appendix B.1. Preventing Posterior Collapse with β-Annealing
| DAX | Noise | Osc. PCA 2 | Osc. PCA 5 | Osc. PCA 10 | |
|---|---|---|---|---|---|
| TempVAE | 20% | 0% | 20% | 20% | 20% |
| TempVAE noAnneal | 0% | 0% | 10% | 20% | 10% |
| DAX | Noise | Osc. PCA 2 | Osc. PCA 5 | Osc. PCA 10 | |
|---|---|---|---|---|---|
| TempVAE | 20.29 | 31.48 | −38.51 | −1.40 | 11.07 |
| TempVAE noAnneal | 27.49 | 31.44 | 3.58 | 2.60 | 13.28 |
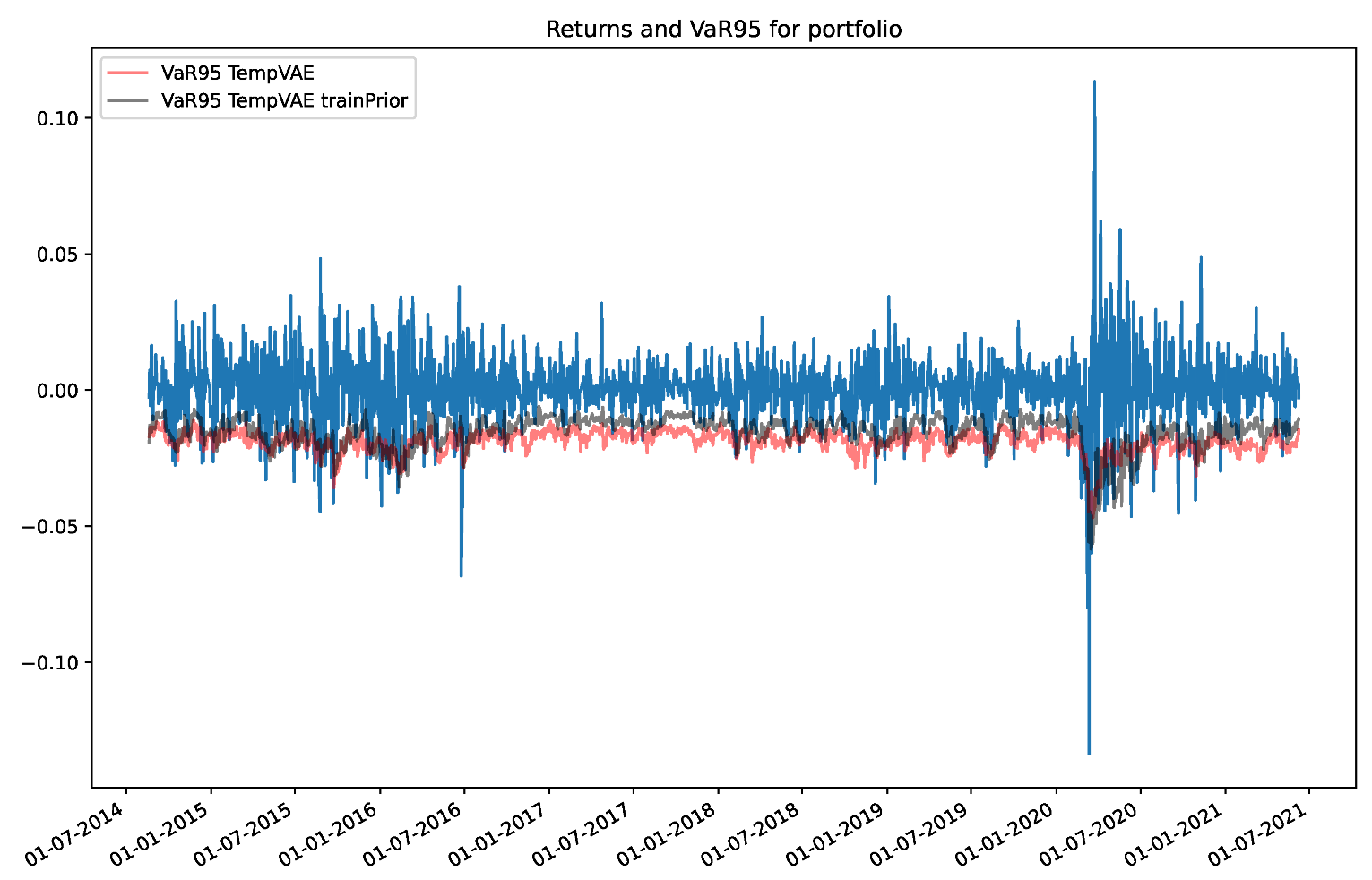
Appendix B.2. Comparison to a Model with Trainable Prior Parameters
| Model | AE95 | AE99 |
|---|---|---|
| TempVAE | 4.8 | 1.3 |
| TempVAE trainPrior | 8.2 | 3.1 |
Appendix B.3. Autoregressive Structure for the Observables Distribution
| DAX | Noise | Osc. PCA 2 | Osc. PCA 5 | Osc. PCA 10 | |
|---|---|---|---|---|---|
| TempVAE | 20.29 | 31.48 | −38.51 | −1.40 | 11.07 |
| TempVAE AR | 22.68 | 32.91 | −34.72 | 25.33 | 69.26 |
Appendix B.4. Using a Diagonal Covariance Matrix
| Model | AE95 | AE99 |
|---|---|---|
| TempVAE | 4.8 | 1.3 |
| TempVAE diag | 5.3 | 1.6 |
Appendix B.5. Setting
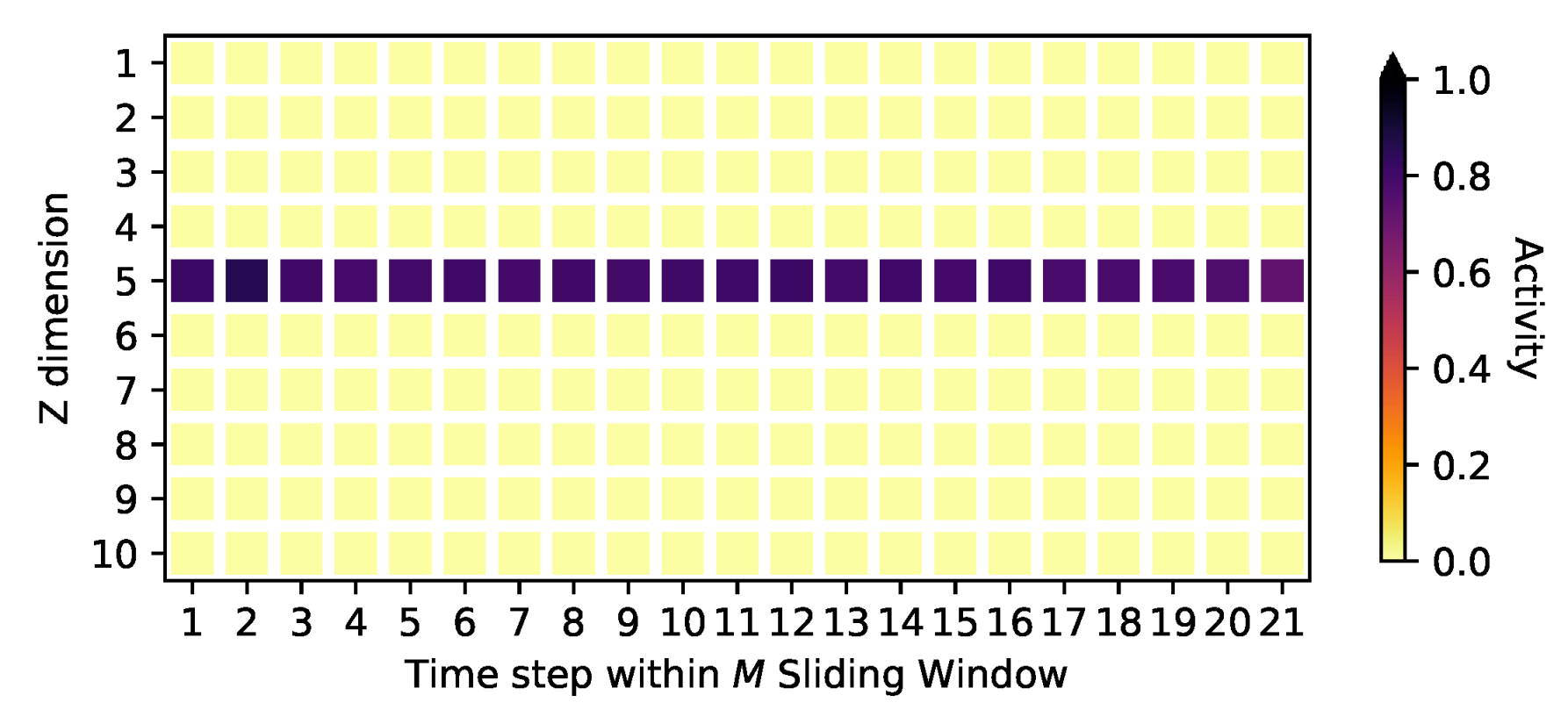
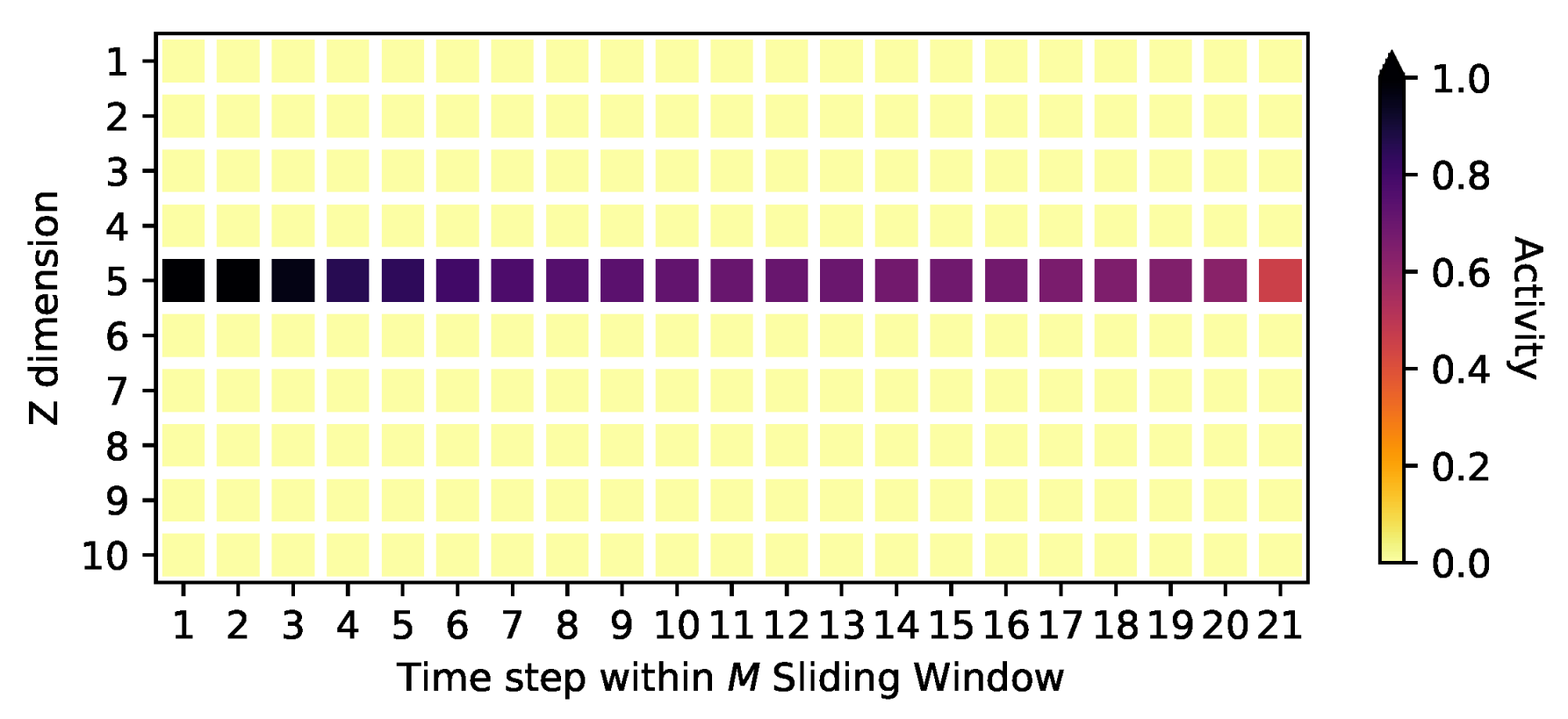
Appendix B.6. Regularization: L2, Dropout and KL-Divergence
- ‘TempVAE’.
- ‘TempVAE det’: The KL-Divergence is switched off and the bottleneck uses only a mean parameter whereas the covariance is set to zero. Therefore, the bottleneck is deterministic and the auto-pruning switched off.
- ‘TempVAE no dropout/L2’: Dropout and L2 regularization are switched off.
- ‘TempVAE no L2’: L2 regularization is switched off.
- ‘TempVAE no dropout’: Dropout is switched off.
- ‘TempVAE det no dropout/L2’: ‘TempVAE det’ and ‘TempVAE no dropout/L2’ combined.
| DAX | Noise | Osc. PCA 2 | Osc. PCA 5 | Osc. PCA 10 | |
|---|---|---|---|---|---|
| TempVAE | 20% | 0% | 20% | 20% | 20% |
| TempVAE det | 0% | 0% | 90% | 81% | 90% |
| TempVAE no dropout/L2 | 20% | 0% | 31% | 76% | 30% |
| TempVAE no L2 | 20% | 6% | 20% | 20% | 30% |
| TempVAE no dropout | 20% | 0% | 31% | 41% | 40% |
| TempVAE det no dropout/L2 | 90% | 90% | 90% | 80% | 90% |
Appendix B.7. Encoder Dependency
| DAX | Noise | Osc. PCA 2 | Osc. PCA 5 | Osc. PCA 10 | |
|---|---|---|---|---|---|
| TempVAE | 20% | 0% | 20% | 20% | 20% |
| TempVAE backwards | 10% | 0% | 10% | 0% | 0% |
Appendix C. GARCH and DCC-GARCH
- GARCH: A GARCH(1,1) model, introduced by Bollerslev (1986).
- DCC-GARCH-MVt: A Dynamic Conditional Correlation GARCH(1,1), with a multivariate distribution assumption for the error term.
Appendix D. Activities on the Oscillating PCA Data Sets
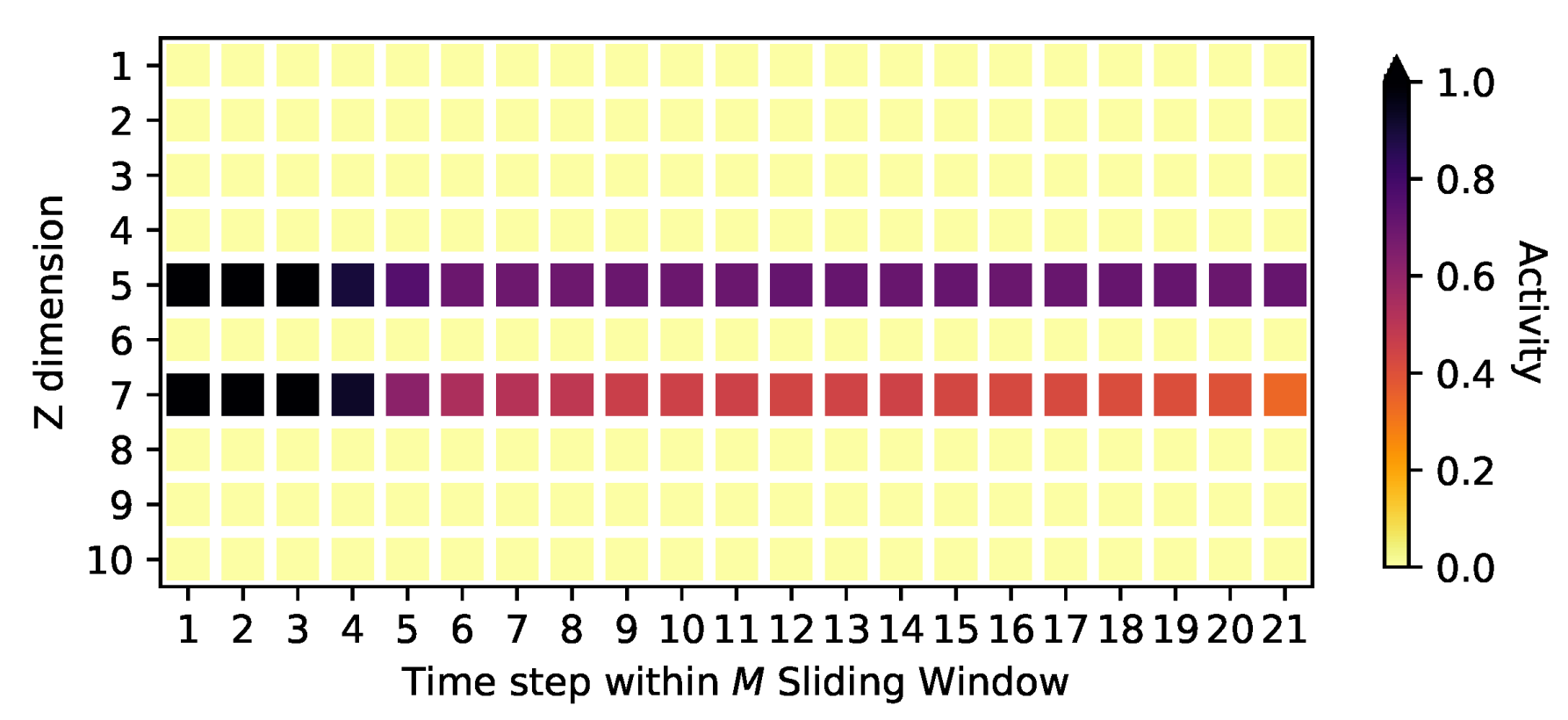
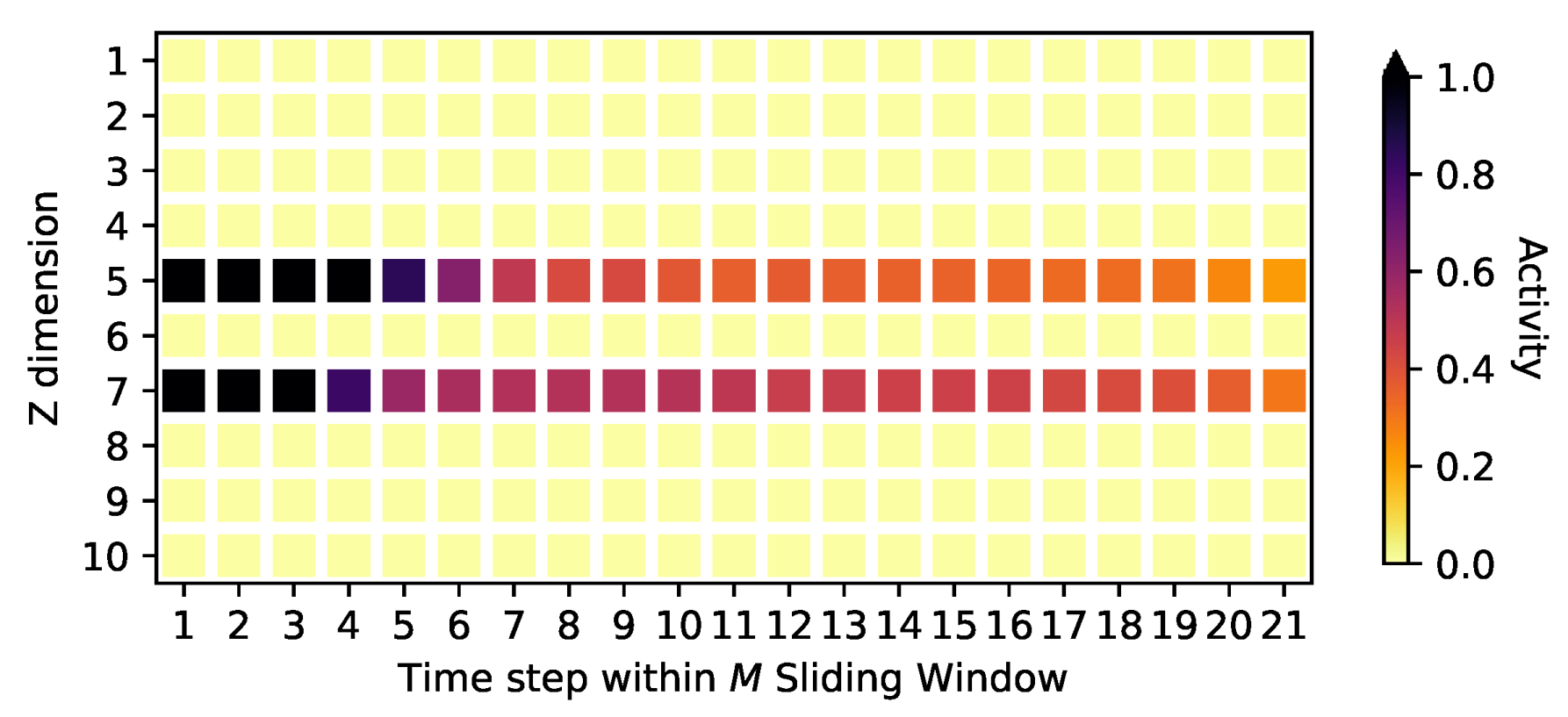
| Score | Osc. PCA 2 | Osc. PCA 5 | Osc. PCA 10 |
|---|---|---|---|
| TempVAE Portfolio NLL | −5.21 | −5.77 | −4.80 |
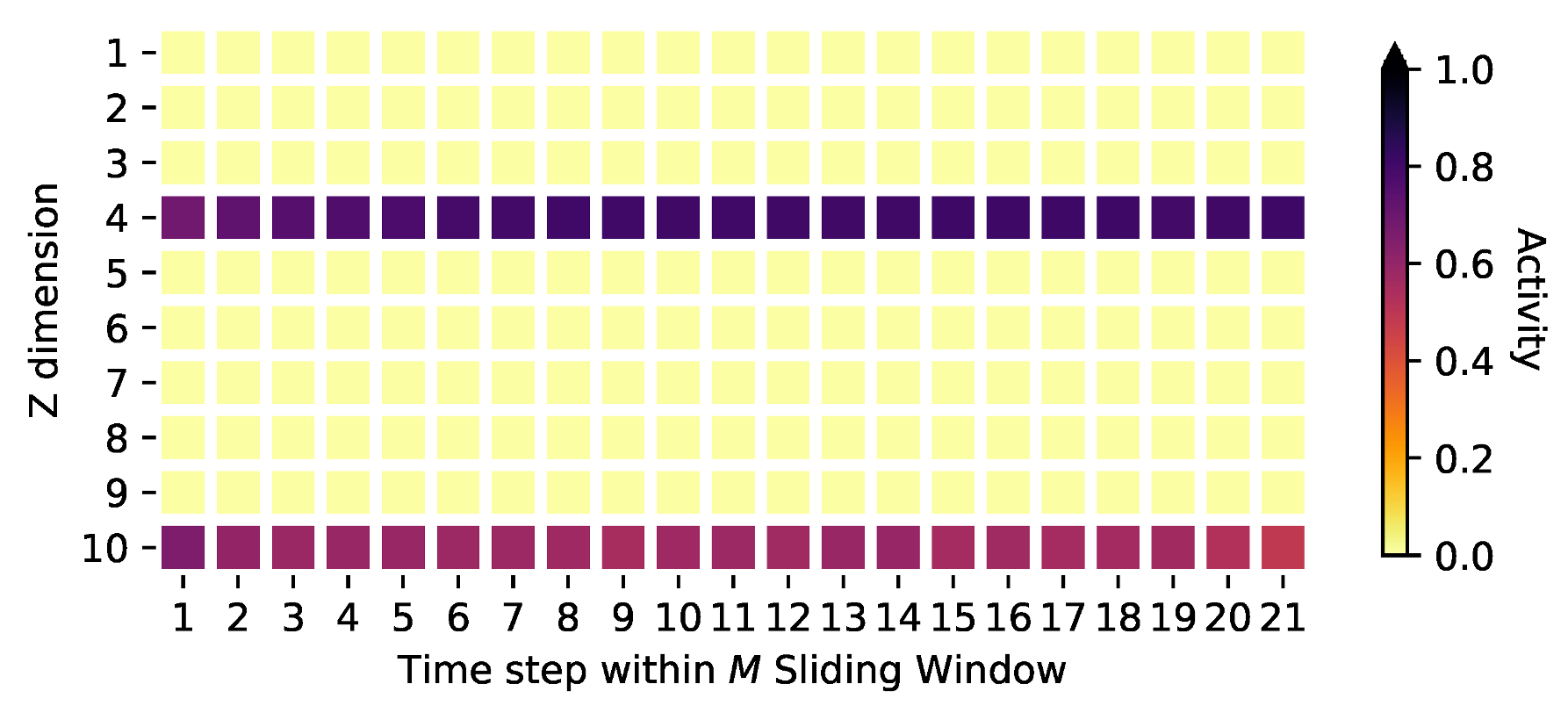
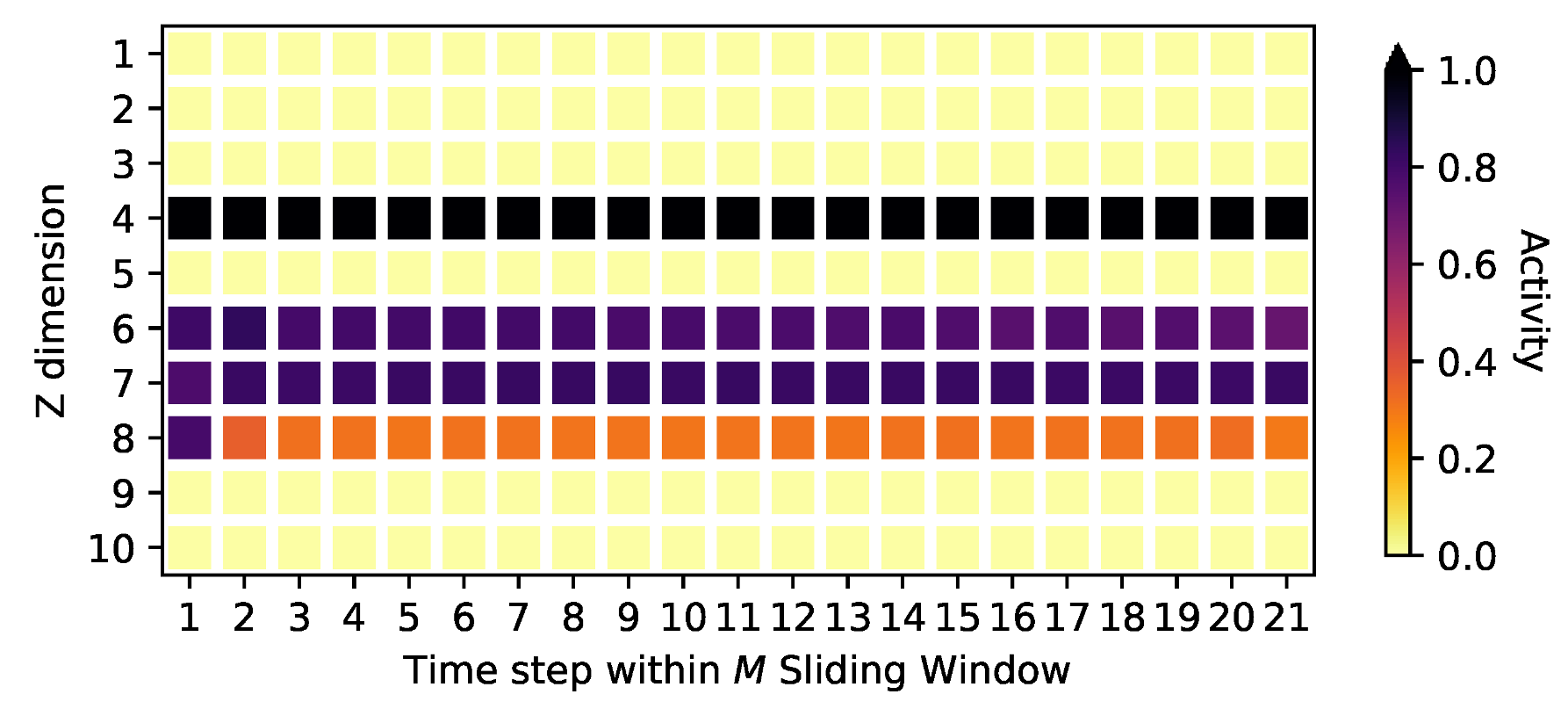
Appendix E. Activities on the Stock Market Data and Model Adaptions for High-Dimensional Data
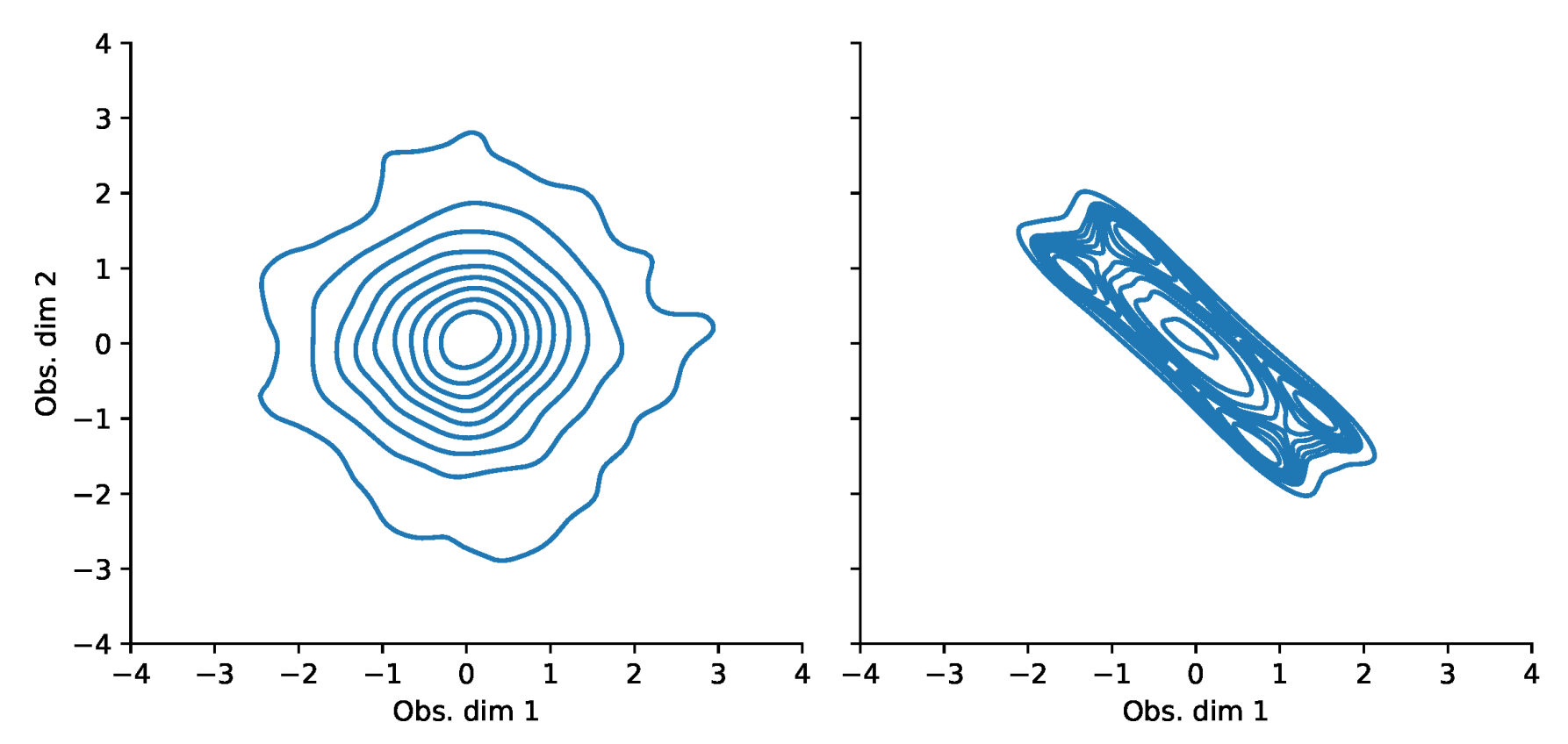
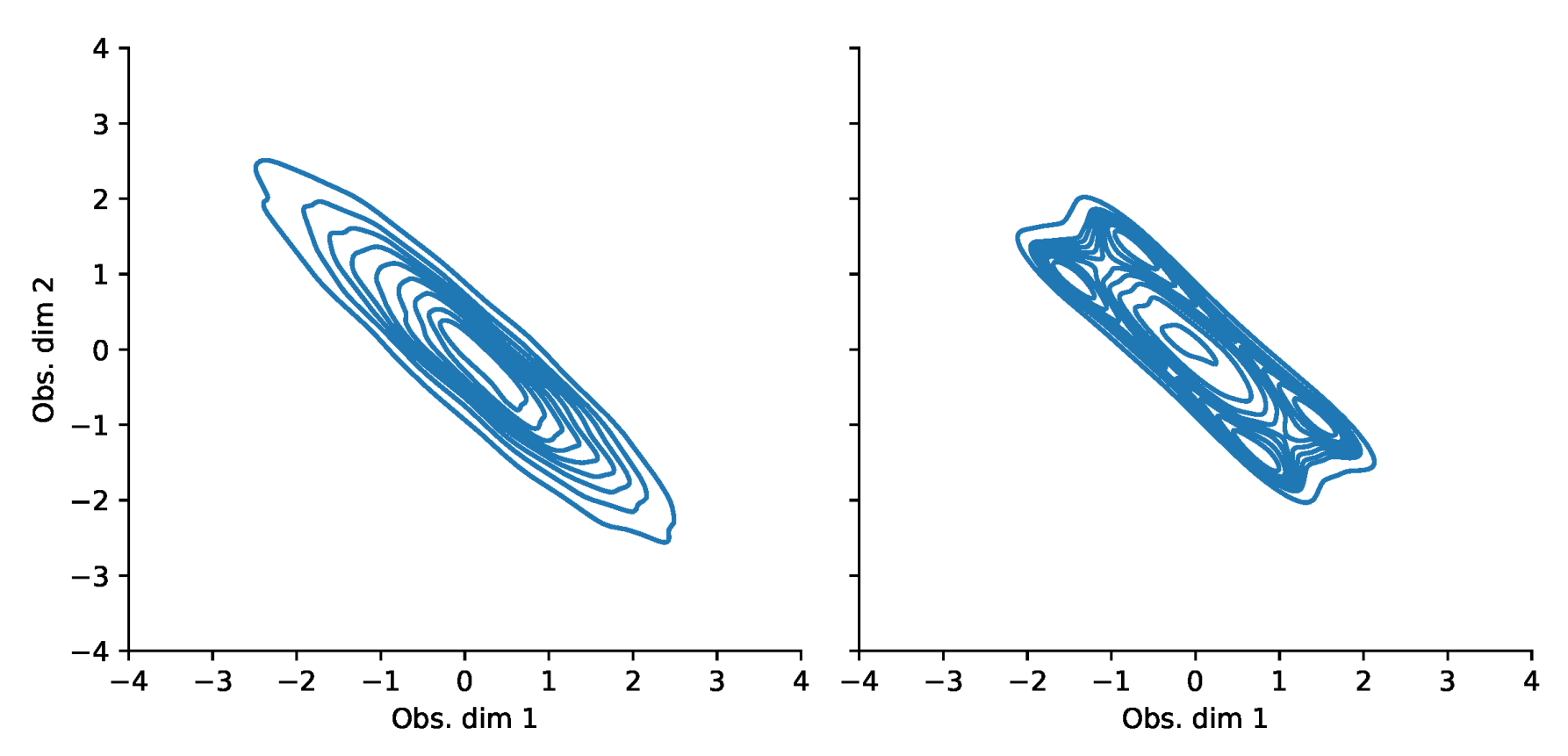
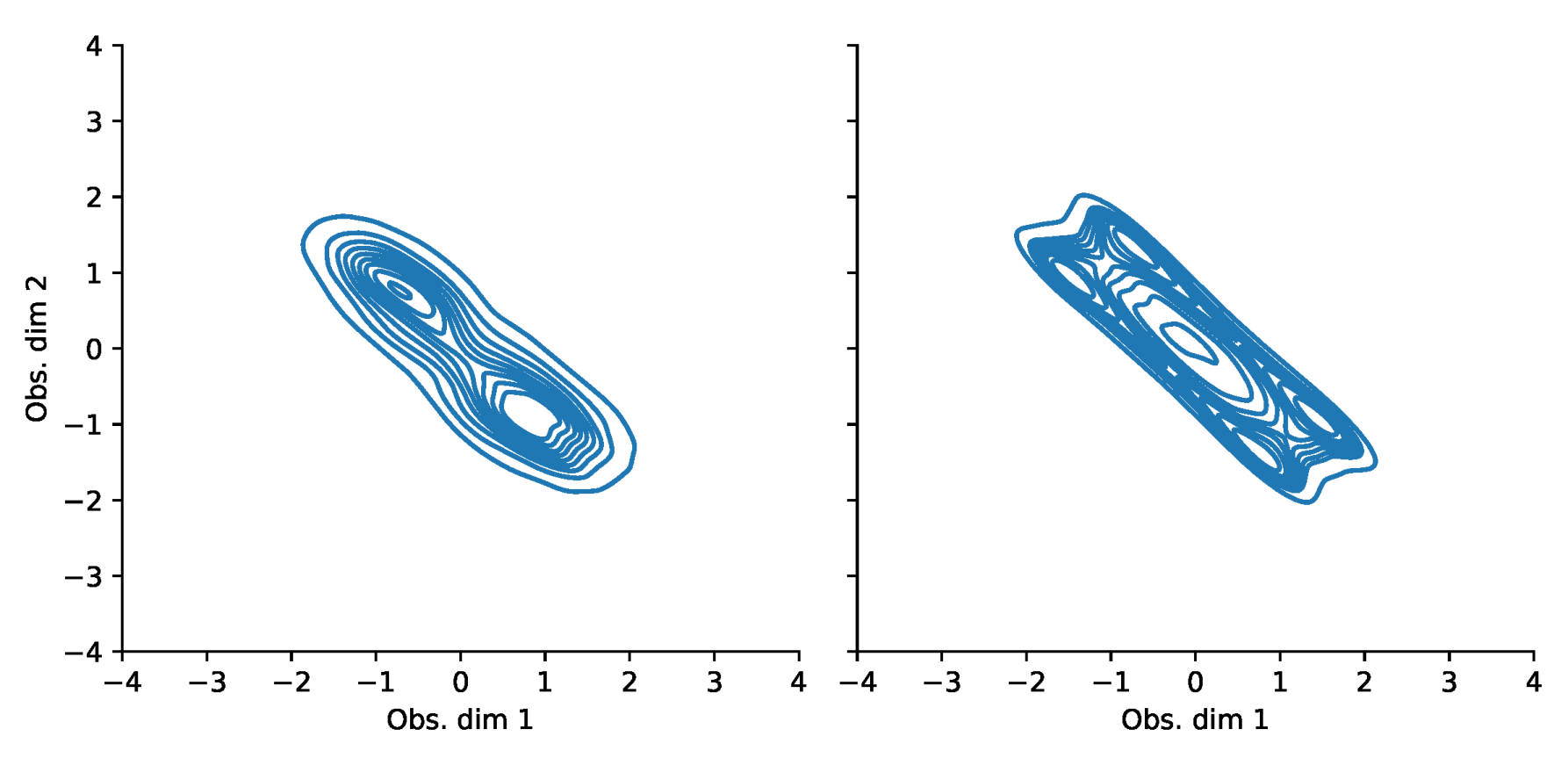
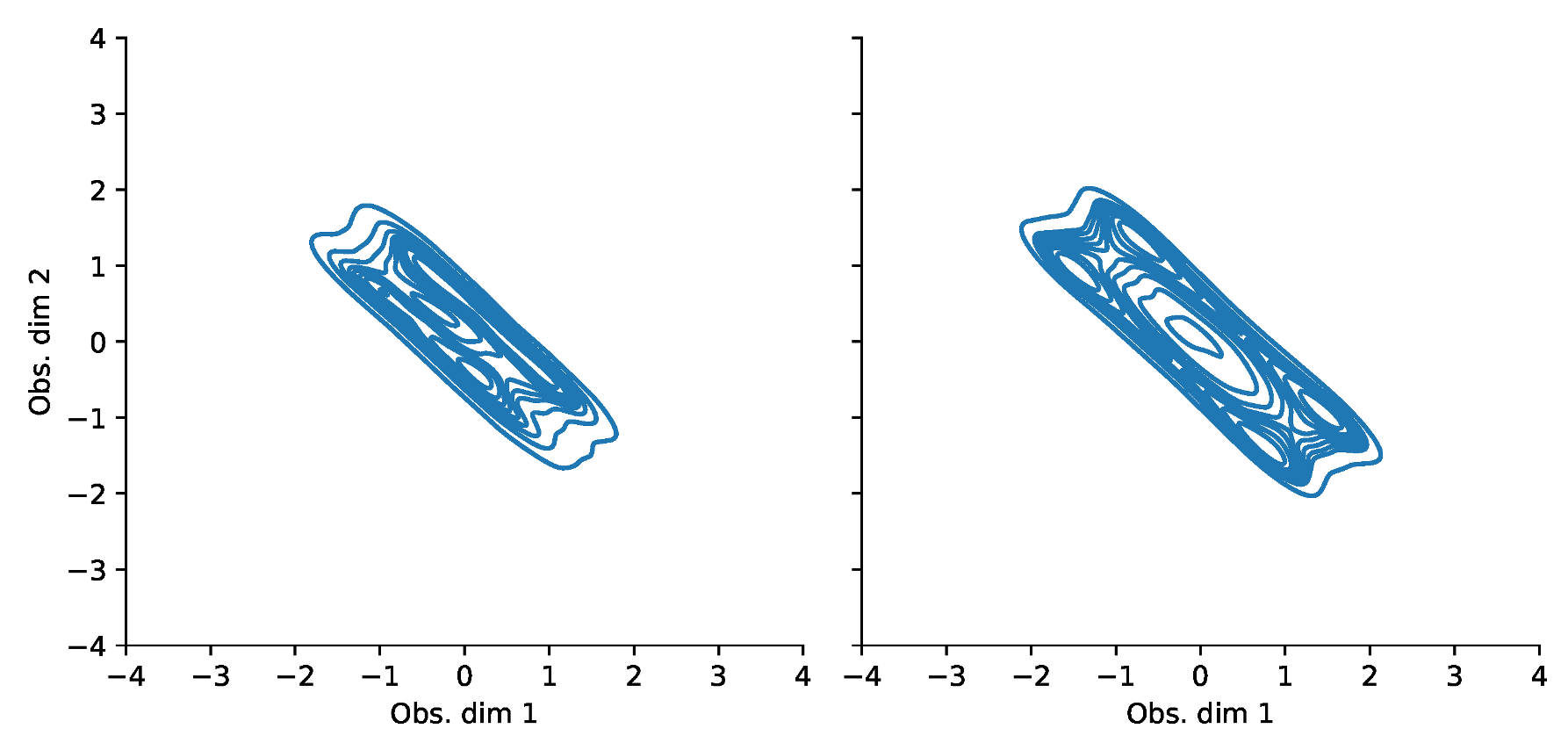
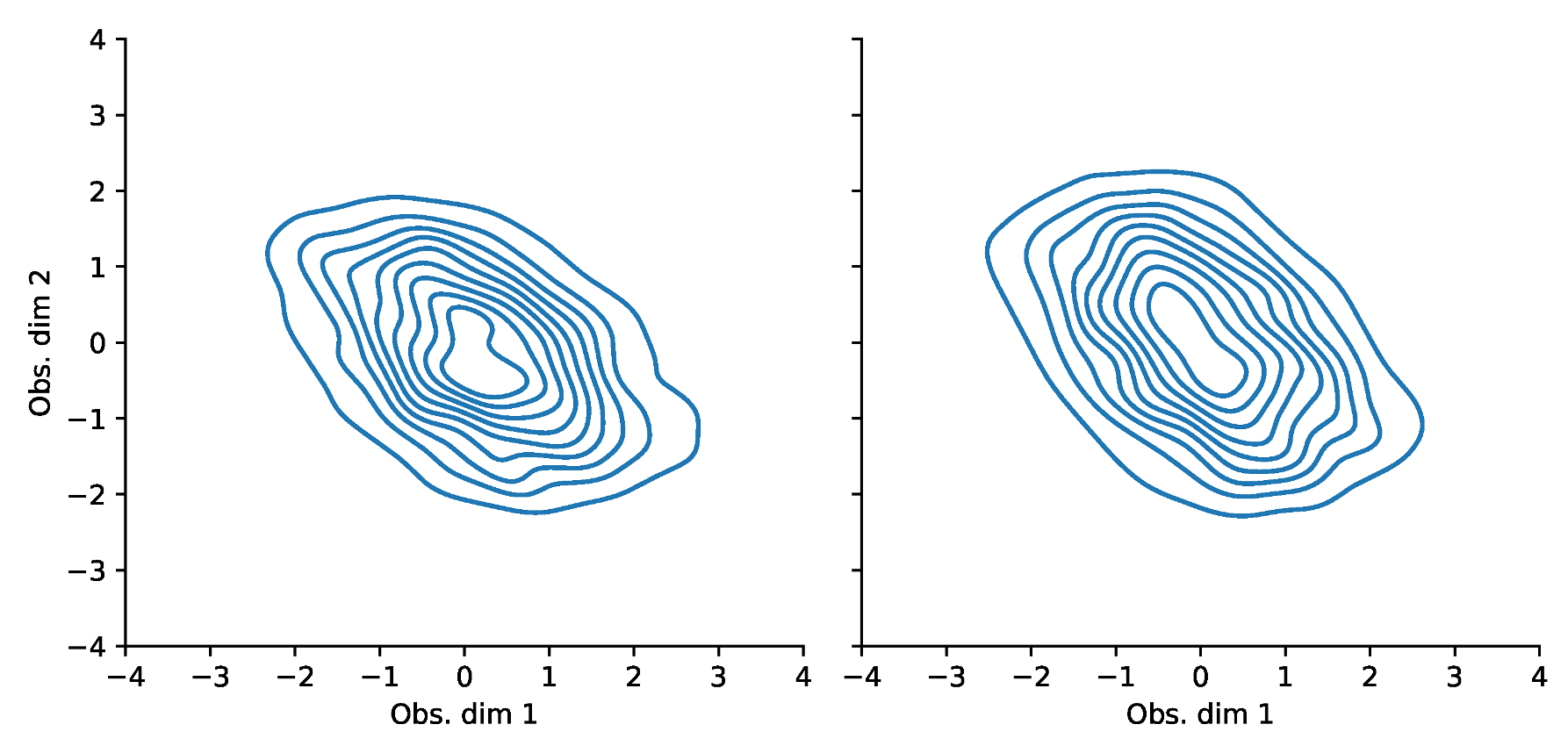
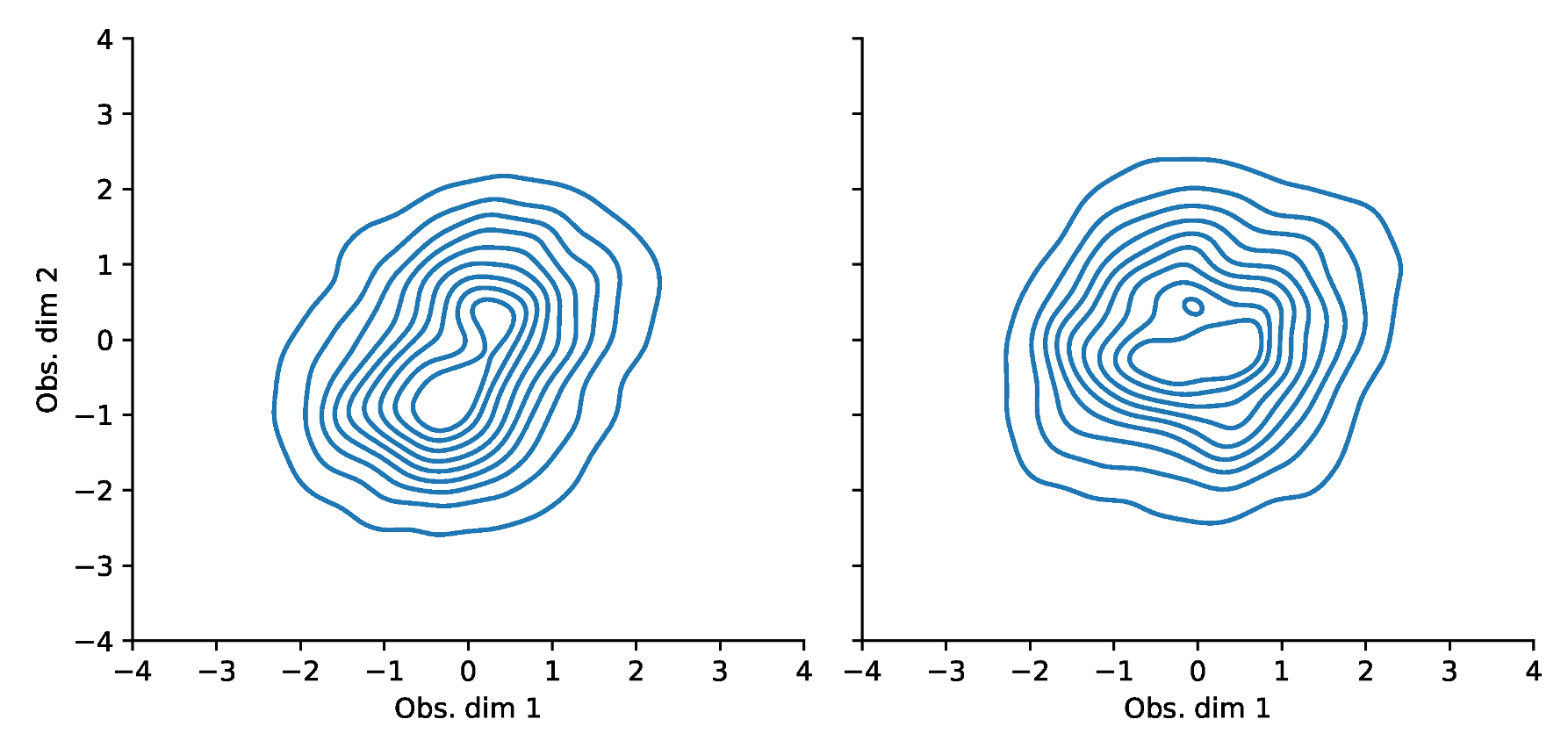
Appendix F. VaR and Scatterplots
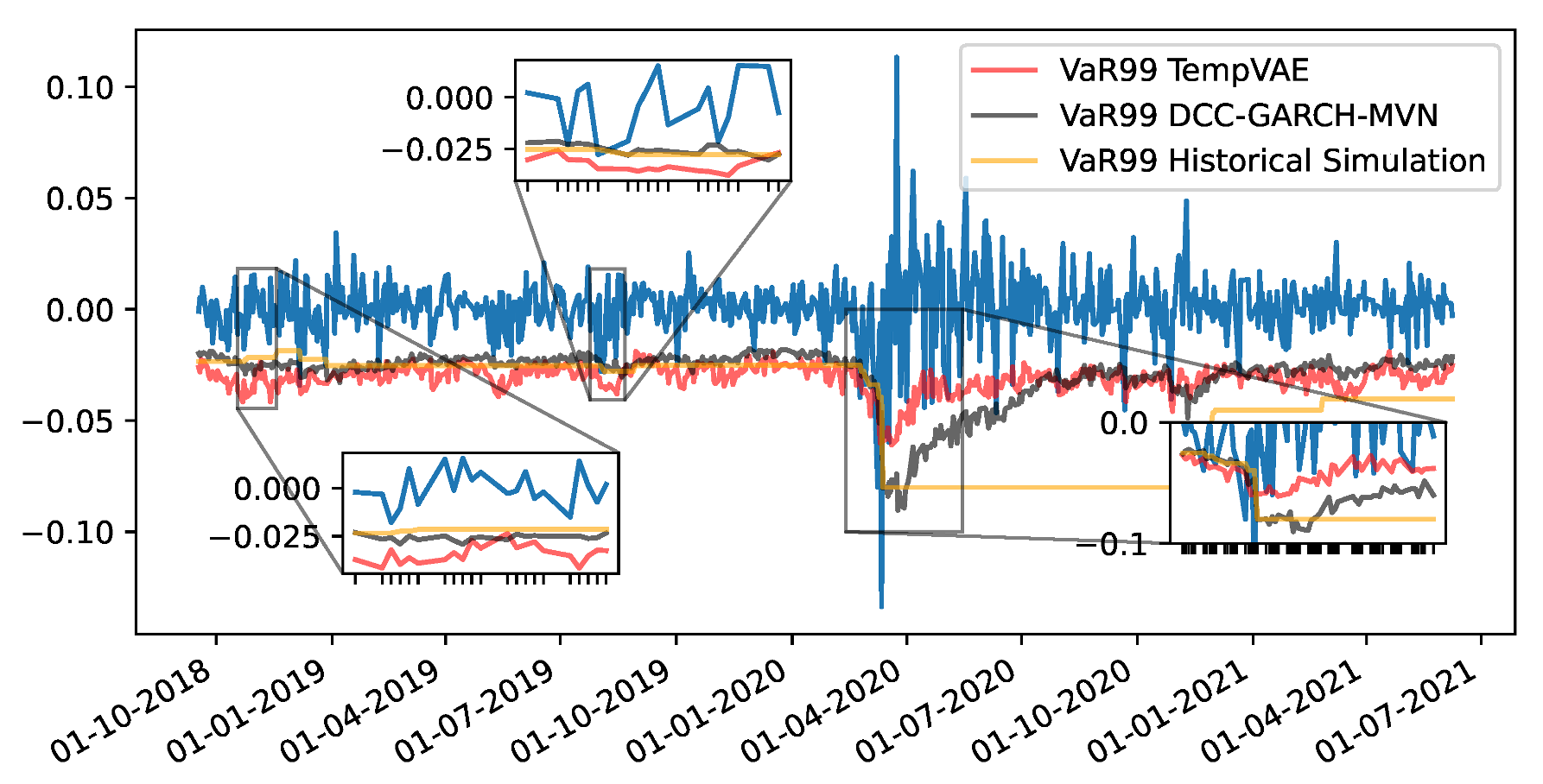
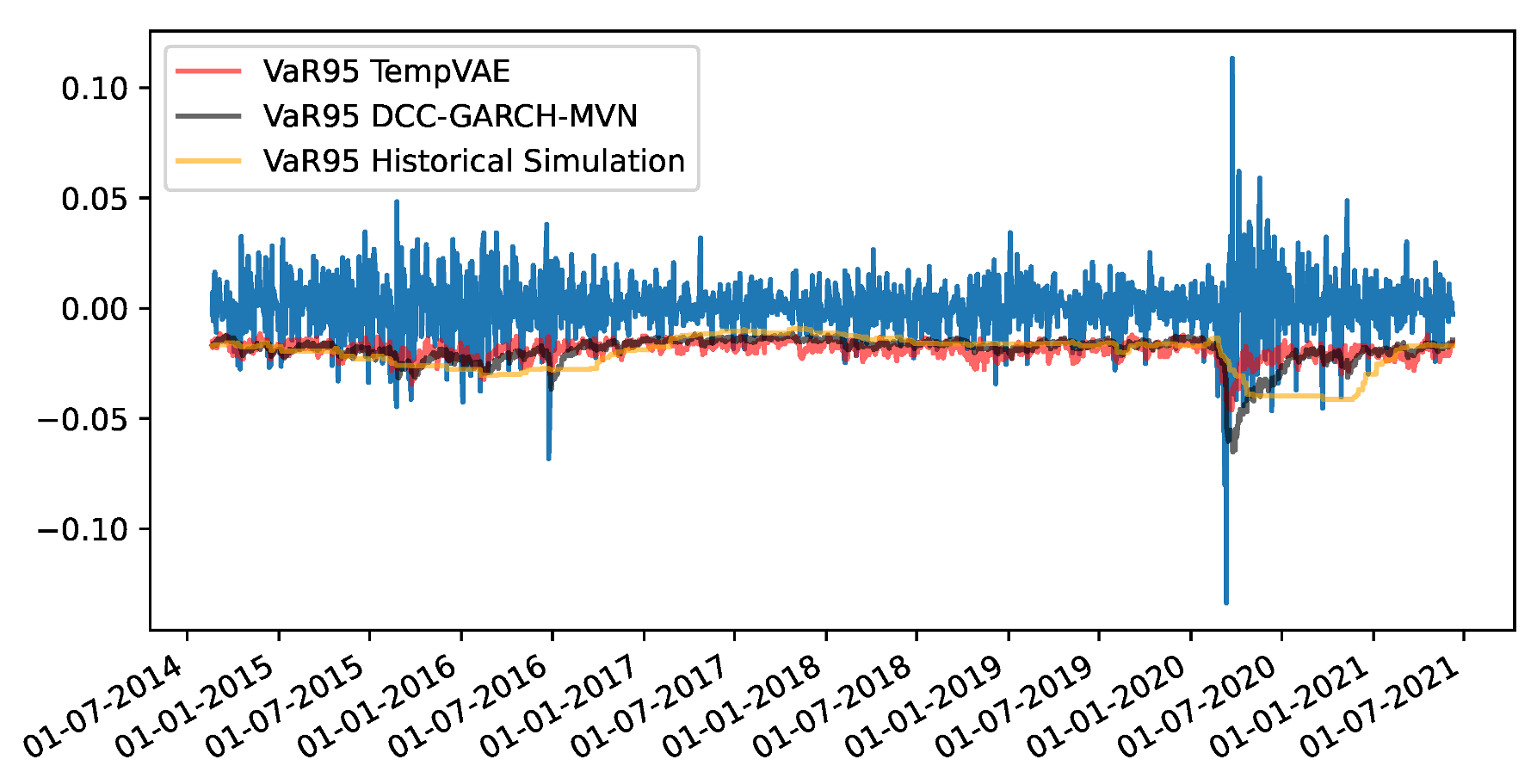
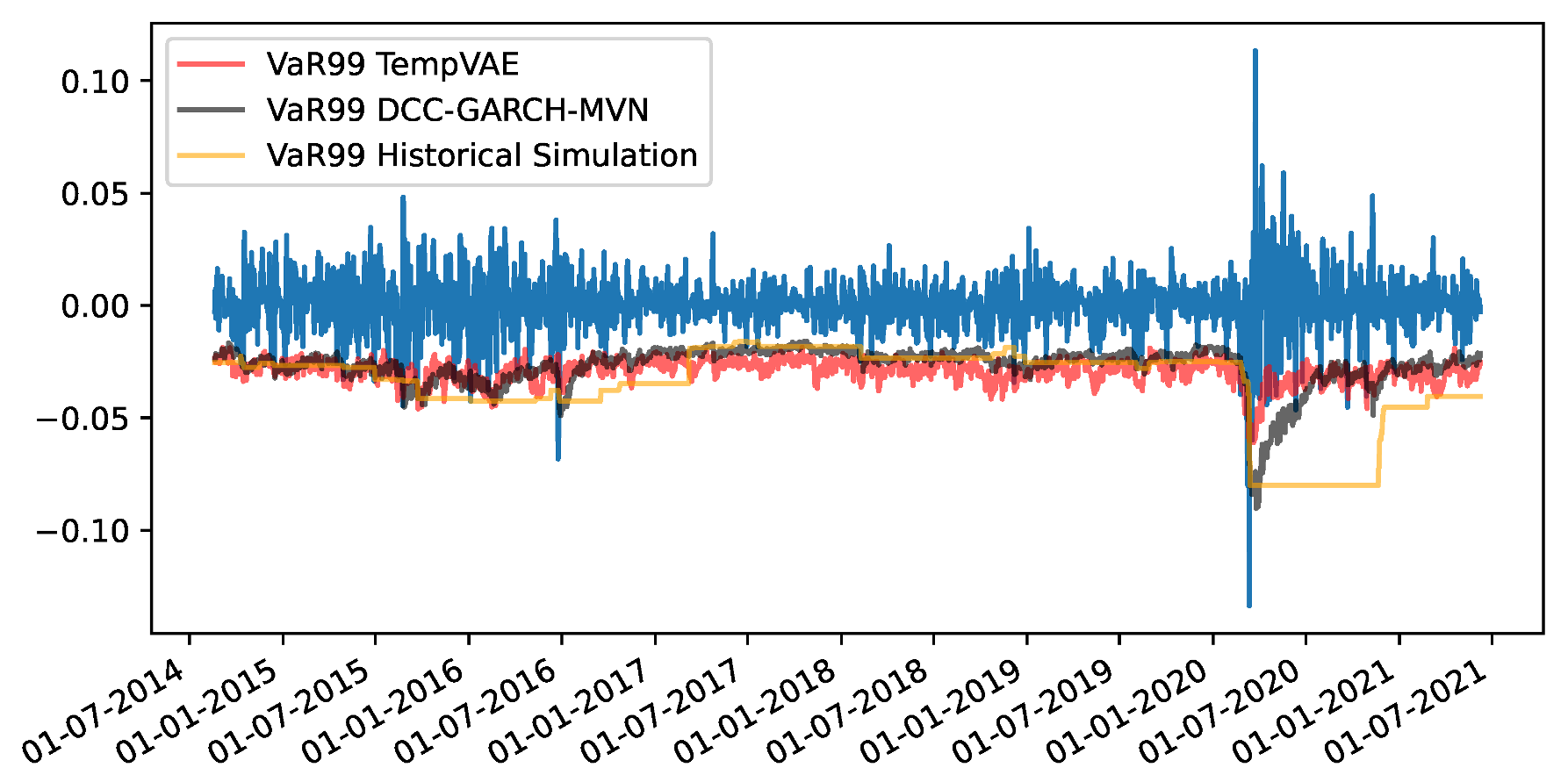
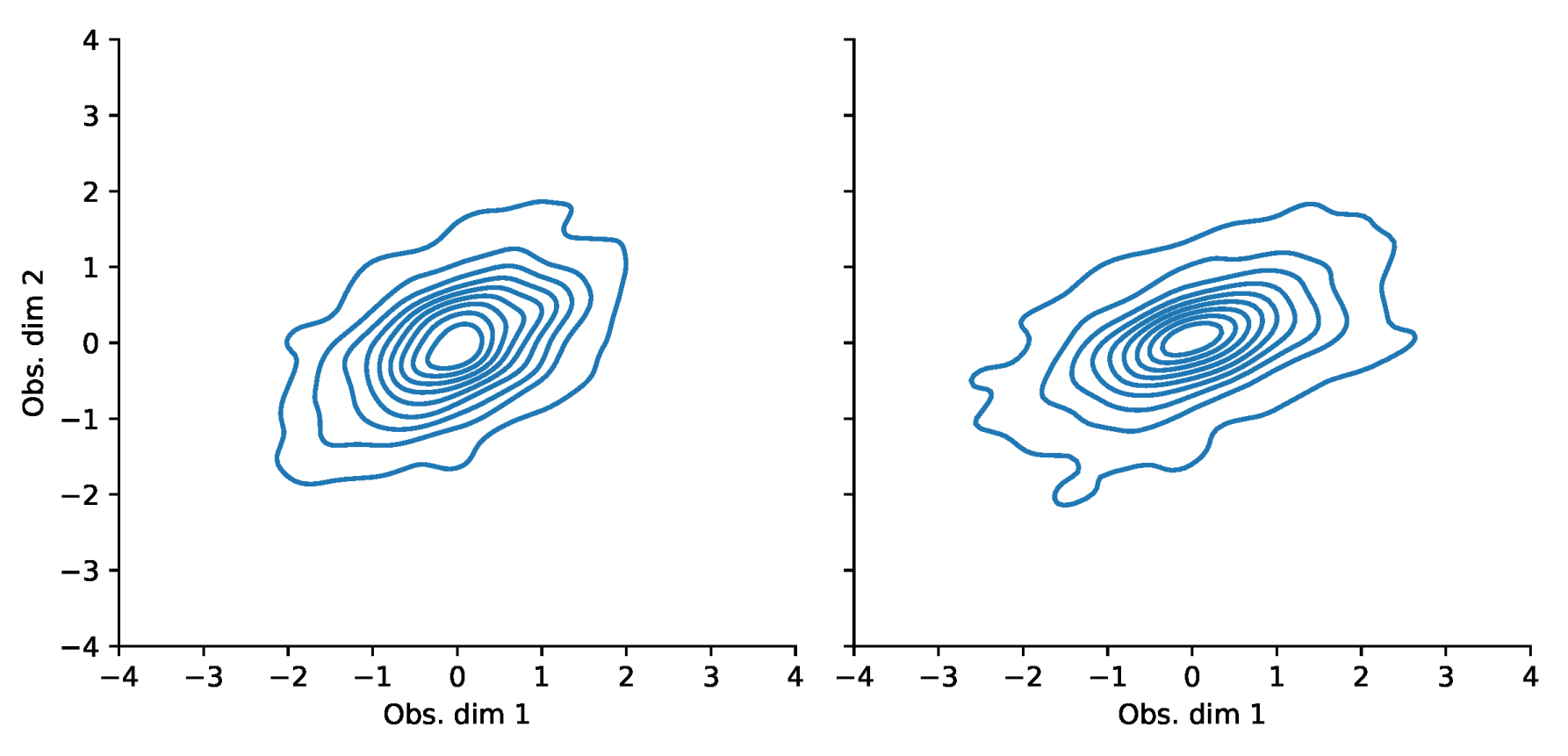
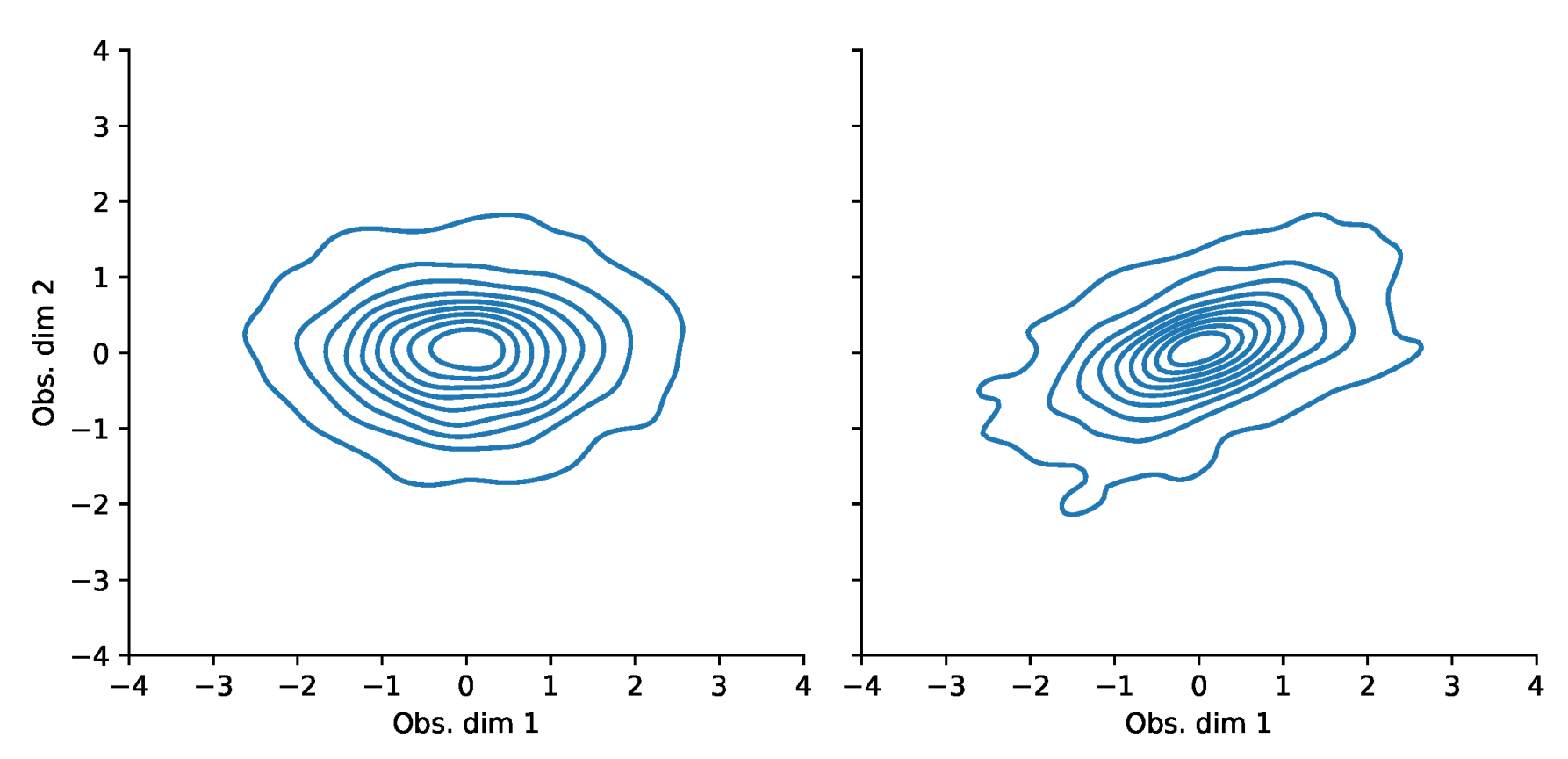
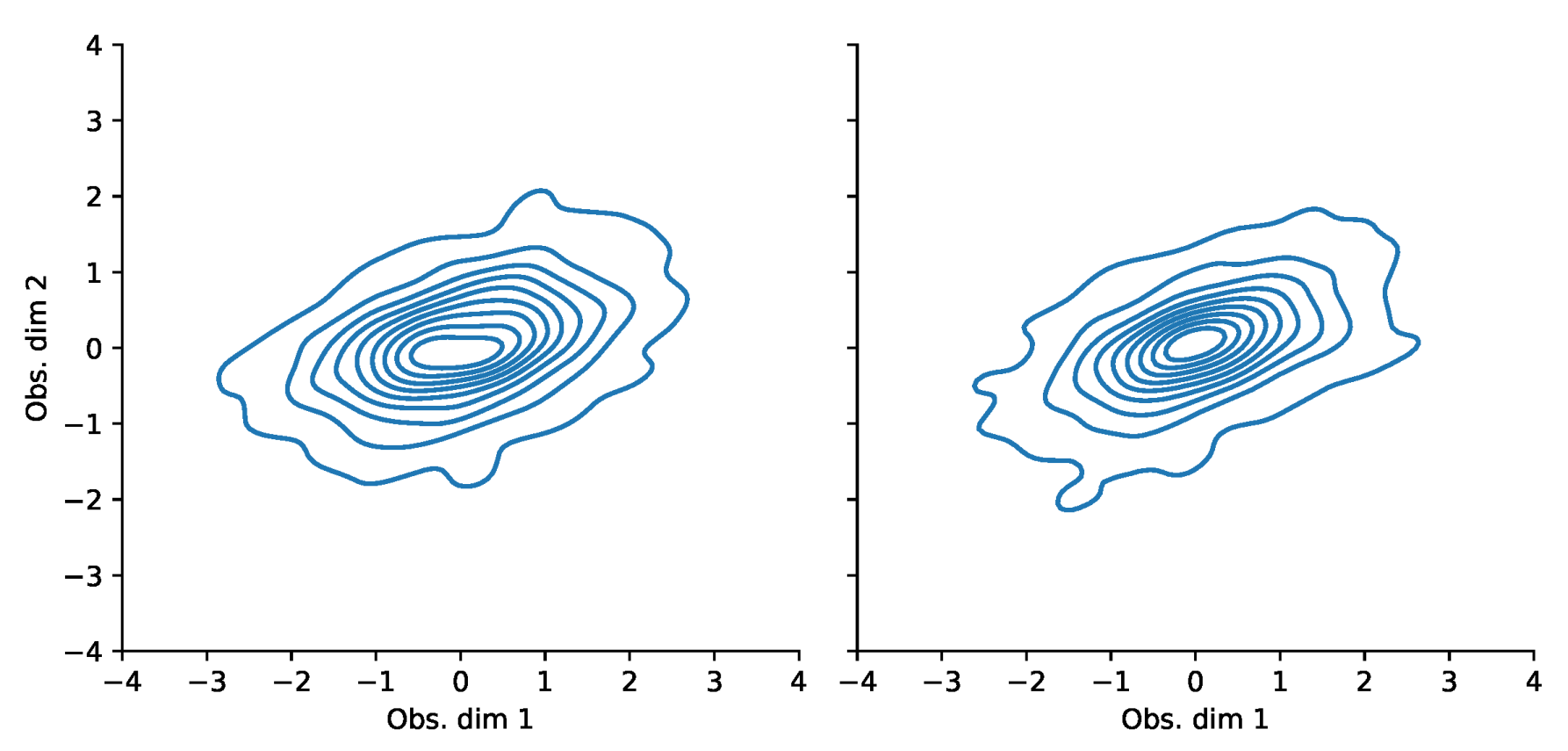
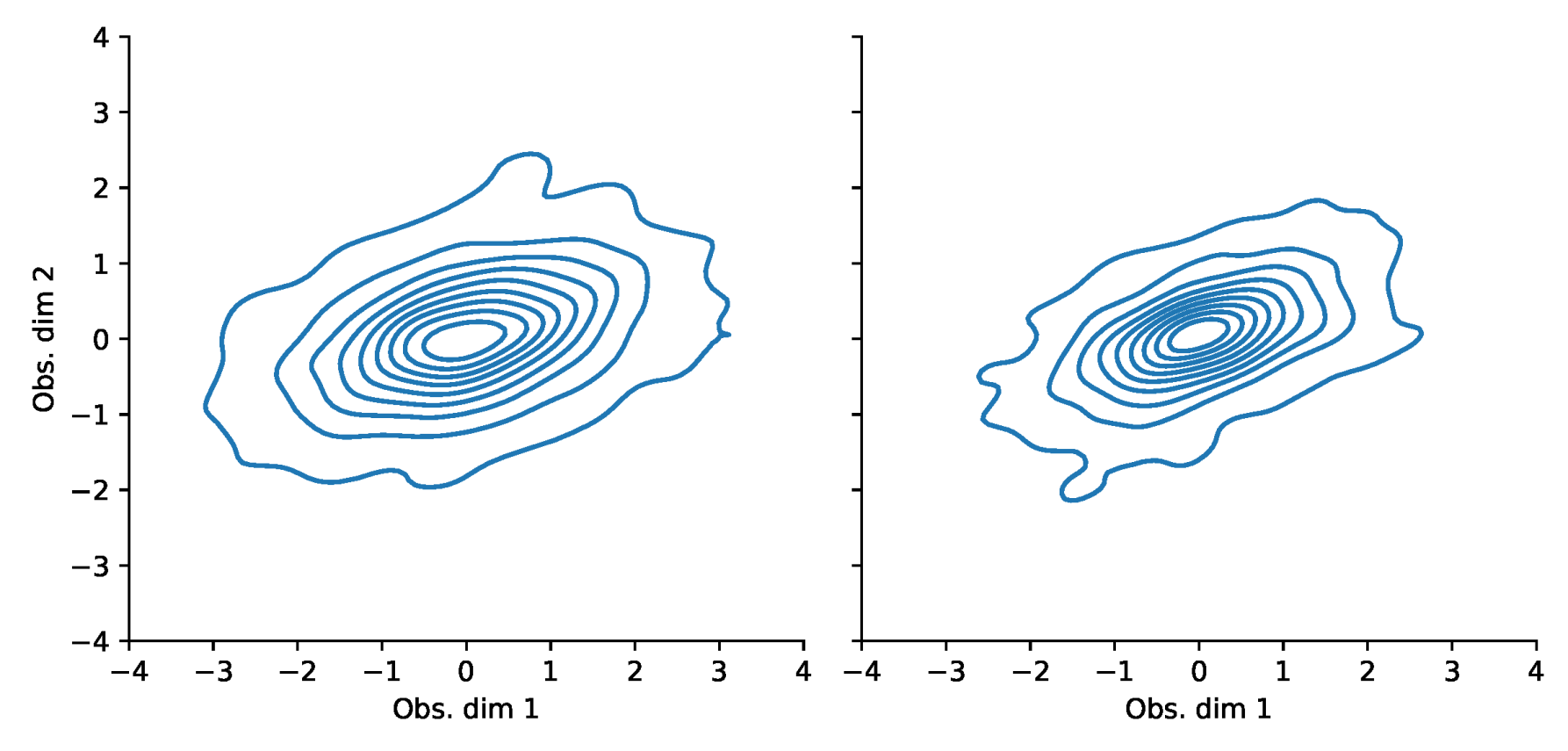
| 1 | i.e., the fact that drift parameters are notoriously hard to estimate while volatility parameters are much easier to obtain. |
| 2 | E.g., . |
| 3 | Then, the assumption is , with for all . |
| 4 | This is common practice when modeling financial data as the increments of the log-stock prices are typically assumed to be independent (or at least uncorrelated) while the price increments are definitely not. For our later application in risk management (the VaR estimation), we therefore transform the log-return forecasts of the models to actual returns by using ) to model the extremes in the data adequately. |
| 5 | The benchmark models are note feasible on the “S&P500” data due to a too high dimension. |
| 6 | We consider a time window of 180 days. |
| 7 | Note that usually one can calculate the VaR estimates for GARCH models analytically. But as we apply a non-linear transform of the modeled log-returns (see expression (24)) this task is not trivially performed. |
| 8 | Indeed, we could get the fractions of mispredictions correct by always predicting the VaR as for the initial fractions of the predictions and then equal to 1 (i.e., a total loss). Of course, this is no reasonable predictor! |
References
- Arian, Hamidreza, Mehrdad Moghimi, Ehsan Tabatabaei, and Shiva Zamani. 2020. Encoded Value-at-Risk: A Predictive Machine for Financial Risk Management. arXiv arXiv:2011.06742. [Google Scholar] [CrossRef]
- Arimond, Alexander, Damian Borth, Andreas G. F. Hoepner, Michael Klawunn, and Stefan Weisheit. 2020. Neural Networks and Value at Risk. SSRN Electronic Journal, 20–7. [Google Scholar] [CrossRef]
- Bayer, Justin, and Christian Osendorfer. 2014. Learning Stochastic Recurrent Networks. arXiv arXiv:1411.7610v3. [Google Scholar]
- Bishop, Christopher M. 2006. Pattern Recognition and Machine Learning. Berlin/Heidelberg: Springer. [Google Scholar]
- Bollerslev, Tim. 1986. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bowman, Samuel R., Luke Vilnis, Oriol Vinyals, Andrew M. Dai, Rafal Jozefowicz, and Samy Bengio. 2015. Generating Sentences from a Continuous Space. In CoNLL 2016—20th SIGNLL Conference on Computational Natural Language Learning, Proceedings. Berlin: Association for Computational Linguistics (ACL), pp. 10–21. [Google Scholar]
- Burda, Yuri, Roger Grosse, and Ruslan Salakhutdinov. 2016. Importance Weighted Autoencoders. Paper presented at International Conference on Learning Representations, ICLR, San Juan, PR, USA, May 2–4. [Google Scholar]
- Chen, Luyang, Markus Pelger, and Jason Zhu. 2023. Deep Learning in Asset Pricing. Management Science. (online first). [Google Scholar] [CrossRef]
- Chen, Xiaoliang, Kin Keung Lai, and Jerome Yen. 2009. A statistical neural network approach for value-at-risk analysis. Paper presented at 2009 International Joint Conference on Computational Sciences and Optimization, CSO 2009, Sanya, China, April 24–26, vol. 2, pp. 17–21. [Google Scholar] [CrossRef]
- Cho, Kyunghyun, Bart Van Merriënboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. 2014. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. Paper presented at EMNLP 2014—2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, October 25–29; pp. 1724–34. [Google Scholar] [CrossRef]
- Chung, Junyoung, Kyle Kastner, Laurent Dinh, Kratarth Goel, Aaron C. Courville, and Yoshua Bengio. 2015. A Recurrent Latent Variable Model for Sequential Data. Advances in Neural Information Processing Systems 28: 2980–8. [Google Scholar]
- Engle, Robert. 2012. Dynamic Conditional Correlation. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Fatouros, Georgios, Georgios Makridis, Dimitrios Kotios, John Soldatos, Michael Filippakis, and Dimosthenis Kyriazis. 2022. DeepVaR: A framework for portfolio risk assessment leveraging probabilistic deep neural networks. Digital Finance 2022: 1–28. [Google Scholar] [CrossRef] [PubMed]
- Fraccaro, Marco, Simon Kamronn, Ulrich Paquet, and Ole Winther. 2017. A Disentangled Recognition and Nonlinear Dynamics Model for Unsupervised Learning. Advances in Neural Information Processing Systems 30: 3602–11. [Google Scholar]
- Fraccaro, Marco, Søren Kaae Sønderby, Ulrich Paquet, and Ole Winther. 2016. Sequential Neural Models with Stochastic Layers. Advances in Neural Information Processing Systems 29: 2207–15. [Google Scholar]
- Ghalanos, Alexios. 2019. rmgarch: Multivariate GARCH models. R Package Version 1.3-7. Available online: https://cran.microsoft.com/snapshot/2020-04-15/web/packages/rmgarch/index.html (accessed on 1 December 2022).
- Girin, Laurent, Simon Leglaive, Xiaoyu Bie, Julien Diard, Thomas Hueber, and Xavier Alameda-Pineda. 2020. Dynamical Variational Autoencoders: A Comprehensive Review. Foundations and Trends in Machine Learning 15: 1–175. [Google Scholar] [CrossRef]
- Goyal, Anirudh, Alessandro Sordoni, Marc-Alexandre Côté, Nan Rosemary Ke, and Yoshua Bengio. 2017. Z-Forcing: Training Stochastic Recurrent Networks. Advances in Neural Information Processing Systems 2017: 6714–24. [Google Scholar]
- He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. Paper presented at The IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, December 7–13. [Google Scholar]
- Kingma, Diederik P., and Jimmy Lei Ba. 2015. Adam: A method for stochastic optimization. Paper presented at 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, May 7–9. [Google Scholar]
- Kingma, Diederik P., and Max Welling. 2014. Auto-Encoding Variational Bayes. Paper presented at 2nd International Conference on Learning Representations, ICLR, Banff, AB, Canada, April 14–16; Technical Report. Available online: https://arxiv.org/pdf/1312.6114.pdf (accessed on 1 December 2022).
- Kingma, Diederik P., Danilo J. Rezende, Shakir Mohamed, and Max Welling. 2014. Semi-supervised Learning with Deep Generative Models. Paper presented at the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, December 8–13. [Google Scholar]
- Krishnan, Rahul, Uri Shalit, and David Sontag. 2017. Structured Inference Networks for Nonlinear State Space Models. Paper presented at AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, February 4–9, vol. 31. [Google Scholar]
- Laloux, Laurent, Pierre Cizeau, Marc Potters, and Jean-Phillippe Bouchard. 2000. Random Matrix and Financial Correlations. International Journal of Theoretical and Applied Finance 3: 391–97. [Google Scholar] [CrossRef]
- Liu, Yan. 2005. Value-at-Risk Model Combination Using Artificial Neural Networks. In Emory University Working Paper Series. Atlanta: Emory University. [Google Scholar]
- Luo, Rui, Weinan Zhang, Xiaojun Xu, and Jun Wang. 2018. A Neural Stochastic Volatility Model. Paper presented at AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, February 2–7, vol. 32. [Google Scholar]
- Rezende, Danilo Jimenez, Shakir Mohamed, and Daan Wierstra. 2014. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. Paper presented at the 31 st International Conference on Machine Learning, Beijing, China, June 21–26; pp. 1278–86. [Google Scholar]
- Sarma, Mandira, Susan Thomas, and Ajay Shah. 2003. Selection of Value-at-Risk Models. Journal of Forecasting 22: 337–58. [Google Scholar] [CrossRef]
- Sicks, Robert, Ralf Korn, and Stefanie Schwaar. 2021. A Generalised Linear Model Framework for β-Variational Autoencoders based on Exponential Dispersion Families. Journal of Machine Learning Research 22: 1–41. [Google Scholar]
- Xu, Xiuqin, and Ying Chen. 2021. Deep Stochastic Volatility Model. arXiv arXiv:2102.12658. [Google Scholar]
| Model | Diagonal NLL | NLL | Portfolio NLL |
|---|---|---|---|
| GARCH | 22.76 | 22.84 | −0.51 |
| TempVAE | 25.79 | 20.35 | −3.04 |
| DCC-GARCH-MVN | 25.03 | 18.69 | −3.07 |
| DCC-GARCH-MVt | 25.44 | 19.17 | −3.05 |
| Model | RLF95 | RLF99 | AE95 | AE99 |
|---|---|---|---|---|
| GARCH | 44.47 | 32.35 | 24.3 | 17.8 |
| TempVAE | 12.64 | 5.96 | 4.8 | 1.3 |
| DCC-GARCH-MVN | 13.15 | 7.10 | 5.4 | 2.1 |
| DCC-GARCH-MVt | 10.23 | 4.14 | 3.9 | 0.6 |
| HS | 14.57 | 7.43 | 5.1 | 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buch, R.; Grimm, S.; Korn, R.; Richert, I. Estimating the Value-at-Risk by Temporal VAE. Risks 2023, 11, 79. https://doi.org/10.3390/risks11050079
Buch R, Grimm S, Korn R, Richert I. Estimating the Value-at-Risk by Temporal VAE. Risks. 2023; 11(5):79. https://doi.org/10.3390/risks11050079
Chicago/Turabian StyleBuch, Robert, Stefanie Grimm, Ralf Korn, and Ivo Richert. 2023. "Estimating the Value-at-Risk by Temporal VAE" Risks 11, no. 5: 79. https://doi.org/10.3390/risks11050079
APA StyleBuch, R., Grimm, S., Korn, R., & Richert, I. (2023). Estimating the Value-at-Risk by Temporal VAE. Risks, 11(5), 79. https://doi.org/10.3390/risks11050079






