Backward Deep BSDE Methods and Applications to Nonlinear Problems
Abstract
1. Introduction
2. FBSDE for Nonlinear Problems
2.1. Backward Time-Stepping
2.1.1. Exact Backward Time-Stepping
2.1.2. Time-Stepping from Taylor Expansion
3. Deep BSDE Approach
3.1. Forward Approach
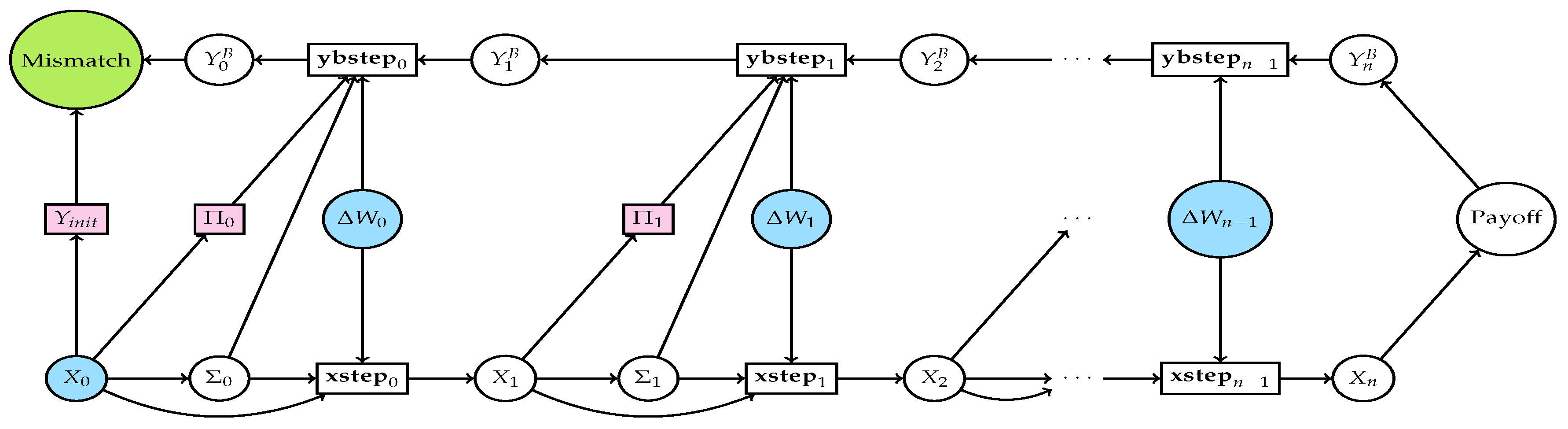
3.2. Backward Approach
| Algorithm 1 The pathwise Backward deep BSDE Method |
|
4. Results
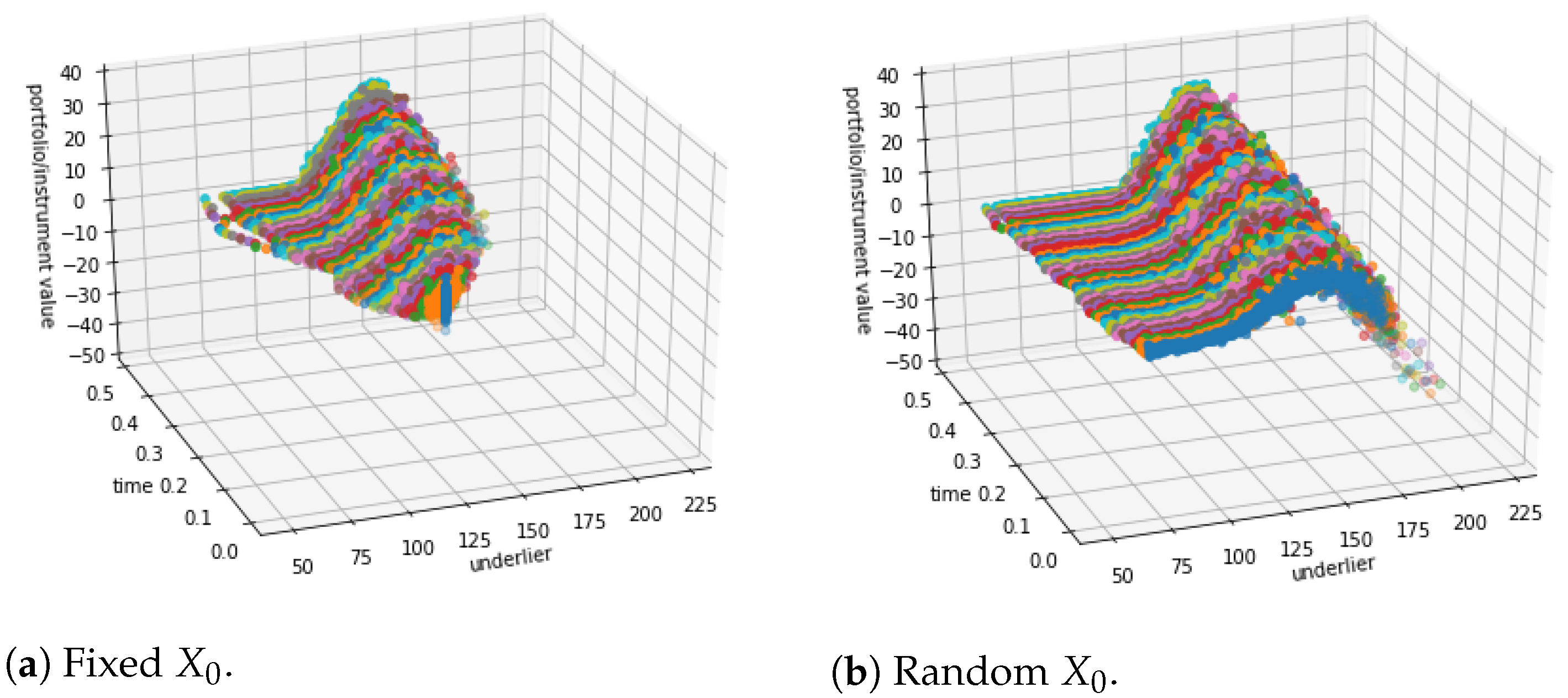
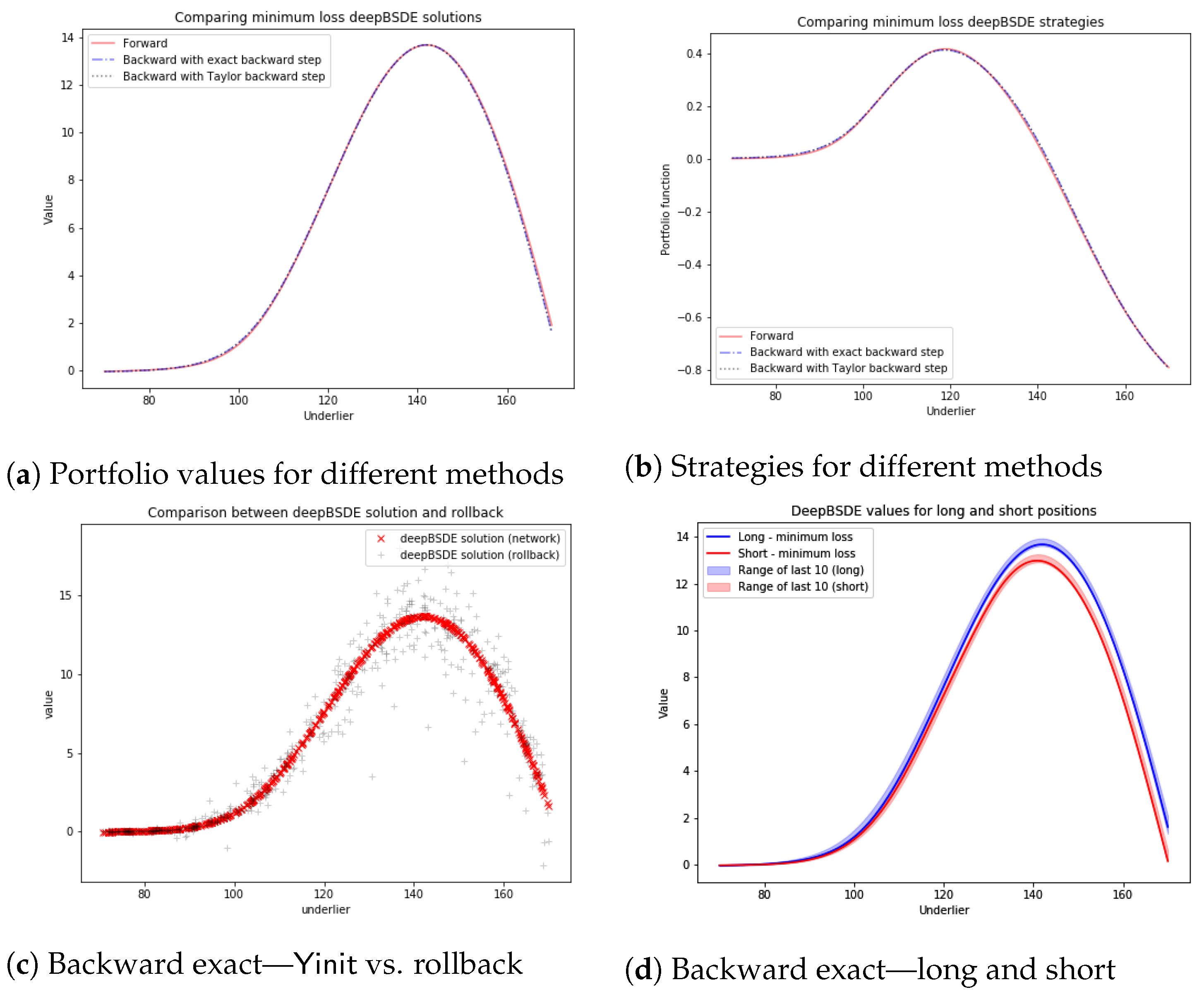
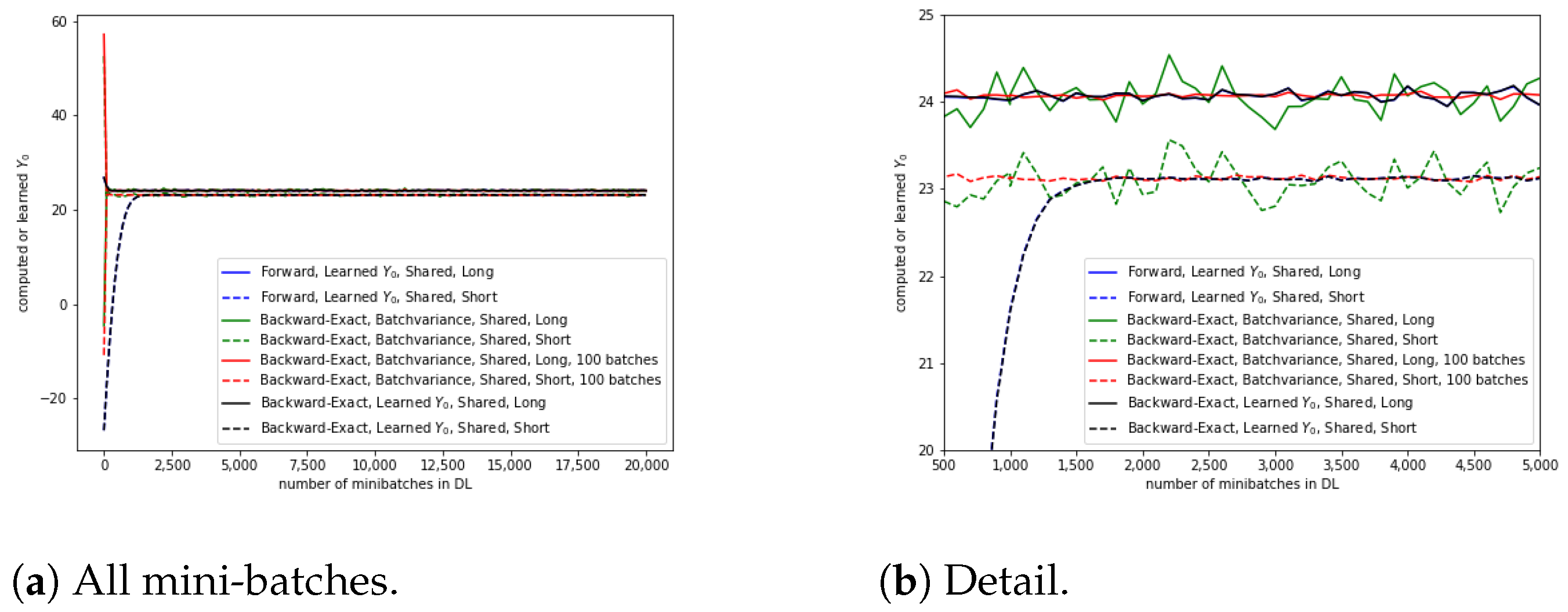
4.1. Call Combination
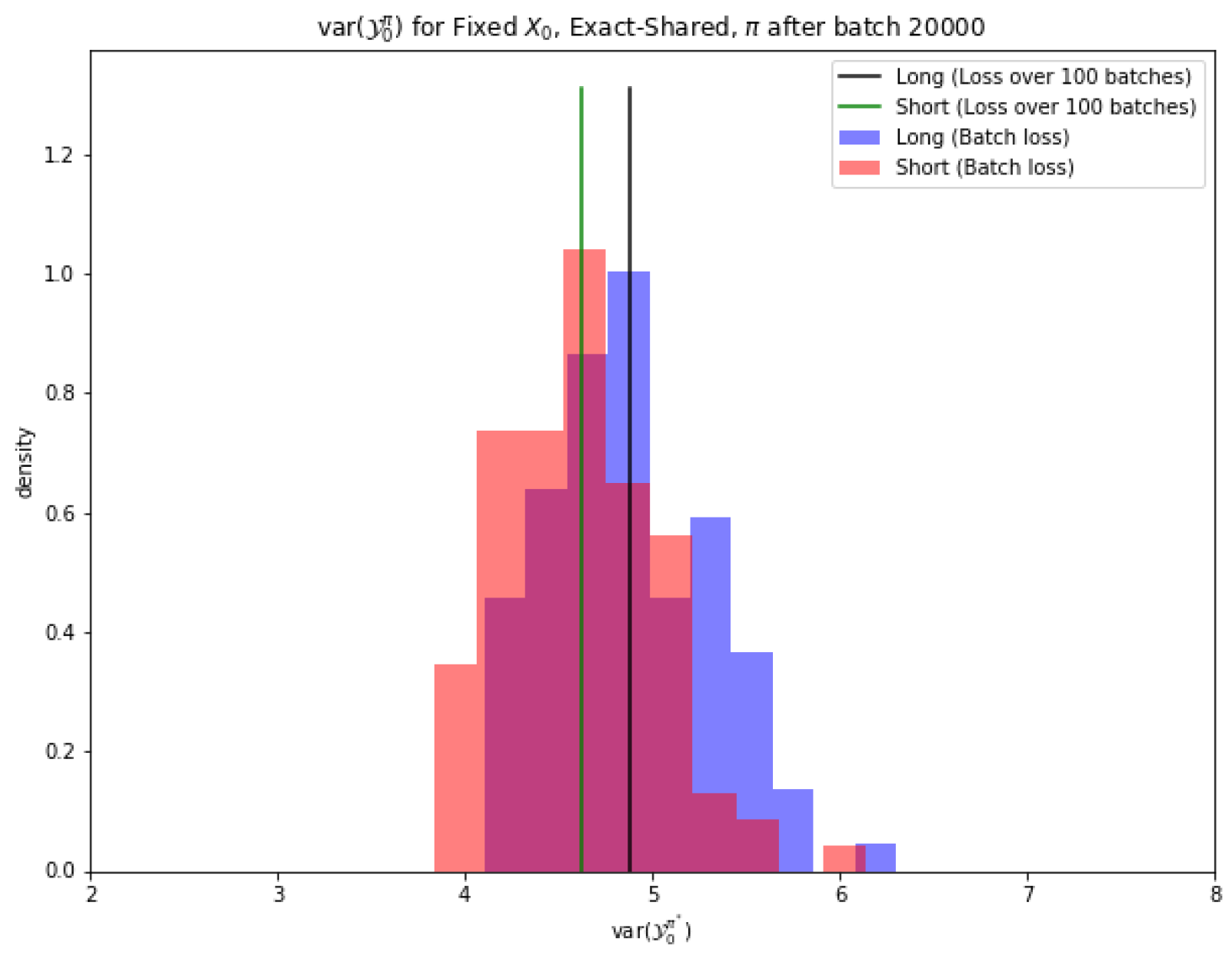
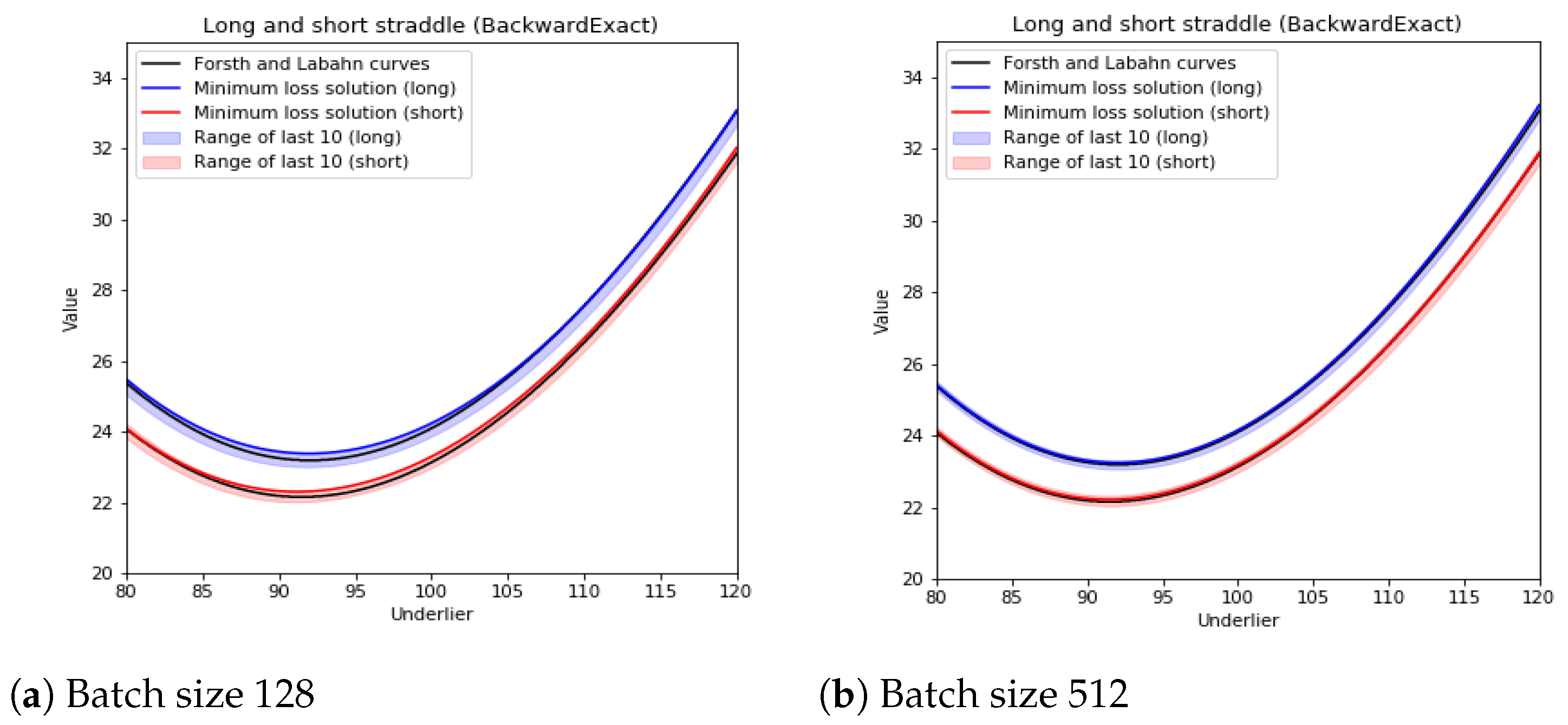
4.2. Straddle
5. Conclusions
6. Disclaimer
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Set and . Then, (Pardoux 1998, Theorem 2.2) with this and shows that one can construct a solution and of the BSDE from a classical solution of a corresponding PDE and a solution . Rewriting the PDE and BSDE in terms of instead of and using function f rather than gives the form reported below. For the opposite direction, (Pardoux 1998, Theorem 2.4) shows how a solution of the BSDE (corresponding to a X that starts at x at time t) gives a continuous function , which is a viscosity solution of the corresponding PDE. |
| 2 | In general, the terminal condition could be given as a random variate that is measurable with respect to the information available of time T (i.e., the sigma algebra generated by with ). The FBSDE approach then will be more general than the PDE approach. If there is an exact (or approximate) Markovianization with a Markov state , the strategy and the solution would in general be functions and of that Markov state. We only treat the usual final value case here. |
| 3 | |
| 4 | This is actually the expectation of the conditional variance over the distribution of . |
| 5 | Here, we consider the 1-dimensional case, while Han and Jentzen (2017) consider the 100-dimensional case. |
| 6 | Notice that (Forsyth and Labahn 2007, Figure 1) do not give the number of space or time-steps used for their plot. |
References
- Forsyth, Peter A., and George Labahn. 2007. Numerical methods for controlled Hamilton-Jacobi-Bellman PDEs in finance. Journal of Computational Finance 11: 1–44. Available online: https://cs.uwaterloo.ca/~paforsyt/hjb.pdf (accessed on 15 March 2023). [CrossRef]
- Ganesan, Narayan, Yajie Yu, and Bernhard Hientzsch. 2022. Pricing barrier options with deep backward stochastic differential equation methods. Journal of Computational Finance 25. Available online: https://ssrn.com/abstract=3607626 (accessed on 15 March 2023). [CrossRef]
- Han, Jiequn, and Arnulf Jentzen. 2017. Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations. Communications in Mathematics and Statistics 5: 349–80. [Google Scholar]
- Han, Jiequn, Arnulf Jentzen, and Weinan E. 2018. Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences 115: 8505–10. [Google Scholar] [CrossRef] [PubMed]
- Hientzsch, Bernhard. 2021. Deep learning to solve forward-backward stochastic differential equations. Risk Magazine. February. Available online: https://ssrn.com/abstract=3494359 (accessed on 15 March 2023).
- Huré, Côme, Huyên Pham, and Xavier Warin. 2020. Deep backward schemes for high-dimensional nonlinear PDEs. Mathematics of Computation 89: 1547–79. [Google Scholar] [CrossRef]
- Liang, Jian, Zhe Xu, and Peter Li. 2021. Deep learning-based least squares forward-backward stochastic differential equation solver for high-dimensional derivative pricing. Quantitative Finance 21: 1309–23. Available online: https://ssrn.com/abstract=3381794 (accessed on 15 March 2023). [CrossRef]
- Mercurio, Fabio. 2015. Bergman, Piterbarg, and beyond: Pricing derivatives under collateralization and differential rates. In Actuarial Sciences and Quantitative Finance. Berlin: Springer, pp. 65–95. Available online: https://ssrn.com/abstract=2326581 (accessed on 15 March 2023).
- Pardoux, Étienne. 1998. Backward stochastic differential equations and viscosity solutions of systems of semilinear parabolic and elliptic PDEs of second order. In Stochastic Analysis and Related Topics VI. Berlin: Springer, pp. 79–127. [Google Scholar]
- Raissi, Maziar. 2018. Forward-backward stochastic neural networks: Deep learning of high-dimensional partial differential equations. arXiv arXiv:1804.07010. [Google Scholar]
- Wang, Haojie, Han Chen, Agus Sudjianto, Richard Liu, and Qi Shen. 2018. Deep learning-based BSDE solver for LIBOR market model with application to bermudan swaption pricing and hedging. arXiv arXiv:1807.06622. Available online: https://ssrn.com/abstract=3214596 (accessed on 15 March 2023). [CrossRef]
- Warin, Xavier. 2018. Nesting Monte Carlo for high-dimensional non-linear PDEs. Monte Carlo Methods and Applications 24: 225–47. [Google Scholar] [CrossRef]





| Method | Upper Price | Lower Price |
|---|---|---|
| Results from Forsyth and Labahn-101 nodes | ||
| Fully Implicit HJB PDE (implicit control) | 24.02 | 23.06 |
| Crank–Nicolson HJB PDE (implicit control) | 24.05 | 23.09 |
| Fully Implicit HJB PDE (pwc policy) | 24.01 | 23.07 |
| Crank–Nicolson HJB PDE (pwc policy) | 24.07 | 23.09 |
| Forward deep BSDE—20,000 batches, size 256 | ||
| Learned (shared) | 24.06 (23.99–24.14) | 23.10 (23.02–23.17) |
| Learned (separate) | 24.07 (24.01–24.12) | 23.10 (23.06–23.15) |
| Backward deep BSDE—20,000 batches, size 256 | ||
| Batch variance/1 (shared) | 24.14 (23.98–24.30) | 23.19 (23.00–23.37) |
| Batch variance/100 (shared) | 24.08 (24.06–24.09) | 23.13 (23.09–23.16) |
| Batch variance/1 (separate) | 24.06 (23.94–24.19 *) | 23.10 (22.95–23.25) |
| Batch variance/100 (separate) | 24.07 (24.06–24.09 *) | 23.12 (23.10–23.13) |
| Learned (shared) | 24.06 (23.99–24.14) | 23.10 (23.02–23.17) |
| Learned (separate) | 24.06 (24.01–24.11 *) | 23.10 (23.06–23.15) |
| Method | Upper Price | Lower Price |
|---|---|---|
| Results from Forsyth and Labahn—101 nodes | ||
| Fully Implicit (implicit control) | 24.02 | 23.06 |
| Crank–Nicolson (implicit control) | 24.05 | 23.09 |
| Fully Implicit (pwc policy) | 24.01 | 23.07 |
| Crank–Nicolson (pwc policy) | 24.07 | 23.09 |
| Backward deep BSDE—20,000 batches, size 512, five seeds | ||
| Batch variance/1 (shared) | 24.02–24.08 (23.87–24.29) | 23.06–23.12 (22.91–23.33) |
| Batch variance/100 (shared) | 24.06–24.07 (24.03–24.09) | 23.11–23.12 (23.09–23.15) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Ganesan, N.; Hientzsch, B. Backward Deep BSDE Methods and Applications to Nonlinear Problems. Risks 2023, 11, 61. https://doi.org/10.3390/risks11030061
Yu Y, Ganesan N, Hientzsch B. Backward Deep BSDE Methods and Applications to Nonlinear Problems. Risks. 2023; 11(3):61. https://doi.org/10.3390/risks11030061
Chicago/Turabian StyleYu, Yajie, Narayan Ganesan, and Bernhard Hientzsch. 2023. "Backward Deep BSDE Methods and Applications to Nonlinear Problems" Risks 11, no. 3: 61. https://doi.org/10.3390/risks11030061
APA StyleYu, Y., Ganesan, N., & Hientzsch, B. (2023). Backward Deep BSDE Methods and Applications to Nonlinear Problems. Risks, 11(3), 61. https://doi.org/10.3390/risks11030061




