Abstract
A vast majority of Loss Given Default (LGD) models are currently in use. Over all the years since the new Capital Accord was published in June 2004, there has been increasing interest in the modelling of the LGD parameter on the part of both academics and practitioners. The main purpose of this paper is to propose new LGD estimation approaches that provide more effective results and include the unresolved cases in the estimation procedure. The motivation for the proposed project was the fact that many LGD models discussed in the literature are based on complete cases and mainly based on the estimation of LGD distribution or regression techniques. This paper presents two different approaches. The first is the KNN non-parametric model, and the other is based on the Cox survival model. The results suggest that the KNN model has higher performance. The Cox model was used to assign observations to LGD pools, and the LGD estimator was proposed as the average of realized values in the pools. These two approaches are quite a new idea for estimating LGD, as the results become more promising. The main advantage of the proposed approaches, especially kNN-based approaches, is that they can be applied to the unresolved cases. In our paper we focus on how to treat the unresolved cases when estimating the LGD parameter. We examined a kNN-based method for estimating LGD that outperforms the traditional Cox model. Furthermore, we also proposed a novel algorithm for selecting the risk drivers.
1. Introduction
According to the Advanced Internal Rating Based (AIRB) approach (CEBS 2006), institutions use their own internal resources and data to estimate three risk parameters: the Probability of default (PD), Exposure at Default (EAD), and Loss Given Default (LGD). These estimates are made following minimal technical standards and guidelines published by the Basel Committee on Banking Supervision (BCBS 2017).
As one of the risk parameters required to be estimated for capital assessment and provisioning, credit loss modelling, namely LGD, is the most difficult type of parameter modelling. This parameter expresses the potential loss expected from defaulted customers and that is why it is so important for a financial institution. Typically, LGD data are managed manually. There is often a substantial amount of time needed between an event of default and the moment of final recoveries. In the guidelines, four basic standards for the calculation of LGD can be found (BCBS 2017). The most frequently used method is known as the workout approach. According to this approach, the discounted value of realized cash flows to when the time of default is measured, relative to the EAD date. Another technique is the historical LGD, based on information about total losses and PD estimates. The two remaining methods are market-based approaches. They are derived from non-defaulted bond prices by means of an asset pricing model. The problematic aspect of the workout approach is the precise identification and calculation of the recovery amounts. It is recommended that all observed defaults from a relevant time period should be taken into account, including cases where the process has started but has not been completed at the time the model is estimated (i.e., incomplete recoveries).
The aim of this paper is twofold. The first is to build a model that can be used to estimate LGD using the unresolved cases. The motivation was the fact that the majority of studies focus on LGD estimation using only resolved cases. This paper addresses the shortfall in this research. The other aim is to apply a kNN-based algorithm. The proposed algorithm allowed us not only to select important variables for the final LGD model, but also to choose the optimal number of neighbours. A wide range of neighbours was considered, from 1 to 70. We compared the results obtained with the model based on the survival approach, namely the Cox proportional hazard model.
The contribution of this paper addresses a real problem regarding treating the unresolved cases when estimating the LGD parameter. We examine a kNN method for estimating LGD that provides better performance than the traditional Cox model. Furthermore, this work presents a new algorithm for choosing the risk drivers.
A novelty proposed in this paper is a novel algorithm for selecting the risk drivers, which uses MSEOOB and MSE generated in the SAS hpforest procedure. We proposed a new ranking method described later in this paper. To the best of our knowledge, none of the studies examined the problem from the perspective of kNN. Therefore, this paper presents the use of kNN for LGD including resolved historical cases with a possibility of it to be applied to unresolved cases.
The remaining part of the paper is structured as follows. The Section 2 reviews recent developments in building LGD models using both resolved and unresolved cases. In Section 3, the data set and methodology used is described, including the undertaken approach. Our proposed algorithm for selecting variables is presented. Section 4 describes the conducted simulation and results obtained. Section 5 provided discussion and Section 6 presents the conclusions.
2. Literature Review
Due to the specific nature of the LGD distribution, a large variety of LGD models are currently in use. Within the empirical literature, we can distinguish parametric and non-parametric approaches in LGD modeling. The simplest parametric approach is using linear regression models based on debt characteristics and macroeconomic variables (Gupton and Stein 2002), (Bastos 2010, pp. 2510–17), (Altman et al. 2006). However, the linear model generally produces poorer predictive results. This is the reason that other parametric models have been tried for LGD estimation. Another popular method for estimating LGD parameters is logistic regression. It is better suited to LGD data because most observations are concentrated around two extreme values: 0 and 1. Two logistic models can be built to predict two extreme values of LGD parameter and they can be combined into one linear formula. This is an example of how predictions used for continuous and discrete targets can be combined together to estimate a continuous, bimodal LGD parameter.
Qi and Zhao (2011, pp. 2842–55), compared six methods for modelling LGD and found that non-parametric methods performed better than parametric ones. This approach was expanded by Li et al. (2016, pp. 17–47), who analysed some parametric models which were adjusted to the given bounded and bimodal distribution of the LGD parameter. According to their findings, advanced parametric models are not significantly superior to the simpler ones both in prediction or in rank-ordering. It was assumed that the model should be based on data specificity, ease of implementation and performance.
An approach that has been well established recently in estimating LGD is survival analysis. Before this occurred, survival analysis was evaluated in the credit risk models for the previous thirty years. The first attempt to employ this method in credit risk industry was made by (Narain 1992, pp. 109–21) and it was later expanded upon by others, namely: (Banasik et al. 1999, pp. 1185–90; Stepanova and Thomas 2002, pp. 277–89; Baesens et al. 2005, pp. 1089–98). When Basel II (BCBS 2006) requirements of the LGD parameter came into force, survival attracted attention for this parameter estimation. Some researchers, (Witzany et al. 2010, pp. 6–27; Privara et al. 2014; Zhang and Thomas 2012, pp. 204–15) proposed modelling the recovery process of a defaulted loan as a survival process using a Cox semi-parametric model.
Joubert et al. (2018, pp. 107–32) proposed the usage of survival analysis instead of traditional logistic regression. The results were compared using the mean squared error, bias and variance, and showed that the use of survival analysis increases the model’s predictive power. The proposed survival analysis approach was applied to two simulated and two retail bank datasets. This approach not only outperformed the logistic regression but also allowed usage of the censored observations and probability prediction over varying outcome periods. This approach was later extended by Joubert et al. (2021, pp. 1–17), who used the default weighted survival analysis (DWSA) method to estimate the LGD for the International Financial Reporting Standard’s (IFRS) 9 impairment requirements. Using the retail portfolio of a South African bank, the forward-looking LGD values in various macroeconomic scenarios were used and expected credit losses were calculated.
Eighteen years have passed since the new Capital Accord was published in June 2004. Over all of those years, there has been increasing interest in LGD modelling on the part of both academics and practitioners. Although there is an extensive literature about modelling and estimating LGD parameters, only a few studies have focused on taking incomplete recovery rates into account. According to the Global Credit Data report, LGD models must include unresolved defaults in the modelling process to avoid resolution bias (GCD 2020). The authors also point out that LGD models based only on the complete cases do not take recent developments into account, which in turn leads to the underestimation of recent losses. Extrapolations of historical recovery cash flows refined by the usage of risk drivers were proposed.
All of these assumptions follow from Article 181(1) of Regulation (EU) No 575/2013 (2013). This states that in relation to the use of all defaults observed during the historical observation period within the data sources for LGD estimation, institutions should ensure that the relevant information from incomplete recovery processes is taken into account in a conservative manner. The LGD estimation should be based on the long-run average LGD. Under paragraph 147 of the EBA Guidelines on PD and LGD, default observations that are very close to the time of the LGD estimation process (recent defaults close to the LGD time that is estimated) are part of the historical observation period and should be part of the reference dataset. The treatment of incomplete recovery processes for these recent defaults is more complex and could cause uncertainty to the LGD estimates. (Paragraph 158 of the EBA GL on PD and LGD) According to the ECB, institutions, to mitigate this risk, can establish a minimum period during which the default should be observed to be included in the calculation of the observed average LGD. This minimum period should be justified and all relevant information regarding defaults observed for a shorter period are considered in the LGD estimates. In any case, this period should not be longer than twelve months.
Rapisarda and Echeverry (2010) proposed a non-parametric estimator that aggregates complete and incomplete recovery profiles to produce unbiased estimates of LGD. According to them, this approach allows more efficient estimates of LGD than estimates obtained from the estimator based on resolved cases only. According to the authors, the incorporation of incomplete recoveries into LGD estimation implies the introduction of the recovery dynamics in terms of partial recovery at a given time after default. This allows for the breaking down of recovery histories into observation windows where they can be compared regardless of whether they relate to a complete or incomplete workout. According to Orlando and Pelosi (2020, pp. 1–22) LGD estimates should reflect the practice of each institution. Moreover, recovery times affect the level of loss. Therefore, in order to increase the recovery amount, the time of the recovery process should be minimized.
A conservative approach was presented by Baesens et al. (2016), who considered the incomplete cases as complete ones. However, there is a risk in this approach of revaluation of the final LGD values.
On the other hand, Starosta (2020, pp. 195–225) proposed the usage of parametric and non-parametric methods in order to estimate partial recovery rates for the incomplete defaults. For this purpose, the mossing recovery rate was calculated in pre-defined time intervals in order to move to the modelling process. Moreover, it was shown that risk drivers change with the age of the default.
Unresolved cases are incorporated by means of an estimator based on Kaplan and Meier (1958, pp. 457–81) and their study of mortality rates. It has been applied to estimate default rates (Altman (2006); Altman and Suggitt (2000, pp. 229–53)) and to the estimation of recovery rates (Dermine and Neto de Carvalho (2006, pp. 1219–43); Bastos (2010, pp. 2510–17)).
Betz et al. (2021, pp. 619–44) also considered resolved and unresolved cases, and for modelling purposes, used a Bayesian hierarchical modelling framework. The proposed method is applicable to the duration of recovery processes in general where the final outcomes depend on the duration of the process and are affected by censoring (unresolved cases). The authors also found that longer workout processes are connected with higher losses. The hierarchical approach diminishes parameter biases due to the exclusion of censored observations in a pure typical LGD model and, thus, enables adequate unconditional LGD predictions for the non-defaulted exposure and consistent conditional LGD predictions for the defaulted exposure within one modelling framework.
LGD estimation was also performed for the leasing data. Hartmann-Wendels et al. (2014, pp. 364–75) compared the effectiveness of parametric and non-parametric methods in and out of the sample to estimate the values of the LGD parameter for unperformed lease contracts. According to the authors, hybrid mixed models that attempt to reproduce the LGD distribution perform well for in-sampled estimation, but have produced poor out-of-sample results. In contrast, non-parametric models provided fairly accurate in-sample estimates and performed best out-of-sample. The obtained results suggest that the number of observations in the dataset affects the relative performance of the estimation methods. Moreover, sophisticated non-parametric estimation techniques achieved good results for large datasets, while they achieved simple OLS regression for smaller datasets. Other research focused on the leasing data was carried out by Kaposty et al. (2020, pp. 248–66). The authors found that advanced methods such as random forest, as well as updating information, improve the prediction accuracy. Moreover, it was indicated that outstanding exposure at the time of default, internal rating, types of standards and lessor industries seem to be significant factors affecting LGD predictions.
3. Research Methodology
LGD estimation is performed on the mortgage data from one financial institution for a period longer than ten years. The motivation to use mortgage data was due to the low default portfolio and long workout period (unresolved cases). The data was generated in 2021 and it includes both resolved and unresolved cases at this point. The share of unresolved cases in the entire sample is about 30%. The main goal of the methodology approach is to incorporate both types of observations into a single survival formula or to build a non-parametric kNN model to predict LGD for the whole population including unresolved cases.
The development data set is prepared for the performing customers who will enter default status in the next twelve months. All variables with more than 10% of missing values were removed from the data set. The missing values were replaced with the mean of the covariate. The entire dataset contains approximately 1770 observations and 380 variables which can be potentially used as model variables. The data set was then split into train and test samples at a proportion of 70/30.
For the building part of the kNN model, the train data set was limited to the resolved cases only, but the further usage of the model was devoted to the unresolved cases. The exclusion of unresolved cases from the development sample is necessary and obvious for the kNN model because the model builds the LGD estimator on the basis of historically collected and completed collection processes. Comparing the regression model with the kNN approach, the regression model built on the population of resolved cases uses the risk drivers and estimated weights based only on that portion of the whole population, while the kNN model builds final LGD estimation based on the customer’s characteristics and collateral and looks for similar historical cases. Our results of the kNN approach can be used to estimate the LGD of unresolved cases despite the fact that we did not use these cases in the estimation procedure.
The initial step of model building is the selection of significant variables. It was made using the Hpforest SAS procedure. This is a known, effective procedure to select important variables for the model building process. The following variables in Table 1 have been selected as the most significant ones and the further estimation procedure is based only on the selected set of variables.

Table 1.
Quality statistics of variables.
Table 1 shows the most significant variables selected by quality statistics produced by the Hpforest procedure such as:
- MSE—mean square error,
- AAE—absolute error,
- MSEOOB—mean square error out of bag,
- AAEOOB—absolute error out of bag,
- Rank—the final rank used for the variables’ selection based on MSEOOB and MSE generated by the SAS hpforest procedure.
As the number of trees increases, the fit statistics usually improve (decrease) at first and then level off and fluctuate in a small range. Forest models provide an alternative estimate of average square error and misclassification rate, called the out-of-bag (OOB) estimate. The OOB estimate is a convenient substitute for an estimate that is based on test data and is a less biased estimate of how the model will perform on future data. The list shows that the OOB error estimate is worse than the estimate that evaluates all observations on all trees.
For the purposes of this paper, a combination of two statistics, MSEOOB and MSE, was used. The resulting rank statistic is then used to estimate the importance of all variables. The proposed approach was used because the MSEOOB seems to produce inadequate results for variables due to the limited number of observations in the out of bag sample, otherwise it would be the best choice for final ranking (Table 1). We assumed a 0.7 weight for it.
The rank is defined as follows:
where
Rank = ((MSEOOB, 0.000001) × 0.7 + (MSE, 0.000001) × 0.3, 0.00001);
- (.,0.00001)—mathematical rounding down transformation to 6 decimal places,
- MSE—mean square error calculated on the train sample,
- MSEOOB—mean square error calculated on the out of bag sample,
Hpforest SAS procedure was used with the following parameters:
hpforest(maxtrees = 300 vars_to_try = 50 seed = 600 trainfraction = 0.6
maxdepth = 50 leafsize = 6 alpha = 0.1)
maxdepth = 50 leafsize = 6 alpha = 0.1)
Ultimately, the data set was randomly split into the train and test data set to ensure 70% observations in the train data set. The above selection of variables was applied to both models built in the paper.
3.1. Non-Parametric Approach
The kNN model was built assuming the following Euclidian metric between observations in the test and train sample:
where:
- x = (x1, … xn) is the vector of variables for the observation from the test sample
- y = (y1, …yn) is the vector of variables for the observation from the train sample
- n is the number of variables.
The test set is separate from the train data set. It includes the cases for which neighbours from the train set are selected. The share of the test set in the population is 30%, while the share of the train is 70%.
The model was built in SAS but the original proprietary algorithm was implemented as there is no KNN regression procedure in SAS except the KRIEGE2D procedure, which is very limited in our application. The built algorithm helps to select important variables for the model and to choose the optimal number of neighbours as well as the number of variables in the model.
Before the metric was applied, all variables were normalized due to the following transformation to ensure the same meaning of distance calculation.
The kNN algorithm finds for each observation in the test set the neighbourhood included in the train set and calculates the average LGD on this basis. The kNN model was performed many times for the number of neighbours (from 1 to 70) and number of variables used in the Euclidian metric from 1 to 20. In total it was used 1400 times. The results of R2 for all choices are shown in the figures included in Table 2. In each iteration of the model sequence, only the variables correlated on the level lower than 70% in terms of the Pearson coefficient were adopted for the model.

Table 2.
KNN model structure.
For each observation from the test data set, the neighbours, the metric and the predicted LGD were assigned based on the observations from the train data set and then compared to the realized LGD. All these iterations and the proposed approach help to find the final model structure with the best quality, and this means that a set of variables and number of neighbours will be selected for further use for LGD estimation. Next, the selected model is ready for use in production, e.g., for unresolved cases.
3.2. Survival Approach
In the semi-parametric model, the so called Cox proportional hazards model, only the regression part is parametrically specified, while the time distribution is not parametrically specified (non-parametric approach). It is assumed that the continuous variable T means the time until the occurrence of the event, in this case the end of the workout period. For the Cox regression model, the hazard function is given by:
where:
- h0(t)—base hazard, parametrically non-specified function of time,
- x1, x2, … xk—explanatory variables.
Cox (1972, pp. 187–220) proposed using the novel approach based on the partial maximum likelihood method to estimate the semi-parametric models. In this approach, the integrity function is divided into two parts: the first part only containing the parameters, and the second part containing the parameters and the hazard function as well.
The main advantage of the Cox model is the assessment of the explanatory variables’ dependence on the process without the necessity of the specification of the baseline hazard h0(t). However, the main disadvantage of the Cox model is the proportionality assumption (Blossfeld and Rohwer 2002). This assumption requires the hazard rate to be fixed for each pair of individuals at any time. When the proportionality assumption is violated, the additional time-dependent variables can be included. In this case, the model is named the non-proportional hazards Cox regression model. The results of Cox model estimation are not only the parameters describing the dependence of explanatory variables on the probability and on the base hazard, but it is also possible to include censored information about the customer. This is the main advantage in incorporating unresolved cases (unfinished workout period). All assumptions applied in typical regression models, such as the: normality assumption, noncollinearity assumption, etc. continue to apply in this case as well.
4. Results of Application on Real LGD Data
4.1. Results for kNN Non-Parametric Model
The dependency between the number of neighbours and the value of R2 was analysed, and the results are presented in Table 2. It can be seen that the increasing number of neighbours (k) influences this dependency. For a smaller number of neighbours (1–10), the R2 values do not exceed 0.2, and the lines presenting the value of k are divergent.
As the number of neighbours increases, the relationship becomes greater and more visible. In addition, there are also visible jumps in this relationship if we increase the number of variables, more or less when the variables increase by five. Once the variable level of 10 is reached, subsequent increases are not so visible. The greatest increase is for the first five variables (up to 0.22) and then for 10 (up to 0.24). As the number of neighbours grows, the curves representing the relationships smooth out, and they get closer and closer until they practically coincide for the neighbours in the last category (where k is between 61 and 70). This is a completely different relationship than for the number of neighbours between 1 and 10, which are practically separate. As the number of neighbours (k) increases, the lines representing dependencies get closer.
The final model was established in accordance with the principle of minimizing the number of neighbours and the number of variables, while not reducing the quality of the model. The highest R2 obtained was around 25% and relates to the number of variables from 6 to 15 and the number of neighbours around 40–70 (Figure 1 and Figure 2). The proposed model follows the above principle and assumes six variables and 25 neighbours and gives an R2 equal to 23.8%. The drop in the quality of the model is meaningless but the number of neighbours decreased significantly. The structure of the model is shown in Table 2. The first column contains the variable name, the second column contains the mean of the variable, and the third one contains the standard deviation of the variable. The final LGD estimation is based on the average of LGD for neighbours, where the metric is calculated from Formula (2), but variables are normalized due to Formula (3).
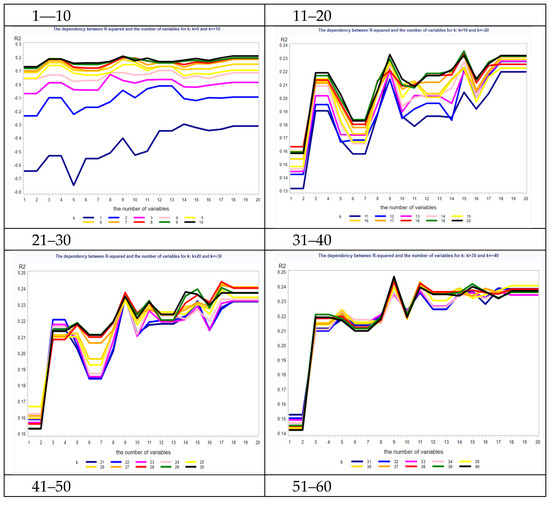
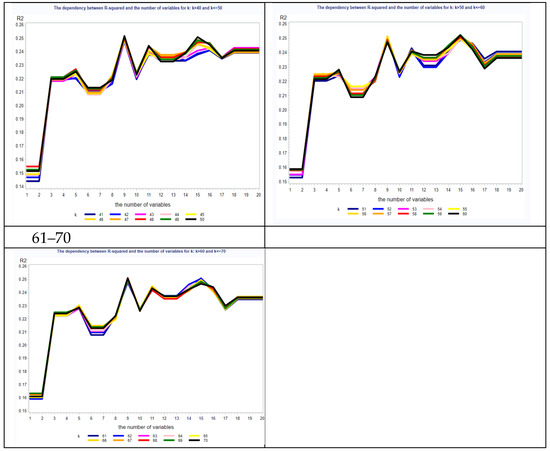
Figure 1.
Results of discriminatory power of the model split by the number of neighbors in the batches.
Figure 2.
Results of discriminatory power of the model split by the number of variables used in the metric in the batches.
Published studies Zhang and Thomas (2012, pp. 204–15), Matuszyk et al. (2010, pp. 393–98) show that LGD predictions based on linear or logistic regression do not have high performance values, usually obtaining a value of R2 around 10%. In comparison, results obtained by Witzany et al. (2010, pp. 6–27) confirmed that the survival methods utilizing partial recovery observations provide significantly better ex ante predictions with R2 exceeding 15%. The authors proposed the modification of the survival methods, in particular the pseudo Cox model, based on the minimization of squared differences on the last known recovery rates, which outperformed all of the other methods.
4.2. Results for Survival Cox Regression Model
For Cox regression, only the first 20 variables with highest rank values were used (see Table 1). Once the correlated and insignificant variables were eliminated, there were four final variables in the model (see Table 3). The end of the workout process (resolved) n = 1516 was set up as the event, and all observations with an unfinished workout period (unresolved) were censored n = 722 (32.26%).

Table 3.
Cox model results.
The estimate of the linear predictor was split into four buckets using the values of the quantiles which divided the data into four parts. The first quartile (Q1) = −0.5592632, the second quartile (Q2) median = −0.3201044, the third quartile (Q3) = −0.0791387. According to this the following four PI groups were created:
- PI1 for predictor < −0.5592632
- PI2 for predictor≥ −0.5592632 and predictor < −0.3201044
- PI3 for predictor ≥ −0.3201044 and predictor < −0.0791387
- PI4 for predictor ≥ −0.0791387
For each PI group the product-limit survival curves were generated and compared.
Plots of Kaplan-Meier product limit estimates of survival for each distinguished group (PI1–PI4) are presented in Figure 3. Customers grouped in PI1 appear to have a higher survival rate than customers in the other remaining groups. The median survival time for those grouped in PI1 appears to be 1800 days versus about 1400 days in PI2, 700 in PI3, and 550 in PI4.
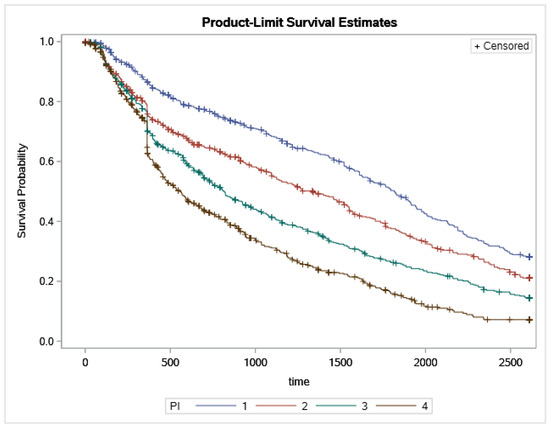
Figure 3.
Product-Limit Survival Curves.
To compare survival between groups we used the log-rank test. The null hypothesis is that there is no difference in survival between the groups or that there is no difference between the groups in the probability of default at any point.
The results of the homogeneity tests across PI groups are given in Table 4. The log-rank and Wilcoxon statistics and their corresponding covariance matrices are displayed. Table 5 consists of the approximate chi-square statistics, degrees of freedom, and p-values for the log-rank, Wilcoxon, and likelihood ratio tests. All three tests indicate strong evidence of a significant difference among the survival curves for four PI groups (p < 0.001). Calculations were obtained from the Lifetest procedure in SAS.

Table 4.
Testing Homogeneity of Survival Curves.

Table 5.
Testing the Homogeneity of Survival Curves.
Mean values of the empirical LGD for pools in the Cox model. Pools were created as deciles of predictor values. Pools 6 and 7 were merged as well as pools 9 and 10 in order to achieve the monotonicity.
5. Discussion
The main purpose of this research is to propose new LGD estimation approaches that provide more effective results and include the unresolved cases in the estimation procedure. The motivation for the project was the fact that many LGD models discussed in the literature are based only on the complete cases. There is a risk that such an approach can underestimate the recent losses. Our proposal proved the usefulness of our approach for LGD modelling, because the approach of treating incomplete cases as complete does not produce the best results (Baesens et al. 2016). Furthermore, according to Rapisarda and Echeverry (2010), consideration of the complete and incomplete cases allows more efficient estimates of mean LGD than those obtained from the estimator based on resolved cases only.
For this purpose, we built a model based on the kNN method and estimated LGD including resolved cases, but it could be used for unresolved cases as well. According to the results obtained, the proposed approach outperformed the traditional Cox model. The main advantage, however, of the survival approach is the straightforward incorporation of unresolved cases into the model (Dermine and Neto de Carvalho 2006; Bastos 2010). As mentioned in Baesens et al. (2016), considering only complete observations creates the risk of the overestimation of the LGD. In our research we decided to apply a methodology that allows the usage of incomplete observations in order to reduce such bias.
We also propose a novel algorithm for selecting the risk drivers which is based on MSEOOB and MSE generated by the SAS hpforest procedure. To the best of our knowledge, this algorithm has never been applied in research.
Results for the non-parametric approach suggest that the relationship between number of neighbours (k) and values of R2 become greater and more visible. Moreover, as the number of neighbours increases, the lines representing dependencies get closer. This finding confirms results achieved in the research done by Qi and Zhao (2011), where the non-parametric approach outperformed the parametric one.
The final model was established in accordance with the rule minimizing the number of neighbours and the number of variables while not reducing the quality of the model. The highest R2 obtained was approximately 25% and relates to the number of variables from 6 to 15 and the number of neighbours being about 40–70. For comparison, the highest performance values usually obtained a value of R2 around 10% for banking data (Zhang and Thomas 2012; Matuszyk et al. 2010). In comparison, results obtained by Witzany et al. (2010) confirmed that the survival methods utilizing partial recovery observations provide significantly better ex ante predictions, with R2 exceeding 15%, which is still significantly below the 25% obtained in our model.
The successful application of the survival analysis in other studies for LGD modelling (Witzany et al. 2010; Privara et al. 2014; Zhang and Thomas 2012; Joubert et al. 2018) encouraged us to apply this approach in our analysis. In the case of the survival Cox regression model, we approached comparison differently because we treated the end point of the workout period as the event in our model and the unfinished workout period as censored cases. In a Cox model, the linear predictor was split into four buckets, using the values of the quantiles, and the data was divided into four equal groups. For each group, the product-limit survival curves were generated and compared. The median survival time for customers was different in each group, ranging from 550 to 1800 days. To estimate LGD, we calculated empirical LGD in pools and proposed those values as LGD approximation.
Despite the lower values of R2 achieved for the Cox survival model compared to the kNN method, we can still consider the model to be at the medium performance level and to provide the advantage of the inclusion of unresolved cases. For future research, we would like to delve into survival modelling incorporating randomness such as random survival trees. As survival approach was outperformed by the kNN method, we will also concentrate on finding a way to optimize this algorithm.
6. Conclusions
In our paper, we considered the use of unresolved cases when estimating the LGD parameter. We examined a new non-parametric kNN method for estimating LGD that provides better performance than the traditional semi-parametric Cox survival model. The final model was established in accordance with the rule minimizing the number of neighbours and the number of variables, while not reducing the quality of the model. The highest R2 obtained equals approximately 25%. For comparison, the highest performance values of R2 were usually around 10% for real banking data. The performance of this model gives an advantage in LGD modelling. Furthermore, we also propose a novel algorithm for selecting the risk drivers, which seems promising in terms of further research. Despite the fact that we analysed only one portfolio, our proposal can be applied in practice. Using the kNN method for estimating LGD is applicable in the banking system, as banks have access to more and more data available on a daily basis, in addition to having more powerful computers to perform such analyses.
Author Contributions
Conceptualization, A.P.-C. and P.K.; methodology, A.P.-C. and P.K.; software, A.P.-C. and P.K.; validation, A.P.-C., P.K. and A.M.; formal analysis, A.P.-C. and P.K.; investigation, A.P.-C.; resources, A.P.-C.; data curation, P.K.; writing—original draft preparation, A.P.-C., P.K. and A.M.; writing—review and editing, A.P.-C. and A.M.; visualization, A.P.-C. and P.K.; supervision, A.P.-C.; project administration, A.P.-C.; funding acquisition, Not Applicabe. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Altman, Edward I. 2006. Default Recovery Rates and LGD in Credit Risk Modeling and Practice: An Updated Review of the Literature and Empirical Evidence. Working Paper. New York: NYU Salomon Center, November. [Google Scholar]
- Altman, Edward I., and Heather J. Suggitt. 2000. Default rates in the syndicated bank loan market: A mortality analysis. Journal of Banking and Finance 24: 229–53. [Google Scholar] [CrossRef]
- Altman, Edward I., Andrea Resti, and Andrea Sironi. 2006. Default Recovery Rates: A Review of the Literature and Recent Empirical Evidence. NYU Working Paper No. S-CDM-03-11. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1295797 (accessed on 2 March 2022).
- Baesens, Bart, Daniel Roesch, and Herald Scheule. 2016. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Hoboken: John Wiley & Sons. [Google Scholar]
- Banasik, John, Jonathan N. Crook, and Lyn C. Thomas. 1999. Not if but when will borrowers default. The Journal of the Operational Research Society 50: 1185–90. [Google Scholar] [CrossRef]
- Baesens, Bart, Tony van Gestel, Maria Stepanova, and Jan Vanthienen. 2005. Neural network survival analysis for personal loan data. Journal of the Operational Research Society 59: 1089–98. [Google Scholar] [CrossRef]
- Bastos, Joao. 2010. Forecasting bank loans loss-given-default. Journal of Banking & Finance 34: 2510–17. [Google Scholar] [CrossRef]
- BCBS. 2006. Basel II: International Convergence of Capital Measurement and Capital. Standards: A Revised Framework-Comprehensive Version. Available online: https://www.bis.org/publ/bcbs128.htm (accessed on 2 March 2022).
- BCBS. 2017. Basel Committee on Banking Supervision, Guidelines on PD Estimation, LGD Estimation and the Treatment of Defaulted Exposures. Available online: https://www.bis.org/bcbs/publ/d423.pdf (accessed on 2 November 2022).
- Betz, Jennifer, Ralf Kellner, and Daniel Rösch. 2021. Time matters: How default resolution times impact final loss rates. Journal of the Royal Statistical Society Series C, Royal Statistical Society 70: 619–44. [Google Scholar] [CrossRef]
- Blossfeld, Hans-Peter, and Gotz Rohwer. 2002. Techniques of Event History Modeling: New Approaches to Causal Analysis, 2nd ed. London: Psychology Press. [Google Scholar]
- Committee of European Banking Supervision. 2006. Guidelines on the implementation, validation and assessment of Advanced Measurement (AMA) and Internal Ratings Based (IRB) Approaches. London: Committee of European Banking Supervision. [Google Scholar]
- Cox, David R. 1972. Regression Models and Life-Tables. Journal of the Royal Statistical Society. Series B (Methodological) 34: 113–20. [Google Scholar] [CrossRef]
- Dermine, Jean, and Cristina Neto de Carvalho. 2006. Bank loan losses-given-default: A case study. Journal of Banking and Finance 30: 1219–43. [Google Scholar] [CrossRef]
- Global Credit Data. 2020. Report—Unresolved Defaults LGD Study. Available online: https://globalcreditdata.org/gcd_library/unresolved-defaults-lgd-study-2020 (accessed on 2 March 2022).
- Gupton, Greg, and Roger Stein. 2002. LossCalcTM: Model for predicting loss given default (LGD), Moody’s Rating Methodology. Available online: https://admin.epiq11.com/onlinedocuments/trb/examinerreports/EX%200299.pdf (accessed on 2 November 2022).
- Hartmann-Wendels, Thomas, Patrick Miller, and Eugen Töws. 2014. Loss given default for leasing: Parametric and nonparametric estimations. Journal of Banking and Finance 40: 364–75. [Google Scholar] [CrossRef]
- Joubert, Morne, Tanja Verster, and Helgard Raubenheimer. 2018. Making use of survival analysis to indirectly model loss given default. ORiON 34: 107–32. [Google Scholar] [CrossRef]
- Joubert, Morne, Tanja Verster, Helgard Raubenheimer, and Willem D. Schutte. 2021. Adapting the default weighted survival analysis modelling approach to model IFRS 9 LGD. Risks 9: 103. [Google Scholar] [CrossRef]
- Kaplan, E.L., and Paul Meier. 1958. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association 53: 457–81. [Google Scholar] [CrossRef]
- Kaposty, Florian, Johannes Kriebel, and Matthias Löderbusch. 2020. Predicting loss given default in leasing: A closer look at models and variable selection. International Journal of Forecasting 36: 248–66. [Google Scholar] [CrossRef]
- Li, Philip, Min Qi, Xiaofei Zhang, and Xinlei Zhao. 2016. Further Investigation of Parametric Loss Given Default Modeling. Journal of Credit Risk 12: 17–47. [Google Scholar] [CrossRef]
- Matuszyk, Anna, Christophe Mues, and Lyn C. Thomas. 2010. Modelling LGD for unsecured personal loans: Decision tree approach. Journal of the Operational Research Society 61: 393–98. [Google Scholar] [CrossRef]
- Narain, B. 1992. Survival Analysis and the Credit Granting Decision. In Credit Scoring and Credit Control. Edited by Lyn C. Thomas, Jonathan N. Crook and David B. Edelman. Oxford: Oxford University Press. [Google Scholar]
- Orlando, Giuseppe, and Roberta Pelosi. 2020. Non-Performing loans for Italian companies: When time matters. An empirical research on estimating probability to default and loss given default. International Journal of Financial Studies 8: 68. [Google Scholar] [CrossRef]
- Privara, Samuel, Marek Kolman, and Jiri Witzanty. 2014. Recovery Rates in Consumer Lending: Empirical Evidence and the Model Comparison. Available online: https://ssrn.com/abstract=2343069 (accessed on 2 November 2022).
- Qi, Min, and Xinlei Zhao. 2011. Comparison of modeling methods for Loss Given Default. Journal of Banking and Finance 35: 2842–55. [Google Scholar] [CrossRef]
- Rapisarda, Grazia, and David Echeverry. 2010. A Non-Parametric Approach to Incorporating Incomplete Workouts into Loss Given Default Estimates. MPRA Paper No 26797. Edinburgh: Royal Bank of Scotland. [Google Scholar]
- Regulation (EU) No 575/2013 of the European Parliament and of the Council of 26 June 2013 on Prudential Requirements for Credit Institutions and Investment Firms and Amending Regulation (EU) No 648/2012 Text with EEA Relevance. 2013. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex%3A32013R0575 (accessed on 2 November 2022).
- Starosta, Wojciech. 2020. Modelling recovery rate for incomplete defaults using time varying predictors. Central European Journal of Economic Modelling and Econometrics 12: 195–225. Available online: https://ideas.repec.org/a/psc/journl/v12y2020i2p195-225.html (accessed on 2 March 2022).
- Stepanova, Maria, and Lyn C. Thomas. 2002. Survival analysis methods for personal loan data. Operations Research 50: 277–89. [Google Scholar] [CrossRef]
- Witzany, Jiri, Michal Rychnovsky, and Pavel Charamza. 2010. Survival analysis in LGD modeling. European Financial and Accounting Journal 7: 6–27. [Google Scholar] [CrossRef]
- Zhang, Jie, and Lyn C. Thomas. 2012. Comparisons of linear regression and survival analysis using single and mixture distributions approaches in modelling LGD. International Journal of Forecasting 28: 204–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).