A Forward-Looking IFRS 9 Methodology, Focussing on the Incorporation of Macroeconomic and Macroprudential Information into Expected Credit Loss Calculation
Abstract
1. Introduction
2. Literature Review
3. Methodology
- Perform PCA on the explanatory variables to obtain the principal components , where and the orthonormal set of eigenvectors. Then, select a subset , with , where and the th eigenvalue of .
- Regress the observed vector of outcomes on the selected principal components as covariates, , using ordinary least squares regression to obtain a vector of estimated regression coefficients, , with dimension equal to the number of selected principal components
- Transform the vector back to the scale of the actual covariates , using the selected PCA loadings (the eigenvectors corresponding to the selected principal components) to obtain the final PCR estimator (with dimension equal to the total number of covariates) for estimating the regression coefficients characterising the original model.
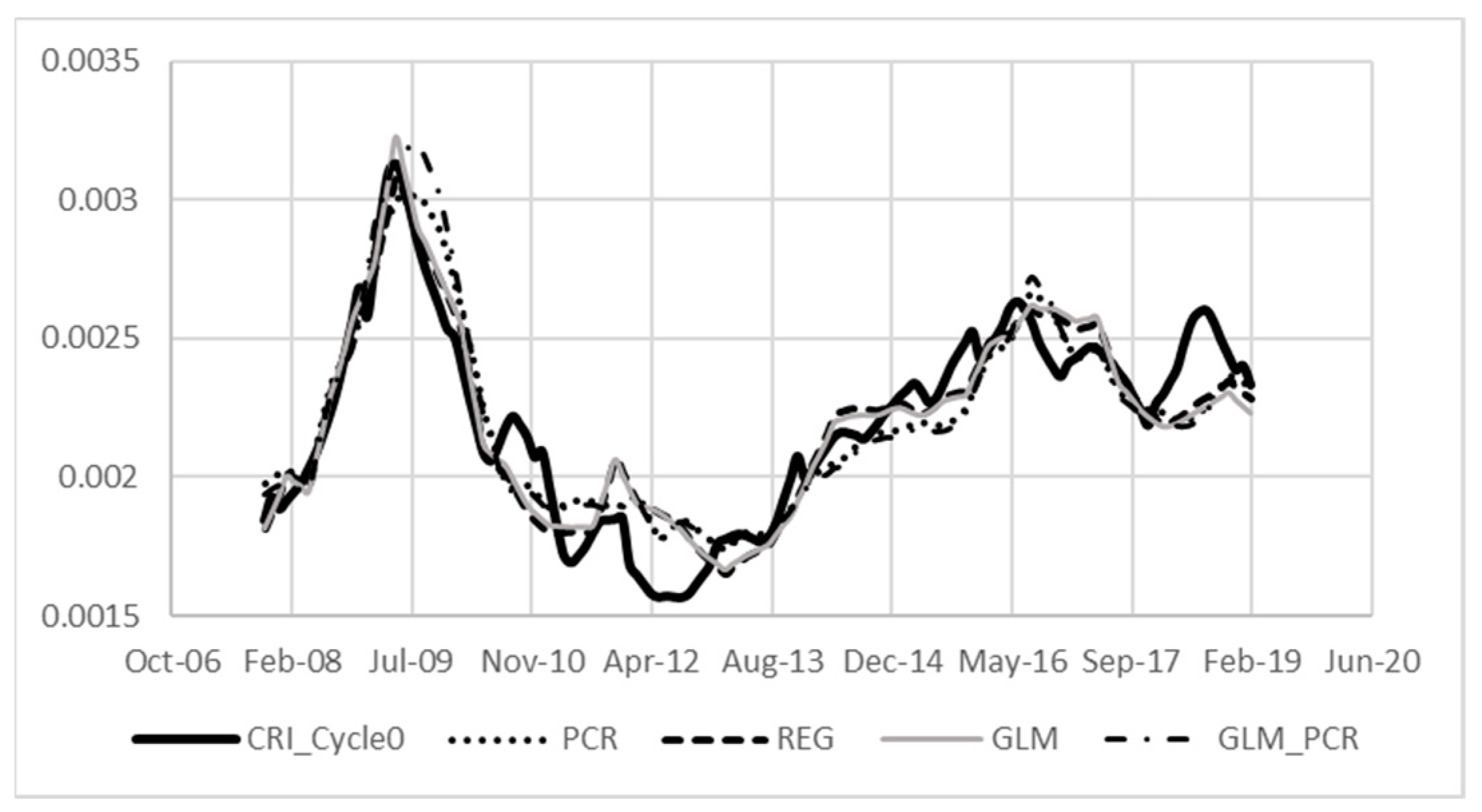
3.1. Credit Risk Index
- Limiting the CRI to the observation that was observed in the last 12 months ensures having the same “horizons” for all observation months. If it is not limited to the last 12 months, some months will have a different number of observation months, and the denominator will not be equal over time.
- Using 12 months ensures that the changes in macroeconomic conditions are reflected in more recent populations and not confused with the behaviour far in the past (i.e., more than 12 months ago).
- The CRIs included in the development data are based only on up-to-date accounts. This is due to the assumption that an increase in credit risk has already impacted accounts that have missed at least one payment, and the behaviour of these accounts is thus more likely to be driven by a deteriorated probability of default than a deteriorated economic outlook. In addition, these up-to-date accounts have an expected lifetime of 12 months according to IFRS 9 principles (i.e., Stage 1), which serve as further motivation for specifically using a 12-month outcome period in the CRI calculation.
3.2. Principal Component Regression
- The estimated sign for the regression coefficients of the macroeconomic variables should be in line with economic expectations. For example, the estimated sign for the GDP coefficient should be negative since we expect default rates to decrease when GDP increases (see Durović 2019).
- All estimated coefficients of are statistically significant at significance level, for example, (see Durović 2019).
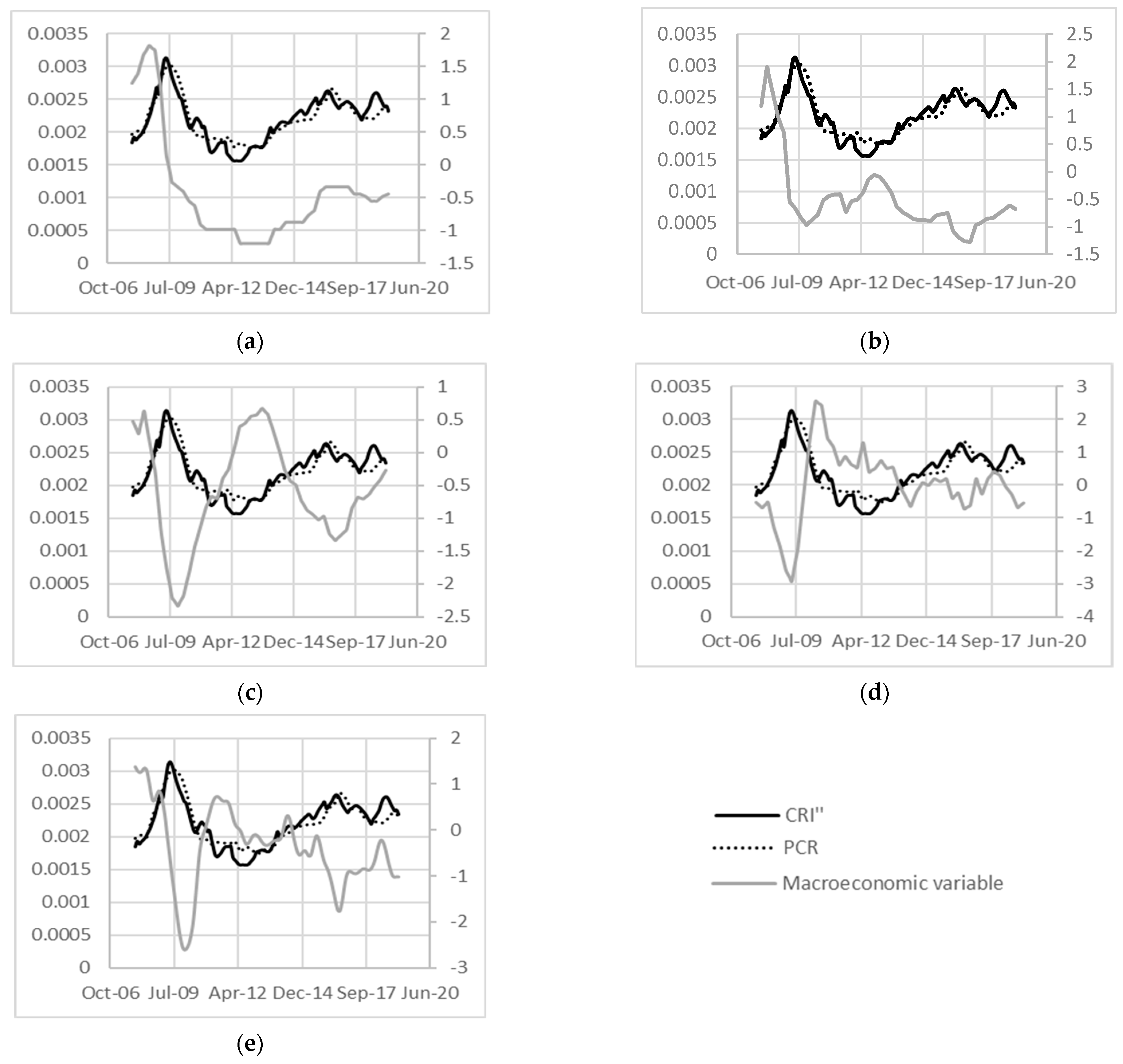
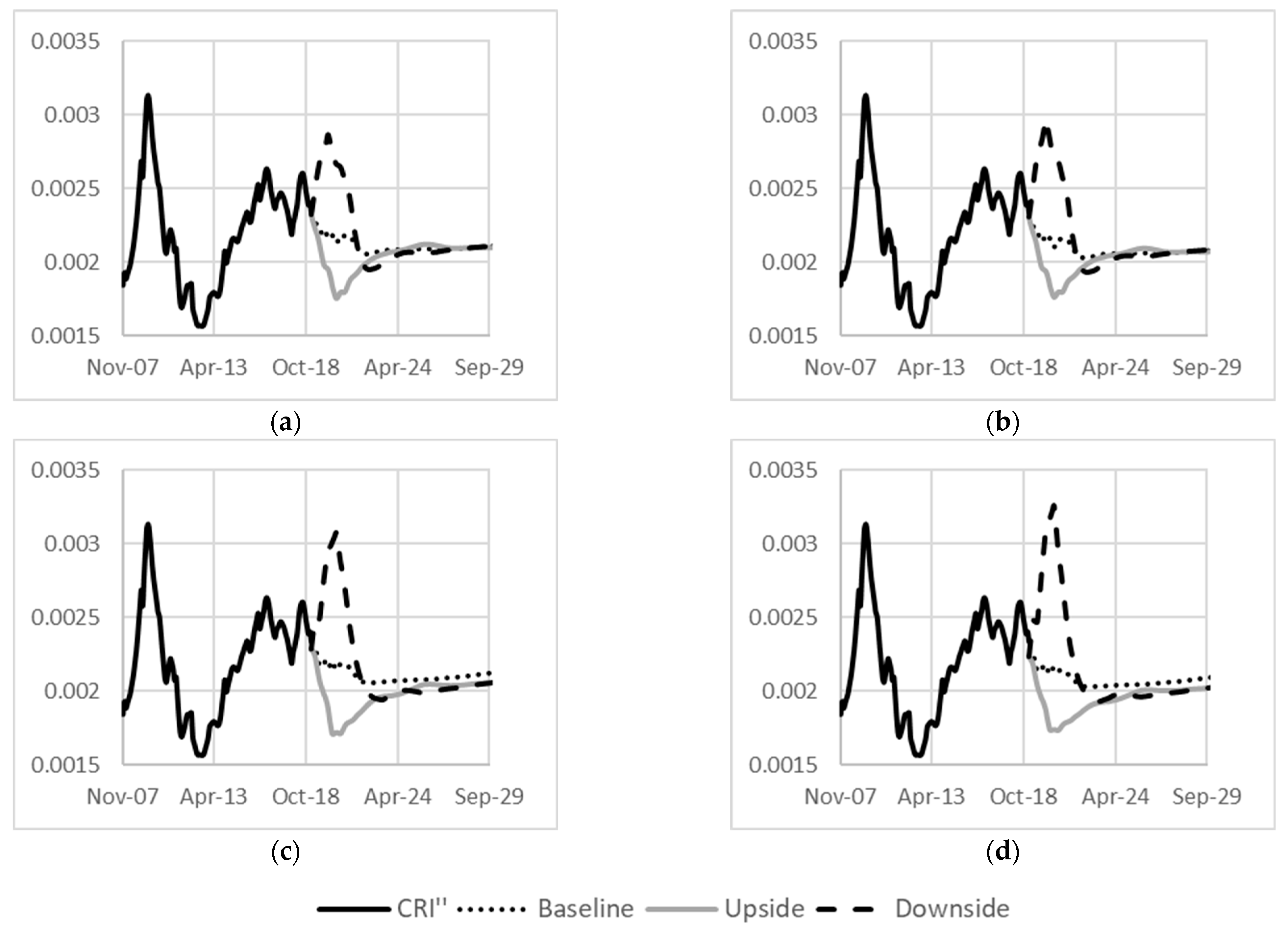
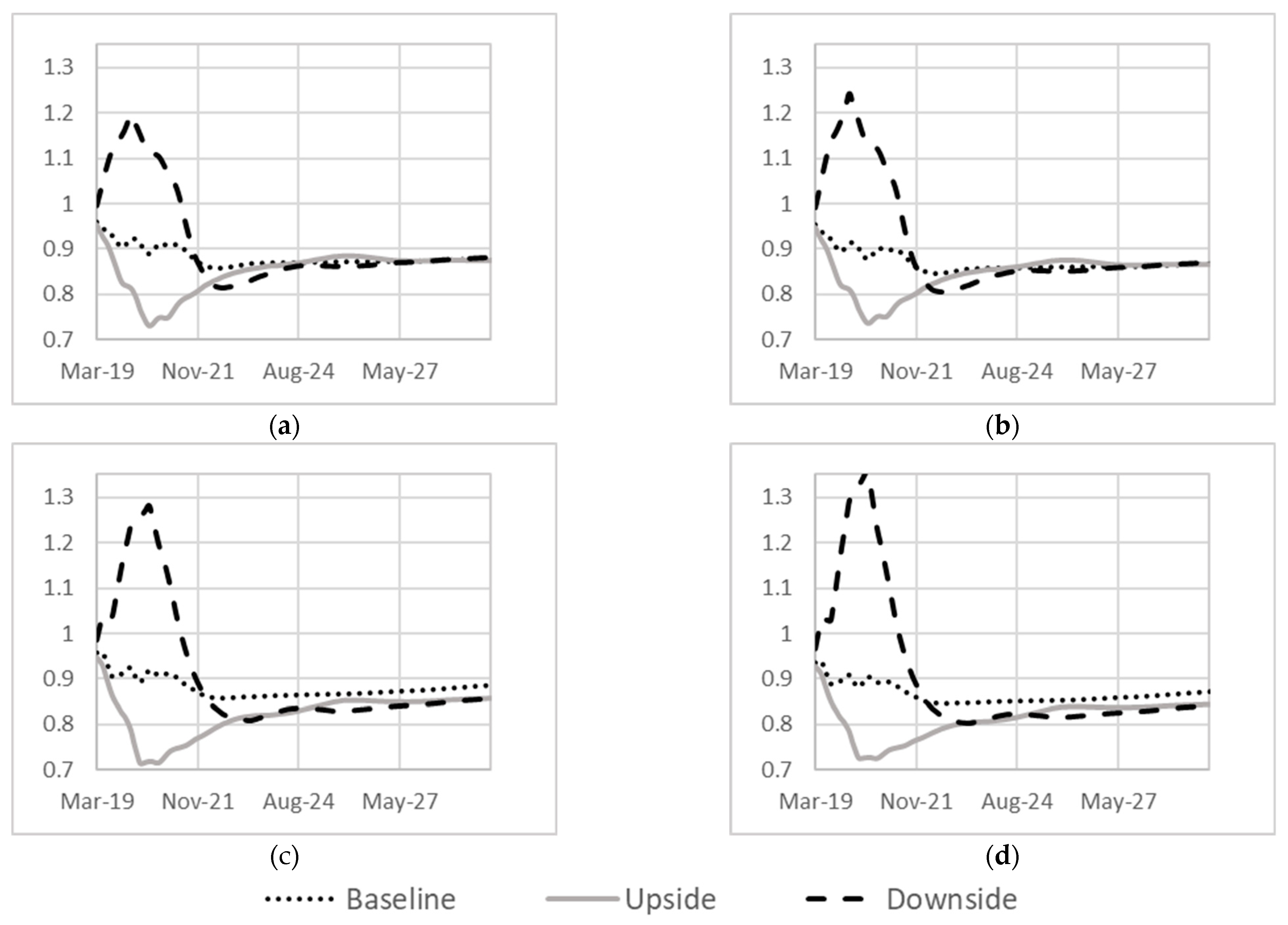
3.3. Derivation of the Macroeconomic Scalar
4. Case Study
4.1. Data
- Real gross domestic product (GDP);
- Nominal gross domestic product (NGDP);
- Consumer price index (CPI);
- House price index (HPI);
- Prime rate (PR);
- Total disposable household income (DHI);
- Household debt to disposable income (HDDI);
- Debt Service Ratio (DSR);
- New vehicle sales (NVS);
- Credit extended to households (CEH);
- Monetary credit extended (MCE);
- Instalment debtors (ID);
- Overdrafts and loans (OL).
4.2. PCR
4.3. Macroeconomic Scalar
5. Conclusions & Future Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bellini, Tiziano. 2019. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS, 1st ed. London: Elsevier. [Google Scholar]
- Bellotti, Tony, and Jonathan Crook. 2013. Forecasting and stress testing credit card default using dynamic models. International Journal of Forecasting 29: 563–74. [Google Scholar] [CrossRef]
- Black, Barnaby. 2016. Probability-Weighted Outcomes Under A Macroeconomic Approach. Available online: https://www.moodysanalytics.com/webinars-on-demand/2016/probablility-weighted-outcomes-macroeconomic-approach (accessed on 9 January 2023).
- Breed, Douw Gerbrand, Niel van Jaarsveld, Carsten Gerken, Tanja Verster, and Helgard Raubenheimer. 2021. Development of an Impairment Point in Time Probability of Default Model for Revolving Retail Credit Products: South African Case Study. Risks 9: 208. [Google Scholar] [CrossRef]
- Cleveland, William S. 1979. Robust Locally Weighted Regression and Smoothing Scatterplots. Journal of the American Statistical Association 74: 829–36. [Google Scholar] [CrossRef]
- Cleveland, William S. 1981. LOWESS: A program for smoothing scatterplots by robust locally weighted regression. The American Statistician 35: 54. [Google Scholar] [CrossRef]
- Crook, Jonathan, and Tony Bellotti. 2010. Time varying and dynamic models for default risk in consumer loans. Journal of the Royal Statistical Society: Series A (Statistics in Society) 173: 283–305. [Google Scholar] [CrossRef]
- Durović, Andrija. 2019. Macroeconomic Approach to Point in Time Probability of Default Modeling—IFRS 9 Challenges. Journal of Central Banking Theory and Practice 1: 209–23. [Google Scholar] [CrossRef]
- Engelmann, Bernd. 2021. A Simple and Consistent Credit Risk Model for Basel II/III, IFRS 9 and Stress Testing when Loan Data History Is Short. Available online: http://dx.doi.org/10.2139/ssrn.3926176 (accessed on 14 February 2022).
- Fine, Jason P., and Robert J. Gray. 1999. A Proportional Hazards Model for the Subdistribution of a Competing Risk. Journal of the American Statistical Association 94: 496–509. [Google Scholar] [CrossRef]
- Global Public Policy Committee (GPPC). 2016. The Implementation of IFRS 9 Impairment Requirements by Banks: Considerations for Those Charged with Governance of Systemically Important Banks. Global Public Policy Committee. Available online: http://www.ey.com/Publication/vwLUAssets/Implementation_of_IFRS_9_impairment_requirements_by_systemically_important_banks/$File/BCM-FIImpair-GPPC-June2016%20int.pdf (accessed on 7 September 2021).
- Hotelling, Harold. 1933. Analysis of a Complex of Statistical Variables into Principal Components. Journal of Educational Psychology 24: 417–441, 498–520. [Google Scholar] [CrossRef]
- IFRS. 2014. IRFS9 Financial Instruments: Project Summary. Available online: http://www.ifrs.org/Current-Projects/IASB-Projects/Financial-Instruments-A-Replacement-of-IAS-39-Financial-Instruments-Recognitio/Documents/IFRS-9-Project-Summary-July-2014.pdf (accessed on 31 January 2016).
- Jacobs, Michael. 2019. An Analysis of the Impact of Modeling Assumptions in the Current Expected Credit Loss (CECL) Framework on the Provisioning for Credit Loss. Journal of Risk & Control 6: 65–112. [Google Scholar]
- Jiang, Yixiao. 2022. A Primer on Machine Learning Methods for Credit Rating Modeling. In Econometrics-Recent Advances and Applications. London: IntechOpen. [Google Scholar] [CrossRef]
- Jolliffe, Ian T. 1982. A note on the Use of Principal Components in Regression. Journal of the Royal Statistical Society, Series C 31: 300–3. [Google Scholar] [CrossRef]
- Lessmann, Stefan, Bart Baesens, Hsin-Vonn Seow, and Lyn Thomas. 2015. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. European Journal of Operational Research 247: 124–36. [Google Scholar] [CrossRef]
- Pearson, Karl. 1901. On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine 6: 559–72. [Google Scholar] [CrossRef]
- PWC. 2017. In Depth IFRS 9 Impairment: How to Include Multiple Forward-Looking Scenarios. London: PWC. [Google Scholar]
- SAS Institute. 2013. SAS/STAT 13.1 User’s Guide: The LOESS Procedure. Cary: SAS Institute Inc. [Google Scholar]
- Schutte, Willem Daniel, Tanja Verster, Derek Doody, Helgard Raubenheimer, and Peet Jacobus Coetzee. 2020. A proposed benchmark model using a modularised approach to calculate IFRS9 expected credit loss. Cogent Economics & Finance 8: 1735681. [Google Scholar]
- Simons, Dietske, and Ferdinand Rolwes. 2009. Macroeconomic Default Modeling and Stress Testing. International Journal of Central Banking 5: 177–204. [Google Scholar]
- Tasche, Dirk. 2013. The art of probability-of-default curve calibration. Journal of Credit Risk 9: 63–103. [Google Scholar] [CrossRef]
- Tasche, Dirk. 2015. Forecasting Portfolio Credit Default Rates. Available online: https://www.bayes.city.ac.uk/__data/assets/pdf_file/0015/256101/TASCHE-Dirk-10.02.2015.pdf (accessed on 22 April 2022).

| Observation Date | Performing Accounts | Months after Observation (t) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 201509 | 1167 | 4 | 7 | 12 | 41 | 45 | 40 | 34 | 41 | 32 | 36 | 35 | 35 |
| 201510 | 1180 | 4 | 7 | 10 | 46 | 42 | 35 | 44 | 36 | 40 | 38 | 37 | 40 |
| 201511 | 1208 | 4 | 7 | 20 | 45 | 38 | 45 | 38 | 43 | 40 | 42 | 42 | 40 |
| 201512 | 1221 | 3 | 13 | 18 | 40 | 48 | 38 | 43 | 44 | 43 | 44 | 43 | 34 |
| 201601 | 1220 | 7 | 10 | 13 | 49 | 39 | 41 | 42 | 43 | 44 | 44 | 34 | 36 |
| 201602 | 1251 | 5 | 8 | 19 | 40 | 44 | 42 | 45 | 47 | 48 | 38 | 38 | 51 |
| 201603 | 1295 | 4 | 13 | 14 | 47 | 48 | 48 | 52 | 53 | 43 | 44 | 58 | 49 |
| 201604 | 1311 | 7 | 10 | 15 | 49 | 49 | 48 | 53 | 44 | 46 | 59 | 51 | 60 |
| 201605 | 1329 | 6 | 11 | 13 | 52 | 54 | 51 | 45 | 49 | 63 | 54 | 63 | 69 |
| 201606 | 1367 | 6 | 9 | 9 | 56 | 55 | 46 | 52 | 66 | 57 | 67 | 74 | 59 |
| 201607 | 1421 | 6 | 7 | 9 | 58 | 54 | 59 | 76 | 65 | 76 | 85 | 69 | 67 |
| 201608 | 1461 | 4 | 6 | 8 | 57 | 64 | 79 | 69 | 81 | 93 | 73 | 74 | 64 |
| Variable Name | Expected Sign |
|---|---|
| Real gross domestic product (GDP) | Negative |
| New vehicle sales (NVS) | Negative |
| Total disposable household income (DHI) | Negative |
| Consumer price index (CPI) | Positive |
| Debt Service Ratio (DSR) | Positive |
| Prime rate (PR) | Positive |
| Instalment debtors (ID) | Negative |
| House price index (HPI) | Negative |
| Credit extended to households (CEH) | Negative |
| Description | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Combination number | 32680 | 3819 | 32483 |
| PC used | 2 | 2 | 2 |
| AIC | −1914.20 | −1910.28 | −1909.75 |
| AICC | −1913.89 | −1909.98 | −1909.44 |
| BIC | −1902.55 | −1898.63 | −1898.10 |
| RMSE | 0.000206 | 0.000209 | 0.000210 |
| Number of variables | 5 | 4 | 5 |
| Variable 1 | NVS | NVS | NVS |
| Variable 2 | PR | PR | PR_L3 |
| Variable 3 | CEH | CEH | CEH |
| Variable 4 | ID | ID_L3 | ID |
| Variable 5 | GDP_L6 | GDP_L6 | |
| Intercept | 0.00208 | 0.00205 | 0.00208 |
| Coefficient of variable 1 | −0.00022 | −0.00028 | −0.00020 |
| Coefficient of variable 2 | 0.00017 | 0.00019 | 0.00019 |
| Coefficient of variable 3 | −0.00009 | −0.00021 | −0.00009 |
| Coefficient of variable 4 | −0.00026 | −0.00036 | −0.00025 |
| Coefficient of variable 5 | −0.00018 | −0.00017 |
| Description | PCA1 | PCA2 |
|---|---|---|
| Coefficient of NVS | −0.24520 | 0.60779 |
| Coefficient of PR | 0.41841 | −0.54217 |
| Coefficient of CEH | 0.57044 | 0.03736 |
| Coefficient of ID | 0.40922 | 0.50460 |
| Coefficient of GDP_L6 | 0.52148 | 0.28396 |
| Description | PCR | GLM_PCR | REG | GLM |
|---|---|---|---|---|
| Combination number | 32680 | 32680 | 3181 | 3181 |
| PC used | 2 | 2 | NA | NA |
| RMSE | 0.000206 | 0.000233 | 0.000188 | 0.000195 |
| Number of variables | 5 | 5 | 4 | 4 |
| Variable 1 | NVS | NVS | NVS | NVS |
| Variable 2 | PR | PR | DSR | DSR |
| Variable 3 | CEH | CEH | CEH_L3 | CEH_L3 |
| Variable 4 | GDP_L6 | GDP_L6 | GDP_L3 | GDP_L3 |
| Variable 5 | ID | ID | ||
| Intercept | 0.00208 | −4.08182 | 0.00182 | −4.17746 |
| Coefficient of variable 1 | −0.00022 | −0.07228 | −0.00015 | −0.04021 |
| Coefficient of variable 2 | 0.00017 | 0.05578 | 0.00054 | 0.19122 |
| Coefficient of variable 3 | −0.00009 | −0.02992 | −0.00066 | −0.23253 |
| Coefficient of variable 4 | −0.00018 | −0.06145 | −0.00014 | −0.03765 |
| Coefficient of variable 5 | v0.00026 | −0.08667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breed, D.G.; Hurter, J.; Marimo, M.; Raletjene, M.; Raubenheimer, H.; Tomar, V.; Verster, T. A Forward-Looking IFRS 9 Methodology, Focussing on the Incorporation of Macroeconomic and Macroprudential Information into Expected Credit Loss Calculation. Risks 2023, 11, 59. https://doi.org/10.3390/risks11030059
Breed DG, Hurter J, Marimo M, Raletjene M, Raubenheimer H, Tomar V, Verster T. A Forward-Looking IFRS 9 Methodology, Focussing on the Incorporation of Macroeconomic and Macroprudential Information into Expected Credit Loss Calculation. Risks. 2023; 11(3):59. https://doi.org/10.3390/risks11030059
Chicago/Turabian StyleBreed, Douw Gerbrand, Jacques Hurter, Mercy Marimo, Matheba Raletjene, Helgard Raubenheimer, Vibhu Tomar, and Tanja Verster. 2023. "A Forward-Looking IFRS 9 Methodology, Focussing on the Incorporation of Macroeconomic and Macroprudential Information into Expected Credit Loss Calculation" Risks 11, no. 3: 59. https://doi.org/10.3390/risks11030059
APA StyleBreed, D. G., Hurter, J., Marimo, M., Raletjene, M., Raubenheimer, H., Tomar, V., & Verster, T. (2023). A Forward-Looking IFRS 9 Methodology, Focussing on the Incorporation of Macroeconomic and Macroprudential Information into Expected Credit Loss Calculation. Risks, 11(3), 59. https://doi.org/10.3390/risks11030059





