Abstract
The purpose of this paper is to examine the issue of portfolio optimization. Optimization consists of minimizing the risk for a given rate of return or achieving a bigger return for a given level of risk. We use historical data from the Bank of Greece to calculate the net return and the standard deviation (std) for each type of property that is available. The objective is to maximize the economic value added (EVA) of a property’s assets portfolio under a specific rate of standard deviation, following the classic Markowitz model (M-V). The stochastic procedure entry in the model uses the Monte Carlo Simulation method with debt to equity (DTE) following PERT distribution for the portfolio’s invested budget, and the net return for the normal distribution with the mean of the expected return and std are taken from historical data, correspondingly. The returns verify that they follow the base assumption of normality through the Lilliefors test in the Greek real estate market. We observe the maximization of EVA and the expected return maximizing concurrently, but the minimizing risk of EVA is diversified with the minimization of portfolio risk. We observe that the max weight that a residential asset takes is 22.7% because a bigger percent reduces both mean and std. The study provides an explicit portfolio optimization procedure under uncertainty in the real estate market and enriches the academic debate about EVA and revenue.
1. Introduction
The real estate market has emerged as an important factor of financial stability during the crisis period, contributing significantly to the economic activity of the country. Changes in property prices have a direct influence on the various financial indicators and therefore play an important role in formulation of monetary policy with a direct interaction with economic developments.
In recent years, the demand for private capital for real estate investments, as it has risen, spiraled, playing many times as security by taking on the role of banks at one point. Especially in Greece, due to the decadal economic crisis and the current crisis of coronavirus it is appropriate that the limited budget should be distributed as rationally as possible and optimally if possible. Operational research is the field of mathematics that implements the above process by providing important information to managers for the decision-making process.
In recent years, in the real estate market a dominant role has been played by real estate management companies such as Real Estate Investments Trusts (REITs) where they must manage large portfolios of real estate. A typical case of an optimal portfolio is Markowitz (1952) (M-V), which defines as risk the std of the portfolio. Many scientific studies have been occupied with this topic, including Lee (1992), Tobin (1965, 1967), Sharpe (1964, 1966), and Mansini and Speranza (1999), but in Greece it has not yet received the appropriate attention.
We will deal with the real estate sector of Greece, which is one of the most important parts of the country’s economy, but the decisions are still based on experience without using scientific tools. The literature review and the main characteristics for the selection of the real estate sector are provided, as well as conclusions and the relevant discussion.
Real estate in many countries such as Greece historically plays a crucial role in economic activity as it acts as a safe investment, and people prefer to invest their money in properties rather than deposit it in banks. The commercial property is characterized by significant heterogeneity not only in terms of use but also in terms of investment characteristics. In addition, in small markets, such as Greece, especially in times of economic recession and crisis, the recording of real transactions becomes even more difficult, while the price levels at which the transactions are completed may not reflect commercial values, but “fire sales” values. In Greece, it is imperative to use a more scientific perspective of investment portfolios in the real estate market because the decision making mainly depends on experience of managers. Markowitz (1952) created an optimal portfolio theory with two conflicting objectives, minimizing risks and simultaneously maximizing returns. The optimal structure of our portfolio is constituted from a variation of M-V model, either maximum mean of EVA under uncertainty for a given level of risk (std of EVA) or minimum risk for a given level of mean of EVA according to perceptions of managers. The purpose of our article is the use of EVA as a performance indicator (objective function) for the entire portfolio instead of the revenues of the portfolio in general and the introduction of the restriction of funding, in the optimization problem of Markowitz and the std of EVA as a risk measure against the classical std of portfolios in the Greek real estate market case. The introduction of uncertainty in our model through the Monte Carlo Simulation method transformed our model into a stochastic one. Our theoretical research problem is the investigation and elimination of the crisis effect in the real estate market in the 2006–2021 period, based on Draper and Smith (1998) and Suits (1957) and the different behavior of EVA and std of EVA as an objective function against the classical Markowitz model (revenue and std of portfolio, respectively). Moreover, the investigation and validation of the hypothesis of normality of return is a topic we address due to the stability of Greek real estate market.
Our research organized as follows: first we analyze the literature referring to the variations of the Markowitz model and the hybrid method using Markowitz with the Monte Carlo Simulation. After we provide the classical Markowitz model, we transform it by introducing EVA as return in objective function. Many restrictions are provided to clarify the above target such as cost of a portfolio’s funding. The classical return of Markowitz model is substituted with . This attempt is an innovation based on other attempts that are provided in the literature review. In order to clarify the base request of the Markowitz model, we investigate the hypothesis of normality of return. After we use data from the Greek real estate market, especially in Athens in which existing problems in the time horizon, we investigate problems that arise due to availability of data from the Bank of Greece because the Bank of Greece provided data till 2006. In this investigation period also, a huge financial crisis existed in the Greek economy with a huge volatility impact. In order to face this problem, we eliminated the crisis impact from our data using a dummy variable (binary) in a time series model based on Kaminsky and Reinhart (1999), Bordo et al. (2001), and Harding and Pagan (2011). The trend component is a low-variational function of time t; the method we will use to estimate it is the least squares method through linear regression assuming that the trend can be a polynomial of time (t) of degree p. After the examination of estimations for the trend, we choose that with higher explanation () and significant estimations (lower p-value). Taking into account the effect of the crisis, the equation for calculating the trend is derived. For the returns in three categories of property assets, which are included as assets in our portfolio, we calculate the average and std for each category. The above estimations are used as input variables, which follow normal distribution and are calculated through the Monte Carlo Simulation method. We use the Monte Carlo Simulation and DTE in order to produce EVA, ROIC, and WACC using PERT distribution after the analysis of real estate companies’ data in Greek Market1 for the index of DTE to implement the above distribution function using specific values for minimum maximum and most likely as input parameters. For the cost of capital (), we use the value of research of Damodaran2. For the cost of debt (), we use the most recent existing real estate loan interest rate from the Bank of Greece3 and other resources4. Finally, for the corporate tax we use the existing tax rate (φ) from tax authorities of Greece5, and for the average rental return we use comparative research from the companies of the Greek Real Estate market6.
All the above-mentioned parameters were used in our model for the maximization of mean of EVA and minimization of std of EVA; we also produced the appropriate efficient frontiers curves. A similar approach is provided by Shadabfar and Cheng (2020) for stock portfolios, and we contribute by implementing the approach with real estate portfolios. In every trial for calculation, the Monte Carlo Simulation ran for every input variable, and we estimated the mean and std for different levels of risk and return, respectively, and we provided the efficient frontiers curves, which are not significantly diversified in previous studies that used portfolios of stock assets, as in the work of Ivanova and Dospatliev (2017). We used property assets with a similar procedure as provided by Lee (2019). Finally, we summarized the implications of our study and our conclusions, respectively. More detailed analysis is provided in the following sections of our study.
Our article contributes to the debate first for the use of EVA against revenue and the use of suitable data in a unique stochastic Markowitz model that be used by professionals and academics for real estate portfolios. Our attempt began by using data from the Greek real estate market and could be implemented in other countries’ real estate markets.
2. Literature Review
Portfolio theory investigates and manages portfolios of investment products, aiming at the simultaneous accomplishment of two opposite goals: maximizing the expected return and minimizing risk. The attempt focuses on estimating the expected return on E(R) and the std of the portfolio (where R is the total return on investment), considering the correlation between the investment’s alternates . Two basic concepts introduced by Markowitz (1952) are the effective portfolio and the effective whole. A portfolio is characterized as effective when there is no one else that has a greater return and less or equal risk than it. Markowitz (1952) defines the problem of portfolio optimization as a problem of quadratic programming, defining std to determine risk. The Markowitz diversified portfolio is based on the basic concept that returns are random variables, as the number of assets increases the degree of the covariance table and increases at a greater rate, playing the key role in formulation of the overall portfolio risk. Markowitz makes the following two assumptions about the exact way that the investor will choose his optimal portfolio:
- Select the maximum return for a given level of risk;
- The least risk to a given level of return.
The basic assumptions of Markowitz model are the following:
- Τhe probability function of the returns can be estimated by investors;
- The basic principle is to maximize the utility function of investor;
- Investors tend to avoid risk in pursuit of profit;
- Financial markets are smooth;
- The existence of transaction cost and taxes is absent.
the yield vector.
The vector of the expected returns is obtained:
Suppose that .
and
This matrix contains variances, its main diagonal, and covariances between all pairs of assets in other items.
where
Suppose that the weights vector of the portfolio.
unitary vector.
For a given level of return to minimize risk, the model is defined as follows:
For a given level of risk, the model to maximize return is:
The procedure of portfolio optimization is very important in investments of the finance sector, as shown in the work of Best (2010), Gambrah and Pirvu (2014), and Quintana et al. (2017). The objective of portfolio management is to increase an investor’s income through the formulation of a rational financial plan, as stated by Gruszka and Szwabiński (2020). Investors in real estate, according to modern portfolio theory (MPT) Markowitz (1952), focus on creating an optimal portfolio based on the best selection of assets available, as stated by Lee (1992). The MPT seeks the highest level of return for each level of risk, calculating the mean value and std using historical data. Applying MPT to an ex-ante framework leads to ex-post results with poor performance because the input variables are uncertain, which creates different optimal distributions between periods. This creates portfolios with extreme solutions giving some assets zero weight (corner solutions), according to the work of Black and Litterman (1992), which goes against the basic principle of diversification. One way to overcome this problem is to put restrictions (upper and lower limits) on the asset’s contribution rate to the optimal portfolio, as shown by Byrne and Lee (1995) and Stevenson (2000). In addition, the average performance is significantly influenced by the period of data selection, as opposed to the measurement error in variance and covariances, as the parameters are relatively stable over time, offering high accuracy in the estimations, as shown in the work of Kalberg and Ziemba (1984) and Chopra and Ziemba (1993). It is obvious that the optimal portfolio calculated with historical data from a particular period is not easy to generalize to future ones. This is confirmed by the work of Myer and Webb (1991), Mueller and Laposa (1995), and Pagliari et al. (1995).
Several scientific studies have tried to test the effectiveness of results at future times in both equity and real estate markets, according to Logue (1982). Madura and Abernathy (1985) dealt with the global equity portfolio through weekly stock index returns from 1978 to 1981 for a total of eight countries. The data were divided into five equal subperiods using the M-V optimization algorithm. Starting from the first period, the optimal weights of this period were the basis for the application of the model in the next period fully incorporating the information of the previous period. Madura and Abernathy (1985) divided this into three types of risk-efficient portfolios, with their analysis according to Sharpe Ratio Sharpe (1966, 1994). A first observation was that the yields and standard deviations of each country were different in each time period; there was an absence of the concept of stationarity of data. The conclusion was that the difference in findings between an ex-post analysis with an ex-post analysis may be significant.
The three main studies in the real estate market that dealt with the effectiveness of MPT portfolios in future periods were as follows: Myer and Webb (1991) were the first to analyze the period from 1978 to 1988 using the returns of the National Council of Real Estate Investments Fiduciaries (NCREIF) for various types of properties. The conclusion was that the optimal combinations differ in each time period because of the nature of returns, so an optimal distribution over a certain period may not remain optimal at future times.
Mueller and Laposa (1995) worked on the optimal strategy that investors should allocate to various types of real estate: retail, office, apartments, and warehouses using quarterly data in the US. Mueller and Laposa (1995) agreed that the returns of each type of property are influenced by economic cycles of previous periods. So, they decided to divide the NCREIF data into different periods based on three cyclical indicators: total returns, capital appreciation, and GDP growth. The results showed a different allocation both of assets selected in the optimal portfolio and the weights that were attributed to them between different periods.
Pagliari et al. (1995) used quarterly returns for 15 years by data segmentation into three five-year subperiods; the authors concluded that MPT portfolios work optimally in ex-post strategy while an ex-ante strategy gives ambiguous results. The effective implementation of an ex-ante strategy of the MPT largely depends on the accuracy of the portfolio input variables. Therefore, for the correct application of MPT in the process of building a real estate portfolio it is necessary during the optimization process to consider the estimation risk.
A simulation analysis by Jorion (1985) showed that the mean-variance portfolio (MVP) is less affected by measurement errors than the classic tangency portfolio, because the results depend only on the sample covariance matrix, which does not change significantly over time.
Many extensions of the Markowitz models have been produced, and the main characteristic of all of them is the use of alternative objective function either for minimization against std or maximization against revenue-return. Of particular importance are Fama (1965), who treated the distribution of returns as a generalized Pareto distribution, and Rockafellar and Uryasev (2000), whoe focuds on the Conditional Var (CVaR) model for minimizing the Conditional Value at Risk-CVaR. A contemporary approach with C-Var as a risk measure wasbadopted by Cui et al. (2020) with a stochastic approach. Konno and Yamazaki (1991) proposed an alternative to the classic MV model to address the problem of creating a large quadratic programming problem, which has a large cost of solving, and they chose the Mean Absolute Deviation-MAD instead of std. Fulton and Bastian (2019) adopted an incorporation of appropriate time-series components with downside MAD as the risk measure in a case study from 2003 to 2013. The basic limitation of the MV approach is the assumption of the normal distribution of returns. For this reason, Estrada (2008) developed an alternative approach and used as a risk indicator the downside risk. Kroencke and Schindler (2010) presented an international application to securitized real estate stock markets. The M-V model has a wide application especially in finance, and Gottschlich and Hinz (2014) created a method for the increase of the earnings rate of a stock investment using Markowitz’s portfolio model, and Jung and Kim (2015) used Markowitz’s model to improve the investment earnings rate considering the time variance of the market. A method for selection between projects within an acceptable level of risk for a given budget was created by Zhou et al. (2014). A classical study of the M-V model in a wmarket with limited application was provided by Ivanova and Dospatliev (2017) for Bulgarian stock market from 2013 to 2016.
The most existing studies on portfolio optimization procedure are occupied with a deterministic approach for the problem formulation, but this is unacceptable in reality because the unknown nature of the uncertainty of market data is so large that it cannot be ignored, according to Chan (2017) and Shadab Far and Wang (2016). Hence, an alternative method is appropriate to incorporate the uncertain nature of the problem; this is the probabilistic approach devised by Dutra et al. (2014). In this way, after the deterministic approach, in order to introduce the uncertainty in our model, we use the Monte Carlo sampling method based on Glasserman (2004) and Thomopoulos (2014). Lee (2019) created a financing method for real estate and infrastructure development using Markowitz’s portfolio selection model in combination with the Monte Carlo Simulation to improve the investment earnings rate for financing. A probabilistic approach for optimal portfolio selection using a hybrid Monte Carlo Simulation and Markowitz mode was created by Shadabfar and Cheng (2020) for the Shanghai stock market, considering the uncertainty in the return and risk values on a daily basis from January 2014 to December 2018. Zanjirdar (2020) and Milhomem and Dantas (2020) provided a comprehensive study on the portfolio optimization model with new approaches and constraints that exist.
3. Data
We use data from Bank of Greece; the data used are the semester price indicator and rental indicator for three sectors:
- Residential;
- Office;
- Retail.
The property area data are divided into three zones:
- Athens;
- Thessaloniki;
- Rest of Greece.
According to Eichholtz et al. (1995) and the Bank of Greece, three-property type and three “sub-regional” segmentation provide a rational portfolio investment strategy for investors in Greece; the data covers the period from 2006 to 2021 biannually with a total of 32 observations. We use data only for Athens because this is only region with full data for the entire time period.
We calculate returns according to:
The quantity of returns is 30 observations because we calculate the change (%) with a corresponding index of the previous year and specifically the rental indicator of residential properties based on 75% of the annual change of the consumer price index (cpi) according to methodology of the Hellenic Statistical Authority. We consider for the creation of a fund the amount of equity available as EUR 2.000.000, and using the process of leveraging through the variable DTE (Debt to Equity) we produce the WACC (Weight Cost Of Capital) of the total investment. We calculate the ROIC (return on invested capital), and through it the EVA according Liapis (2010), to produce an EVA vector of each project; EVA® is a variant of residual income marketed by Stern Stewart & Co., a New York consulting firm, with the purpose of promoting value–maximizing behaviour in corporate managers, as described by Stewart (2009):
The charts representing the progress of returns over the time under consideration are presented below (Figure 1, Figure 2 and Figure 3):
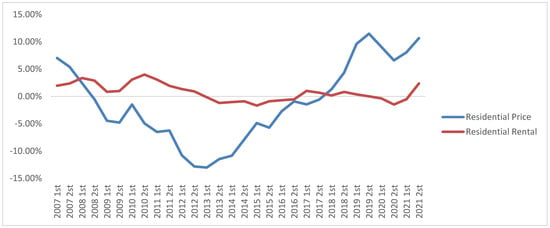
Figure 1.
Residential Net Yield Index.
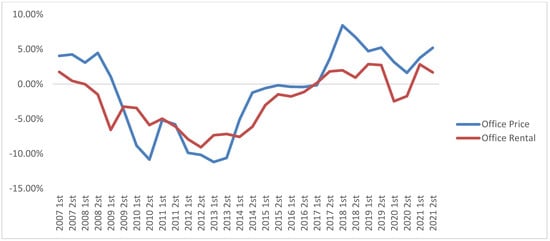
Figure 2.
Office Net Yield Index.
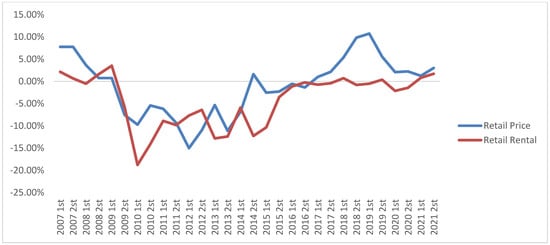
Figure 3.
Retail Net Yield Index.
4. Methodology
We calculate the expected return (mean) and the std (risk) of return for each type of property. The data shows a degree of risk and return volatility, rejecting stationarity in the expected return vector and the variance/covariance matrix. A large period of 30 years or more is necessary to make a realistic forecast of the risk and expected return; unfortunately, the data from the Bank of Greece in the real estate market does not have such a long history.
We calculate the trend taking into account the effect of the crisis for each type of property for rent and the price indicator, respectively. Trends are calculated according to the following equation:
where the variable is defined as the binary variable, as in the work of Bliss et al. (2015), which takes the numerical value 1 for years of financial crisis, capital controls, and coronavirus crisis and zero otherwise.
For price indicators, the dummy variable is 0 for years 2007–2008 and years 2017–2021 and 1 for years 2009–2016.
For rental indicators of residential, the dummy variable is 0 for years 2007–2010, years 2017–2018, and year 2021 and 1 for years 2011–2016 and years 2019–2020.
For rental indicators of office, the dummy variable is 0 for years 2007–2008, years 2017–2018, and year 2021 and 1 for years 2009–2016 and years 2019–2020.
For rental indicators of retail, the dummy variable is 0 for years 2007–2008, years 2017–2018, and year 2021 and 1 for years 2009–2016 and years 2019–2020.
The price of property is not affected by the crisis of coronavirus in contrast with rental indicator, due to traffic restrictions and the implementation of remote work. Residential property has time a lag (2 years) compared to commercial property.
Subtracting the dummy (crisis) by (13), we have the net yield without the effect of crisis. The terms and are optional depending on data:
The yield vector after subtracting the effectiveness of the crisis, represents the type of property, and represents the indicator price or rental.
The weighted return is extracted according to:
The rental indicator of properties is based on a fixed yield of this type of property plus the growth rate of return in this period.
The Theoretical Point of View of Our Model
Our final model takes the following form:
Model 1:
- Apartment;
- Offices;
- Retail.
Model 2:
- Apartment;
- Offices;
- Retail.
We choose the EVA (Economic Value Added) as the maximizing objective function, based on the work of Engels (2004), against a classical rate of return based on Markowitz (1952).
We suppose that for the input parameters (returns) in type (10) for each type of property that follows normal distribution with mean, the expected return of weighted return and the corresponding std and DTE follows PERT distributions with probability . The type of probability distribution function can have a significant effect on the results; for this, we must check if our data population is generated from normal distribution through a Lilliefors test, based on the work of Lilliefors (1967). The Monte Carlo Simulation process runs individually and generates random returns for every trial (possible solution). The main purpose of this study is to maximize mean of EVA and minimize the risk (std of EVA) against the classical Markowitz model to maximize the return and minimize the std of return of the portfolio. Therefore, two objective functions are required to define the problem; we could formulate the problem individually for two objective functions, but this does not cover a coherent approach. We try to produce a model to cover both objectives at the same time. Different methodologies’ specific intelligent algorithms, in combination with the Monte Carlo analysis, areadopted to solve the portfolio optimization problem, but this procedure has a high computational cost. The deterministic approach implemented by Markowitz method MVP can be used with the Palisade decisional tool addition to Excel. The data obtained from bank of Greece from three different types of real estate property market has according results. From the biannual return in each year, we estimate the expected return and the standard deviation, which represent the risk. The investors can choose the best combination according to their preferences by specifying the maximum risk or minimum expected return.
5. Estimations-Empirical Analysis
5.1. Estimations
The presentation of the empirical results from the analysis of benefits from diversification according to the Markowitz (1959) framework first examines the effect of crisis in the real estate market. According to Equation (14), we calculate the adjusted indicators without the effect of crisis, and the results are presented below:
Table 1 presents the results of trend valuation of return of both price and rental for each type of property.

Table 1.
Trend calculation.
Because the data is divided biannually and does not contain tourist accommodations and hotels, the existence of seasonality is rejected; thus, the return depends only on trend, which is a low-degree function of time. When the trend in a time series can be described by some known or estimated function of time named, it is called a deterministic trend. Usually, the trend is linear, but it can be a polynomial of t degree p, and we use the least squares method for the determination of trend. We observe that all trends, except the residential rental, present as non-linear; the rental indicator of residential properties is based on 75% of annual change of consumer price index (cpi) according to methodology of the Hellenic Statistical Authority.
We observe according to Table 2 that retail has the max expected return, and the residential has the min, respectively.

Table 2.
Expected weighted return and std for each type of property.
The graphical representation of the trend of adjusted returns for each type of property without the effect of crisis is presented below (Figure 4):
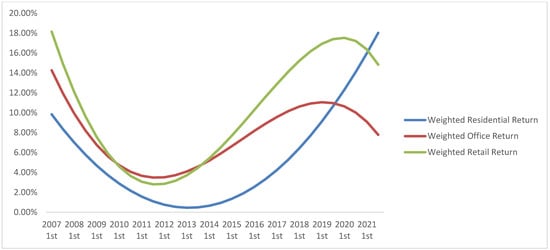
Figure 4.
Trend of weighted return.
In our paper, the Monte Carlo Simulation method is used to implement the probabilistic analysis of our problem. In this procedure, each input variable for the calculation of EVA should be defined as a random variable (Weighted Returns and DTE). With simulation analysis, many possible scenarios would be examined, and the uncertainties of input parameters would be imported to the problem formulation. The type of probability distribution function is very important for the analysis results and should be selected according to the actual data.
We use the Lilliefors test Lilliefors (1967) to check if our data population was generated from normal distribution, and the results are provided below in Table 3.

Table 3.
Lilliefors test.
We observe that in a low level of significance, up to 5% at least, we can assume that data follow normal distribution in Figure 5. We observe that for a large number, up to 200, observations the data did not fit well.
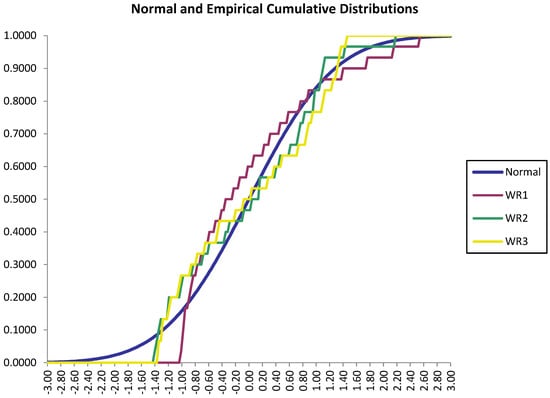
Figure 5.
Lilliefors test.
5.2. Portfolio Optimization Results
The accuracy of Monte Carlo simulation analysis is the most important point, and this is directly connected with the number of random samples and the number of iterations we select. We apply the Monte Carlo Simulation approach with a number of 1000 iterations for each trial; this covers the number of 200 trials according to the Lilliefors test, and for each trial we calculate mean and std for 1000 trials. In every trial for calculation, the Monte Carlo simulation is run for every input variable, and we estimate the mean and std for a different level of risk and return, respectively. The best combination of risk yield is called the tangency portfolio. The different combinations of the tangency portfolio with guaranteed yields give us the efficient portfolios, which achieve the best balance between risk and return. The set of points on the curve that has an expected return at least as large as the MVP is called an efficient frontier. Portfolios belonging to this limit are called mean-variance efficient portfolios. Efficient frontier, from a mathematical point of view, is the intersection of set of portfolios with minimum risk and a set of portfolios with maximum return, according to Chen et al. (2020) and Haugen and Baker (1990).
First, we present the efficient frontier for minimizing the risk of EVA. In Figure 6, we present the efficient frontier for minimum risk of EVA, and the precise weights for component assets in the minimum risk (EVA) for specific level of mean of EVA are shown in Table 4. The perceptions of investors play a key role for the selection of an optimal portfolio; if investors have low risk tolerance, they should select a combination of risk and return located on the left of the frontier, and, conversely, if they accept a high degree of risk, they should select s combination on the right of the frontier, as described by Ivanova and Dospatliev (2017). In Figure 7, we present the efficient frontier for maximum mean of EVA, and the precise weights for component assets in the maximum mean (EVA) for specific levels of risk portfolio are shown in Table 5.
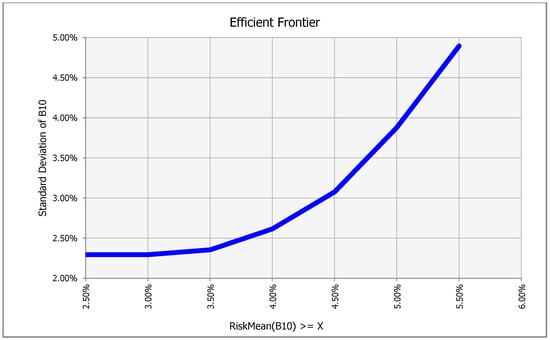
Figure 6.
Efficient frontier minimizing risk of EVA portfolio.

Table 4.
Minimum-risk EVA portfolio.
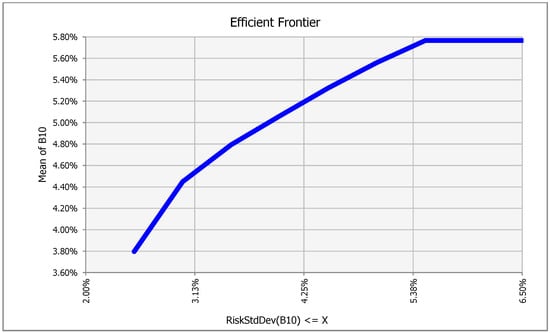
Figure 7.
Efficient frontier maximizing mean of EVA portfolio.

Table 5.
Maximum mean EVA portfolio.
In Figure 7, we observe that the max weight that residential asset takes is 22.7% because for a bigger percent, it reduces both mean and std. The optimal structure depends on the perception of the investor, but it is obvious that for up to 3.07% of risk the rate of increase of the mean is lower than std. For the 3.07% risk level, the optimal mean of EVA is 4.5%; this is possibly an optimal combination according to mathematical approach.
6. Discussions and Conclusions
6.1. Discussions and Key Findings
The paper aims to extend the existing literature on portfolio optimization in real estate markets. The proposed model is developed based on the use of the Monte Carlo Simulation with the M-V model with EVA as objective function. This study has several findings.
First, the data of input values were compiled on a biannual basis from 2006 to 2021. We calculate the weighted returns, and, for them, the mean and std were calculated and imported to the Monte Carlo algorithm, validating that the random weighted return variable follows normal distribution. According to study of Shadabfar and Cheng (2020), at stock portfolios confirm that normal distribution for returns is most suitable, but we calculate the weighted return against daily return, and we import these as random variables.
Second, in this paper a stochastic formulation of portfolio optimization for the real estate market in Greece was provided, considering the uncertain nature of return and risk values. The uncertainty is introduced through the Monte Carlo Simulation according to Shadabfar and Cheng (2020); the returns are modeled as random variables following normal distribution and DTE with PERT Distribution.
Third, the objective function is maximizing the economic added value (EVA) against the classical expected return in the optimal portfolio using as risk std of EVA. According to the mathematical approach, maximum average return of EVA is approximately 4.5% for a 3.07% risk level. We observe that if maximizing EVA, the expected return maximizes concurrently, but the minimizing risk of EVA is diversified by the minimization of portfolio risk. We observe that the max weight that a residential asset takes is 22.7% because a bigger percent reduces both mean and std.
Fourth, comparing Figure 1, Figure 2 and Figure 3 for the Greek economy, where it includes both the yields and the value of rents, and Figure 4 that also contains the goodwill (increase of value of property assets) without the impact of the crisis, we observe that the trends of yields continue to show a cycle that coincides with the economic crisis of 2007–2012. While corporate assets show a next phase of cycle starting in 2020, due to COVID-19 restrictions, residential has not been affected.
Finally, we produce the efficient frontiers curves, which are not significantly diversified from previous studies that used portfolios of stock assets, as in the work of Ivanova and Dospatliev (2017). Max average return of EVA follows a hyperbolic form for a different level of risk, and minimum risk of EVA follows a parabolic form for a different level of average return of EVA.
6.2. Theoretical Implication-Practical Implication
This study enriches the theoretical research of portfolio optimization of real estate markets. This paper extracts the crisis’s effect of data return before the implementation of the model using the data in the Greek market because if we use the actual returns, the outcomes are not valid. We calculate the weighted returns, we introduce these in a stochastic procedure, and the uncertainty is introduced through the Monte Carlo Simulation. Afterwards, by generating random numbers for each random variable, 1.000 random scenarios were defined for each trial, and the optimal results were separately calculated for each one for the maximization mean of EVA or minimization std of EVA. The practical application depends on the fact that the model we developed is not a theoretical model explaining the trend of yields but a model of operational research for market practitioners. An investor or a fund wanting to achieve a return, knowing how to leverage the rental returns and the returns of goodwill and the volatility of these can help them to proceed to the creation of a portfolio maximizing EVA for various levels of risk and for control and monitoring of already formed portfolios. According to agent theory and Stewart EVA, it seeks to build a portfolio that satisfies all three parties (banks, shareholders, managers) because investors handle money from funds and form portfolios from managers, so it is more appropriate to choose the EVA that managers use to secure their fees, and when EVA is positive, both managers and creditors are satisfied. The specific data refer to Greece, especially Athens, but any international investor can use the model by importing data from another economy. A future investigation would be in the case of international investors investing in various markets by introducing country risk diversification.
6.3. Restrictions and Future Work
Although this study provides useful insights, there are some restrictions. First, the data of Bank of Greece are quite limited. The data of input values was compiled on a biannual basis from 2006 to 2021. A greater data segmentation (possible monthly) will increase the number of observations, significantly improving the results, because the dimension of covariance matrix increases extremely for each next observation. Second, the nonstationarity nature of data, although it does not influence our procedure, must be examined with a KPSS test, as devised by Kwiatkowski et al. (1992), and corrected with the appropriate transformation. Finally, it is obvious that the optimal portfolio calculated with historical data of a particular period is not easy to generalize to future ones; because of this, we must check the effectiveness of results through the out-of-sample performance analysis over a sufficient time horizon, as demonstrated by Lee and Stevenson (2005). Furthermore, time could be introduced as a variable to check the degree of depreciation of the property through the Gordon–Shapiro valuation process, as developed by Liapis et al. (2011).
An extension of our research in the future would be the introduction of the theory of representation and the constraints it defines between the management–shareholder–banking relations. We will try to construct a specific portfolio for an investment company in the real estate market with, as an objective, the maximization of EVA though Knapsack problem formulation, as formulated by Dantzig (2007), and take as restrictions the weights that produce an optimal portfolio based on the above procedure. Comparative research with data from other real estate markets is imperative and a very interesting topic for understanding the differences between countries’ markets and the specific characteristics of the Greek economy. Whether residential has a higher yield than corporate after 2020 is a matter for future research. According to the modification of Liapis et al. (2011), we will introduce the cost of utilities and maintenance in our model.
Author Contributions
K.L., in collaboration with T.P., conceived the idea and wrote the conclusions. T.P. wrote the introduction, the literature review, and the empirical results. K.L. and E.T. performed the empirical evidence and wrote the final text. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data we used for our calculations are available in the webpage of the Bank of Greece (bankofgreece.gr) accessed on 25 August 2022.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | We use the median of stock exchange listed companies on Greek Real Estate Market by ICAP database. |
| 2 | Cost of Capital (nyu.edu) accessed on 25 August 2022. |
| 3 | (bankofgreece.gr) accessed on 25 August 2022. |
| 4 | See note 1 above. |
| 5 | The corporate tax rate reduced from 24% to 22% in 2021 year. |
| 6 | RE/MAX 2021 (remax.gr) accessed on 25 August 2022. |
References
- Best, Michael. 2010. Portfolio Optimization. Boca Raton: CRC Press. [Google Scholar]
- Black, Fischer, and Robert Litterman. 1992. Global portfolio optimization. Financial Analysts Journal 48: 28–43. [Google Scholar] [CrossRef]
- Bliss, Barbara A., Yingmei Cheng, and David J. Denis. 2015. Corporate payout, cash retention, and the supply of credit: Evidence from the 2008–2009 credit crisis. Journal of Financial Economics 115: 521–40. [Google Scholar] [CrossRef]
- Bordo, Michael, Barry Eichengreen, Daniela Klingebiel, and Maria Soledad Martinez-Peria. 2001. Is the crisis problem growing more severe? Economic Policy 16: 52–82. [Google Scholar] [CrossRef]
- Byrne, Peter, and Stephen Lee. 1995. Is there a place for property in the multi-asset portfolio? Journal of Property Finance 6: 60–83. [Google Scholar] [CrossRef]
- Chan, Bertram K. C. 2017. Applied Probabilistic Calculus for Financial Engineering: An Introduction Using R. New York: John Wiley & Sons. [Google Scholar]
- Chen, Wei-Peng, Huimin Chung, Keng-Yu Ho, and Tsui-Ling Hsu. 2020. Portfolio optimization models and meanvariance spanning tests. In Handbook of Quantitative Finance and Risk Management. Edited by Cheng-Few Lee, Alice C. Lee and John Lee. Boston: Springer, pp. 165–84. [Google Scholar]
- Chopra, Vijay Kumar, and William T. Ziemba. 1993. The effect of errors in means, variances and covariances on optimal portfolio choice. Journal of Portfolio Management 19: 6–11. [Google Scholar] [CrossRef]
- Cui, Tianxiang, Ruibin Bai, Shusheng Ding, Andrew J. Parkes, Rong Qu, Fang He, and Jingpeng Li. 2020. A hybrid combinatorial approach to a two-stage stochastic portfolio optimization model with uncertain asset prices. Soft Computing 24: 2809–31. [Google Scholar] [CrossRef]
- Dantzig, Tobias. 2007. Number: The Language of Science. The Masterpiece Science ed. New York: Plume Book. ISBN 9780452288119. [Google Scholar]
- Draper, Norman R., and Harry Smith. 1998. Applied Regression Analysis. New York: John Wiley & Sons, vol. 326. [Google Scholar]
- Dutra, Camila Costa, José Luis Duarte Ribeiro, and Marly Monteiro de Carvalho. 2014. An economic–probabilistic model for project selection and prioritization. International Journal of Project Management 32: 1042–55. [Google Scholar] [CrossRef]
- Eichholtz, Piet M. A., Martin Hoesli, Bryan D. MacGregor, and Nanda Nanthakumaran. 1995. Real estate diversification by property-type and region. Journal of Property Finance 6: 39–62. [Google Scholar] [CrossRef]
- Engels, Marnix. 2004. Portfolio Optimization: Beyond Markowitz. Master’s thesis, University of Leiden, Leiden, The Netherlands. [Google Scholar]
- Estrada, Javier. 2008. Mean-semivariance optimization: A heuristic approach. Journal of Applied Finance 18: 57–72. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1965. Portfolio analysis in a stable Paretian market. Management Science 11: 404–19. [Google Scholar] [CrossRef]
- Fulton, Lawrence V., and Nathaniel D. Bastian. 2019. Multiperiod stochastic programming portfolio optimization for diversified funds. International Journal of Finance & Economics 24: 313–27. [Google Scholar]
- Gambrah, Priscilla Serwaa Nkyira, and Traian Adrian Pirvu. 2014. Risk measures and portfolio optimization. Journal of Risk and Financial Management 7: 113–29. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2004. Monte Carlo methods in Financial Engineering. New York: Springer, vol. 53, pp. xiv+–596. [Google Scholar]
- Gottschlich, Jörg, and Oliver Hinz. 2014. A decision support system for stock investment recommendations using collective wisdom. Decision Support Systems 59: 52–62. [Google Scholar] [CrossRef]
- Gruszka, Jarosław, and Janusz Szwabiński. 2020. Best portfolio management strategies for synthetic and real assets. Physica A: Statistical Mechanics and Its Applications 539: 122938. [Google Scholar] [CrossRef]
- Haugen, Robert A., and Nardin L. Baker. 1990. Dedicated stock portfolios. Journal of Portfolio Management 16: 17–22. [Google Scholar] [CrossRef]
- Harding, Don, and Adrian Pagan. 2011. An econometric analysis of some models for constructed binary time series. Journal of Business & Economic Statistics 29: 86–95. [Google Scholar]
- Ivanova, Miroslava, and Lilko Dospatliev. 2017. Application of Markowitz portfolio optimization on Bulgarian stock market from 2013 to 2016. International Journal of Pure and Applied Mathematics 117: 291–307. [Google Scholar] [CrossRef]
- Jorion, Philippe. 1985. International portfolio diversification with estimation risk. Journal of Business 58: 259–78. [Google Scholar] [CrossRef]
- Jung, Jongbin, and Seongmoon Kim. 2015. An adaptively managed dynamic portfolio selection model using a time varying investment target according to the market forecast. Journal of the Operational Research Society 66: 1115–31. [Google Scholar] [CrossRef]
- Kalberg, Jerry, and William Ziemba. 1984. Misspecification in portfolio selection problems. In Risk and Capital. Berlin and Heidelberg: Springer, pp. 74–87. [Google Scholar]
- Kaminsky, Graciela L., and Carmen M. Reinhart. 1999. The twin crises: The causes of banking and balance-of-payments problems. American Economic Review 89: 473–500. [Google Scholar] [CrossRef]
- Konno, Hiroshi, and Hiroaki Yamazaki. 1991. Mean absolute deviation portfolio optimization model and its application to Tokyo stock market. Management Science 37: 519–31. [Google Scholar] [CrossRef]
- Kroencke, Tim-Alexander, and Felix Schindler. 2010. Downside risk optimization in securitized real estate markets. Journal of Property Investment & Finance 28: 434–53. [Google Scholar]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Lee, Chijoo. 2019. Financing method for real estate and infrastructure development using Markowitz’s portfolio selection model and the Monte Carlo simulation. Engineering, Construction and Architectural Management 26: 2008–22. [Google Scholar] [CrossRef]
- Lee, S. L. 1992. Emerging Concepts for the Management of Portfolios and the Role of Research: Property in the Portfolio Context. London: Society of Property Researchers. [Google Scholar]
- Lee, Stephen, and Simon Stevenson. 2005. Real estate portfolio construction and estimation risk. Journal of Property Investment & Finance 23: 234–53. [Google Scholar]
- Liapis, Konstantinos J. 2010. The Residual Value Models: A Framework for Business Administration. European Research Studies 13: 83–102. [Google Scholar]
- Liapis, Konstantinos J., Manolis S. Christofakis, and Harris G. Papacharalampous. 2011. A new evaluation procedure in real estate projects. Journal of Property Investment & Finance 29: 280–96. [Google Scholar]
- Lilliefors, Hubert W. 1967. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American statistical Association 62: 399–402. [Google Scholar] [CrossRef]
- Logue, Dennis E. 1982. An experiment in international diversification. Journal of Portfolio Management 9: 22–27. [Google Scholar] [CrossRef]
- Madura, Jeff, and Gordon Abernathy. 1985. Playing the international stock diversification game with an unmarked deck. Journal of Business Research 13: 465–71. [Google Scholar] [CrossRef]
- Mansini, Renata, and Maria Grazia Speranza. 1999. Heuristic algorithms for the portfolio selection problem with minimum transaction lots. European Journal of Operational Research 114: 219–33. [Google Scholar] [CrossRef]
- Markowitz, Harry M. 1952. Portfolio selection. Journal of Finance 7: 77–91. [Google Scholar]
- Markowitz, Harry. 1959. Portfolio Selection: Efficient Diversification of Investments. New York: Wiley. [Google Scholar]
- Milhomem, Danilo Alcantara, and Maria José Pereira Dantas. 2020. Analysis of new approaches used in portfolio optimization: A systematic literature review. Production 30. [Google Scholar] [CrossRef]
- Mueller, Glenn R., and Steven P. Laposa. 1995. Property-type diversification in real estate portfolios: Size and return perspective. The Journal of Real Estate Portfolio Management 1: 39–50. [Google Scholar] [CrossRef]
- Myer, Neil, and James Webb. 1991. Estimating allocations for mixed-asset portfolios using the bootstrap technique. Paper presented at the American Real Estate Society Meeting, Sarasota, FL, USA. [Google Scholar]
- Pagliari, Joseph L., James R. Webb, and Joseph J. Del Casino. 1995. Applying MPT to institutional real estate portfolios: The good, the bad and the uncertain. The Journal of Real Estate Portfolio Management 1: 67–88. [Google Scholar] [CrossRef]
- Quintana, David, Roman Denysiuk, Sandra Garcia-Rodriguez, and António Gaspar-Cunha. 2017. Portfolio implementation risk management using evolutionary multiobjective optimization. Applied Sciences 7: 1079. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 2: 21–41. [Google Scholar] [CrossRef]
- Shadab Far, Mahdi, and Yua Wang. 2016. Approximation of the Monte Carlo sampling method for reliability analysis of structures. Mathematical Problems in Engineering 2016: 572656. [Google Scholar] [CrossRef]
- Shadabfar, Mahboubeh, and Longsheng Cheng. 2020. Probabilistic approach for optimal portfolio selection using a hybrid Monte Carlo simulation and Markowitz model. Alexandria Engineering Journal 59: 3381–93. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar]
- Sharpe, William F. 1966. Mutual fund performance. Journal of Business 39: 119–38. [Google Scholar] [CrossRef]
- Sharpe, William F. 1994. The Sharpe ratio. Journal of Portfolio Management 21: 49–58. [Google Scholar] [CrossRef]
- Stevenson, Simon. 2000. Constraining optimal portfolios and the effect on real estate’s allocation. Journal of Property Investment & Finance 18: 488–506. [Google Scholar]
- Stewart, Bennett. 2009. EVA Momentum: The One Ratio That Tells the Whole Story. Journal of Applied Corporate Finance 21: 74–86. [Google Scholar] [CrossRef]
- Suits, Daniel B. 1957. Use of dummy variables in regression equations. Journal of the American Statistical Association 52: 548–51. [Google Scholar] [CrossRef]
- Thomopoulos, Nick T. 2014. Essentials of Monte Carlo Simulation: Statistical Methods for Building Simulation Models. Berlin and Heidelberg: Springer. [Google Scholar]
- Tobin, James. 1965. The Theory of Portfolio Selection. In The Theory of Interest Rates. Edited by F. H. Hahn and F. P. R. Brechling. London: Macmillan. [Google Scholar]
- Tobin, James. 1967. Life Cycle Saving and Balanced Growth. In Ten Economic Studies in the Tradition of Irving Fisher. New York: Wiley, pp. 231–56. [Google Scholar]
- Zanjirdar, Majid. 2020. Overview of portfolio optimization models. Advances in Mathematical Finance and Applications 5: 419–35. [Google Scholar]
- Zhou, Bei, Li Zongzhi, Harshingar Patel, Arash M. Roshandeh, and Yuanqing Wang. 2014. Risk-based two-step optimization model for highway transportation investment decision-making. Journal of Transportation Engineering 140: 04014007. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).