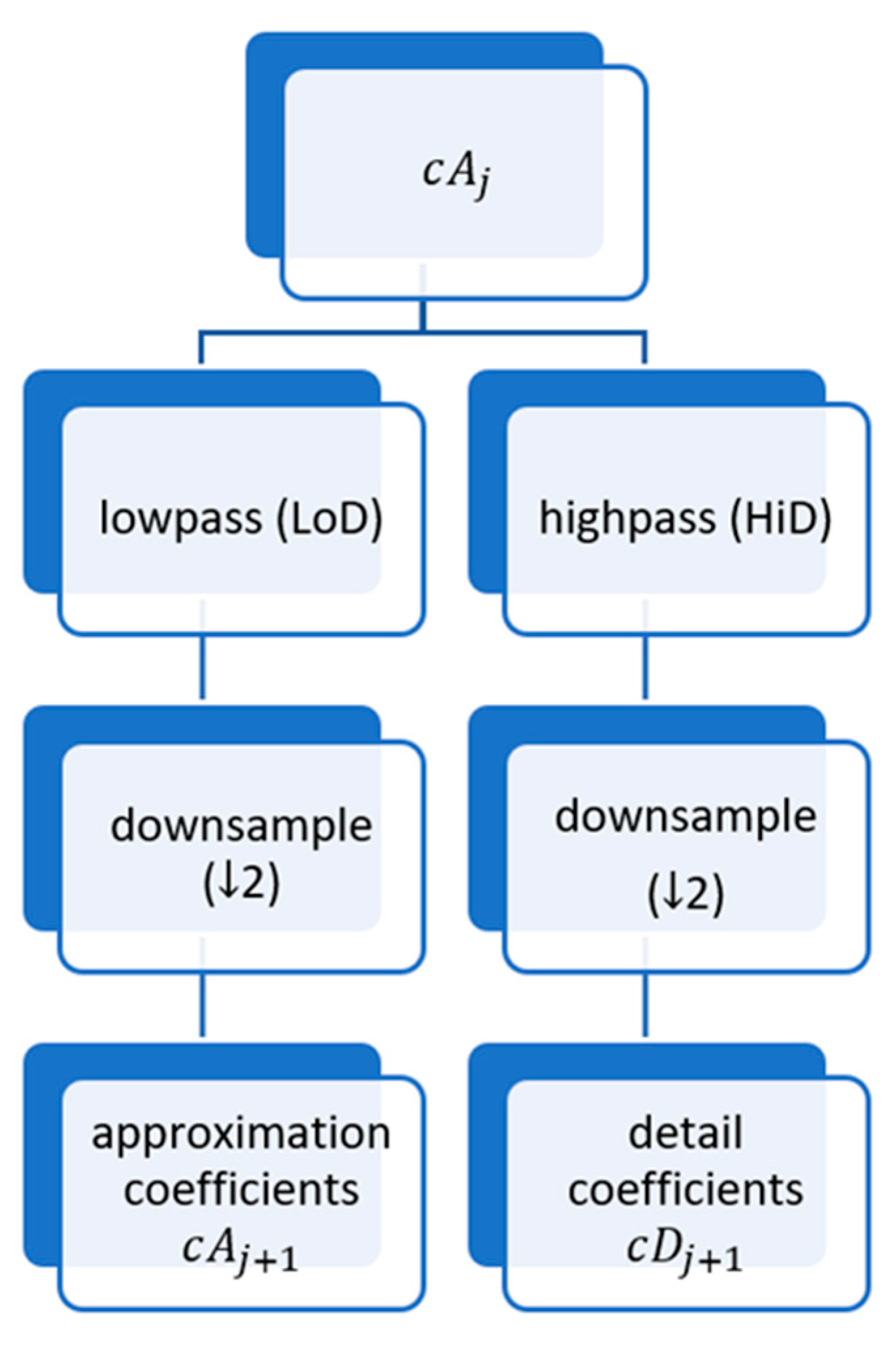
Figure 2.
Wavelet decomposition of the signal s analysed at level 3.
Figure 2.
Wavelet decomposition of the signal s analysed at level 3.
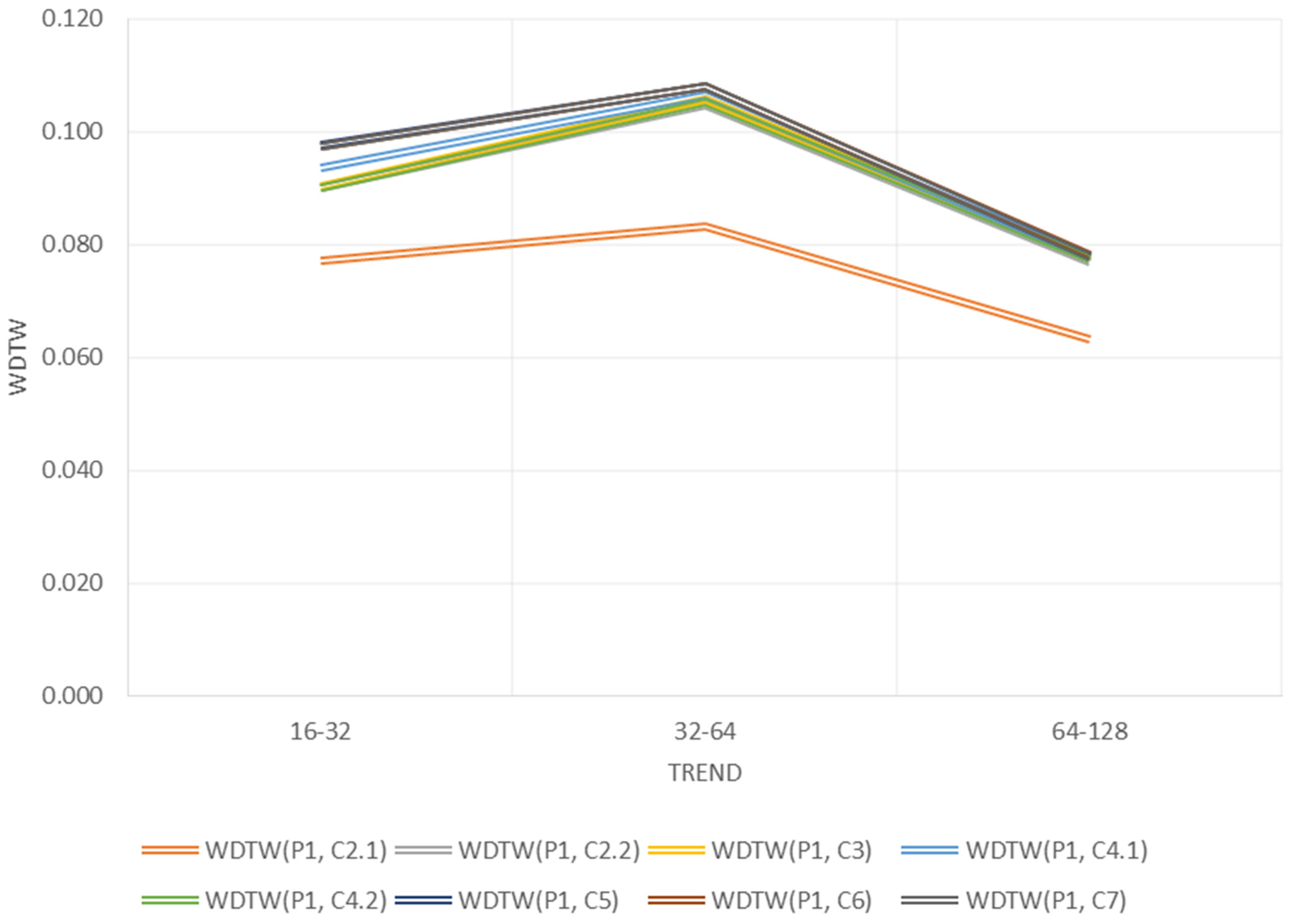
Figure 3.
One-Dimensional DTW.
Figure 3.
One-Dimensional DTW.
Figure 4.
Volatility coefficient for individual green bonds.
Figure 4.
Volatility coefficient for individual green bonds.
Figure 5.
Quarter range for individual green bonds. Source: Own calculations.
Figure 5.
Quarter range for individual green bonds. Source: Own calculations.
Figure 6.
The current rate of income (in %) for W2 green bonds issued in Hungary. Source: Own calculations.
Figure 6.
The current rate of income (in %) for W2 green bonds issued in Hungary. Source: Own calculations.
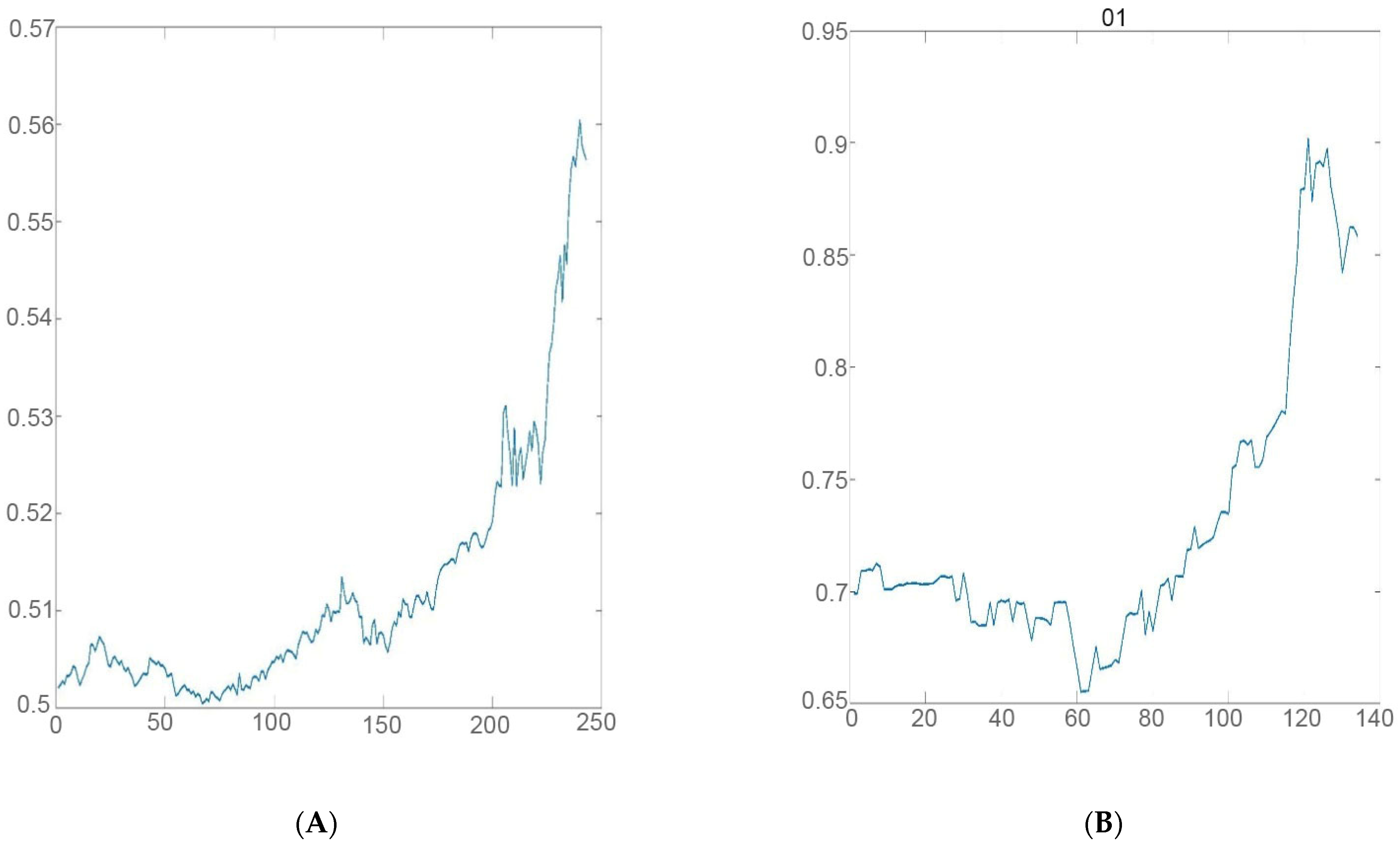
Figure 7.
The current rate of income (in %) for W1 green bonds issued in Hungary. Source: Own calculations.
Figure 7.
The current rate of income (in %) for W1 green bonds issued in Hungary. Source: Own calculations.
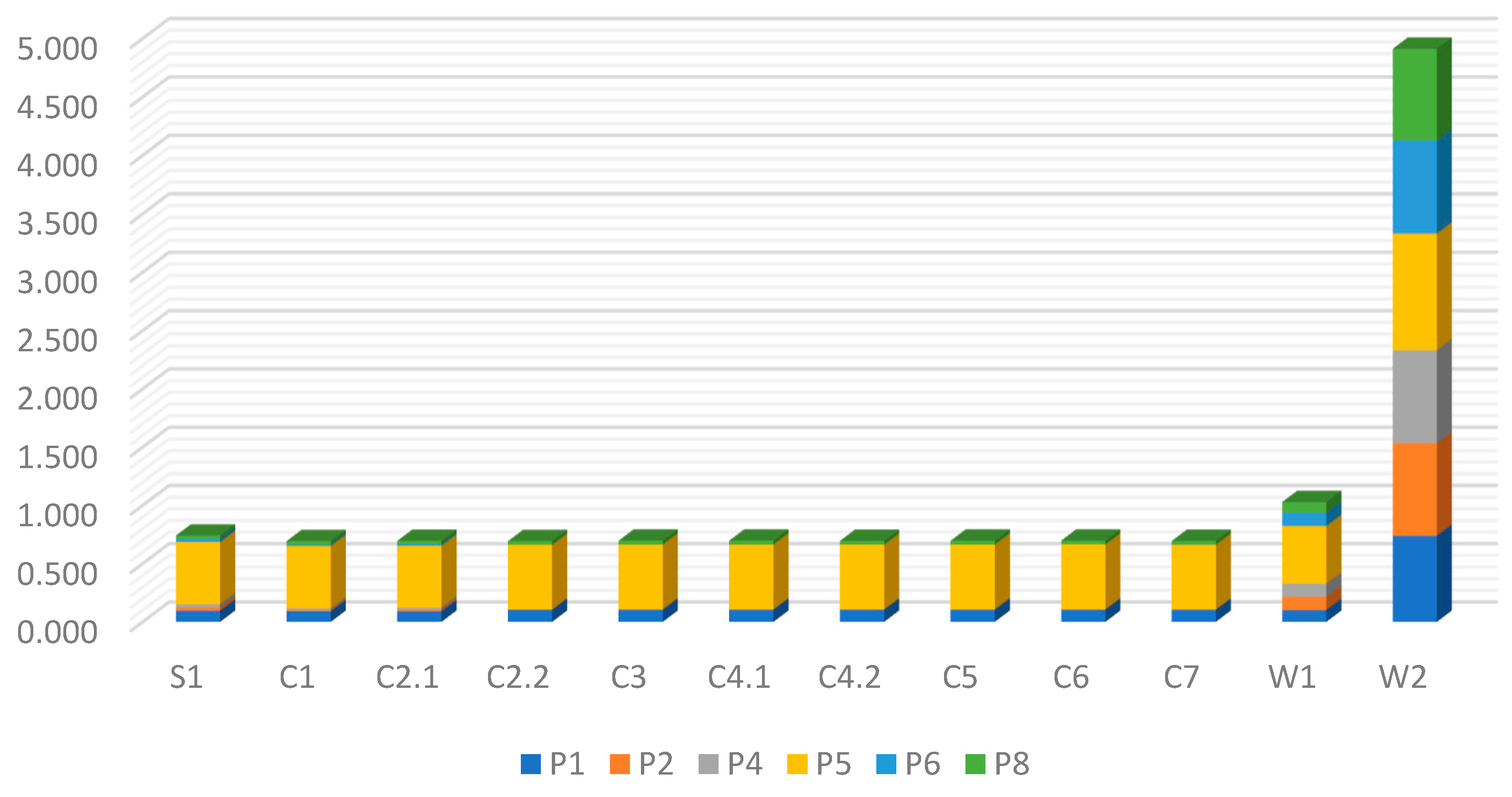
Figure 8.
WDTW index for individual bonds using only the first level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of the analysis of all analysed bonds. Source: Own calculations.
Figure 8.
WDTW index for individual bonds using only the first level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of the analysis of all analysed bonds. Source: Own calculations.
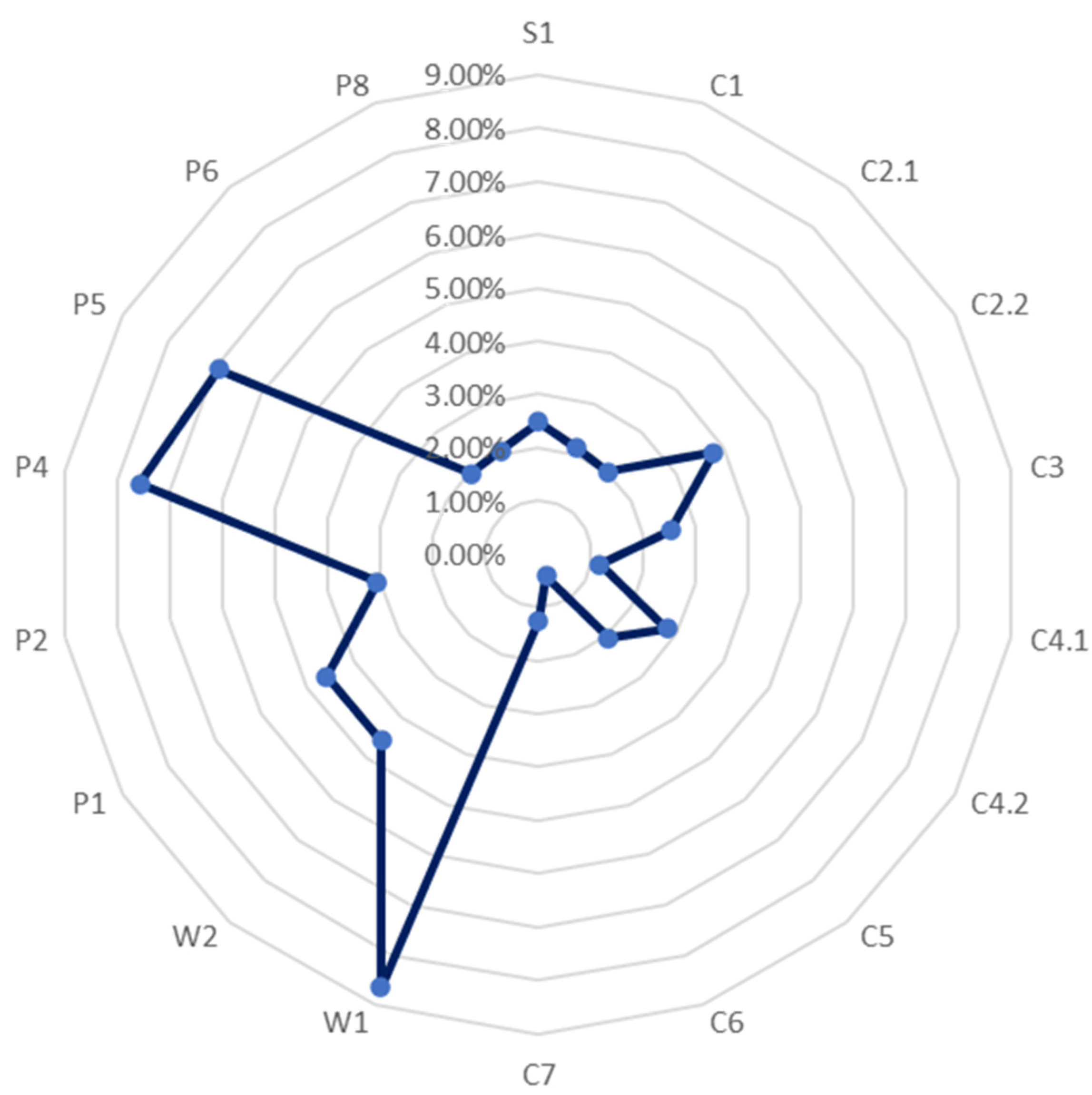
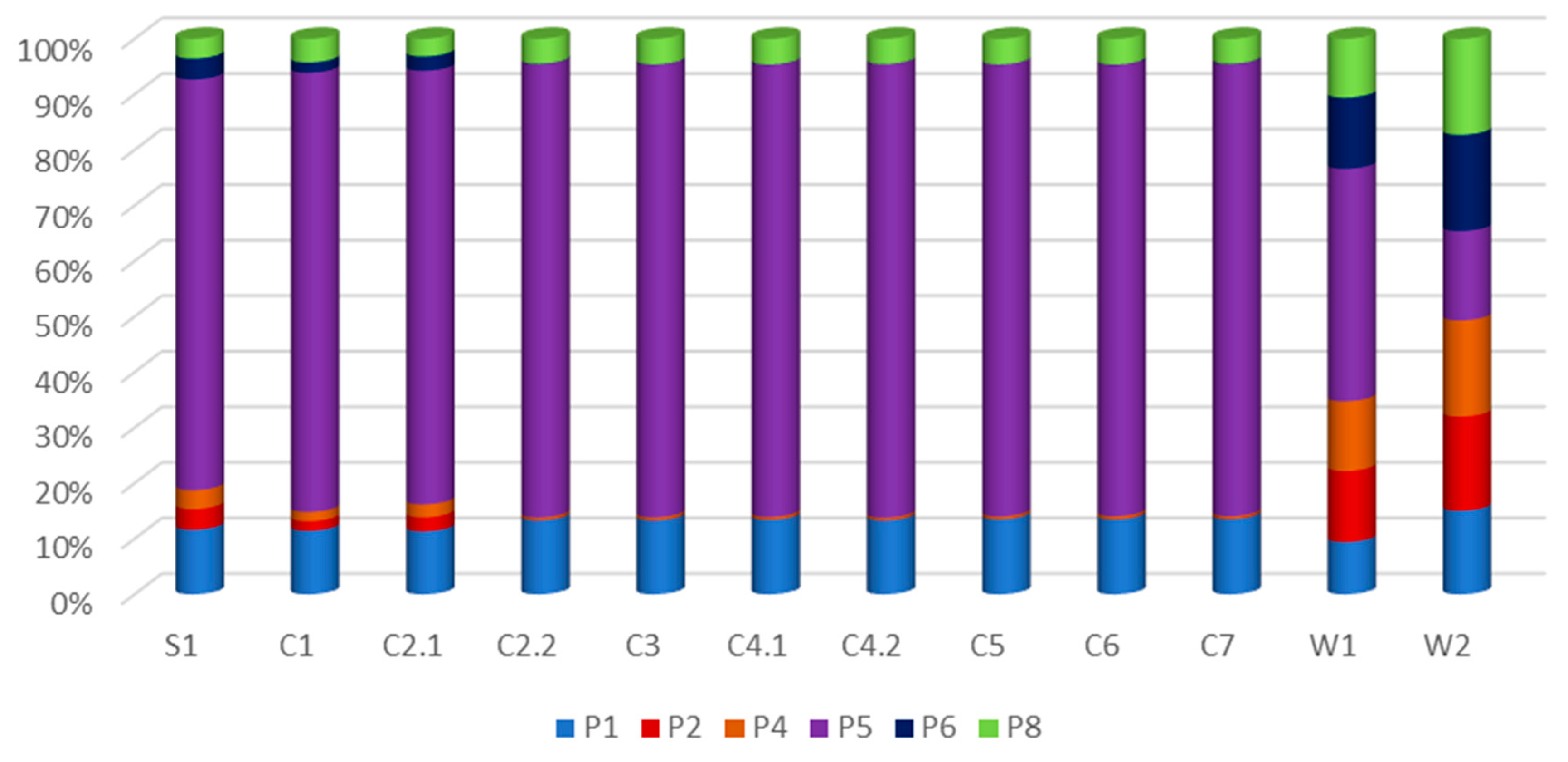
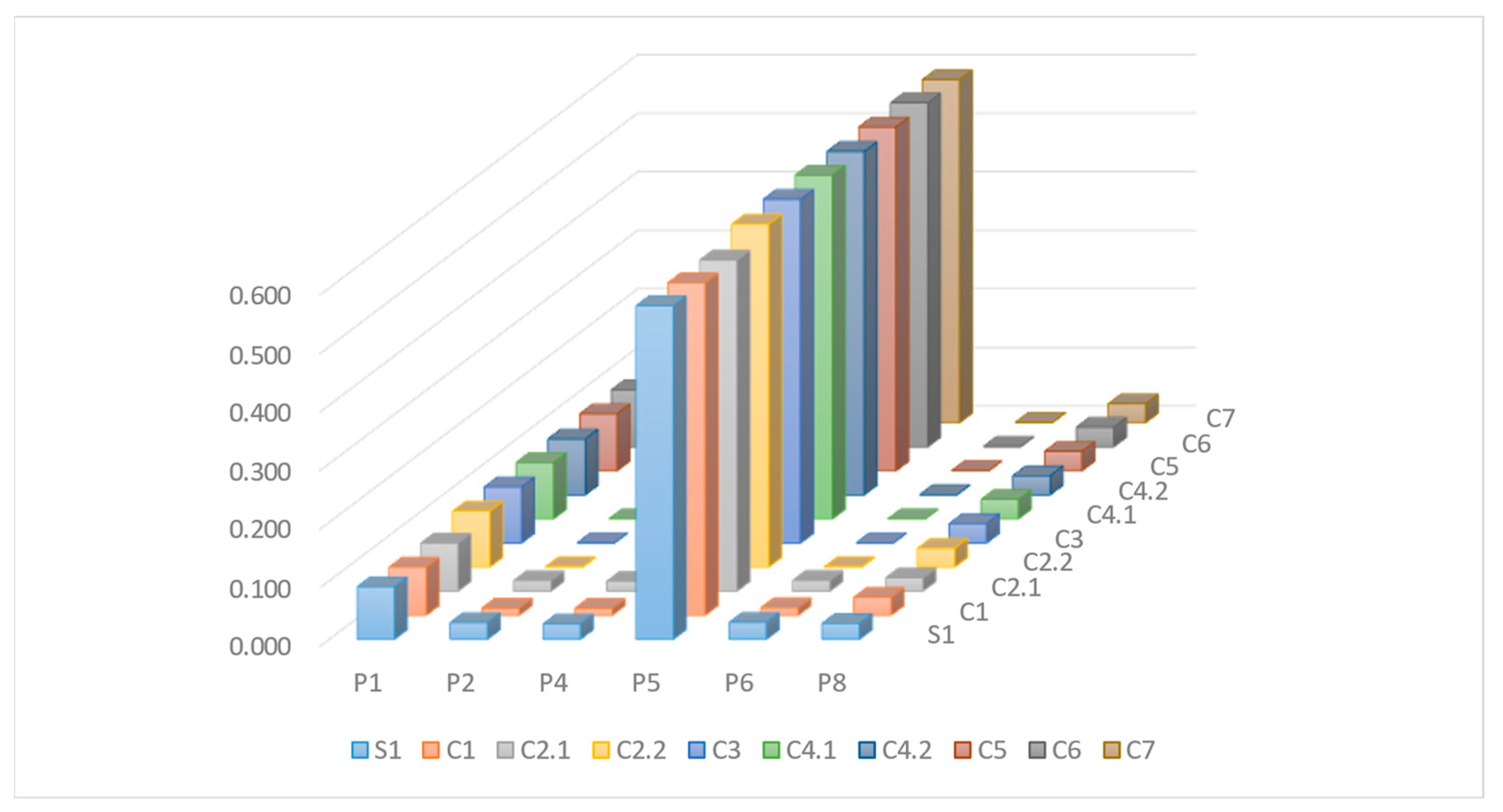
Figure 9.
WDTW index for individual bonds using only the first level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of P1, P2, P4, P5 P6, and P8 bonds. Source: Own calculations.
Figure 9.
WDTW index for individual bonds using only the first level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of P1, P2, P4, P5 P6, and P8 bonds. Source: Own calculations.
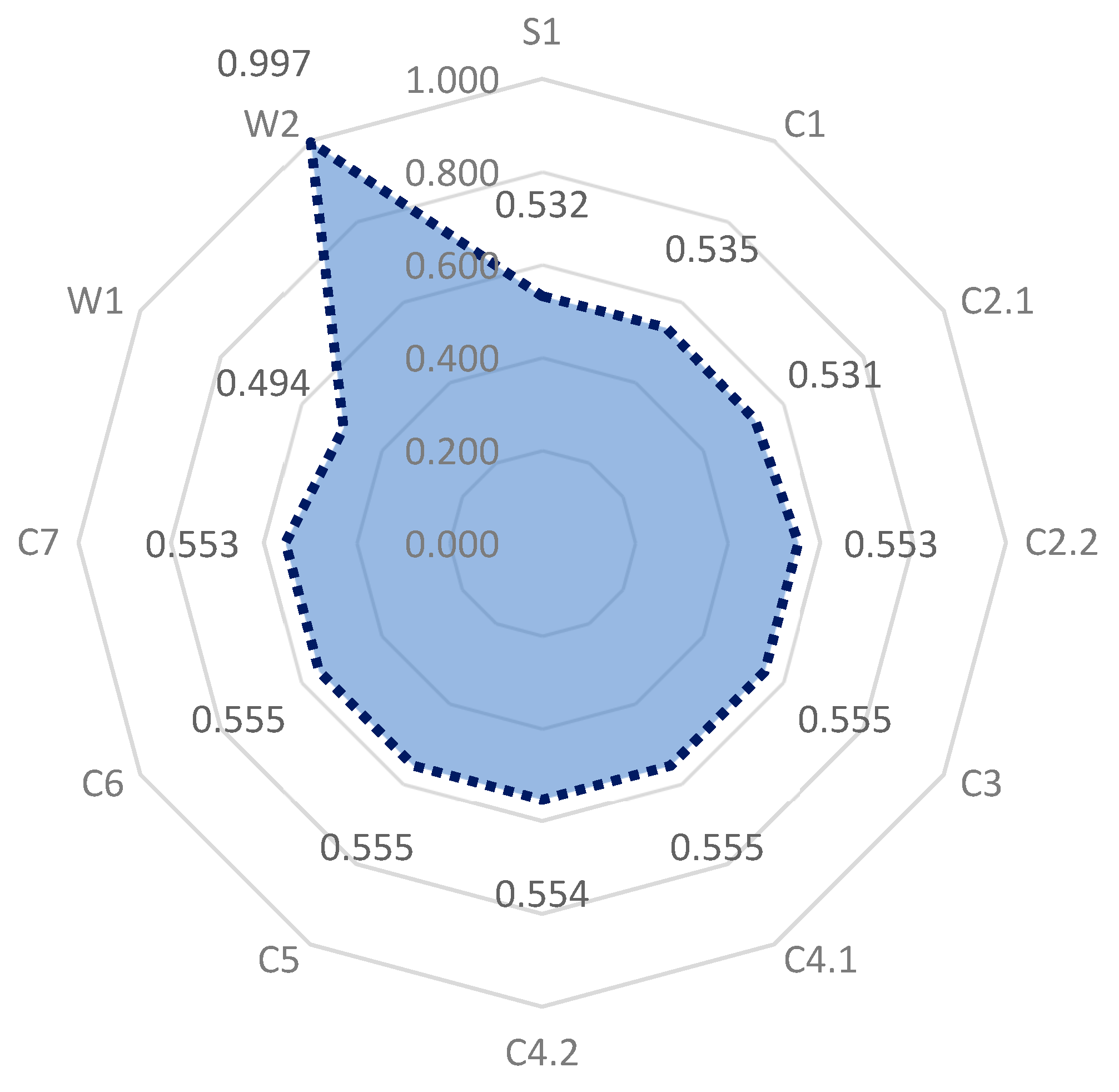
Figure 10.
Values of the proprietary WDTW index between the S1 bond and the P1, P2, P4, P5, P6, and P8 bonds, using only the first level of wavelet decomposition in the algorithm. Source: Own calculations.
Figure 10.
Values of the proprietary WDTW index between the S1 bond and the P1, P2, P4, P5, P6, and P8 bonds, using only the first level of wavelet decomposition in the algorithm. Source: Own calculations.
Figure 11.
The current rate of income (in %) for green bonds issued in Poland and Slovakia. (A) The current rate of income (in %) for S1 green bonds issued in Slovakia. (B) The current rate of income (in %) for P1 green bonds issued in Poland. Source: Own calculations.
Figure 11.
The current rate of income (in %) for green bonds issued in Poland and Slovakia. (A) The current rate of income (in %) for S1 green bonds issued in Slovakia. (B) The current rate of income (in %) for P1 green bonds issued in Poland. Source: Own calculations.
Figure 12.
Values of the proprietary WDTW index between the P5 bond and green bonds issued by the Czech Republic, Hungary, and Slovakia, using only the first level of wavelet decomposition in the WDTW algorithm. Source: Own calculations.
Figure 12.
Values of the proprietary WDTW index between the P5 bond and green bonds issued by the Czech Republic, Hungary, and Slovakia, using only the first level of wavelet decomposition in the WDTW algorithm. Source: Own calculations.
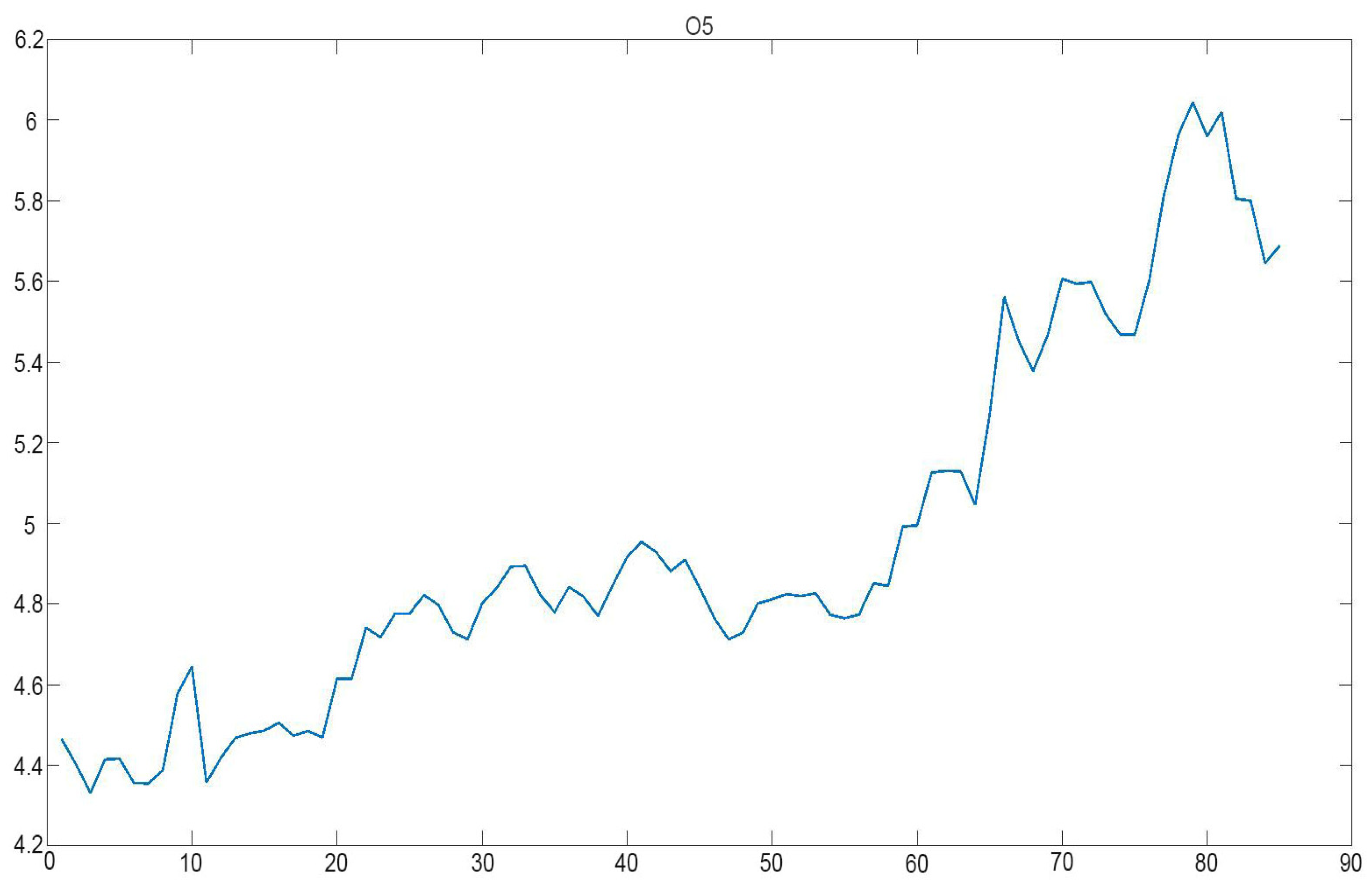
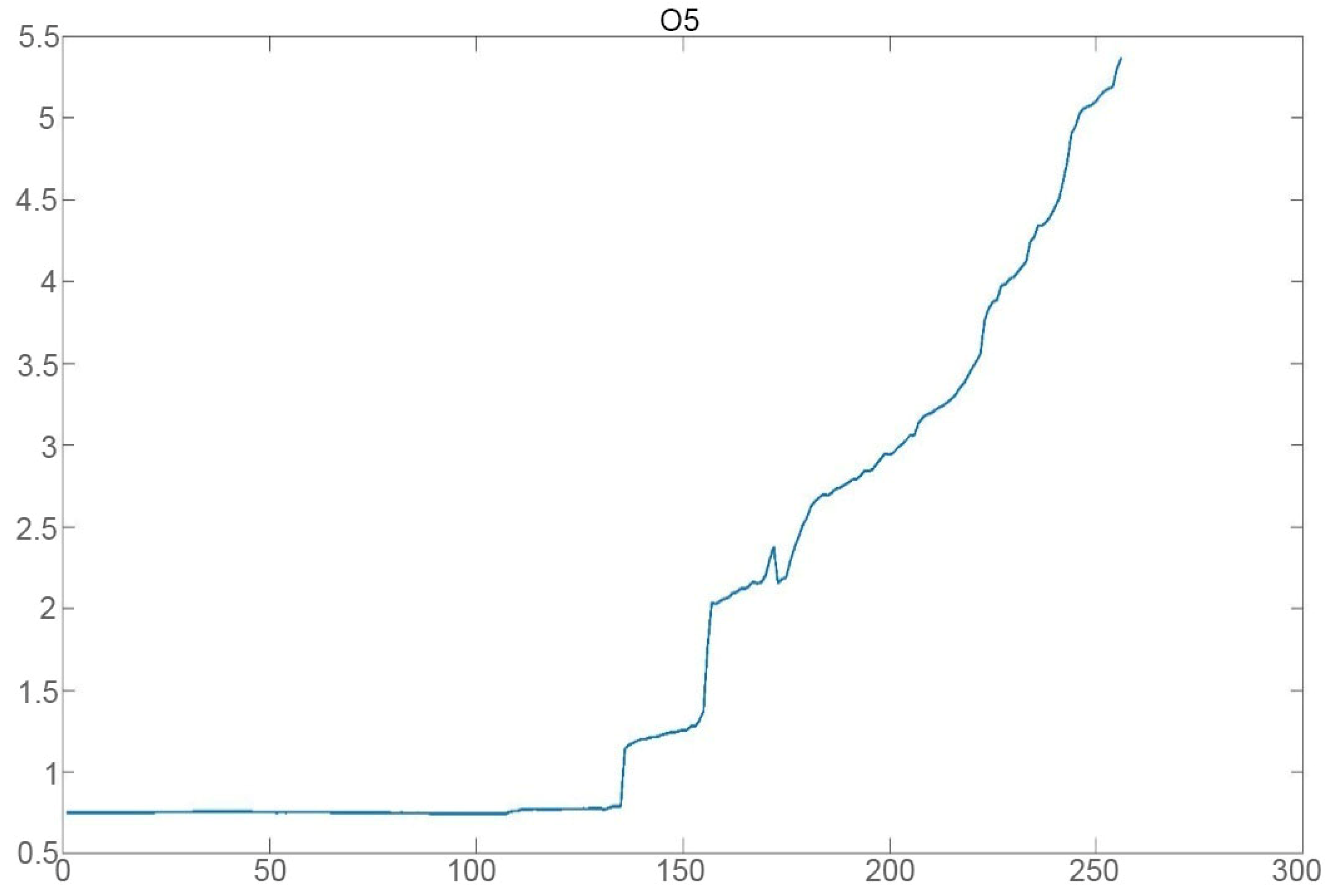
Figure 13.
The current rate of income (in %) for P5 green bonds issued in Poland.
Figure 13.
The current rate of income (in %) for P5 green bonds issued in Poland.
Figure 14.
Values of the proprietary WDTW index between bonds W1, W2 and bonds P1, P2, P4, P5, P6, and P8, using the second level of wavelet decomposition in the WDTW algorithm. Source: Own calculations.
Figure 14.
Values of the proprietary WDTW index between bonds W1, W2 and bonds P1, P2, P4, P5, P6, and P8, using the second level of wavelet decomposition in the WDTW algorithm. Source: Own calculations.
Figure 15.
WDTW index for individual bonds using the second level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of the analysis of all analysed bonds. Source: Own calculations.
Figure 15.
WDTW index for individual bonds using the second level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of the analysis of all analysed bonds. Source: Own calculations.
Figure 16.
WDTW index for individual bonds using the second level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of P1, P2, P4, P5 P6, and P8 bonds. Source: Own calculations.
Figure 16.
WDTW index for individual bonds using the second level of wavelet decomposition in the WDTW algorithm. Percentage analysis in the context of P1, P2, P4, P5 P6, and P8 bonds. Source: Own calculations.
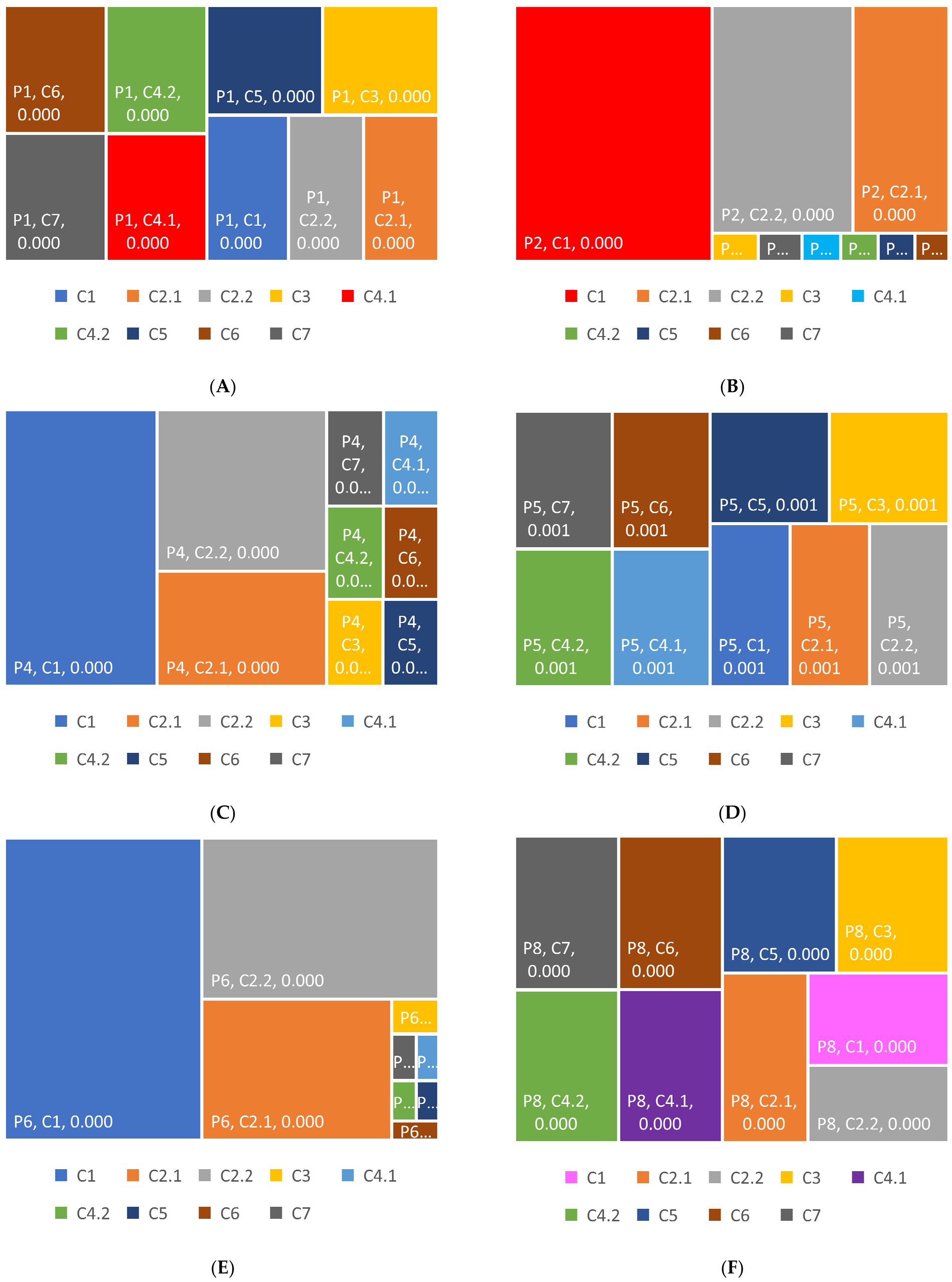
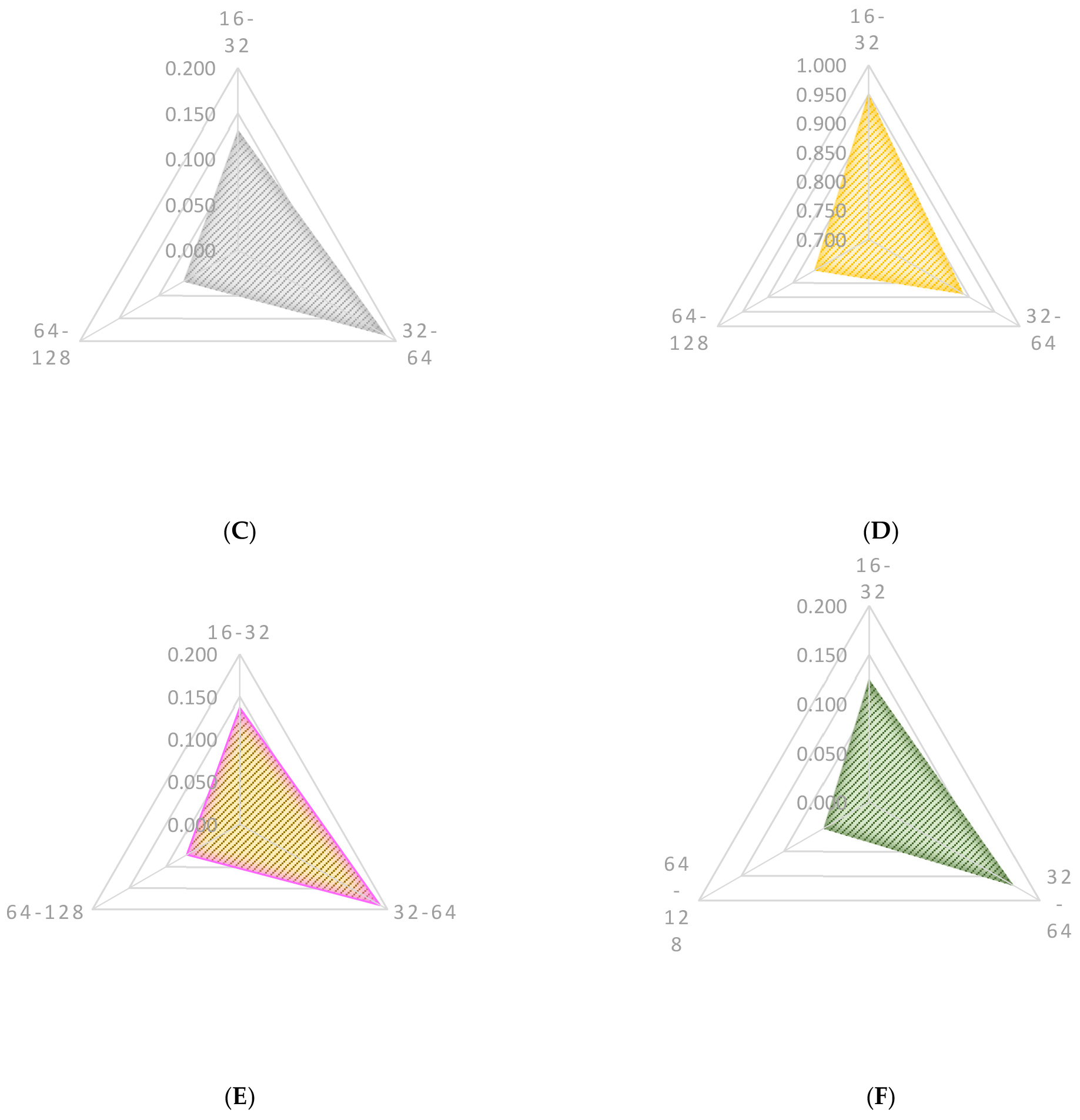
Figure 17.
Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic and bonds issued in Poland in the weekly trend. (A) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P1 bond. (B) Treemap showing the strength of the relationship between the current rate of income for a holder of bonds issued in the Czech Republic with the P2 bond. (C) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P4 bond. (D) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P5 bond. (E) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P6 bond. (F) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P8 bond. Source: Own elaboration based on calculations in the Matlab program.
Figure 17.
Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic and bonds issued in Poland in the weekly trend. (A) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P1 bond. (B) Treemap showing the strength of the relationship between the current rate of income for a holder of bonds issued in the Czech Republic with the P2 bond. (C) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P4 bond. (D) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P5 bond. (E) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P6 bond. (F) Treemap showing the strength of the relationship between the current rate of return for a holder of bonds issued in the Czech Republic with the P8 bond. Source: Own elaboration based on calculations in the Matlab program.
![Risks 11 00214 g017]()
Figure 18.
WDTW index between S1 and P1, P2, P4, P5, P6, and P8 using second level wavelet decomposition in the WDTW algorithm. Source: Own calculations.
Figure 18.
WDTW index between S1 and P1, P2, P4, P5, P6, and P8 using second level wavelet decomposition in the WDTW algorithm. Source: Own calculations.
Figure 19.
WDTW ratio between bonds issued in the Czech Republic and Hungary and bonds issued in Poland using the second level of wavelet decomposition in the WDTW algorithm. Source: Own calculations.
Figure 19.
WDTW ratio between bonds issued in the Czech Republic and Hungary and bonds issued in Poland using the second level of wavelet decomposition in the WDTW algorithm. Source: Own calculations.
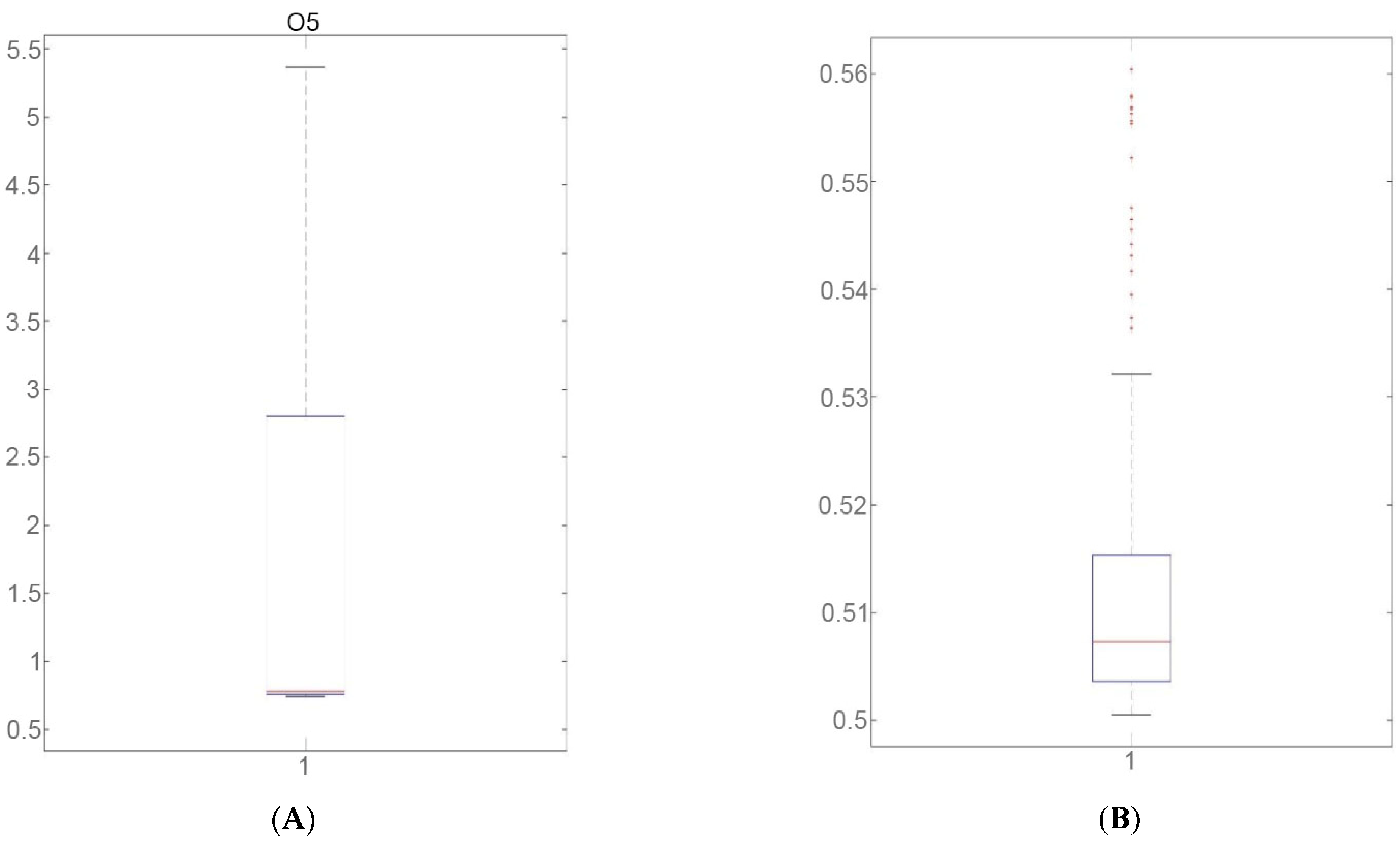
Figure 20.
Histograms presenting the current rate of income (in %) for individual analysed green bonds issued in Poland. Source: Own calculations. (A) Histogram presenting the current rate of income (in %) for P5 green bonds issued in Poland. (B) Histogram presenting the current rate of income (in %) for S1 green bonds issued in Slovakia. Source: Own calculations.
Figure 20.
Histograms presenting the current rate of income (in %) for individual analysed green bonds issued in Poland. Source: Own calculations. (A) Histogram presenting the current rate of income (in %) for P5 green bonds issued in Poland. (B) Histogram presenting the current rate of income (in %) for S1 green bonds issued in Slovakia. Source: Own calculations.
Figure 21.
WDTW index between a bond issued in Slovakia and bonds issued in Poland, using the WDTW algorithm in the trends 16–32 days, 32–64 days, 64–128 days. Source: Own calculations.
Figure 21.
WDTW index between a bond issued in Slovakia and bonds issued in Poland, using the WDTW algorithm in the trends 16–32 days, 32–64 days, 64–128 days. Source: Own calculations.
Figure 22.
Quantile analysis. The current rate of income (in %) for the analysed green bonds issued in Poland. (A) Quantile analysis. The current rate of income (in %) for P5 green bonds issued in Poland. (B) Quantile analysis. The current rate of income (in %) for S1 green bonds issued in Slovakia. Source: Own calculations.
Figure 22.
Quantile analysis. The current rate of income (in %) for the analysed green bonds issued in Poland. (A) Quantile analysis. The current rate of income (in %) for P5 green bonds issued in Poland. (B) Quantile analysis. The current rate of income (in %) for S1 green bonds issued in Slovakia. Source: Own calculations.
Figure 23.
WDTW between green bonds issued in the Czech Republic and P1 green bonds issued in Poland. Source: Own calculations.
Figure 23.
WDTW between green bonds issued in the Czech Republic and P1 green bonds issued in Poland. Source: Own calculations.
Figure 24.
WDTW between green bonds issued in the Czech Republic and P2 green bonds issued in Poland. Source: Own calculations.
Figure 24.
WDTW between green bonds issued in the Czech Republic and P2 green bonds issued in Poland. Source: Own calculations.
Figure 25.
WDTW between green bonds issued in the Czech Republic and P4 green bonds issued in Poland. Source: Own calculations.
Figure 25.
WDTW between green bonds issued in the Czech Republic and P4 green bonds issued in Poland. Source: Own calculations.
Figure 26.
WDTW between green bonds issued in the Czech Republic and P5 green bonds issued in Poland. Source: Own calculations.
Figure 26.
WDTW between green bonds issued in the Czech Republic and P5 green bonds issued in Poland. Source: Own calculations.
Figure 27.
WDTW between green bonds issued in the Czech Republic and P6 green bonds issued in Poland. Source: Own calculations.
Figure 27.
WDTW between green bonds issued in the Czech Republic and P6 green bonds issued in Poland. Source: Own calculations.
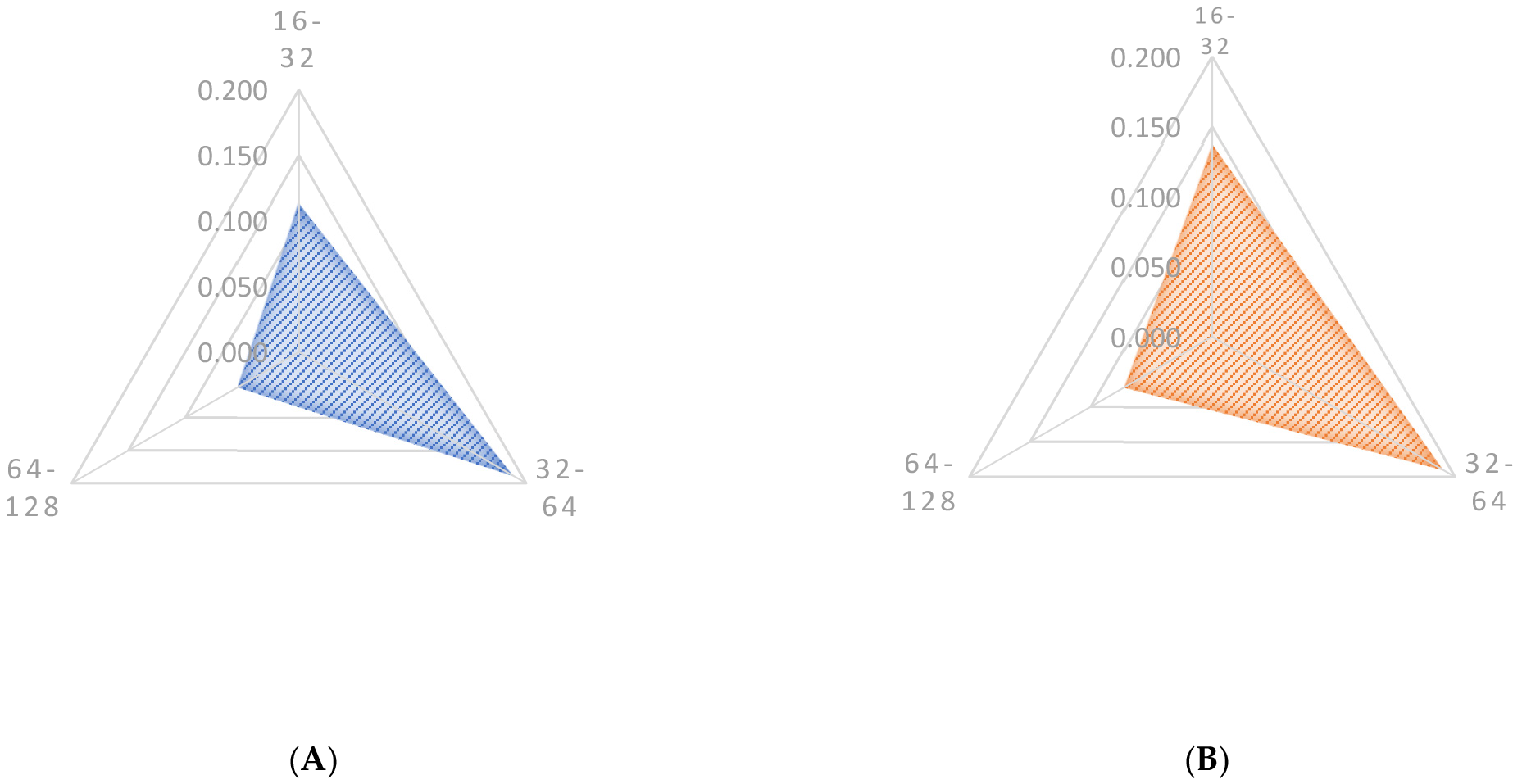
Figure 28.
WDTW between W1 green bonds issued in Hungary and green bonds issued in Poland. (A) WDTW(W1, P1). (B) WDTW(W1, P2). (C) WDTW(W1, P4). (D) WDTW(W1, P5). (E) WDTW(W1, P6). (F) WDTW(W1, P8). Source: Own calculations.
Figure 28.
WDTW between W1 green bonds issued in Hungary and green bonds issued in Poland. (A) WDTW(W1, P1). (B) WDTW(W1, P2). (C) WDTW(W1, P4). (D) WDTW(W1, P5). (E) WDTW(W1, P6). (F) WDTW(W1, P8). Source: Own calculations.
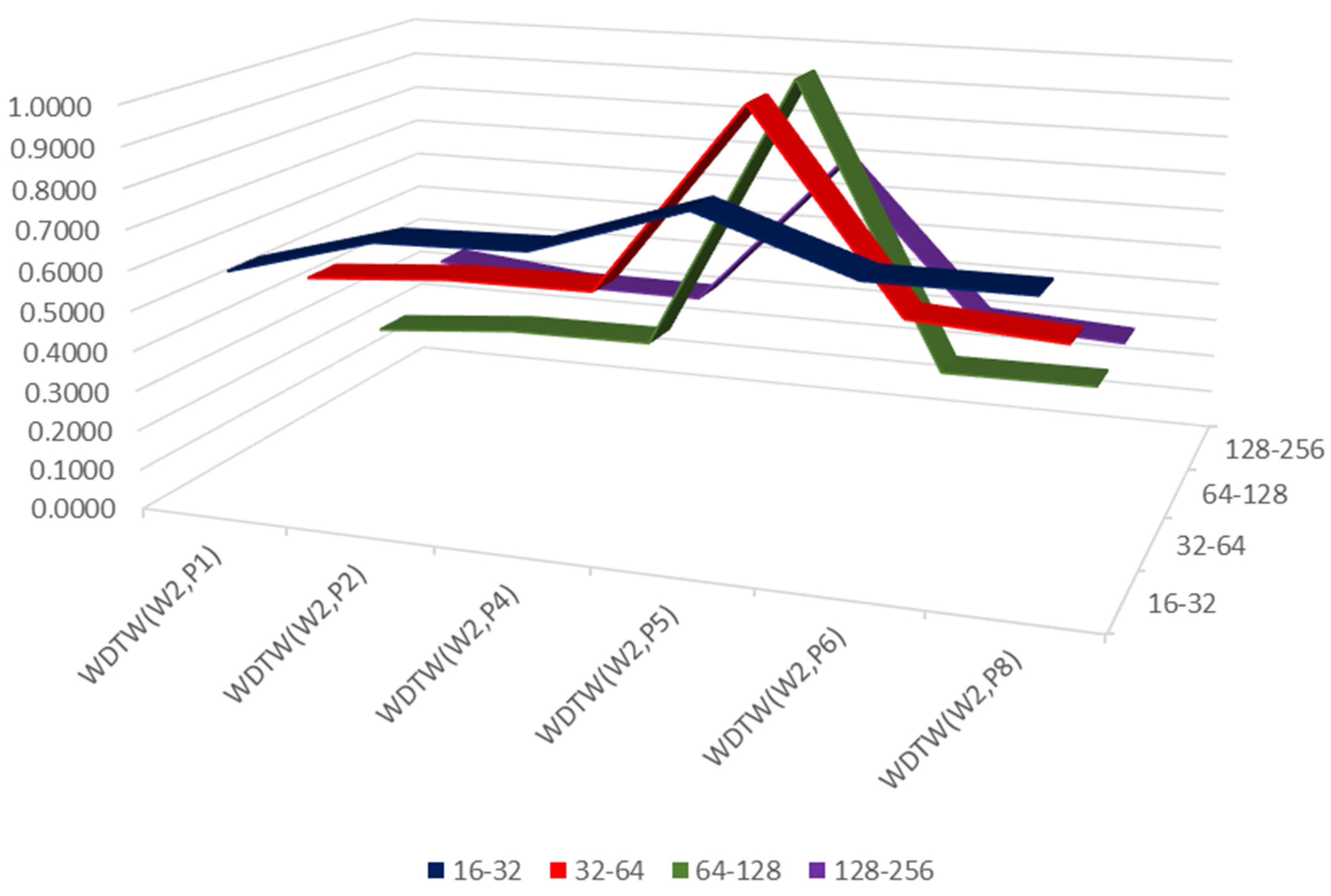
Figure 29.
WDTW between W2 green bonds issued in Hungary and green bonds issued in Poland. Source: Own calculations.
Figure 29.
WDTW between W2 green bonds issued in Hungary and green bonds issued in Poland. Source: Own calculations.
Table 1.
Green bond issue in Poland (private sector).
Table 1.
Green bond issue in Poland (private sector).
| Issuer | Settlement Date | Maturity Date | Profitability | Value | Code in Empirical Analysis |
|---|
| mBank | 20 September 2021 | 21 September 2027 | 3 m EURIBOR + 1.25%. | 500 m EUR (590.65 m USD) | P1 |
| PKN Orlen | 21 May 2021 | 27 May 2028 | 1.13% | 500 m EUR (607.30 m USD) | P2 |
| Cyfrowy Polsat | 14 February 2020 | 12 February 2027 | 6 m WIBOR + 165 bps | 1 bn PLN | P3 |
| Bank PKO BP | 27 November 2019 | 2 December 2024 | 3 m WIBOR + 51 bps | 250 m PLN (63.85 m USD) | P4 |
| Bank PKO BP | 10 June 2019 | 30 September 2024 | 3 m WIBOR + 0.6% | 250 m PLN (65.70 m USD) | P5 |
Table 2.
Government green bond issue in Poland.
Table 2.
Government green bond issue in Poland.
| Issue Number | Settlement Date | Maturity Date | Profitability | Value | Code in Empirical Analysis |
|---|
| 1 | 7 March 2019 | 7 March 2049 | 2% | 500 m EUR | P6 |
| 2 | 7 March 2019 | 7 March 2029 | 1% | 1707.06 m USD | P7 |
| 3 | 7 February 2018 | 7 October 2026 | 1.13% | 1 m EUR (1243 m USD) | P8 |
| 4 | 19 December 2016 | 19 December 2021 | 0.5% | 750 m EUR (791.89 m USD) | Emissions have not been subject to empirical analysis |
Table 3.
Green bond issue in Czech Republic.
Table 3.
Green bond issue in Czech Republic.
| Issuer | Settlement Date | Maturity Date | Profitability | Value | Code in Empirical Analysis |
|---|
| CTP | 20 January 2022 | 20 January 2026 | 0.875% | 700 m EUR | C1 |
| CTP | 27 September 2021
(issue in 2 tranches) | 27 September 2026 | 0.625% | 500 m EUR (585.9 m USD) | C2.1 |
| 27 September 2031 | 1.5% | 500 m EUR (585.9 m USD) | C2.2 |
| Ceska Sporitelna AS | 13 September 2021 | 13 September 2028 | 0.50% | 500 m EUR | C3 |
| CTP | 21 June 2021 (issue in 2 tranches) | 21 June 2025 | 0.5% | 500 m EUR (593.10 m USD) | C4.1 |
| 21 June 2029 | 1.25% | 500 m EUR (593.10 m USD) | C4.1 |
| CTP | 18 February 2021 | 18 February 2027 | 0.75% | 500 m EUR(603 m USD) | C5 |
| CTP | 27 November 2020 | 27 November 2023 | 0.0625% | 400 m EUR (476.58 m USD) | C6 |
| CTP | 25 September 2020 | 1 October 2025 | 2.1250% | 650 m EUR (757.80 m USD) | C7 |
Table 4.
Green bond issue in Hungary.
Table 4.
Green bond issue in Hungary.
| Issuer | Settlement Date | Maturity Date | Profitability | Value | Code in Empirical Analysis |
|---|
| Republic of Hungary | 22 April 2021 | 28 April 2051 | 4% | 30 m HUF | W1 |
| Republic of Hungary | 5 June 2020 | 5 June 2035 | 1.75% | 1500 m EUR (1643.10 m USD) | W2 |
Table 5.
Green bond issue in Slovakia.
Table 5.
Green bond issue in Slovakia.
| Issuer | Settlement Date | Maturity Date | Profitability | Value | Code in Empirical Analysis |
|---|
| Tatra Banka | 23 April 2021 | 23 April 2028 | 0.5% | 300 m EUR (361.38 m USD) | S1 |
Table 6.
Individual series representing the current rate of return on green bonds.
Table 6.
Individual series representing the current rate of return on green bonds.
| Slovakia | Czech Republic | Hungary | Poland |
|---|
| S1 | C1 | C2.1 | C2.2 | C3 | C4.1 | C4.2 | C5 | C6 | C7 | W1 | W2 | P1 | P2 | P4 | P5 | P6 | P8 |
| 244 | 30 | 111 | 111 | 31 | 181 | 81 | 246 | 246 | 246 | 257 | 85 | 134 | 218 | 256 | 256 | 256 | 256 |
Table 7.
Selected statistical measurements of green signage quotations in individual countries of the CEE group.
Table 7.
Selected statistical measurements of green signage quotations in individual countries of the CEE group.
| Country Name | Shortcut | Average | Variance | Kurtosis | Skewness | Min | Max |
|---|
| Slovakia | S1 | 97.66 | 5.86 | 2.95 | −1.84 | 89.22 | 99.90 |
| Czech Republic | C1 | 98.03 | 4.28 | 0.61 | −1.30 | 91.59 | 100.13 |
| C2.1 | 98.07 | 3.94 | 0.58 | −1.29 | 92.00 | 100.17 |
| C2.2 | 95.59 | 13.16 | 0.18 | −1.22 | 85.63 | 99.68 |
| C3 | 97.16 | 5.95 | 0.20 | −0.96 | 89.90 | 100.10 |
| C4.1 | 99.52 | 1.35 | 1.77 | −1.67 | 95.69 | 100.71 |
| C4.2 | 98.36 | 7.48 | 0.82 | −1.27 | 89.75 | 101.31 |
| C5 | 98.31 | 4.06 | 1.87 | −1.43 | 91.17 | 100.75 |
| C6 | 100.98 | 0.20 | 5.79 | −2.31 | 98.99 | 101.47 |
| C7 | 105.45 | 1.74 | 1.65 | −1.51 | 100.90 | 106.93 |
| Hungary | W1 | 81.41 | 49.62 | −0.58 | −0.55 | 66.19 | 92.36 |
| W2 | 103.48 | 22.35 | 1.39 | −1.59 | 90.51 | 108.54 |
| Poland | P1 | 96.57 | 19.68 | 1.62 | −1.68 | 84.11 | 100.11 |
| P2 | 100.17 | 9.42 | 2.70 | −1.89 | 89.56 | 103.29 |
| P4 | 119.35 | 82.03 | 3.12 | −1.97 | 89.10 | 129.77 |
| P5 | 105.46 | 53.19 | 3.99 | −1.99 | 0.00 | 109.06 |
| P6 | 105.18 | 4.27 | 1.07 | −1.46 | 99.69 | 107.00 |
| P8 | 105.07 | 4.67 | 0.73 | −1.38 | 99.56 | 107.00 |
Table 8.
Quartile analysis.
Table 8.
Quartile analysis.
| Country Name | Shortcut | Q1 | Q2 | Q3 |
|---|
| Slovakia | S1 | 96.995 | 98.57 | 99.28 |
| Czech Republic | C1 | 97.62 | 98.83 | 99.415 |
| C2.1 | 97.725 | 98.79 | 99.4 |
| C2.2 | 95.22 | 96.97 | 98.145 |
| C3 | 95.705 | 98.18 | 98.895 |
| C4.1 | 99.465 | 99.84 | 100.31 |
| C4.2 | 97.5 | 98.99 | 100.54 |
| C5 | 97.49625 | 98.74 | 99.6725 |
| C6 | 100.998 | 101.10 | 101.22 |
| C7 | 104.92 | 105.85 | 106.295 |
| Hungary | W1 | 77.97 | 82.95 | 85.51 |
| W2 | 103.31 | 104.94 | 106.225 |
| Poland | P1 | 95.3025 | 98.81 | 99.2525 |
| P2 | 100.1675 | 101.19 | 101.7213 |
| P4 | 119.0675 | 122.82 | 124.695 |
| P5 | 105.33 | 107.02 | 107.775 |
| P6 | 104.69875 | 106.29 | 106.7175 |
| P8 | 104.66 | 106.25 | 106.7 |
Table 9.
Values of the proprietary WDTW index for the indicated bonds, using only the first level of resolution in the algorithm.
Table 9.
Values of the proprietary WDTW index for the indicated bonds, using only the first level of resolution in the algorithm.
| Bond Name Code | P1 | P2 | P4 | P5 | P6 | P8 |
|---|
| C1 | 0.0923 | 0.0115 | 0.0126 | 0.5348 | 0.0122 | 0.0302 |
| C2.1 | 0.0918 | 0.0156 | 0.0158 | 0.5305 | 0.0161 | 0.0259 |
| C2.2 | 0.1041 | 0.0010 | 0.0026 | 0.5526 | 0.0009 | 0.0316 |
| C3 | 0.1052 | 0.0006 | 0.0032 | 0.5547 | 0.0004 | 0.0333 |
| C4.1 | 0.1052 | 0.0006 | 0.0032 | 0.5547 | 0.0004 | 0.0333 |
| C4.2 | 0.1047 | 0.0006 | 0.0029 | 0.5538 | 0.0005 | 0.0327 |
| C5 | 0.1052 | 0.0006 | 0.0030 | 0.5545 | 0.0004 | 0.0331 |
| C6 | 0.1053 | 0.0007 | 0.0033 | 0.5549 | 0.0005 | 0.0334 |
| C7 | 0.1047 | 0.0009 | 0.0028 | 0.5534 | 0.0006 | 0.0325 |
Table 10.
Brief characteristics of the P5 green bond.
Table 10.
Brief characteristics of the P5 green bond.
| Name | Issuer Swap Vert | Pricing Date Swap Vert | Settlement Date Swap Vert | Maturity Date Swap Vert | Coupon |
|---|
| P5 | PKO BP | 5 June 2019 | 10 June 2019 | 30 September 2024 | 3M WIBOR + 0.6% |
Table 11.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P2 bonds.
Table 11.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P2 bonds.
| | TREND (IN DAYS) |
|---|
| 16–32 | 32–64 | 64–128 |
|---|
| WDTW(P2,C1) | 0.0148 | - | - |
| WDTW(P2, C2.1) | 0.0206 | 0.0156 | 0.0089 |
| WDTW(P2, C2.2) | 0.0008 | 0.0008 | 0.0006 |
| WDTW(P2, C3) | 0.0004 | 0.0004 | 0.0003 |
| WDTW(P2, C4.1) | 0.0004 | 0.0004 | 0.0004 |
| WDTW(P2, C4.2) | 0.0005 | 0.0005 | 0.0002 |
| WDTW(P2, C5) | 0.0004 | 0.0004 | 0.0003 |
| WDTW(P2, C6) | 0.0005 | 0.0005 | 0.0004 |
| WDTW(P2, C7) | 0.0007 | 0.0003 | 0.0003 |
Table 12.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P4 bonds.
Table 12.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P4 bonds.
| | TREND (IN DAYS) |
|---|
| 16–32 | 32–64 | 64–128 |
|---|
| WDTW(P4, C1) | 0.017 | - | - |
| WDTW(P4, C2.1) | 0.021 | 0.014 | 0.006 |
| WDTW(P4, C2.2) | 0.005 | 0.002 | 0.003 |
| WDTW(P4, C3) | 0.005 | 0.003 | 0.003 |
| WDTW(P4, C4.1) | 0.005 | 0.003 | 0.003 |
| WDTW(P4, C4.2) | 0.005 | 0.003 | 0.003 |
| WDTW(P4, C5) | 0.005 | 0.003 | 0.003 |
| WDTW(P4, C6) | 0.005 | 0.003 | 0.003 |
| WDTW(P4, C7) | 0.005 | 0.003 | 0.003 |
Table 13.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P5 bonds.
Table 13.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P5 bonds.
| | TREND (IN DAYS) |
|---|
| 16–32 | 32–64 | 64–128 |
|---|
| WDTW(P5,C1) | 0.978 | - | - |
| WDTW(P5, C2.1) | 0.968 | 0.910 | 0.833 |
| WDTW(P5, C2.2) | 0.998 | 0.924 | 0.844 |
| WDTW(P5, C3) | 0.999 | 0.926 | 0.844 |
| WDTW(P5, C4.1) | 1.000 | 0.926 | 0.844 |
| WDTW(P5, C4.2) | 0.999 | 0.925 | 0.844 |
| WDTW(P5, C5) | 0.999 | 0.926 | 0.844 |
| WDTW(P5, C6) | 1.000 | 0.926 | 0.844 |
| WDTW(P5, C7) | 0.999 | 0.925 | 0.844 |
Table 14.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P6 bonds.
Table 14.
Values of the proprietary WDTW index between the current yield rate of bonds issued in the Czech Republic and the current yield rate of P6 bonds.
| | TREND (IN DAYS) |
|---|
| 16–32 | 32–64 | 64–128 |
|---|
| WDTW(P6, C1) | 0.01560 | - | - |
| WDTW(P6, C2.1) | 0.02076 | 0.01553 | 0.00840 |
| WDTW(P6, C2.2) | 0.00072 | 0.00065 | 0.00026 |
| WDTW(P6, C3) | 0.00042 | 0.00036 | 0.00033 |
| WDTW(P6, C4.1) | 0.00038 | 0.00037 | 0.00029 |
| WDTW(P6, C4.2) | 0.00047 | 0.00032 | 0.00039 |
| WDTW(P6, C5) | 0.00033 | 0.00039 | 0.00023 |
| WDTW(P6, C6) | 0.00045 | 0.00042 | 0.00035 |
| WDTW(P6, C7) | 0.00062 | 0.00042 | 0.00016 |
Table 15.
Values of the proprietary WDTW index between the current rate of return on W1 bonds and the current rate of return on bonds issued in Poland.
Table 15.
Values of the proprietary WDTW index between the current rate of return on W1 bonds and the current rate of return on bonds issued in Poland.
| TREND | WDTW(W1, P1) | WDTW(W1, P2) | WDTW(W1, P4) | WDTW(W1, P5) | WDTW(W1, P6) | WDTW(W1, P8) |
|---|
|
16–32
| 0.114 | 0.137 | 0.132 | 0.951 | 0.137 | 0.125 |
|
32–64
| 0.189 | 0.19 | 0.188 | 0.889 | 0.19 | 0.17 |
|
64–128
| 0.054 | 0.073 | 0.069 | 0.808 | 0.072 | 0.054 |
Table 16.
Values of the proprietary WDTW index between the current rate of return on W2 bonds and the current rate of return on bonds issued in Poland.
Table 16.
Values of the proprietary WDTW index between the current rate of return on W2 bonds and the current rate of return on bonds issued in Poland.
| TREND | WDTW(W2, P1) | WDTW(W2, P2) | WDTW(W2, P4) | WDTW(W2, P5) | WDTW(W2, P6) | WDTW(W2, P8) |
|---|
|
16–32
| 0.5870 | 0.6892 | 0.6996 | 0.8241 | 0.6974 | 0.6982 |
|
32–64
| 0.4792 | 0.5079 | 0.5111 | 0.9998 | 0.5129 | 0.4889 |
|
64–128
| 0.2424 | 0.2745 | 0.2779 | 0.9999 | 0.2752 | 0.2783 |
|
128–256
| 0.3459 | 0.3079 | 0.3052 | 0.7068 | 0.3078 | 0.2869 |